Questo articolo è stato inserito nella sezione d'archivio "Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo"

 

L’uso della funzione esponenziale, in particolare di quella che si basa sul numero e, permette di descrivere la celebre spirale logaritmica, di cui abbiamo ampiamente parlato ampiamente in QUESTO articolo e nei link ad esso collegati. Essa rappresenta un passo in più rispetto a quella di Archimede, anche se è altrettanto semplice ed è la curva più utilizzata nel Cosmo, a tutti i livelli di grandezza. Oltretutto, ha anche influenzato le proporzioni armoniose dei monumenti, delle statue e delle pitture, a partire dai capolavori greci (rettangolo aureo). Ovviamente, ha a che fare con i numeri di Fibonacci.

Dalle lumache alle galassie

Userò un’introduzione leggermente diversa da quella che viene usata normalmente. Dato che la nuova spirale prende il nome di logaritmica, mi sembra giusto partire proprio da questa funzione. L’equazione semplificata della spirale di Archimede aveva equazione (in coordinate polari):

s = p φ

Ebbene, possiamo ottenere la nuova curva, sostituendo al valore di s quello del suo logaritmo (e lo scegliamo in base e, anche se si potrebbe fare con qualsiasi base). Abbiamo, quindi una funzione del tipo:

ln s = p φ     …. (4)

Cosa vuol dire praticamente scrivere il logaritmo al posto della distanza? Beh… se il logaritmo di un numero segue la spirale di Archimede, il numero deve seguire una funzione inversa a quella del logaritmo, ossia un’esponenziale. Per sapere come si muove la lunghezza del bastone s, basta, allora eseguire l’operazione esponenziale su entrambi i membri:

e ^{(ln s)} = e ^pφ

Ma, per la stessa definizione di esponenziale, segue che il primo membro non è altro che s.

Ricordate, infatti, che scrivere y = e^x vuol dire scrivere x = ln y, ossia: y = e^{ln y}; le due funzioni si annullano essendo una l’inversa dell’altra.

Segue quindi che

s = e ^{(ln s)} = e ^pφ

Riscriviamola per comodità:

s = e ^pφ     …. (5)

Questa equazione è equivalente alla (4) e rappresenta la spirale logaritmica (in particolare in base e).

In cosa differisce, praticamente, da quella di Archimede? Beh… basta calcolare (se è possibile)  il suo passo d. Esso era dato da:

d = s_i+1 – s_i = 2πp = cost (per qualsiasi valore di i, ossia per ogni giro completo 2π dell’angolo φ) .

In altre parole, la distanza tra le spire era costante.  La relazione che dava la costanza di d, poteva essere scritta:

s_i+1 = s_i + 2πp     …. (6)

ossia diceva che per passare da una distanza s a quella successiva (dopo che l’angolo aveva girato  di 2π) bastava aggiungere sempre la stessa quantità costante 2πp.

Cosa succede adesso?

s_i = e^pφi

s_i+1 = e^pφ(i+1) = e^{p(φi +2π)} = e^pφi e^2πp          (per una proprietà delle potenze che abbiamo già imparato)

Facendo la differenza, otteniamo il passo d della spirale:

d = s_i+1 – s_i = e^pφi e^2πp – e^pφi   …. (7)

la (7), dopo banali sostituzioni, diventa:

s_i+1 = s_i + e^pφi e^2πp – e^pφi  = s_i + s_i e^2πp - s_i = s_i e^2πp

ossia:

s_i+1 = s_i e^2πp     …. (8)

Confrontiamo la (8) con la (6). La (6) diceva che, per ottenere la distanza successiva, dopo aver compiuto un giro completo dell’angolo φ, bastava aggiungere sempre la stessa quantità costante. La (8), invece, dice che, ogni vola che l’angolo φ compie un giro, la distanza s viene moltiplicata per un fattore costante. Vogliamo fare un esempio?

Poniamo che s₁ valga ad esempio 3 e che e^2πp valga, invece, 5 (sono numeri presi del tutto a caso…). Dopo un giro completo s₁ diventa s₂ e vale 3 · 5 = 15 (la differenza, ossia il “primo” passo d₁₂) vale, quindi, d₁₂ = s₂ – s₁ = 15 – 3 = 12.

Facciamo fare un altro giro a φ e otteniamo s₃ che deve valere s₂ · 5 = 15 · 5 = 75. Calcoliamo il nuovo passo d₂₃ = s₃ – s₂ = 75 – 15 = 60. Come volevasi dimostrare, il passo NON è più costante, è passato da 12 a 60 e continua ad aumentare.

Torniamo a termini più generali. La (8) ci dice che le distanze dall’origine, per ogni giro completo dell’angolo φ, vengono moltiplicate per una costante, ossia aumentano in progressione geometrica di ragione e^2πp. Il passo non è assolutamente costante! Potremmo scrivere il risultato, riferendoci alla prima distanza considerata s₁.  Avremmo:

s₂ = s₁ e^2πp,   s₃ = s₂ e^2πp = s₁ e^2πp e^2πp = s₁ e^4πp , e via dicendo…

Ciò si traduce in una spirale che si apre sempre di più, come quella riportata in Fig. 61.

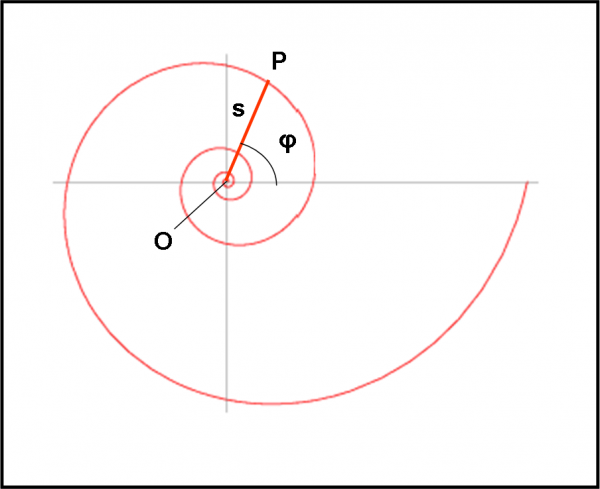
Cosa significa, in modo estremamente semplice e intuitivo, il fatto che la distanza cresca in progressione geometrica? Ogni nuova distanza y del punto della spirale dall’origine si ottiene moltiplicando quella precedente (x) per una costante m (ragione). Questa definizione non è certo nuova e descrive esattamente una retta nel piano x,y di equazione y = mx. Ad esempio, per m (coefficiente angolare) = 5 e per x iniziale uguale a 3 (l’esempio pratico di prima), la retta ci dice che:

x₁ = 3 , da cui y₁ = 3 · 5

x₂ = y₁ = 3 · 5  = 15 , da cui y₂ = 3 ·5 · 5 = 75

Esattamente lo stesso risultato. La retta esprime perfettamente ciò che succede alla nuova spirale.

D’altra parte, cari ragazzi, questo risultato ce lo potevamo aspettare già da un po’… Andiamo, infatti, a riprendere la (8):

s_i+1 = s_i e^2πp

Basta porre, come abbiamo appena detto:

m = e^2πp,  s_i = x,  s_i+1 = y e la (8) diventa:

y = mx

Niente da fare, girate le cose come volete, ma la matematica non si fa ingannare e torna sempre al punto di partenza.

Ammetto di aver girato fin troppo attorno a questa nuova spirale (ma d’altra parte una spirale “gira proprio attorno”…). Potevo cavarmela con una frase o poco più. Tuttavia, ho voluto insistere per “costringervi” a qualche ripasso forzato e per mostrare ancora una volta che esistono sempre varie possibilità, apparentemente diverse, per esprimere matematicamente uno stesso concetto. Esse, però, devono portare allo stesso risultato. Questo è il bello della matematica: non tradisce mai e ogni strada (se corretta) vi conduce sempre a casa!

Torniamo alla nostra spirale logaritmica, ricca di tante meravigliose proprietà. Nel quadro del nostro discorso generale sulla matematica non possiamo, però, farci distrarre più di tanto (al limite ci torneremo sopra in seguito) e occupiamoci di una sua caratteristica importantissima che la diversifica enormemente da quella di Archimede e che ci riporta prepotentemente al concetto di limite.

Riscriviamo ancora una volta la spirale di Archimede:

s = pφ

da come l’abbiamo scritta (un po’ semplificata), per φ che tende a zero anche s tende a zero. Non vi è nemmeno bisogno di passare al limite … basta inserire φ = 0 e si ottiene subito s = 0. D’altra parte zero moltiplicato per una costante è uguale a zero. Prima di far girare il bastone esso è esattamente un punto, l’origine della spirale. Se, invece, l’angolo tende a infinito, è altrettanto facile trovare che anche la lunghezza del bastone va a infinito. Infatti: ∞ · p = ∞

Cosa succede, invece, alla spirale logaritmica?

s = e ^pφ

Nessun problema per φ che tende a infinito:

lim s_{φ →∞} = lim e^pφ _{φ →∞} = e^p∞ = e^∞  = ∞

L’ho fatta un po’ lunga, ma è ovvio che elevare un numero (e è un numero maggiore di uno) a infinito vale infinito (andate a vedere le prime lezioni…).

Cosa capita, invece, per φ = 0? Niente di speciale e possiamo calcolarlo facilmente senza bisogno di passare al limite.

s = e^p0 = e⁰ = 1

Qualsiasi numero elevato a zero (ed e è un numero a tutti gli effetti) vale 1. Un risultato apparentemente banale, ma di importanza fondamentale.

Vediamo la situazione in Fig. 62. La spirale sembra partire dal valore 1 (si ottiene 1 perché abbiamo preso una spirale semplificata, se no avremmo un certo valore costante a…) e poi andare verso infinito avvolgendosi con spirali sempre più larghe. Una curva che sembra troppo “parziale”. Noi siamo estremamente interessati, invece, a cosa succede a mano a mano che s tende a zero… Esiste la curva oppure no? Esiste, esiste e come! Basta far girare φ al contrario, verso valori negativi, e la spirale tende a stringersi sempre di più. Bene, abbiamo capito… dobbiamo far tendere φ a -∞. Proviamo subito…

lim s_{φ →- ∞} = lim e^pφ _{φ →- ∞} = e^-p∞ = e^-∞  = 1/e^∞ = 1/∞ = 0

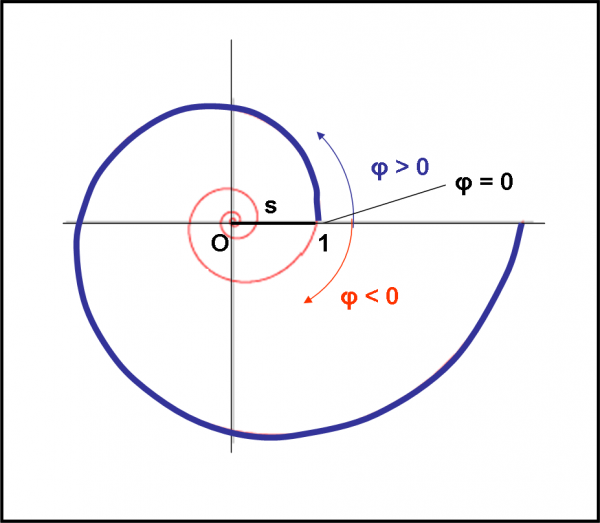
Tutto bene? Anche in questo caso la curva finisce (o comincia, come volete) nell’origine O. Sì, sì, ma essa tende a zero solo per un angolo che tende a infinito e non quando assume un valore ben definito. Cosa vuol dire, in altre, parole? Che la curva continua ad attorcigliarsi sempre più strettamente, ma raggiungerà l’origine solo quando l’angolo arriverà a infinito (girando in verso orario). Questo tipo di frase la conosciamo molto bene… ricordate Achille e la tartaruga? Non ci facciamo più prendere in giro. Matematicamente il punto O è il “sogno” della curva che continua ad avvicinarsi a lui, ma non lo raggiunge mai. Ossia, è il limite per un angolo che continua a crescere (negativamente) e che deve arrivare a infinito per vedere realizzato il suo scopo e, quindi, matematicamente … mai!

Questa fantastica caratteristica della spirale logaritmica ci porta immediatamente a molti altri argomenti di carattere ben più generale. Immaginate di prendere un microscopio e guardare la curva che si avvicina al centro. La situazione è perfettamente uguale a quella che si vede a occhio nudo: una spirale che si stringe sempre più. Potreste cambiare il microscopio con uno ancora più potente. Niente da fare: l’immagine sarebbe sempre la stessa. La spirale logaritmica ripete la sua forma a qualsiasi scala. Otteniamo, infatti, la stessa situazione anche allontanandoci sempre più dall’origine. Vi ricorda qualcosa una situazione del genere? Beh… non possiamo dilungarci, ma la risposta è ovvia per molti: i frattali.

E, conseguentemente, di più, molto di più. La spirale logaritmica è il simbolo stesso dell’evoluzione. La Natura la ama e la segue costantemente. Solo pochi esempi, che però potete facilmente moltiplicare da soli.

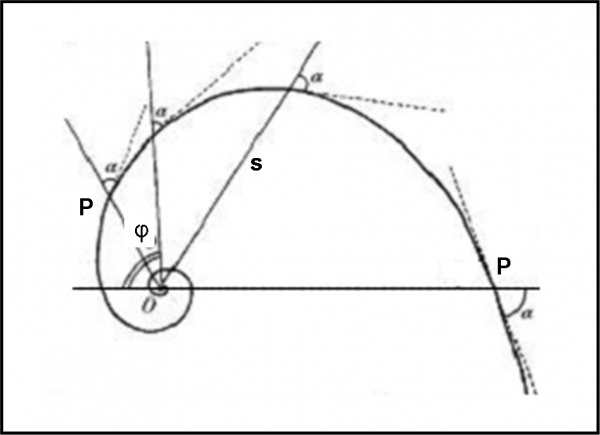
Innanzitutto, il guscio di una lumaca e di mille altre creature simili, come i nautili marini.  In questo caso la spirale risponde perfettamente a un’esigenza di crescita dell’animale che occupa il suo interno. Lo stesso comportamento lo notiamo però nella struttura di molti fiori e nella disposizione delle foglie di un albero. Gli esempi sarebbero infiniti. Anche passando a qualcosa di più dinamico, che tenda sempre a mostrare un’evoluzione del movimento. Gli insetti si avvicinano a una sorgente di luce eseguendo curve a spirale logaritmica, perché vogliono sfruttare un’altra proprietà della spirale, quella di mantenere costante, in ogni suo punto, l’angolo tra la tangente alla curva e la direzione del centro (Fig. 63), la direzione della sorgente di luce. Per motivazioni analoghe il falco pellegrino si avvicina alla sua preda “spiraleggiando”.

Spiraleggiando… spiraleggiando… quante volte abbiamo usato questo verbo parlando dei dischi di accrescimento attorno a una stella o a un buco nero galattico. Non solo nei pressi del centro, però. Tutta la struttura di certe galassie è proprio una spirale logaritmica (si chiamano appunto galassie a spirale). Questa forma indica da un lato la stessa evoluzione della galassia (dall’interno verso l’esterno), ma anche qualcosa che potrebbe essere più profondo. Fatemi volare un po’ con la fantasia (ma è solo fantasia?). La spirale che continua verso il centro della galassia tende verso l’orizzonte degli eventi del buco nero centrale. Poi le cose, apparentemente, cambiano e le conosciamo ben poco. Fatemi pensare che la spirale continui andando verso il suo punto origine, un punto che non riesce mai a raggiungere, il vero e proprio buco nero centrale, il “solito” punto singolare che matematicamente si definisce solo con un limite. Torniamo sempre ad Achille e alla tartaruga e a considerazioni simili.

Volevo anche parlarvi della spirale armonica, che altri non è che una particolare spirale logaritmica, ottenuta cambiando le costanti che la caratterizzano. Magari lo faremo in un articolo dedicato. Diciamo solo che attraverso di lei si può benissimo costruire il rettangolo aureo che ha sempre dato armonia ed eleganza alle costruzioni artistiche attraverso i millenni della cultura umana. O -se preferite- il viceversa: dalla regola aurea si deriva facilmente una spirale logaritmica. Gli stessi numeri di Fibonacci danno luogo a una spirale logaritmica (e viceversa, ovviamente).

Concludendo, spirale uguale a evoluzione, ripetizione, ottimizzazione, ma anche armonia e perfezione… E se anche la nostra intelligenza usasse (o -almeno-  cercasse di usare), per evolversi, una spirale logaritmica …

Basta, dobbiamo interrompere il discorso e tornare alle nostre lezioni che ci porteranno verso la derivata. Ci rimane solo da parlare delle funzioni trigonometriche e poi potremo fare il grande salto…

Finiamo con un aneddoto abbastanza divertente. La spirale logaritmica venne descritta la prima volta da Descartes nel 1638, ma fu Bernoulli, pochi anni dopo, a sviscerarne le più importanti proprietà. Ne fu talmente entusiasta che la definì Spira Mirabilis, ossia Spirale Meravigliosa e chiese espressamente che venisse incisa sulla sua tomba insieme a un motto che anticipava i frattali: “Eadem mutata resurgo” (benché con dimensioni diverse, rinasco sempre uguale a me stessa). Così fu fatto, ma l’incisore non era sicuramente un grande matematico ed ecco, in Fig. 64, ciò che si vede sulla lastra tombale: una spirale sì, ma quella di Archimede! Chissà quante volte Bernoulli avrà tirato i piedi all’incisore… dall’aldilà!

Domandina finale: Che valore deve assumere il parametro p della spirale logaritmica ((4) o (5)), perché la spirale degeneri in una circonferenza? Direi che è veramente facile…

Appendice: quanto è lunga una spirale?

Inserisco questa parte come appendice, dato che una trattazione completa ci porterebbe troppo lontani. Vale, però, la pena accennare a un risultato che sembrerebbe -a prima vista- paradossale.

Abbiamo visto che, a partire da una certa posizione P, per esempio quella che si ottiene ponendo l’angolo φ = 0, il percorso verso l’origine della spirale è un’impresa senza speranza. L’angolo continua girare e a crescere (negativamente), ma la spirale continua a spiraleggiare senza mai arrivare al termine. Il punto O è solo un limite irraggiungibile della curva.

Se considerassimo la cosa senza ragionarci troppo sopra, diremmo che è impossibile sapere quanto è lungo il tratto di spirale così descritto. Invece, Evangelista Torricelli, celebre scienziato del diciassettesimo secolo, riuscì a compiere la prima “rettificazione” moderna di una curva. Egli dimostrò che si può costruire un segmento la cui lunghezza (misurabile) è esattamente uguale alla lunghezza della spirale (considerata immisurabile). Evitiamo la dimostrazione che sarebbe estremamente complessa -e in fondo inutile- e vediamo il risultato dell’opera di Torricelli, descritto nella Fig. 65.

In modo decisamente analogo a quanto fatto da Archimede per la sua rettificazione della circonferenza, si deve tracciare la tangente alla curva nel punto P (inizio del tratto considerato) e la perpendicolare alla direzione OP. Le due rette s’incontrano in un punto L. Ebbene, PL è esattamente uguale alla lunghezza della spirale da P fino al suo limite O. Per noi questo non è più un paradosso, come non lo è più il problema di Achille e della tartaruga. Sappiamo benissimo che una cosa è una lunghezza matematica e un’altra è una lunghezza fisica. Misurare un segmento rettilineo ha sempre e comunque un limite di accuratezza (fisico) che non è altro che l’incapacità (fisica) di raggiungere il punto O. Fisicamente il paradosso non esiste. Matematicamente, ci troviamo di fronte al solito problema del limite e la soluzione ha un senso solo attraverso questa operazione. In realtà, anche il segmento OL non è mai perfettamente misurabile, se vogliamo scrivere tutti i suoi decimali…

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica