Questo articolo è stato inserito nella sezione d'archivio "Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo"

 

I numeri di Fibonacci restano ancora un meraviglioso mistero. E’ indubbio, però, che la Natura sembra conoscerli molto bene. E forse molto di più di quanto immaginiamo.

Questo articolo è molto vecchio, ma mi è tornato in mente avendo parlato di spirali nell’Universo (QUI). Le abbiamo anche trattate nella Matematica (QUI e QUI), ma in modo molto più tecnico.

Introduciamo brevemente un personaggio a dir poco eccezionale: Leonardo Fibonacci. Non ha scoperto niente di estremamente utile per l’uomo, né ha contribuito alla conoscenza di ciò che ci circonda, però ha insinuato dei dubbi e delle emozioni sulle regole che la Natura si ostina a seguire.

Egli è stato un matematico, ma quello che più conta è che è vissuto in un’epoca abbastanza anonima della storia umana. Nato a Pisa (sarà un caso? Anche Galileo è di Pisa…) nel 1180 e morto nel 1250, è relativamente celebre per i suoi “numeri” e per avere fatto conoscere in Europa i numeri indo-arabici, come abbiamo raccontato QUI. Non è un’epoca celebre per gli studi scientifici ed è abbastanza anomalo che un uomo del medioevo sia riuscito a concepire, nel 1202, una straordinaria regolarità in una serie costruita molto semplicemente. Scriviamo questi numeri:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

Che legame hanno tra loro? Facilissimo: ognuno è la somma dei due precedenti.

1+1=2, 1+2=3, 2+3=5, 3+5=8, ecc., ecc.

“Ebbene?”, direte voi, “Non sembra niente di speciale…!”

Facciamo, allora, il rapporto tra questi numeri

1:2 = 0.5

2:3 = 0.667

3:5 = 0.6

5:8 = 0.625

8:13 = 0.615
…
34:55 = 0.618

Dopo piccole variazioni il rapporto diventa costante e sempre uguale a 0.618. In termini matematici, il limite di questo rapporto tende a 0.618.

Un numero non qualunque, ma già ben conosciuto nell’antichità e legato a tutte le forme di arte. Deriva dal numero irrazionale ((5)^1/2-1)/2 che è universalmente noto come Numero Aureo e viene definito come il rapporto della Sezione Aurea, considerata come la legge universale dell’armonia.

Pochi esempi: le piramidi egiziane, il Partenone, le cariatidi dell’Eretteo sono definite attraverso un rettangolo aureo le cui proporzioni sono proprio date dal rapporto aureo. Ed è anche facilissimo da costruire sia verso il piccolo che verso il grande, come indica la Fig.1. Se si parte da un rettangolo aureo, basta disegnare un quadrato che abbia il lato uguale al lato minore del rettangolo e si otterrà un nuovo rettangolo aureo e via dicendo.

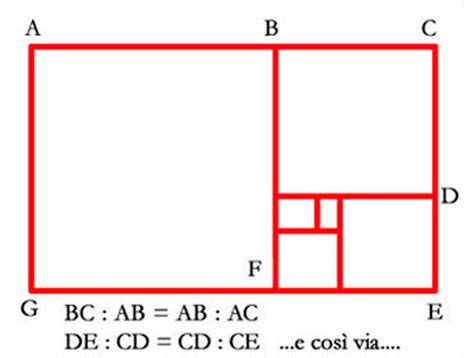
Il rettangolo aureo fu sempre seguito e nel Rinascimento divenne regola fondamentale di bellezza e armonia. Le dimensioni della Gioconda e di molti altri celebri quadri e sculture sono regolate da proporzioni auree. Perfino il palazzo di vetro dell’ONU segue la stessa geometria.

Fibonacci ha quindi espresso con una serie di numeri ciò che gli antichi avevano intuito attraverso la geometria e la proporzione.

La musica classica ha fatto spesso uso della sequenza di Fibonacci, come nelle fughe di Bach, nelle sonate di Mozart, nella Quinta di Beethoven, ecc. Insomma, il rapporto 0.618 o il suo inverso 1.618 (sarà un caso…?) sono simbolo dell’armonia delle costruzioni dell’uomo e la sequenza da cui derivano può regalare assonanze e melodie sublimi.

Fin qui la Scienza c’entra poco… ma, attraverso la serie di Fibonacci, si può facilmente costruire una figura a spirale, la spirale di Fibonacci o logaritmica, appunto. Essa è riportata in Fig. 2

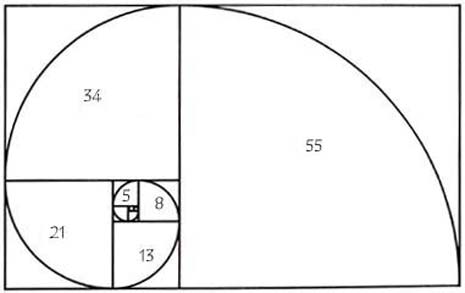
Bella, eh? Ma non solo quello… Senza nemmeno parlare, guardate alcune creazioni della Natura e traetene le conclusioni… (Fig.re 3-7).

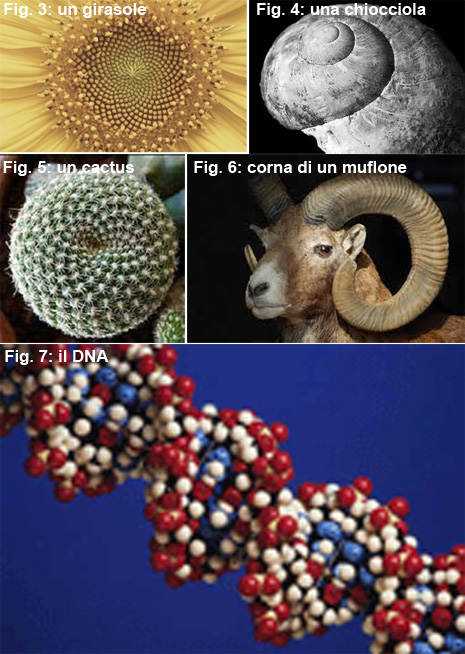
Questi sono solo alcuni esempi, ce ne sarebbero infiniti altri, come questo splendido esemplare di Aloe Polyphylla fotografato dal nostro amico Frank nel regno del Lesotho (Sudafrica)

 

Ma non solo nel piccolo … (Fig.re 8 e 9)

E non parliamo poi dei frattali (come, per esempio, abbiamo visto QUI, QUI e QUI) e cose del genere, tipo le caustiche…

Ma veniamo all’ultima riflessione che mi ha fatto scrivere questo articolo. Vogliamo rappresentare i coni di luce che partono dal Big Bang, seguendo la rappresentazione che ho usato spesso per rappresentare lo Spazio-Tempo dell’Universo, che ormai conoscete molto bene (ad, esempio QUI)?

Guardate come apparirebbe considerando moltissimi coni di luce…

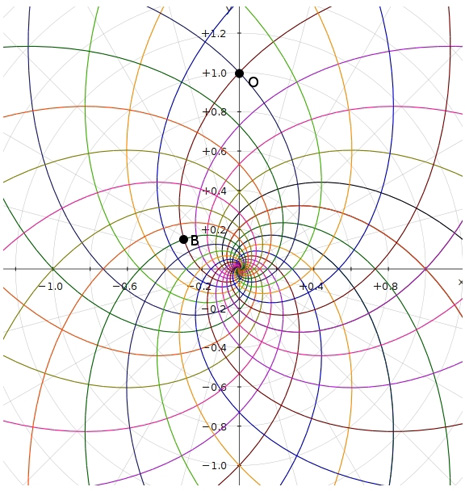
Ben poco da aggiungere, soprattutto se paragoniamo il girasole  di Fig. 3 con la rappresentazione dell’Universo di Fig. 10.

Armonia, bellezza, regolarità, parole che hanno un senso ben più profondo di quanto si possa immaginare…

Forse l’uomo ha scoperto l’armonia attraverso la sezione aurea, ma sicuramente l’Universo le conosce entrambe già da molto più tempo…

 

 

La spirale logaritmica non finirà mai di stupirci: QUI un'applicazione alla relazione che sembra legare massa del buco nero galattico e ampiezza dei bracci della galassia a spirale che lo ospita.

QUI una spiegazione matematica della spirale logaritmica

E se volete andare a spasso tra matematica e arte in compagnia del numero aureo, potete farlo QUI