Questo articolo è stato inserito nelle pagine d'archivio "Sezione Aurea, Spirale di Fibonacci e altre forme ricorrenti nell'Universo" e "Antichi Greci, che passione!"

Come già detto, prima di arrivare alla spirale logaritmica, legata strettamente al numero e, soffermiamoci un momento su una spirale più “semplice” che ha, però, permesso ad Archimede di risolvere problemi matematici che sembravano insuperabili. Ci serve anche per fare un po’ di sano esercizio “matematico”.

Un bastone che gira accorciandosi (o allungandosi)

Sappiamo quanto erano bravi gli antichi greci nell’usare un semplice bastone per risolvere problemi addirittura … astronomici. Nel 275 a.C. nasce Eratostene, che, per mezzo di un bastone (e di un dromedario regolare come un orologio svizzero), riesce a determinare con grande precisione la circonferenza della Terra. Pochi anni prima (287 a.C.) nasce Archimede che, attraverso un bastone un po’ più raffinato, introduce una figura geometrica che apre la strada a sorelle un po’ più complicate, che, si scoprirà, sono sicuramente le più utilizzate dalla Natura a tutte le scale di grandezza. Sto ovviamente parlando delle spirali.

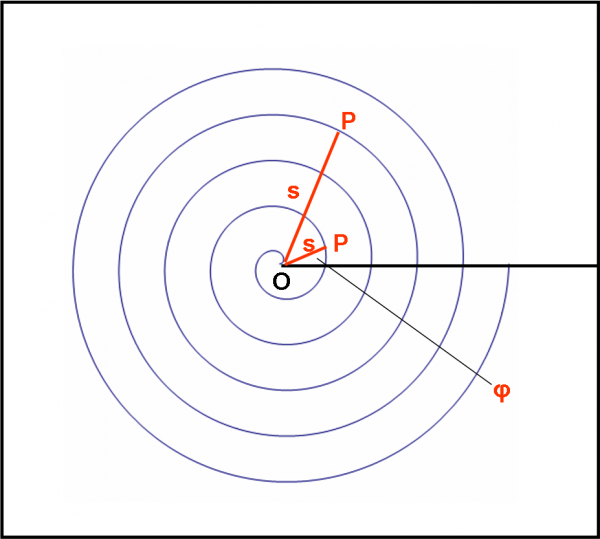
Vediamo com’è fatto il “bastone” di Archimede. Innanzitutto non deve stare fermo ma, fissato in una sua estremità (O), esso inizia a ruotare in modo uniforme, ossia descrive angoli uguali in tempi uguali. Beh, niente di speciale, come vediamo in Fig. 53. Immaginiamo di vedere il movimento nel piano della figura e, in particolare, seguire cosa succede al punto P, estremo “libero” del bastone. Mi vergogno quasi a dirlo: il punto P descrive ovviamente una circonferenza di raggio uguale a OP. Dopo una rotazione di 360° la circonferenza si chiude e, se continuo a far girare il bastone, non faccio altro che ripassare sopra la stessa circonferenza. Beh, se non altro ho trovato un facile metodo per disegnare una circonferenza, anche se, in fondo, non ho fatto altro che utilizzare una specie di compasso.

Fatemi fare un piccolo cambiamento. Invece di considerare angoli espressi in gradi, utilizzo angoli espressi in radianti, ossia numeri puri. D’altra parte sarebbe imbarazzante moltiplicare numeri per gradi… Cos’è il radiante? Non è altro che il rapporto tra la misura “lineare” dell’arco di una circonferenza diviso per il raggio. A ogni angolo φ, espresso in gradi, corrisponde, quindi, un certo arco “normalizzato” φ, espresso in radianti. Dovreste sapere molto bene che a 360° corrisponde il numero 2π. Basta, allora, scrivere la proporzione:

2π : 360° = φ (rad):  φ°

Per ottenere il valore dell’angolo espresso in radianti, basta scrivere:

φ (rad) = (φ°/360°) 2π

D’ora in poi, quando parleremo di angoli, ci riferiremo ad angoli espressi in radianti. Ciò vuol dire che compiere un giro completo (360°) vuole anche dire descrivere un angolo di 2π radianti.

Torniamo al bastone che ruota attorno a O. Tutto lì il genio di Archimede? No di certo, dato che vi ho già detto che il bastone ha una caratteristica molto particolare. La sua lunghezza varia con il tempo, in modo uniforme. In altre parole, mentre il bastone gira, la sua lunghezza s diminuisce  (o cresce) in modo uniforme. Ossia, anche la lunghezza s , come l’angolo φ, si accorcia o si allunga (a seconda del senso di rotazione) di una quantità uguale in tempi uguali.

Basta poco per capire la situazione, ma ciò che descrive il punto P diventa subito di estremo interesse. Non può certo disegnare una circonferenza dato che il raggio varia costantemente. In Fig. 54 abbiamo fatto decrescere la lunghezza del bastone a mano a mano che l’angolo gira in verso antiorario (positivo). Ai nostri occhi appare una curva che si avvicina sempre di più al centro O. Essa evidenzia molto bene che se osserviamo la situazione a intervalli di tempo uguali, il bastone, oltre a descrivere angoli uguali, si accorcia di una quantità costante. Se continuassimo in questo operazione arriveremmo, per un certo angolo, ad annullare del tutto il bastone, ossia a farlo coincidere con il punto O. Potremmo, però, anche eseguire l’operazione in senso inverso, partendo proprio dall’origine O e allungare costantemente la lunghezza s del bastone.

In poche parole, disegneremmo la nostra curva allontanandoci dal centro, ottenendo la Fig. 55, che ben rappresenta la spirale di Archimede. Notate una cosa molto importante: la curva parte dal punto O, ossia questo punto fa parte della curva. In particolare, in quel punto, il bastone si riduce a un punto. Ci torneremo presto sopra…

Abbiamo giocato un po’, ma adesso possiamo (anzi dobbiamo) applicare le nozioni matematiche che abbiamo acquisito e scrivere qualcosa di più rigoroso. In poche parole, ricavare l’equazione della funzione spirale di Archimede.

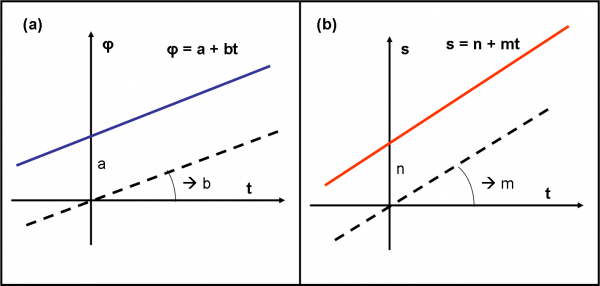
Partiamo da lontano (facendo un po’ di ripasso). Come si può scrivere il fatto che l’angolo φ varia in modo uniforme col tempo? Basta ricordarsi l’equazione di una retta nel piano cartesiano e l’applicazione che ne avevamo dato per definire la velocità di un punto che si muove di moto rettilineo uniforme. L’angolo φ deve, perciò, descrivere una retta in funzione del tempo. Ossia, seguire una legge del tipo:

φ = a + bt         ….  (1)

Al variare di t, φ descrive una retta, come riportato in Fig 56(a).

Non spaventatevi… abbiamo solo sostituito y con φ e x con t (tanto φ è diventato un numero…). Tutto il resto rimane tale e quale…

Cosa rappresentano i coefficienti (costanti) a e b? Dovreste saperlo bene (andate a rileggere i capitoli sulla funzione retta): b non è altro che il coefficiente angolare della retta e ci indica quanto rapidamente cambia φ in funzione del tempo (la pendenza della retta, insomma). a, invece, è la distanza dall’origine della retta al tempo zero. Nel nostro caso ci dice soltanto che all’istante iniziale, il bastone è già  ruotato di un certo angolo (per t = 0 la (1) ci dice che φ = a). Se scegliessimo a = 0, faremmo passare la retta per l’origine o -se preferite- il bastone di Archimede giacerebbe sull’asse delle ascisse all’istante iniziale (per t = 0 anche φ = 0).

Qualcuno starà pensando: “Perché complicare un qualcosa che sembrava così semplice? Avevo capito così bene come si costruiva la curva e adesso, invece, si sta complicando tutto.”. la risposta è facilissima. Vogliamo "raccontare" i fenomeni attraverso la matematica e non attraverso semplici descrizioni. DOBBIAMO, perciò, scrivere anche le relazioni più intuitive con il linguaggio matematico. Solo così sarà facile generalizzare il risultato, studiare i casi particolari, e proseguire verso situazioni più elaborate.

Abbiamo scritto la prima condizione che caratterizza la nostra curva. Passiamo alla seconda, che ci dice che la lunghezza del “bastone” varia anch’essa in modo uniforme con il tempo. Vale, allora, nuovamente, una relazione simile alla precedente (Fig. 56(b)):

s = n + mt               …. (2)

dove s è la lunghezza. m ci dice, nuovamente, quanto è ripida la retta, ossia quanto cambia velocemente la lunghezza del bastone a parità di tempo. n è invece la lunghezza del bastone all’istante zero.

La relazione (1) e (2) devono valere entrambe per ogni istante t e quindi basta scriverle ricavando per entrambe il tempo t. Possiamo, però, fare prima una doppia semplificazione: consideriamo che l’angolo parta dall’asse delle x, ossia, come abbiamo visto prima, che il coefficiente a valga 0. Si ha:

t = φ/b

Nella seconda relazione, poniamo, invece, che il bastone sia un punto al tempo 0 (l’origine O) e che cresca al crescere del tempo. Si ha n = 0 e quindi:

t = s/m

In poche parole, abbiamo considerato le due rette che descrivono la variazione dell’angolo e della lunghezza come rette passanti per l’origine degli assi cartesiani.

Non ci resta che uguagliare le due ultime relazioni in modo da eliminare il tempo, ossia:

φ/b = s/m

e, ancora:

s = (m/b) φ  = p φ      …. (3)

m e b sono costanti e il loro rapporto è, quindi, anch’esso una costante, che posso chiamare p. In pratica, p confronta le velocità di variazione della lunghezza e dell’angolo del bastone. Potrei prenderlo uguale a 1 e considerare il caso in cui angolo e lunghezza variano con la stessa legge rispetto al tempo. Un caso particolare, niente di più. L’equazione diventerebbe, però, estremamente semplice. Direbbe soltanto che la lunghezza s è sempre uguale all’angolo φ, espresso in radianti. Banale ma geniale… bravo Archimede!

In ogni modo, l’equazione (3) descrive perfettamente la spirale di Archimede.

Come vedete non è definita attraverso le “normali” ascisse e ordinate  del punto P, ma attraverso l’angolo rispetto a x della congiungente O con il punto P (ossia, l’angolo φ formato dal bastone) e la distanza s di P da O (la lunghezza del bastone). Queste coordinate si chiamano polari. Tuttavia, poco importa, dato che una loro coppia permette di identificare ogni punto del piano, come facevano le x e le y. I punti P che hanno la coppia di coordinate legate dalla (3) descrivono la curva in questione. Niente di diverso concettualmente dall’espressione y = f(x), usata finora.

Per esercizio, possiamo scrivere i facilissimi casi particolari della retta e della circonferenza in coordinate polari? Sicuramente… e diventano molto semplici. La retta è data da φ = cost. Infatti ogni punto di essa è descritta da una coppia di numeri in cui, qualsiasi sia la distanza s dall’origine, l’angolo deve rimanere sempre lo stesso, P(s, φ = cost). La circonferenza diventa invece r = cost. infatti, qualsiasi sia l’angolo φ, la distanza s deve rimanere costante P(s = cost, φ).

Vi posso solo dire che le coordinate polari permettono di scrivere abbastanza facilmente l’equazione di un ellisse che abbia l’origine degli assi in un fuoco. Noi non lo faremo, ma questa equazione è quella che permette di descrivere istante per istante la posizione di un corpo planetario rispetto al Sole, che è posto nel fuoco.

In breve, a seconda di quale funzione si vuole descrivere, può convenire usare un sistema di coordinate cartesiane o di coordinate polari.

Come si fa a passare da un sistema all’altro? Il modo è semplicissimo e si basa proprio sulle funzioni trigonometriche, che ormai conosciamo “abbastanza” bene.  Andate a rileggervi la loro definizione e tutto risulterà banale. Ve lo mostro, comunque, nella Fig. 57, che abbiamo già usato in varie occasioni. Essa mostra come sia facile passare da φ e s a x e y. Basta scrivere che:

x = s cos(φ)

y = s sin(φ)

Possiamo anche dire che la x e la y sono le componenti del segmento s, come ci insegna la trigonometria più elementare.

Ve bene, torniamo alla spirale del grande matematico greco, riscrivendo l’equazione, in coordinate polari, della sua spirale:

s = p φ

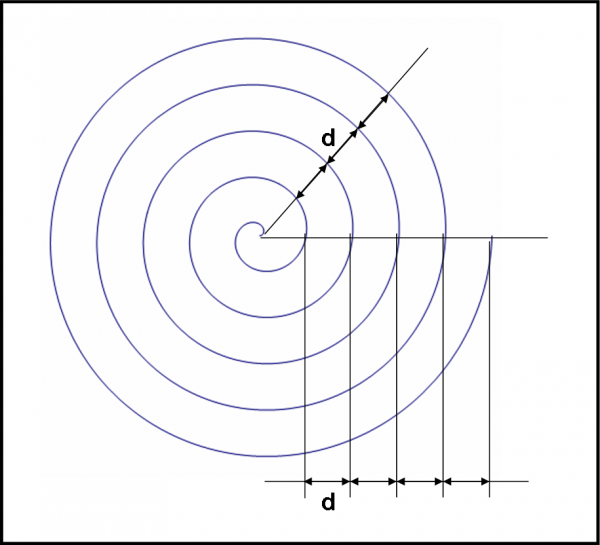
Quali sono le caratteristiche più evidenti? Innanzitutto si vede facilmente (e si ricava altrettanto semplicemente) che la distanza tra i suoi bracci rimane costante. In altra parole, ogni volta che l’angolo compie una rotazione completa (ossia 2π) la distanza d tra i due punti della curva corrispondenti è costante. In formula, infatti, si ha:

d =  s₁ – s₂ = s₃ – s₂ = …. = s_n – s_n-1 = p(φ +2π) – pφ = 2πp

d è detto passo della spirale e vale 2πp, ossia è una costante, come lo sono sia p che 2π. Al suo variare, si ha una concentrazione o una dilatazione delle “spire” della spirale.

Il passo è descritta nella Fig. 58.

La spirale di Archimede ha un’importanza matematica impressionante, dato che è servita in tempi antichi a risolvere problemi che sembravano insolubili. Potrei scrivere per ore. Mi limito a un paio di essi. Il primo è quello di dividere un angolo qualsiasi in tre parti uguali. L’utilizzo della spirale ci riesce egregiamente e facilmente. Tuttavia, quello che considero il più geniale è la rettificazione della circonferenza, ossia la misura lineare della circonferenza.

Purtroppo non posso dimostrarlo, dato che avrei bisogno delle derivate (magari ci torneremo sopra). Ma come? Archimede conosceva le derivate? No, no, non ancora… ma metodi di analisi numerica, fatti con tentativi e con ragionamenti iterativi, permetteva ai grandi scienziati dell’antichità di arrivare a risultati fondamentali anche senza l’utilizzo di una matematica superiore. Oggi, nell’epoca dei calcolatori elettronici, non ci accontenteremmo più e ci sembrerebbe un gioco da bambini.

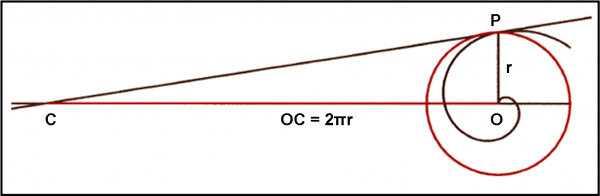
Archimede riuscì a rettificare la circonferenza, ossia a misurare direttamente la lunghezza di una circonferenza. Pensateci bene e capirete la difficoltà di questo problema. Oggi utilizziamo il π e tutto sembra ovvio. Ma allora il π era uno degli attori più controversi e ambigui. Archimede lo conosceva bene, anche se non l’aveva ancora definito perfettamente (si chiama anche costante di Archimede e questo fatto la dice lunga…), ma ne fa a meno e risolve geometricamente il problema come è rappresentato in Fig. 59. Prendiamo una spirale e facciamogli fare un giro completo, ossia ruotiamo φ di 2π. Tracciamo la circonferenza rossa che ha per raggio la distanza tra l’origine O e l’ultimo punto descritto dalla curva (P). Disegniamo la perpendicolare a OP (nel caso della figura coincide proprio con l’asse delle ascisse). Tracciamo, adesso, la tangente alla spirale nel punto P e prolunghiamola fino a incrociare l’asse delle x. Si otterrà un punto C. Bene, OC è proprio la lunghezza della circonferenza rossa. Meraviglioso!

La Natura ama le spirali, come sappiamo già molto bene, ma non tanto quella di Archimede, con il suo passo costante.  Tuttavia, almeno un animale molto comune la utilizza perfettamente. Qual è il vantaggio di questa spirale? Quello di mantenere costante la distanza tra le spire. In parole terra-terra, se un insetto non passa tra le spirali vicino al centro, non passa nemmeno ai bordi. Avete già capito chi sfrutta questa proprietà? Facile… il ragno con la sua tela che è effettivamente una spirale di Archimede (Fig. 60). Chissà se il grande scienziato greco ha osservato a lungo i piccoli tessitori prima di descriverla matematicamente.

Ben più utilizzata in Natura è un’altra spirale, quella che tende ad allargare sempre più le sue spire. Bene, per definirla correttamente dobbiamo fare uso del famoso numero e o, quantomeno, di una funzione esponenziale. Finalmente siamo arrivati al punto chiave…

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica