Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Un simpatico esercizio di cinematica, che ci porta velocemente nel mondo delle spirali che tanta importanza hanno per l'Universo. Noi ci limitiamo, per il momento, a una volpe e a un coniglio...

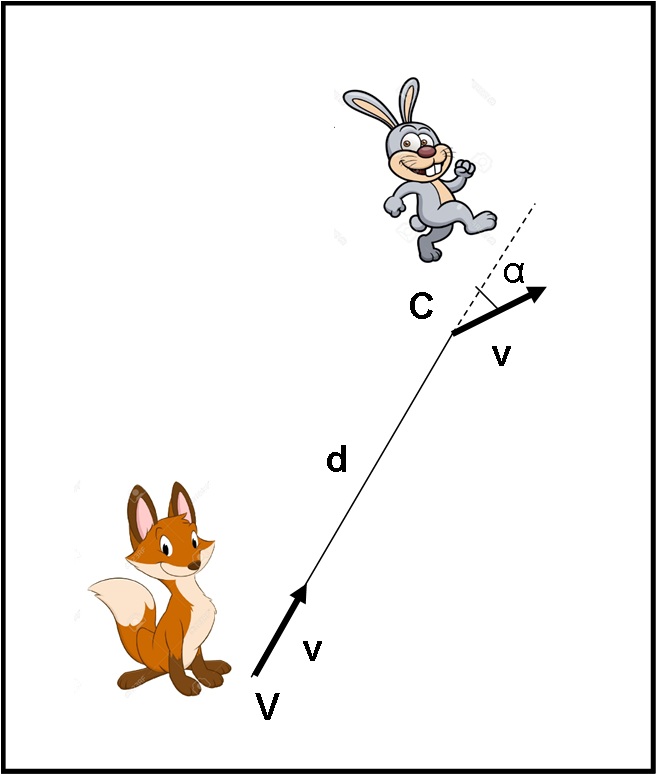
Una volpe e un coniglio si trovano in due posizioni qualsiasi della prateria. Sono entrambi fermi quando la volpe individua il coniglio e inizia la caccia… La loro distanza è uguale a d. Entrambi vanno alla stessa velocità. La volpe si dirige sempre verso la preda, mentre il coniglio corre in direzione opposta alla posizione della volpe (si allontana istantaneamente da lei). Cercando di complicare la vita alla volpe, si sposta sempre dello stesso angolo α rispetto alla direzione istantanea (per semplicità, anche nello stesso verso). La velocità v della volpe e del coniglio sono costanti in modulo e uguali tra di loro.

La volpe raggiungerà sempre il coniglio?

E, se sì, dopo quanto tempo?

Un quiz che pone un interessante problema di cinematica, ma che aiuta anche a fare una stretta conoscenza con curve che abbiamo già trattato nel corso di matematica

Le domande hanno scatenato vari approcci che possono sicuramente aiutare nel cercare la soluzione, anche se nel contempo possono distogliere dalla via più sicura e semplice. D'altra parte, la fisica ci insegna che spesso e volentieri un problema può essere risolto in vari modi... Chi volesse trarre spunto da questi vari approcci può leggere i commenti di questo articolo (il quiz originario), ma io consiglierei ai nuovi arrivati di seguire il loro ragionamento senza farsi troppo influenzare. I commenti e le soluzioni alternative parziali, più o meno corrette, possono creare confusione come capita spesso nei "forum". Noi, invece, vogliamo, alla fine, sintetizzare e dare una o anche più soluzioni che siano esatte, descritte esaurientemente e che servano per fare del problema un bagaglio culturale in più per avvicinarsi con passione alla fisica.

In questo articolo vi è, perciò, la soluzione più semplice (senza calcoli sofisticati) sia della prima parte che della seconda. Esiste, comunque, una soluzione analitica della seconda parte, che abbisogna di integrali per passare da velocità a posizione, ma qui viene presentata quella tipica di una volpe, furba, decisa e senza tanti ghirigori… Alla fine si è aggiunto anche l'approccio, forse più approssimato, fornito da Arturo.

La prima parte è relativamente semplice e si risolve inserendosi nel sistema di riferimento istantaneo volpe-coniglio. La seconda parte è un po’ più complicata, soprattutto perché è di difficile resa grafica. Bisogna ragionare in termini di situazione istantanea e non dare la precedenza al moto della volpe o del coniglio. Non per niente la via più rigorosa avrebbe bisogno di ragionare sulla velocità e sulla sua direzione istantanea, per poi passare all’integrale capace di regalarci la posizione finale. Tuttavia, si può arrivare facilmente alla soluzione con un po’ di ragionamento e di logica “simmetrica”.

QUANDO

Ci serviamo della Fig. 1. A sinistra abbiamo la posizione alla partenza. Il tempo è zero e la distanza è d. Possiamo pure disegnare le due frecce della velocità, ma bisogna ricordarsi che esse agiscono contemporaneamente: la volpe è sempre diretta verso il coniglio che, a sua volta, è sempre diretto in una direzione che è piegata di α rispetto a quella istantanea volpe-coniglio.

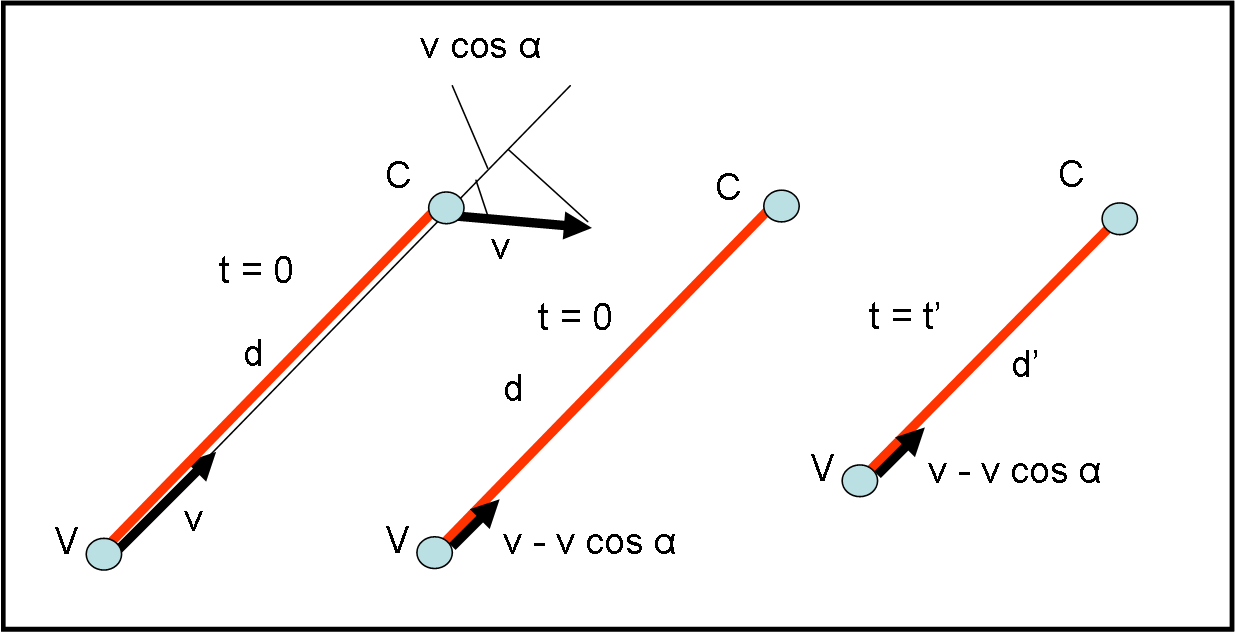
Tuttavia, qualsiasi suo tentativo di piegare viene immediatamente annullato dalla volpe per mantenere sempre una direzione rettilinea che congiunga le loro posizioni in un qualsiasi tempo t. Tutto ciò vuole solo dire che in ogni istante il sistema volpe-coniglio deve stare su una retta, ossia in un sistema che appare come un segmento rettilineo.

Dato che ci interessa  il QUANDO, possiamo trascurare la direzione di questo segmento e lavorare solo sulla riduzione della sua lunghezza fino al valore zero. E’ un sistema in movimento continuo, in cui noi ci sistemiamo stabilmente, come in un satellite che gira attorno alla Terra. Noi ci consideriamo fermi e vediamo solo i movimenti relativi tra volpe e coniglio nel sistema di riferimento (siamo in una navicella orbitante, all’interno della quale si svolge un inseguimento tra due animali muniti di una velocità propria… non tiriamo, però, in ballo la forza di Coriolis!). In altre parole, ancora, il sistema volpe-coniglio è un sistema rigido, come se i due animali fossero uniti da una sbarra di ferro, ma la cui lunghezza continua  a diminuire.

Nella parte centrale della Fig. 1 disegniamo quello che avviene veramente al tempo zero e in qualsiasi altro istante. La componente della velocità ortogonale alla direzione istantanea sposta solo il sistema di riferimento, ma non cambia la distanza relativa. Quella che conta è la velocità del coniglio nella direzione volpe-coniglio, dato che quello è il sistema di riferimento istantaneo. La componente della velocità nella direzione istantanea è data da v cos α. Nel sistema rettilineo va allora calcolata la velocità relativa della volpe rispetto al coniglio ed essa è data da:

v_REL = v – v cosα = v(1 – cosα)

A questo punto il problema è di una semplicità estrema, sapendo che

v_REL = Δd/Δt

Nella parte destra della figura precedente, vi è la situazione in un qualsiasi istante t’, nel quale si può scrivere:

d’ = d - v_REL (t’- 0)    (la distanza diminuisce col tempo)

Sostituendo il valore della v_REL, si ottiene:

d’ = d - v(1 – cos α) (t’- 0)

Basta imporre d’ = 0 (volpe che acchiappa il coniglio) e si ottiene il tempo t_FIN, ossia quello in cui la volpe raggiunge il coniglio:

0 – d = - v(1 – cos α) t_FIN

t_FIN =  d/v(1 – cos α)

Qualche risultato numerico?

v = 1 m/sec

d = 10 m

α = 90°           t_FIN = 10 sec

α = 60°           t_FIN = 20 sec

α = 30°           t_FIN = 75 sec

α = 0°             t_FIN = ∞             (la velocità relativa è uguale a zero e la distanza rimane invariata)

DOVE

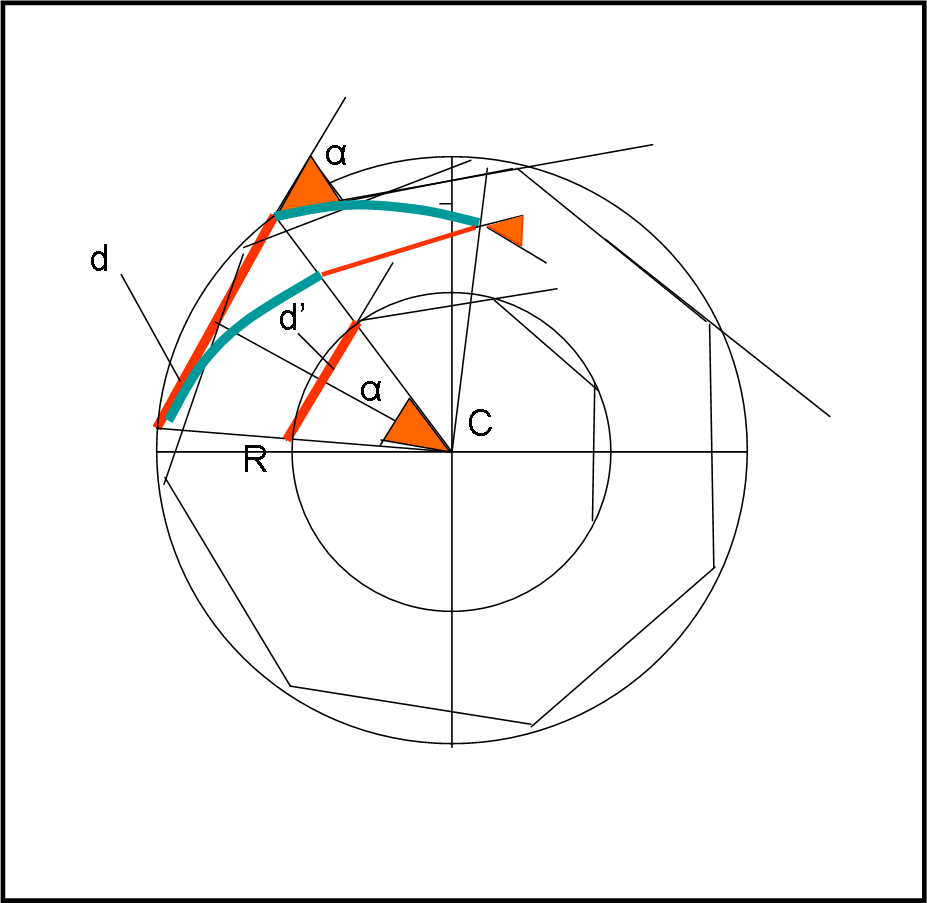
Per risolvere il problema graficamente conviene capire bene le posizioni relative di volpe e coniglio, per varie posizioni nel piano della figura (a parità di distanza d e di angolo α).

Prendiamo la volpe V e il coniglio C iniziali e sistemiamoli dove vogliamo, come rappresentato in Fig. 2. Immaginiamo, adesso che il coniglio sia diventato una volpe che insegue un alto coniglio alla stessa distanza e con lo stesso angolo di “fuga”. E poi ancora e ancora. La nostra linea spezzata  di lato d continua girare, a scatti di α, e tutti i suoi punti volpe e coniglio descrivono una circonferenza di centro C.

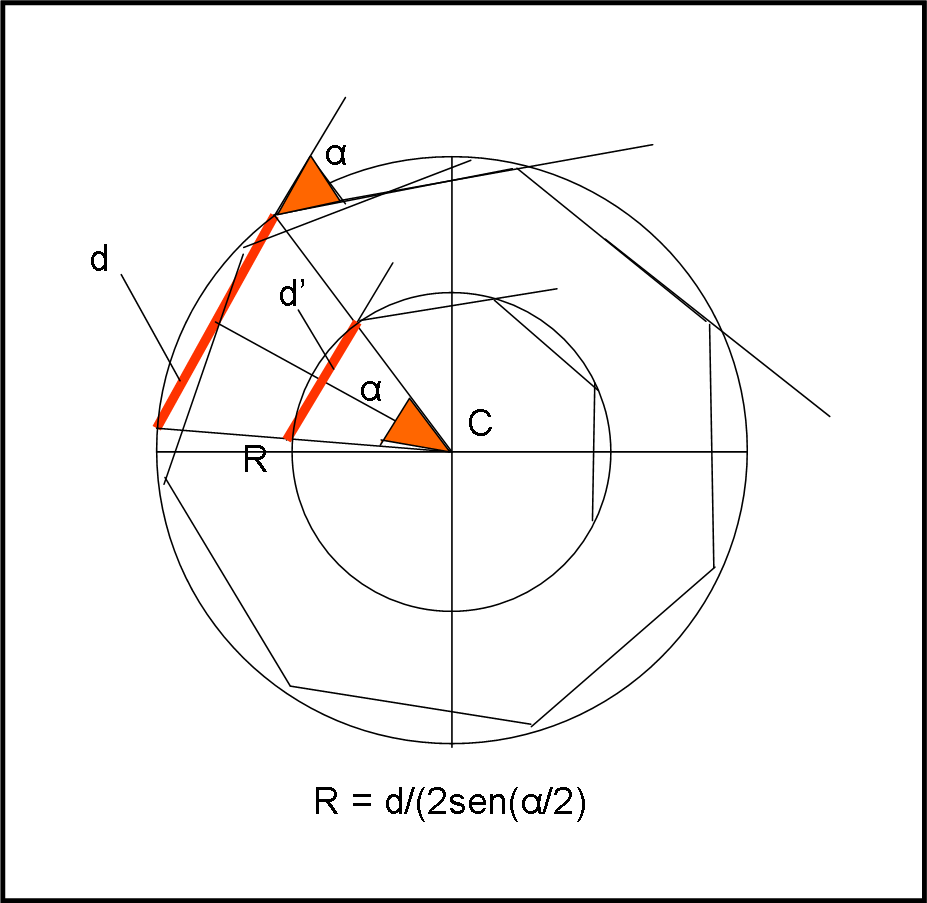
Questo avviene per una d costante. I triangoli formati dalle posizioni di volpe e coniglio in un certo istante e il centro del cerchio sono ovviamente isosceli e il loro angolo al centro è proprio α (si dimostra facilmente… provate… magari aiutati dalla Fig. 3).

Immaginiamo adesso di diminuire la distanza d e di rifare lo stesso gioco, mantenendo fisso l’angolo α. Troveremo nuovamente un cerchio che ha lo stesso centro di quello precedente e i soliti triangoli isosceli, ma il lato sulla circonferenza è ora d’ < d.

Cosa succede alla nostra volpe e al nostro coniglio iniziali? Essi fanno proprio ruotare di α la loro congiungente (ricordiamoci che essa deve sempre rimanere rettilinea!) e seguirebbero il cerchio, ma la velocità relativa ci dice che deve diminuire la distanza d. Ciò vuol dire che non solo ruota la loro congiungente, ma si sposta verso valori di d sempre minori. In poche parole, la congiungente spiraleggia verso il centro della circonferenza, come rappresentato “rozzamente” dalle traiettorie verdi della Fig. 4. Ricordiamoci anche  che il coniglio e la volpe hanno dimensioni finite e non sono punti senza dimensioni...

Vi è una a fine a tutto ciò? Sicuramente sì, dato che sappiamo esattamente quando d diventa zero. Ma se d diventa zero il cerchio relativo si riduce al punto centrale C. In altre parole, volpe e coniglio si devono sempre incontrare nel punto C.

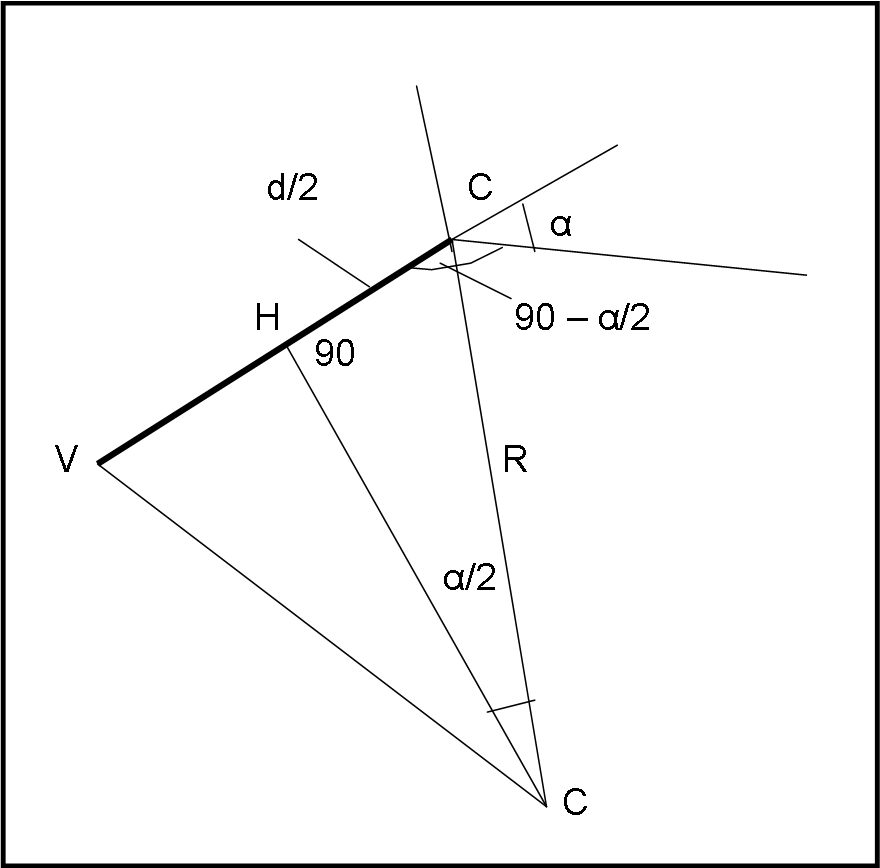
Non è certo difficile calcolare la posizione di C rispetto alla posizione della volpe iniziale (o del coniglio): non è altro che il raggio R del cerchio!

Esso si può scrivere facilmente (dal triangolo VHC) come:

R = d/(2 sen(α/2))

Se α = 0, R, ovviamente, diventa infinito, dato che la velocità relativa è nulla e il cerchio diventa una retta.

Se α = 90,  R = 0.7 d. Il triangolo è rettangolo in C, come mostrato nella Fig. 5, fornitami gentilmente da Arturo e che rappresenta l’intera caccia.

Se α = 180, R =d/2.  Il coniglio va incontro alla volpe con la sua stessa velocità e si incontrano a metà strada senza nessuna rotazione… un coniglio che ha preferito sacrificarsi subito, piuttosto che girare invano…

Chi, poi, vuole divertirsi con le spirali può andare QUI, QUI e QUI. Infine, come già detto, si potrebbe risolvere il problema descrivendo analiticamente il moto della volpe (o del coniglio) legati sempre in modo indissolubile. La variazione di direzione della velocità di una è legata a quella dell’altro (in particolare è importante la componente ortogonale della velocità del coniglio, ossia quella che fa spostare la coppia). Direi che non ce n’è bisogno, avendo trovato una soluzione più che logica e comprensibile.

Ho aggiunto i link alla spirale (sia di Archimede che logaritmica) proprio perché il problema è quasi esattamente lo stesso. Fisicamente il punto O esiste sempre... infatti, la congiungente si può misurare e può andare a zero, così come una spirale può sempre essere misurata attraverso un segmento finito (Torricelli e Archimede insegnano...). Tuttavia, la spirale si vede bene mantenendo il coniglio fisso (è lui che trascina la volpe nella sua spirale). Ma, in realtà... il coniglio si muove anch'esso e allora ecco che il triangolo isoscele risolve la questione...

Il moto del coniglio dipende dalla sua velocità che è legata a quella della volpe... o, se preferite, è vero anche il viceversa...

Mi hanno detto, in gran segreto, che la volpe in oggetto è una volpe vegetariana. La sua caccia è solo un modo per passare il tempo e per scaldarsi i muscoli. Il tutto finisce con un bello spavento per il coniglio e una sana risata liberatoria dei due animali.

Contributo di Arturo

Questa è una soluzione approssimata, a cui sono giunge per via grafica.

Prima che venga dato il via alla caccia, la volpe e il coniglio sono fermi, distanziati tra loro di una certa lunghezza che indichiamo con d.

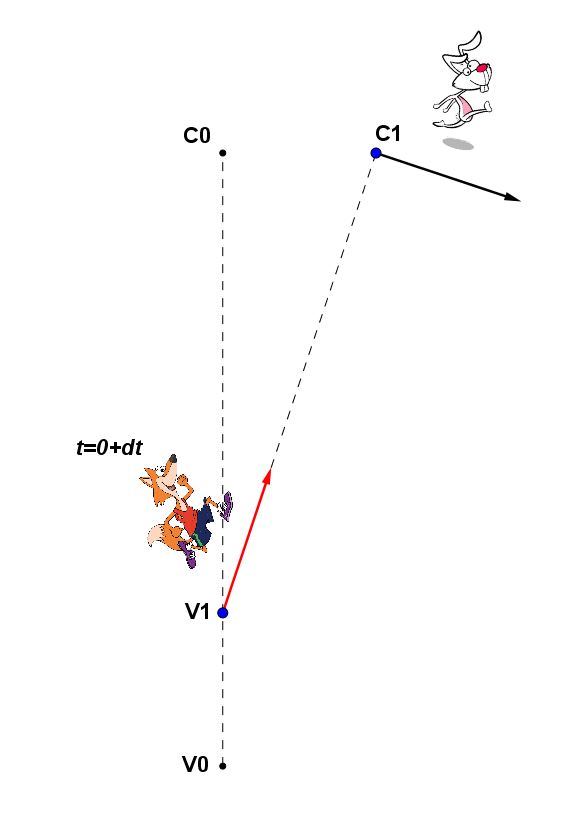
All’istante t=0, la volpe, visto il coniglio, inizia a correre verso di lui con velocità di modulo pari a v. Il coniglio, avvertito il pericolo, si mette a correre istantaneamente, quindi allo stesso t=0, ad una velocità anche essa di modulo pari a v ma con direzione inclinata di un certo angolo  rispetto alla direzione della volpe. Nel modello grafico si è posto  = 90 gradi, ma potrebbe essere un qualsiasi angolo compreso tra 0 e 180 gradi.

Dopo una frazione di tempo dt dall’inizio della corsa del coniglio, quindi all’istante t=0+dt,  la volpe, vedendo che questo si è spostato un po’ verso destra, corregge la direzione della propria corsa e punta nuovamente verso il coniglio. Ma quest’ultimo se ne accorge istantaneamente e devia nuovamente di un angolo  la direzione della propria fuga, rispetto alla direzione della volpe.

Dopo un ulteriore frazione di tempo dt, quindi all’istante t=0+dt+dt, la volpe ripunta verso il coniglio e questo devia nuovamente dell’angolo :

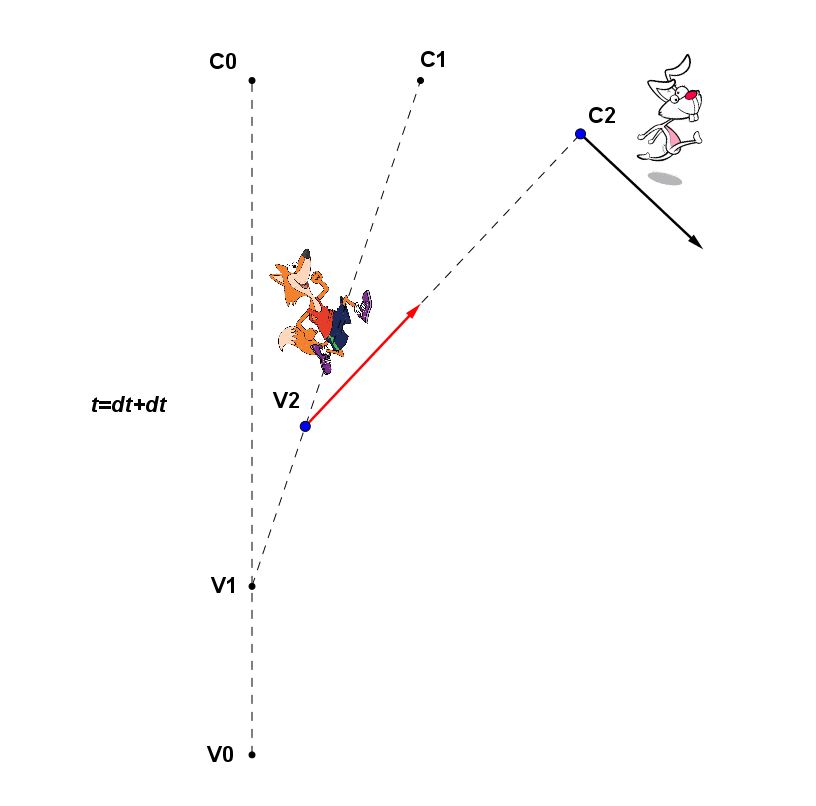
Si può tranquillamente reiterare questo evento per vedere come va a finire. Così, dopo qualche tentativo si capisce che con dt troppo grande (a cui corrispondono tratti elementari ds di traiettoria attraverso la relazione v=ds/dt) sembra quasi che volpe e coniglio, pur avvicinandosi, debbano alla fine restare separati indefinitamente di una certa lunghezza, pari proprio a ds. Riducendo l’intervallino dt, invece, si nota che le due traiettorie seguite rispettivamente da volpe e coniglio, vanno a confluire in un punto, chiamato C nelle figure, situato sull’asse del segmento iniziale  e distanziato da questo di d/2. In perfetta sintonia con la soluzione precedente.

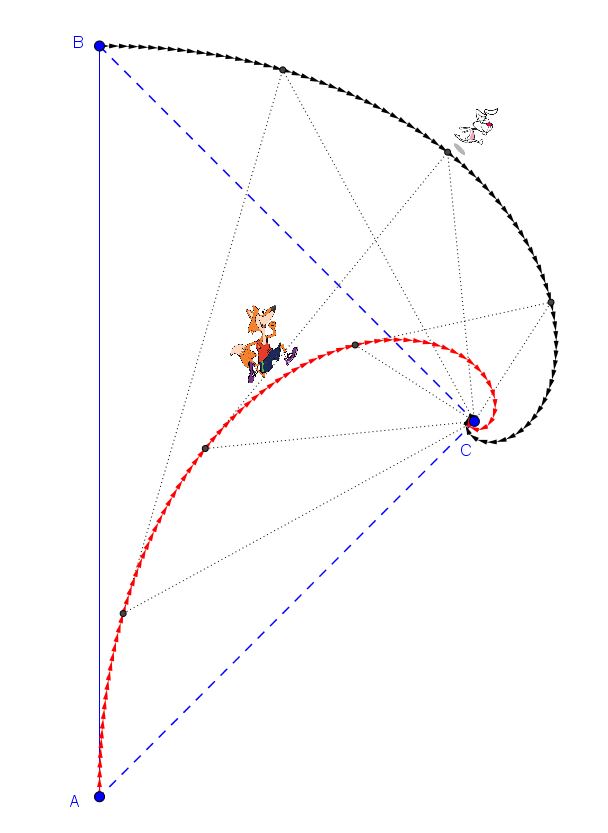
Ma non basta.

Fissato un valore di v pari a 10 m/s, è stato impostato il ds in maniera tale da avere un intervallino elementare di tempo dt pari a ds/v = 0,091/10=0,0091 s, cioè poco meno di 1/100 di secondo.  Fissata una distanza d iniziale pari a 7 metri, si ottiene il risultato grafico suddetto con un numero di passi pari a 80. Si può, perciò,  calcolare il tempo impiegato dalla volpe a raggiungere il coniglio, semplicemente moltiplicando il dt per il numero di passi: 0,0091 x 80 = 0,728 s, in buono accordo con il risultato trovato tramite la formula precedente [d/v(1-cos alfa)].

Dopo 80 passi, la distanza finale tra volpe e coniglio è risulta pari a 0,091 m, cioè circa 9 cm, mentre la distanza della volpe o del coniglio dal punto C  risulta pari a circa 6 cm. Considerate le dimensioni fisiche di una volpe e quelle di un coniglio, che non sono ovviamente quelle puntiformi del modello grafico, possiamo tranquillamente affermare che , anche con l’approssimazione del modello grafico, la volpe riesce a raggiungere il coniglio e lo fa nel punto C.

Un chiaro riferimento al celebre paradosso di Achille e la tartaruga... (QUI)

Inoltre, è possibile calcolare la lunghezza complessiva della traiettoria percorsa dalla volpe, semplicemente moltiplicando il ds per il numero di passi: 0,091 x 80 = 7,28m. Con quale valore confrontare questo dato? Per rispondere bisogna chiedersi cosa rappresenti, geometricamente, la traiettoria della volpe (ma le identiche considerazioni possono farsi per quella del coniglio). Dalla successione dei tratti elementari di traiettoria venuta fuori dal procedimento grafico , nonché dalla constatazione che l’angolo tra la direzione del moto del coniglio e quella della congiungente i due animali si mantiene costante, si giunge alla conclusione che si tratta di una spirale logaritmica. L’equazione generica di una spirale logaritmica in coordinate polari è :

          (1)

dove r è la distanza del generico punto P della spirale dalla sua origine e θ è l’angolo compreso tra la congiungente l’origine della spirale con il generico punto P e l’asse x.

Con riferimento al nostro caso, se la traiettoria della volpe è una spirale logaritmica, essa , per angolo θ = 5/4 π   (225 °)  deve passate per il punto A, cioè deve risultare

Sostituendo i valori nell’equazione (1) e ponendo b=1,  si ricava:

Inoltre, volendo rappresentarla in coordinate cartesiane attraverso le due equazioni parametriche:

si deve tenere conto del fatto che l’origine della spirale non è nell’origine degli assi, ma nel punto C, quindi:

In definitiva, la traiettoria della volpe sarebbe rappresentata dalle equazioni parametriche:

Ebbene, tracciando graficamente tale curva si ottiene il  risultato che segue, dove la spirale è la curva verde.

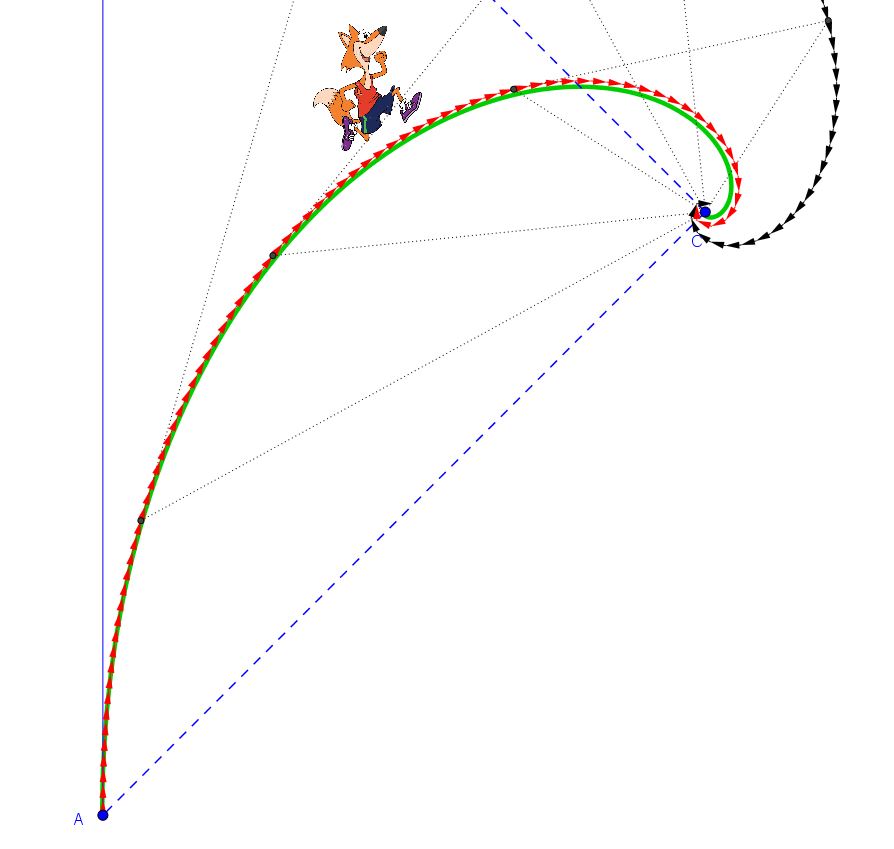
Si nota un’ottima  sovrapponibilità di questa con la traiettoria “discreta” ricavata graficamente. Approssimandoci all’origine della spirale, cioè al punto C, le differenze tra spirale logaritmica e traiettoria discreta diventano un po’ più marcate ma questo dipende dall’entità del dt. Qualora si spingesse la discretizzazione della traiettoria a intervalli ancora più piccoli, alla fine quest’ultima sarebbe pressoché identica alla spirale logaritmica sopra ricavata.

E la traiettoria del coniglio ? E’ anche essa una spirale logaritmica, con origine nel punto C e con lo stesso valore del coefficiente a, ma semplicemente ruotata in senso orario di un angolo pari a 90 gradi. In figura è la curva di colore viola.

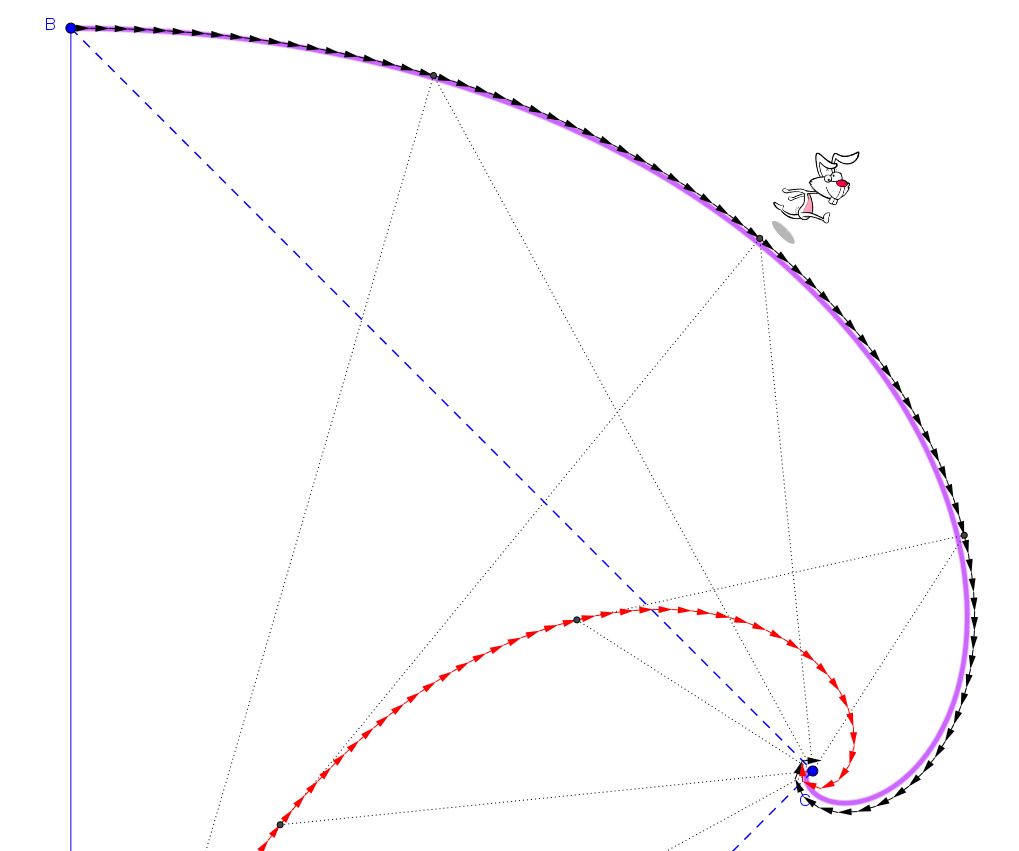
A questo punto, posso calcolare la lunghezza del percorso seguito ad esempio dalla volpe tramite la formula che deriva dalla teoria della spirale logaritmica:

Nel caso che interessa , vogliamo calcolare l’arco di spirale che va dalla sua origine (punto C) al punto A  (in corrispondenza del quale si ha ). Sostituendo i valori già trovati per a e b, alla fine otteniamo s=d=7 metri.

Confronto ora questo valore con quello trovato con la soluzione grafica (7,28m) e noto anche in questo caso una buona approssimazione.

In definitiva, questa soluzione grafica approssimata, collegata alla spirale logaritmica,  risulta in ottimo accordo con quella precedente.