QUIZ: La volpe e il coniglio **
Questo problema rientra nel quadro delle soluzioni ottenibili in collaborazione. Infatti, a partire da una prima semplice risposta, si possono diversificare le risposte relative alle eventuali successive domande. Forza amici e speriamo che vinca il coniglio (ma la vedo dura…).
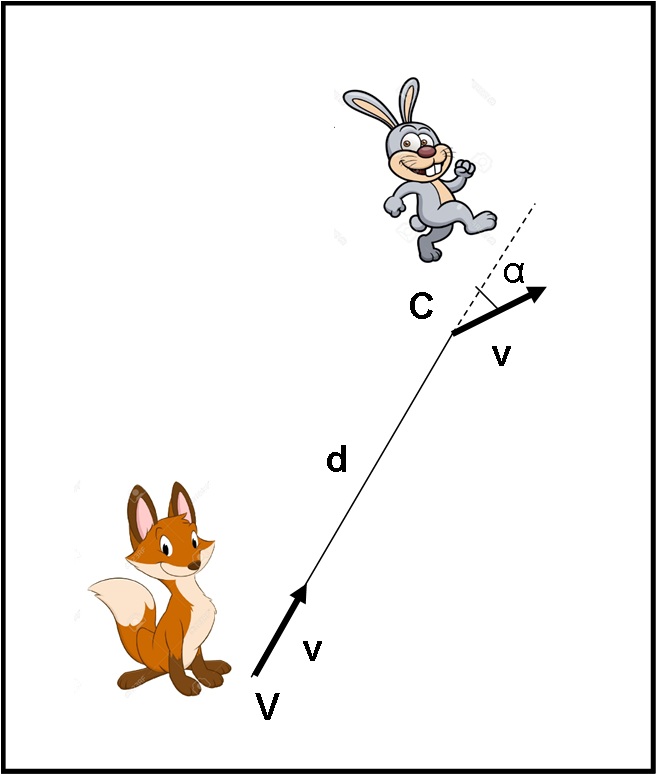
Una volpe e un coniglio si trovano in due posizioni qualsiasi della prateria. Sono entrambi fermi quando la volpe individua il coniglio e inizia la caccia… La loro distanza è uguale a d. Entrambi vanno alla stessa velocità. La volpe si dirige sempre verso la preda, mentre il coniglio corre in direzione opposta alla posizione della volpe (si allontana istantaneamente da lei). Cercando di complicare la vita alla volpe, si sposta sempre dello stesso angolo α rispetto alla direzione istantanea (per semplicità, anche nello stesso verso). La velocità v della volpe e del coniglio sono costanti in modulo e uguali tra di loro.
La volpe raggiungerà sempre il coniglio?
E, se sì, dopo quanto tempo?
La soluzione si trova QUI
52 commenti
Inizialmente mi sembrava facile, almeno la risposta alla prima domanda...
Innanzitutto direi che la scelta del coniglio di iniziare a deviare appare contro-producente: a parita' di velocita' meglio andar dritti...
Siccome pero' il coniglio devia allora la volpe puo' apparentemente percorrere una distanza inferiore, e quindi di raggiungerlo.
Il fatto che la volpe punti sempre il coniglio (e non la sua posizione futura) sembra innescare una situazione paradossale simile al famoso paradosso della tartaruga e della lepre: in questo caso il coniglio percorre una traiettoria chiusa (che tende al cerchio) ... la volpe percorre una spirale, che si avvicina sempre piu', ma che sembra non raggiungerlo mai.
Ho simulato la cosa con questa figura, in cui la curva del coniglio e' formata di piccoli segmenti. I differenti colori sono gli spazi percorsi nell'unita' di tempo, sulle diverse traiettorie (in alto il coniglio in basso la volpe): quella del coniglio forma un poligono regolare ( tendente al cerchio quanto minori sono i gradi di deviazione), quella della volpe una forma a spirale sempre piu' vicina... ma che non si incontra gemoetricamente mai.
Il sistema dei segmenti che ho usato consente di ottenere alcuni casi in cui la volpe raggiunge il coniglio... ad esempio aumentando la distanza di partenza ed ipotizzando che il coniglio stupidamente continui a percorrere la sua traiettoria anche se questa lo avvicina alla volpe, tipo questa.
Credo pero' che questa situazione sia dovuta solo al fatto che ho usato dei segmenti, cioe' degli spazi discreti in cui il coniglio e la volpe cambiano contemporaneamente traiettoria (e la volpe punta la posizione alla fine del segmento). Se la volpe puntasse realmente sempre la posizione istantanea del coniglio, percorrerebbe una curva, e finirebbe comunque per accodarsi al coniglio sulla sua traiettoria spiroidale, ricadendo nella situazione precedente.
come sempre... riuscite a evidenziare risvolti interessanti e stimolanti che fanno già parte della domanda successiva. In ogni modo, il tempo si può calcolare facilmente...
Ho fatto un'altra prova che conferma la mia supposizione: se la volpe punta la posizione istantanea del coniglio finisce per accodarsi anche nel caso il coniglio vada verso di lei (nella figura sotto in giallo cosa accade realmente sull'ultimo segmento).
La volpe non lo acchiappa.
Ho visto il coniglio e la volpe prima di imbarcarmi, così vi dico i miei pensieri "alati" (Poi voglio studiarmi attentamente il ragionamento di Paolo)
Direi che il coniglio farebbe bene ad impegnare le energie solo per scappare, senza deviare, cioè con alfa = zero dovrebbe mantenere la volpe sempre alla stessa distanza.
Con valori di alfa diversi da zero dovrebbe descrivere una spirale ad angolo costante , logaritmica, costringendo anche la volpe ad una traiettoria simile ma distanziata inizialmente di "d"
Ho pensato anche che se il coniglio gira sempre di 90° potrebbe descrivere un cerchio ( che è una spirale molto particolare). Intuitivamente direi che usa tutte le sue energie su una traiettoria che non lo allontana dalla volpe, come se fosse "fermo". Se fosse così, la volpe lo raggiungerebbe in un tempo t= d/v. ma questo l'ho pensato mentre avevo la testa fra le nuvole.
Invece, atterrando, ho pensato che si potrebbe esprimere la distanza tra i due protagonisti in funzione della loro posizione istantanea, in modo iterativo, applicando ogni volta il teorema di Carnot per ottenere la distanza dopo l'intervallo di tempo standard prefissato e utilizzando il risultato per calcolare il passo successivo, Poi, uno bravo potrebbe far tendere a zero il DeltaT ...eccetera e vedere per quale valore di t la distanza si annulla. Naturalmente si dovrebbe anche studiare come cambiano le cose agendo sull'altro parametro , ossia l'angolo di deviazione nella strategia elusiva del coniglio. La distanza iniziale può determinare il tempo più o meno lungo del raggiungimento, ma non penso che cambi il destino. Insomma, a prima vista direi "corri coniglio - sempre dritto e non ti voltare"
Va bene... , la smetto, e vado a studiare cosa ha scritto Paolo, che forse è meglio.
Prima di tutto devo chiarire una cosa: io ho capito che la volpe si muove verso la posizione iniziale del coniglio. Questi si muove su una direzione che forma un angolo "alfa" rispetto alla direzione della volpe. Al passo successivo la cosa si ripete: la volpe punta verso il coniglio e lui scappa in una direzione che forma il solito angolo "alfa" con l'attuale direzione della volpe.
Se è così la traiettoria del coniglio non è una spirale logaritmica perché il centro di rotazione varia continuamente con la posizione della volpe, a sua volta determinata dallo spostamento del coniglio.
Comunque la tra la curva "inseguitrice" e quella di "fuga" la distanza, ad ogni intervallo di tempo, può essere espressa in modo recursivo. Quindi dovrei poter calcolare come essa varia ad ogni passo, fino al suo azzeramento o alla sua stabilizzazione.
Nel modello che potete scaricare a questo indirizzo www.bernardiweb.it/carnot spirali.xls si possono modificare i vari parametri e vedere i passi di iterazione (ne ho previsti 500 ma possono essere estesi a piacere copiando dall'ultima riga in giù).
Ipotesi sulla velocità 10 m/sec ( = 36 Km/ora). l'intervallo temporale è variabile da un secondo a un centesimo di sec ( tempi più piccoli richiederebbero troppe iterazioni)
La distanza iniziale (bisognerebbe chiedere alla volpe) diciamo qualche decina di metri...
Per l'angolo di deflessione direi da 0 (che appare essere la strategia più semplice ed efficace) a 90°.
Restano molti dubbi sulla validità dei risultati perché pare che il coniglio se la cavi sempre, pur con margini talvolta minimi. Insomma la distanza si stabilizza senza azzerarsi. Un caso limite, non contemplato in partenza, è quello di un coniglio Kamikaze che vada verso la volpe (Alfa = 180°). in questo caso non c'è niente da fare, ad un certo istante la distanza vale zero. Ciao, ciao, Coniglio.
Comunicato tecnico: non riseco in questo spazio a inserire figure né allegare file. Ho dovuto pubblicare il file e mettere il link più sopra. Cosa sbaglio? E' il mio browser Chrome che ha perso la cromatura e qualche estensione? O sono io che proprio sono negato? O tutte e due?
Se la volpe punta sempre al coniglio lo prende dopo cinque o sei unità di tempo perché il coniglio va in circolo la volpe ha un angolo che è la metà di quello del coniglio.
Alle traiettorie a spirale seguite da coniglio e volpe ero giunto pure io, utilizzando geogebra come "tavolo da disegno". Ecco il risultato (traiettorie incomplete):
Ora, Maurizio, leggendo il tuo ragionamento, che mi sembra corretto, mi chiedo, a proposito della formula per determinare la distanza all'istante i-esimo: e se , brutalmente, imponessi che tale distanza si annulli ? Ho provato a farlo e, trascurando i termini dt^2 (infinitesimi di secondo ordine) viene fuori:
Questa formula è consistente con il fatto che , per alfa = 0, il tempo tende ad infinito. Infatti se volpe e coniglio procedono nella stessa direzione alla stessa velocità distanziati inizialmente di d, la volpe non raggiungerà mai il coniglio.
Dai, Arturo, ora non ti resta che catturare una volpe e un coniglio, istruirli adeguatamente (casomai ti aiuta Enzo a spiegare loro traiettorie, angoli e velocità) e dare il via all'esperimento!
Ciao Arturo, la formula che hai ottenuto , trascurando credo giustamente i termini di secondo ordine, contiene un valore di distanza relativo al passo precedente (i-1), diverso dal valore della distanza iniziale.
Cosa significa il tempo ( delta t) che si ottiene? Non ne sono certo ... Posso dire che è il tempo di cattura del bersaglio? Ho provato a mettere nel mio modellino l'angolo alfa=60 ° che darebbe al denominatore della formula il valore "v", per cui avremmo
DeltaT = d/v ossia un valore finito
Ho imposto anche distanza iniziale d=30 m , intervallo di iterazione 0,01 sec e velocità 10 m/sec
Al passo n. 613 la distanza si stabilizza al valore di 0,1 m. Sembra che la volpe veda la coda del coniglio a 10 cm ma non riesca a raggiungerlo mai.
Il mistero si infittisce...bisognerebbe uscire dalla logica degli intervalli finiti: passare da una successione recursiva di risultati discreti ad una vera funzione del tempo (parametrizzata con angolo e velocità) e fissando il valore iniziale della distanza.
Chi prepara la polenta ?
Si Maurizio, per questo usavo l'avverbio "brutalmente". Non ne sono convinto nemmeno io
Ieri sera ho provato a scrivere le espressioni di x(t) e y(t) per la volpe e per il coniglio , per poi imporre l'uguaglianza (in pratica per trovare il punto di intersezione tra le due traiettorie). Mi sono venute fuori espressioni con sommatorie di seni e coseni di angoli e differenze di angoli niente male...
E' che il nostro Prof, quando ci si mette, escogita dei quiz davvero intriganti.
Bravissimi Maurizio e Arturo.
Io pero' avevo inteso che il coniglio deviasse rispetto alla sua direzione, non rispetto alla nuova direzione della volpe.
Nel primo caso il coniglio percorre un poligono, nel secondo una spirale, come ipotizzato da Maurizio e da Arturo.
Secondo me pero' la conclusione e' la stessa, cioe' partendo dal presupposto che
Allora la volpe percorrera' una traittoria curva che tendera' ad avviniarsi sempre piu' al coniglio, ma senza mai raggiungerlo (o meglio raggiungendolo asintoticamente all'infinito). E questo e' vero indipendentemente dalla distanza dei punti di partenza e dalla traiettorie iniziali. E quindi che il coniglio cambi direzione o non lo faccia, cio' e' irrilevante, perche' i punti di partenza sono sempre differenti.
Qui sotto una figura che mostra come quand'anche il coniglio si metta a correre quasi nella direzione della volpe, questa non riesca ad acciuffarlo (a lato l'ingrandimento ...)
L'unica eccezione a questa conclusione mi pare il caso in cui il coniglio proceda in linea retta in direzione della volpe, senza deviare affatto.
Infine un commento: e' molto bella la spirale di Arturo... essa rende il fatto che la volpe non riesca a prendere il coniglio ancora piu' paradossale, dato che la spirale si chiude sempre di piu', e quindi costringe il coniglio e la volpe a rimpicciolirsi all'infinito...
Ciao Maurizio, per caricare immagine, fa l'up-load su un sito dedicato. Io uso senza problemi questo sito gratuito:
https://postimage.org/
poi copi/incolli l'indirizzo che ti viene proposto (tra le varie scelte, usa il secondo dall'alto) nell'apposita finestra "inserisci immagine" di questo editor.
Stiamo attenti... questo è un problema fisico. Anche la tartaruga non si fa mai raggiungere da Achille, ma invece fisicamente viene raggiunta senza problemi.
Il coniglio piega ogni volta, Paolo...
Attenzione a tutti!
le velocità sono sempre uguali, così come l'angolo.
Il primo passaggio dona facilmente il tempo necessario per ridurre la distanza di un certo ds. Ma, a questo punto ci ritroviamo esattamente nelle condizioni del primo passaggio, ma con una distanza un po' più corta. E via dicendo. In pratica siamo sempre in una situazione rettilinea (non per niente la volpe punta sempre il coniglio). A me sembra logica... a meno che non sbagli io (cosa possibilissima, ovviamente!!!).
cari tutti!
rileggendo bene, non vorrei avervi complicato le cose non essendo stato abbastanza preciso nel testo (a me sembrava di sì, ma...).
Il succo di tutto è che istantaneamente volpe e coniglio sono sempre lungo la stessa direzione. Proprio su questa devo fare i calcoli. Tuttavia, lungo questa direzione istantanea, ma costantemente ripetitiva, le due velocità non sono più uguali. Quella della volpe è proprio diretta lungo di lei, ma non quella del coniglio. Quella che conta è la velocità relativa lungo la direzione volpe-coniglio e questa vale proprio v - vcos(alpha), come diceva Arturo...
In altre parole, la velocità del coniglio è costantemente v cos(apha) nella direzione volpe-coniglio...
Quindi, il risultato è proprio quello dato da Arturo:
quanto tempo ci mette la volpe a raggiungere il coniglio se la loro velocità relativa è v - v cos(alpha) sempre lungo la stessa direzione?
Beh... proprio
t = d/(v - vcos(alpha))
Scusate se non mi sono espresso bene... ma il mio era un quiz più semplice del previsto, forse...
Accetto critiche e insulti (ma non botte!!!
)
Il problema proposto da Vincenzo è un classico che va sotto il nome di " curva di inseguimento " .
una curva di inseguimento piana è la curva descritta da un punto mobile M ( la volpe) il cui movimento è diretto in ogni istante verso un altro punto mobile M_0 ( il coniglio), la cui traiettoria è detta " curva di fuga" . Si suppone che i moti siano uniformi, cioè il modulo delle velocita sia costante. In generale si pone :
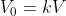
Data la curva di fuga, quella di inseguimento è definita quindi dal fatto che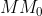
è tangente in M alla curva descritta da M stesso, e l'ascissa curvilinea di M è proporzionale a quella di 
:
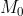La volpe cattura il coniglio se e solo se corre più in fretta : k < 1 . Se le velocità sono uguali , la distanza tra volpe e coniglio tende a un valore costante , e la curva di inseguimento tende a diventare la trattrice della curva di fuga . Un esempio è la trattrice di una retta .
Queste sono le equazioni differenziali ( che ho copiato e incollato da un sito, evidentemente ) :
La trattrice di una retta è detta anche " curva del cane a guinzaglio" . Il padrone segue una retta, per esempio partendo dall'origine (0,0) delle coordinate di un rif. cartesiano , in direzione delle x . Il cane inizialmente si trova sull'asse y , quindi ha coordinate iniziali : (0, L) , dove L è la lunghezza costante del guinzaglio . Spostandosi il padrone , il cane si muove in modo che :
la distanza tra lui e il padrone sia costante e uguale a L
il guinzaglio rimanga tangente alla curva descritta dal cane stesso .
Ma anche la ruota posteriore di una bicicletta segue una curva di inseguimento rispetto alla ruota anteriore . Immaginiamo per esempio di tenere il manubrio della bici ruotato sempre dello stesso angolo : siamo nelle condizioni del coniglio. Anche in questo caso la distanza rimane costante .
Divertitevi a risolvere quelle equazioni differenziali.
caro Pippo,
a me sembra che se la direzione è sempre quella volpe-coniglio, ciò che conta è la velocità relativa lungo questa retta. E la velocità relativa è positiva e quindi il coniglio viene sempre raggiunto. Almeno, io intendo così il problema... Infatti non impongo certo che d istantanea sia costante (come il guinzaglio)... essa varia in base alla velocità relativa.
Ma, forse, mi sbaglio...
Ciao Vincenzo,
sicuramente sbaglio (o forse ho capito male il quiz)... pero' non ho capito la tua osservazione.
Supponiamo che il coniglio cambi direzione una volta sola, e lo faccia con un angolo di addirittura 90 gradi, cioe' diciamo che svolta a destra rispetto alla volpe ... e prosegua su quella direzione indeterminatamente.
La volpe vedra' il coniglio svoltare a destra con un angolo retto, e siccome lei punta la sua posizione istantanea, essa sara' costretta a descrivere una curva (che ritengo sia asintotica sempre piu' vicina al parallelismo), ma senza mai raggiungerlo, cioe' qualsiasi sia il tempo il risultato e' infinito, che e' molto diverso dal paradosso di Achille, che sembra un paradosso solo perche' si prendono tempi sempre piu' piccoli. In questo caso invece al salire del tempo la distanza e' sempre piu' piccola... ma per quanto piccola, c''e' ne sempre un po'.
Fatico a metterla in una funzione... ma sbaglio ragionamento ?
Se non sbaglio, il fatto che il coniglio cambi ancora direzione non cambia i presupposti del problema, la volpe ridurra la sua distanza e percorrera' un'altra curva, ma le caratteristiche asintotiche della curva permangono...
Infatti il mio dubbio è su quella d iniziale : non può rimanere costante , evidentemente, se vogliamo che la volpe catturi il coniglio .
Qui tutti possiamo sbagliare , questo è implicito ed è inutile sottolinearlo ogni volta.
Ma non me la sento di risolvere quelle equazioni differenziali, che d'altronde ritengo siano corrette . Lascio il compito ad Arturo o altri matematici !
E pensare che ieri sera , in un lampo di lucidità post cena, l'avevo pure incorniciata:
ci ero arrivato però partendo da lontano, andando cioè a sommare i dt relativi a passi successivi della traiettoria (formula che si intravede più sopra nel foglio) e poi ponendo appunto beta = 90 gradi (che significa mettersi istantaneamente nella direzione volpe-coniglio) trovavo proprio la suddetta espressione del tempo necessario ad annullare la distanza. Ma non ne ero sicuro, così non l'ho proposta. Però ora resta da capire cosa rappresenta la possibile soluzione proposta da Maurizio, che neppure mi sembra peregrina. Tra l'altro, tra la formula derivata dal teorema di Carnot da lui applicato e quella indicata sopra vi è un 1/2 di differenza. Cioè, nel caso della formula derivata dal post di Maurizio, il tempo per acchiappare il coniglio si dimezzerebbe, mica bruscolini..
Il coniglio piega sempre rispetto alla congiungente e quindi esiste sempre una sola linea che unisce volpe e coniglio. Su questa linea la velocità della volpe è maggiore e quindi non può che raggiungerlo...
Penso che siano due modi diversi di vedere la faccenda...
Infatti, Pippo, la mia non rimane costante... e diventa zero per il t citato sopra.
Cerco di ripetere il mio ragionamento.
La volpe e il coniglio partono insieme, ma la volpe segue sempre il coniglio che continua a piegare rispetto a questa direzione istantanea. Bloccandola, vedo subito (senza Carnot) che la velocità relativa lungo questa retta, che è quella che accompagna sempre la coppia, è data dalla velocità v della volpe (diretta sempre in quella direzione) meno la componente della velocità del coniglio (che forma sempre un angolo alpha con lei) che è data, istantaneamente, solo da vcos(alpha). Ne segue che lungo queste retta istantanea sempre uguale (non c'è bisogno di ruotarla), la volpe viaggia con una certa velocità rispetto al coniglio e quindi diminuisce sempre la distanza fino a raggiungerlo. Lo raggiunge quando ha guadagnato, con questa velocità relativa, la distanza d. da cui:
v - vcos(alpha) = (d- 0)/(t- 0)
Non c'è bisogno di asintoti o di equazioni differenziali...
Vincenzo, ho letto dopo la tua precisazione.
Come tu dici pero' la volpe non punta istantaneamente il coniglio, punta la sua posizione futura prima del prossimo cambio di direzione. In tal caso credo possa raggiungerlo, ma non sono sicuro accada sempre... la prova dei segmenti che avevo fatto (e che riproduce la situazione che dici) non sembrava darmi sempre risultato positivo... cioe' se i due segmenti non si intersecano entro un intervallo tra due cambi di direzione, essi sembrano non potersi intersecare piu' e dare origine a qualcosa di sempre piu simile al parallelismo...
Dipende credo dall'intervallo tra cambi di direzione (piu sono lunghi piu la volpe puo' puntare una posizione futura e guadagnare piu spazio) e dalla loro entita' in gradi...
Ci pensero' ancora...
Perché, Paolo, parli di posizione "futura"? A t = 0 sono fermi. A t = t1, la direzione è unica e la volpe continua ad andare dritta verso il coniglio (per definizione) che istantaneamente sta facendo un angolo rispetto a quella direzione. Avvengono insieme le due cose e non una prima dell'altra...
Siamo riusciti a creare un bello scompiglio... quasi quasi userei un bel fucile per fare scappare la volpe e il coniglio in due direzioni opposte
Ciao Vincenzo,
ho capito quello che tu dici, ma non mi quadra: se il coniglio si sposta in linea retta, ma con un certo angolo rispetto alla volpe, la volpe (se punta la posizione istantanea) deve necessariamente compiere una curva. La traiettoria della volpe non puo' mai essere rettilinea perche ad ogni istante infinitesimo il suo bersaglio non e' piu' allineato con la retta che stava percorrendo, deve deviare... e deve farlo continuativamente.
In pratica anche se il coniglio percorre una retta, la volpe deve continuamente cambiare direzione e percorrere una curva. Stasera provo a fare un disegno... ora devo scappare. Bellissimo questo quiz !!!!
Sono stato dal dentista, adesso ci sta pensando anche lui ....
Comunque ringrazio tanto Paolo per avermi spiegato come inserire le immagini e gli allegati.
Poi, dico, non si può lasciarvi soli un momento che ne succedono di tutti i colori. Certo, Vincenzo ha gettato un macigno nello stagno....
Allora lascerei perdere per il momento Achille e la tartaruga, problema che conosco anche in una habitat quantistico e di cui magari proverò a raccontare qualcosa in un altro momento.
Tornando al nostro coniglio, che è lì che aspetta di conoscere il suo destino, mentre ero sotto anestesia (locale) mi è venuto in mente che se parto dalla formula iterativa che mi da la distanza in ogni istante discreto (i) e scrivo :&space;-&space;d(i))/\Delta&space;t)
, poi ne calcolo il limite per 
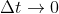dovrei avere la derivata della funzione che cerco, cioè la derivata di... distanza = f(t).
Se integro dovrei trovare la funzione. La costante da aggiungere non è altro che la distanza iniziale.
A questo punto dovrei avere una funzione monotona decrescente che parte dal valore "d" iniziale e , forse, va a zero, oppure no. Comunque, se impongo l'annullamento di questa funzione, dovrei o trovare l'istante in cui lepre e coniglio occupano lo stesso punto (concettualmente) o non riuscire a trovare nessun punto reale.
Se mi dite che è una corbelleria non ci penso più e mi oriento su qualcosa d'altro...
Scusate, ho scritto "lepre e coniglio" invece di "volpe e coniglio" per via dell'anestesia. Ovviamente volevo dire Volpe e Coniglio, a meno che la soluzione non sia proprio cambiare animale...
denti permettendo, direi che va bene... il problema, come vedrai dai commenti, è che le condizioni di partenza ci trovano un po' discordi... Dovremmo chiedere alla volpe e, magari, anche al coniglio... Forse un bel fucile è la soluzione migliore...
Per il vino ci pensi tu?
senz'altro... un bel barolo direi?!
La volpe in A punta verso il coniglio in B.
.
Al tempo t la distanza relativa è D(t).
Al tempo t+dt il coniglio si sposta di una angolo alfa verso C di un tratto vdt (primo lato del triangolo ABC).
Contemporanemente la volpe percorre un tratto pari a vdt quindi la sua distanza diviene D(t) -vdt (secondo lato) .
L'angolo fra essi compreso è
La domanda è: quanto vale D(t+dt) ?
Applichiamo un semplice Carnot al triangolo ABC:
da cui ricordndo le proprietà degli angoli complementari:
Da questa eliminiamo i termini infinitesimi di grado superiore
poiché alfa è compreso tra 0 e
, il coseno può essere positivo o negativo e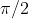
.
la distanza al quadrato diminuisce o incrementa al passare del tempo.
La strategia vincente del coniglio è quindi quella di deviare di un angolo avente coseno negativo cioè >
Mi fermo qui (citazione) e lascio agli altri l'onere/onore di completare lo sviluppo del problema.
PS il coniglio ovviamente descrive una spirale logaritmica intorno al suo predatore , contrariamente a ciò che fa invece il falco con la sua preda.
Mi correggo :
tutte le strategie del coniglio sono vincenti in quanto (1- cos
) non è mai negativo. eh eh eh
Accidenti , il latex editor mi ha fregato ancora una volta.
L'espressione esatta è
il terzo termine è costantemente negativo.
Quindi la distanza diminuisce costantemente come l'esimio Professore ha affermato.
Proseguendo
Dalla precedente si calcola la derivata di)
:
adesso poniamo)
}{\mathrm{d}&space;t}&space;=&space;v&space;\left&space;(&space;cos&space;\alpha&space;-1&space;\right&space;))
f(t) =
quindi
ma
quindi
che ha per soluzione
-1) t
D(t) = v (cos
inaspettatamente lineare in t , monotona decrescente.
Fine prima parte
Più precisamente
D(t) = D(0) + v (cos
-1) t
D(0) è la distanza iniziale tra coniglio e volpe
Riprendendo le premesse di Leandro e la valutazione della distanza istantanea con Carnot, che mi vede concorde, ho eseguito una simulazione con alfa = 90°, distanza iniziale 30 metri, velocità, tipica dei conigli e volpi = 36 km/ora (= 10 m/sec). il tempo di campionamento è di un decimo di secondo.
Dopo 36 iterazioni (3,6 secondi) la volpe si è avvicinata al coniglio riducendo la distanza ad un metro e da lì non è più riuscita ad avvicinarsi oltre. Indipendentemente dalle traiettorie che possono essere descritte ricorrendo a vari sistemi di riferimento (dice bene Leandro, spirale logaritmica "attorno alla volpe" che è un centro mobile) la distanza non decresce più.
Questa simulazione la trovate all'indirizzo riportato in fondo.
Se però provate a ripetere la simulazione mettendo come intervallo un millesimo di secondo, a parità di tutto il resto, dopo poco più di 3.000 iterazioni ( 3 secondi) avrete un risultato diverso, la volpe è ad un centimetro dal coniglio.... e sembra che da lì non guadagni più terreno.
Si potrebbe dedurre che facendo tendere a zero l'intervallo temporale, in quei tre secondi la volpe riesca ad avvicinare il coniglio fino a toccarlo.
Pensandoci un attimo, alla velocità di 10 m/sec occorrono 3 secondi per fare 30 metri...in linea retta.
Che abbia ragione l'enoico??? Sarebbe un vero disastro!
http://www.bernardiweb.it/carnot spirali.xls simulazione (salvo errori ed omissioni)
usa un runge kutta del quarto ordine.
Per chi non ci crede ancora... facendo riferimento al caso di "alfa = 90°" nel post precedente.
immaginate che ci sia un tubo perfettamente trasparente ai cui estremi ci sono la volpe e il coniglio.
Dalla parte della volpe il tubo è incernierato al piano, può ruotare come la lancetta di un orologio.
Al via la volpe si infila nel tubo e corre alla velocità v. Contemporaneamente il coniglio si mette a girare in cerchio con raggio uguale al tubo, alla velocità periferica v, trascinando la sua estremità del tubo in un moto circolare. Il coniglio non si allontana per niente dalla imboccatura del tubo, la sua velocità radiale è nulla.
Dopo il tempo necessario a compiere a velocità v la lunghezza del tubo (distanza iniziale) sbuca fuori la volpe e ciao.
Per un osservatore esterno (come noi) il coniglio ha tracciato un arco di cerchio piegando ad ogni istante la sua traiettoria di 90° e la volpe ha compiuto una traiettoria "non rettilinea" ma curva. Per quanto riguarda la volpe (vista soggettiva) è sempre andata dritta, dentro la "metropolitana" verso il coniglio, come dice il Professore. (una vera volpe anche lui)
Per i casi di alfa diverso da 90° il più facile è "alfa=0". Qui il coniglio se ne frega del tubo, si guarda bene dal farlo girare e pensa solo a correre nella direzione del prolungamento, prima che arrivi la volpe. (ha capito!)
Per i casi intermedi di "alfa" vedrei due componenti di velocità una radiale v cos(alfa), con cui il coniglio "vero" si allontana prudentemente, sempre allineato con la direzione istantanea del tubo, e una velocità tangenziale v sen(alfa), con la quale un "coniglio clone" fa ruotare il nostro tubo, ma la notte incombe e lascio a voi il problema di una formalizzazione rigorosa di questo ragionamento "del tubo".
Runge Kutta del quarto ordine, già ... L'ultima volta che l'ho usato è stato nel dicembre del 1970, o forse era un Predictor Corrector? In ogni caso ha funzionato bene....era per un modello che simulava il funzionamento di una colonna di distillazione a piatti. Quanti eoni sono passati....
Vedo che siete andati avanti parecchio. Finalmente un po' di diatriba...
Ho visto la soluzione di Leandro ... anch'essa contrasta coi dati di Maurizio. Il primo dice che lo prende, il secondo sperimentalmente dice di no...vedo che si stanno creando due fazioni...
Premetto che non sono in grado di mettere in discussione i passaggi di Leandro, che e' bravissimo, ma secondo me in questo caso sbaglia approccio, perche' la volpe non percorre il lato del triangolo che lui disegna. Il suo ragionamento tornerebbe se la volpe puntasse la posizione di arrivo del coniglio trascorso il tempo t, ma in realta' la volpe non punta la posizione di arrivo del coniglio, la volpe punta il coniglio in ogni istante... e quindi percorre una curva... tipo questa.
I segmenti rettilinei sono la traiettoria del coniglio, che cambia direzione con un angolo di 60 gradi ogni 10 secondi. La curva interna e' invece la volpe... che cambia direzione continuamente. La distanza si riduce, ma sempre meno e sembra non annullarsi mai.
A mio modestissimo parere trovo l'approccio di pippo della curva trattore piu fedele al problema. L'esempio delle ruote della bicicletta (con quella posteriore che insegue su traiettoria diversa quella anteriore) mi sembra che calzi abbastanza, con la differenza che nella bici il telaio impone distanza costante tra le ruote, e quindi la ruota posteriore in curva e' costretta a girare piu piano, in questo caso invece e' imposta la velocita costante, ed infatti la volpe si avvicina... ma solo fino ad un certo punto.
Secondo me val la pena di fare un esempio numerico condiviso, magari con dati forniti da Vincenzo e confrontare le soluzioni.
Paolo
per me la curva di fuga e la curva di inseguimento sono entrambe curve ( scusate il gioco di parole!) , perchè fai cambiare direzione al coniglio solo ogni 10 secondi ? Se è una tua scelta, d'accordo. Ma mi sembra che i termini del problema non fossero questi . In ogni posizione della curva di fuga del coniglio , la congiungente col corrispondente punto della curva di inseguimento della volpe è tangente alla curva di inseguimento stessa in quel punto.
Io mi trovo d'accordo col disegno che ha fatto Arturo Lorenzo il 6 dicembre con Geogebra. Avrei voluto fare anch'io un disegno con geometra, ma non sono cosí bravo . E allora ho fatto questa schifezza a mano , con righello e penna , su foglio quadrettato :
La spezzata
rappresenta la traiettoria " discreta" del coniglio , ogni segmentino rappresenta la velocità nel punto , pari a 2 quadratini . La spezzata 
rappresenta la corrispondente traiettoria della volpe , i segmentino sono uguali per ipotesi del problema .
Le congiungenti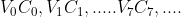
rappresentano le direzioni istantanee ( queste sono tracciate in istanti ben definiti , discreti , ovviamente) che congiungono le posizioni istantanee di V e C . La prima , cioe 
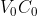, rappresenta la distanza iniziale, che ho assunto pari a 10 quadratini .
La distanza diminuisce col tempo, si vede .
Però non sono d'accordo su una cosa , mi pare che l'abbia detta Vincenzo , e cioè che la componente della velocità di C sulla direzione di ciascuna congiungente è sempre uguale a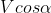
: non è vero , perchè l'angolo che tale velocità forma in un certo istante con la congiungente V-C non è affatto costante ed uguale ad 
iniziale assegnato !
Io ho preso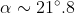
(la tangente è 2/5 , facilmente disegnabile col righello ) . È evidente per esempio che la velocità di C nel punto 
, uguale a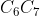 
, è quasi perpendicolare al segmento 
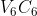. Quindi forma un angolo ben maggiore di 21º.8 .
E perciò , per me la soluzione in cui la velocità risulta pari a)
, che ho visto scritta da varie parti, non mi sembra giusta .
Non sono in grado di fare di più , però . Avrei voluto scrivere le equazioni delle due curve , i due assi cartesiani servivano a questo , ma non ne sono capace . Posso solo dire che :
e che i segmenti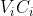
sono tangenti alla curva di inseguimento della Volpe . Ma non so scrivere l'equazione di questa curva, nè di quella di fuga .
Ciao.
Al primo momento, con la simulazione (alfa 90°) basata su intervalli di un decimo di secondo ho avuto la sensazione che la distanza si stabilizzasse dopo tre secondi ad un certo valore. Ripetendo però la simulazione con un intervallo 100 volte più piccolo, di un millisecondo, dopo tre secondi ottengo una apparente stabilità ad un livello di distanza molto più piccolo. insomma c'è da pensare che infittendo i punti l'azzeramento si possa ottenere, proprio in tre secondi. (=D/v). Ha ragione Leandro, bisognerebbe usare un metodo efficace di integrazione numerica che converga più rapidamente ad un risultato più preciso di una semplice iterazione. La funzione ottenuta da Leandro poi,in linea con quanto dicevo anche io in alcuni interventi precedenti, mi sembra corretta.
Ma posso anche vedere le cose in un altro modo: prendiamo sempre il caso di alfa = 90°. Il coniglio corre in un cerchio di raggio pari alla distanza iniziale, ogni istante piega di 90° per restare sulla circonferenza, la sua velocità tangenziale è v. la volpe all'istante zero, quando il coniglio è ancora fermo, è allineata sul raggio che conduce a lui. Nell'istante successivo dovrebbe compiere uno spostamento laterale per non perdere il raggio verso il coniglio e uno spostamento radiale per avvicinarlo. La cosiddetta "velocità della volpe" v è solo la componente radiale, se calcoliamo la velocità lungo la traiettoria curva che di fatto percorre, devo comporre questa componente con la componente ad essa ortogonale che rappresenta la velocità di spostamento angolare. il vettore risultante sarà in modulo superiore a v, e crescerà quanto più la volpe si allontana dal punto di partenza. Insomma la velocità "costante" = v è quella radiale. Calcolare la distanza tra volpe e coniglio mi consente di valutare ( se la forzo a zero) in quanto tempo si conclude l'inseguimento ma nulla mi dice sulla velocità della volpe "lungo la sua traiettoria". ( questo secondo me, e anche secondo qualcuno di voi. Ah, Pirandello...)
direi che piano piano stiamo convergendo... Potrebbero mettersi in contatto i vari Maurizio, Leandro, Arturo, Paolo (direi che Pippo la pensa in modo decisamente diverso...) e provare a mettere insieme un loro modo di vedere la faccenda (quella del tubo flessibile mi sembra molto interessante).
In ogni modo lascerei stare Carnot, dato che non esiste realmente un triangolo, ma sempre solo e soltanto una retta istantanea, lungo cui una velocità è costretta a ridursi in funzione del coseno di alpha... Potremmo dire che ci si può mettere nel sistema di riferimento della volpe, che vede sempre il coniglio dritto davanti a sé, e si accorge del suo spostamento laterale solo per la riduzione della sua velocità.
E poi, se proprio volete farvi del male, potreste anche trovare il DOVE si incontrano. Io l'ho risolto (forse) in modo un po' empirico... se qualcuno ha idee migliori ben vengano!
Giovanotti,
richiamo l'attenzione su un fatto importante , ripetendomi: la componente della velocità di C sul raggio vettore condotto da V non è affatto costante, ma diminuisce col tempo, perché aumenta l' angolo e quindi diminuisce il coseno dell' angolo! Altro che \ alpha! L' angolo è funzione crescente del tempo !
La distanza tra V e C può diminuire proprio perché la velocità relativa di V rispetto a C aumenta.
Nella figura da me disegnata, ogni segmentino che rappresenta velocità rappresenta anche spostamento in 1 secondo , giusto?
Arturo, che conosce benissimo Geogebra, potrebbe fare un disegno dando coordinate iniziali , velocità iniziale, e angolo \alpha iniziale; Geogebra è capace da solo di calcolare le coordinate cartesiane dei punti e dare pure distanze e angoli, e li riporta anche sul disegno, volendo.
Ci proverò anch' io, ma non conosco bene il programma.
Insomma, direi che ognuno ha la sua visione diversa del problema. Per me l'angolo rispetto alla congiungente VC rimane costante ed è uguale ad alpha. Se mi metto nel sistema VC, istante per istante ,la componente della velocità del coniglio va sempre ridotta col coseno di alpha. Il tutto si riduce a una retta in cui la volpe continua a guadagnare terreno fino a raggiungere il coniglio. Non dobbiamo dimenticare che la volpe non si dirige verso una posizione precedente o posteriore del coniglio, ma verso la sua posizione istantanea che, rispetto a questa direzione, forma sempre un angolo alpha (come scritto nel problema). Sono contento che anche Pippo ha lasciato da parte la prima ipotesi che voleva una d costante. ma se d non è costante il coniglio non ha scampo. Perché non provate con un gatto e un topolino (finto ovviamente che tenda a ruotare continuamente)
.
Secondo me, la migliore figura è quella rettilinea con V e P allineati SEMPRE (per definizione del problema), ma con un coniglio che continua spostarsi di alpha rispetto a QUESTA configurazione (alpha costante e non si somma).
Dai, facciamo una bella cosa. Inserire nuovi commenti un po' saltellanti e con figure diverse non aiuta a far capire. Invito tutti i partecipanti a stendere una loro relazione con belle figure, farle girare tra loro, discutere e vedere a quali conclusioni arrivano. Prometto che le inserirò tutte come articoli risolutivi (sempre che non compaiano errori rispetto ai dati di partenza). Adesso mando un mail a tutti voi, in modo che abbiate le email di tutti...
Abbiate pazienza, ma io di più non riesco a fare, dato che devo andare avanti con le news e con la RG e altro ancora (la sabbia da esempio). Forza miei prodi e vinca il coniglio migliore! (o la volpe?????).
Cari TUTTI,
vista la frenesia raggiunta nel quiz ( non ho ancora capito se il tifo è per la volpe o per il coniglio
) ho deciso di dire STOP ai commenti degli scatenati risolutori (Pippo, Leandro, Paolo Salvini, Maurizio e Arturo -spero di essermeli ricordati tutti...) e di invitarli a rispondere contattandosi e proonendo soluzioni alternative, ma chiare e comprensibili a tutti.
Ovviamente, chi non ha ancora risposto e ha altre idee per la soluzione può continuare a inserirle, ma in modo tale che siano chiare e non frammentarie. Altrimenti si rischia una confusione enorme...
Mi ha chiamato la volpe, dicendomi che le gira la testa e non sa più dove dirigersi... Ma anche il coniglio sta per svenire... Non vorrei si fermassero e ci mandassero al diavolo!!!!!!!!
Grazie a tutti per l'aiuto e per l'interesse sempre più tangibile. Il circolo è fiero di VOI!!!!!!!!!!
Amici, per risolvere questo problema ci vuole la fiducia (in chi chiaramente l'ha posto) e un po' di farina ( quella scura). Per me la volpe raggiunge il coniglio , ma trovare quando è un po' complicato.E' inutile fare altri disegni, come dice Vincenzo, quello del quiz va benissimo.Bisogna fare dei calcoli. Proverò anche io.
Bisognerebbe fare i calcoli,per chi li sa fare,come fossero due circonferenze,una piccola per il coniglio una più grande che la contiene,per la volpe unite a tangente.Quando si sposta Rabitt,Fox si sposta in avanti e misura L' angolo sul radiante del coniglio,fino a che Fox mangia Rabitt.
Non avevo letto i commenti.. non sapevo che fossa già stata data la soluzione, pensavo a qualcosa di complesso, poi ho visto che aveva solo due **, e sono giunto alla conclusione.
Provo: “una prima semplice risposta”
Per esempio la semplice risposta del tornitore: Se devo filettare un foro fondo 10 mm, passo 1 mm, conto i 10 giri del trapano!
In questo caso, per esempio:
Considero la distanza d = 200 metri
Considero v = 100 metri/minuto, e che il coniglio si allontana di 80 metri/minuto.
Cambia angolo la volpe, cambia angolo il coniglio. Sempre 80 metri/minuto sono. Quindi ci mette 10 minuti?
Ora traccio il percorso del coniglio (si fa presto a scriverlo) e calcolo dove si trova dopo 10 minuti.