In questo articolo vi è la soluzione più semplice (senza calcoli sofisticati) sia della prima parte che della seconda, verso cui si era già scatenato un bel manipolo di concorrenti (Arturo, Leandro, Maurizio, Paolo Salvini, Pippo e Umberto). La seconda parte era trapelata nei commenti e riguarda il DOVE la volpe prende il coniglio.  Esiste, comunque, una soluzione analitica della seconda parte, che abbisogna di integrali per passare da velocità a posizione, ma qui viene presentata quella tipica di una volpe, furba, decisa e senza tanti ghirigori…

La prima parte è relativamente semplice e si risolve inserendosi nel sistema di riferimento istantaneo volpe-coniglio. La seconda parte è un po’ più complicata, soprattutto perché è di difficile resa grafica. Bisogna ragionare in termini di situazione istantanea e non dare la precedenza al moto della volpe o del coniglio. Non per niente la via più rigorosa avrebbe bisogno di ragionare sulla velocità e sulla sua direzione istantanea, per poi passare all’integrale capace di regalarci la posizione finale. Tuttavia, si può arrivare facilmente alla soluzione con un po’ di ragionamento e di logica “simmetrica”.

QUANDO

Ci serviamo della Fig. 1. A sinistra abbiamo la posizione alla partenza, simile a quella data nel quiz. Il tempo è zero e la distanza è d. Possiamo pure disegnare le due frecce della velocità, ma bisogna ricordarsi che esse agiscono contemporaneamente: la volpe è sempre diretta verso il coniglio che, a sua volta, è sempre diretto in una direzione che è piegata di α rispetto a quella istantanea volpe-coniglio.

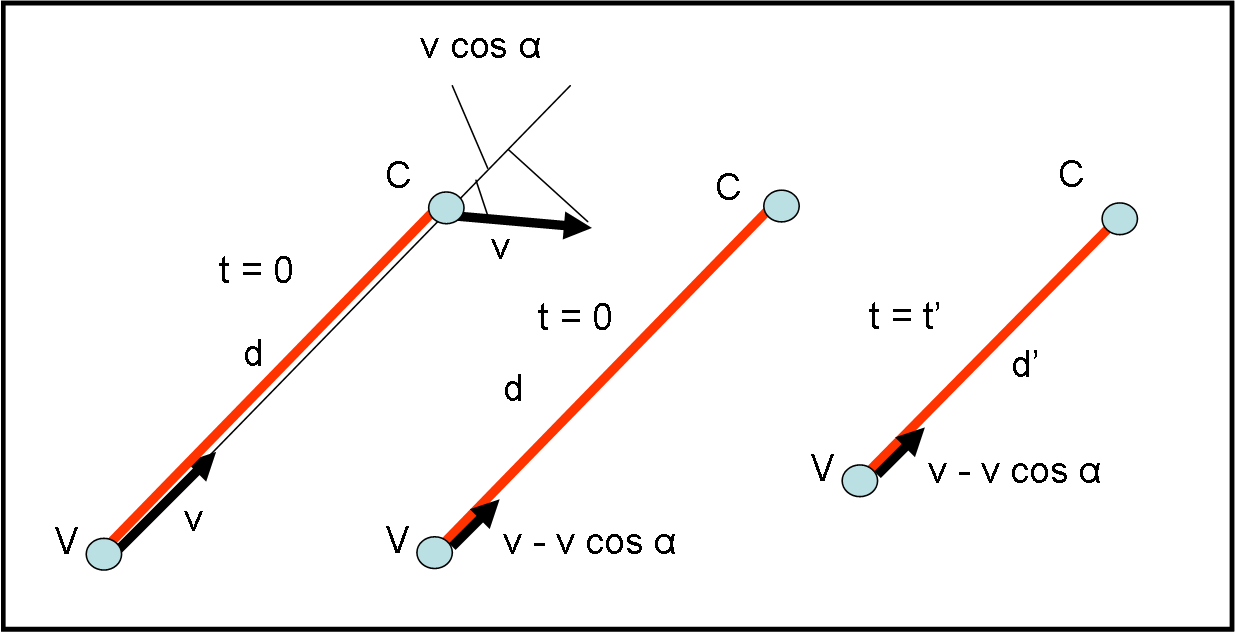
Tuttavia, qualsiasi suo tentativo di piegare viene immediatamente annullato dalla volpe per mantenere sempre una direzione rettilinea che congiunga le loro posizioni in un qualsiasi tempo t. Tutto ciò vuole solo dire che in ogni istante il sistema volpe-coniglio deve stare su una retta, ossia in un sistema che appare come un segmento rettilineo.

Dato che ci interessa  il QUANDO, possiamo trascurare la direzione di questo segmento e lavorare solo sulla riduzione della sua lunghezza fino al valore zero. E’ un sistema in movimento continuo, in cui noi ci sistemiamo stabilmente, come in un satellite che gira attorno alla Terra. Noi ci consideriamo fermi e vediamo solo i movimenti relativi tra volpe e coniglio nel sistema di riferimento (siamo in una navicella orbitante, all’interno della quale si svolge un inseguimento tra due animali muniti di una velocità propria… non tiriamo, però, in ballo la forza di Coriolis!). In altre parole, ancora, il sistema volpe-coniglio è un sistema rigido, come se i due animali fossero uniti da una sbarra di ferro, ma la cui lunghezza continua  a diminuire.

Nella parte centrale della Fig. 1 disegniamo quello che avviene veramente al tempo zero e in qualsiasi altro istante. La componente della velocità ortogonale alla direzione istantanea sposta solo il sistema di riferimento, ma non cambia la distanza relativa. Quella che conta è la velocità del coniglio nella direzione volpe-coniglio, dato che quello è il sistema di riferimento istantaneo. La componente della velocità nella direzione istantanea è data da v cos α. Nel sistema rettilineo va allora calcolata la velocità relativa della volpe rispetto al coniglio ed essa è data da:

v_REL = v – v cosα = v(1 – cosα)

A questo punto il problema è di una semplicità estrema, sapendo che

v_REL = Δd/Δt

Nella parte destra della figura precedente, vi è la situazione in un qualsiasi istante t’, nel quale si può scrivere:

d’ = d - v_REL (t’- 0)    (la distanza diminuisce col tempo)

Sostituendo il valore della v_REL, si ottiene:

d’ = d - v(1 – cos α) (t’- 0)

Basta imporre d’ = 0 (volpe che acchiappa il coniglio) e si ottiene il tempo t_FIN, ossia quello in cui la volpe raggiunge il coniglio:

0 – d = - v(1 – cos α) t_FIN

t_FIN =  d/v(1 – cos α)

Qualche risultato numerico?

v = 1 m/sec

d = 10 m

α = 90°           t_FIN = 10 sec

α = 60°           t_FIN = 20 sec

α = 30°           t_FIN = 75 sec

α = 30°           t_FIN = ∞             (la velocità relativa è uguale a zero e la distanza rimane invariata)

DOVE

Per risolvere il problema graficamente conviene capire bene le posizioni relative di volpe e coniglio, per varie posizioni nel piano della figura (a parità di distanza d e di angolo α).

Prendiamo la volpe V e il coniglio C iniziali e sistemiamoli dove vogliamo, come rappresentato in Fig. 2. Immaginiamo, adesso che il coniglio sia diventato una volpe che insegue un alto coniglio alla stessa distanza e con lo stesso angolo di “fuga”. E poi ancora e ancora. La nostra linea spezzata  di lato d continua girare, a scatti di α, e tutti suoi punti volpe e coniglio descrivono una circonferenza di centro C.

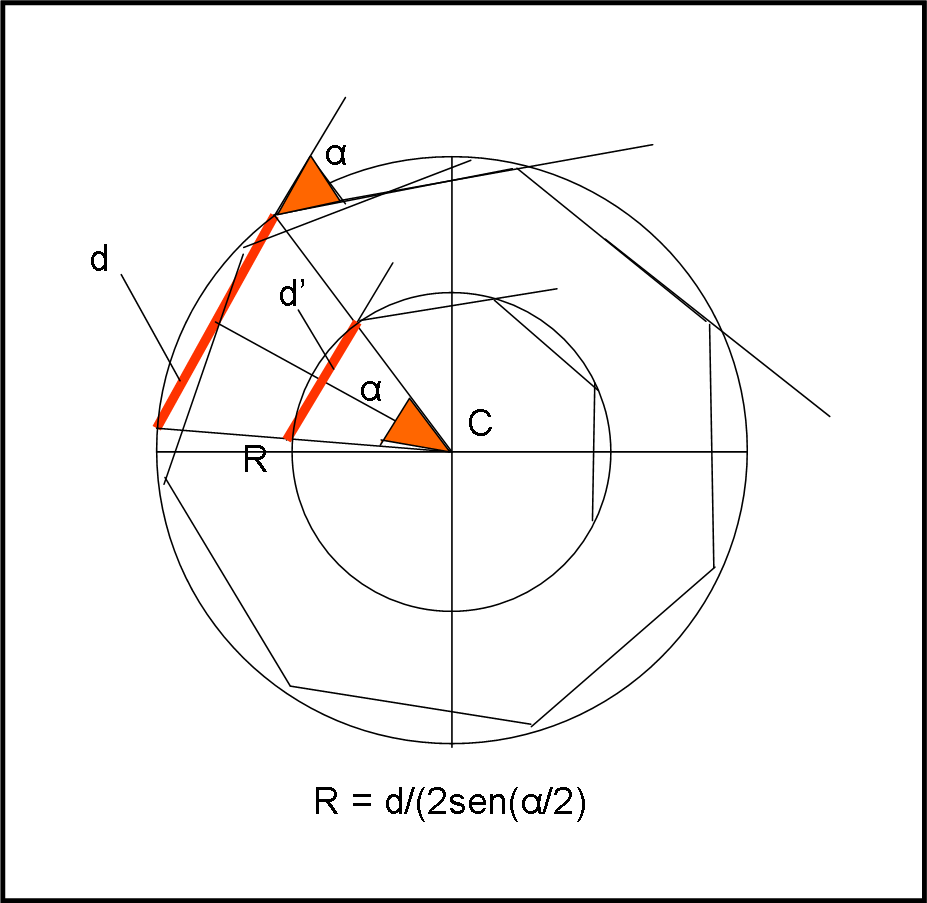
Questo avviene per una d costante. I triangoli formati dalle posizioni di volpe e coniglio in un certo istante e il centro del cerchio sono ovviamente isosceli e il loro angolo al centro è proprio α (si dimostra facilmente… provate… magari aiutati dalla Fig. 3).

Immaginiamo adesso di diminuire la distanza d e di rifare lo stesso gioco, mantenendo fisso l’angolo α. Troveremo nuovamente un cerchio che ha lo stesso centro di quello precedente e i soliti triangoli isosceli, ma il lato sulla circonferenza è ora d’ < d.

Cosa succede alla nostra volpe e al nostro coniglio iniziali? Essi fanno proprio ruotare di α la loro congiungente (ricordiamoci che essa deve sempre rimanere rettilinea!) e seguirebbero il cerchio, ma la velocità relativa ci dice che deve diminuire la distanza d. Ciò vuol dire che non solo ruota la loro congiungente, ma si sposta verso valori di d sempre minori. In poche parole, la congiungente spiraleggia verso il centro della circonferenza, come rappresentato “rozzamente” dalle traiettorie verdi della Fig. 4. Ricordiamoci anche  che il coniglio e la volpe hanno dimensioni finite e non sono punti senza dimensioni...

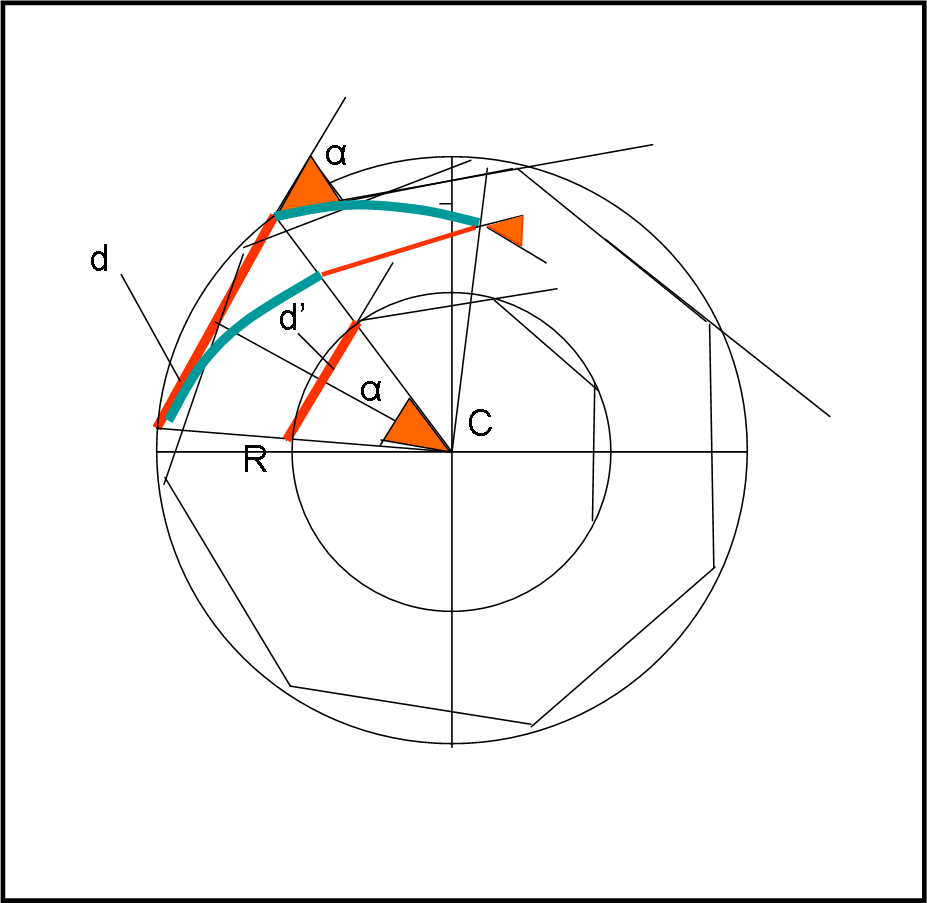
Vi è una a fine a tutto ciò. Sicuramente sì, dato che sappiamo esattamente quando d diventa zero. Ma se d diventa zero il cerchio relativo si riduce al punto centrale C. In altre parole, volpe e coniglio si devono sempre incontrare nel punto C.

Non è certo difficile calcolare la posizione di C rispetto alla posizione della volpe iniziale (o del coniglio): non è altro che il raggio R del cerchio!

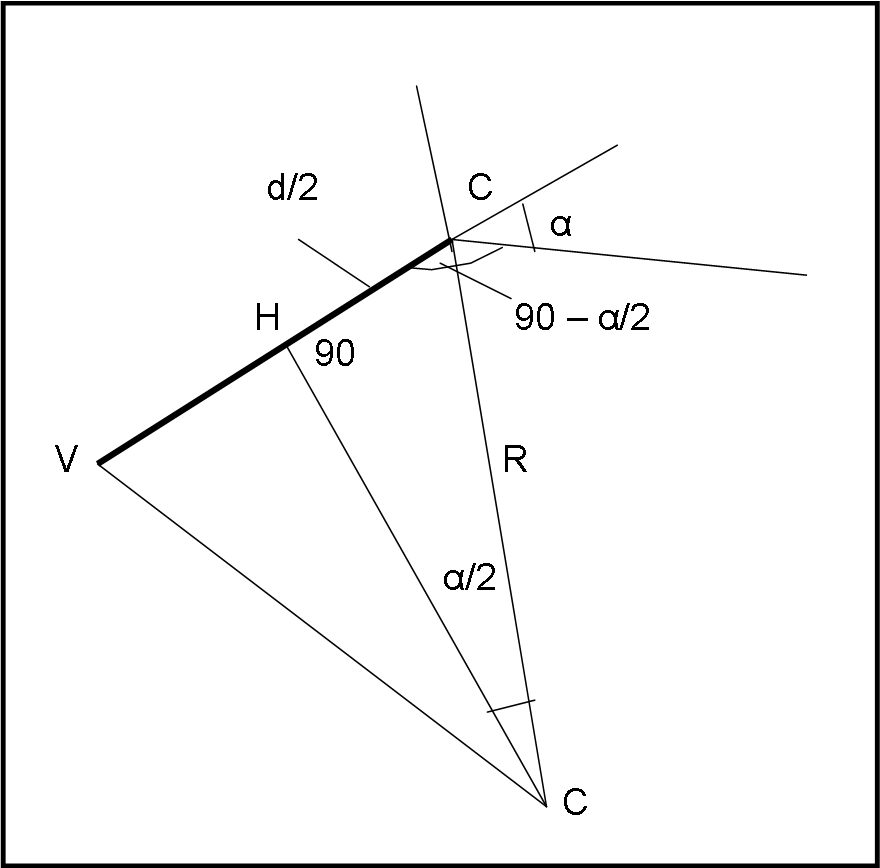
Esso si può scrivere facilmente (dal triangolo VHC) come:

R = d/(2 sen(α/2))

Se α = 0, R, ovviamente, diventa infinito, dato che la velocità relativa è nulla e il cerchio diventa una retta.

Se α = 90,  R = 0.7 d. Il triangolo è rettangolo in C, come mostrato nella Fig. 5, fornitami gentilmente da Arturo e che rappresenta l’intera caccia.

Se α = 180, R =d/2.  Il coniglio va incontro alla volpe con la sua stessa velocità e si incontrano a metà strada senza nessuna rotazione… un coniglio che ha preferito sacrificarsi subito, piuttosto che girare invano…

Chi, poi, vuole divertirsi con le spirali può andare QUI, QUI e QUI. Infine, come già detto, si potrebbe risolvere il problema descrivendo analiticamente il moto della volpe (o del coniglio) legati sempre in modo indissolubile. La variazione di direzione della velocità di una è legata a quella dell’altro (in particolare è importante la componente ortogonale della velocità del coniglio, ossia quella che fa spostare la coppia). Direi che non ce n’è bisogno, avendo trovato una soluzione più che logica e comprensibile. Chi volesse cimentarsi lo faccia pure, ma l’importante é che invii (a me direttamente o nei commenti) una soluzione rigorosa, comprensibile e completa. Soluzioni parziali, confuse e non spiegate chiaramente, saranno “cancellate”, per non creare inutile confusione… Ricordiamoci che il nostro è un Circolo aperto a tutti, ma NON è un "forum".

Mi hanno detto, in gran segreto, che la volpe in oggetto è una volpe vegetariana. La sua caccia è solo un modo per passare il tempo e per scaldarsi i muscoli. Il tutto finisce con un bello spavento per il coniglio e una sana risata liberatoria dei due animali.

il QUIZ lo trovate QUI