Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Esiste la forza centrifuga? Se io rispondessi di no, qualcuno potrebbe dire che la Luna sta cadendo sulla Terra. Troppo spesso, infatti, si sente dire che la Luna non cade perché la forza centrifuga si oppone a quella centripeta. Purtroppo, c’è molta confusione a riguardo. Non ci resta che utilizzare la Luna per risolvere il problema. In questo articolo si ripassano velocemente i principi della dinamica e non solo. E’, quindi, estremamente sintetico. Ogni frase (anche se ripetuta, come mio solito) va compresa appieno perché definisce, spesso, concetti fondamentali per la comprensione della meccanica classica.

Introduzione

La forza centrifuga ha messo in crisi molti professori e gli studenti ne sono stati, ovviamente, influenzati. Non parliamo, poi, di quello che si legge nella rete… Direi che è giunta l’ora di fare chiarezza una volta per tutte.

Posso già anticipare che la confusione nasce da un’errata applicazione del terzo principio della dinamica: ad ogni azione corrisponde una reazione uguale e contraria.

Inoltre, non si pensa mai abbastanza al sistema di riferimento in cui si descrive il moto. Ciò che sembra perfetto e stabile in uno è invece “disturbato” e anomalo in un altro.

Per comprendere questo problema basterebbe pensare alla relatività, ma non a quella di Einstein, bensì a quella perfettamente descritta da Galileo Galilei. Se un sistema di riferimento si muove rispetto a un altro, di moto rettilineo uniforme, le leggi della meccanica possono essere spiegate esattamente nello stesso modo in entrambi i sistemi. Ciò vuole dire che non posso assolutamente capire se un osservatore è fermo o è in moto rettilineo uniforme.

Se, però, uno dei due sistemi non si muove di moto rettilineo uniforme rispetto a un altro, le cose cambiano. Dato che il fenomeno fisico che sta avvenendo non può essere diverso nei due casi, esso deve venire spiegato in modo diverso se riferito a uno o all’altro dei due sistemi. La spiegazione è relativa al sistemo di riferimento. Spero di avervi fatto venire l’acquolina in bocca… e allora iniziamo il nostro “giallo”.

Il movimento: una storia di malavita, di guardie del corpo, di sicari e di mandanti

Un breve antefatto è necessario per arrivare al problema di fondo. Il primo principio della dinamica dice che ogni corpo tende allo stato di quiete o di moto rettilineo uniforme se nessuna forza ESTERNA viene a disturbarlo. Esso è anche chiamato principio d’inerzia, in quanto implica che un corpo è soggetto a una specie di “azione” d’inerzia che lo obbliga o -ancora meglio- lo aiuta a mantenere un moto rettilineo e uniforme. Uniforme vuol dire “a velocità costante”, per cui è compreso anche il caso di quiete assoluta, in cui la velocità vale zero.

Sappiamo, però, molto bene che non vi è niente di veramente fermo nell’Universo e, quindi, che qualsiasi corpo, che non sia soggetto a forze agenti su di esso, resta in balia dell’inerzia e si muove a velocità costante. In realtà, l’inerzia non è una vera forza, ma una proprietà della materia e viene normalmente quantificata con la massa. Essa ha il compito di opporsi a qualsiasi azione di disturbo e difendere la tranquillità del corpo. Possiamo immaginarci l’inerzia come una vera guardia del … corpo, che non si nota quando tutto va bene, ma che entra in azione in caso di pericolo. Reagisce in modo simile a una forza solo e soltanto quando il corpo è soggetto a un’altra forza. Non agisce assolutamente se il corpo è in movimento rettilineo con velocità costante. Il nostro “personaggio” vive una vita perfetta e regolare grazie alla sua inerzia.

Tutti i sistemi di riferimento che permettono di descrivere questo movimento, per un corpo libero da forze esterne, sono detti inerziali. E’ facile intuire che i sistemi di riferimento inerziali sono tutti quelli che si muovono uno rispetto all’altro di moto rettilineo uniforme. In altre parole, in un sistema di riferimento inerziale qualsiasi, il corpo, soggetto solo alla sua inerzia, si vede sempre muovere di moto rettilineo e uniforme, ossia segue il primo principio della dinamica. Cambia solo la velocità, che rimane però costante.

E’ facile intuire che è sempre possibile sceglierne uno rispetto al quale il corpo risulti immobile. Ciò che si muove di moto rettilineo uniforme in un sistema, può essere considerato fermo in un altro. Nessun corpo può rendersi conto se è in movimento o è fermo, dato che le leggi della meccanica rimangono perfettamente uguali. Questa constatazione, che chiunque può provare da solo, è la base della relatività galileiana. Se versate dell’acqua in un bicchiere ci riuscite sia se siete fermi in una stazione, sia se siete sopra un treno che viaggia velocissimo ma con moto rettilineo uniforme (nessuna brusca frenata o accelerazione e nemmeno una curva).

Ho detto forse cose ovvie, ma fondamentali per tutta la fisica da Galileo in poi. La relatività galileiana dice praticamente che le leggi della meccanica rimangono immutate in qualsiasi sistema inerziale o -se preferite- possono essere descritte in modo perfettamente identico. E’ lo stesso postulato usato da Einstein nella sua teoria della relatività. Egli accetta completamente il postulato di Galileo e ne aggiunge solo un altro che dice che la velocità della luce nel vuoto rimane sempre la stessa in qualsiasi sistema di riferimento. Una sola frase in più e tutto è stato cambiato e stravolto. Tuttavia, questa semplice verità ci deve far comprendere che il valore e i risultati della meccanica classica rimangono invariati se non ci avviciniamo a fenomeni che prevedono velocità simili a quella della luce.

Prima di procedere, è veramente fondamentale aver capito cosa s’intende per sistema inerziale. Se vi rimane qualche dubbio, fatelo subito presente e cercherò di eliminarlo fin dall’inizio.

La vittima innocente

Un corpo qualsiasi è quindi soggetto a una velocità, il cui valore dipende dal sistema di riferimento inerziale che è stato scelto per descriverlo. Passando da uno ad un altro, le leggi della meccanica devono rimanere le stesse. Scusate se ripeto ancora questo concetto, ma è alla base della “strana” caratteristica della forza centrifuga.

E’ solo e soltanto la velocità che caratterizza il movimento di un corpo. Anche se non ve ne sarebbe bisogno, ricordiamo, infatti, che la velocità è data dallo spostamento del corpo rispetto al tempo. E’, quindi, lei che determina il movimento. Senza di lei non ci sarebbe movimento. Se non intervengono forze esterne, la velocità resta costante. La massa (la guardia del corpo) cerca di aiutare il corpo a mantenerla in questo stato. Un corpo in movimento rettilineo uniforme è un personaggio tranquillo e inoffensivo, sempre che rimanga abbastanza isolato. Possiamo considerarlo come una vittima innocente.

Purtroppo, la massa, per attenta e preparata che sia, non riesce a controbattere azioni di disturbo esterne. Se questo succede, la prima cosa che varia è proprio la velocità del corpo e, come conseguenza, il suo movimento. Una grandezza meravigliosa (ma poco richiamata) che lega perfettamente la velocità e la sua guardia del corpo (massa) è la quantità di moto. Nient’altro che il prodotto tra velocità e massa. Un qualcosa che rimane anch’essa sempre uguale a se stessa fintanto che niente viene a disturbare il corpo in movimento. Una coppia veramente affiatata, dato che la sua costanza impone una legge fisica fondamentale: la conservazione della quantità di moto. Peccato non conoscerla meglio, ma dobbiamo proseguire nel nostro cammino giocoforza molto semplificato e abbreviato.

Vista l’importanza della velocità, conviene, però, definirla per bene, introducendo un vettore che la rappresenti.  Un vettore è caratterizzato da un certo valore numerico (modulo) che ne definisce l’intensità. La lunghezza del vettore rappresenta quantitativamente il modulo. Il vettore ha anche una direzione, che identifica la direzione del moto. Se esso è rettilineo la direzione del vettore è quello della retta lungo cui si svolge il moto. Se, invece, la traiettoria descritta è una curva, la direzione della velocità istantanea è, in ogni punto, la tangente alla curva (ecco perché ho dovuto aspettare la derivata e il suo significato geometrico). L’ultima caratteristica del vettore è il verso che indica se il moto avviene verso valori positivi o negativi, rispetto al sistema di riferimento che si sta utilizzando. Il verso può essere “inglobato” nel modulo, facendogli assumere valori positivi o negativi a seconda del verso del moto.

Da quanto abbiamo detto e da quanto avete già imparato dai primi due capitoli della derivata, possiamo tranquillamente dire che la velocità istantanea del corpo, in un certo punto P, non è altro che la derivata dello spostamento del corpo rispetto al tempo e possiamo scrivere:

v = ds/dt       …. (1)

dove ds e dt sono intervalli piccolissimi che tendono a zero.

Notale che ho scritto v e ds in grassetto, dato che rappresentano vettori, mentre dt è uno scalare, ossia un numero (d’altra parte la direzione del tempo è una e una soltanto e anche il suo verso). La derivata vettoriale contiene tutte le informazioni, ma non è eseguibile matematicamente in modo diretto. Conviene allora separare il modulo ds del vettore ds dalla direzione e scrivere:

v = ds/dt       …. (1bis)

In questo modo ricavo il modulo v della velocità v. Spesso, i vettori sono anche indicati con una freccetta sopra la lettera. Questo comporta problemi nella scrittura del testo e, allora, utilizzo il metodo del “grassetto”. In articoli precedenti non avevo tenuto conto di questa possibilità, dato che non parlavamo di vettori. Adesso, però, starò molto attento e quando vedrete una lettera scritta in grassetto saprete che rappresenta un vettore.

Vale la pena fare una piccola, ma importantissima, riflessione per eliminare possibili confusioni. Se il moto del corpo descrive una curva y = f(x), la derivata f ’(x), calcolata nel punto P occupato dal corpo, identifica il coefficiente angolare della retta tangente al curva. In altre parole, determina la direzione del vettore velocità. La derivata dello spostamento lungo la curva rispetto al tempo determina, invece, il modulo della velocità, ossia quanto è lungo il vettore. Stiamo bene attenti a non confondere le due cose.

Nel caso del moto rettilineo uniforme, la direzione della tangente alla “curva” è la retta stessa, mentre il valore della velocità si determina dalla variazione della distanza (misurata lungo la retta) divisa per l’intervallo di tempo. Essa risulta una costante, ovviamente, ma niente ha, comunque, a che vedere con la traiettoria della retta in cui avviene il moto. La stessa velocità (in modulo), infatti, si può ottenere su qualsiasi retta. Il modulo della velocità resta costante, ma cambia la direzione. Una cosa analoga, anche se leggermente più complicata, si ha per una traiettoria curva.

Riflettete bene su questo punto, perché non deve assolutamente portarvi a confusioni “deleterie”. Riassumendo ancora: la derivata, rispetto al tempo, dello spazio percorso lungo la traiettoria determina il modulo della velocità; la derivata, rispetto a x, della funzione traiettoria espressa come y = f(x), determina il coefficiente angolare della retta (tangente) che ha la direzione della velocità. Mi raccomando… capite bene questa differenza.

Il sicario prezzolato

Sembrerebbe, da quanto detto, che anche su una curva qualsiasi si può avere una velocità di modulo costante. Questo è sicuramente vero, ma non basta per soddisfare il principio d’inerzia che voleva un moto rettilineo e non solo uniforme. Ciò vuol dire che qualsiasi corpo si trovi a descrivere una traiettoria che non sia rettilinea deve sicuramente essere soggetto a un disturbo esterno. I vettori velocità, punto per punto, mantengono -magari- lo stesso modulo, ma cambiano direzione e quindi sono diversi. In modo analogo, anche se il corpo descrive una retta non è detto che accontenti il principio d’inerzia. Infatti, la velocità ha sempre la stessa direzione, ma potrebbe variare il proprio modulo. Il moto sarebbe rettilineo ma non uniforme. Niente da fare, l’inerzia, ossia la massa, non si accontenta di mezzo bicchiere, lo vuole sempre intero!

In un modo o nell’altro, sia che la velocità non rimanga costante in modulo, sia che cambi la direzione, il principio d’inerzia non è verificato e quindi sul corpo DEVE agire qualcosa di fastidioso e pericoloso.

Qual è la grandezza che caratterizza la variazione della velocità istantanea, ossia che impone una variazione al moto rettilineo uniforme? Essa prende il nome di accelerazione istantanea e non è altro che la variazione della velocità rispetto al tempo, nel punto P, ossia è la derivata della velocità rispetto al tempo, calcolata in P. Si può quindi scrivere:

a = dv/dt       …. (2)

Il calcolo del modulo di un’accelerazione è meno semplice del previsto e passa attraverso la scomposizione del vettore lungo due direzioni particolari e perpendicolari tra di loro: una tangenziale (quella che aumenta o diminuisce il modulo della velocità lungo la tangente) e una normale (quella che varia la direzione del moto ed è diretta verso il centro del raggio di curvatura istantaneo). Dato che il nostro problema di fondo è un caso particolare, evitiamo la trattazione completa e le formule relative. Resta, comunque, il fatto che, nel caso più generale possibile, l’accelerazione si fa proprio in due per disturbare il primo principio della dinamica.

Prima di proseguire, ribadiamo un concetto molto importante. L’accelerazione non fa realmente muovere un corpo, ma fa solo variare la velocità. E’ la velocità -e solo la velocità- l’unica che riesce in questo compito (la massa risponde solo a lei… come un cane ben addestrato). Un corpo che cade per terra ha una certa velocità iniziale, magari proprio zero. Tuttavia, essa è soggetta all’accelerazione di gravità (che possiamo considerare una costante vicino alla Terra) e quindi è costretta a variare il proprio modulo in modo crescente (moto rettilineo UNIFORMEMETE accelerato, dato che l’accelerazione è costante). L’accelerazione causa un aumento nella velocità, ma è sempre lei e soltanto lei che dirige il movimento, portandosi dietro la guardia del corpo massa. Anzi, nel caso della caduta dovuta alla gravità, la massa non ha nessuna importanza e non riesce a rispondere “apparentemente” in alcun modo. Subisce e basta. Ho appena enunciato il concetto del tutto “contro intuitivo” della caduta dei gravi: una piuma o una palla di piombo cadono alla stessa velocità. State tranquilli che tra non molto risolveremo anche questo enigma…

Come si determina, nei casi più generali, la direzione dell’accelerazione? Non è cosa facilissima, ma viene in aiuto la regola della somma (e differenza) dei vettori. D’altra parte la relazione (2) indica proprio che l’accelerazione si determina facendo una differenza di vettori velocità (dv). Il fatto di dividere per un numero come dt può solo cambiare il modulo del vettore finale, ma non la sua direzione. Per sommare o sottrarre due vettori si usa la ben nota regola del parallelogramma. Prima di applicarla ricordiamo che il verso di un vettore è dato, in realtà, dal segno del suo modulo: se è positivo va in un certo verso, se è negativo nel verso opposto. Ne segue che per passare da un vettore v a uno –v basta invertire il verso, mantenendo uguale modulo e direzione.  Usiamo la Fig. 1 per definire la regola.

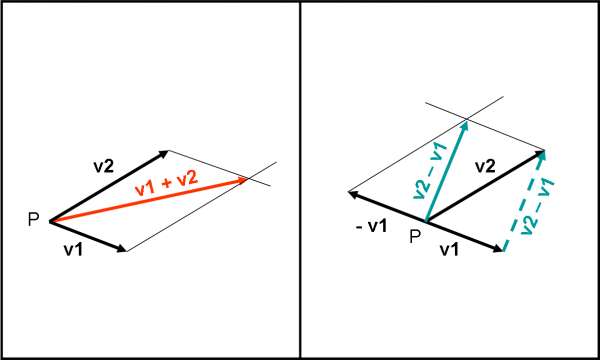
A sinistra, vediamo come si esegue la somma dei due vettori v1 e v2. Essa risulta uguale a una diagonale del parallelogramma; a destra vediamo come si esegue la differenza tra v2 e v1. Notate che in questo secondo caso non ho fatto altro che disegnare il vettore –v1 e sommarlo a v2. Risulta che il vettore differenza è l’altra diagonale del parallelogramma.

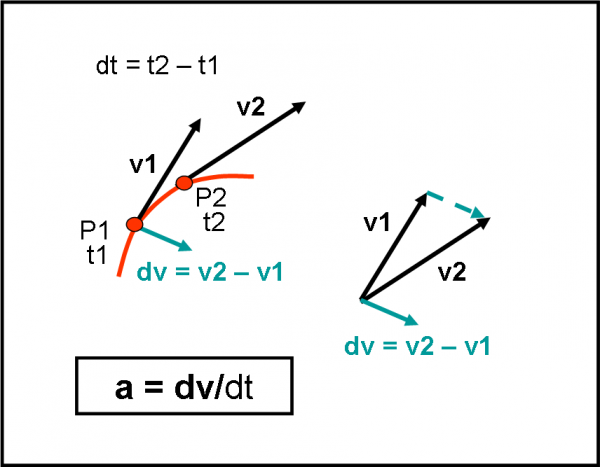
In Fig. 2, applichiamo quanto appena imparato al caso della velocità e dell’accelerazione. Immaginiamo che i punti P1 e P2 siano vicinissimi e che v2 non sia altro che v1 + dv (dv piccolo a piacere). La differenza vettoriale v2 – v1 e proprio uguale a dv e, di conseguenza, è la direzione dell’accelerazione.

A questo punto basta trovare le componenti del vettore lungo due direzioni particolari (quella tangenziale e quella normale) per risolvere completamente la faccenda, come mostrato in Fig. 3. Vi informo che la componente normale si chiama anche accelerazione centripeta e questo nome la dice già lunga… Notiamo, inoltre, che ogni componente ha un suo ben preciso compito. Quella tangenziale modifica solo il modulo della velocità; quella centripeta modifica solo la direzione. Cose già dette, ma troppo importanti per rischiare di perderle per strada…

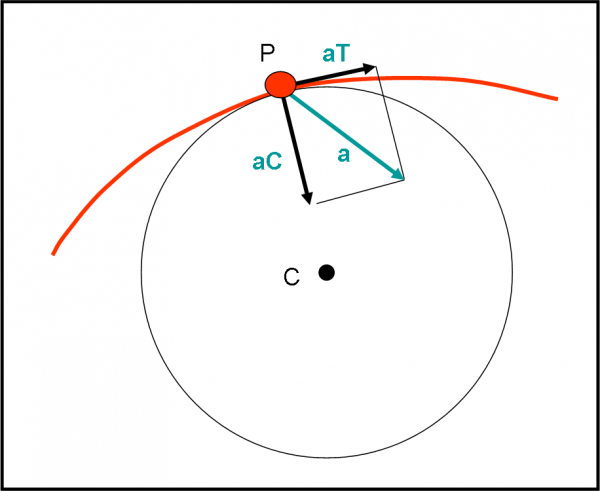
Avrete notato che ho inserito tranquillamente il cerchio osculatore, alla curva traiettoria, nel punto P. Ormai lo conosciamo bene, dato che è lui che ci permette di definire geometricamente la tangente a una curva senza mettere in ballo la derivata. Ovviamente, la componente centripeta è istante per istante diretta verso il suo centro, mentre la componente tangenziale è sempre, istante per istante, normale a questa direzione.

Un moto curvilineo qualsiasi lo possiamo anche immaginare come la traiettoria che ha in ogni suo punto la velocità come tangente, una specie di inviluppo delle velocità. La velocità non cambia per niente? E allora il moto è rettilineo e uniforme. La velocità cambia direzione e modulo? E allora la traiettoria è obbligata a curvare. La velocità cambia solo il modulo? E allora la traiettoria rimane una retta, ma viene percorsa più o meno velocemente. La velocità cambia solo direzione, ma non modulo? E allora la traiettoria è …. No, lo diremo tra poco, dato che è proprio il caso che c’interessa!

Possiamo definire l’accelerazione come una specie di sicario, che colpisce la velocità ma non influisce direttamente sul moto. Non si sporca le mani fino a quel punto. Comunque, essendo solo un sicario, pagato per colpire la vittima, è assai più importante trovare il mandante del crimine che ha infastidito al tal punto il moto rettilineo uniforme inerziale.

Alla ricerca del mandante

Riassumiamo in modo molto intuitivo. Un corpo si muoverebbe sempre secondo un moto rettilineo uniforme, ossia manterrebbe la sua velocità costante con la stessa direzione e verso. Se ci accorgiamo che il vettore velocità cambia, vuol dire che esiste qualcosa che lo disturba (lo devia o l'allunga o l'accorcia). L’unica cosa che può far variare la velocità è il “sicario” accelerazione. In particolare, se il movimento comincia a non essere rettilineo siamo più che sicuri che esiste un’accelerazione, dato che varia la direzione della velocità (è inutile controllare quanto vale il modulo). Se il moto resta rettilineo bisogna invece controllare se varia il modulo. Ribadiamo ancora che la presenza di un’accelerazione, ossia di un sicario, vuole dire, con la massima sicurezza, che esiste un mandante, ossia qualcosa che agisce sul corpo attraverso l’accelerazione. Il mandante prende nome di forza esterna. Come può agire il corpo per ribellarsi a questa imposizione esterna? L’unica sua arma è la massa (inerziale), ossia quel qualcosa che cerca di ridurre gli effetti del crimine. A parità di mandante, più la massa è grande è più è debole l’azione del sicario accelerazione. Con l’ultima frase abbiamo introdotto anche il secondo principio della dinamica… Torneremo, però, su quest’ultimo concetto, dato che, a volte, la massa gioca di … nascosto.

Prima di andare avanti, fatemi riassumere un concetto di massima, a volte, non viene completamente digerito: l’inerzia di un corpo. Abbiamo detto che possiamo considerare la massa come il segno più indicativo di questa caratteristica di ogni oggetto celeste (e non solo), ma il concetto ha una valenza estremamente generale e fondamentale. La richiamo ancora: ogni corpo tende a muoversi di moto rettilineo uniforme se nessun disturbo esterno lo viene a perturbare. In altre parole: ogni corpo cerca in tutti i modi di mantenere questo stato di PIGRIZIA, ossia di inerzia. Qualsiasi cosa si cerchi di fare a un corpo, vuol dire lottare contro la sua inerzia. Anche se alla fine cede e si adegua, la sua inerzia deve entrare in gioco. Non dimentichiamolo mai!

Una sfida all’ultimo sangue

Stavamo cercando il mandante del sicario accelerazione, l’unico capace di variare quella velocità costante che permetterebbe al corpo di accontentare la sua inerzia. Non è difficile risalire al mandante, una volta che conosciamo il sicario (almeno nella fisica). Basta fare uscire allo scoperto i due contendenti principali: la massa del corpo (l’inerzia) che tende a ribellarsi ai disturbi esterni e il mandante che cerca, invece, di andare contro la pigrizia del corpo. E’ una specie di braccio di ferro o di duello da Far West. La massa affronta il mandante e il duello ha inizio. Purtroppo, sappiamo già chi è il vincitore, dato che quasi tutti i corpi celesti non sono in moto rettilineo uniforme. Il mandante vince sempre, ma la massa riesce a limitare i danni. Una vittoria più o meno eclatante che dipende da quanto sia resistente la massa. Non è difficile avere un’idea della sfida: basta fare il rapporto tra mandante e massa. Fatemi chiamare il mandante forza e indicarlo con F. La sfida si può rappresentare quindi come:

F/m

A cosa è uguale questo rapporto (occhio che F è un vettore, dato che ha modulo, direzione e verso così come il suo sicario)? Beh, deve essere qualcosa che indichi chiaramente quanto la vittoria della forza sia netta e decisiva. Vi faccio un esempio banalissimo che ci tornerà presto utile. La Terra, intesa come pianeta, cerca di disturbare il Sole e fargli cambiare velocità (che possiamo immaginare, in prima approssimazione, come uniforme e diretta sempre lungo una retta). Lo scontro è tra la forza che la Terra esercita sul Sole e la massa del Sole. Anche in questo caso, la vittoria della Terra é sicura (come al solito), ma le costa molto cara e, praticamente, nessuno se ne accorge. Se invece  lascio libero un bicchiere  davanti a me, la battaglia avviene tra la forza esercitata dalla Terra sul bicchiere e la massa del bicchiere. Sapete tutti la conclusione di una sfida davvero impari. La vittoria è così netta che il bicchiere va in mille pezzi sul pavimento. Ci torneremo presto…

Il rapporto potrebbe quindi essere qualcosa di estremamente piccolo, ma anche di estremamente grande. Un lieve schiaffetto o un pugno massacrante. Che cosa esce fuori dallo scontro all’ultimo sangue? Beh… solo e soltanto il sicario che ha via libera di agire sulla povera velocità. La massa ha fatto il possibile, limitando i danni, ma poi deve accettare la sconfitta con grande cavalleria e umiltà. Ha vinto il più forte e il sicario è libero di andare a compiere la sua azione. La “violenza” del sicario è proprio ciò che esce fuori dalla sfida. Possiamo, perciò scrivere:

F/m = a

Potremmo anche scriverla così:

m = F/a

Il significato sarebbe: la massa indica quanto la forza del mandante è costretta a ridurre l’azione che il suo sicario può compiere sulla vittima. Più la massa è grande, più piccola è l’azione del sicario accelerazione, a parità di mandante. Potremmo anche dare un’altra definizione: se il mandante aumenta la propria forza verso un corpo di massa m, la sua accelerazione deve aumentare ma solo in modo che il loro rapporto, ossia la massa m, rimanga costante. In altre parole, per permettere al sicario accelerazione di aumentare la sua violenza sulla vittima deve anche aumentare la forza che comanda il sicario. La massa regola questo rapporto che non può cambiare, dato che essa è sempre la stessa, per un certo corpo.

Il secondo principio della dinamica

Potremmo scrivere un libro sul modo di interpretare il secondo principio della dinamica. Basta, però, con gli scherzi e scriviamo il principio nella sua forma più nota:

F = ma

Essa ci dice che l’accelerazione che agisce su un corpo è direttamente proporzionale alla forza che l’ha generata ed è inversamente proporzionale alla massa del corpo. Ben poco da aggiungere: Newton era proprio un GENIO, oltre che un detective fantastico. E’ riuscito con una banale formuletta a legare sicario e mandante, solo conoscendo l’inerzia della vittima.

Una vendetta cosmica

Non ci rimane che introdurre anche il terzo principio della dinamica, ossia il principio della … vendetta. Passatemi questa parola anche se siamo in un ambiente che non segue le squallide reazioni umane. State bene attenti al suo enunciato, perché può causare, a volte, confusione o false interpretazioni. Ecco, perché ho usato la parola “vendetta”. Se un corpo A agisce su un altro corpo B attraverso una forza F, il corpo B reagisce agendo sul corpo A con una forza uguale e contraria. Molta attenzione a chi agisce e dove agisce. Se un corpo A agisce su B, il corpo B deve agire su A. La forza è uguale e contraria, ma chi la subisce non è lo stesso corpo. Questa precisazione sarà utilissima nello spiegare la forza centrifuga.

Bene, abbiamo concluso la nostra … premessa. Se andavo avanti così avrei descritto tutta la meccanica classica. Meglio che mi fermi e torni a ... "bomba".

Sezioniamo il sicario

Tuttavia, non mi sento ancora tranquillo e in pace con me stesso. Avevo promesso di utilizzare le derivate per risolvere il problema dell’accelerazione. Sarebbe comodo girarci intorno come avevo fatto nella "Fisica addormentata nel Bosco". Però, una promessa è una promessa. Allora, facciamo così: utilizzerò entrambi i metodi, quello più avanzato e professionale e quello approssimato e -forse- più intuitivo. In qualche modo, tutti avranno in mano la soluzione.

Riassumiamo, ancora una volta, la situazione a cui siamo arrivati. Un corpo celeste tende a mantenere per sempre il suo stato di moto rettilineo e uniforme.

Appena subentra un'azione di disturbo, la massa (ossia l’inerzia del corpo a mantenere il suo moto rettilineo e uniforme) sfida a singolar tenzone la forza (il mandante) in modo da limitare l’azione violenta operata dal sicario (accelerazione). Tuttavia, la massa può solo limitare i danni ed è costretta ad accettare il cambiamento della situazione. Il modo più sicuro per capire se un corpo ha subito l’azione di un mandante è la variazione della sua velocità e, in particolare, della sua traiettoria. Se capita quest’ultima situazione siamo certi che sta agendo un’accelerazione. Se il moto continua a essere rettilineo bisogna controllare se la velocità aumenta o diminuisce il proprio modulo. Nel caso di una traiettoria curva abbiamo sicuramente un’accelerazione centripeta, normale alla tangente alla traiettoria nel punto P; nel caso che il moto resti rettilineo, ma non uniforme, abbiamo soltanto un’accelerazione tangenziale. Il caso più generale è ovviamente quello in cui cambia sia il modulo che la direzione della velocità, per effetto del sicario accelerazione.

Data un certa traiettoria curvilinea e una certa velocità, vogliamo calcolare l’accelerazione che subisce il corpo nel punto P. Abbiamo già descritto la situazione, ma adesso vogliamo eseguire il calcolo matematico. Vi sono due modi. Uno che sfrutta le derivate e uno che, sebbene approssimato, conduce allo stesso risultato. Li descrivo tutti e due, ricordando che il secondo è quello descritto nella "Fisica addormentata nel Bosco". Chi non se la sente può saltare la parte che segue fino al prossimo paragrafo.

Facciamo un ulteriore passo avanti. Abbiamo visto che un vettore ha dentro di sé tre caratteristiche: il modulo, la direzione e il verso. In particolare, il modulo è un numero, vincolato, però, al vettore. Ne consegue che scrivere v è cosa diversa  dallo scrivere v. Su v posso eseguire calcoli matematici semplici, su v è più complicato.

Posso, però, utilizzare un piccolo trucco. Introdurre un vettore unitario, ossia un vettore che abbia modulo unitario (in relazione all’unità di misura usata) e moltiplicarlo per il modulo. Questo vettore unitario lo chiamo versore. Ho creato una specie di “chiocciola” che si porta dietro un “guscio”. La chiocciola è il versore che può girare e cambiare verso, il modulo è il guscio che viene trascinato senza poter agire direttamente. Chiamiamo u il versore. Posso allora scrivere che la velocità v è data da:

v = vu

Sono riuscito a separare il modulo dal versore, in modo da poterli trattare separatamente. Tuttavia, la velocità (o un vettore, in generale) non perde la sua identità.

Consideriamo la Fig. 4, in cui abbiamo una traiettoria curvilinea qualsiasi. Ovviamente, guardiamo la situazione da un sistema di riferimento inerziale, ossia tale che potrei sempre cambiarlo spostandolo di moto rettilineo uniforme. Un sistema, in particolare, che NON SUBISCE accelerazioni di sorta da nessun mandante inopportuno. Ciò che subisce il corpo P è visto nello stesso modo in uno qualsiasi di questi sistemi. Ricordiamolo sempre, mi raccomando!

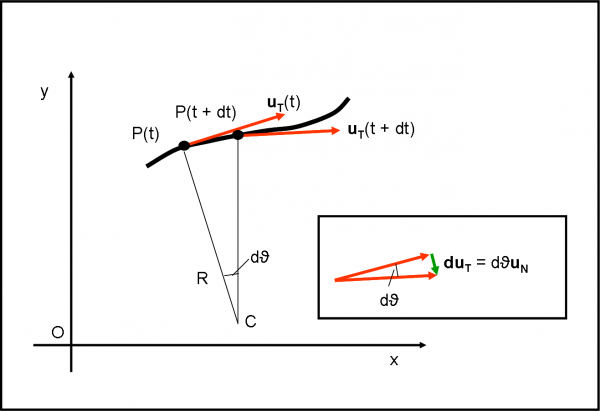
Il punto P(t) si sposta in P(t + dt) di una quantità piccolissima che, misurata sulla curva, è uguale a un certo ds. Ciò lo fa in un intervallo di tempo dt. Un ds talmente piccolo che può essere approssimato perfettamente dal cerchio osculatore in P alla curva. Ne segue che la distanza tra P(t) e P(t + dt) dal centro istantaneo C del cerchio osculatore è sempre uguale a R. Visto dal centro C il trattino ds, corrisponde a una variazione piccolissima dell’angolo ϑ. Posso scrivere tranquillamente che:

ds = R dϑ    …. (1)

Adesso disegniamo qualche vettore. Iniziamo con le velocità in P(t) e P(t+dt). Consideriamo solo il loro versore, dato che per adesso c’interessa solo la variazione di direzione. Il versore velocità in P(t) lo chiamiamo u_T(t) e quello in P(t + dt), u_T(t + dt). Sono, ovviamente entrambi funzione del tempo, hanno lo stesso modulo unitario, mentre l’indice T indica solo che essi devono essere diretti lungo la tangente alla curva. L’angolo dϑ, definito prima, è esattamente lo stesso formato tra le direzioni di u_T(t) e u_T(t + dt), dato che sono entrambe perpendicolari al raggio R.

Definito u_T posso immediatamente definire u_N, ossia il versore diretto verso il centro C che deve essere, per definizione, perpendicolare a u_T. Nel quadratino a destra eseguo la solita differenza di vettori, anzi di versori. I due versori che considero non sono altro che quelli relativi alle due velocità in P(t) e P(t + dt), che, come detto, formano tra di loro un angolo dϑ. Posso quindi scrivere senza problemi  (ricordando la (1)):

du_T= (dϑ ·1)u_N     (il modulo del versore u_T è uguale a 1)

Dovremmo avere tutti i dati per passare alla vera velocità e all’accelerazione che è stata in grado di trasformarla da quella che era in P(t) a quella che è adesso in P(t + dt). Come avete visto, finora non abbiamo parlato di moduli, ma abbiamo solo lavorato con versori, ossia solo con direzione e verso delle velocità.  Torniamo, quindi alla relazione:

v = v u_T   …. (2)

Ho scritto u_T perché so di sicuro che la velocità deve avere la direzione del versore tangente. Che cos’è l’accelerazione? Ormai lo sappiamo bene: essa si calcola facendo la derivata della velocità rispetto al tempo. Non ci resta, allora che fare la derivata della (2) rispetto al tempo. Compaiono dei vettori e degli scalari? Poco importa, basta ricordarsi che la derivata di un vettore rimane un vettore così come la derivata di uno scalare rimane uno scalare. Dopo tanta fatica, ecco che finalmente capite perché ho aspettato di descrivere la derivata di un prodotto. Infatti, devo eseguire:

a = dv/dt = d(v u_T)dt

Ossia scrivere la derivata di un prodotto (v u_T). Ormai sappiamo come fare:

a = d(v u_T)/dt = (dv/dt) u_T + v (du_T/dt)    …. (3)

(ricordate? y’ =  f ’(x)g(x) + f(x) g’(x)).

Avete sicuramente notato che la velocità v compare solo come modulo. Alla direzione e al verso ci pensa il versore.

La relazione di prima può essere elaborata, dopo tutto il lavoro che abbiamo svolto poco fa.

Abbiamo, infatti trovato che:

du_T= dϑ u_N  

e quindi anche:

du_T/dt= (dϑ/dt) u_N

Sostituendo nella (3):

a = (dv/dt) u_T + v (dϑ/dt) u_N

Avevamo, però, anche ricavato che:

ds = R dϑ,   ossia:    dϑ = ds/R

Sostituisco ancora e ottengo:

a = (dv/dt) u_T + (v/R)(ds/dt) u_N

Cos'è, però, ds/dt ? Lo sappiamo bene, fin dalla volta scorsa: non è altri che la velocità (in modulo). Infatti: v = ds/dt.

Ultima sostituzione e otteniamo infine la relazione fondamentale e generale per l’accelerazione agente su un corpo che si muove di moto curvilineo qualsiasi:

a = (dv/dt) u_T + (v²/R) u_N

Essa ci dice proprio che l’accelerazione si può scomporre lungo due direzioni perpendicolari tra di loro (tangenziale e normale o centripeta). La componente lungo la tangente (indicata dal versore u_T) ha modulo dv/dt, ossia proprio la variazione del modulo della velocità (possiamo chiamarla accelerazione tangenziale). Questo vuol dire che se la velocità non cambia in modulo passando da P(t) a P(t + dt), questo termine va a ZERO. In altre parole, non esiste accelerazione tangenziale.

La componente lungo la direzione normale alla tangente, ossia verso il centro del cerchio osculatore istantaneo, ha un modulo estremamente importante che vale v²/R. Esso indica l’intensità, dell’accelerazione centripeta. Se il moto è curvilineo questa componente esiste sempre. Ossia, come già detto precedentemente, un moto curvilineo ci assicura che esiste un’accelerazione normale alla tangente alla traiettoria.

Due precisazioni. Abbiamo usato la scrittura dy/dx per indicare la derivata. In questo modo l’abbiamo sempre indicata come un rapporto tra grandezze infinitesime. Il solo scrivere dy/dx, però, non indica solo un rapporto tra segmenti o tratti di curva o di tempo piccolissimi, ma indica già che  queste grandezze stanno tendendo a zero, ossia proprio il concetto di derivata. Tuttavia, la scrittura permette anche di sostituire, ai singoli intervalli piccolissimi, valori corrispondenti in cui appaiano altre grandezze.  Al posto di dϑ abbiamo potuto, ad esempio, scrivere ds/R. Un grande aiuto nel calcolo, pur non variando assolutamente il concetto e il risultato della derivata. In parole matematiche lo scrivere:

a(t) = dv/dt

significa:

a(t) = lim _dt→0 (v(t + dt) – v(t))/dt

La seconda precisazione è un po’ più complessa. Nel calcolo precedente abbiamo fatto la derivata di un versore, ossia di un qualcosa che ha sempre modulo costante e unitario. Alla fine abbiamo trovato che (a parte le costanti numeriche che l’hanno moltiplicato) si è trasformato in un versore normale a quello di partenza. Questo fatto ci permette di concludere che la derivata di un versore è un versore perpendicolare al primo. Potremmo parlare per ore di versori e dimostrare questa conclusione in altri modi, ma direi di non esagerare… non vorrei che la forza centrifuga resti un sogno irraggiungibile.

Aggirare un ostacolo non è sempre dignitoso, ma a volte semplifica la vita

Ammetto che le derivate di vettori non sono un esercizio molto facile, anche perché bisognerebbe prendere dimestichezza con i versori e con le componenti, lungo essi, del modulo. Vi ripropongo, allora, il metodo usato nel libro, anche perché a noi, in fondo, interessa solo il valore finale della accelerazione centripeta. Fate, però attenzione che è valido solo nel caso che il modulo della velocità non vari col tempo.

Consideriamo la Fig. 5, in cui il modulo della velocità resta costante (varia solo la direzione). Il triangolo isoscele PP’C è simile al triangolo formato dalle due velocità in P e P’. La differenza delle velocità e data da dv.

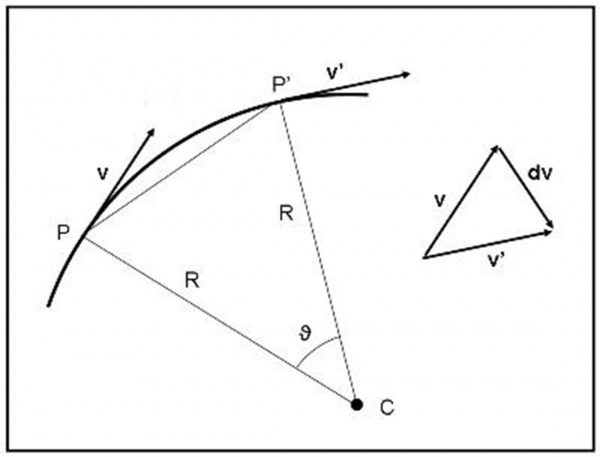
Dai triangoli simili posso scrivere (in modulo):

dv/v = PP’/R

A questo punto possiamo assumere, in prima approssimazione, che PP’ diviso per dt tenda al modulo della velocità v.  Ossia:

PP’ = v dt

E quindi:

dv/v = v dt/R

Attenzione: dv è il modulo della differenza di velocità e non la differenza dei moduli che sarebbe uguale a 0, per definizione di velocità a modulo costante. E’ immediato che:

dv = v² dt/R

Ma dv/dt è il modulo dell’accelerazione centripeta e, concludendo, si ha che:

a_C= v²/R

Il risultato è lo stesso ottenuto precedentemente. Non abbiamo usato vettori e versori, ma solo moduli, ossia scalari. Tuttavia, si sono fatte approssimazioni che diventano trascurabili solo se si fanno tendere a zero certe quantità, il che ci porta nuovamente al concetto di derivata. Teniamo anche presente che questa modo di agire è valido solo se la velocità ha modulo costante.

Dato che è proprio questo il caso che c’interessa, l’importante è che, in un modo o nell’altro, siamo stati capaci di ricavare l’accelerazione centripeta in un punto P.

La determinazione dell’accelerazione centripeta ci permette di entrare, finalmente, nell’argomento che volevamo trattare, ossia nel moto circolare uniforme, proprio quello che ci aiuta a capire se la Luna cade oppure no. Vi invito già a pensare a quello che sarà il problema fondamentale legato alla forza centrifuga. Un moto circolare uniforme non è un moto rettilineo uniforme. Se uso un sistema di riferimento inerziale, la descrizione del fenomeno deve essere diversa rispetto alla descrizione fatta in un sistema di riferimento che segue il moto circolare. Questo è un obbligo per far sì che il fenomeno fisico resti identico.

Direi che l’ho fatta lunga… mi dispiace, ma dovrete aspettare ancora un po’ per toccare con mano la forza centrifuga. Ho preferito, però, essere, come al solito, lungo e ripetitivo per cercare di farvi arrivare al nocciolo della questione in condizioni ottimali. Tra parentesi, vi assicuro che non vi sarà più bisogno di derivate…

Bene, siamo pronti a far cadere la … Luna sulla Terra? Purtroppo, sì e … no. Insomma, mi sono accorto che era meglio affrontare il problema sia arrivando “da fuori” che “da dentro”. Raccontiamo il primo modo.

Una descrizione senza volere sapere il perché

Ancora prima, però, dobbiamo imparare a descrivere un moto a cui sono soggetti moltissimi corpi celesti (la nostra “casa” per prima). Attenzione, però: descriviamo solo il moto senza voler sapere chi o cosa lo causi e perché. Ci limitiamo a fare cinematica, ossia descrizione. Non parliamo ancora di vittime, sicari e mandanti. Facciamo solo una banale descrizione basata sulle definizioni di velocità e accelerazione e sui loro legami con la traiettoria descritta. Lasciamo quindi da parte l’inerzia del corpo e la sua voglia di reagire, di difendersi e di fare vendetta.

Ciò che stiamo guardando dal nostro sistema di riferimento inerziale è solo e soltanto un fenomeno “asettico”, descritto da un punto senza massa. Questo moto è molto simpatico, perché è ripetitivo e continuo e quindi la situazione da studiare è sempre la stessa. Lo possiamo fare molto semplicemente.

Ciò che osserviamo (Fig. 6) è un punto P che si muove attorno a un punto C mantenendo sempre la stessa distanza R. Beh… non ci vuole molto a capire che stiamo guardando un moto circolare. Non solo, però. Ci accorgiamo anche che la velocità del punto è uniforme. Come possiamo renderci conto di questo fatto? Beh, basta notare che l’angolo (o l’arco) descritto dal raggio R (o dal punto P) è sempre lo stesso per intervalli di tempo costanti.

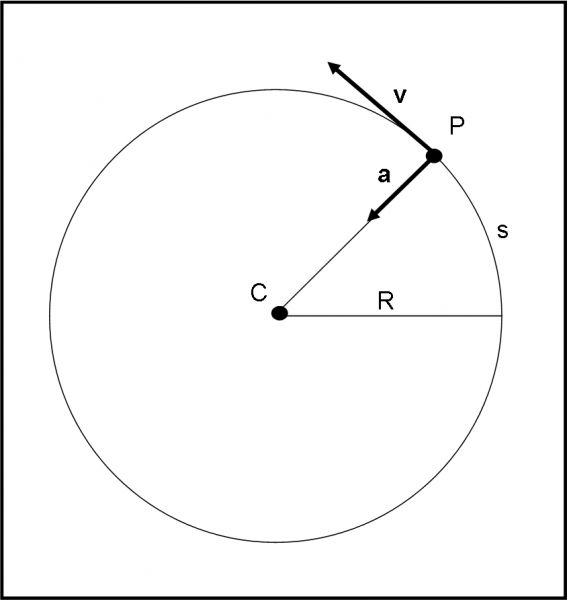
Senza sapere ancora scrivere le formule relative al moto, possiamo già enunciare alcuni dati di fatto che abbiamo imparato a conoscere nei primi due capitoli. La velocità del punto è sempre tangente alla circonferenza. Tuttavia, dato che cambia continuamente direzione deve esistere un’accelerazione centripeta che regoli questo continuo spostamento della direzione. Infine, non deve esistere alcun accelerazione tangenziale dato che il modulo della velocità rimane costante.

Cosa possiamo concludere da queste semplici constatazioni? Che un punto può permettersi di girare in modo indefinito a velocità costante attorno a un altro punto, mantenendo da lui sempre la stessa distanza, solo se esiste in  ogni punto della traiettoria un’accelerazione centripeta, ossia diretta verso il centro del cerchio osculatore, che, però, in questo caso è sempre lo stesso ed è proprio definito, in ogni punto, dal cerchio su cui il punto descrive il moto. Veramente una situazione semplicissima.

Quanto vale la velocità del punto P? Non è certo difficile ricavarla da una semplicissima considerazione. Posso misurare il tempo T che è necessario affinché il punto P compia un giro completo attorno a C. Che percorso descrive il punto P? Beh… è ovvio, la circonferenza, ossia 2πR. Ora basta chiedersi quale tratto ds della circonferenza descrive nell’intervallo di tempo dt, attraverso la proporzione:

2πR : T = ds : dt

Ossia

ds/dt = 2πR/T

Ormai siamo esperti e sappiamo benissimo che scrivere ds/dt vuole dire scrivere il modulo della velocità, costante per definizione, quindi:

v = 2πR/T

A questo punto, non abbiamo nemmeno bisogno di usare triangoli e/o segmenti vari, dato che sappiamo già bene quanto vale l’accelerazione centripeta che fa variare la direzione della velocità punto per punto. L’abbiamo ricavata la volta scorsa in due modi. Essa vale, in modulo:

a_C = v²/R   …. (1)

Dato che la traiettoria è una circonferenza anche l’accelerazione deve essere una costante, come d’altra parte è dimostrato dalla formula precedente che dipende da v (costante) e da R (costante).

Cosa possiamo concludere? Che stiamo guardando un moto estremamente semplice in cui vi è un punto che, per potersi muovere di moto circolare uniforme attorno a un punto C, deve subire costantemente un’accelerazione centripeta che è legata alla velocità v del punto P dalla relazione (1).

Cosa vuol dire tutto ciò? Che, ad esempio, se la velocità aumentasse, dovrebbe aumentare anche l’accelerazione centripeta. O, inversamente, se aumentasse l’accelerazione centripeta dovrebbe aumentare la velocità del punto P. Un perfetto gioco di squadra. Sembra che il  “crimine” nascosto si risolva in una reciproca pacifica convivenza.

Per un osservatore esterno, in un sistema inerziale, la faccenda è di una semplicità incredibile. Basta misurare il periodo di rivoluzione e la distanza tra C e P (costante) è ogni grandezza in gioco è completamente individuata. Attenzione, però, che per poter arrivare a questa conclusione è stato necessario imparare come calcolare l’accelerazione in grado di causare un moto curvilineo.

Purtroppo, questa è una visione molto superficiale, che descrive, ma non si chiede il perché e il come. Non può quindi accorgersi del dramma che si nasconde dietro a una “danza” regolare e senza fine.

Una ragnatela costruita a regola d’arte

Lasciamo quindi da parte la cinematica (ci servirà dopo) che, malgrado sia  un modo apparentemente semplicistico di valutare i fenomeni, è utilissima e fondamentale, e diamo al punto P una sua concretezza fisica. In parole povere, diamogli una massa, ossia un’inerzia tale da farlo muovere di moto rettilineo uniforme rispetto al nostro sistema di riferimento. Il punto di massa m se ne andrebbe per i fatti suoi, ma ecco che cade nella “tela di un ragno”. Parlo di tela di un ragno, ma non deve essere considerata una delle mie solite similitudini “poetiche”. Senza che il nostro corpo di massa m lo sappia, non troppo lontano da lui, vi è un corpo O di massa M ben maggiore, che ha proprio steso la sua rete attorno a lui.

Che tipo di rete è? Una rete “vettoriale”! In particolare, una rete composta da infinite accelerazioni pronte ad agire sul malcapitato che ha la sventura di entrarci dentro. La forza che O esercita si traduce in una rete di sicari in attesa di una vittima.  Che tipo di forza può possedere un corpo di massa M, tale che possa agire anche a distanza, ossia senza nemmeno toccare la vittima? Beh… ha un nome ben conosciuto: gravità. Essa viene definita attraverso una formula che è uno dei capolavori della fisica descritta dall’uomo. Descriviamola a parole e poi attraverso la matematica. Ogni corpo di massa M esercita una forza su un corpo di massa m che è data dal prodotto tra le due masse diviso il quadrato della reciproca distanza.

F = GMm/r²  …. (2)

Ovviamente, per il terzo principio della dinamica, se M esercita una forza su m, anche m deve esercitare una forza uguale contraria su M. La prima agisce su m, la seconda su M. Fate molta attenzione a questa frase, perché verrà utile quando comparirà la forza centrifuga.

Nel nostro caso, però, chi comanda il gioco è M, mentre m subisce. La sua reazione, ossia la sua vendetta, è cosa veramente ridicola… In realtà, la forza è la stessa, ma può fare ben poco su una massa come M. Ricordate cosa abbiamo precedentemente? Vediamo, allora, come è stato predisposta la ragnatela di O.

Innanzitutto, dobbiamo tener conto del secondo principio della dinamica, che abbiamo ricavato abbastanza facilmente. Esso dice:

F= m a   …. (3)

La formula è già stata investigata in lungo e in  largo e sappiamo che può esprimersi, tra l’altro, con la frase: l’accelerazione causata da F è “regolata” da m, ossia dalla pigrizia di P a cambiare il proprio movimento. La F che compare nella (2) e nella (3) è la stessa, ossia la forza del “ragno” O. Basta uguagliarle e ricaviamo immediatamente:

GMm/r² = ma

Semplificando la massa m, si ricava immediatamente l’accelerazione che agisce su di lei, ossia il sicario predisposto da O. Si ha che:

a = GM/r²   …. (4)

La costruzione della ragnatela, composta da tutte le accelerazioni che aspettano m al varco, diventa, allora, cosa banale ed è rappresentata in Fig. 7.

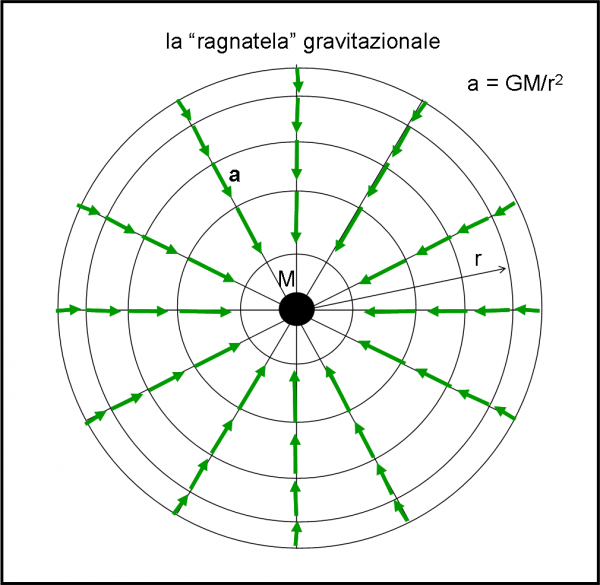
In ogni punto dello spazio attorno al “ragno” O, si può inserire un sicario accelerazione che non aspetta altro che far deviare l’ignaro corpo P. La potenza del sicario dipende solo dalla distanza rispetto al ragno. Più si è lontani dal mandante e meno efficace è l’azione del sicario. Cosa cerca di fare ogni sicario? Solo e soltanto attirare la vittima verso il ragno. L’accelerazione è quindi diretta verso il corpo O. E’ facilissimo disegnare questa ragnatela, che NON dipende da quanto vale la massa m che vi cade dentro e che perde di vigore spostandosi verso l’esterno. A ogni punto si associa un vettore accelerazione a, di modulo (4) e diretto verso O. Esso rappresenta l’azione del sicario, ossia l’operazione di spostarlo verso il centro. La ragnatela prende il nome di campo gravitazionale del corpo O di massa M.

Piuma o macigno per me pari sono

Ribadiamo ancora (è troppo importante) che il valore dell’accelerazione, ossia della capacità di spostare una certo corpo P, di massa m, verso O è INDIPENDENTE dalla massa m. Il che vuole anche dire che qualsiasi corpo capiti nella rete subisce la stessa accelerazione verso O, a parità di distanza da O. Lasciatemi, quindi, enunciare un fatto importantissimo che Galileo Galilei ha cercato di dimostrare in tutti i modi. Se facciamo cadere verso la Terra un macigno di molte tonnellate e una piuma leggerissima, esse sono soggette alla stessa accelerazione e quindi, senza attriti o altre cose del genere, cadono al suolo con la stessa velocità.

Immaginate, infatti, di portare a una certa altezza h sia il macigno che la piuma. Essi hanno velocità ZERO rispetto al suolo perché li teniamo fermi. Poi li lasciamo liberi di subire la forza del ragno O (la Terra). Essendo alla stessa distanza da lui, l’accelerazione, ossia la variazione della loro velocità, è la stessa, indipendentemente dalla massa che hanno. Essi partono con v₀ = 0, al momento t₀ = 0 e quindi, dopo un certo intervallo di tempo, i due corpi acquistano la stessa velocità istantanea v = v₀ + dv = dv, dato che dv è dettato dalla stessa accelerazione (dv/dt = a). I due corpi cadono alla stessa velocità verso il ragno, indipendentemente dalla loro massa. Risultato sicuramente contro intuitivo, ma dimostrabile in modo facilissimo e impeccabile. Se non vi piace… prendetevela con la forza gravitazionale!

Vale la pena chiarire una frase che ho letto spesso in giro e che è fondamentalmente errata. Si dice che la caduta di due gravi  di massa diversa avviene alla stessa velocità, dato che l’accelerazione di gravità è costante (la famosa g). Non è assolutamente vero! Il fatto che g (ossia GM/R²) possa essere considerata costante nelle vicinanze della Terra è un’approssimazione più che plausibile (la distanza dal centro della Terra è praticamente sempre la stessa), ma questa semplificazione fa solo sì che il moto verso il suolo possa considerarsi uniformemente accelerato (ossia ad accelerazione costante), ma non è certo una condizione per ottenere una identica velocità di caduta. Se lasciassimo cadere gli oggetti da un’altezza enormemente più grande, benché l’accelerazione non potrebbe più essere considerata costante, le velocità di caduta dei due corpi di massa diversa sarebbero comunque identiche. E’ bene smentire subito false conclusioni…

Come districarsi nella ragnatela

Torniamo alla ragnatela e vediamo come riesce ad agire su un corpo P che non parte da fermo ma che è -ovviamente- in moto rettilineo uniforme rispetto al nostro sistema inerziale (primo principio della dinamica).

Potremmo scrivere subito le condizioni che permettono al corpo P di seguire perfettamente un moto circolare uniforme attorno a O. Sappiamo, infatti, benissimo di cosa abbiamo bisogno, ricordando la descrizione cinematica. Di solito si fa così e lo farò anch’io, ma prima voglio farvi vedere cosa succede realmente durante l’avvicinamento di P a O. Si capiranno meglio le condizioni favorevoli per ottenere una specie di “stallo”, ossia una parità tra i due corpi in gioco.

Sappiamo che quello di massa minore deve subire la forza di quello più grande (malgrado cerchi di vendicarsi, come vedremo a tempo debito) o -meglio- dei suoi sicari sparsi per lo spazio. Tuttavia, per certi valori della velocità e dell’accelerazione, si potrebbe ottenere una specie di pareggio. Qualcosa di simile a uno stallo nel gioco di scacchi. Magari un giocatore è ridotto al lumicino, mentre l’altro è ancora pieno di pezzi importanti. Sebbene risulti chiara la maggiore “potenza” del secondo, il primo potrebbe trovare una situazione di ripiego, ossia trovare lo stallo. E’ chiaramente in netta inferiorità, ma il suo Re riesce a evitare lo scacco matto e può sopravvivere per sempre, adattandosi alla configurazione raggiunta. La partita, benché “ai punti”, sembrerebbe stravinta dal secondo giocatore, ma DEVE essere, invece,  dichiara “patta”. Non esiste un vincitore ufficiale.

La stessa cosa capita al nostro corpo P. Esso, volente o nolente, subisce l’accelerazione del corpo più massiccio O. Un’accelerazione diretta verso di lui, con lo scopo (non certo misterioso) di far cadere P su O. Tuttavia, malgrado sia in balia di questa accelerazione, la velocità v del corpo P può riuscire ad arrivare a uno stallo. Anzi, se essa fosse sufficientemente alta e diretta nel modo giusto, P potrebbe anche sopravvivere e andarsene per la sua strada, vincendo addirittura la sfida. Una vittoria molto dura, dato che è stato costretto, comunque, a cambiare il suo moto rettilineo uniforme. A noi interessa, soprattutto, la situazione di stallo, ma vale la pena cercare di analizzare anche le altre due (più comuni) soluzioni: quella della fuga e quella della caduta catastrofica.

Vi prego di notare, ancora una volta, che in tutto questo gioco la massa m non compare per niente, dato che la ragnatela non si cura di lei e agisce comunque. Questa è una caratteristica del campo gravitazionale e non certo di tutte le forze della Natura. Ricordiamocelo bene. Tuttavia, non è un risultato veramente strano. In  realtà, la massa m, anche se non si vede, svolge il suo compito, dato che il confronto tra forza gravitazionale e inerzia del corpo continua implacabile. L’accelerazione sicario si è “ridotta” a quella che conosciamo, proprio perché la massa m è scomparsa per dar luogo all’accelerazione di gravità. Anche se non si vede, la massa m esiste e come. Se non avesse massa, il corpo P non subirebbe la gravità di O.

Giochiamo con i vettori

Questo paragrafo può essere saltato da chi vuole andare al sodo e non vuole perdere tempo a cercare di rappresentare il “dramma” che si svolge tra il corpo P e la ragnatela. In altre parole, da chi vuole subito studiare il moto circolare uniforme, ossia la posizione di “stallo”. Chi invece vuole divertirsi con un "filmato" molto grossolano di ciò che capita durante tutto il passaggio del corpo P attraverso la ragnatela di O, alzi le antenne e mi segua!

Immaginiamo un corpo P che viaggia tranquillo lungo la sua traiettoria rettilinea uniforme con una velocità v costante in modulo e direzione. Il corpo O è ancora lontano e non si fa sentire. Tuttavia, posso usare la distanza tra P e O per definire la velocità. Infatti, le distanze tra O e due punti P1 e P2 possono essere considerati dei vettori e la loro differenza (vettoriale) ci fornisce, come al solito, la direzione della velocità. Seguiamo questa prima fase nella Fig. 8.

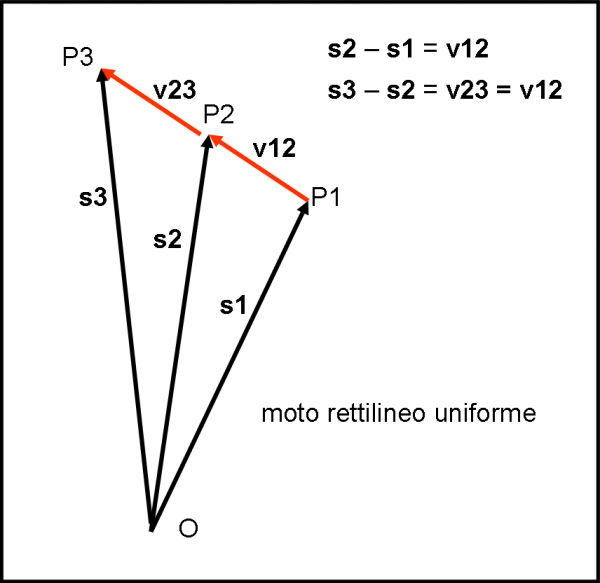
Vale la ovvia relazione:

v12 = ds12/dt = (s2 – s1)/dt

Posso, però, eseguire ancora una semplificazione: prendere dt = 1 (basta scegliere la giusta unità di misura). In questo modo considero lo spostamento dal punto P1 a P2 uguale alla velocità del corpo tra P1 e P2. In altre parole, data la velocità nel tratto P1 - P2, posso disegnare immediatamente la posizione del punto P2. Dato che ripetersi non fa mai male, riscriviamo la relazione che spiega direttamente  la procedura da seguire:

v12 = s2 – s1

O, se preferite:

s2 = s1 + v12

Conoscendo la velocità v12 e la posizione P1 (data da s1), trovo immediatamente la posizione s2 e quindi la posizione P2, attraverso una somma vettoriale.

Come già detto, finché la ragnatela non entra in azione, la semplificazione non crea assolutamente problemi. Dato che la velocità è sempre la stessa, in modulo e direzione, considerare traiettorie rettilinee durante intervalli di tempo, piccoli o grandi che siano, non cambia il risultato. In altre parole, la lunghezza e la direzione dello spostamento del corpo, nell’intervallo  dt = 1, può benissimo essere considerato uguale alla velocità del corpo.

Noi, però, continueremo a usare lo stesso approccio anche quando v comincerà a cambiare, sia in direzione che modulo. Avremo un insieme di tratti rettilinei continui che indicheranno  “approssimativamente” la traiettoria seguita dal corpo P.

Spieghiamo come fare. Il punto P di massa m, entra, finalmente, nella ragnatela. Rappresentiamo il suo limite esterno come un cerchio di raggio R. Prima approssimazione! La ragnatela non comincia a un raggio preciso, ma si estende fino all’infinito, diventando sempre meno attiva. Noi, però, la facciamo entrare in azione in modo improvviso.

Consideriamo la Fig. 9.

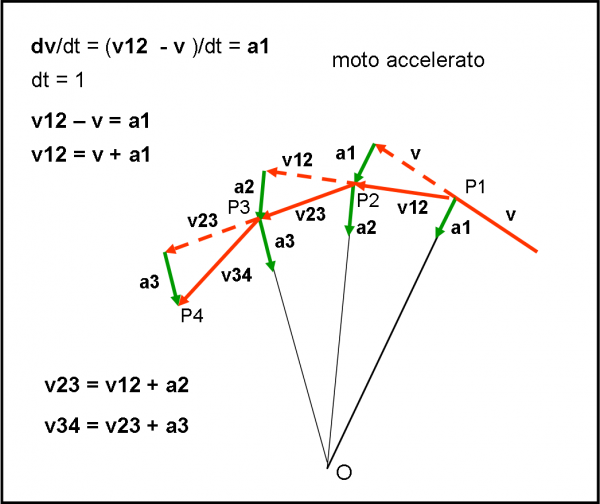
In P1 entra in azione l’accelerazione di gravità a1, che tende ad attirare il corpo P verso O. La velocità v, costante e tranquilla, subisce uno spostamento nel tragitto da P1 a P2 e diventa v12. Questo spostamento è proprio comandato dall’accelerazione subita in P1 che vale:

a1 = dv/dt = (v12 – v)/dt

ma, avendo posto dt = 1, abbiamo anche:

a1 = v12 – v

Conoscendo la v precedente e la a1 (la ragnatela), posso disegnare subito la v12, in direzione, intensità e verso, attraverso la regola del parallelogramma (attenzione: sto sommando o sottraendo dei vettori e non dei moduli!), dato che:

v12 = v + a1

Dato che dt = 1, il tragitto percorso dal corpo P può essere approssimato dalla nuova velocità v12 (come fatto fuori dalla ragnatela) e quindi di determina subito P2.

Occhio, però, che stiamo facendo differenze di vettori e non di moduli di vettori! Il modulo della velocità è uguale al modulo del vettore somma (o differenza) e NON è uguale alla differenza dei moduli dei vettori.

Non è difficile continuare il nostro gioco dinamico. In P2 il corpo subisce una nuova accelerazione  a2 che è maggiore di quella precedente, dato che il corpo si è avvicinato a O: la ragnatela acquista potenza. Come faccio a trovare la nuova velocità v23 e il punto P3? Basta rifare il procedimento di prima, dato che:

v23 = v12 + a2

E via dicendo…

In questo modo  possiamo descrivere la traiettoria del corpo P sotto l’effetto del campo gravitazionale di O, ossia della sua ragnatela. Quello che stiamo eseguendo è comunque solo una specie di gioco, dato che ha un senso compiuto solo finché la velocità resta costante. Quando inizia a variare dovrei considerare dei tratti curvilinei piccolissimi, mentre, invece, continuiamo a usare tratti rettilinei tra i punti raggiunti (prendendoli anche molto grandi). Teniamo quindi ben presente che è un gioco valido in prima approssimazione! Comunque, più si restringe l’intervallo degli spostamenti e più ci si avvicina alla realtà. Nelle figure precedenti ho allungato il vettore accelerazione "a occhio" e senza seguire la formula che ne determina il modulo (GM/r²). Le figure precedenti e soprattutto quelle che seguono vanno, quindi, prese solo come indicative, mi raccomando…

Facciamo tre esempi veramente “brutali”, ma chi vuole può divertirsi a stringere gli intervalli e a variare velocità e accelerazioni a piacere. Notate che ho anche descritto in questo modo così “infantile” anche una traiettorie a spirale attorno al corpo O, come capita attorno ai buchi neri, o attorno a una stella che mangia la materia della compagna. Io, adesso, ve li mostro e poi voi potrete divertirvi a piacere (anche trovare l’effetto fionda…).

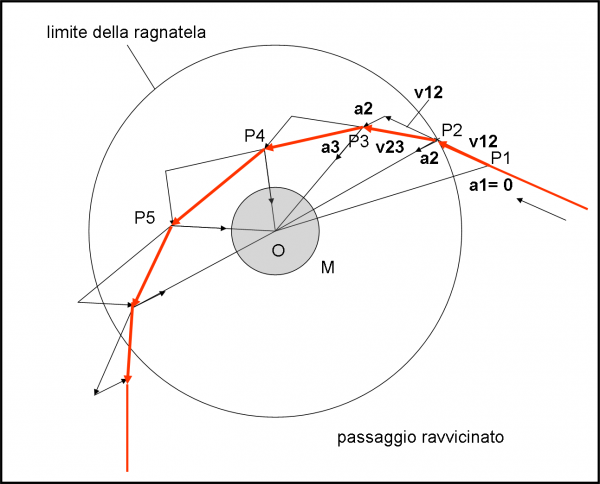
In Fig. 10, la velocità iniziale del corpo ha una direzione e un'intensità tali da superare l’attrazione di O. Alla fine, il corpo P, dopo essere stato costretto a cambiare la traiettoria iniziale, esce dalla ragnatela e può tornare al suo moto rettilineo uniforme, anche se diverso da quello iniziale. Questo è il caso di un passaggio ravvicinato di un asteroide con la Terra. Nessun impatto, ma l’asteroide ha dovuto cambiare drasticamente traiettoria.

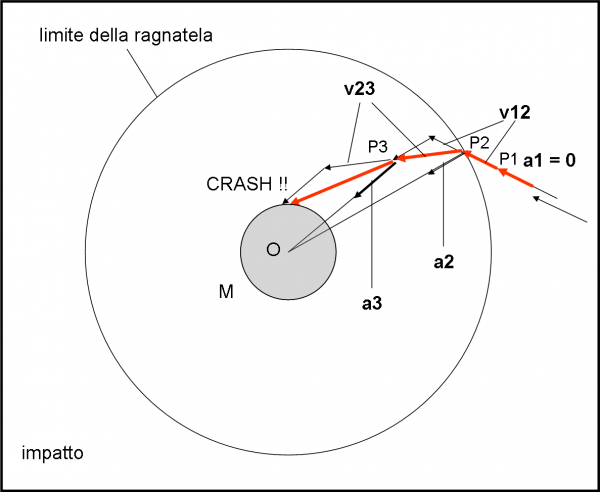
In Fig. 11, la velocità iniziale non riesce a controbattere l’accelerazione di gravità e il corpo non può fare altro che impattare velocemente su di esso.

In Fig. 12, il gioco tra velocità iniziale e ragnatela ha uno svolgimento più lungo, una specie di tira e molla. Alla fine, vince l’accelerazione, ma si genera una bellissima traiettoria a spirale. Tenete presente che la distorsione della traiettoria dipende in gran parte dall’approssimazione brutale del metodo usato. Tuttavia, dà già un’idea della situazione piuttosto chiara e … divertente.

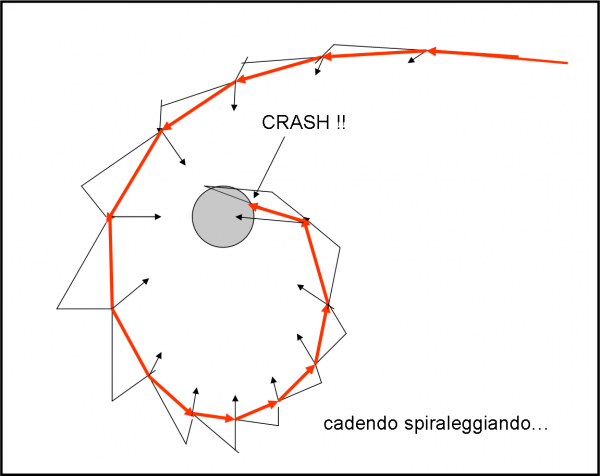
Nel fare qualche esercizio, ricordatevi che non basta il modulo della velocità per difendersi dalla gravitazione di O. Conta anche la sua direzione. Se la componente della velocità, nella direzione di O, ha lo stesso verso dell’accelerazione non fa altro che aiutare P a essere mangiato dal “ragno”. Se, invece, il verso è opposto, la lotta è molto più lunga e magari P riesce a vincere.

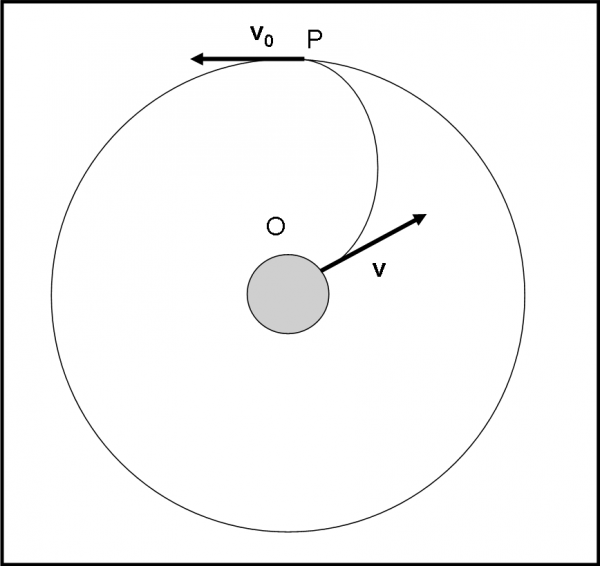
Se scegliete l’intervallino piccolo piccolo e una velocità abbastanza particolare, tale che diventi, a un certo istante, perfettamente perpendicolare alla congiungente P con O, otterrete anche che l’accelerazione è TUTTA perpendicolare alla velocità. Cambierebbe la direzione della velocità, ma non il modulo. Questa situazione la conosciamo molto bene dalla cinematica del moto circolare uniforme! Il corpo P ha ottenuto lo stallo e si mette in orbita attorno ad O. Ovviamente, lo può fare a qualsiasi distanza da O, sempre che il modulo e direzione della sua velocità siano quelli giusti. Sappiamo, infatti, benissimo come i moduli di velocità e accelerazione devono essere legati tra loro: ce lo dice la (1), ossia:

a_C = v₀²/r

da cui si ricava immediatamente il valore di v₀, capace di mantenere il corpo P in moto circolare uniforme attorno ad O.

v₀ = (a_C r)^1/2

Ma noi conosciamo benissimo il modulo della a_C, dato che si ricava dalla ragnatela, ossia dal campo gravitazionale di O. Esso vale:

a_C = GM/r²

Sostituendo:

v₀ = (GMr/r²)^1/2

E, infine:

v₀ = (GM/r)^1/2    …. (5)

Ho lavorato con i moduli, dato che so benissimo che il vettore è tangente in ogni punto al cerchio di raggio r.

Stallo!

Trascurando del tutto il racconto del dramma, possiamo arrivare subito al caso di stallo, ossia a quando la velocità del corpo che giunge sulla tela del ragno è tale da immetterlo su un’orbita circolare, dove può muoversi di moto circolare uniforme attorno a O. Quali sono le condizioni particolari perché questo succeda? Le formule sono sempre le stesse. La variazione di velocità impartita dall’accelerazione di gravità deve avvenire solo  agendo sulla direzione e non sul modulo. Esattamente quello che avevamo visto trattando il moto circolare uniforme dal punto di vista cinematico. In altre parole, l’accelerazione, dovuta alla ragnatela, deve essere uguale all’accelerazione che si ha in un moto circolare uniforme. Ciò capita per una certa distanza r di P rispetto a O. La prima vale GM/r², la seconda v²/r. Basta uguagliare e si ottiene:

GM/r² = v²/r

Semplificando:

v₀ = (GM/r)^1/2    …. (6)

Ovviamente, la (5) e la (6) sono identiche. La prima l’abbiamo ottenuta seguendo tutto lo svolgimento del crimine, la seconda cercando solo la posizione di “stallo”, di pareggio, di moto circolare uniforme.

Abbiamo comunque ricavato una relazione fondamentale. Affinché un corpo P si metta in orbita attorno a un corpo O di massa M, il modulo della sua velocità deve essere quello dato dalla (5) e la sua direzione deve essere perpendicolare alla direzione di O. In parole più tecniche: in ogni punto della traiettoria il cerchio osculatore deve rimanere sempre lo stesso e coincidere  con il cerchio di raggio R che ha per centro O.

Come vedete la (5) dipende dalla massa del corpo che ha creato la ragnatela, ma anche dalla distanza rispetto a lui. In altre parole, per entrare in orbita circolare (stallo), la velocità deve aumentare se la distanza r diminuisce. Più si va vicini a O e più grande è l’accelerazione che subisce P. Per riuscire a mantenersi in moto circolare uniforme deve aumentare la v₀. Teoricamente, perciò, se non vi fosse atmosfera o cose del genere, un corpo potrebbe ruotare intorno a un altro a qualsiasi distanza dalla massa centrale, sempre che abbia la giusta velocità.

Dall’esterno non è facile

Il moto circolare uniforme è perciò un caso estremamente fortunato per un corpo che arrivi dall’esterno rispetto alla ragnatela. Se la velocità di P fosse troppo alta e diretta in un certo modo, dopo una deviazione più o meno significativa della sua traiettoria, il corpo riuscirebbe a scappare e a tornare a un moto rettilineo uniforme. La velocità, infatti, cambierebbe solo durante l’azione dell’accelerazione di gravità, ma quando quest’ultima diventasse praticamente nulla, l’oggetto P tornerebbe alla sua situazione dominata solo dall’inerzia. Se, invece, la velocità fosse sempre troppo bassa e diretta in un certo modo, non potrebbe che cadere tragicamente su O.

E’ stato confermato ancora una volta il principio fondamentale. Chi comanda il movimento di un corpo è sempre e soltanto la velocità (non per niente è lo spazio percorso nell’unità di tempo). Chi può disturbarla, anche gravemente, è l’accelerazione, la sola che può agire su di lei, allungandola, accorciandola, piegandola. Una lotta tra una caratteristica insita nel corpo e un’azione comandata dal mandante. La vera sfida concettuale è tra le masse, ma la battaglia sul campo vede solo la vittima e il sicario.

Esiste un caso particolarissimo che ormai sappiamo inquadrare molto bene: La velocità del corpo P è ZERO rispetto al corpo O. L’accelerazione (anche se ha un valore costante g) ha gioco facile ad applicargli velocità via via crescenti fino a farla giungere ad O e schiantarsi. Un caso veramente eccezionale e irrealistico. Chi potrebbe mai avere velocità zero al momento dell’ingresso nella ragnatela? Doveva averla anche prima, ma allora non sarebbe mai arrivato fino alla ragnatela. No, un corpo che arriva dal “di fuori” deve comunque lottare e non può cadere come una mela! La Luna, se fosse arrivata da fuori, sarebbe potuta anche cadere, ma solo dopo una dura lotta tra i fili della ragnatela. Tuttavia, sappiamo benissimo che NON è caduta e nemmeno se n’è andata, per cui l’unico caso possibile è che sia riuscita a pareggiare la partita a scacchi, trovando lo stallo. Può anche essere, ma è un caso molto fortunato… forse troppo!

Due considerazioni rapide, rapide:

Dato che raggiungere la velocità necessaria al moto circolare uniforme è un caso fortunato, è molto difficile catturare un corpo vagante attraverso l’accelerazione gravitazionale. Il corpo, normalmente, o cade o fugge. Avremmo avuto bisogno di decine e decine di lune che avessero tentato l’aggancio e, alla fine, magari una ci sarebbe riuscita. Ma, trovare tanti oggetti delle dimensioni della Luna pronti a fare questa gara così vicine alla Terra, non era molto probabile nemmeno quando il Sistema Solare era molto più popolato e disordinato.

Teoricamente, sappiamo che la ragnatela stesa dal corpo O non ha mai fine e può arrivare ovunque nell’Universo. Un corpo P lontanissimo potrebbe, perciò, mettersi in orbita anche a distanza enorme da O. Sarebbe necessaria anche  una velocità v₀ molto bassa. Tuttavia, nello Spazio non esistono solo P e O, ma tantissimi altri corpi con le loro ragnatele. Ne segue che la somma di tutte queste, anche se molto  lontane, bastano e avanzano per trascinare via il corpo P dalla ragnatela di O, quando essa è ormai troppo debole.

Perché il Sole ci è riuscito?

Qualcuno potrebbe dirmi: “Ma come... dici che è praticamente impossibile essere immesso in un’orbita circolare attorno a O, e, invece, vediamo che i pianeti, e non solo, rivolvono tranquillamente attorno al Sole!”. La differenza fondamentale è che i pianeti si sono formati all’interno del disco che circondava la stella Sole, ossia i granelli di polvere che li hanno formati rivolvevano già attorno al Sole fin dalla nascita della stella. La velocità era già quella giusta! Se non fosse stata quella giusta, la polvere se ne sarebbe andata per sempre o sarebbe caduta sul Sole. Insomma, non sarebbe servita a formare i pianeti! In realtà ciò è parzialmente successo:  molta polvere del disco è finita realmente sul Sole o se ne è andata verso altre stelle.

In ogni modo, ovunque nel disco, sarebbe possibile, teoricamente, avere un corpo che gira attorno al Sole. Lo vediamo con gli asteroidi: si frantumano l’uno con l’altro, ma i loro frammenti continuano a stare in orbita, tranne casi particolari, dove subentra il caos dinamico… ma questa è un’altra storia, ben più complicata. Le velocità sono quelle giuste per restare nella ragnatela per tempi anche molto lunghi.

Ben diversa sarebbe la situazione se una stella arrivasse vicino al Sole. Ci sarebbe una lite furibonda, ma alla fine (dato che le velocità relative tra le stelle sono molto alte), se ne andrebbe facilmente per la sua strada. La stessa cosa capita per un meteoroide che si avvicina alla Terra. Tutto dipende dalla componente della velocità nella direzione della Terra, che si può sommare o sottrarre all’azione dell’accelerazione gravitazionale della Terra, aiutando la caduta se il verso è uguale o ostacolandola se il verso è opposto.

Insomma, ragazzi, la Luna non cade perché la sua velocità rispetto alla Terra soddisfa le condizioni di moto circolare uniforme. E’ caduta nella ragnatela e ha ottenuto uno stallo? Insomma, la Luna ha avuto (o forse ancora più la Terra) una fortuna enorme? Tutto è possibile nell’Universo, ma il troppo è troppo. Forse la Luna non è venuta dal “di fuori”, ma è partita dal “di dentro”.

In generale, però, tenete conto che stiamo parlando di velocità relative tra Terra e Luna. Entrambi i corpi ruotano attorno al Sole e quindi posseggono una certa velocità. Tuttavia, possiamo considerare, in prima approssimazione, che questo movimento comune sia rettilineo uniforme. Possiamo, perciò, cambiare tranquillamente il sistema di riferimento inerziale e sceglierne uno che viaggi alla velocità della Terra. Ne segue che la velocità “residua” della Luna è quella del satellite rispetto a noi. La stessa cosa che capita a una pietra lasciata cadere. Essa viaggia alla stessa velocità della Terra e quindi quando la lascio libera può considerarsi a velocità zero rispetto alla Terra e subisce senza pietà la sua accelerazione di gravità senza colpo ferire. Se invece la lancio per aria, prima di cadere descrive una certa traiettoria. Le ho impresso una certa velocità che, finché può, cerca di ribellarsi all’accelerazione di gravità. Questo caso particolare ci conduce a quel genio infinito di Newton e alla scoperta della legge di gravitazione universale. Come sotto prodotto, questo fenomeno ci porta alla formazione “endogena” della Luna, ossia dal “di dentro”, proprio come fosse una pietra lanciata verso lo spazio.

P.S.: Prima che qualcuno me lo chieda... Ho sempre parlato di moto circolare uniforme e mai di orbite ellittiche. La legge di gravitazione rimane la stessa e i risultati non cambiano assolutamente. Cambiano, invece, i passaggi matematici e i vettori si ingarbugliano ancora di più. Insomma, vi prego di fidarvi e di non pretendere una trattazione completa.

A furia di tirar pietre

Mettiamoci, quindi, sul corpo O e proviamo a lanciare la nostra pietra P. Per lanciarla, dobbiamo, ovviamente, impartirle una certa velocità, che è l’unica cosa che riesce a far muovere una massa m. Per fare ciò impartiamo con il braccio una forza F alla pietra che si trasforma in un’accelerazione che, a sua volta, origina una velocità. Infatti, la pietra parte con velocità zero, ma, a seguito dell’accelerazione che le abbiamo dato, passa a una velocità v diversa da zero. Ricordiamo che l’accelerazione crea una differenza di velocità dv in un certo intervallo di tempo dt. Acquistare una velocità vuol dire permettere al corpo P di spostarsi di uno spazio ds in un intervallo di tempo dt, anche se lungo una traiettoria rettilinea (accelerazione tangenziale). Otteniamo, praticamente, un moto.

Ovviamente, l’accelerazione dura un attimo, quello che basta per regalare la velocità v (costante) alla pietra P. A questo punto il sasso si sta muovendo di moto rettilineo uniforme, cercando disperatamente di allontanarsi dal corpo O. La faccenda non è certo semplice, dato che P è costretto a muoversi all’interno della ragnatela creata da O. Cosa succede, in pratica? La pietra è soggetta a una velocità che è obbligata a deviare la sua direzione e a cambiare il modulo sotto l’azione dell’accelerazione di gravità. Se disegnassimo una figura simile a quelle descritte precedentemente, avremmo una soluzione drammatica: la pietra cadrebbe su O, in breve tempo (Fig. 12).

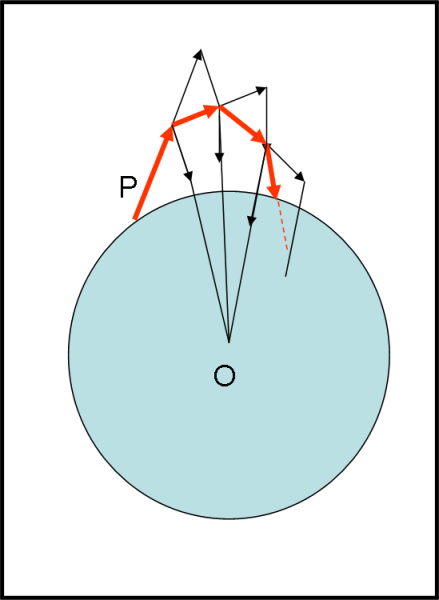
Non sarebbe difficile descrivere questa traiettoria, dato che è una parabola come quella descritta da un proiettile sparato da un cannone. Proprio attraverso un cannone molto più potente, potremmo aumentare la velocità della pietra. In questo modo ritarderemmo la sua caduta. Non basta ancora? Beh… perché non usare una rampa di lancio per missili e sparare il sasso nello spazio? Potremmo ottenere una velocità tale che la pietra si metta in condizioni di stallo rispetto alla ragnatela. Non è certo difficile ricavare la velocità necessaria: l’abbiamo già visto la volta scorsa.

Quando raggiungiamo questa velocità, l’accelerazione diventa puramente centripeta, dato che la velocità è sempre tangente a un cerchio di centro O. Agendo dal “di dentro”, abbiamo, perciò, ottenuto lo stesso stallo dell’altra volta, descrivendolo in modo diverso. Siamo riusciti a lanciare una pietra che continua a girare attorno a O. In realtà, essa continua a cadere verso di lui (la velocità si piega verso il basso), ma non lo raggiunge mai. Magnifico!

Per farvi capire la semplicità e profondità di questo processo mentale, basta inserire la Fig. 13, disegnata proprio da Newton per spiegare il concetto generale. Se spariamo con le modalità giuste, la pietra raggiunge la giusta velocità e la caduta non si verifica più. La pietra resta sospesa a galleggiare ruotando nella ragnatela di O. Il caso riportato da Newton usava proprio la velocità tangenziale fin dalla partenza. Essendo su una montagna altissima si poteva sparare in direzione orizzontale ed essa era già quella giusta per entrare in orbita.

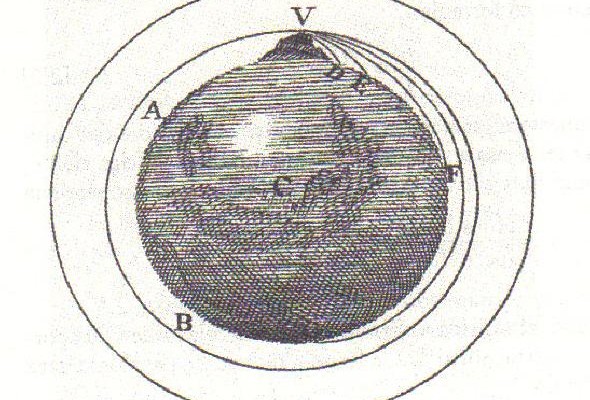
Quando si lanciano i satelliti si spara verso l’alto e quindi la velocità necessaria  si ottiene dopo che l’accelerazione della ragnatela l’ha costantemente deviata fino a che non sia diretta perpendicolarmente alla direzione PO. In parole più tecniche si parla di orbita di trasferimento (Fig. 14), ma lasciamo perdere se no Lampo ci picchia! Sciocchezze, comunque, per i “cannoni” di oggi. Resta il fatto che la Fig. 13 è un vero capolavoro. Pensate che è stata ideata senza ancora conoscere la legge di gravitazione universale. Anzi è stata proprio usata per dimostrarla!

Qualcuno potrebbe chiedermi: “Sì, sì, tutto molto bello… ma cosa cambia rispetto alla volta scorsa? Abbiamo ottenuto le identiche formule del moto circolare uniforme!”. Avrebbe sicuramente ragione (d’altra parte volevamo proprio quello), ma siamo NOI questa volta a cercare di dare alla pietra la velocità giusta e non sperare solo che il corpo che viene da fuori riesca ad ottenerla per puro caso. In poche parole, abbiamo scelto NOI la velocità necessaria a mettere sicuramente la pietra-satellite in orbita e anche all’altezza che vogliamo raggiungere. Non abbiamo aspettato che la lotta tra la velocità di un corpo esterno e la ragnatela decida se e dove il corpo P può mettersi in moto circolare uniforme. Abbiamo preparato a tavolino la nostra difesa!

Come appena detto, non solo abbiamo la sicurezza della riuscita della missione, ma possiamo anche scegliere l’altezza che vogliamo raggiungere: basta, infatti, cambiare la velocità! Se la v, tangente al cerchio, cresce, la formula ci dice che anche la distanza r da O deve crescere. E tutto ciò lo otteniamo, qualsiasi sia la massa che mandiamo verso lo spazio. Un attimo, un attimo. L’unico momento in cui la massa da inviare gioca un ruolo decisivo è all’atto della forza da imprimere al sasso-satellite per farlo muovere alla giusta velocità. La forza necessaria a dargli la giusta accelerazione, e quindi velocità e spostamento, dipende (e come!) dalla massa m da inviare nello spazio (é o non è F = ma, secondo principio della dinamica?).

OK, OK, siamo capaci di inserire in orbita tutte le pietre che vogliamo, ma cosa c’entra con la Luna? Ebbene, una Luna che viene “da fuori” avrebbe una velocità “di crociera” frutto del suo passato. Una che viene “da dentro” sarebbe composta da materiale (tante pietre) che partono da O con velocità molto diverse tra loro. Molte ricadrebbero perché la velocità è troppo bassa. Altre se ne andrebbero nello spazio perché la velocità è troppo alta. Ma moltissime si sistemerebbero su orbite circolari, avendo raggiunto la giusta velocità per ottenere lo stallo a una certa distanza. Insomma, si creerebbe un disco di materia, come il disco che si è formato attorno al Sole. A quel punto giocherebbe la velocità relativa (piccola) tra le varie pietre ed esse inizierebbero a scontrasi tra loro diventando un corpo sempre più grande. La gravità della prossima Luna riuscirebbe a vincere quella del lontano corpo O. Due insetti innamorati, intrappolati in due punti molto vicini della ragnatela, non riuscirebbero a scappare, ma potrebbero muoversi quel poco che li farebbe sopravvivere uniti nella loro configurazione di stallo. Ricordiamo, infatti, che pur aumentando la massa della proto Luna non cambierebbe assolutamente l’accelerazione-ragnatela di cui è vittima.

Ricapitoliamo: lavorando dal “di dentro” potremmo non solo scegliere volontariamente la velocità necessaria allo stallo (satelliti artificiali), ma anche aspettarci che le pietre, scappate in modo naturale dopo un impatto catastrofico, riescano a coprire un intervallo di velocità tale da contenere anche quelle giuste per avere un moto circolare uniforme. Non una sola velocità decisa “da fuori”, ma un “range” enorme di velocità tra cui selezionare quelle adatte a sopravvivere per sempre nella ragnatela.

In questo secondo caso, molto più realistico, potremmo proprio dire che la Luna continua a cadere verso la Terra, ma ritarda all’infinito il momento dell’impatto.

Abbiamo quindi risposto alla domanda fondamentale: "Perché la Luna non cade sulla Terra". Facile: " la Luna continua teoricamente a cadere verso la Terra, ma la stessa ragnatela, che cerca di trascinarla verso di noi, le permette di non cadere mai, dato che la velocità della Luna non è zero". Tutto ciò sempre, e comunque, senza attriti, perturbazioni ed effetti mareali dovuti a corpi non perfettamente rigidi. Ma questo è tutto un altro discorso che abbiamo già affrontato varie volte.

La reazione c’è ma non si vede

Come avete visto abbiamo ottenuto un moto circolare uniforme senza mai fare entrare in ballo altre forze che non siano quella di gravitazione universale, che si traduce nell’unica accelerazione esistente, quella centripeta. Escludiamo, infatti, quella necessaria a lanciare il corpo nello spazio, dato che agisce solo per un istante e poi scompare immediatamente.

Tutto questo giallo ha un finale essenzialmente positivo per entrambi i contendenti. La massa O riesce a non farsi scappare il corpo P e quindi la sua ragnatela funziona. Il corpo P riesce a non essere inghiottito e a trovare una situazione di pacifica sopravvivenza. Tutti felici e contenti. Non potendo ottenere il massimo, ci si deve accontentare di una via di mezzo che in fondo regala soddisfazione a entrambi gli avversari, ossia al mandante e alla vittima.

Tuttavia, immaginiamo che l’intero dramma (o meglio commedia…) sia vista da un alieno di passaggio (che si tiene a debita distanza dalla ragnatela, che non guarderebbe in faccia nessuno). Cosa conclude? Un corpo P è riuscito a girare attorno a un corpo O di massa ben più grande sotto l’effetto di un’unica forza, quella che cerca di attirarlo verso O. Una forza che dà luogo a una sola accelerazione. L’accelerazione è centripeta e tale è anche la forza che la crea.

Ma dov’è finito il terzo principio della dinamica? Dov’é la reazione uguale e contraria che la massa m deve esercitare per ribellarsi alla forza della massa M? Insomma, non esiste nessuna “vendetta”? C’è, c’è, non preoccupiamoci. E, a questo punto, bisogna leggere bene il terzo principio. Esso dice che se P subisce una forza, si vendica applicando a O una forza uguale e contraria. Capito il concetto fondamentale? La reazione non si applica a P, ma a O.

In realtà, O subisce una forza uguale e contraria a quella che esercita su P, ma l’accelerazione che cerca di smuoverlo, e quindi il suo spostamento, è troppo piccolo per essere notato. Infatti, l’accelerazione di O nasce dalla stessa forza di gravità che agisce anche su P, ma deve essere divisa per M. Ciò che resta è, quindi, un’accelerazione ridicola e praticamente invisibile. In altre parole, anche P crea la sua piccola ragnatela, ma il corpo O se ne ride bellamente e non ci pensa nemmeno.

Ciò non è più vero quando le masse diventano comparabili, dato che la reazione diventa ben visibile e misurabile. Il moto circolare si complica (apparentemente, perché lui resta sempre lo stesso), facendo girare entrambe le masse attorno a un punto particolare, un punto che è come la Svizzera durante i conflitti mondiali, un punto del tutto neutrale, capace di proseguire nel suo moto rettilineo uniforme rispetto al sistema inerziale degli alieni. Parliamo, ovviamente, del baricentro… ma evitiamo di approfondire la questione, se no saremmo obbligati a introdurre energie, momenti angolari e … tutta la meccanica classica. Torniamo alla nostra pietra che gira attorno alla Terra. Ne abbiamo a sufficienza di cose da dire!

Una forza che non esiste! Parola degli alieni…

Ricapitoliamo il pensiero degli alieni. La pietra è soggetta solo e soltanto alla forza o –meglio- all’accelerazione centripeta. Non vi sono altre accelerazioni e, di conseguenza, nessun’altra forza in gioco (ricordiamo ancora una volta che l’esistenza di una forza implica un’accelerazione e l’esistenza di un’accelerazione implica l’esistenza di una forza: non possono mai esistere separate!). E’ solo lei che causa una variazione nel moto di una pietra qualsiasi, che altrimenti se ne andrebbe tranquillamente secondo il primo principio della dinamica, ossia con un pacifico e inoffensivo moto rettilineo uniforme.

Insomma, cari ragazzi, non esiste nessuna forza centrifuga. Non ce n’è assolutamente bisogno. Tutto è stato spiegato perfettamente e lei non ha mai fatto la sua comparsa. Essa NON è certamente la reazione alla forza gravitazione (ossia centripeta) che attrae il corpo P verso O. La reazione, sempre esistente, ma praticamente invisibile nel caso Terra-pietra,  viene applicata su O e deve essere considerata anch’essa una forza centripeta diretta da O verso P.  Tenete ben presente questo concetto per non fare confusione quando parleremo di forza centrifuga. Sì, ne parleremo, anche perché non possiamo certo far finta di niente e cancellarla da tutti i libri!

Senza peso, ma non senza forza

L’ affrontiamo in modo indiretto, in modo da sfatare un altro possibile fraintendimento, che, a volte, viene proprio creato da qualche professore…  Immaginiamo che la nostra pietra sia una navicella vuota al cui interno vi sia una pietra più piccola o -se preferite- un  astronauta. Che bello vederlo galleggiare nella capsula senza peso. Beh…. ovvio… è talmente distante dalla Terra che non risente della sua gravità. Mamma mia, che errore grossolano! (E la Luna, allora, che è ancora più distante?). Se fosse così, come mai la capsula spaziale continua a girare attorno alla Terra in balia della sua accelerazione gravitazionale? No, no, la ragnatela c’è ancora, statene certi. La mancanza di gravità non è assolutamente dovuta alla distanza. Ci vorrebbe ben altro.

Il fatto è che l’astronauta ha la stessa velocità della capsula e quindi rispetto a lei non si muove: subiscono entrambi, astronauta e capsula, la stessa accelerazione. In altre parole, ancora: se l’astronauta si sente senza peso, la stessa cosa sente anche la navicella (potesse parlare, lo direbbe!). Se la corda di un ascensore si rompe, siete o non siete costretti a cadere insieme a lui. Restate sempre al vostro posto rispetto all’ascensore, ma alla fine vi schianterete come lui! Se il satellite dovesse improvvisamente ridurre a zero la sua velocità orbitale, il povero astronauta sentirebbe, e come, l’accelerazione centripeta che lo porterebbe tragicamente verso la Terra.

L’assenza di gravità per un astronauta è quindi un fenomeno apparente che ci introduce molto bene verso la forza centrifuga. Ricordate, però, che, benché la descrizione fatta dall’astronauta e quella fatta dall’alieno siano nettamente diverse, il fenomeno fisico che avviene è lo stesso. Due modi diversi per raccontare la stessa identica storia. In un caso c’è bisogno di introdurre un certo “mago” per far tornare le cose (ossia per usare sempre le stesse leggi della dinamica), nell’altro assolutamente no. Questa apparente discrepanza ha un solo colpevole, come già detto fin dall’inizio: il sistema di riferimento inerziale! Lui ha le sue regole e non tutti possono seguirle.

Chi gira non è in moto inerziale!

Non ci resta che prendere anche noi una navetta spaziale e raggiungere l’astronauta in orbita. Pensavamo di aver capito perfettamente la situazione e di essere freddi e logici fino in fondo e, invece, ci sentiamo confusi. Accidenti, siamo proprio senza peso e vediamo la Terra girare laggiù sotto di noi. In altre parole, noi ci sentiamo completamente fermi ed è il resto che si muove.

Ma come facciamo a stare fermi se subiamo un’accelerazione centripeta? No, niente da fare. Per stare fermi vuol dire che su di noi agisce un’accelerazione uguale e contraria a quella centripeta. Attenzione però. Non abbiamo bisogno di una reazione uguale a contraria alla forza che ci spinge vero la Terra, ma una forza che annulli quest’ultima. Non è il terzo principio della dinamica di cui abbiamo bisogno, ma solo e soltanto di una forza magica che annulli quella centripeta. Entrambe devono essere applicate su di noi.

In altre parole, per mantenere la nostra posizione immobile, devono agire due forze (o due accelerazioni) che si annullino tra di loro. Solo così possiamo descrivere il nostro stato di quiete (apparente) completa. Questa forza la devo introdurre assolutamente e la chiamo forza centrifuga. Se non lo facessi dovrei stravolgere i principi della fisica e questo non posso farlo.

Va bene, va bene, ma esiste davvero o è solo una nostra invenzione dovuta alla scarsa preparazione fisica? No, signori miei, esiste e come. Ma esiste solo e soltanto nel sistema di riferimento che ruota insieme alla navicella. Per descrivere il nostro moto dobbiamo usare una descrizione diversa da quella dell’alieno. Ma non dobbiamo stupirci più di tanto. E’ una conclusione ovvia: siamo su un sistema di riferimento che non è inerziale, in quanto è soggetto a un’accelerazione e la nostra velocità, benché sia costante come modulo, non è assolutamente costante come direzione. La forza centrifuga ci permette di descrivere in modo diverso un fenomeno che deve essere lo stesso sia per noi che per l’alieno!

Ciò che avviene è esattamente la stessa cosa e anche la legge fisica che lo governa.

Seguitemi in questa dimostrazione “matematica”, poco sfruttata, ma che per me è la migliore possibile. Per mostrarla uso formule che abbiamo già ricavato e usato. Facciamo parlare prima l’alieno e poi l’astronauta.

Alieno: l’astronauta ruota attorno alla Terra con una velocità tale da permettergli di mantenere un moto circolare uniforme. Io sto assistendo direttamente a questo spettacolo e non posso sbagliarmi. Il fatto stesso che la sua traiettoria sia curvilinea e sia descritta con velocità costante mi dimostra che esiste un’accelerazione centripeta che agisce su di lui e questa accelerazione è data da:

a = v²/r

Basta un po’ di cinematica per ottenerla. Se esiste un’accelerazione deve, però, esistere anche una forza che la origina. Essa può essere scritta, in base al secondo principio della dinamica, come

F = ma = mv²/r

dove m è la massa dell’astronauta

Potrei fermarmi qui se non conoscessi Newton e la sua legge. Ma, sono ben preparato e, quindi, so benissimo che questa forza non è altra che la forza di gravità che vale

F = GMm/r²

Posso permettermi di uguagliare le due espressioni precedenti e ottengo:

GMm/r² = mv²/r    …. (1)

Adesso non ho altro da dire, dato che ho espresso ciò che capita con una formula completa che tiene in conto tutte le grandezze in gioco.

Astronauta: Che bella la Terra laggiù in basso! Mi sono addormentato già prima della partenza e non so come sono arrivato fin quassù, ma è veramente una meraviglia. Non sono un grande esperto di fisica, ma ho imparato che a questa altezza (r, come dice la strumentazione di bordo) dovrei subire la forza di gravità della Terra e invece mi sento completamente fermo. Non posso certo essere uscito dal suo campo gravitazionale: se guardo dall’oblò vedo la Luna molto più distante e se lei subisce la gravità della Terra, devo subirla anch’io. Fatemi scrivere la forza di gravità. Fino a lì c’arrivo anch’io:

F = GMm/r².

Insomma, dovrei cadere verso di lei a velocità incredibile e, invece, sono fermo, immobile. C’è una sola spiegazione! In questa navicella in cui mi trovo deve esistere qualche marchingegno che mi permette di non cadere. Da quel poco che ho letto di fisica, so che per poter stare fermo esistono solo due modi: o non sono soggetto ad alcuna forza o la somma di tutte le forze che agiscono su di me deve essere uguale a ZERO. Il primo caso non può andar bene, dato che ho la certezza che esiste la forza di gravità che mi attira verso la Terra. E’ quindi assolutamente necessario che esista un’altra forza, che chiamo F’, che sommata a F dia come risultato ZERO. Non c’è bisogno di essere Einstein per arrivarci. Sono o non sono immobile nello spazio? Tutto è risolto e posso scrivere:

F + F’ = 0

O, tanto per far vedere che non sono poi così ignorante:

GMm/r² + F’ = 0     …. (2)

Ho cercato dappertutto, ma non ho trovato nessun razzo e nemmeno cavi che mi leghino a qualche astronave. Boh … qualcuno prima o poi mi dirà che mistero è mai questo. Magari sono sotto l’effetto di una magia. In un modo o nell’altro, però, sono felice che ci sia. Se guardo verso la Terra mi vengono i brividi a pensare di cadere in picchiata fino a laggiù.

La chiamerei forza della salvezza, qualcosa, insomma, che riesce a non farmi cadere sulla Terra. No, troppo poco scientifico. Un attimo, un attimo… so che la forza gravitazionale è anche una forza centripeta, che vuol dire diretta verso un centro, la Terra o qualsiasi altra massa. E, allora, dato che questa forza è proprio il suo opposto, la chiamerò forza centrifuga, ossia che si allontana dal centro.

Gli astronauti ci scuseranno se li abbiamo presi un po’ in giro, ma era solo per farci raccontare la situazione da uno che non aveva assolutamente idea di ciò che stava capitandogli.

Tocca a noi adesso far vedere che sia l’astronauta che l’alieno hanno detto la stessa identica cosa. Beh… non è certo difficile. La (2) si scrive anche:

GMm/r² = -F’    …. (3)

Affinché la (3) sia uguale alla (1) basta che si abbia

F’ = - mv²/r

La stessa identica legge si ottiene nei due casi (meglio dire “punti di vista”) accettando che la forza centrifuga sia veramente una forza che agisce sull’astronauta, uguale e opposta alla forza centripeta.

Una forza “vera”, perciò, o -quantomeno- realmente avvertita dall’astronauta. Essa è però, in realtà, anche “fittizia” perché serve a spiegare all’astronauta come può stare fermo, immobile, apparentemente senza subire la gravità. L’alieno non ne ha bisogno per spiegare la situazione che vede, l’astronauta invece sì. Se non esistesse  questa forza il povero astronauta cadrebbe sulla Terra. Tuttavia, in questo caso, la legge espressa dalla (1) non si applicherebbe anche al viaggiatore spaziale. Alla fisica non piacerebbe e ancor meno a Newton!

Se leggendo le righe precedenti vi siete sentiti presi in giro, dato che ho detto delle banalità e ho girato sempre attorno alla stessa formula, non arrabbiatevi. E’ il primo passo per capire la differenza tra sistema inerziale e sistema non inerziale. Nel secondo sistema la descrizione deve essere diversa, ma si continua a parlare dello stesso fenomeno.

Capisco, comunque, che, pur avendo seguito e capito i passaggi e i ragionamenti precedenti, alla prima occasione ci si possa trovare nuovamente spiazzati. Vedremo meglio la prossima volta, con casi più “pratici” questa situazione apparentemente assurda nella sua semplicità. Parleremo di giostre, di curve pericolose, di ruote di von Braun e non solo. Magari anche di Coriolis (chi era costui?).  Nel frattempo, vi lascio un problemino per farvi divertire un po’.

Sapete benissimo quanto vale la velocità necessaria per restare in orbita a una certa distanza r dalla Terra. Sapete anche quanto vale il periodo di rotazione della Terra (24 ore). Vi chiedo, allora: a che altezza deve stare un satellite in modo da rimanere fermo rispetto alla Terra, ossia sempre sopra allo stesso punto della superficie terrestre? Tecnicamente, qual è l’altezza per avere un satellite geostazionario? Avete tutti i dati e l’unica incognita è proprio la distanza r… Buona fortuna! Se proprio non ci arrivate… chiedetelo a Caronte, lui è proprio un satellite geostazionario di Plutone… (o è meglio dire plutostazionario?). I “fan” di Plutone non possono non saperlo!

P.S.: mi accontento anche solo della formula risolvente e non del valore numerico. In ogni modo, la costante G vale 6.674 · 10^-11 m³/(kg sec)² e la massa della Terra è = 6 ·10²⁴ kg.

Direi che ormai abbiamo introdotto e capito il vero significato della forza centrifuga, una vera e propria “pezza” che si deve inserire per fare in modo che un fenomeno fisico rimanga se stesso sia in un sistema di riferimento inerziale che in uno rotante. Abbiamo anche capito il ruolo fondamentale dell’inerzia di un corpo, inerzia che si traduce nella sua ferrea volontà di mantenere una velocità costante e un moto rettilineo. La lotta tra ragnatela formata dall’accelerazione di gravità e l’inerzia di un viaggiatore solitario finisce a volte in pareggio. Più facile è ottenere lo “stallo” lavorando dal di dentro, ossia scegliendo come lanciare il viaggiatore. Abbiamo anche imparato che l’assenza di gravità di un astronauta è solo una piccola magia che compie la forza centrifuga o -se proprio non vi piace- la forza centripeta e la velocità che abbiamo dato alla navicella che lo ospita. In fondo è la stessa identica cosa che capiterebbe in un ascensore che venga fatto cadere verso il suolo, tagliando magari le corde. Vi sentireste senza peso, dato che cadete insieme all’ascensore, alla stessa velocità, ma al momento dell’arrivo al suolo vi accorgereste che era solo una impressione e che la gravità esisteva e come!

In generale, però, abbiamo risolto questa doppia faccia della forza centrifuga in un modo che forse ha lasciato un po’ di amaro in bocca. Abbiamo usato formule, facilissime, ma sempre formule matematiche. Come San Tommaso, molti preferirebbero toccare con mano. Dato che non è facilissimo andare direttamente nello spazio a provare l’apparente assenza di gravità vediamo di trovare qualche esempio terra-terra (nel vero senso della parola) che ci metta veramente di fronte a questa “strana” forza che, per chi è in moto circolare, esiste e agisce, ma non per un alieno che assiste da  un’astronave in quiete. Adesso che sappiamo che, in fondo, non esiste, ma è una specie di trucco, saremmo magari convinti di riuscire a farne a meno, o di riconoscere il vero dal falso o -meglio- dal “fittizio”. Rimarremmo molto delusi! Se ci immergiamo in un sistema rotante, la sentiremmo e come! E ne subiremmo anche le conseguenze. Le formule ci sembrerebbero dei ciarlatani che parlano, parlano, ma non sanno quello che realmente capita.

Ho scelto tre esempi, che dicono esattamente la stessa cosa, ma che differiscono nel modo in cui agisce la forza centripeta (l’unica vera forza per l’alieno). Essa, a volte, si nasconde molto bene e lascia spazio libero alla sua amica-nemica forza centrifuga.

Il caso più semplice è quello del lanciatore di martello o  di quelle giostre a seggiolini volanti che fanno ruotare gli audaci (almeno per me) attorno a un palo centrale. Prima di vedere con un semplice schema la situazione, vi faccio una domanda: “Cosa direbbe il “martello” se gli chiedeste dove si sente trascinato?” Sicuramente non avrebbe dubbi: “Verso l’esterno. Meno male che c’è la corda che mi tiene vincolato al lanciatore”. La stessa domanda si può rivolgere a chi sta sul seggiolino della giostra. “Verso l’esterno, accidenti! Verso l’esterno… E non lo dico solo io che sono qui seduto con una paura pazzesca, ma anche il gattino che mi sono messo su una spalla. Le sue unghie piantate profondamente nella carne la dicono lunga: non ha nessuna voglia di essere lanciato verso la folla che ci circonda”.

C’è poco da fare, la forza centrifuga esiste e come! Il caro alieno ha un bel dire che non esiste. Per semplicità annulliamo la forza di gravità che tende a far cadere verso il basso i seggiolini o il martello del lanciatore. In fondo, è solo questione di velocità di rotazione che bisogna imporre all’attrezzo o alla giostra. Caro alieno, dove sarebbe la forza centripeta che comanda la situazione generale? Noi vediamo solo un gatto che cerca di non essere sbattuto fuori dalla giostra!

La Fig. 15 non ha problemi a dare ragione ancora una volta all’alieno, anche se il gatto non si convincerà mai! Il seggiolino ha una certa velocità di partenza che lo porterebbe ad andarsene di moto rettilineo e uniforme, come tutti i corpi di questo magnifico Universo. Chi è che lo costringe a girare come un matto? Solo e soltanto la corda di lunghezza finita. E’ proprio la corda che impartisce la forza centripeta. Una corda non usa la forza gravitazionale che sa lavorare anche a distanza e quindi deve “toccare” il seggiolino. Essa viene applicata direttamente a lui attraverso un contatto diretto che avviene nel punto P. La forza centripeta tende a trascinarlo verso il palo di rotazione. Questa forza genera una reazione uguale e contraria sul palo che si sente tirato verso l’esterno. Nel caso del lanciatore di martello chiedete alla sua mano che strattone subisce! La forza centripeta c’è e basta e avanza per far girare il seggiolino e chi è seduto su di lui (che però si tiene ben stretto), modificandone istante per istante la direzione della velocità.

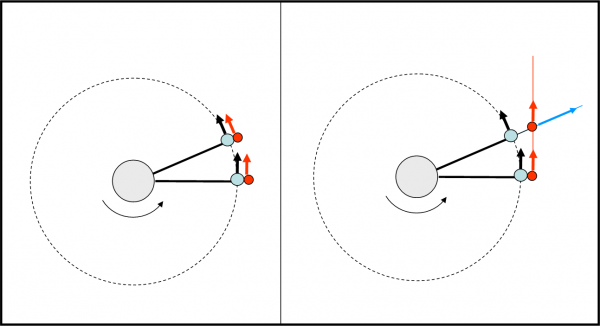
La pallina rossa potrebbe essere il gattino, ma non voglio nemmeno pensarci! Lo sostituiamo con una vera pallina rossa (che ammettiamo, sempre, non subisca la forza di gravità che la farebbe cadere velocemente a terra). Se la teniamo stretta in mano lei viaggia con noi e segue il moto della giostra (a sinistra). Immaginiamo, adesso di lasciarla andare (destra). Per uno che gira sulla giostra la pallina sembra proprio andarsene sempre più lontana, in senso radiale. Può anche misurare in qualche modo la distanza tra lui e la pallina, magari con uno spago o un elastico. Ormai è più che sicuro. La forza centrifuga esiste sicuramente ed è proprio diretta in senso radiale. L’alieno ha torto marcio! Se si slegasse farebbe la stessa fine anche lui. E’ la stessa cosa che succederebbe se qualcuno tagliasse la corda. Il passeggero sarebbe in balia della forza centrifuga dato che è stata abolita la forza centripeta che riusciva a tenerla a freno.

E, invece, l’alieno ha ancora ragione. Per lui, infatti, è successo proprio quello che immaginava. Lasciando la pallina rossa o tagliando la corda, la pallina o tutto il seggiolino (occupante compreso) sono finalmente liberi di andarsene seguendo il tanto amato moto rettilineo uniforme, ossia vanno dritti seguendo la tangente al cerchio che prima la forza centripeta li obbligava a descrivere. D’altra parte, il martello dell’atleta scappa proprio secondo la tangente. Chi assiste all’impresa sportiva allo stadio ne è più che sicuro. Tutti gli spettatori, in quel caso, sono alieni!

Cosa possiamo concludere ancora una volta? E’ il sistema di riferimento che decide se esiste o no la forza centrifuga, ma per chi sta ruotando essa diventa una forza a tutti gli effetti capace di agire direttamente su chi la subisce. Se l’occupante della giostra avesse una borsa al suo fianco sentirebbe e come la forza che cerca di strappargliela di mano! Così come il lanciatore di martello sentirebbe la forza della sfera che cerca di andarsene. L’inerzia è una lottatrice impavida anche quando si trasforma in forza centrifuga!

Il secondo esempio è quello forse più comune: basta andare in automobile su una strada a curve. Nel sedile posteriore c’è sempre qualcosa che può scivolare (magari la solita pallina rossa). Durante una curva verso destra il guidatore sente ben poco (è seduto e stringe il volante), ma la pallina inizia ad andarsene verso sinistra fino a sbattere contro la portiera. Il guidatore sarebbe più che sicuro: la pallina si è mossa perpendicolarmente alla direzione del moto. E invece, il solito alieno, direbbe di no. La pallina ha solo proseguito il suo moto rettilineo uniforme, ossia ha obbedito solo e soltanto alla sua inerzia. La Fig.16 fa capire la situazione molto bene. A destra, ciò che “vede” il guidatore; a sinistra, ciò che realmente succede per un alieno che osserva da un sistema inerziale. Chi ha ragione? Tutti e due, ancora una volta. La forza centrifuga ha agito molto bene sulla pallina (potesse parlare lo direbbe anche lei che è sbattuta violentemente contro la portiera). Qual è in questo caso la forza centripeta, l’unica vera forza osservata dall’alieno? L’attrito delle ruote con il terreno. E’ proprio questo che vieta all’automobile di andare dritta e la obbliga a curvare. Se, infatti, ci fosse del ghiaccio sulla strada vedremmo benissimo come sparirebbe la forza centripeta e … addio curva! La ruota, ovviamente, si ribella screpolando l’asfalto (il solito terzo principio della dinamica).

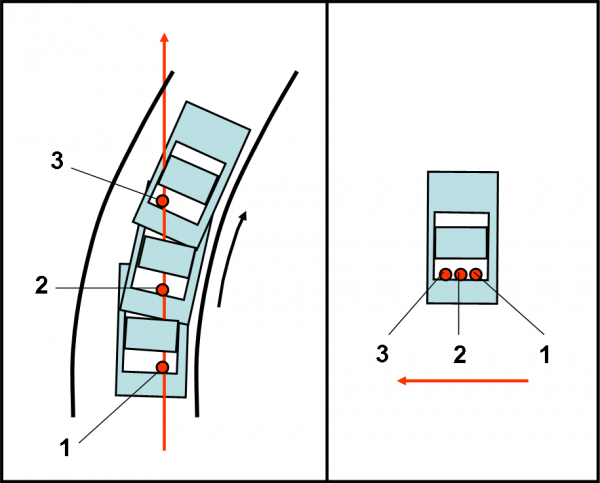
Facciamo attenzione che in questo caso la vettura non esegue effettivamente un moto circolare uniforme (le curve non sono cerchi perfetti) e, quindi, ci sarà anche una componente tangenziale dell’accelerazione che fa variare il modulo della velocità e non solo la sua direzione. In generale, dobbiamo dire che vi è un sistema di riferimento inerziale (alieno) e uno accelerato (non solo ti tipo circolare uniforme) in cui gli stessi fenomeni vanno trattati in modo diverso. Pensate, ad esempio anche solo a un moto rettilineo che subisce un’accelerazione o una decelerazione solo nel senso della traiettoria. Non avremmo curve, ma la velocità cambierebbe continuamente. La pallina rossa non andrebbe di lato, ma avanti e/o indietro, dato che la sua inerzia tenderebbe a farla proseguire di moto uniforme. Perché mai usiamo le cinture? Proprio per evitare gli effetti “locali”, ma ultra reali, di una improvvisa decelerazione. La velocità che avevamo acquisito prima della brusca frenata ci farebbe andare, per accontentare l’inerzia, contro il vetro!

Il terzo esempio riguarda uno sport invernale (ma non solo, ovviamente): il bob o lo slittino. La velocità di discesa è data normalmente dalla spinta e dalla gravità terrestre. Ma, immaginiamo, come al solito, per non complicare la trattazione, che sia solo dovuta a una spinta che riesce a far viaggiare il bob con velocità rettilinea uniforme. Si para davanti una curva a sinistra. Il bob andrebbe tranquillamente dritto, ma la parete della pista lo ferma e piega il bob che -a furia di continui scontri con il ghiaccio- esegue la curva e torna al moto rettilineo uniforme per un breve tratto (magari brevissimo). Altra curva e altro muro di ghiaccio che blocca l’uscita del bob e così via fino alla fine. L’alieno non ha problemi: per lui l’unica cosa che ha evitato la fuoriuscita del bob e gli ha permesso di eseguire le curve è stata la forza centripeta. Basta e avanza. Il muro ghiacciato impartisce la forza centripeta al bob e lo costringe a curvare. Il bob lascia il segno sul muro attraverso delle belle strisciate (tanto per cambiare, per il terzo principio). Chiedete al bobbista una volta che è arrivato in fondo, soprattutto se non è molto bravo ad assecondare le curve con lo sterzo e ad agire sul freno, se si è sentito tranquillo e riposato. Vi dirà, magari ancora balbettando, che ha sentito a ogni curva una forza terribile che cercava di farlo uscire di pista. Forza centrifuga e molto forte anche! Meno male che il muro l’ha annullata.  La Fig.17 mostra la situazione vista dall’alieno. In questo caso è il muro inteso come ostacolo a fare la parte della fune del lanciatore di martello e dell’attrito sulle ruote dell’automobile.

Quest’ultimo esempio ci porta sulla ruota di von Braun, illustrata in Fig. 18. Immaginiamo che sia lontano da pianeti e da stelle, nel vuoto più vuoto che c’è. Tutto è immobile o -più realisticamente- viaggia di moto rettilineo uniforme. Nessuna forza, nessuna gravità e nessun peso. Al suo interno si galleggia liberamente. Non è bello, però, vivere così. Meglio sfruttare la forza centrifuga come una specie di gravità artificiale. Sappiamo benissimo che chi vive all’interno del sistema la sentirebbe sicuramente. Mettiamo in rotazione l’intera ruota fino a che la forza centrifuga (che dipende come sappiamo bene dalla velocità che abbiamo impartito alla ruota) non sia sufficiente a spingere le persone contro la parete esterna. Non poco, ma  nemmeno troppo, se no sai quante “sardine” spiaccicate sulle pareti (e poi dicono che è una forza fittizia!). Si potrebbe benissimo fare in modo di ottenere una gravità uguale a quella che ci regala la Terra, basta agire sulla velocità.

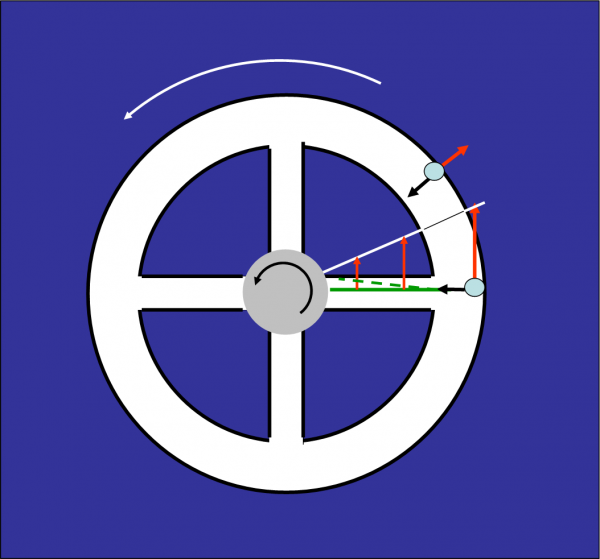
In realtà, l’alieno, che ormai ci perseguita, dice che le persone all’interno della ruota non fanno altro che sbattere contro la parte come il bob di prima. Solo la parete evita che vengano lanciate nello spazio lungo la tangente alla ruota. Le persone, all’interno, invece, si sentono pesanti come a casa loro. Tutto bene? Non tanto, in verità. Immaginate che uno voglia recarsi verso il centro della sfera lungo uno dei quattro raggi-corridoio (magari ci sono i bagni…). Poverino, sarebbe sbattuto contro la parete laterale. Non se lo sarebbe aspettato, dato che non conosceva un’altra forza fittizia (ma per lui MOLTO reale): la forza di Coriolis. Non posso illustrarvi anche questa (vi invito veramente, se siete interessati, ad acquistare la Fisica addormentata nel Bosco…), ma posso solo dire che, andando verso il centro, l’individuo cambierebbe la propria velocità tangenziale (diminuisce la distanza dal centro). La sua inerzia lo porterebbe a continuare come prima e un bella facciata contro il muro del corridoio non glielo toglierebbe nessuno! Meglio prevedere qualche bel cartello che indichi: “Attenzione, Coriolis in agguato!”

Forza fittizia? Sì, sì, ma che dà luogo a un fenomeno che deve esistere anche se visto dal di fuori. Pensate solo ai cicloni terrestri e alle correzioni che deve fare un pilota di aereo che parte da alte latitudini e deve raggiungere basse latitudini. A mano a mano che viaggia, cambia la velocità tangenziale terrestre e nasce … Coriolis.

Volete un esempio più indicativo? Mettetevi su una piattaforma girevole e cercate di giocare a golf. Davanti a voi, sempre sulla piattaforma, c’è la buca. E’ lì, la vedete benissimo, e gira assieme a voi, sempre nella stessa posizione.  Pronti, via, ed ecco un bellissimo tiro. Ma che succede? Siete  sicuramente un vero asso del golf, ma non di fisica. La pallina non va verso la buca, ma compie una curva allontanandosi dalla meta. Che figura! Purtroppo, fareste una figuraccia anche se visto dall’onnipresente alieno. Voi, grande campione, avreste lanciato in modo perfettamente rettilineo, ma mirando un punto ben lontano dalla buca. Che schiappa!

La spiegazione non è proprio banale, ma quasi. Se proprio non volete comprarvi il libro, prima o poi ve la spiegherò… oppure cercate di arrivarci da soli. I mezzi per farlo, in effetti, ce li avete tutti.

Anche vivendo sulla Terra e stando tranquilli in poltrona, siamo soggetti a una forza centrifuga. Non dimentichiamoci, infatti, che il nostro pianeta oltre che a creare la ragnatela gira come una trottola attorno al suo asse. E anche in modo piuttosto veloce, dato che all’equatore percorre ben 40 000 km in sole 24 ore. Bene o male questo fatto implica che, essendo in un sistema rotante, dobbiamo subire una forza centrifuga. Da che cosa è causata? Beh… ormai lo sapete benissimo: per annullare la forza centripeta che ci spinge verso l'asse di rotazione.

Meno male che la Terra è solida e si rifiuta di accoglierci. Noi, nel nostro piccolo, però, la schiacciamo al massimo delle nostre possibilità. Quanto riusciamo in questo ingrato compito dipende solo e soltanto dalla nostra massa e dalla forza di gravità. Attenzione, non sto parlando di accelerazione, ma proprio di forza e quindi chi ha più massa deve risentire di più della forza di gravitazione.

Essa vale, infatti:

F = GMm/r²

In realtà la formula a cui pervenne Newton non è questa ma un'altra (che abbiamo illustrato QUI). Egli , infatti, non riuscì mai a determinare il valore della sua costante gravitazionale G. Dovette quindi accontentarsi solo di rapporti di forze, in modo da eliminare quella scomoda costante, il cui valore fu ricavato solo un secolo e mezzo dopo grazie a sofisticatissimi strumenti di laboratorio e a piccole masse che, però, non servirono subito a determinare G, bensì la densità della Terra. Insomma, la storia di G è una lunga avventura nella quale il ruolo del protagonista è ricoperto dall'esperimento di Henry Cavendish del 1797-98 e ne parliamo QUI.

Al variare di m varia la forza che ci attira verso il centro della Terra e quindi anche la forza che noi applichiamo sul suolo. Stiamo, infatti, bene attenti che la forza di gravità sa agire anche a distanza, ma dato che noi calpestiamo il suolo, in questo caso agisce nel punto di contatto con il pavimento, dove lui si ribella e non ci fa passare (terzo principio, come sempre). La forza che noi esercitiamo sul pavimento è proprio la forza di gravità o forza centripeta. Normalmente la chiamiamo anche forza peso p e indica il peso di ciascuno di noi. Attenzione, quindi: il peso p è una forza. Se è una forza dipende dalla massa m, ma può cambiare indipendentemente dal suo valore, dato che compare anche la massa M e la distanza r. Anzi possiamo dire che il rapporto tra peso e massa di un corpo è proprio l’accelerazione di gravità. Infatti:

p/m = GMm/mr² = GM/r² = g

Chiamiamo l’accelerazione di gravità al suolo g, dato che è una costante se il corpo che la genera (g è un’accelerazione e quindi fa parte della ragnatela) è perfettamente sferico e omogeneo. Diciamo, normalmente, che g è una costante anche per i corpi che cadono al suolo, dato che le altezze raggiungibili dalle cose terrene sono ridicole rispetto al raggio r della Terra. Il peso diviso per la massa è quindi proprio g.

La massa è sempre la stessa, ovunque si vada nello Spazio, mentre il peso dipende dal corpo che ci attira verso di sé.

Per definire questa forza non c’è assolutamente bisogno che la Terra ruoti. La gravità esiste, comunque, insieme a tutta la sua bella ragnatela di accelerazione, che al suolo vale proprio g. Ripetiamo ancora:  un corpo che poggi sulla superficie di un pianeta (la Terra, ad esempio) è soggetto alla forza di gravità e alla sua accelerazione e quindi vorrebbe proseguire verso il baricentro del pianeta, ma ne è ostacolato dal terreno, una materia troppo dura per essere perforata. Il corpo spinge verso di lui e il terreno si ribella seguendo la terza legge della dinamica e ci fa sentire il peso che abbiamo. In realtà, il peso si sente proprio per la reazione che il terreno applica su di noi.

Immaginate una mela che ci cade in testa (tanto per non dimenticare il signor Newton). La mela ha un suo peso, ossia, una sua forza peso che è quella che l’attira verso il centro della Terra, regalandogli la famosa accelerazione di gravita che la fa cadere verso il basso. Se la nostra testa si frappone a questa caduta, agisce come il terreno agisce su di noi: ferma la caduta della mela. La forza peso della mela si trasferisce sulla nostra testa che “sente” il peso della mela  e dà luogo a un bel bernoccolo. Se la reazione della testa  (o del suolo) non è sufficiente a bloccare il movimento della mela, il suolo si deforma (si forma un buco, ad esempio) e/o la testa si rompe.

Con queste idee ben chiare, guardiamo cosa succede sul nostro pianeta. Immaginiamo che esso sia una sfera perfetta e che non ruoti. Qualsiasi abitante della Terra è soggetto alla stessa accelerazione di gravità. Per trovare il suo peso basta moltiplicare la massa per una costante tipica della Terra, l’accelerazione g. Se due corpi hanno la stessa massa hanno anche uguale peso, dovunque si trovino.

Mettiamo, adesso, in rotazione il pianeta e lo facciamo ruotare attorno a un asse che passa per il centro. Gli abitanti sono adesso soggetti a una rotazione che li trascina insieme al terreno. Conviene risolvere il problema relativamente alla persona che ruota. Sappiamo benissimo che, pur dovendo inserire una forza fittizia, il fenomeno rimane sempre lo stesso. Cosa succede alla persona P che si trova a una certa latitudine? Lui sente nettamente una forza centrifuga che lo spinge verso l’esterno. Noi sappiamo che è una “fittizia” reazione a una forza centripeta, ma sappiamo anche che essa è una forza reale per l’osservatore che ruota. Che cos’è che riesce a fare stare fermo la persona P? Ovviamente la reazione alla forza centrifuga che è una forza centripeta. Tuttavia, la forza centripeta che può agire è la gravità terrestre. Essa, però, è diretta verso il centro della sfera e non è perpendicolare all’asse di rotazione. Dobbiamo, allora, scomporre questa forza di gravità in due componenti: Una è quella centripeta che pareggia la forza centrifuga, l’altra è ciò che rimane della forza di gravità, ossia della forza peso della persona.

In Fig.19, basta fare il solito diagramma vettoriale e trovare la risultante di questa somma di forze. Una, quella centrifuga è diretta in direzione perpendicolare all’asse di rotazione, l’altra, quella di gravità è diretta verso il centro della Terra, Non ci resta che sommarle e troveremo ciò che resta della forza di gravità a cui è soggetta la persona P. Ricordiamoci, infatti, che una parte della forza peso è servita a compensare la forza centrifuga e fare sentire FERMA la persona P. La forza di gravità finale non è più diretta verso il centro della Terra ed è diminuita come modulo. Cosa succede all’equatore? Beh… la forza centrifuga è diretta in direzione opposta alla gravità. La forza peso si ottiene proprio togliendo al modulo della forza di gravita il modulo della forza centrifuga. Il peso è quindi minimo.

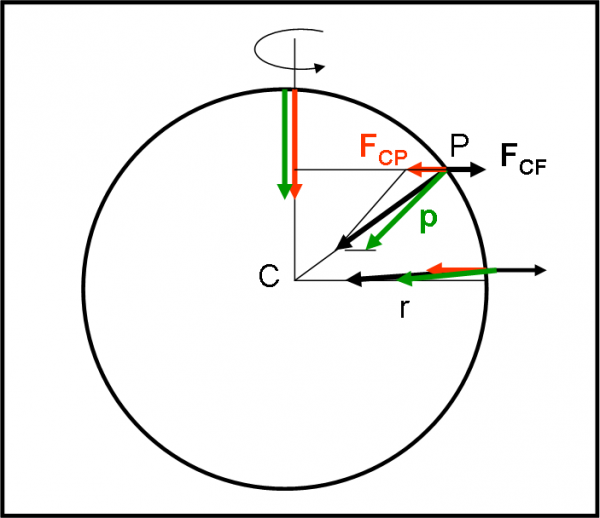
Dato che la massa è sempre la stessa, possiamo dire che a causa della rotazione la g non è più costante sulla Terra, dato che essa è proprio il rapporto tra forza peso e massa del corpo. E se la forza peso cambia, deve cambiare anche g, ricordando che:

p/m = g

Il peso di un corpo è massimo ai poli, dove la forza centrifuga è uguale a zero e quindi il peso è esattamente uguale alla forza di gravità, diretta proprio verso il centro della Terra.

Solo un cenno ulteriore al fatto che quanto abbiamo raccontato vale per un corpo perfettamente rigido. In realtà la Terra è composta soprattutto da acqua che può spostarsi, ossia non è vincolata al terreno. Capita, allora, che una goccia d’acqua a grandi latitudini tende a essere spostata verso l’equatore. Abbiamo infatti visto che la direzione della forza di gravità NON è perpendicolare alla tangente alla sfera terrestre nel punto P. Ciò vuol dire che esiste una componente che applica un’accelerazione diretta verso il basso e trascina la goccia con sé (la goccia può scorrere sulle altre, essendo un liquido). In poche parole, le gocce tendono a concentrarsi verso l’equatore dove si devono fermare perché in quel punto sparisce la componente della gravità che non è perpendicolare alla tangente. Ai poli la Terra si schiaccia e all’equatore si gonfia. Chi ha giocato questo scherzetto? Nuovamente la forza centrifuga che ha comandato la variazione della direzione della forza di gravità risultante e ha fatto subire un’accelerazione diretta verso l’equatore (freccia azzurra). La situazione è riassunta nella Fig. 20.

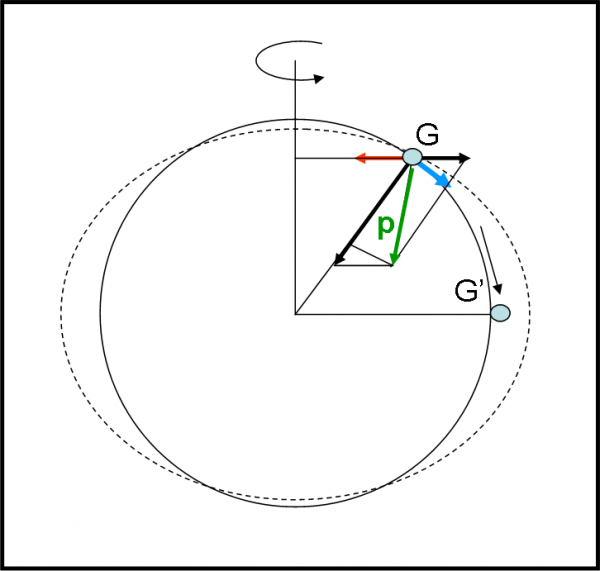
Se non avete capito bene come si può scorrere verso il basso, pensate a una discesa asciutta e a una discesa ghiacciata. Nel primo caso, se qualcuno vi spinge leggermente verso il basso riuscite, comunque, a stare fermo; nel secondo caso, invece, scivolate senza speranza.  Siete, in pratica, svincolati dal terreno. Qualcosa di simile a quanto abbiamo visto con l’automobile sul ghiaccio… Questa forma ellittica della Terra gioca ulteriormente sul peso di un corpo, dato che la gravità cambia anche a causa della variazione del raggio r della Terra che è massimo all’equatore e minimo ai poli.

Non voglio girare il coltello nella piaga… ma una goccia che scivola su una superficie rotante è soggetta anche a un’altra forza “fittizia”, quella di Coriolis, come già accennato prima. Vi faccio un ultimo esempio su Coriolis. Immaginate di essere su un autobus. Come già visto, quando è in curva sentite la forza centrifuga che vi spinge verso il finestrino. Provate, adesso, a muovervi lungo il corridoio. State facendo come la pallina da golf sulla piattaforma rotante. Non sarà facile camminare perché alla forza centrifuga si aggiunge anche quella di Coriolis… Insomma, voglio proprio farvi venire voglia di acquistare il libro…. ah ah ah… Tra parentesi, dopo le lezioni sulla matematica non dovreste più vere paura delle formule…

Va bene. Abbiamo concluso la nostra lunga disquisizione sulla caduta della Luna che ci ha portato ben più lontani. La risposta più giusta alla domanda di partenza è allora: “Sì, la Luna continua a cadere verso la Terra, ma la sua inerzia, ossia la sua velocità che cerca di mantenerla in moto rettilineo uniforme, ritarda indefinitamente il momento della caduta”. Vale , però, anche l’altra risposta: “No, la Luna se se ne sta andando per la sua strada, ma è attirata istante per istante verso la Terra e riesce a non scappare e a girare indefinitamente intorno al pianeta”. Insomma, avete capito il succo dell’intero discorso? Ciò che conta nella descrizione è solo e soltanto il sistema di riferimento. La Luna non fa altro che seguire lo stesso identico fenomeno: un moto circolare uniforme attorno alla Terra. A questo punto, il suo moto si potrà anche spiegare, e discutere, attraverso altre grandezze fisiche, come il momento angolare e l’energia…

 

 

“Le lune e i pianeti sembravano dunque governati da una regola semplice e l’uomo l’aveva capita. Con questa regola l’uomo è stato in grado di prevedere il movimento dei pianeti e questa sarà la base del successo della Scienza negli anni a seguire, perché ha reso plausibile la speranza che altri fenomeni, nel mondo, siano governati da leggi semplici e meravigliose”. Questo ci dice Gatto Gualtiero (tradotto dal suo insostituibile collaboratore Alan) a proposito della Legge di Gravitazione Universale, in QUESTO VIDEO che di riduttivo ha solo il titolo… non perdetevelo!

Mela o non mela… questo è il problema! QUI  una semplice e divertente spiegazione di Curiuss, coadiuvato dal fido assistente micio Gualtiero, sulla genialità dell’intuizione di Newton circa la Legge di Gravitazione Universale.