Riportiamo la soluzione del quiz che va oltre alla semplice spiegazione e che apre interessanti sviluppi sia per la fisica newtoniana che per l’ottica geometrica applicata ai telescopi. Un articolo da leggere… e con un nuova proposta di quiz.

La rotazione di un secchio d’acqua è uno dei classici della fisica e comporta una configurazione di perfetto equilibrio del liquido. Si dimostra abbastanza facilmente che la forma assunta dal liquido è quella di un paraboloide di rotazione, l’ideale per eliminare il difetto principale di un obiettivo a specchio sferico: l’aberrazione sferica.

Un po’ di storia…

I telescopi a specchio liquido rappresentano una soluzione teorica  (messa sovente anche in pratica) per ottenere una superficie riflettente capace di far convergere tutti i raggi luminosi, tra loro paralleli, in un unico fuoco (situazione non ottenibile con uno specchio sferico QUI). La forma necessaria per il liquido è quella del paraboloide di rotazione.

Il liquido (generalmente mercurio) è inserito in un contenitore di diametro prefissato che viene fatto ruotare attorno a un asse verticale con una velocità angolare costante ω. Il liquido è soggetto ad alcune forze che lo inseriscono in equilibrio quando esso assume la forma del paraboloide di rotazione.

Newton aveva già avuto l’idea per realizzare un simile strumento, ma non riuscì mai a costruirlo per problemi nella stabilizzazione della rotazione. Solo nel 1850, Ernesto Capocci sviluppò il sistema pratico che venne realizzato praticamente nel 1872 in Nuova Zelanda.

Ovviamente, se il telescopio viene usato mentre avviene la rotazione, esso può puntare solo verso lo zenit. Ciononostante, un telescopio di questo tipo, di ben sei metri di diametro, è in uso in Canada.

Si possono anche usare liquidi che diventino solidi senza perdere l’accuratezza della forma e che, quindi, possano venire trasportati. Oggi, con i telescopi a tasselli e con le tecnologie ultra precise, i telescopi parabolici vengono costruiti in modo diverso. Rimane, comunque, la genialità dell’intuizione.

Tuttavia, il quiz mira soprattutto a dimostrare che il liquido in rotazione assuma la forma di paraboloide. Il che vuole anche dire, per semplicità di descrizione, che la sua sezione verticale sia una parabola (QUI).

Vi sono vari metodi per arrivare al risultato, estremamente simili tra loro, che dipendono soprattutto dal considerare un sistema di riferimento rotante oppure no. Il “nostro “ Arturo è stato bravissimo nella sua ultima risposta a mettersi in un sistema rotante e a far giocare al meglio la forza centrifuga e la forza peso. Noi lo seguiamo senza esitazione… In ogni modo, la forma del liquido assume una configurazione stabile e questo rende semplice qualsiasi trattazione.

Consideriamo, in Fig. 1, i due assi x e y aventi l’origine in V. Il liquido ruota attorno all’asse y.

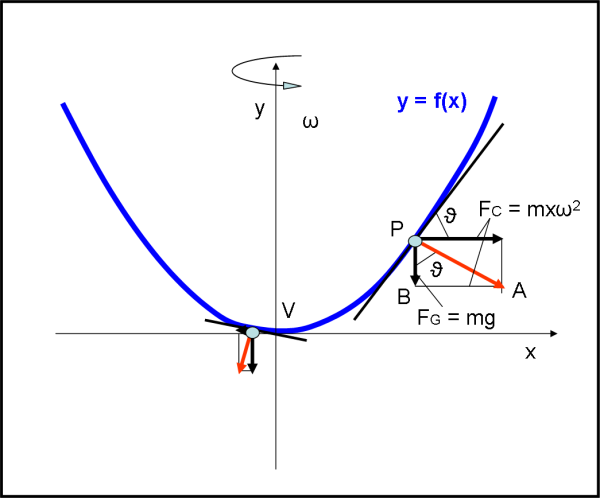
Sia P una particella di liquido di massa m, estremamente piccola. Durante la rotazione, su di essa agiscono la forza centrifuga F_C e la forza peso F_G. La risultante delle due forze corrisponde a quella che la particella esercita sul resto del liquido. Per l’equilibrio della configurazione  questa forza è bilanciata dalla forza che il resto del liquido esercita sulla particella (terzo principio della dinamica). Essa deve essere normale alla tangente alla superficie in P, dato che se esistesse una componente parallela il liquido scorrerebbe e non sarebbe in equilibrio.

Quello che dobbiamo fare è trovare l’equazione y = f(x) della sezione sul piano del foglio della superficie di rotazione.

Sia ϑ l’angolo che la tangente in P forma con l’asse x.

Attenzione: la tangente trigonometrica di questo angolo non è altro che la derivata (QUI e QUI), nel punto P, della funzione y = f(x), ossia della curva cercata.

In parole matematiche:

dy/dx = tan(ϑ)    …. (1)

Consideriamo il triangolo PAB. L’angolo in P è uguale a ϑ, dato che è formato da rette perpendicolari all’asse x e alla tangente.

Ne segue che:

tan(ϑ) = AB/PB    …. (2)

Tuttavia, il segmento AB non è altro che il modulo della forza centrifuga che vale mxω², mentre il segmento PB è il modulo della forza peso che vale mg. Sostituendo nella (2), si ha:

tan(ϑ) = xω²/g

Ma, per la (1), si ha:

dy/dx = xω²/g        …. (3)

Questa relazione ci dice che la derivata prima in un qualsiasi punto della curva è uguale a una costante (ω²/g) moltiplicata per x. Conoscendo il significato di integrale (inverso della derivata) è immediato ottenere la funzione y, integrando la (3) tra 0 e x (QUI).

y = ∫₀^x xω²/g dx = (ω²/g) ∫₀^x x dx = (ω²/g) x²/2 – 0 = (ω²/2g) x²     …. (4)

Questa non è altro che una parabola che passa per l’origine del tipo y = ax² (QUI)

Dimostrato che il liquido assume la forma di un paraboloide di rotazione, parliamo un poco del suo fuoco…

Innanzitutto, dobbiamo ricordarci qualche proprietà della parabola (QUI) e applicarle a un sistema ottico (QUI). In poche parole, si ottiene che tutti raggi luminosi provenienti da una sorgente all’infinito (e quindi paralleli tra loro) si riflettono in un unico punto detto fuoco.

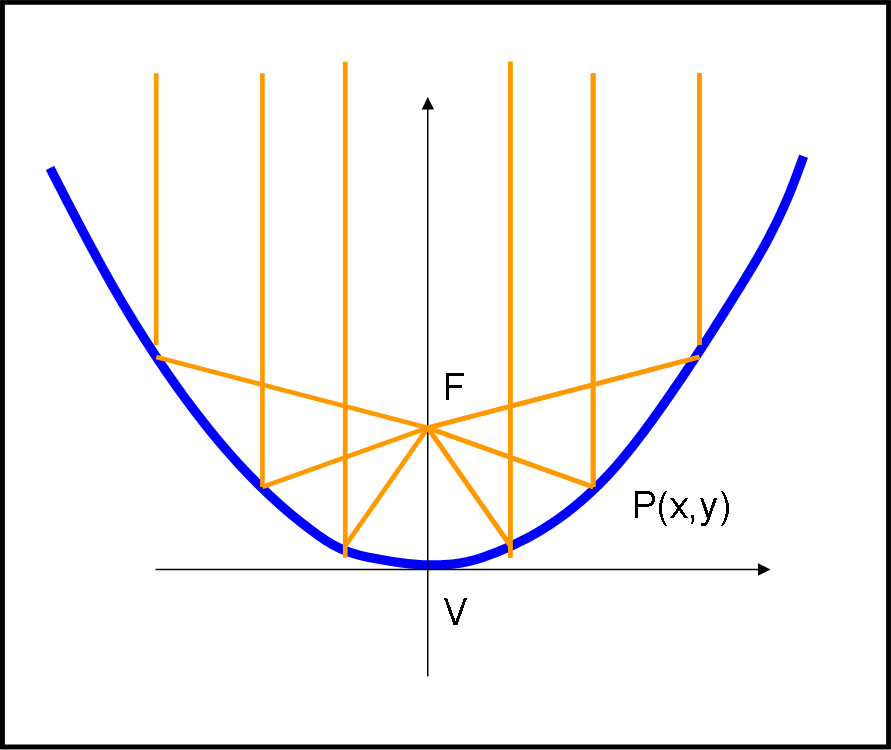
La formula che lega la distanza focale VF = f, l’ordinata y del punto di contatto del raggio e l’ascissa di questo stesso punto è data da (Fig. 2):

4f y = x²        …. (5)       (QUIZ: chi vuole può divertirsi a ricavarla…)

Sostituendo la (4) nella (5) si ottiene:

4f(ω²/2g) x² = x²

2f ω²/g = 1

E infine:

f = g/2ω²

La semplice formula ci permette di calcolare la distanza focale in funzione della sola velocità angolare e, quindi, di avere un telescopio variabile a seconda della rotazione che imprimiamo al liquido.

Peccato, veramente, che questo sistema abbia molte limitazioni, ma resta -comunque- un’idea veramente geniale… alla Newton, che ogni astrofilo che si professa tale dovrebbe conoscere. Sarà vero…?

QUI trovate il quiz