Questo articolo è inserito nella sezione d'archivio "Ottica"

 

Partendo da un pescatore sprovveduto e da un pesce molto furbo, passeremo attraverso i giochi di prestigio della luce, per giungere fino ai telescopi e alle loro caratteristiche.

In fondo, se riusciamo a capire sempre meglio la struttura e gli attori dell’Universo lo dobbiamo ai telescopi sempre più grandi e raffinati. E’ quindi giusto essere in grado di capire quali sono i loro limiti e le loro potenzialità. Parlare di telescopi non vuol dire limitarci, anzi… La vera limitazione è quella di usarli come un qualsiasi telefonino senza sapere come funzionano. L’ottica geometrica e l’ottica ondulatoria ci faranno capire i telescopi, ma ci permetteranno anche degli intriganti paralleli con quanto abbiamo imparato nella MQ e nella QED, in particolare.

Torniamo ancora una volta, allora, a parlare di luce e di sorgenti che la emettono. E' talmente importante che il tornarci sopra non fa mai male.

Iniziamo con la Fig. 1. Essa ci mostra una sorgente che invia le sue onde di luce circolari (in realtà sarebbero sferiche nelle tre dimensioni). Se niente le disturba, si allargano sempre di più andando a spasso per l’Universo. Una parte di esse può raggiungere l’osservatore che, allora, è in grado di “vedere” la stella. In realtà, per vedere la sorgente, si deve  già usare un primo strumento ottico: l’occhio, con tanto di obiettivo, fuoco e lastra “fotografica” o CCD. Ma… andiamo con calma.

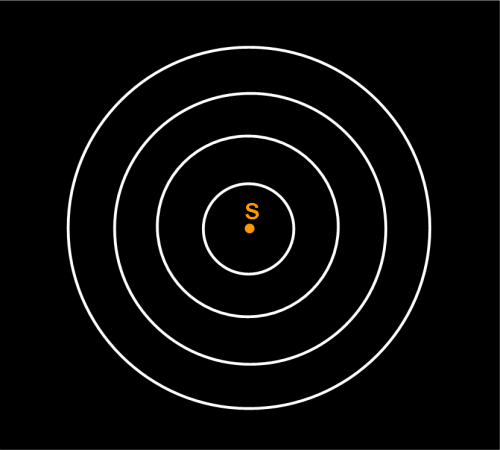
Immaginiamo la nostra stella talmente lontana che le sue dimensioni possano essere considerate trascurabili rispetto alla distanza dell’osservatore. In altre parole, possiamo considerarla una sorgente puntiforme. E quando dico puntiforme dico proprio puntiforme, ossia un vero punto. Talmente piccolo che se riuscissi a vederlo senza alcun difetto dovuto all’occhio, al telescopio, al binocolo o cose del genere dovrei riuscire a vederlo veramente privo di dimensioni (un po’ come il punto matematico …). Tutte le stelle, a parte il Sole, possono essere considerate così. Lasciamo per adesso da parte il “punto” e vediamo di seguire il suo sistema di onde luminose.Teniamo, però, ben presente questa considerazione che tornerà molto utile più avanti (e la tratteremo nell'Appendice)

Consideriamo la Fig. 2 (che è uguale alla Fig. 1) ed eseguiamo un’ulteriore semplificazione. Invece di disegnare tutte quelle circonferenze, possiamo benissimo tracciare solo la direzione che parte dal centro e va verso l’esterno, un po’ come facciamo con il palloncino che rappresenta lo spazio e il tempo che parte dal Big Bang e che definisce istante per istante il raggio del palloncino. In altre parole, invece di disegnare le circonferenze posso disegnare solo le rette che partono dalla stella e che, per definizione, sono sempre perpendicolari alla circonferenza, o, meglio, alla tangente alla circonferenza nel punto in cui la toccano. Esse rappresentano perfettamente le circonferenze: disegnate loro, si possono disegnare subito le circonferenze corrispondenti.

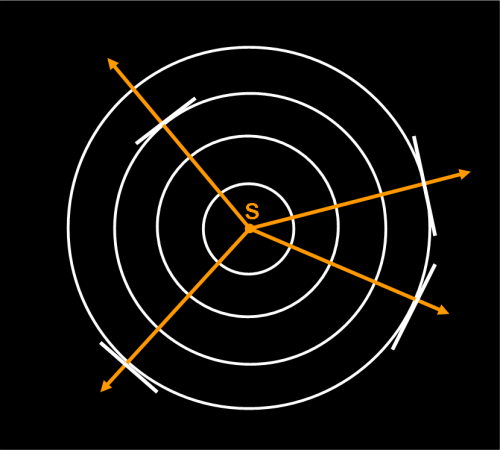
Chi vuole pensare un po’ di più, trova una perfetta corrispondenza con il campo gravitazionale e le sue linee di forza.

Questi raggi vengono chiamati raggi luminosi e sono, molte volte, più che sufficienti a caratterizzare le onde sferiche.  Lasciamo, per il momento, da parte queste ultime e lavoriamo solo con i raggi. Quando ne avremo bisogno sapremo subito come disegnare anche loro. Per essere “tecnici”, questo tipo di studio della luce prende proprio il nome di ottica geometrica ed è più che sufficiente per definire i vari tipi di telescopio e non solo. Si potrebbe anche pensare ai raggi come alle traiettorie dei fotoni, considerando la luce come un  qualcosa trasportato da particelle. La natura ambigua della luce è ben nota, ma ha il vantaggio di descrivere la realtà scegliendo il modo  più comodo per lo scopo che ci si prefigge. La soluzione migliore (e più complessa) sarebbe quella di usare la meccanica quantistica, ma, per lo scopo di questa trattazione, onde e/o raggi sono più che sufficienti.

Se il raggio dei cerchi, che rappresentano le onde, si allunga sempre di più, ossia se la distanza dalla sorgente diventa veramente molto grande, la piccola parte di onda che raggiunge la terra T può essere considerata piana e non circolare. Invece di onde concentriche, potremmo tranquillamente considerare onde rettilinee, tutte parallele fra loro, proprio come in una spiaggia davanti al mare aperto, come rappresentato in Fig. 3, a destra.

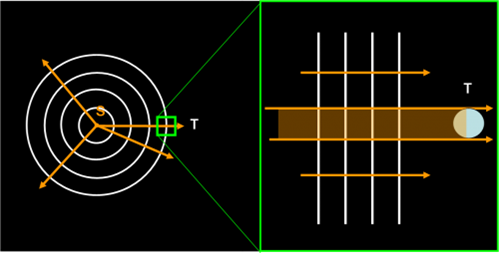
Da che raggi luminosi sono rappresentate queste onde? Facile a dirsi: da un insieme di rette perpendicolari alle linee delle onde, tutte parallele fra di loro. In questo modo abbiamo fatto nostro un primo importantissimo concetto fisico: il fascio luminoso proveniente da una stella può essere disegnato come un insieme di raggi luminosi paralleli tra di loro. Un concetto non così difficile, direi…

Un fascio praticamente infinito, dato che si estende ovunque nello spazio. Le sue dimensioni sono solo limitate dalla parte che colpisce la Terra (parte arancione nella figura), o l’osservatore o, meglio ancora, il  prezioso telescopio personale, ossia l’occhio.

Per semplificare ancora le cose, consideriamo un solo raggio che arrivi fino al suolo terrestre (i suoi amici sono uguali e paralleli). Immaginiamo che sia stato così fortunato da non incontrare molecole di gas o di polvere sospese nell’atmosfera. Esso tocca terra (anzi acqua) in un punto, formando un certo angolo con la perpendicolare alla superficie di  un fiume o di un laghetto limpido e trasparente.

Il raggio si piega: la rifrazione

Cosa fa il nostro raggio dopo tanto cammino? E’ capace di proseguire anche nell’acqua oppure no? Sicuramente sì, anche se deve subire una modifica piuttosto importante.

In Fig. 4. immaginiamo che la retta z sia la perpendicolare alla superficie d’acqua. Il raggio luminoso (giallo), che è arrivato viaggiando nell’aria, forma un certo angolo d’incidenza i con la linea z. Esso penetra nell’acqua, ma viene deviato rispetto alla direzione precedente. In che modo? Semplice, si piega in modo da formare un angolo r (detto di rifrazione) più piccolo, con la retta z, all’interno del liquido.

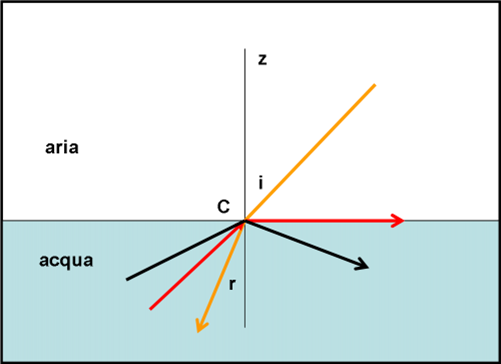
Perché è capitato tutto ciò? Perché l’acqua si oppone in modo diverso al cammino (ottico) del raggio (ossia, il suo percorso). In realtà, ciò che succede è che il contatto con l’acqua modifica il sistema di onde che provengono dalla stella o da ciò che preferite. Lo modifica cambiando apparentemente la direzione di provenienza. Non sarebbe difficile spiegarlo, ma per adesso accettatelo come un dato di fatto, ci torneremo sopra un’altra volta. L’importante è che il raggio luminoso si avvicini alla perpendicolare tracciata alla linea di separazione tra acqua e aria.

Ovviamente, la QED ci ha dimostrato in ben altro modo come questo avviene, ma per le applicazioni pratiche che ci interessano non è il caso di disturbare elettroni e fotoni…

Ogni tipo di sostanza ha un particolare valore che indica quanto il raggio di luce viene deviato al suo interno. Questo parametro si chiama indice di rifrazione: più esso è grande e più il raggio luminoso si avvicina alla perpendicolare z tracciata rispetto al confine tra le due sostanze. In altre parole,  se l’indice di rifrazione di una sostanza cresce, diminuisce l’angolo che il raggio luminoso sottende rispetto alla perpendicolare alla superficie di contatto  tra le due sostanze. In formula matematica : r < i. La stessa cosa capiterebbe, ad esempio, se si passasse dall’aria al vetro. Quest’ultimo è proprio il caso che interessa le lenti e quindi i telescopi a lente.

Ovviamente, vale anche il viceversa: se un raggio passo da una sostanza con indice di rifrazione più alto a una con indice più basso, l’angolo aumenta. r diventa angolo di incidenza e i angolo di rifrazione. Esiste, però, un angolo limite o critico. Se l’angolo r raggiunge un certo valore (per l’acqua è 49° e per il vetro 42°) il raggio rifratto, passando dalla prima sostanza all’aria, diventa esattamente di 90° . Ossia il raggio si propaga proprio lungo la superficie (linea rossa). Se poi si supera quest’angolo il raggio torna indietro, ossia viene riflesso completamente (linea nera). Proprio su questo principio si basano le fibre ottiche. Di specchi e di riflessione parleremo in seguito.

Un pesce e un pescatore

Adesso, vogliamo solo capire perché i pesci vedono meglio di noi e perché l’arte della pesca non è così semplice come potrebbe sembrare. Insomma, facciamo il tifo per il pesce e prendiamo un po’ in giro il pescatore.… E quindi rimandiamo il vetro, le lenti e la riflessione a più tardi. Ovviamente, questo fenomeno nel suo complesso, ossia la deviazione del raggio luminoso quando passa da una sostanza a un’altra, prende il nome di rifrazione.

Prima di iniziare la cattura del pesce, il pescatore prende la canna da pesca e questa, senza volerlo, si immerge nel laghetto per metà. Il poveretto si accorge subito che essa sembra essersi piegata proprio in corrispondenza del punto C in cui tocca la superficie liquida. Accidenti con tutti i soldi che gli è costata è bastato immergerla nell’acqua perché si rompesse! Calma, calma. Non è successo niente di grave. E’ solo un’immagine virtuale, un’illusione visiva simile a un miraggio (parleremo anche di loro in seguito). E’ stata la rifrazione subita dalla luce che la canna immersa manda verso di lui a causare questa specie di miraggio.

Lo vediamo bene nella Fig. 5.

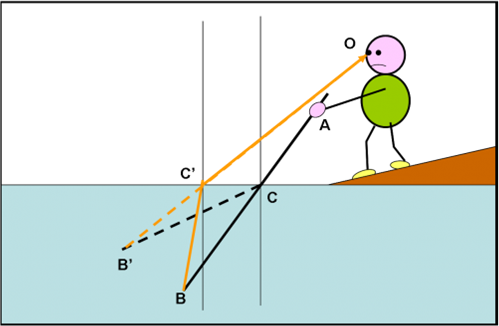
La canna AB è in realtà sempre dritta. Tuttavia il raggio di luce che parte dall’estremità B immersa nell’acqua viaggia verso l’esterno lungo il raggio BC’. Appena tocca la superficie in C’, esso è costretto, però, ad allontanarsi dalla perpendicolare z, a causa della rifrazione della luce, e quindi a seguire la linea C’O, fino a colpire l’occhio del pescatore. Egli, quindi, immagina di vedere la parte sommersa della canna nella direzione CB’ e non in quella vera CB. In altre parole, il punto B viene spostato dalla rifrazione  in B’. In conclusione la canna che appare all’occhio segue la linea spezzata ACB’.

Finché è nell’aria appare normale (AC), poi si piega fino ad arrivare in B’. Almeno questo è quello che percepisce il suo occhio. Se il pescatore conoscesse un minimo di ottica non si sarebbe certo spaventato, ma a lui interessa solo pescare, usando magari le canne e le esche più sofisticate presenti in commercio, l’ottica non gli serve a niente.

Il pescatore solleva la canna dall’acqua con grande rabbia, ma si accorge che è ancora perfettamente integra. Meno male: che spavento! Sicuramente è stato uno scherzo di un maledetto pesce! si riprende dallo shock e si rilassa. Comincia a guardare nel lago ed ecco comparire un pesce veramente eccezionale. Un vero mostro! Ma è proprio così grande?

Consideriamo la Fig. 6.

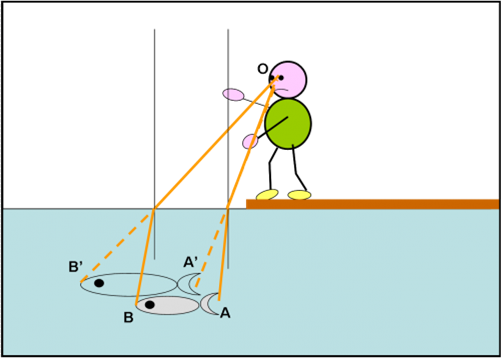
Il pesce “reale” è AB. Tracciamo i raggi luminosi che dalle due estremità del pesce vanno verso il pescatore. Sono quelli arancioni rappresentati dalle linee continue. Esse vengono rifratti con le modalità ormai ben conosciute e giungono all’occhio del pescatore lungo le direzioni B’O e A’O. Al pescatore il pesce AB apparirà nella posizione A’B’, ossia, molto più grande. Che preda! Anche se non riuscirà a catturarlo potrà dire ai suoi amici che era veramente una … balena!

Il pesce, comunque, non ha finito di prendersi gioco del pescatore. Quest’ultimo si accorge di essere troppo vicino al pesce e teme che lo possa vedere. Si allontana di qualche metro e allunga solo la canna. Povero illuso. Sembra proprio uguale ai bambini che giocano a nascondino e pensano di essere al sicuro da occhi indiscreti chiudendo gli occhi e voltandosi verso il muro.

L’ultimo capolavoro del pesce lo vediamo nella Fig. 7. Il pescatore è uscito addirittura dalla figura e si sente molto scaltro. Tuttavia cosa vede realmente il pesce? Ricordiamoci la Fig. 4 e il famoso angolo critico. Un raggio che arriva al pesce con un angolo di 49° deve aver viaggiato nell’aria proprio lungo la superficie. In altre parole il pesce vede entro 49° ciò che all’esterno è compreso in 90°, ossia dallo zenit al terreno. Ne consegue che con due rapide occhiate il pesce riesce a vedere tutto ciò che succede intorno a lui anche a grande distanza: la sua vista copre un angolo di 180° nel piano della figura o, meglio, di 360° nella realtà tridimensionale. Il povero pescatore sarà perfettamente visibile e il pesce si guarderà bene dall’ingoiare qualcosa che proviene dalla sua direzione.

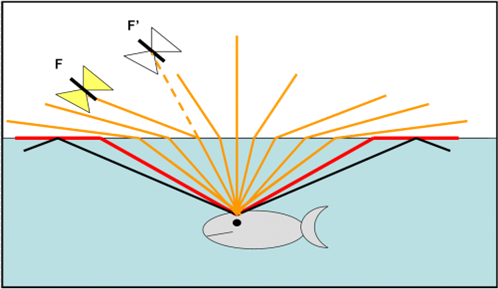
Il campo di vista limite del pesce è segnato dai raggi rossi. Per raggi ancora più inclinati (linee nere) la luce torna indietro nell’acqua.

Qualcuno potrebbe dire: “Il merito non è del pesce, ma della rifrazione che gioca a suo favore. Ammettiamo pure che il pescatore sia molto ignorante in ottica e non capisca assolutamente quanto gli potrebbe essere utile durante il suo hobby. Tuttavia, non è più ignorante del pesce che sfrutta soltanto una serie di situazioni a lui favorevoli”. Ne siete proprio sicuri? Immaginiamo che ci sia una ghiotta farfallina sopra il laghetto. Il pesce la vede distintamente. Tuttavia, la vera posizione dell’insetto è in F, mentre l’immagine che appare al famelico predatore degli abissi è F’.

Il pescatore se ne accorge (anche se forse è pretendere troppo da un uomo normale…) e gioisce tra sé e sé: “Tu mi hai fregato, ma adesso sarai pagato con la stessa moneta.” Una piccola vendetta, tipica della miseria intellettuale di molti uomini odierni. Con grande meraviglia del pescatore, invece, il pesce salta con perfetto tempismo e inghiotte al volo la farfallina. Sembra quasi che durante la ricaduta in acqua strizzi l’occhio al pescatore che si crede tanto furbo con le sue attrezzature di ultima generazione.

Il pesce ha tenuto in conto la rifrazione anche se è solo un pesce… Un concetto insito in chi vive a continuo contatto con la Natura. L’uomo, invece, schiavo ormai della tecnologia a scatola chiusa, non c’è riuscito!

Un pescatore in crisi

La canna è stata buttata per terra e gli occhi del pescatore sono fissi nel vuoto. Accidenti, essere fregati da un pesce è veramente troppo. La sfortuna (e chi altri, se no?) deve proprio averlo seguito. Si guarda attorno, ma non la vede e nemmeno riesce a scorgere il volto dell’ignoranza (forse non vuol vederla…). Lei cerca di mettersi in mostra, di attirarlo a sé, ma… non c’è peggior sordo di chi non vuol sentire.

Proprio in quel momento, di tragica depressione, ecco che l’invisibile sfortuna gli gioca un altro scherzo. Niente da fare ce l’ha proprio con lui. Davanti ai suoi occhi volteggia lentamente una foglia che si è staccata da un albero frondoso. Tutto normale. Il pescatore abbassa casualmente gli occhi verso l’acqua e gli si rizzano i capelli in testa. Del pesce, ovviamente, nemmeno l’ombra, ma, in compenso, ecco due belle foglie in fondo al laghetto. Sembrano perfettamente uguali, anche se una è un po’ più sfumata.

Non ci sarebbe niente di strano, ma il fatto è che un attimo prima non c’erano e che, inoltre, sono perfettamente identiche a quella sospesa in aria. La Fig. 8 illustra questa tragicomica scena. Non ha bevuto niente di alcolico, ma è costretto ad ammettere che non solo ci vede doppio, ma addirittura triplo: la stessa foglia in tre punti diversi. Si sente quasi svenire e meno male che non si accorge che il pesce si sta divertendo un sacco alle sue spalle.

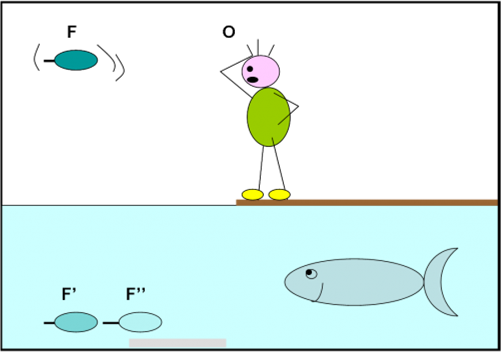
Si accascia al suolo e vorrebbe piangere. Non lo fa, solo per non dare soddisfazione al pesce che sicuramente lo tiene sotto controllo. Arriva il tramonto e poi la notte. Il pescatore, quasi automaticamente, mangia un panino che aveva in  tasca e finalmente si accorge che forse vicino a lui c’è l’ignoranza, anch’essa molto affamata. Alla buon ora! Nessun essere umano lo sta guardando e decide di concedere qualcosa a quella antipatica che lo perseguita giorno e notte.  Non molto, ma quanto basta per vedere apparire una luce improvvisa. E’ lì di fronte a lui, proprio dove nel pomeriggio aveva visto quella maledetta foglia. E’ tutto buio e i suoi occhi sono subito attratti da un’altra luce che è apparsa simultaneamente anche nell’acqua. Non solo, vicino a quest’ultima ce n’è un’altra ancora, appena visibile. Nel suo cervello qualcosa succede. Si apre una porticina e tutto gli appare chiaro e anche facile: l’ignoranza ha fatto un piccolo spuntino!

La Fig. 9 spiega il mistero del pomeriggio riapparso magicamente anche di notte.

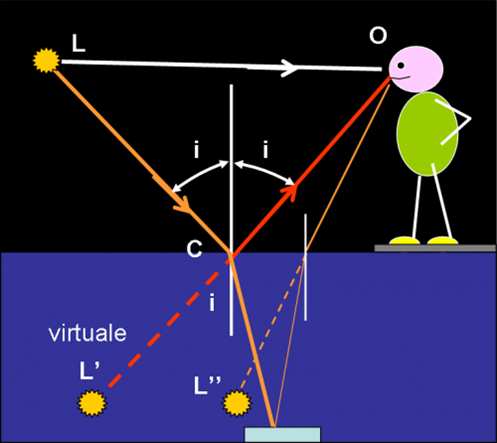
Un raggio partito dalla luce L arriva sulla superficie del laghetto. Tuttavia, sembra sdoppiarsi. Una parte prosegue all’interno del liquido avvicinandosi alla perpendicolare, seguendo la rifrazione che ormai conosciamo molto bene. Un’altra parte, invece, torna indietro lungo una retta che forma lo stesso angolo i rispetto alla perpendicolare. Quest’ultimo raggio, ricacciato verso l’aria, va a colpire proprio l’occhio del pescatore. Cosa vede il nostro sfortunato amico? O, almeno, cosa crede di vedere?

Beh, è facile rispondere: vede la luce nella direzione OC e gli sembra proprio che la sorgente luminosa sia in L’. La luce di L forma due immagini: una si forma nell’occhio del pescatore attraverso il raggio luminoso diretto LO; l’altra, L’, attraverso il raggio luminoso LC riflesso lungo CO. Ovviamente, non esiste niente nella posizione L’. L’ è un’immagine virtuale.

I raggi rimbalzano: la riflessione

Il pescatore, dopo la rifrazione, ha imparato anche la riflessione della luce. La notte porta consiglio e lui la passa cercando di capire anche l’origine di L’’. In  fondo, non è difficile.

Quasi ogni sostanza  accetta entrambe le possibilità dei raggi luminosi. Una parte della luce viene rifratta e un’altra parte viene riflessa. Ci sono, però, quelle che preferiscono far entrare al loro interno quasi tutta la luce e altre che non ne vogliono avere niente a che fare. L’acqua e il vetro accettano entrambe le cose con grande democrazia. Se, però, lavoriamo perfettamente una superficie di vetro, lisciandola al massimo, favoriamo la riflessione. Se, invece, la lasciamo grezza predomina la rifrazione.

Cosa analoga succede all’acqua se è più o meno increspata. Vi sono sostanze meravigliose per la riflessione, come l’argento e l’alluminio. Gli specchi di una casa sono vetri sottili e ben lisci che hanno dietro superfici particolari; i prismi a riflessione sono vetri spessi che stimolano invece la luce a entrare. Insomma, l’uomo è riuscito a sfruttare molto bene le caratteristiche dei raggi luminosi e delle sostanze. I telescopi utilizzano entrambe le possibilità, come vedremo più in là.

Torniamo a L’’. Una parte della luce emessa da L penetra nell’acqua avvicinandosi alla perpendicolare per rifrazione. Sul fondo del laghetto si trova “casualmente” uno specchietto (c’è chi dice che ce l’ha portato il pesce…) che riflette la luce di L. Il raggio torna indietro, tocca la superficie dell’acqua dalla parte interna, passa in una sostanza con indice di rifrazione minore e si allontana dalla perpendicolare, raggiungendo l’occhio del pescatore. Quest’ultimo vede, quindi, un’altra immagine di L in L’’ (in modo simile a quanto abbiamo visto  precedentemente  con la rifrazione). Compri tre e paghi uno! A questo punto è facilissimo capire cosa era successo con la foglia nel pomeriggio, come riporta la Fig. 10

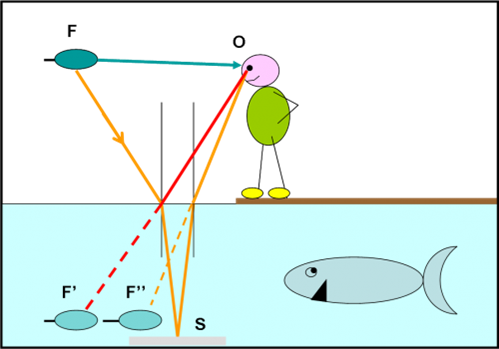
Il pescatore si sente un genio: ha capito tutto! Manda al diavolo l’ignoranza che avrebbe ancora fame e se ne va contento e orgoglioso di sé stesso. Ormai può considerarsi un esperto di ottica e … al diavolo anche i pesci squallidi di piccoli laghetti ancora più squallidi. Il mondo lo aspetta! Non si accorge, però, che il pesce è altrettanto contento. Un altro uomo ha capito che esistono cose più interessanti del pescare per hobby e ha preferito andare alla scoperta della Natura.

La Fig. 11 ci mostra ciò che ha capito finora il pescatore e noi con lui.

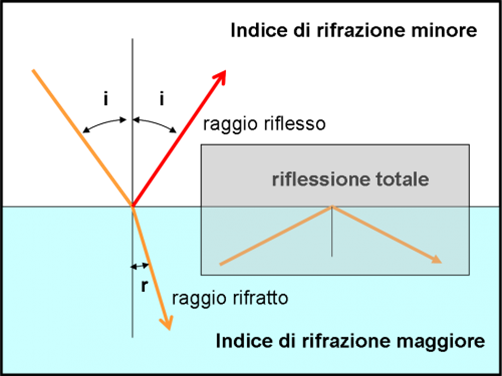
Tuttavia, resta una piccola parte “grigia” che il pescatore ha del tutto trascurato. Se ne accorgerà molto presto. Stiamo parlando, nuovamente, del superamento dell’angolo critico. E’ meglio ripetere il concetto perché ci sarà molto utile tra poco. Quando si è in un mezzo che ha un indice di rifrazione maggiore di quello contiguo, esiste un certo valore critico dell’angolo di incidenza oltre al quale il raggio viene completamente riflesso. Nella Fig. 11, l’acqua ha un indice di rifrazione superiore a quello dell’aria e il raggio, troppo inclinato, non riesce a uscire dall’acqua e viene riflesso, ossia “intrappolato” all’interno del laghetto. Il pescatore ha sbagliato completamente a trascurare questo fenomeno molto particolare ma anche molto efficiente e affascinante.

Miraggi e ... UFO

Sentendosi ormai un dominatore delle leggi dell’ottica, il nostro eroe decide di girare il mondo per indottrinare tutti con il suo “verbo”.  Essendo ancora legato alla pesca, che c’è di meglio che imbarcarsi su una nave che faccia una rotta in cui non sia difficile imbattersi in prede veramente colossali? Decide di  doppiare il Capo di Buona Speranza, una zona spesso colpita da uragani, da nebbie fittissime e soggetta a rapidi cambiamenti di temperatura.

I marinai, scherzando, gli narrano di leggende spaventose nate in quella zona e il pescatore ne rimane piuttosto sconvolto. Ovviamente, non si informa e rimane con la sua paura latente a guardare il mare avvolto nella nebbia che sta diventando tempestoso. Improvvisamente, un’immagine  terrificante gli si para di fronte: è lui, proprio lui! Il terribile vascello fantasma, l’Olandese Volante che a vele spiegate naviga, completamente rovesciato, nel cielo.

Solo dopo parecchi minuti e dopo la scomparsa dell’orribile visione il pescatore riesce a uscire dall’anfratto in cui si era rifugiato e a raccontare la terribile esperienza ai marinai. Fa anche uno schizzo della nave misteriosa (Fig. 12), aggiungendole vele e tanti particolari. I marinai lo guardano scrollando la testa e decidono di farlo sbarcare al più presto: potrebbe diventare molto pericoloso!

Peccato che il nostro eroe sia scappato troppo presto dal laghetto e non abbia scoperto la riflessione completa.

Quella zona di mare ha spesso causato, in tempi antichi, naufragi e molte navi sono state sbattute contro scogli o isolotti.  Ad esempio, un grande galeone olandese si era incagliato non troppo lontano dal capo sudafricano ed era rimasto in quella posizione per secoli, ormai ridotto a una presenza spettrale. Come si diceva prima, la zona è molto nebbiosa e la superficie marina alquanto fredda. Gli strati atmosferici più bassi sono quindi a temperatura inferiore rispetto a quelli degli strati appena superiori. Temperatura inferiore vuol dire aria più densa, pesante e indice di rifrazione  più alto. Aria calda vuole invece dire sostanza più leggera e rarefatta e indice di rifrazione più basso.

Consideriamo la Fig. 13.

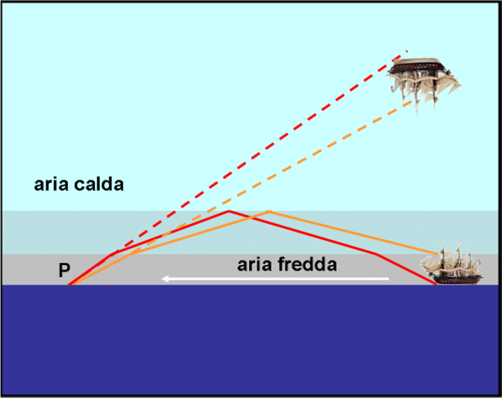
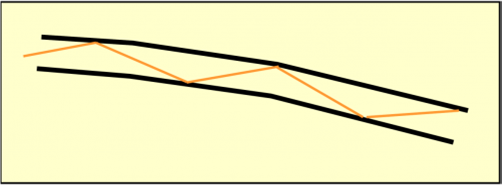
In basso a destra, in mezzo alla nebbia vi è il galeone incagliato. Il raggio luminoso (bianco) che esso invia verso la nave del pescatore P, non riesce ad arrivare a destinazione: troppa nebbia. Più fortunati sono invece i raggi mandati verso l’alto. Essi escono velocemente dalla nebbia fredda e si trovano in un ambiente leggermente più caldo e quindi deviano allontanandosi dalla normale. Continuano, comunque, a salire verso l’alto fino a trovare finalmente aria decisamente più calda, con indice di rifrazione molto più basso. Raggiungono questo strato con una direzione molto inclinata, superiore all’angolo critico della sostanza in cui stanno viaggiando.

Sono costretti, quindi, a subire una riflessione totale e tornano verso il basso, riavvicinandosi alla perpendicolare fino a raggiungere P. Tuttavia, la direzione apparente dei raggi che colpiscono P è diretta verso l’alto ed è proprio lì che si formerà l’immagine del galeone. Essendoci stato un incrocio dei raggi, l’immagine sarà anche capovolta. Tutto lì. Ecco spiegata la nave fantasma! Il fenomeno prende il nome di miraggio superiore, in quanto l’aria calda si trova in uno strato superiore rispetto alla zona di partenza dei raggi.

I raggi possono anche non incrociarsi durante il tragitto e la nave potrebbe vedersi dritta e non capovolta. Spesso l’immagine viene anche ingrandita rispetto all’originale per effetto lente (un po’ come capita per i raggi di luce che passano vicino a una grande massa) anche se, in questo caso, non c’è bisogno di scomodare la relatività. Basta pensare all’effetto causato da una semplice lente di vetro. Ne parleremo, state tranquilli.

A volte il fenomeno può permettere di vedere, apparentemente più vicini, oggetti che si trovano al di sotto della linea dell’orizzonte, come mostrato nella Fig. 14.

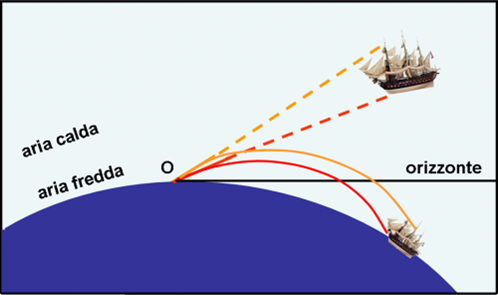
Abbiamo parlato di navi, ma qualsiasi cosa andrebbe bene: scogli, tratti di costa, iceberg, ecc.. Anche il mare non è veramente necessario. Il fenomeno può avvenire anche  su distese ghiacciate o altri luoghi simili. L’importante è che ci sia un’inversione termica rispetto a quella prevista teoricamente salendo verso quote maggiori: aria calda sopra aria fredda.

L’esempio dell’Olandese Volante è stato scelto solo per fare un po’ di “scena” e spaventare il pescatore che ancora non ha capito che… non ha ancora capito molto dell’ottica. Un po’ troppo arrogante. Tuttavia, la leggenda (reale) viene comunemente spiegata in questo modo. Pensate che aveva suggestionato anche il grande Wagner che ne ha scritto un’opera famosa.

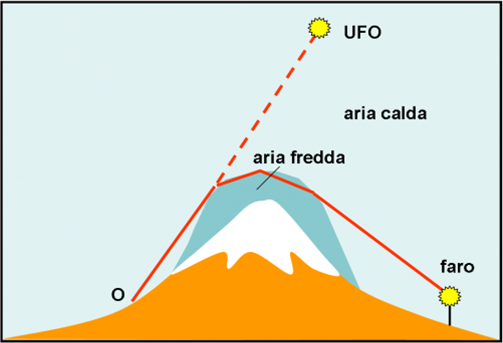
Per i tanti amanti del Cielo e per lo sparuto gruppetto che sicuramente crede agli UFO (ce n'è sempre qualcuno), il miraggio superiore può spiegare molto bene alcuni avvistamenti di Oggetti Volanti non Identificati. Consideriamo la Fig. 15. L’Osservatore è in O e sta osservando stelle e galassie. Improvvisamente, si accende un faro al di là della montagna dalla cima innevata. L’aria fredda che circonda la vetta del monte causa un miraggio superiore e il faro risplende alto nel cielo, aumentando e diminuendo la sua luminosità. Un altro UFO, magari anche fotografato!

Torniamo al nostro pescatore fatto sbarcare senza troppi complimenti in un qualche luogo della Namibia, in prossimità del deserto di Namib, che giunge fino al mare. Ovviamente, si perde quasi subito ed è costretto a percorrere un tratto non indifferente di sabbia arroventata. All’improvviso, quando la sete è ormai diventata un incubo, ecco di fronte a lui un’oasi con tanto di laghetto in cui si specchiano le palme. Finalmente! Si mette a correre come un disperato, ma l’oasi sparisce come era comparsa. Vi è qualche palma rachitica ma assolutamente nessuna pozza d’acqua.

Il nostro eroe si è imbattuto in un miraggio inferiore, quello più comune nelle zone desertiche o in pianure particolarmente assolate. In questo caso, gli starti più bassi dell’atmosfera sono quelli più caldi e diventano freddi molto velocemente salendo di quota (l’aria è tersa e limpida).

Vediamo ciò che è successo nella Fig. 16. Il pescatore scorge perfettamente la palma (raggio di luce diretto). Tuttavia, il raggio che parte dall’albero e va verso il basso incontra strati di aria sempre più caldi, ossia con indice di rifrazione più piccolo. Il raggio tende quindi ad allontanarsi dalla normale pur continuando a scendere. A un certo punto, però, supera l’angolo critico e viene riflesso completamente verso l’alto.

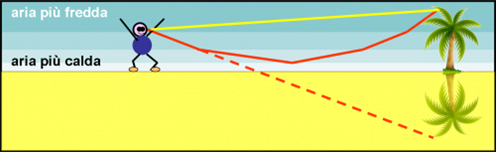
Comincia a salire piegandosi sempre di meno rispetto alla perpendicolare fino a raggiungere l’occhio del pescatore assetato, che quindi vede la palma anche in posizione più bassa, rovesciata rispetto alla vera immagine diretta. L’occhio umano associa immediatamente, per esperienza atavica, due oggetti sovrapposti e ribaltati alla presenza di uno specchio d’acqua (si chiama “specchio” apposta) e quindi crede di vedere l’agognata sostanza liquida proprio ai piedi della palma.

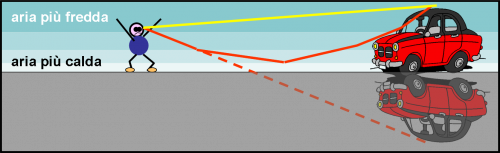
Fortunatamente, una carovana di passaggio lo preleva quando ormai è distrutto e disperato e lo conduce nella città  più vicina, Finalmente la civiltà, le case, le macchine, un albergo dove dormire. Sta per salire in camera quando l’ottica gli gioca il suo ultimo scherzo. Mentre attraversa la strada vede un gruppo di macchine venire verso di lui. Non ci sarebbe niente di strano se non stessero muovendosi proprio sull’acqua. Sperando che riescano a frenare si lancia sul marciapiedi con il cuore in gola. No, non c’era nessuna pozzanghera sulla strada. C’era solo asfalto molto caldo che ha causato uno dei fenomeni di miraggio inferiore  più frequenti nella vita di tutti i giorni. Una macchina che si riflette sulla strada fa nuovamente pensare a una distesa d’acqua, esattamente come ciò che è successo nel deserto con la palma (Fig. 17).

E’ ora di smettere di infierire sul pescatore. Speriamo solo che abbia capito la lezione e non si dimentichi più di sfamare la sua personale ignoranza. Voi ci credete? Io non tanto…

Su qualche testo troverete scritto che il miraggio superiore  viene anche chiamato Fata Morgana. In realtà, non è proprio così. La Fata Morgana è un  miraggio più complesso dovuto a un alternarsi di strati più freddi e più caldi in uno spazio breve. Uno dei luoghi più famosi in cui si verifica è lo stretto di Messina e il nome deriva da una leggenda che racconta come i saraceni giunti a Reggio Calabria abbiano visto la costa siciliana veramente vicina. Decisero, allora, di superare la piccola distanza a nuoto. La Sicilia era invece ben più distante e ciò che avevano visto era un miraggio.

Perirono tutti e nacque la leggenda legata a una fata, Morgana, che avrebbe eseguito il miracolo. La Fig. 18 mostra una foto presa dalla costa calabra, in cui si nota molto bene una costa “apparente” molto più vicina del reale.

Andando a spulciare nella Bibbia, c’è chi pensa che anche il passaggio del Mar Rosso di Mosè  sia legato a un miraggio inferiore, che abbia fatto apparire acqua dove invece non c’era e abbia scoraggiato gli egiziani dall’inseguire gli ebrei.

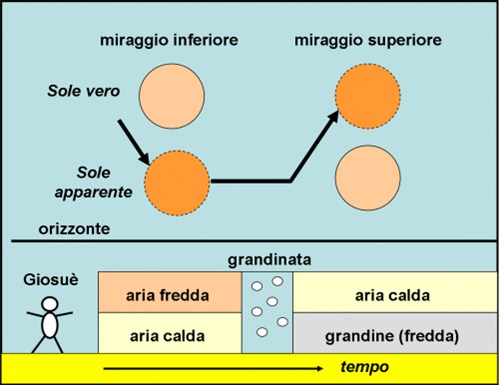
Più complesso potrebbe essere l’episodio di Giosuè che, al tramonto, ferma il Sole e poi lo fa risalire. In  quel caso ci sarebbe prima un miraggio inferiore e poi uno superiore causato da una violenta e improvvisa grandinata.

Giosuè arriva dal deserto. La sabbia calda produce un miraggio inferiore. Il Sole sembra più basso della sua posizione effettiva. Quando si avvicina ai nemici morti inizia a grandinare e si verifica un miraggio superiore. Anche se il Sole vero si è abbassato “naturalmente”, sembra più in alto della sua posizione apparente e quindi Giosuè vede il Sole prima fermarsi e poi, addirittura, tornare indietro. La Figura 19 schematizza il risultato finale. Non aggiungo descrizioni, in quanto potrebbe essere un ottimo esercizio per vedere se i "miraggi" sono stati ben assimilati.

Permettiamoci un’applicazione moderna dell’angolo critico e dell’effetto di riflessione totale. Sto parlando della fibra ottica, in grado di trasportare la luce all’interno di un cavo flessibile. Senza scendere nei particolari tecnici, vediamone uno schema in Fig. 20. La sostanza della parte interna del cavo ha un indice di rifrazione superiore a quello del rivestimento esterno. Se il raggio di luce viene “lanciato” con l’angolo giusto, continua a riflettersi lungo le pareti interne senza mai disperdersi lungo i bordi perché l’angolo è sempre superiore a quello critico e vi è riflessione totale.

Quante cose interessanti e affascinati abbiamo imparato o ricordato solo per esserci dedicati a un angolo, un semplice angolo che ha l’unico pregio di essere un po’ troppo grande. E siamo solo all’inizio dell’ottica.

Ad esempio, non abbiamo nemmeno parlato di lunghezza d’onda, considerando il raggio come se fosse sempre e soltanto composto di luce bianca. E invece…

E’ il momento di parlare di pentole d’oro e di folletti dei boschi…

Lasciamo da parte il nostro pescatore che ha deciso di non vedere più un lago in vita sua. Si è addirittura trasferito al mare e passa il suo tempo sul molo che delimita l’ingresso al porto della città. Si diverte a vedere le persone che con una canna in mano aspettano che qualche bella preda si attacchi al loro amo. Uno strano sorriso gli si dipinge sul volto e nessuno ha ancora capito se faccia il tifo per i pescatori o per i pesci. Lasciamolo in pace. Prima o poi ci tornerà utile, proprio in quella posizione all’imboccatura del porto, dove le onde incontrano un ostacolo imprevisto.

Occupiamoci, invece, di uno dei grandi misteri del mondo e degli uomini: come si forma l’arcobaleno? Vi sono due teorie, una scientifica e una legata alla magica vita che brulica nei boschi e che solo i bambini hanno la fortuna di conoscere. Cominciamo da quest’ultima… poi ognuno sceglierà quella che gli sembra più realistica.

La vera storia dell’arcobaleno

Una volta compresa la verità, bisogna continuare a crederci e a lottare perché non venga occultata. Fatevi aiutare dai bambini che di queste cose se ne intendono molto di più di voi.

Quanti racconti, quante leggende, quante spiegazioni scientifiche sull’origine dell’arcobaleno. D’altra parte quell’arco luminoso e colorato, che attraversa il cielo ancora grigio al termine di un temporale, ha da sempre stimolato la fantasia e l’intelligenza dell’uomo.  Se parlate con gli studiosi, vi diranno delle belle parole sulle gocce d’acqua sospese nell’aria e di come la luce solare si possa scomporre passando attraverso di esse. Fate di sì col capo, fingetevi interessati, ma non credeteci.

Altri vi diranno di correre nel luogo dove nasce l’arcobaleno: troverete una pentola piena di monete d’oro, che vi renderà ricchi. Mi raccomando non andateci! Rovinereste tutto. O almeno, prima di andarci, sentite la vera storia dell’arcobaleno e capirete la mia paura.

Come molti sanno, ma non dicono per cercare di approfittarne in gran segreto, chi fabbrica gli arcobaleni è l’infaticabile folletto ciabattino Leprechaun. Viene descritto come un diavoletto irlandese scherzoso, inaffidabile e perfino maligno. Tutte storie! Dicerie costruite proprio per non sentirsi in colpa nel rubare le sue pentole piene d’oro.

Tutto cominciò dieci giorni prima del passato remoto infinito. Il mondo era grigio e triste, senza colori. Il mare era grigio scuro, le foglie grigio chiaro e il cielo quasi bianco. Anche il Sole e la Luna erano grigi e le nuvole bianche che gli passavano davanti sembravano disegnare delle smorfie sconsolate sul loro volto.

Ogni tanto piangevano singhiozzando e le nubi, che avevano pietà, cercavano di trattenere il loro pianto disperato, ma non sempre ci riuscivano e questo si trasformava in pioggia. Leprechaun era triste, molto triste, e voleva trovare una soluzione. Pensava di giorno e pensava di notte, senza mai dormire. Poi capì che tutto era così grigio perché non vi era gioia. Non sapeva però ancora cos’era la gioia. Iniziò quindi a cercarla con tutta la caparbietà di cui era capace. Provò nel cielo, nel mare, nelle foreste… niente! Nessuno la conosceva.

Provò allora sotto terra. Era difficile muoversi tra tutte quelle rocce, la sabbia e i sassi taglienti. Proseguì comunque senza mai perdere la fiducia. Incontrò finalmente un’enorme goccia liquida. Tuttavia, non era il pianto del Sole o della Luna, era qualcosa di diverso. Era calda e densa e il folletto sperò che fosse la gioia. No, non lo era, ma la goccia sapeva come si poteva crearla.

Accompagnò Lepreachaun a casa sua. Che meraviglia! Non erano più soltanto gocce perché tutte insieme formavano un mare infinito che risplendeva di “colori” brillanti e luminosi. Gli dissero che si trovava nel cuore della Terra e  gli raccontarono che erano nate in un tempo molto più antico, ma che una strega cattiva le aveva nascoste al centro dei pianeti, perché l’uomo non potesse mai conoscerle  e provare la gioia. Solo i colori, infatti, portano gioia. Leprechaun era entusiasta e felice. Bastava che aprisse un foro e facesse uscire tutte quelle gocce, quei colori e con essi la gioia.

No, purtroppo non era così facile. L’incantesimo non l’avrebbe mai permesso. Se fossero uscite allo scoperto, e ogni tanto qualcuna ci provava, avrebbero portato solo distruzione e morte. Dovevano rimanere per sempre laggiù fino a spegnersi per sempre.

Leprechaun pianse fino a che ebbe lacrime. Era arrivato così vicino alla gioia e non poteva portarla con sé. Chiese di rimanere per sempre con quelle gocce e  morire con loro. Le più vecchie e sagge riaccesero, però, una speranza nel povero folletto disperato. Se avesse avuto forza, speranza, fiducia, fantasia, sarebbe forse riuscito a fabbricare da solo i colori anche dove non esisteva quel mare liquido e luminoso. Molto più vicino alla superficie esistevano gli stessi elementi che formavano quell’oceano di luce, solo che erano stati spenti e induriti dalla strega. Ma non erano morti: Leprechaun poteva farli vivere di nuovo. Doveva avvicinarli, unirli, mischiarli tra loro. Solo così sarebbero tornati a risplendere di mille colori e avrebbero “costruito” la gioia.

Leprechaun esultò e non vide l’ora di cominciare il nuovo lavoro. Non lo spaventava niente e nessuno: per ottenere quel risultato avrebbe superato qualsiasi difficoltà. Le gocce gli spiegarono che elementi doveva scegliere, come doveva mescolarli e combinarli. Era una fatica terribile, anche perché fino a che restava sotto terra non avrebbe potuto respirare. Il folletto guardò in faccia la gioia o almeno quello che rimaneva di essa e non ebbe alcuna esitazione. Tornò verso la superficie e cominciò la sua impresa.

Trovò quasi tutto quello che gli serviva, ma mancava soltanto un po’ di oro, che avrebbe permesso di passare dal rosso al giallo e poi al verde. Uscì allo scoperto e chiese aiuto a tutti gli abitanti delle foreste e delle pianure. Lui avrebbe preparato i composti sotto terra e poi sarebbe uscito portandoli dietro di sé lungo un  grande cerchio che avrebbe descritto in cielo. Da quel cerchio sarebbero usciti i colori, che avrebbero dipinto il mondo e con loro sarebbe nata la gioia.

Bastava che gli preparassero una pentola piena di monete d’oro nel punto in cui fosse uscito all’aperto e tutto sarebbe stato perfetto. Lo avrebbe mescolato con il resto e avrebbe disegnato nel cielo un perfetto arcobaleno. E così fu per tanti e tanti anni.

Il Sole e La Luna non piansero più e le nuvole azzurre e rosa che gli passavano davanti creavano curve sorridenti sui loro volti. Le foreste divennero verdi, il grano giallo, i tramonti viola, la terra marrone, la neve bianca. Tutto risplendeva di luce e di gioia.

Purtroppo, un brutto giorno, qualcuno che non voleva la gioia e, quindi, nemmeno i colori, ma solo il grigio del potere e della ricchezza, rubò la pentola. Il mondo tornò grigio e triste. Nessun problema! Ci voleva ben altro per scoraggiare l’eroico Leprechaun. Ricominciò tutto da capo e trovò di nuovo qualcuno pronto a donargli un po’ del suo prezioso metallo.

Ogni volta, però, qualcuno lo rubava e faceva piangere il Sole e la Luna. E, ogni volta, il folletto tornava sottoterra e creava un nuovo arcobaleno con l’aiuto di chi non voleva rinunciare alla gioia. E così continua anche oggi, senza interruzione. Leprechaun spera sempre che nessuno vada più a rubare la sua pentola, ma non ci spera molto ed è sempre pronto a ricominciare.

Adesso che sapete la vera storia dell’arcobaleno, vi chiedo solo di non raccontarla a nessuno: magari lo verrebbero a sapere proprio quelli che preferiscono l’oro alla gioia. Se proprio vi trovate a passare vicino a quel recipiente così importante lasciate cadere una moneta dentro di esso. Leprechaun ve ne sarà grato. Poi proseguite il vostro cammino e spiegate a tutti che l’arcobaleno è dovuto alle piccole gocce d’acqua sospese nell’aria e alla scomposizione della luce solare.

Ai vostri bimbi dite, però, la verità. Loro capiranno e manterranno il segreto.

La visione scientifica: accettiamola ma non dimentichiamoci del folletto.

Sapete come sono gli scienziati? Se non lo sapete ve lo dico io che li conosco molto bene… Quando si mettono in testa qualcosa sono più duri della pietra. Vogliono spiegare tutto con formule, strane figure e termini difficili. Anche quando basterebbe lasciarsi andare alla fantasia. Loro cercano sempre la logica e la ragione. Devo ammettere, però, che, sebbene siano testardi e molto rigidi, molte volte c’azzeccano. Tuttavia, non si deve sempre prendere ciò che dicono come oro colato (tanto per rimanere vicini al prezioso metallo). Spiegazioni basate sull’emozione e sul sogno possono essere altrettanto valide. Basta solo decidere quali sensi si vogliono usare e comprendere che fantasia e logica possono benissimo convivere, basta solo lasciare libera la strada che unisce cuore e cervello. Troppo spesso questa via di comunicazione viene chiusa con l’età. Impariamo dai bambini, loro la mantengono sempre aperta e scorrevole.

In fondo, è un po’ ciò che capita alla luce. Può essere descritta come onde gigantesche che si propagano nello spazio, attraverso un oceano senza confini, ma anche come un insieme di messaggeri piccolissimi (i fotoni) che la trasportano in giro per il Cosmo e la fanno conoscere a tutto e a tutti. Usare i fotoni e un po’ come credere alla leggenda di Leprechaun… a volte vedo proprio il suo volto dolce e furbo, con una candela in mano, quando penso a un fotone. Qual è la verità, allora? Beh…entrambe sono vere. Per la luce, almeno, è così.

La descrizione dell’arcobaleno è  un dilemma molto simile. La spiegazione scientifica è sicuramente valida, ma tenetevi nel cuore e in un piccolo angolo del cervello (ha tanto posto ancora libero) anche la versione che i bambini si raccontano tra loro e che a noi sembra così difficile da capire.

La luce e un pezzo di vetro

Facciamo, allora, un piccolo passo indietro e ripensiamo alla rifrazione  luminosa. Lo facciamo con la solita figura che conosciamo ormai molto bene. Tuttavia, questa volta lasciamo in pace i pesci e i pescatori e consideriamo un pezzo di vetro. Anche il vetro ha in indice di rifrazione maggiore di quello dell’aria e quindi un raggio luminoso che voglia penetrare al suo interno è costretto ad avvicinarsi alla perpendicolare.

Studiamo da vicino cosa succede “veramente” dopo l’ingresso del raggio. Il raggio che arriva, se non abbiamo inserito filtri, è normalmente di luce bianca, ossia un “mix” di tutte le lunghezza d’onda. Non posso ripetere un’altra volta cosa sia la lunghezza d’onda e cosa rappresenti lo spettro della luce. Diciamo solo che ogni colore  ha una sua lunghezza d’onda, ossia le onde che arrivano dalla stella possono essere più o meno “lunghe”.

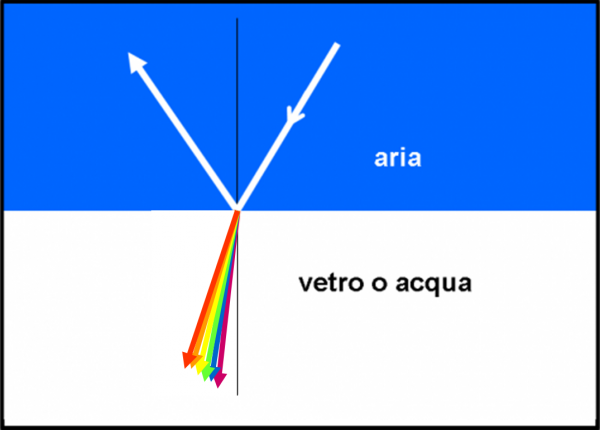
Occupiamoci solo della luce visibile, ossia quella che i nostri occhi riescono a percepire. Essa va dal violetto al rosso ed è solo una piccola parte dell’intero spettro elettromagnetico. Il raggio che arriva è composto di onde di tutti i tipi e appare di color bianco, ma, appena tocca la superficie del vetro (lo stesso capita anche nel laghetto) ogni tipo di onda (ossia colore) segue un suo cammino particolare. I raggi che contraddistinguono le varie onde “colorate” si piegano di più o di meno rispetto alla perpendicolare. Questo fatto lo vediamo nella Fig. 21, dove abbiamo disegnato i due colori estremi accettati dal nostro occhio, il viola e il rosso, e un paio di quelli intermedi (blu e giallo). In realtà i colori sono sette o sei (se non si considera l’indaco) come ho raccontato, a modo mio, QUI e, in modo un po' più serio, QUI.

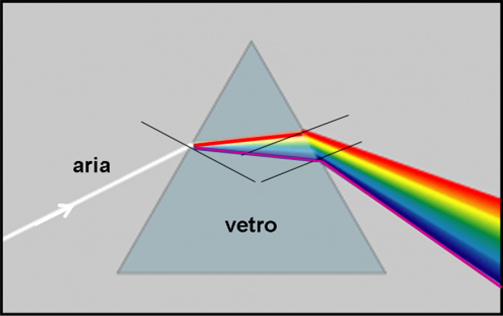
Questo fatto pone alcuni problemi (la luce si disperde all’interno del vetro), ma tanti vantaggi su cui si basa una parte fondamentale dell’astrofisica: la spettroscopia. In poche parole, la possibilità di “aprire” la luce di un astro come fosse un ventaglio e studiare non solo tutte le sue caratteristiche, ma anche e soprattutto la  composizione e le peculiarità dell’oggetto che l’ha inviata o anche soltanto riflessa. Senza spettroscopia l’astrofisica moderna non sarebbe certo arrivata ai livelli odierni. Per ottenere questo risultato prodigioso basta prendere un pezzo di vetro fatto a triangolo, interporlo alla luce da analizzare e aspettare che la luce esca nuovamente allo scoperto, come avviene nella Fig. 22.

Vorrei fare una considerazione molto importante, soprattutto per i telescopi e per chi li usa. Come sapete e come vedremo, vi sono telescopi che usano come obiettivo delle lenti e altri che usano degli specchi. Ciò vuol dire che alcuni basano la formazione dell’immagine sulla rifrazione, altri sulla riflessione. Abbiamo già capito bene che una lente (essendo in pratica un pezzo di vetro) causa una dispersione dei raggi di vario colore. Se questo è molto utile per uno spettroscopio, non lo è più per una visione diretta di un oggetto celeste, che rischia di apparire di tutti i colori, anche sfasati tra loro. In realtà, come vedremo, si devono usare più lenti per cercare di limitare questo danno. Gli specchi, invece, hanno un pregio non trascurabile: la luce che si riflette non si separa nei vari colori. E’ anche facile capire il perché, dato che non vi è un passaggio da una sostanza a un’altra. In altre parole, l’immagine formata da un sistema di specchi non ha il problema del “cromatismo”, ossia della separazione dei colori nell’immagine finale. Comunque ci torneremo sopra, state tranquilli.

Un prisma d’acqua

Qualcuno potrebbe dirmi: “Abbiamo già finito. Altro che folletto dei boschi, basta un pezzetto di vetro per fabbricare un bellissimo arcobaleno!”. In parte avrebbe ragione. Tuttavia, nell’atmosfera c’è un po’ di tutto, dalla polvere alle particelle elementari, dai pezzi di missili ai satelliti artificiali. Nessuno però ha la forma esatta di un triangolo. Ci vuole qualcosa che ne faccia le veci. Non è difficile capire cosa può essere questo “qualcosa”. Soprattutto, pensando che l’arcobaleno si vede normalmente dopo un temporale, quando il Sole torna a rallegrare la Natura. Temporale vuol dire pioggia e pioggia vuol dire goccioline d’acqua.

Ecco trovato ciò che fa le veci del triangolino di vetro: una goccia d’acqua di forma sferica (questa è proprio la loro forma prima di cadere al suolo). Nessuno può realmente vedere nel cielo quello che accade, ma solo ammirare il risultato finale. Eppure, già nel 1200, gli arabi sapevano descrivere perfettamente il fenomeno.

Occupiamoci prima dell’arcobaleno principale, quello più luminoso che, a volte, è l’unico che si vede. Tuttavia, spesso esso è accompagnato da uno secondario, più debole ma altrettanto suggestivo. Iniziamo a spiegare il fenomeno nella Fig. 23, limitandoci a due raggi luminosi, quello rosso e quello blu. Non ho preso quello viola perché potrebbe confondersi con il rosso, ma immaginate pure di sostituire il blu con il viola. Insomma, consideriamo i raggi estremi della luce visibile.

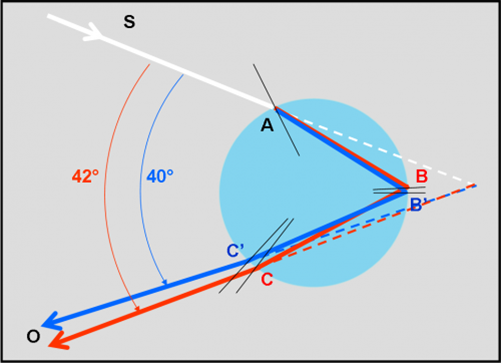
Un raggio solare (bianco) arriva da sinistra e incontra una goccia d’acqua sferica sospesa in aria, dato che il temporale sta finendo o è finito da pochissimo. Il punto di contatto è A. Come detto precedentemente, penetrando nell’acqua il raggio rosso si piega di meno di quello blu. Il raggio rosso colpisce la superficie interna della goccia in B. Una parte prosegue uscendo dall’acqua e ritornando in atmosfera, allontanandosi dalla perpendicolare, ma una parte tornerà indietro sfruttando la riflessione. Non quella totale, ma solo e soltanto la riflessione normale.

State molto attenti, a questo riguardo. In molti testi si trova  scritto che la riflessione è causata solo da quella totale, ossia si è superato l’angolo critico. Non è vero! Sappiamo, infatti, che un raggio di luce si scompone sempre in uno che si rifrange e in uno che si riflette. Quale dei due predomini sull’altro dipende dalla sostanza e dalla geometria . In questo caso a noi interessa solo quello che si riflette, dato che la parte che si rifrange si dirige in una zona di cielo che non produce immagini visibili da terra. E’ solo una parte, ma ancora abbastanza vigorosa.

La stessa cosa fa anche il raggio blu. I raggi blu e rosso si intersecano tra loro (non succede niente, state tranquilli, ognuno continua per la sua strada) e arrivano a toccare nuovamente la superficie interna della goccia in C’ e C rispettivamente. Questa volta, consideriamo i raggi che subiscono la rifrazione e che escono all’aria. Il gioco è fatto.

Essi si dirigono verso l’osservatore (in basso) mantenendosi nettamente separati tra loro. Abbiamo ottenuto una cosa analoga al triangolo usato in spettroscopia, ma utilizzando soltanto una naturalissima gocciolina d’acqua.

Vale la pena dare qualche numero. Sappiamo benissimo quanto valgono gli angoli di rifrazione all’interno dell’acqua e di quanto si discostino a seconda del colore. Sembrerebbe facile calcolare l’angolo formato tra il raggio incidente (proveniente dal Sole S) e quello finale diretto verso l’osservatore O, sia per la luce rossa che per quella blu. Ovviamente, tutto dipende anche dall’inclinazione dei raggi solari. Il calcolo si complica se vogliamo che la parte riflessa e/o rifratta sia quella predominante nelle varie situazioni. Ci vuole un bel po’ di matematica e di fisica per ottenere la risposta. Accontentiamoci del risultato finale.

Gli angoli che permettono una visione distinta dell’arcobaleno sono di 42° per il rosso e di 40° per il blu.

L’arcobaleno primario è quindi spiegato da due rifrazioni e da una riflessione su una goccia d’acqua sferica. Tuttavia, quando un raggio entra in una goccia ha voglia di divertirsi e può essere “difficile” farlo uscire. Se pensiamo che sia un fotone a fare questo viaggetto, possiamo immaginarcelo come il folletto della favola e vederlo sorridere mentre salta da una parte all’altra della goccia d’acqua, come in una piscina!

Parlando seriamente, consideriamo un altro possibile percorso del raggio di luce bianca che proviene dal Sole. Consideriamolo parallelo a quello precedente, dato che la luce solare può essere considerata composta da un fascio di raggi paralleli. Il Sole, pur non essendo distante come una stella qualsiasi, è pur sempre abbastanza lontano da accettare questa approssimazione.

Guardiamo, quindi, la Fig. 24. Il raggio entra in A e si separa come al solito. Si riflette in B e B’ e poi ancora in C e C’ (una volta in più). Infine, decide di uscire e lo fa in D e D’. Come prima, abbiamo usato solo la parte che ci interessa, ma in ogni punto si ha sia un  raggio riflesso che uno rifratto. In ogni modo la conclusione è simile a quella di Fig. 23. Tuttavia, ci sono alcune differenze non certo trascurabili. Innanzitutto, la luce che esce sarà più debole di quella precedente a causa della riflessione in più che hanno subito i raggi vagabondi. Poi, i raggi si sono invertiti: il rosso è quello che esce più in alto, mentre il blu esce più in basso.

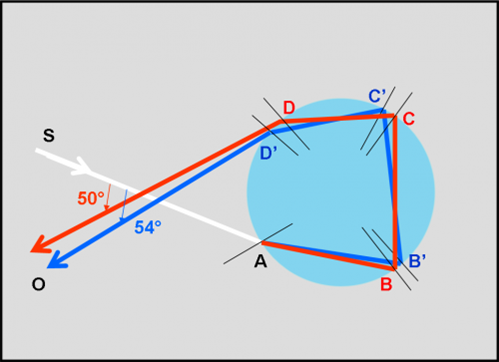
Nella Fig. 23 avveniva esattamente il contrario. Infine, gli angoli tra raggio incidente e raggi finali sono leggermente più grandi : 54° per il blu e 50° per il rosso. Ciò vuol dire che l’arcobaleno è più “largo” di quello precedente. Comunque, tra poco, spiegherò meglio la situazione.

In pratica, avremmo finito. Tuttavia, vale la pena costruire meglio ciò che vede il nostro occhio. In particolare, bisogna evitare una fonte abbastanza “normale” di confusione. Le figure che ho fatto precedentemente mostrano contemporaneamente cosa capita al raggio rosso e a quello blu e, analogamente, potrebbero fare lo stesso anche per gli altri colori. Sembrerebbe, quindi, che l’intero arcobaleno nasca da una singola goccia d’acqua. Questo non è assolutamente vero.

Se ci pensate un attimo, vedete che gli angoli di uscita dei raggi blu e rosso sono molto simili, ma diversi tra loro. Il nostro occhio non riuscirebbe mai a catturarli entrambi. Ciò che capita in realtà è che ogni goccia ci invia uno e un solo raggio. Ci sono quelle specializzate nel blu, quelle specializzate nel rosso, nel giallo, nel verde, nell’arancione, ecc. Parlando più seriamente, dalle gocce che formano un certo arco nel cielo vedremo giungere la luce rossa, da quelle che ne descrivono un altro vedremo quella blu e via dicendo. Proprio questo ragionamento ci spiega anche perché l’arcobaleno ha  la forma di un … arco.

La Fig. 25 mostra chiaramente quanto ho detto per entrambi gli arcobaleni. Come vedete, ogni gocciolina ci manda un certo colore. Tutte assieme ci mostrano la meravigliosa immagine del doppio arcobaleno.

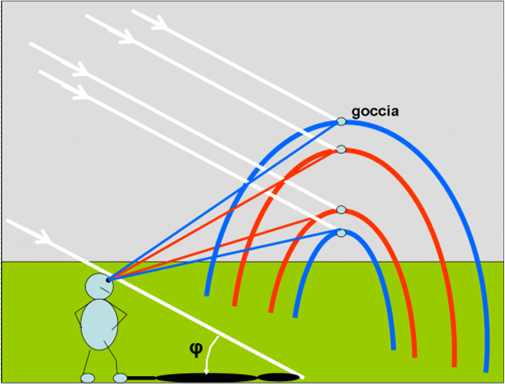
Si vedono sempre entrambi gli arcobaleni? Come già detto, non sempre, a causa della minore luminosità del secondario. Tuttavia, può capitare benissimo che si veda soltanto il secondario. Questa situazione non dipende più dalla quantità di luce, ma da considerazioni puramente geometriche.

Giochi di prestigio

La luce solare, però, sa fare giochi ancora più complicati e misteriosi. Per dimostrarlo ne prendiamo due piuttosto appariscenti. Nel primo caso dobbiamo far ghiacciare le gocce e nel secondo dobbiamo tornare vicino al nostro laghetto.

Guardando l’immagine seguente (Fig. 26),  non possiamo che meravigliarci: non  due, ma addirittura tre Soli nel cielo!

Presentiamo, innanzitutto, gli attori principali di questi giochi di prestigio. Li vediamo rappresentati nella Fig. 27. Non sono altro che cristalli di ghiaccio a sezione esagonale (la Natura sa creare forme perfette quando vuole…). Essi sono molto frequenti nelle nuvole sottili, dette cirri, dove la temperatura è molto bassa. A volte, possono anche formarsi a bassa quota e prendono il nome di polvere diamante (diamond dust) che dà luogo a nevicate con cielo sereno o a nebbie che non bloccano la visuale. Ovviamente, sono frequenti nei paesi artici o molto freddi. Tuttavia, quelli che servono ai giochi solari (e lunari) sono quelli molto alti.

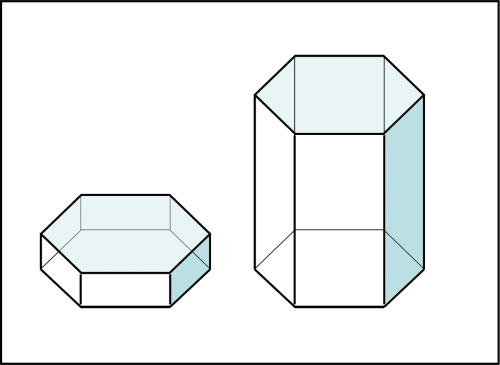
Vediamo, allora come si formano i tre Soli o i cani solari, come li chiamano in inglese. Chi li causa sono cristalli esagonali molto sottili (come quelli a sinistra della Fig. 1) che si piazzano orizzontalmente. Ne segue che il risultato migliore si ha quando il Sole è molto basso, ossia se è quasi sull’orizzonte. Ciò che avviene è mostrato nella Fig. 28. I raggi solari attraversano i piccoli cristalli, si rifrangono ed escono con un angolo finale che non può essere minore di 22°. Questo vincolo si può dedurre dall’indice di rifrazione del ghiaccio e sapendo che l’angolo tra due facce di un esagono, non adiacenti e non parallele tra loro, misura 60°. L’angolo minimo di 22° si ha quando il raggio rifratto, interno al cristallo, è parallelo al lato adiacente a quello di entrata (a sinistra di Fig. 28).

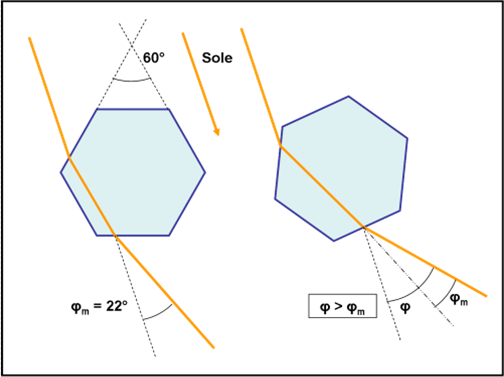
Cos’avviene nel Cielo? Lo vediamo dall’alto in Fig. 29. I raggi solari si dirigono verso l’osservatore O, formando l’immagine “normale”. Tuttavia, anche i raggi che incontrano i cristalli, messi nel modo giusto, eseguono la loro rifrazione  e raggiungono  l’osservatore, producendo due immagini del Sole che distano un angolo di 22° da quella vera.

Spesso i cani del Sole sono colorati a causa della dispersione causata dalla rifrazione, ma non sempre, in quanto la debole luce di ogni singolo cristallo può non attivare i selezionatori dei colori dell’occhio e quindi le immagini appaiono bianche.

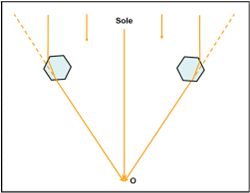
Tuttavia, nell’aria, vi sono anche piccoli cilindretti esagonali, non piatti come quelli precedenti (a destra di Fig. 27). Loro possono assumere varie inclinazioni rispetto al piano orizzontale, pur dando luogo a immagini finali non più vicine di 22° rispetto al Sole. Ne deriva, quindi, un cerchio completo attorno alla nostra stella (ma anche alla Luna), come mostrato in Fig. 30. Attenzione a non confonderlo con la corona che si vede sovente e che è dovuta alla diffusione della luce su gocce d’acqua sospese in aria.

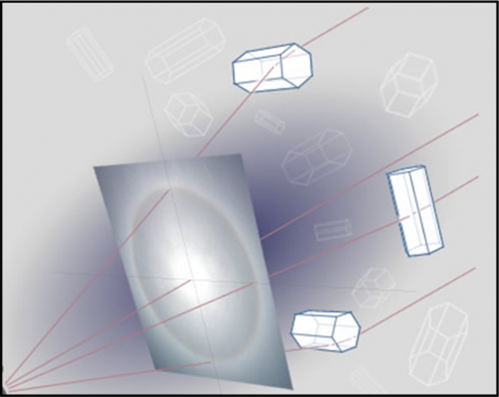
Fermiamoci a questi due fenomeni che sono spesso assai suggestivi e visibili ad alte latitudini, senza dimenticare, però, che gli stessi cristalli e giochi più complicati tra rifrazione e riflessione  possono dar luogo a figure ancora più complicate, come quelle mostrate in Fig. 31.

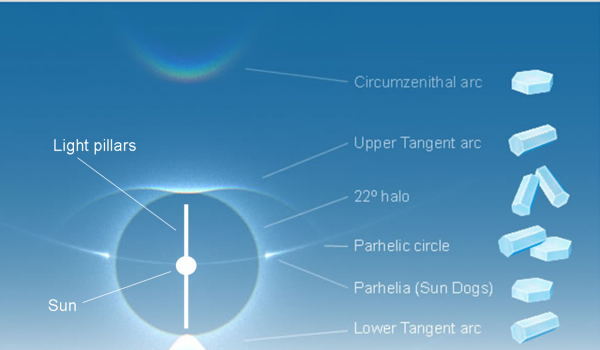
In Fig. 32  vi è una vera foto di quasi tutti i possibili fenomeni causati dai nostri simpatici esagoni ghiacciati.

Per tornare agli UFO… immaginate che vi siano delle nuvole che coprano il Sole vero o intrappolino l’immagine dei due “cagnolini”. Luci strane, colorate che sembrano muoversi e spegnersi improvvisamente. L’UFO diventerebbe la più ovvia conclusione e potrebbe anche essere fotografato!

Basta invece qualche gocciolina d’acqua e un lago alle spalle per osservare uno stupendo arcobaleno doppio (oltre a quello secondario che già conosciamo bene), addirittura inclinato rispetto al primo, come quello di Fig. 33.

Chissà quanti ne avrà visti il nostro celebre pescatore… La luce del Sole, che colpisce la goccia G, si rifrange e fa vedere, all’osservatore O, l’arcobaleno normale A (Fig. 34). Tuttavia, la luce del Sole colpisce anche la superficie liquida e si riflette in S. E’ come se vi fosse un nuovo Sole in S’. Il raggio riflesso che sembra provenire da S’ colpisce la goccia G’, si rifrange, e mostra all’osservatore anche l’arcobaleno A’, che si chiama arcobaleno di riflessione. Facilissimo a spiegare senza bisogno di pensare di rivolvere attorno a una stella doppia!

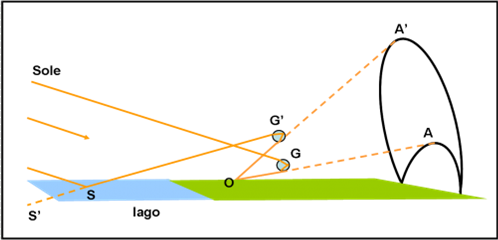
Finirà mai di stupirci l’Universo? Basta un cristallino di ghiaccio, un po’ d’acqua, una banda di allegri fotoni e il gioco è fatto!

Dopo questi fenomeni a metà tra Scienza e poesia, è ora di tornare dal nostro pescatore, seduto all’ingresso del porto. Cosa aspetta? Beh… la luce di una stella. I raggi non gli bastano più e vuole guardare le onde.

All’entrata del porto

Il pescatore non solo ha cambiato modo di passare il tempo, ma è diventato estremamente attento e riflessivo. Le brutte avventure vissute a causa della scarsa conoscenza dell’ottica lo hanno reso dapprima guardingo e timoroso, ma poi sempre più curioso e interessato ai fenomeni che lo circondano. Non solo interesse, però, ma anche voglia di capire e interpretare. Per la gente del molo è ormai un punto di riferimento e tutti si fidano della sua perspicacia. Il suo arrivo, di fronte all’immensità del mare, è sempre un momento di festa per tutti e lui si diverte in quello scambio continuo di conoscenza e di partecipazione collettiva. Lo studio della Natura e delle sue leggi aiuta in molte cose, non solo scientifiche. Ridendo e scherzando, il nostro eroe (possiamo ormai chiamarlo così) riesce addirittura a dare un significato ben più ampio all’effetto che nota guardando le onde che entrano nel porto (Fig. 35) e ad applicarlo perfino alla sua nemica-amica  ottica.

Questa parte della nostra avventura nell’ottica è senza dubbio una delle più importanti e complicate. Tuttavia, ho cercato di renderla il più semplice possibile, tralasciando qualsiasi formula e/o concetto un po’ astruso. Penso di avere ottenuto il massimo con il minimo sforzo (vostro). Non pensate, però, che una trattazione di questo tipo possa risolvere tutti i problemi legati alla luce che attraversa una fenditura o un’apertura qualsiasi.  Per descrivere compiutamente tutti i fenomeni sarebbe necessario un libro corposo e forse più di un uno. Basti dire che non possiamo più accontentarci dell’ottica geometrica. L’importanza, però, è enorme e non si limita certo alla definizione dell’immagine di un oggetto celeste data da uno strumento ottico, sia naturale (occhio) che artificiale (telescopio).

Per chi è più esperto basterebbe ricordare l’interferometria e i reticoli di diffrazione: le applicazioni teoriche e tecnologiche  apparirebbero in tutta la loro vastità. Niente paura, noi ci fermeremo ai concetti base, quelli che poi possono permettere a chiunque di entrare più a fondo nelle varie problematiche collegate. Mi raccomando, non andate avanti senza prima aver digerito questa parte!

Facciamo una breve premessa alla storia del pescatore. Ormai sapete bene che la luce può essere decritta in due modi altrettanto validi: quello corpuscolare (fotoni) e quello ondulatorio. Tuttavia, quando si ha a che fare con l’interazione della luce con qualche ostacolo, la teoria basata sulle simpatiche particelle che la trasportano non riesce più a dare una spiegazione valida. Diventa obbligatoria la trattazione in termini di onde che si propagano. La MQ spiega che le due visioni sono in pratica la stessa cosa, ma noi scegliamo di immergerci in un... mare agitato.

Per darne un’idea concreta, immaginiamo che la luce proveniente da una stella, ossia da una sorgente puntiforme che produce a grande distanza un fascio di raggi paralleli  si avvicini a un ostacolo. Esso è rappresentato da due muri che lasciano libera solo una piccola apertura. Proprio quello che fa il molo che separa il porto dal mare aperto.

Disegnare dei raggi luminosi è  molto simile a rappresentare la luce attraverso particelle che viaggiano in linea retta. In poche parole,  il percorso di queste ultime (sempre i fotoni, ovviamente)  possono essere descritte perfettamente dai raggi luminosi che abbiamo imparato a usare finora. Un fascio di questi raggi sarebbe quindi un fascio di fotoni che si muovono tutti insieme nello stesso verso e paralleli tra loro, come rappresentato in Fig. 36.

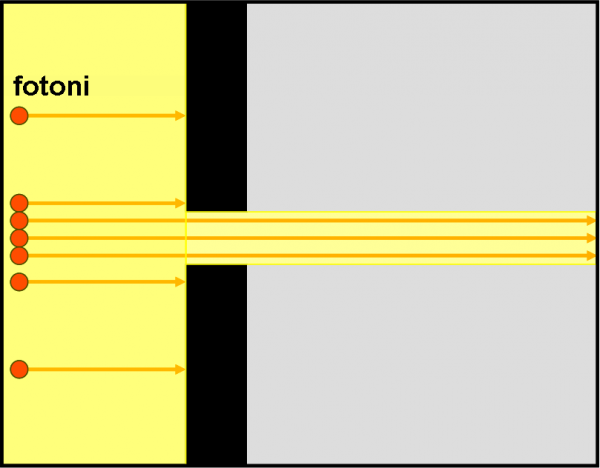
Essi si trovano di fronte due muri neri che lasciano libera solo una piccola apertura. I fotoni non hanno una grande scelta, dato che possono muoversi SOLO in linea retta. Quelli che vanno contro il muro si devono fermare (o si riflettono o si rifrangono, ma conta poco adesso). Riescono a passare solo quelli che sono diretti proprio verso l’apertura aperta. Muovendosi in linea retta, essi proseguono il loro cammino. Ne segue che il fascio di luce che entra nell’apertura ha esattamente la sezione dell’apertura. Solo questo fascio, sempre composto da rette parallele tra loro, trasporta la luce. Tutt’attorno c’è il buio.

Chi fosse nella zona grigia non vedrebbe niente perché nessun raggio di luce potrebbe colpirlo. Nella parete di fondo (a destra) il fascio illuminerebbe esattamente una zona con la forma dell’apertura. E questa parte illuminata avrebbe i contorni perfettamente definiti, con un errore pari alle dimensioni di un fotone, quindi zero, senza penombra o cose simili. Infatti, il fotone o passa o non passa, ossia o vi è luce o vi è buio.

La Fig. 36 sarebbe molto semplice e forse anche comoda (ma non avrebbe permesso tante scoperte e tante conquiste scientifiche). Sicuramente permetterebbe a uno strumento ottico di concentrare la luce in modo perfetto. Purtroppo -o per fortuna- non capita questo. Ciò che succede realmente, in modo molto semplificato e approssimativo, è rappresentato nella Fig. 37. Non solo la luce entra e prosegue lungo il fascio orizzontale, ma tutta la zona che dovrebbe essere al buio risulta più o meno illuminata. Chi o che cosa può illuminare questa parte nascosta dai due muri? I fotoni  (o -se preferite- i raggi luminosi rettilinei) non possono di certo averlo fatto.

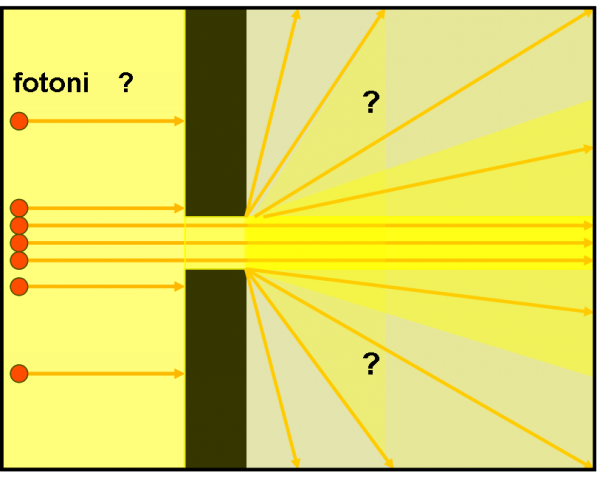
L’unica conclusione è che non possiamo più trattare la luce soltanto come raggi paralleli (fotoni o non fotoni), ma come qualcosa che risente in modo macroscopico del fatto di essere entrata all’interno di un’apertura più o meno piccola. Attenzione: questo avviene sempre e non dipende assolutamente da riflessioni “strane” che avvengono all’interno del “porto”, ossia nella zona dopo l’apertura. L’unico modo per descrivere la realtà è abbandonare i nostri simpatici fotoni (o raggi rettilinei) e considerare la rappresentazione ondulatoria della luce. L’ottica geometrica non ci basta più.

A questo punto possiamo tranquillamente tornare dal nostro pescatore che sta chiacchierando allegramente con i suoi amici sul molo d’ingresso al porto della sua nuova città. E’ una giornata abbastanza ventosa e le onde che si susseguono sono piuttosto alte. La situazione è quella di Fig. 38, dove il molo M e il pescatore P sono visti dall’alto.

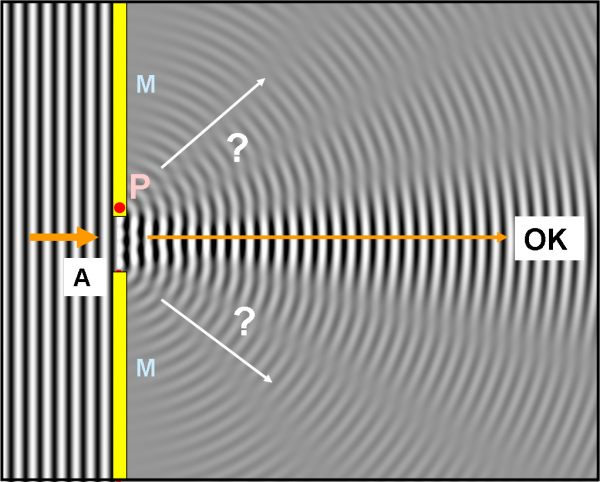
Le onde piane e parallele arrivano fino all’apertura A del porto. Potrebbero benissimo essere rappresentate da linee, a loro perpendicolari, anch’esse tutte parallele, proprio come abbiamo fatto nell’ottica geometrica con la luce di una stella puntiforme lontanissima. In altra parole, anche le onde marine potrebbero essere descritte da un fascio di raggi paralleli alla freccia arancione.

Inseriamo un bellissimo video dell'amico Frank che illustra molto bene come la Natura ci insegni sempre meglio e di più dei  nostri disegni...

https://www.dropbox.com/s/9hs4tatnpypsmjs/MVI_2044.wmv?dl=0

In realtà, le onde entrano nel porto e sembrano proseguire come prima dell’apertura. Ma non tutte.

Si crea una strana forma del moto ondoso. Le onde non sono più piane e parallele, ma sembrano girare attorno ai punti d’entrata. La visione generale assomiglia a una circonferenza o qualcosa di simile. L’origine di questa struttura ondulatoria sembra provenire proprio dall’apertura. Se si tracciassero i raggi perpendicolari alle onde questi andrebbero in tutte le direzioni. Non solo, ma l’altezza delle onde sembra anche variare come se “interferissero” tra loro, ossia si disturbassero a vicenda.

Il pescatore si accorge subito che sta assistendo a un fenomeno generale non solo causato dal vento o da qualche situazione peculiare. Ormai è diventato troppo curioso e non può più dare una scrollata di spalle e dire: “Boh… che sia quel che sia”. Decide di verificare ciò che ha visto in condizioni analoghe in cui, però, l’apertura dovuta al molo sia di dimensioni diverse. E’ convinto che il segreto stia proprio lì, nella larghezza dell’apertura A. Girando per il porto trova facilmente altri moli che soddisfino le condizioni che sta cercando. Ne traccia dei disegni e poi li confronta tra loro nella Fig. 39, mettendoli in ordine di apertura decrescente.

Aveva proprio ragione. Esiste proprio una serie di onde circolari che nascono in corrispondenza dell’apertura tra i moli. E più il buco di entrata è piccolo e più è nitida la struttura delle onde. Analizza ancora meglio le quattro situazioni. Nella prima sembrerebbe che l’onda entri e si mantenga piana come nel mare aperto. A prima vista però. Guardando meglio vede ciò che è indicato dalla freccia bianca: in prossimità dei moli l’onda diventa circolare, come se volesse girare attorno all’ostacolo presentato dai muri del molo. La stessa configurazione che aveva notato nel molo iniziale.

Non è allora l’apertura a causare quello strano gioco di onde, ma le sue due estremità. Ovviamente, se l’apertura è molto piccola le onde che nascono dalle due estremità si accavallano e sembrano diventare una sola, quasi circolare, come nell’ultima immagine a destra. Si ferma, posa i suoi disegni e guarda verso il mare. No, non sta più cercando il pesciolino dispettoso, sta solo pensando e riflettendo. Onde marine e onde luminose. Sono simili in tante cose perché non anche nei loro comportamenti attraverso le aperture più o meno strette? Corre a casa, prende una risma di fogli di carta e una matita e si dirige ormai sorridente verso i suoi amici del molo. Ne vuole discutere con loro, ma ormai le idee gli si sono chiarite. E’ ovvio, accidenti. In fondo c’era proprio da aspettarselo!

Si siede su uno dei gradoni e chiama a raccolta i pescatori che posano volentieri le loro canne per imparare qualcosa di nuovo: i pesci possono anche aspettare. Pochi minuti e il nostro “esperto” in ottica ondulatoria disegna la Fig. 40. Sembra un po’ caotica, ma lui la spiega con grande precisione e semplicità. Riporto una sintesi della sua descrizione.

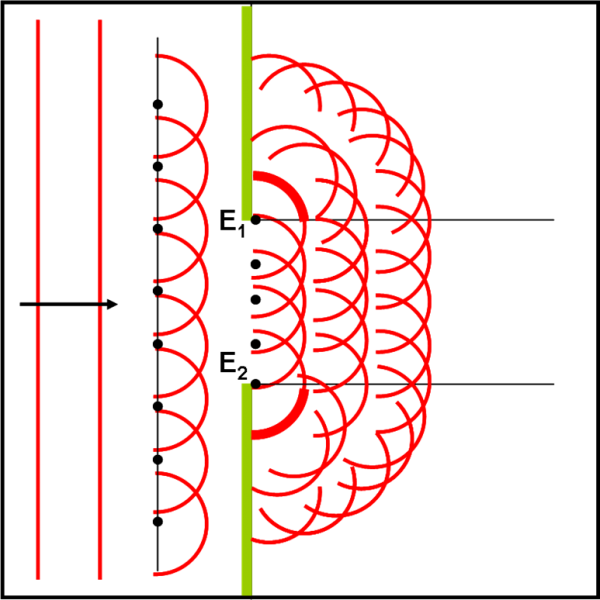
Immaginiamo che ogni onda luminosa che proviene da una stella lontana sia come l’onda del mare e possa essere disegnata come una retta verticale rossa. La sua direzione è data dalla freccia nera. Immaginiamo adesso che ogni punto dell’onda sia capace di generare una nuova onda che si propaghi verso l’esterno come quella che è nata dalla stella che l’ha originata, ossia abbia forma circolare. In altre parole, come se ogni punto generasse un cerchio di onde che si allarga come quando buttiamo un sasso nell’acqua. Ogni punto diventerebbe, quindi, una sorgente luminosa. Miliardi di miliardi di piccoli sassi che producono miliardi di miliardi di onde concentriche tutte uguali tra loro.

Piccolo inciso: il pescatore non lo sa ancora, ma sta enunciando nientemeno che il principio di Huygens che recita così: “Ciascun punto di un fronte d’onda si può considerare come una sorgente elementare di altre onde che si propagano nella medesima direzione del fronte d’onda stesso. Il fronte d’onda successivo è il risultato dell’inviluppo totale di tutte le onde elementari”.

Non possiamo disegnare miliardi di punti, ma possiamo semplificare le cose e disegnarne solo qualcuno a una certa distanza tra loro. Può bastare per capire cosa succede. L’onda, che sembra una linea, avanza ed è composta da tanti cerchi tutti uguali che si propagano in avanti e si intersecano tra loro. In realtà, nel vuoto dello spazio o nel mare aperto, le cose non cambiano di molto rispetto all’insieme di onde rettilinee e/o dei raggi perpendicolari che le possono rappresentare nell’ottica geometrica. Abbiamo, comunque un “fronte” d’onda che è formato da tutte le onde nate da tutti i punti dell’onda totale. La situazione ha solo cambiato la sua essenza profonda ma non l’aspetto esteriore. E così continuerebbe a essere se la luce non si trovasse di fronte il molo.

I punti E₁ ed E₂ sono gli estremi in cui possano ancora nascere onde nel modo appena descritto. Dopo di loro c’è il muro del molo e le onde s’infrangono e non possono proseguire. Ma se, come ipotizzato, anche nei punti E₁ ed E₂ nascono due sistemi di onda circolari essi determinano una curvatura del fronte d’onda che gira intorno ai due punti e si propaga anche nelle zone interne,  teoricamente “riparate” dai moli. E’ proprio come nella Fig. 38 che abbiamo disegnato poco fa.

La luce o l’acqua gira attorno ai limiti del molo e si propaga dove non potrebbe andare se fosse formata da particelle libere di muoversi sono in linea retta (i nostri “raggi”). Teoricamente, se il porto fosse completamente asciutto e si aprisse improvvisamente la porta che chiude l’apertura del molo, l’acqua dovrebbe entrare secondo onde piane e parallele e proseguire solo nella direzione dell’apertura come disegnato, per la luce, nella Fig. 36.

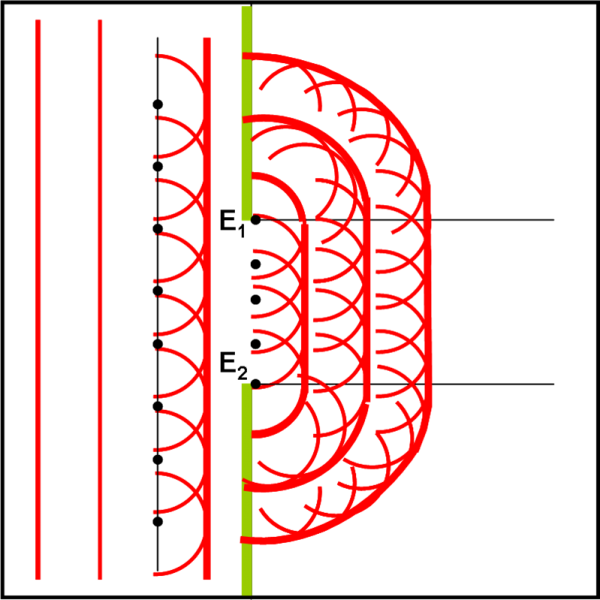
E, invece, l’acqua riesce in fretta a giungere anche nelle zone più nascoste del porto e non perché qualcuno la spinge o perché c’è troppo vento. No, solo perché alle estremità del molo si generano onde circolari che si propagano anche negli angoli più riparati. Basta disegnare nuove onde circolari anche nella parte delle onde che vanno oltre l’apertura e che girano attorno a E₁ ed E₂. Onde circolari che nascono da punti che sono già essi su linee curve “piegate” rispetto a quelle originarie. Le due estremità E₁ ed E₂ hanno creato due strutture di onde concentriche che originano nuove strutture allargando il fronte d’onda diretto verso l’interno del porto. Cosa si vedrà alla fine? Non certo tutte le onde formate da ogni singolo punto, ma l’inviluppo di loro come disegnato nella Fig. 41.

La teoria ondulatoria ha permesso di spiegare un fenomeno che sembrava impossibile con quella puramente geometrica ( in altre parole, questa frase dice anche che i fotoni non possono sempre essere considerati come particelle). Il pescatore ormai esperto in ottica tira un grande sospiro di soddisfazione e guarda casualmente verso l’acqua. Sarà un effetto ottico, ma gli sembra che un numero incredibile di pesci, di tutte le grandezze e colori, gli stiano facendo una specie d’inchino! Ah, quest’ottica… quanti scherzi è capace di fare. Ma lui non ci casca più!

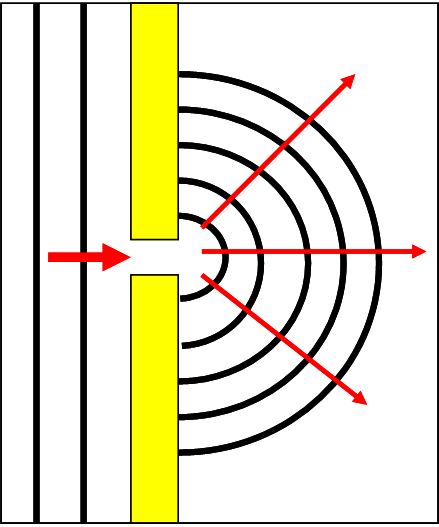
A questo punto non gli è nemmeno difficile disegnare ciò che capita dopo un molo con un’apertura estremamente stretta e la fa con molta facilità nella Fig. 42. L’apparenza è proprio quella di un onda piana che si trasforma in un sistema di onde circolari concentriche. Che magia la luce e le sue leggi!

Le onde viste “di taglio”

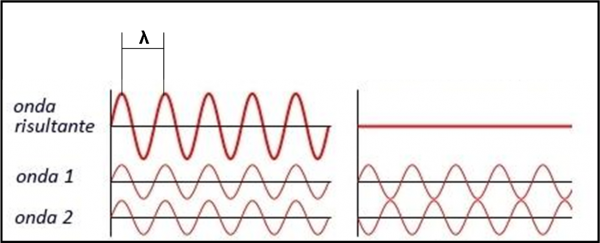
Per capire meglio la magia ricordiamo come sono fatte le onde del mare e quelle della luce (e non solo) viste di taglio e non dall’alto. Esse sono come quelle dalla Fig. 43, in alto a sinistra: un linea che sale e che scende in continuazione. La distanza tra due massimi è chiamata lunghezza d’onda λ e caratterizza il tipo di luce (ricordate i colori?). Le linee rette (e anche quelle circolari) viste dall’alto si riferiscono, ad esempio, ai punti più alti del saliscendi. Tra una linea e l’altra vi è la zona di minimo di luce.

In realtà l’onda sferica che avanza è molto più complicata di quello che sembra, ma per affrontare questa parte bisognerebbe fare ricorso a formule matematiche molto complicate. Non ce n’è, però, veramente bisogno. Si può cercare di capire cosa succede attraverso un paio di ragionamenti, estremamente semplici.

Consideriamo la Fig. 44 e immaginiamo che l’apertura sia veramente piccola, piccola come la lunghezza d’onda. La sua larghezza sia D. La distanza tra l’apertura e uno schermo p varia a seconda della direzione dei raggi luminosi perpendicolari in ogni punto all’onda circolare che si origina nell’apertura (o dai suoi bordi che però sono praticamente coincidenti). La distanza apertura-schermo è minima andando dritti, mentre cresce se consideriamo raggi che piegano rispetto alla linea orizzontale (stiamo parlando di triangoli rettangoli, di cateti e di ipotenusa).

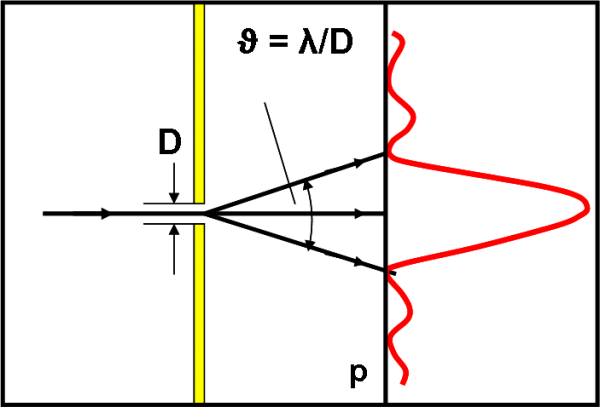
La differenza di lunghezza del percorso fatto dalla luce ci indica anche che mentre si ottiene un massimo di luce con la linea dritta, la linea diagonale arriva sullo schermo con un minimo di luce. La differenza tra di loro è, per costruzione, dell’ordine della lunghezza d’onda e non è difficile calcolare quanto vale l’angolo ϑ tra i due minimi esterni rispetto al massimo centrale di luce sullo schermo.

L’angolo è anche una misura angolare delle dimensioni della zona centrale più luminosa, dato che va da un minimo a un altro e confina proprio con la parte luminosa centrale. Vogliamo scrivere la formula risultante per questo angolo? Non pretendo di ricavarla, ma è talmente importante che è fondamentale ricordarsela (ci sarebbe un seno dell’angolo, ma per angoli piccoli si può sostituirlo con lo stesso angolo espresso in radianti):

 ϑ = λ/D

Anche se non è facile ricavarla, la stessa formula vale anche per una fenditura larga. Tutti coloro che guardano il cielo dovrebbero conoscerla, sia che usino l’occhio sia che usino un telescopio. Che cos’è infatti D? Nient’altro che l’ingresso al sistema ottico, l’apertura dello strumento. Poi ci penserà lui a concentrare la luce in un punto e farcela vedere direttamente o tramite lenti e specchi.

Come mai sullo schermo p non abbiamo una linea che sale e che scende, mantenendo sempre lo stesso livello dei massimi? Beh, come dicevo prima, la trattazione dell’onda che si genera nei punti, dopo che la luce è entrata nel porto,  è più complicata di quello che può sembrare. Ne potete avere un’idea guardando la Fig. 38, dove si vede bene che spostandoci dalla zona centrale vi sono zone più chiare e più scure. Questo vuole anche dire che i massimi diventano sempre meno alti andando verso i bordi.

Perché capita questo? Non è semplice, ma possiamo immaginare qualcosa di molto simile a quello che vediamo nella Fig. 43 nella sua parte bassa, sia a destra che a sinistra. Due onde “sfasate” tra loro possono dar luogo sia a un’onda risultante che è la somma delle due si a una che è praticamente nulla, dato che i massimi di una capitano in corrispondenza nei minimi dell’altra. Mentre le onde generate dalle due estremità dell’apertura avanzano, interagiscono tra loro e l’onda finale risultante assume un aspetto irregolare nella sua altezza. Non è proprio esatto, ma è abbastanza veritiero e sufficientemente comprensibile, In altre parole, stiamo parlando di interferenza.

Un cerchietto irriducibile

Tuttavia, qualsiasi cosa riesca a fare lo strumento, con il fascio di luce che è entrato attraverso l’apertura, non potrà mai vietare che l’immagine finale sia formata da una serie di massimi e minimi di luce. La parte più visibile è quella centrale che viene considerata come immagine finale. Se ricordiamo che tutto è partito da una stella puntiforme, l’immagine a saliscendi dello schermo è proprio l’immagine della stella, che è più grande della stessa apertura, quando questa è molto stretta.

Cosa si vedrà, allora, sullo schermo se immaginiamo che anche quel poco di luce che filtra attraverso l’apertura sia sufficiente a proiettare un’immagine sullo schermo anche senza essere concentrata?  Una struttura a strisce più chiare e più scure, dove quella centrale, relativa al massimo principale, è più luminosa delle altre relative ai massimi successivi, sempre meno luminosi. Una struttura sì, ma con quale forma? La forma finale, proprio per come si è ottenuta, dipende solo e soltanto dalla forma dell’apertura.

Per lo studio dell’ottica ondulatoria e delle interferenze tra onde sfasate e cose del genere si usano fenditure molto strette o un insieme di fenditure (reticolo). Nei telescopi si usano invece fenditure (aperture) più larghe, di forma circolare. Nei telescopi formati da tanti tasselli, le forme di questi ultimi danno la forma finale di una sorgente puntiforme, ad esempio ad ottagono. La Fig. 45 mostra le immagini per diversi tipi di apertura. Per questa -forse- inaspettata conclusione (stelle di diversa forma?) rimando all’appendice finale.

Quella circolare viene chiamata disco di Airy ed è la più piccola immagine di una stella puntiforme che si può ottenere. Il suo diametro angolare è proprio l’angolo ϑ e questo ci dice la grandezza minima di qualsiasi immagine puntiforme. E’ un limite invalicabile in natura che non dipende né dall’atmosfera, né dal vetro o dalla lente né dalla distanza focale. Essa dipende solo e soltanto dalla lunghezza d’onda della luce che vogliamo vedere e -soprattutto- dal diametro dell’apertura del telescopio, D.

Più esso è grande e più piccolo é il diametro dell’immagine centrale (e più deboli sono gli anelli che la circondano nel caso di apertura circolare).

Fatemi ripetere questo concetto fondamentale. L’ottica ondulatoria ci costringe ad avere sempre un’immagine non puntiforme di una sorgente puntiforme. Si può solo cercare di ridurre il suo diametro angolare aumentando le dimensioni dell’obiettivo del telescopio (D). Niente di più. Una stella apparirà sempre come un dischetto luminoso di dimensioni piccole ma non nulle.

Se l’apertura è piccola, è più facile distinguere anche gli anelli più deboli e concentrici che accompagnano la parte centrale più luminosa. Questa figura che nel caso di un obiettivo circolare (occhio,telescopio, binocolo) ci porta al disco di Airy si chiama figura di diffrazione.

Il fenomeno causato dalla luce che passa attraverso un’apertura viene chiamato diffrazione della luce e su di essa si basano un numero enorme di strumenti astronomici.

Nel caso di apertura circolare una lunga e faticosa trattazione matematica porta a una formula dell’angolo ϑ (il diametro del disco di Airy), che è leggermente diversa da quella trovata per la fenditura stretta e lineare:

ϑ = 2.44 λ/D

Una formuletta che tutti coloro che hanno un telescopio dovrebbero conoscere come le loro tasche. E’ infatti lei che definisce il valore minimo dell’immagine finale di una stella puntiforme.

Attenzione, però. Il disco di Airy non ha niente a che vedere con l’aberrazione sferica, il coma, l’astigmatismo, il seeing atmosferico e mille altri problemi che rendono estesa un’immagine stellare. Contro la diffrazione non c’è niente da fare. Ce la dobbiamo tenere. Tuttavia, è perfettamente controllabile e può servire per determinare distanze piccolissime nel Cosmo, quando si usa per gli interferometri o per simulare telescopi virtuali di dimensioni anche planetarie.

La capacità di distinguere

A questo punto diventa ovvia la definizione di potere risolutivo di un telescopio (ma anche dell’occhio). Si è stabilito che due stelle puntiformi siano ancora visibili come dischetti separati tra loro quando il massimo della figura di diffrazione di una coincide con il primo minimo dell’altra. Questa separazione prende il nome di potere risolutivo di un telescopio. Ovviamente dipende in parte dalla lunghezza d’onda, ma, a parità di questa, dal diametro dell’obiettivo: più è grande e maggiore è il  potere risolutivo.

La Fig. 46 ci mostra quanto detto a parole e mostra  l’intensità luminosa di una coppia di stelle che abbiano una distanza pari al potere risolutivo. Esse rappresentano il limite per essere separate da un certo telescopio. Limite teorico, ovviamente, dato che si può facilmente peggiorare la grandezza del disco di Airy. Tuttavia, vi sono stati (e vi sono forse tuttora) grandi osservatori di stelle doppie visuali che riuscivano ad andare anche sotto il potere risolutivo del proprio telescopio sulla base di piccole deformazioni dell’immagine osservata. Attenzione, però. Sto parlando non solo di accorgersi che una stella è “probabilmente” doppia, ma di riuscire a misurare la distanza tra le due componenti. Tra parentesi, malgrado io sia un planetologo da sempre, nel lontano 1986 avevo collaborato a un articolo scientifico sul potere risolutivo (QUI), scoprendone un “effetto” particolare che potrebbe anche interessare qualche osservatore odierno di stelle doppie.

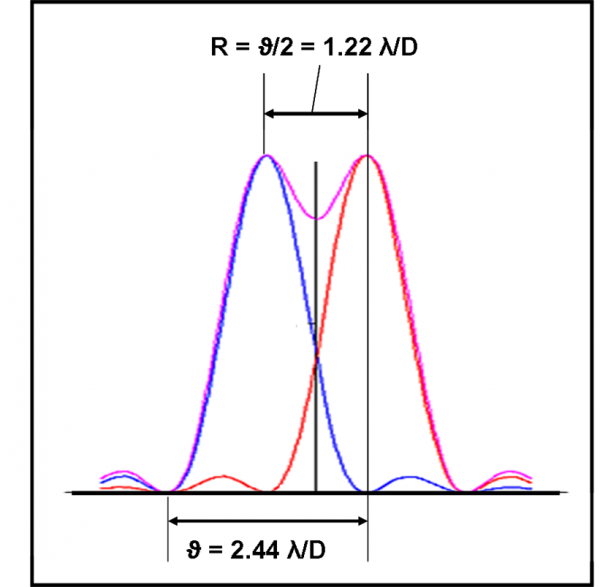
Il potere risolutivo è quindi dato da:

 R = ϑ/2 = 1.22 λ/D

Per come è stato definito è, ovviamente, la metà del disco di Airy.

La Fig. 47 riporta le immagini di una serie di stelle doppie a distanza diverse.

Ovviamente, non solo un’apertura crea figure di diffrazione. L’importante per farla nascere è che ci siano dei “bordi” di un qualcosa che ostacola la propagazione della luce. Vale quindi anche per un ostacolo che la luce deve, per così dire, “aggirare”, come, ad esempio, uno specchio secondario inserito all’interno del cammino ottico di un telescopio.

Vediamo ciò che capita nella Fig. 48. A sinistra la classica apertura singola, a destra un ostacolo, con le due onde circolari che si formano ai bordi dell’ostacolo e che in breve interferiscono per creare poi un’ onda finale più complicata.

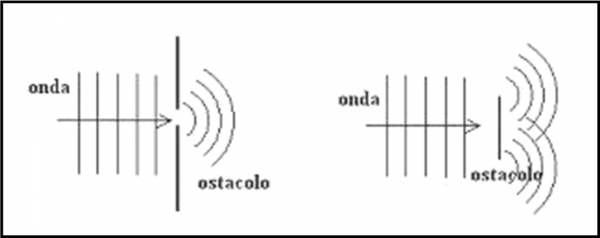
Come si manifesta, in pratica, l’inserimento di un ostacolo circolare in un telescopio ad apertura circolare? Vediamone l’immagine finale per varie combinazioni nella Fig. 49. In alto, senza alcuno ostacolo e il classico disco di Airy. Scendendo, cresce il diametro dello specchio secondario e la figura di diffrazione si complica mettendo in rilievo anche i cerchietti secondari. Nell’ultima in basso, l’inserimento di sostegni per il lo specchio secondario e l’apparizione dei raggi luminosi che sembrano “sparati” da un’immagine stellare piuttosto luminosa. In qualche modo ne viene riprodotta la forma.

Sui telescopi, comunque, torneremo prestissimo. Dobbiamo, infatti, ancora cercare di mandare verso un solo punto (più o meno) i raggi luminosi che entrano da un apertura larga ed è necessario usare un obiettivo. Il nostro occhio è veramente fantastico, malgrado abbia un’apertura molto piccola: riesce a cambiare la forma dell’obiettivo a seconda di cosa deve guardare, quasi fosse un sistema ad ottica “adattiva” (ne abbiamo già parlato in un vecchio articolo).

Ripeto ancora che questa parte abbastanza difficoltosa è fondamentale per creare le basi necessarie all’utilizzo consapevole di un telescopio e di quello che può mostrarci. Ho cercato di rendere la trattazione elementare, ma l’argomento è tutt’altro che semplice. La diffrazione impone un limite a qualsiasi telescopio! L’unico modo di eliminarla e avere un diametro … infinito. Ma, per adesso, è un sogno da folletto dei boschi…

Applichiamo la diffrazione a un vero telescopio

Per facilitare la comprensione di una parte abbastanza  difficile, ma fondamentale, riassumiamo tutto il fenomeno appena descritto, applicandolo a un caso veramente pratico, ossia a un vero telescopio. Per semplicità di descrizione usiamo uno strumento classico: il riflettore Newton, ossia quello che ha per obiettivo uno specchio parabolico. Vedremo in seguito perché ha proprio questa forma. Per adesso lo usiamo solo per costruire la figura di diffrazione. Un riassunto e un’applicazione pratica.

Avevamo concluso, con l’aiuto della perspicacia del pescatore, che un’apertura attraverso cui passa un fascio di onde piane e parallele crea un fronte d’onda che non è più piano. O -almeno- non completamente. Avevamo anche visto che il vero colpevole non è l’apertura in sé, ma i suoi bordi, ossia i punti dove si forma una discontinuità. Il pescatore aveva capito tutto ipotizzando che ogni punto dell’onda è, a sua volta, sorgente di una fascio d’onda circolare che si mescola con quelli dei punti vicini e fa apparire l’onda complessiva come piana. Tuttavia, quando l’onda attraversa un’apertura, una parte continua il suo percorso tranquillamente, mentre le onde che si originano nei punti che toccano i bordi introducono un disturbo che non riesce a essere amalgamato nell’onda piana.

Dopo il passaggio attraverso la fenditura, l’onda piana si sovrappone a quelle circolari generati nei punti che la delimitano. Questo mix crea il fenomeno della diffrazione

Per metterlo meglio in mostra si usa normalmente un’apertura estremamente piccola, dell’ordine della lunghezza d’onda, in modo che ciò che esce fuori da essa è solo l’onda circolare generatasi nei bordi, mentre quella piana praticamente non riesce a passare.

I casi di apertura larga e stretta li rivediamo nella Fig. 50: a sinistra la fenditura larga, a destra quella stretta. Nel secondo caso è come se avessimo messo in evidenza SOLO ciò che capita nei bordi della fenditura, mentre nel primo caso questo effetto si sovrappone velocemente all’onda piana che continua il suo cammino all’interno della fenditura.

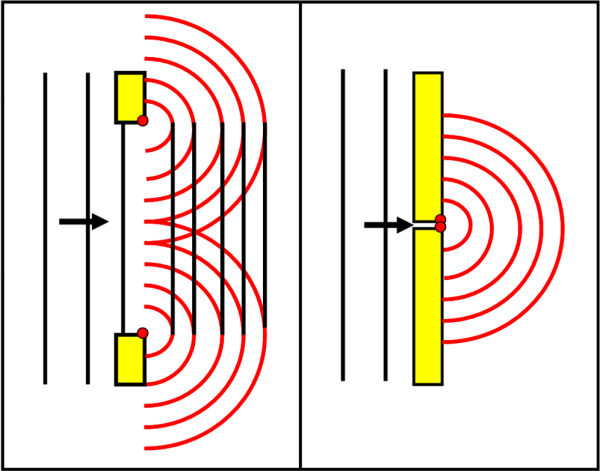
Un altro sistema per studiare le onde generatesi ai bordi di una fenditura è quello mostrato nella Fig. 51. Consideriamo un “molo” con due aperture strette, separate tra loro (parte sinistra). Ognuna di esse produce praticamente solo l’onda circolare tipica dei bordi di una fenditura. Possiamo con relativa facilità studiare le loro sovrapposizioni e interferenze. La somiglianza di questa configurazione con quella di un’unica fenditura estesa (a destra) è più che evidente. L’unica cosa che le fa differire è il “treno” d’onda piana che prosegue oltre la fenditura (disegnato in nero), ma che non modifica più di tanto la figura di diffrazione dato che mantiene una luminosità costante lungo tutto l’asse verticale.

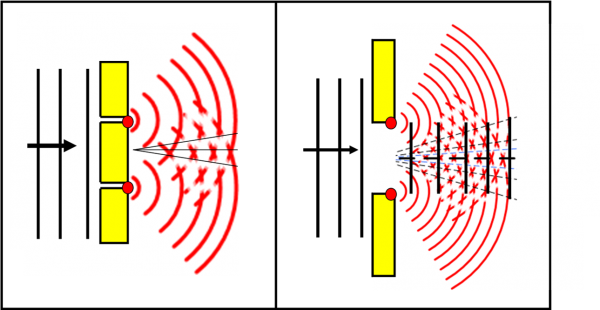
E’ quasi inutile dire che allargando e stringendo le due fenditure e/o modificando la loro distanza si ottengono figure sempre diverse che permettono uno studio accurato del fenomeno della diffrazione e di quello conseguente dell’interferenza fra onde, con una serie ininterrotta di applicazioni di estremo interesse scientifico. Ma a noi importa (per adesso) solo come questo fenomeno deformi l’immagine finale data da un telescopio (e anche dall’occhio che ha i suoi bordi come qualsiasi altro obiettivo artificiale).

La Fig. 52 introduce (finalmente !) il telescopio. Come detto, per semplicità di descrizione, consideriamo il telescopio a specchio (ossia il riflettore)  più comune e semplice: il telescopio di Newton che è formato da un obiettivo la cui superficie riflettente è di forma parabolica in modo da trasformare le onde piane e parallele che giungono da una stella in un insieme di onde circolari che hanno il loro centro in un punto detto fuoco.

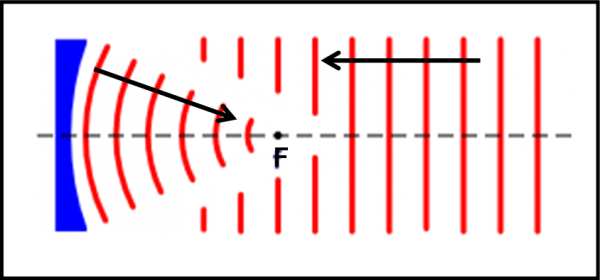
Concentriamo la luce

Ricordate che la parabola, intesa come curva, ammette la presenza di un fuoco che ha certe caratteristiche geometriche. Attenzione, però, a non confondere quanto detto finora: le onde circolari, che si originano ai bordi di un’apertura (o di un obiettivo), e che caratterizzano la diffrazione, hanno il loro centro proprio nel punto al bordo della fenditura. In questo caso, invece, l’onda circolare è “opposta”, ossia ha il suo centro in un punto (fuoco) lontano dall’obiettivo. Questa è un’onda che concentra la luce raccolta dall’obiettivo in un solo punto (o quanto di più simile a un punto possa essere).

Per essere ancora più chiari scomponiamo, nelle due parti della Fig. 53, ciò che fa il telescopio (tralasciando, per adesso, la diffrazione). Nella parte alta vediamo le onde piane, disegnate in nero, che provengono dalla stella puntiforme e lontanissima. Sono anche disegnati i raggi luminosi (già introdotti nell’ottica geometria), sempre perpendicolari all’onda piana e anch’essi disegnati in nero. Nella parte bassa l’onda piana colpisce lo specchio e viene riflessa e trasformata in onda circolare rossa (vedremo in seguito come avviene esattamente questa riflessione). Anche in questo caso ho disegnato i raggi rossi perpendicolari alle onde circolari (in realtà non sono proprio circolari, ma possiamo tranquillamente considerarle tali…). I raggi convergono in un punto dove si forma l’immagine della stella e la cui luminosità dipende da quanti raggi sono riuscito a fare convergere, ossia da quanto è grande l’obiettivo.

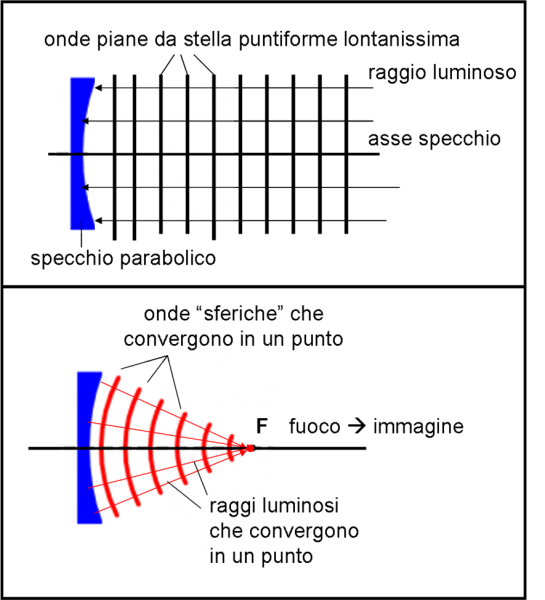
Avete notato? Dopo la diffrazione, anche la quantità di luce che si può raccogliere dipende dal diametro D dell’obiettivo del telescopio. Niente da fare: un grande diametro è la soluzione migliore!

Questo schema funziona perfettamente se non introduciamo la diffrazione. Penso che ormai abbiate capito questo concetto. Senza tener conto del fenomeno della diffrazione potremmo teoricamente ottenere un’immagine puntiforme di una stella puntiforme. In pratica, non è mai vero, in quanto uno specchio introduce comunque delle imperfezioni nell’immagine, sia per la sua lavorazione sia per questioni puramente geometriche. Inoltre l’atmosfera fa “ballare” l’onda piana della stella che l’attraversa (o -se preferite- i raggi luminosi che le rappresentano). I telescopi spaziali superano quest’ultimo inconveniente (e quasi del tutto quelli tecnici), ma… non possono fare niente, comunque, con la diffrazione: anche loro hanno dei bordi!

Riassumiamo l’intero tragitto della luce, sia come onde, sia come raggi luminosi, dalla stella fino al fuoco del telescopio. Lo facciamo con la Fig. 54. L’intervallo in anni luce, in cui ho interrotto il percorso della luce, è quello che permette alle le onde sferiche originali di essere, alla fine, considerare come onde piane a causa della distanza enorme e del piccolo angolo che ci raggiunge.

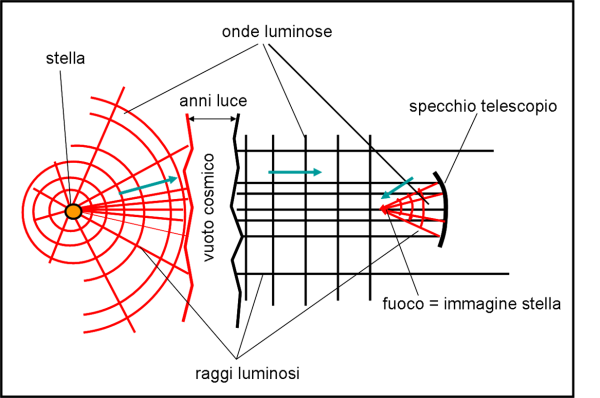
A questo punto, non ci resta che introdurre la diffrazione, l’effetto che si origina ai bordi dell’obiettivo e di cui ormai sappiamo tutto (o quasi).

Dividiamo i due effetti che giocano sulla formazione dell’immagine nella Fig. 55. In alto riportiamo quanto abbiamo appena visto: l’onda piana si riflette sullo specchio e torna indietro come onda circolare fino a formare un’immagine teoricamente perfetta. In basso, consideriamo solo le parti di onda piana che toccano i bordi dell’obiettivo.

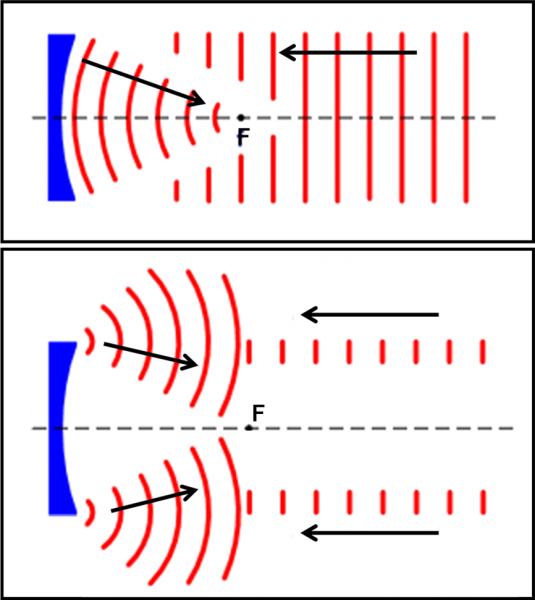
Esse seguono le leggi della diffrazione e i due punti estremi originano due onde sferiche che si allargano andando verso il fuoco. Come già visto esse interagiscono tra loro e formano la figura di diffrazione già abbondantemente analizzata.

Non ci resta che mettere tutto assieme e seguire l’onda finale che giunge al fuoco. Lo facciamo in Fig. 56. Sommando le onde di diffrazione a quelle di pura riflessione si ottiene un onda di forma ben più complessa che forma nel fuoco la figura di diffrazione finale.

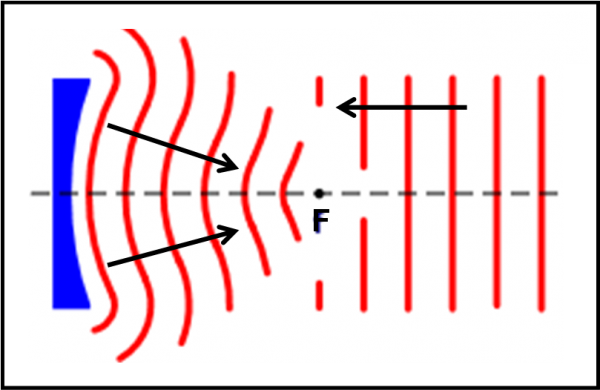
Il disco di Airy è più nitido e piccolo, e senza l’accompagnamenti marcato dei cerchietti concentrici, quanto più il diametro del telescopio è grande (ossia quanto i due punti estremi sono distanti tra loro, come visto precedentemente). Contemporaneamente, l’immagine è anche più luminosa, ossia ha raccolto più luce della stella lontana, quanto più il diametro cresce. Non è difficile notare che la quantità di luce raccolta cresce con l’area dell’obiettivo, ossia cresce con il diametro al quadrato. Su questo punto, comunque ci torneremo.

Cercate di comprendere bene questa parte. Non la richiameremo più, ma deve rimanervi bene in testa il seguente concetto: mai e poi mai potete ottenere un’immagine puntiforme di una sorgente di luce puntiforme, qualsiasi sia il telescopio, l’obiettivo, gli oculari, la lunghezza focale, ecc., ecc. E’ inutile usare diaframmi, allungatori di focale, lenti di Barlow e mille e uno marchingegni.

Tra poco cominceremo a parlare veramente dei vari tipi di telescopi e di ciò che riescono a fare. Ci basterà utilizzare di nuovo l’ottica geometrica, ossia quella che usa solo i raggi luminosi. Tutto sarà più semplice (tranne qualche formula in più).

Ingrandimenti…? No grazie, meglio tanta luce

La maggior parte di ciò che segue è una trattazione abbastanza tecnica e interessa sicuramente coloro che hanno un telescopio o che vogliono capire come funziona. Potrebbe sembrare un po’ noiosa agli altri, ma…  una rapida lettura la consiglio a tutti.

Il telescopio subisce ancora il fascino di Galileo Galilei. Malgrado siano passati secoli, molti continuano a pensare che esso serva per vedere più vicini, e quindi ingranditi, gli oggetti celesti. Se questo scopo era valido nel 1600, oggi il telescopio ha acquistato un significato ben diverso e decisamente più importante. Un telescopio scientifico serve solo e soltanto a raccogliere più luce possibile e non certo a ingrandire gli oggetti celesti.

Quanta delusione ho visto negli occhi di tanti sprovveduti appassionati quando a un telescopio gigantesco gli è apparsa una stella  o un pianeta. “Tutto lì… !”. Ebbene, questa è la vera differenza tra chi si vuole divertire con un telescopio amatoriale e chi vuole fare Scienza. Entrambe sono scelte personali e validissime, ma cerchiamo di non confonderle. Un telescopio di 8 metri di diametro non permette di ingrandire visivamente molto di più di un telescopio di pochi centimetri, ma raccoglie un’informazione che è straordinariamente più grande e ha un potere risolutivo di ben altra accuratezza.

Già alla fine del 1800 ci si accorse che il telescopio aveva ben altre caratteristiche che non quelle di far vedere vicino ciò che era lontano. Quest’ultima possibilità era solo un “di più”, di interesse sempre meno attraente. Anche perché non è certo l’ingrandimento che può far superare i limiti intrinseci di un’immagine telescopica.

L’unica caratteristica di importanza astronomica è il diametro dello strumento. Solo da esso dipendono i due vantaggi fondamentali: la quantità di luce che può raccogliere (e quindi l’informazione fisica) e la capacità di distinguere due stelle molto vicine (o i particolari di uno stesso oggetto). Tutto il resto è solo una “manipolazione” più o meno evidente di ciò che fornisce l’apertura. Una manipolazione che, se non conosciuta adeguatamente, può portare a errori, confusioni e conclusioni del tutto fuorvianti.

Oggi, l’occhio umano è praticamente inutile nell’osservazione astronomica e si preferiscono ricevitori molto più specialistici che variano a seconda dell’informazione che si vuole ottenere: lastre fotografiche o CCD, spettrometri, fotometri, polarimetri, interferometri, ecc., ecc.

L’occhio rimane fondamentale solo per coloro che desiderano “guardare” gli oggetti celesti, cercando di seguire le orme di Galileo, ossia tentare di ingrandirli il più possibile.

Tuttavia, bisogna ricordare che senza una conoscenza delle caratteristiche dell’immagine che si vuole ingigantire si fanno sforzi spesso del tutto inutili  Solo una precisa conoscenza del sistema ottico usato e della figura di diffrazione possono evitare insuccessi spesso dolorosi. Non fidiamoci nemmeno troppo della tecnologia che ci viene offerta ovunque e per chiunque. Quando si tratta di vendere, si gira sovente intorno ai veri problemi e le parolone, le promesse e -purtroppo- i prezzi alti sono sovente soltanto uno specchietto per le allodole e sfruttano facilmente la scarsa preparazione del compratore.

In questo contesto, non solo il disco di Airy diventa un ostacolo insormontabile, ma anche gli altri difetti tipici degli obiettivi. Essi prendono il nome di aberrazioni e deformano o alterano l’immagine raccolta nel piano focale. Non esiste un telescopio perfetto che riesca a eliminare TUTTE le aberrazioni. Quali cancellare dipende essenzialmente dal tipo di risultato che si vuole raggiungere. Proprio questa scelta permette di decidere che tipo di strumento è più vicino alle proprie aspirazioni. Ovviamente, vale lo stesso discorso anche per i “giganti” professionali.

Cos’è un telescopio?

Come già detto varie volte, un telescopio è formato da un sistema ottico in grado di raccogliere quanta più luce possibile da un astro posto praticamente all’infinito, i cui raggi possano, perciò, essere considerati paralleli. In quest’articolo non specifichiamo il tipo di obiettivo (lo faremo la prossima volta), ma ci limitiamo solo alle sue caratteristiche essenziali.

L’importante è che sia in grado di far convergere tutti i raggi verso un solo punto o in “qualcosa” che gli assomigli il più possibile. Il limite di questo punto è l’ormai ben noto disco di Airy, che è definito dalla diffrazione  ed è funzione soltanto del diametro e della lunghezza d’onda. Se a qualcuno risulta ancora un po’ “fantasioso” e misterioso questo fenomeno, legato all’ottica ondulatoria, basta ricordare che deriva essenzialmente dal secondo principio della termodinamica.

Tra le sue tante implicazioni, esso dice che non è possibile trasferire l’energia emessa da una sorgente estesa, come una stella, in un punto fisicamente perfetto.

La Fig. 57  mostra un telescopio generalizzato. I raggi rossi provengono da un oggetto posto all’infinito, incontrano l’obiettivo OB di diametro D, vengono deviati e convergono verso il punto F, detto fuoco. I raggi rossi della stella S₁ sono diretti esattamente come l’asse AO dell’obiettivo. I raggi, sempre paralleli tra loro, di un’altra stella S₂, separata dalla prima di un angolo ϑ, colpiscono l’obiettivo inclinati e sono fatti convergere in un altro punto che sta, comunque, nel piano passante per F e perpendicolare all’asse dello strumento.  Tale piano è detto piano focale ed è il luogo delle immagini che si formano attraverso l’obiettivo. La distanza, tra il centro di simmetria dell’obiettivo e il fuoco, è detta distanza focale f_OB.

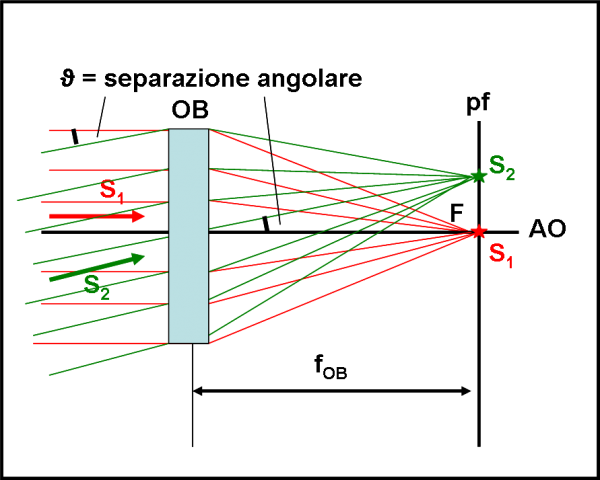
Il “vero” telescopio termina, teoricamente, a questo punto. Non vi sarebbe alcuna necessità di aggiungere altra strumentazione ottica. Si possono solo inserire le apparecchiature più idonee per lo studio dell’immagine suddetta. In altre parole, l’immagine contiene tutto ciò che può servire per la tecnologia più sfrenata.

Se, invece, vogliamo imitare il grande Galileo, e guardare direttamente con l’occhio l’immagine che si è formata, è necessario introdurre un nuovo dispositivo ottico in grado di trasformare nuovamente i raggi convergenti in un fascio parallelo, adatto alle condizioni di massimo rilassamento dell’occhio. L’obiettivo svolge il ruolo fondamentale di immagazzinare molta più luce di quanta possa riceverne direttamente l’occhio, l’oculare serve per adattarla alla visione dell’occhio e cercare di ingrandirla angolarmente. Avete mai visto un telescopio, che vuole fotografare o fare spettroscopia o qualche altra cosa di chiaro interesse scientifico, avere un oculare nel suo fuoco?

Questo fatto dimostra immediatamente che un oculare è un oggetto usato quasi unicamente  da astrofili senza interessi scientifici. Non ci occuperemo, perciò, dei dettagli di questa parte che ha quasi infinite variazioni sul tema. Alcune utili e necessarie, altre (e sono ben più numerose) del tutto inutili e secondarie rispetto al telescopio vero e proprio.

Lo schema obiettivo + oculare è mostrato in Fig. 58, dove la parte arancione è quella che ci interessa.

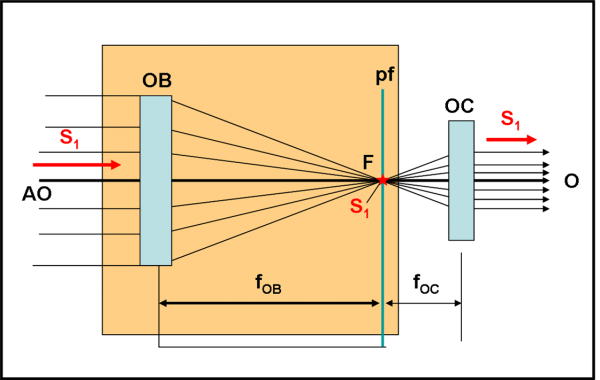
Vale, comunque, la pena descrivere brevemente uno degli apparenti vantaggi dell’oculare: ingrandire le immagini formatesi nel piano focale dell’obiettivo. Attenzione, però: ingrandire NON vuol dire fornire più dettagli. Tutta l’informazione che si riceve con l’occhio attraverso l’oculare è già presente nell’immagine ottenuta sul piano focale. Ciò che il dischetto di Airy ci permette di analizzare è lasciato inalterato.  L’oculare regala la soddisfazione di vedere più “grandi” particolari comunque presenti nell’immagine.

Se due stelle non sono state separate dall’obiettivo, non c’è oculare che possa farlo. In altre parole, un oculare non può fare miracoli e superare i limiti dell’ottica ondulatoria.

Come si calcolano, comunque, gli ingrandimenti di un sistema obiettivo + oculare? Ce lo mostra la Fig. 59.

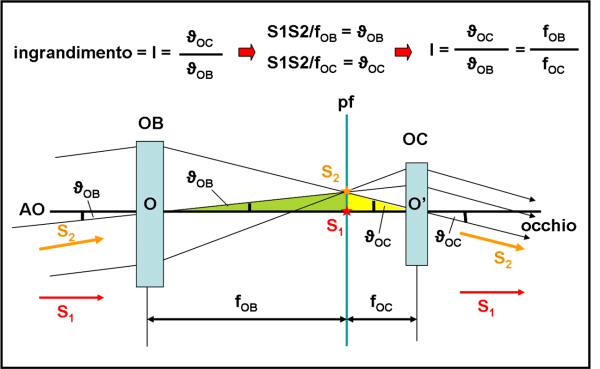
L’angolo, ossia la distanza angolare tra due oggetti o tra due particolari di uno stesso oggetto, è dato dall’angolo ϑ_OB. Sul piano focale questa distanza angolare è rappresentata dalla distanza lineare S₁S₂, ma le distanze tra oggetti celesti sono in realtà espresse solo e soltanto come angoli. L’oculare OC ritrasforma le immagini in fasci di raggi paralleli che formano tra loro un angolo diverso, ϑ_OC. L’oculare è normalmente costruito in modo che questo angolo sia maggiore di quello relativo ai fasci originari delle due stelle. Si definisce come ingrandimento del sistema obiettivo + oculare il rapporto tra ϑ_OC e ϑ_OB. Esso dice proprio quanto una distanza angolare viene aumentata nella visione diretta dell’occhio. Possiamo scrivere, perciò, che l’ingrandimento I è dato da:

I = ϑ_OC /ϑ_OB

Tuttavia, dal triangolo S₁S₂O, abbiamo anche:

S₁S₂ = f_OB ϑ_OB

e da quello S₁S₂O’:

S₁S₂ = f_OC ϑ_OC

In realtà, al posto dell’angolo bisognerebbe mettere la tangente dell’angolo, ma dato che gli angoli sono estremamente piccoli si può tranquillamente inserire l’angolo stesso espresso in radianti.

Le ultime due relazioni ci dicono che:

f_OB ϑ_OB =  f_OC ϑ_{OC ,}  e quindi:

I = ϑ_OC /ϑ_OB = f_OB/f_OC

che è la classica formula usata per calcolare gli ingrandimenti, conoscendo le distanze focali dell’obiettivo e dell’oculare.

La Fig. 60 mostra due visioni di Giove. La prima è stata ottenuta dalla seconda ingrandendola attraverso un oculare. E’ facile notare che si è guadagnato in dimensioni, ma non certo nei dettagli. L’informazione contenuta  nella seconda non è cambiata, ma si è solo fatta più confusa per varie ragioni fisiche.

Mettiamo da parte gli oculari  e procediamo nell’analisi del nostro telescopio vero e proprio.

Un lungo cammino verso il fuoco

Assodato una volta per tutte il concetto che il vero parametro fondamentale di un obiettivo è il suo diametro, da cui dipendono sia la quantità di luce concentrata nel piano focale sia il potere separatore, possiamo passare ad analizzare un altro parametro di grande interesse, la distanza focale. Infatti, a parità di diametro, a seconda del tipo dell’obiettivo, si possono avere distanze focali anche molto diverse.

La distanza focale è un parametro che va scelto sulla base dei risultati che si vogliono ottenere. E’, in qualche modo, un artificio che “manipola” l’informazione, rendendo più o meno leggibili certi suoi risvolti. Facciamo tre esempi che mettono in evidenza pregi e difetti di una distanza focale più o meno lunga.

Consideriamo in Fig. 61 il nostro solito obiettivo di diametro D, ma con due diverse distanze focali, f e f’, e i corrispondenti piani focali pf e pf’, dove si formano le immagini. Consideriamo anche due stelle che formino, rispettivamente, angoli ϑ₁ e ϑ₂ con l’asse ottico. Nel piano focale pf le immagini si formano in S₁ e S₂, mentre nel piano focale pf’ si formano in S₁’ e S₂’. E’ immediato notare che la distanza angolare ϑ1 - ϑ2, misurata in millimetri o centimetri o quello che volete, aumenta se la focale cresce. In altre parole, un millimetro corrisponde a una separazione angolare decrescente aumentando la focale dell’obiettivo. Il numero che ci dice quanti secondi d’arco corrispondono a un millimetro viene chiamata scala dell’obiettivo.

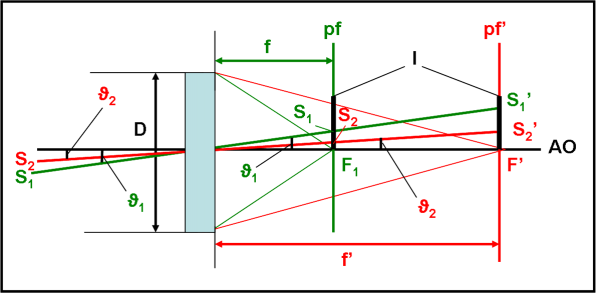
spieghiamo meglio questa semplicissima considerazione. Sia l una lastra fotografica o un CCD o una qualsiasi superficie su cui sia possibile analizzare le immagini. La lunghezza lineare di l è, ovviamente, sempre la stessa sia che essa sia posta in F che in F’.

Vediamo nella Fig. 62 cosa succede sui due piani focali. Immaginiamo di dividere la superficie di l in tanti quadratini (come fossero i pixel di un CCD) e studiamo la situazione. I due “quadrati” della Fig. 62 rappresentano le due superfici che giacciono sul piano focale, viste “di fronte”. Esse sono rappresentati solo come linee l nella Fig. 61 (viste di “taglio”).

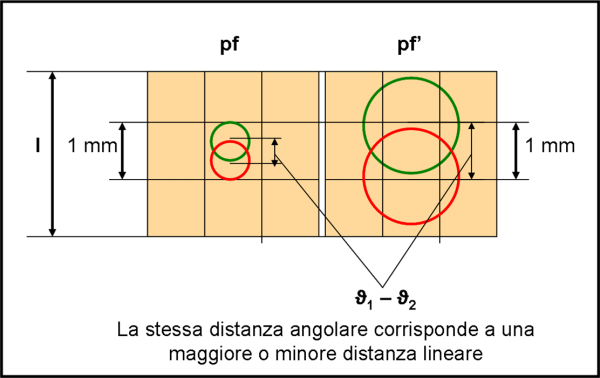
La distanza angolare tra le due immagini stellari è sempre la stessa ed è data da ϑ₁ - ϑ₂. Tuttavia, come detto precedentemente, la distanza lineare tra di loro aumenta all’aumentare della focale. Non illudiamoci, però. Al crescere della distanza lineare crescono anche le dimensioni del disco di Airy (sarebbe troppo bello!). La situazione di pf’ ha però dei notevoli vantaggi rispetto a quella di pf. Quando si misurano le posizioni relative tra due stelle si cerca di misurare il centro di ciascuna immagine (fotocentro). Se essa è una figura perfettamente simmetrica l’aumentare del diametro non influisce proporzionalmente sulla precisione della posizione del fotocentro.

In altre parole, se si commette un errore di 0.1 mm nel piano pf, si commette un errore circa uguale anche in pf’. Gli errori di misura si definiscono, ovviamente, in termini lineari. Tuttavia, 0.1 mm su pf corrisponde a un angolo maggiore che in pf’. Ricordiamo, infatti, che 1 mm su pf’ corrisponde a un valore più piccolo di separazione angolare. Ne consegue che l’errore finale espresso come angolo (in secondi d’arco, ad esempio) è nettamente più piccolo se si lavora con grandi lunghezze focali.

Ma, ancora più importante, è il fatto che, lavorando su angoli piccoli, l’intera lastra o il CCD è quasi immune dai difetti legati ai raggi  inclinati rispetto all’asse ottico.  Vedremo che esse sono le aberrazioni fuori asse, tra cui il coma è la più importante. Telescopi di grande lunghezza focale (a parità, ovviamente di diametro) sono usati per  misure di grande precisione.

Non sempre, però, lo scopo che si vuole ottenere è quello appena descritto. Vediamo, ad esempio, un problema non trascurabile che viene introdotto da obiettivi con grandi distanza focali. Lo schema ottico è sempre quello di Fig. 61, ma adesso consideriamo nella Fig. 63 cosa succede all’immagine di una singola stella nei due piani focali su una stessa lastra o CCD, di dimensioni uguali a l.

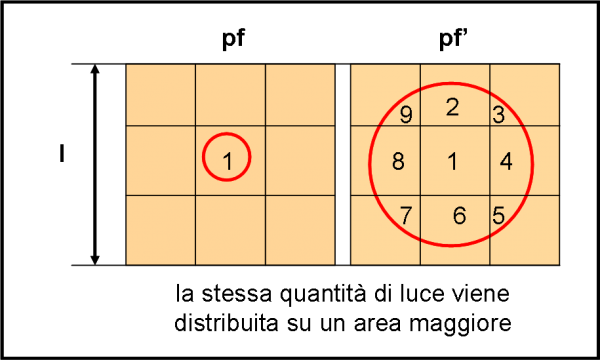
Dividiamo sempre le due superfici in quadratini. L’immagine della stella in pf è agevolmente contenuta all’interno di un singolo quadratino. La stessa stella va invece a coprire un’area ben maggiore nel piano focale pf’. Essa interessa ben nove quadratini.

Cosa vuol dire questo? Sappiamo benissimo che la quantità di luce raccolta da un obiettivo di diametro D non cambia al variare della focale. Ne consegue che, quando si usa una focale più lunga, la stessa quantità di luce viene distribuita su una superficie maggiore . Ogni singolo quadratino su pf', colpito dalla luce stellare,  mostra un’intensità minore di quello in pf, colpito da tutta la luce della stella.

Si suole dire che una focale più corta è più luminosa, perché le immagini stellari sembrano più luminose. In realtà, come già detto, l’intensità totale rimane invariata, ma nel secondo caso tutta la luce è concentrata in un quadratino e non viene dispersa su nove di essi. Focali corte possono quindi essere scelte quando si vogliono avere immagini apparentemente più luminose e quando non interessa molto la separazione tra le immagini e nemmeno i problemi dovuti alle aberrazioni fuori asse.

Ritorniamo per un attimo alla Fig. 62. Le immagini delle due stelle cadono entrambe all’interno di un solo quadratino nel piano pf. Ciò vuole anche dire che vedremmo una singola stella e non due, anche se l’intensità luminosa è molto elevata. Insomma, ogni soluzione ha un suo pro e suo contro.

Riflettete sopra a queste varie considerazioni. Ad esempio, cosa vuol dire che entrambe le immagini stellari cadono all’interno di un quadratino? Beh… solo che il singolo pixel è ben più grande del disco di Airy della stella. Ciò potrebbe essere un vantaggio per una visione globale di un certo campo stellare, ma non permetterebbe al telescopio di arrivare al potere separatore dell’obiettivo: la tecnica ucciderebbe l’informazione.

Una focale corta comporta un altro vantaggio, che spesso è molto utile: coprire con una sola immagine un campo di cielo il più vasto possibile. Poco importa se alcune stelle non vengono separate o se le aberrazioni fuori asse diventano molto grandi. L’importante è avere una visione contemporanea di una vasta regione di cielo. Ad esempio, per scovare qualche oggetto di cui non si sa l’esatta posizione o coprire l’intera forma di una struttura molto estesa.

Disegniamo la Fig. 64.

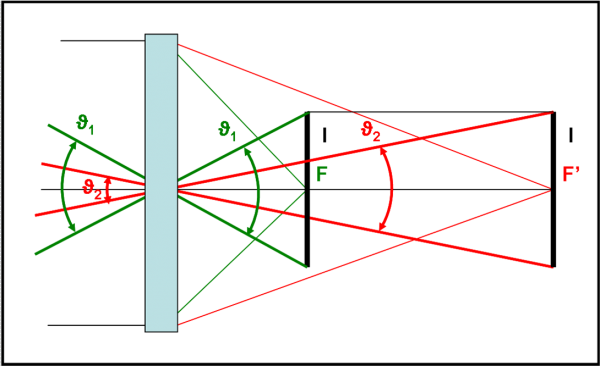
Una lastra fotografica o un CCD di dimensioni l copre una zona di cielo ben diversa se posto in pf o in pf’, come mostrato in Fig. 65. In pf il CCD copre un angolo uguale a ϑ₁ più grande di ϑ₂, ossia ha un campo angolare più esteso. Al suo interno vi saranno molte più stelle che non in quello posto in pf’.

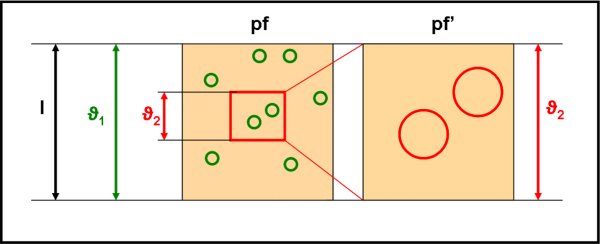
La distanza focale, quindi, pur avendo un ruolo decisamente secondario rispetto al diametro, può dar luogo a soluzioni più o meno vantaggiose a seconda di ciò che si vuole studiare e a seconda delle aberrazioni che si vogliono trascurare o eliminare.

Devo comunque fare una precisazione. Gli esempi fatti precedentemente sono oltremodo semplificati e non rappresentano situazioni realistiche al 100%. Hanno un valore puramente divulgativo e, giocoforza, estremizzato. Spero che siano, però, sufficienti per una comprensione qualitativa dei concetti di base.

Lenti, specchi e tanti difetti

Finora, abbiamo trascurato l’obiettivo, considerandolo solo un qualcosa che concentra la luce di una stella in un punto il più piccolo possibile. Non ci rimane, adesso, che analizzarlo in dettaglio, entrando nel mondo delle lenti, degli specchi e dei loro difetti. Vedremo che gli obiettivi a più lenti non si costruiscono per farli pesare di più e che le forme degli specchi non sono fantasiose scelte estetiche o soluzioni legate alla facilità di lavorazione.

I problemi che nascono nel cercare di concentrare i raggi luminosi di un astro lontano in un’immagine che assomigli il più possibile a un punto non si limitano soltanto alla diffrazione. Tuttavia, mentre per quest’ultima l’unica soluzione (palliativa) è ingrandire il diametro dell’obiettivo, per tutti gli altri è possibile ottenere ottimi risultati lavorando sul tipo di obiettivo e sulla sua forma. Ovviamente, non esiste una soluzione perfetta e si sceglie quella che meglio soddisfa lo scopo dell’osservazione programmata. O, invertendo il discorso, ogni telescopio ha una sua ben precisa funzione.

Accettato il fatto che contro la diffrazione non vi è niente da fare, vediamo ora i tipi di obiettivo che sono normalmente utilizzati nelle osservazioni astronomiche.

Vi sono solo due fenomeni capaci di deviare un raggio luminoso dal suo percorso rettilineo: la rifrazione e la riflessione. E’ ovvio, quindi, che un obiettivo, il cui scopo è proprio quello di fare convergere raggi tra loro paralleli, debba sfruttare uno di loro.

In realtà, anche la gravità riesce a ottenere lo stesso risultato, ma l’uomo deve andare a cercare la “lente” tra quelle già costruite dell’Universo e non può certo elaborarla per i propri scopi. Possiamo quindi tralasciare la lente gravitazionale tanto utile per lo studio delle galassie più lontane. Non possiamo nemmeno pensare di utilizzare laghi e laghetti che il nostro amico pescatore conosce molto bene. Meglio dedicarsi al vetro, all’argento, all’alluminio e a sostanze più moderne e attraenti.

Per far ciò prendiamo due oggetti molto comuni nella vita di tutti i giorni: una lastra di vetro e uno specchio. Cosa riescono a fare se inseriti lungo il percorso della luce che proviene da una stella? Lo vediamo nella Fig. 66, anche se ormai dovremmo saperlo molto bene.

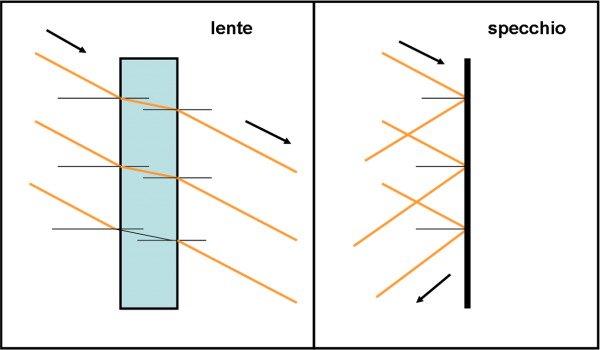
Una lastra di vetro di un certo spessore devia il raggio luminoso avvicinandolo alla normale alla superficie di contatto tra aria e vetro, ma, poi, è costretta a farlo di nuovo allontanare in modo esattamente uguale e contrario a quanto fatto all’entrata, quando la luce esce nuovamente allo scoperto. Conclusione? I raggi si sono spostati leggermente ma sono rimasti paralleli tra loro.

Sappiamo che succede anche qualcos’altro (prisma o goccia d’acqua), ma per adesso tralasciamolo.

Proviamo, adesso, a inserire lo specchio. Il raggio torna nella direzione da cui è venuto formando un angolo uguale a quello di incidenza tra lui e la normale alla superficie. Anche questo fenomeno lo conosciamo molto bene, ma, ancora una volta, i raggi restano paralleli anche se deviano nettamente il loro percorso primitivo. Ogni raggio del fascio segue perfettamente ciò che fanno i compagni di viaggio.

Dobbiamo, perciò, concludere che la superficie da interporre al raggio di luce deve essere curvilinea per sperare che ogni raggio segua un percorso diverso da quello dei fratelli paralleli. Scusate se la trattazione può sembrare banale e quasi infantile, ma è sempre importante avere le idee chiare fin dall’inizio.

Una curva ha in ogni suo punto una perpendicolare alla tangente, tracciata per quel punto, che differisce da quella del compagno vicino. Non abbiamo ancora risolto niente, ma, almeno, siamo riusciti a deviare i raggi in modo diverso tra loro, dato che sappiamo benissimo che o si rifrangono avvicinandosi alla normale o si riflettono formando un certo angolo con lei.

Prendiamo allora il pezzo di vetro a facce piane e parallele e lavoriamo queste ultime in modo che diventino entrambe una porzione di superficie sferica. Abbiamo ottenuto una lente. Se la mettiamo contro i raggi del Sole vediamo che formano un punto molto luminoso su un foglio di carta.

Spostando il foglio, in avanti o indietro, può anche capitare che prenda fuoco. Evviva! Abbiamo concentrato i raggi luminosi in un punto. La spiegazione “tecnica” ce la mostra la Fig. 67. la rifrazione e le perpendicolari sempre diverse tra loro hanno compiuto il miracolo. L’immagine della stella si è formata in un punto (o quasi, ricordando la diffrazione). Tutto ciò che è stato descritto  precedentemente è diventato realtà.

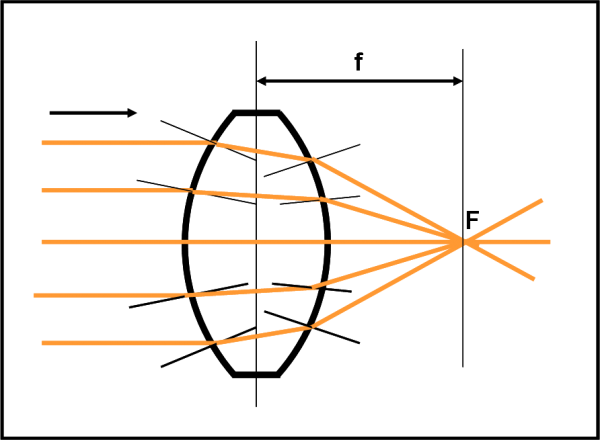
Ovviamente, sorgono dei problemi. Se vogliamo diminuire il disco di Airy dobbiamo aumentare le dimensioni della lente. Il vetro purtroppo pesa e una lente anche. Oltretutto, più è grande la superficie e più difficile è riuscire a farla diventare perfettamente sferica. Non possiamo permetterci di fare un lavoro approssimativo. Tutto deve essere preciso se vogliamo almeno arrivare ai limiti imposti dalla diffrazione. La prova di quanto detto si ha notando che il telescopio a lente più grande del mondo non supera il metro di diametro. Valore enorme per una lente, ma ridicolo se si vuole raccogliere veramente molta luce e spingersi ai confini dell’Universo, raccogliendo anche quella partita miliardi di anni fa.

Ci si potrebbe anche accontentare, per osservare oggetti vicini, ma sorgerebbe comunque un problema molto evidente che conosciamo bene e che viene sfruttato egregiamente per altri scopi sia dalla tecnica umana che dalla Natura. Quale? Basta ricordare il prisma e l’arcobaleno. Ogni lunghezza d’onda si avvicina o si allontana dalla perpendicolare in modo diverso. La Fig. 68 ci mostra quello che succede alla luce che esce dalla lente. I raggi rossi convergono verso un fuoco diverso da quello della luce verde e della luce blu (e lo stesso vale anche per gli altri colori). La nostra immagine stellare si colora magicamente.

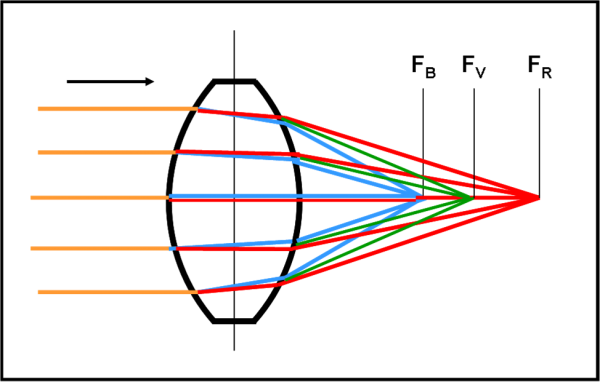
Può anche essere molto suggestivo, ma è sicuramente un difetto che deteriora l’osservazione. Siamo di fronte a un primo tipo di aberrazione che è intrinseca della lente, ossia del fenomeno della rifrazione: l’aberrazione cromatica.

Se questo difetto poteva anche essere accettato da Galileo Galilei, non può più esserlo oggi. Cosa fare, allora? Non è teoricamente difficile. Basta inserire un’altra lente dopo la prima e far convergere nello stesso punto sia la luce rossa che quella blu (i due estremi del visibile, violetto permettendo), come vediamo nella Fig. 69, in alto.

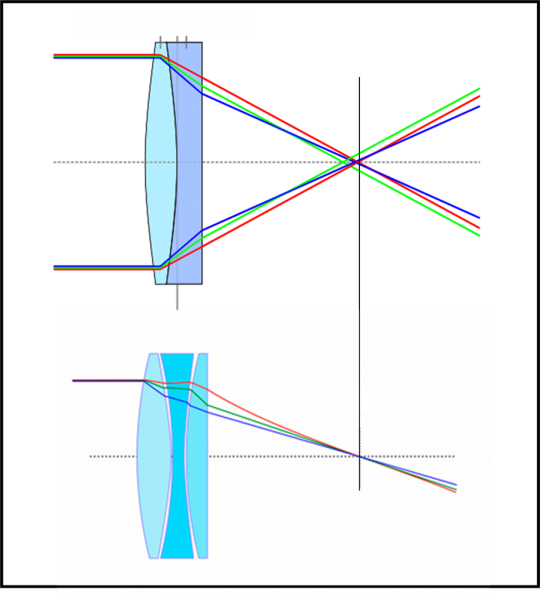
Purtroppo, far convergere gli estremi non vuol dire far convergere anche le altre lunghezze d’onda. Se volessimo aggiungere anche quella verde dovremmo aggiungere ancora una lente (in basso). Oltretutto le lenti dovrebbero anche essere di vetro diverso e di forma diversa. Oggi tutto è possibile, ma il peso aumenterebbe e anche il costo di lavorazione. Non solo, però. Dover percorrere un tragitto sempre più lungo nel vetro porta a dispersione di luce (riflessioni interne e cose più complicate) e quella finale perderebbe parte della sua energia. Insomma, le lenti, in astronomia osservativa, hanno perso molto del loro antico fascino.

Prima di abbandonarle del tutto (almeno nella nostra trattazione elementare) utilizziamone una per introdurre visivamente un’altra fonte di disturbo, ossia un’altra aberrazione di tipo geometrico: l’aberrazione di sfericità. Purtroppo è ancora qualcosa che aumenta le dimensioni del disco di Airy e peggiora il potere separatore.  La vediamo in modo schematico nella Fig. 70. I raggi che colpiscono la lente vicino ai suoi bordi  si dirigono a un fuoco che è più vicino all’obiettivo di quanto non sia quello relativo ai raggi vicini all’asse ottico. Ogni coppia di raggi considerati nella figura ha un suo fuoco personale.

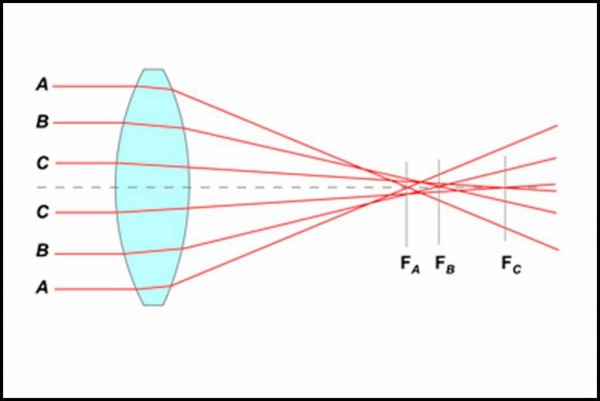
Vale la pena studiare in dettaglio questa situazione abbastanza critica. Lo faremo, però, introducendo il secondo tipo di sistema ottico, quello che utilizza uno specchio. Tuttavia, ricordiamo, prima, che l’aberrazione di sfericità può essere annullata (o quasi) lavorando sulla singola lente. Un lavoro non certo facile. Bisogna intervenire trasformando la superficie in qualcosa di molto più complesso che in qualche modo vada a deformare l’onda piana che arriva all’obiettivo in modo che quella uscente, dopo la rifrazione, sia perfettamente sferica e abbia un solo punto di convergenza. Passando ai raggi (sempre perpendicolari alla superficie dell’onda, ricordate?) avremmo quanto rappresentato nella Fig. 71. La lente assume una forma strana e non certo facile da ottenere. Ne vale la pena? Vedremo che la risposta è positiva, ma in casi ben diversi da quelli legati a una lente usata come obiettivo.

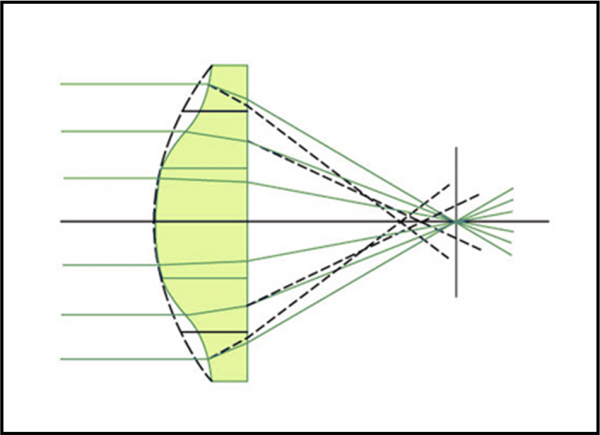
Lo studio delle aberrazioni è oltremodo complesso e necessita di una geometria non banale. Ho cercato di renderlo elementare, almeno per quanto riguarda la più importante tra loro, quella di sfericità. Ciò che sto per mostravi richiede solo una minima attenzione, ma non si va oltre al teorema di Pitagora e alle proprietà dei triangoli simili. Roba da scuola media.

Chi vuole seguirmi non farà una gran fatica e comprenderà meglio cosa s’intende veramente per aberrazione. In mancanza di voglia o capacità o tempo può passare direttamente alla conclusione.

Consideriamo allora uno specchio di forma sferica, come quello rappresentato nella Fig. 72. Il raggio luminoso proviene dalla stella S ed è parallelo all’asse ottico. Sia C il centro della circonferenza che rappresenta la sezione dello specchio sferico. Il raggio luminoso, che colpisce lo specchio in P, forma un angolo α con il segmento PC, che è proprio il raggio della circonferenza r. Il raggio luminoso viene riflesso, tornando indietro e formando con il segmento PC un angolo uguale ad α (riflessione).

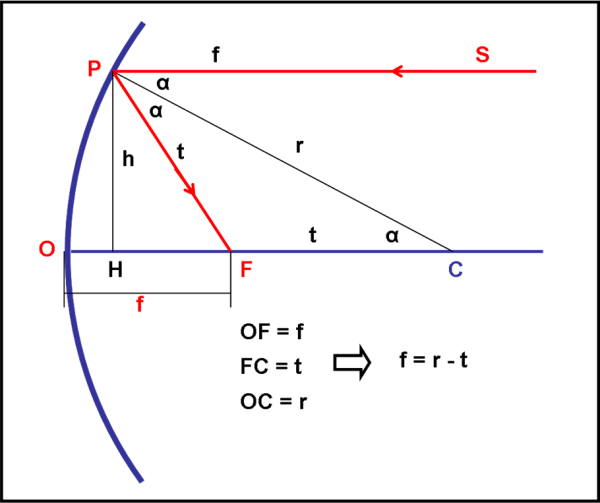
Ricordiamo che il segmento PC è perpendicolare alla tangente tracciata alla circonferenza nel punto P, ossia è proprio la perpendicolare di riferimento per la riflessione. Il raggio luminoso prosegue il suo cammino fino a incontrare l’asse ottico nel punto F. Esso rappresenta il fuoco per il raggio luminoso considerato, che dista h dal punto P di contatto (PH = h). OF è, quindi, la distanza focale corrispondente.

L’angolo PCF è uguale all’angolo SPC in quanto alterni interni di rette parallele e vale, quindi, α.

Per definizione di riflessione, anche l’angolo CPF è uguale a SPC e vale ancora α. Consideriamo il triangolo PFC. Esso ha due angoli uguali (quello in P e quello in C) e quindi risulta essere un triangolo isoscele. Ma se è isoscele devono essere uguali anche i lati opposti ai due angoli uguali, ossia PF = FC. Chiamiamo t questi segmenti. Ne consegue che la distanza focale f (OF) è data anche dalla differenza tra il raggio della circonferenza-specchio (OC) e il segmento FC, uguale a t. ossia:

f = r – t

Passiamo, adesso, alla Fig. 73.

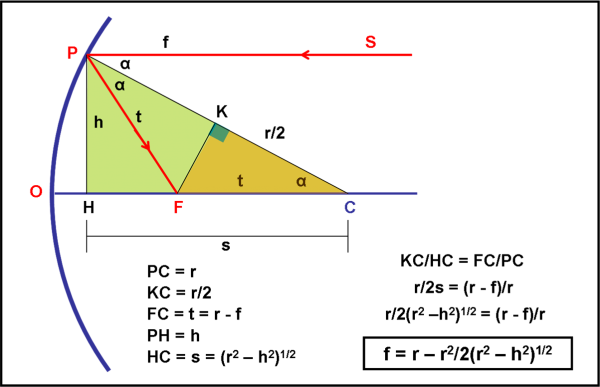
Tracciamo da F la perpendicolare al raggio della circonferenza CP. I due triangoli che si ottengono sono rettangoli e uguali tra loro (due angoli e due lati uguali). Vale quindi KC = PK = r/2. Rivolgiamoci al triangolo FKC. La sua ipotenusa FC vale t e il suo cateto più lungo vale r/2. Consideriamo, ora, il triangolo rettangolo PHC. Il suo cateto più lungo HC (s) può essere ricavato applicando il teorema di Pitagora, ossia:

HC² = PC² – PH² , e quindi:

s² = r² – h²  o, ancora, s = (r² – h²)^1/2

I triangoli FKC e PHC sono simili tra loro, in quanto hanno due angoli uguali (e quindi di conseguenza anche il terzo). Se sono simili vale allora anche la proporzionalità tra i lati corrispondenti, ossia: il cateto più lungo del primo sta al cateto più lungo del secondo come l’ipotenusa del primo sta all’ipotenusa del secondo. In termini matematici:

KC/HC = FC/PC , ossia:

r/2s = t/r = (r – f)/r

Ricordando il valore di s, si ottiene:

r/2(r² – h²)^1/2 = (r – f)/r

Con semplici passaggi, si arriva a scrivere la relazione che lega la distanza focale f  al raggio della circonferenza (una costante dello specchio) e all’altezza del punto P (in cui il raggio luminoso tocca lo specchio) rispetto all’asse ottico (h).

In altre parole, la relazione che permette di calcolare la distanza focale f , per ogni distanza h del raggio luminoso dall’asse ottico. Essa vale:

f = r – r²/2(r² – h²)^1/2

Nel caso in cui il raggio luminoso abbia altezza h uguale a zero (ossia coincida con l’asse ottico) si ha subito:

f = r – r²/2r = r – r/2 = r/2

il fuoco, per i raggi prossimi all’asse ottico, è un punto che sta proprio a metà del raggio della circonferenza-specchio. Ossia: OF = OC.

All’aumentare dell’altezza h si può facilmente calcolare che il fuoco si avvicina sempre di più al punto O, ossia la distanza focale si accorcia. Chi si vuole divertire può provare a calcolare il caso limite in cui l’angolo α è di 45°, ossia h = s. Troverà che il fuoco si sposterà fino ad H.

Questa semplice relazione ci permette di descrivere in modo oltremodo elementare gli effetti dell’aberrazione di sfericità  al crescere della distanza dei raggi luminosi dall’asse ottico.

Come si traduce, in pratica, questa variabilità della distanza focale? Lo vediamo bene nella Fig. 74.

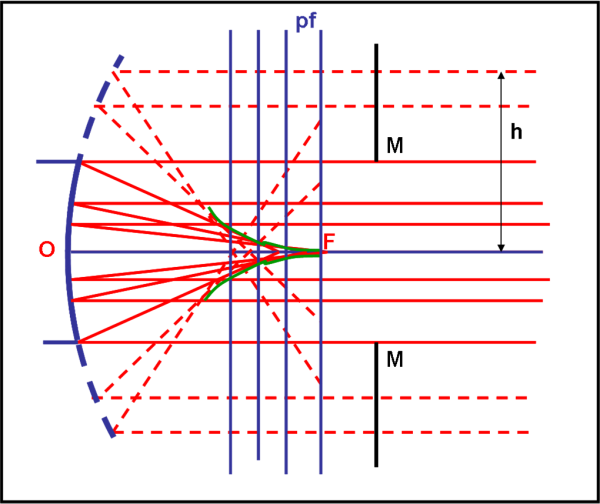
A mano a mano che spostiamo il piano focale pf  l’intersezione dei raggi, che convergono verso fuochi diversi, creano immagini a forma di disco che si allargano o si stringono. Il fuoco F dei raggi vicini all’asse non dà certo l’immagine migliore, dato che raggi molto lontani, come quelli tratteggiati, arrivano sul suo piano focale molto distanti dal centro.

I casi sono due: o si cerca il disco di minore estensione su un piano focale intermedio o si limita l’altezza dei raggi incidenti, utilizzando, ad esempio, un diaframma M inserito prima del contatto con la superficie sferica.

Diaframma, però, vuole dire diffrazione (ricordate?). Insomma, uno specchio sferico comporta problemi non indifferenti che alterano non poco il disco di Airy teorico. L’unico vantaggio indiscusso è che la riflessione non introduce aberrazione cromatica. Inoltre, ovviamente, può permettere diametri dell’obiettivo ben maggiori di quelli delle lenti.

La figura mostra anche una curva verde, sopra e sotto l’asse ottico. Essa rappresenta una superficie che è l’inviluppo dei raggi che convergono verso i vari fuochi e definisce perfettamente l’aberrazione di sfericità. Essa prende il nome di caustica e la sua trattazione in termini analitici è oltremodo “divertente”, anche se non proprio immediata. Lo dico con cognizione di causa dato che su queste superfici di aberrazione era basata la mia tesi di laurea, tanti, tanti anni fa.

La Fig. 75  mostra un’immagine priva di aberrazione di sfericità (a sinistra) e una “raccolta”  in un fuoco intermedio in presenza dell’aberrazione (a destra). Povera figura di diffrazione!

Fortunatamente la geometria viene in aiuto ai problemi che stanno riversandosi sulla nostra povera immagine stellare. Altro che punto perfetto! Assumo che chiunque legga queste pagine sappia cosa sono le coniche, ossia quelle curve che nascono dal taglio di un cono con piani più o meno inclinati. I loro nomi “propri” sono sicuramente più conosciuti: ellisse, parabola, iperbole. Nel caso le trovate spiegate in dettaglio nella sezione matematica. Tutti gli amanti del Cosmo sanno benissimo che esse rappresentano i vari tipi di orbita che un corpo planetario può descrivere attorno alla sua stella.

Ogni curva ha tutta una serie di caratteristiche esprimibili in vari modi. A noi interessano, adesso, quelle di tipo puramente geometrico. L’ellisse è quella curva chiusa tale che per ogni suo punto la distanza da due punti detti fuochi  rimane costante. In campo astronomico un pianeta descrive normalmente un’ellisse con il Sole posto in uno dei due fuochi. Un caso limite dell’ellisse è la parabola, una curva “aperta” simile all’ellisse, in cui si può immaginare che uno dei due fuochi vada all’infinito. Lasciamo per il momento da parte questa visione ben più generale e istruttiva e torniamo al nostro specchio sferico e ai suoi difetti di convergenza dei raggi paralleli.

Il telescopio di Newton

Se, invece di una sezione sferica, introducessimo una sezione parabolica? Succederebbe qualcosa? Sicuramente sì. Proprio per definizione di parabola. Provare per credere. Prendete un fascio di raggi paralleli che incidono su uno specchio parabolico e costruite i raggi riflessi. Qualsiasi sia l’altezza dei raggi rispetto all’asse ottico trovereste che i raggi riflessi convergono verso un unico punto, che è proprio il fuoco dell’obiettivo parabolico, ma anche il fuoco della parabola. Vi sono tanti modi per dimostrarlo in modo analitico. Io preferisco quello legato proprio alle onde luminose che giungono fino al telescopio.

Uno dei criteri per definire una parabola è la relazione che dice che la distanza da una retta perpendicolare all’asse di simmetria (asse ottico) fino al fuoco, toccando la parabola, è una costante.

Considerando la Fig. 76, possiamo scrivere questa relazione in semplicissime forme matematiche:

QP + PF =  Q’P’ + P’F = cost.

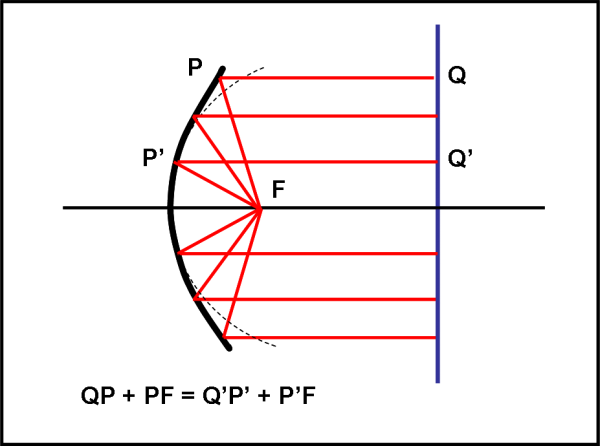
Ma la retta perpendicolare QQ’ rappresenta perfettamente un’onda luminosa piana che sta arrivando da una stella lontana. La relazione di prima cosa dice allora? Che un raggio luminoso, che sia perpendicolare all’onda piana, è obbligato a toccare la superficie parabolica e convergere nel punto F. Non solo, ma anche che tutti i raggi paralleli devono fare la stessa cosa. In poche parole, un fascio di raggi paralleli all'asse, dopo la riflessione su una superficie parabolica, converge in un unico punto.

Le condizioni che fanno nascere l’aberrazione di sfericità sono state cancellate e quindi possiamo concludere che uno specchio parabolico non presenta questo tipo di aberrazione. Vi pare poco?

Capite allora perché questo tipo di telescopio ha avuto tanto successo. Il suo nome proprio è telescopio di Newton. Esso è ottimo finché si rimane su campi abbastanza piccoli, ossia non si considerano raggi stellari troppo inclinati rispetto all’asse ottico. In altre parole: se la distanza focale è molto più grande del diametro del telescopio (ricordate il capitolo precedente). Torneremo su questo problema tra poco.

Vediamo adesso un altro tipo di problema legato al telescopio puramente parabolico. Come avete visto, il fuoco, ossia il luogo dove si forma l’immagine, è posto davanti allo specchio rispetto alla sorgente luminosa. Per guardare cosa succede nel fuoco dovremmo entrare dentro al telescopio e bloccare la luce che viene dalla stella. Bisogna fare qualcosa. La soluzione più ovvia è quella di inserire uno specchietto piano che devi i raggi che stanno dirigendosi verso il fuoco e ne crei uno esterno al telescopio. Proprio quello che si vede nella Fig. 77.

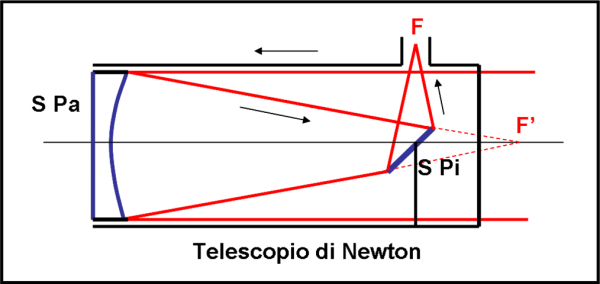
Ovviamente, se vogliamo analizzare l’immagine finale non con l’occhio, ma con altri sensori non avremo nessun bisogno di deviare i raggi e potremmo introdurre lo strumento che guarda le immagini direttamente nel fuoco reale F’. Vi sarà un piccolo ingombro, ma non quanto quello causato comunque dallo specchietto piano S Pi. Inoltre, tenete sempre a mente che introdurre uno specchietto vuole dire introdurre un ostacolo con dei margini e quindi … diffrazione!

Un altro problema del telescopio di Newton è quello dovuto al suo ingombro. Abbiamo visto che può lavorare abbastanza bene se la distanza focale è lunga rispetto al diametro. Ne segue che la lunghezza del tubo del telescopio è notevole, poco meno della distanza focale. Se il diametro cresce troppo, il tubo diventa enorme, pesante e può subire flessioni.

Il telescopio Cassegrain

Per ridurre l’ingombro e poter, comunque, mantenere una distanza focale notevole nasce una variante importantissima del riflettore Newton, il telecopio Cassegrain. Esso sfrutta la convergenza dei raggi assiali in un unico punto data dallo specchio parabolico, ma inserisce uno specchio secondario lungo l’asse dello specchio primario. Qual è lo scopo di questa “intrusione”? Semplice: rispedire indietro i raggi luminosi e farli convergere in un punto che stia oltre il primario.

Sicuramente il sistema diventa più complicato: bisogna costruire e inserire uno specchietto secondario e poi bisogna fare un buco nel primario per permettere ai raggi di convergere all’esterno, dove poter analizzare tranquillamente l’immagine finale. E’ vero, abbiamo introdotto un ostacolo alla luce che arriva dalla stella, ma abbiamo ottenuto un fuoco facilmente raggiungibile e una grande lunghezza focale con un ingombro del tubo nettamente minore.

La distanza focale finale, infatti, è quella relativa a tutto il percorso del raggio, da S Pa a S Ip, fino al fuoco F, decisamente più lunga di quella originaria da S Pa a F’. La Fig. 78 mostra una classica combinazione Cassegrain. La lunghezza del telescopio è circa la metà della distanza focale, ma può anche essere minore. Un gran bel vantaggio!

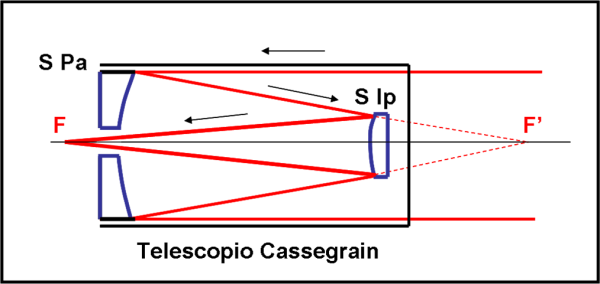
Avete visto che lo specchio secondario l’ho chiamato S Ip, che sta per specchio iperbolico. In  realtà, la forma della sua superficie riflettente è proprio un’ iperbole.

Si potrebbe usare anche uno specchio piano (il telescopio astrometrico dell’Osservatorio di Torino usa questa semplice soluzione), ma la lunghezza focale resterebbe inalterata, con un ingombro del tubo pari alla metà di essa.

I raggi si inclinano

Vi siete accorti che stiamo facendo di tutto per avere grandi lunghezze focali, ossia campi di vista molto ridotti. Soluzione perfetta per misurazioni molto precise, ma meno interessante per coprire larghe zone di cielo. Sembra quasi che si abbia paura a ricevere immagini da stelle molto inclinate rispetto all’asse ottico, ossia tali che i loro raggi formino angoli abbastanza grandi con l’asse ottico dello strumento. In effetti, è proprio così.

Se l’angolo comincia a crescere fa la sua comparsa la prima aberrazione fuori asse, il coma. Essa dipende dall’angolo di inclinazione ϑ che il raggio forma con l’asse ottico e, in parte, anche dall’altezza del raggio nel suo punto di contatto con la superficie rifrangente o riflettente dell’obiettivo. E’ una specie di mix tra aberrazione di sfericità (che dipende solo dall’altezza del raggio parallelo all’asse) e la deformazione dovuta all’angolo che i raggi formano con l’asse.

Insomma, un bel pasticcio. Non chiedetemi la trattazione analitica che non potrebbe essere comunque banale. Vediamo, invece, in Fig. 79, uno schema molto semplificato di quello che succede per un fascio di raggi paralleli inclinati di un angolo ϑ rispetto all’asse ottico.

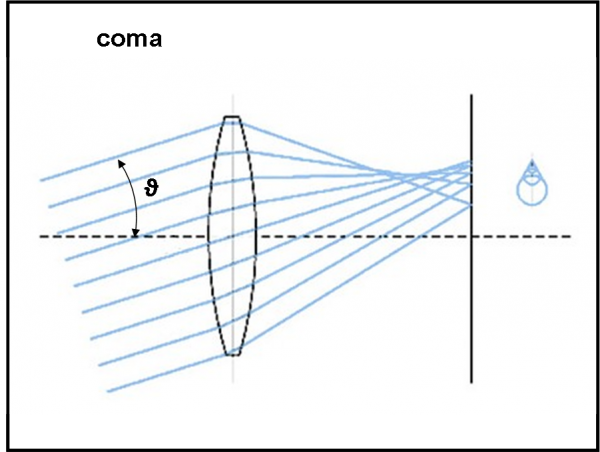
Il fuoco non è certamente unico e nasce una strana figura a “goccia”, tipica delle immagini stellari poste ai bordi di telescopi che non fanno niente per annullare quest’aberrazione. La goccia la vediamo in dettaglio nella Fig. 80 e un campo largo, affetto da coma, lo vediamo in Fig.81.

Telescopio Ritchey-Chretien

Si può fare qualcosa per il coma? Sicuramente sì, basta studiare le superfici di due specchi che possano essere qualsiasi e vedere se esistono soluzioni che permettano di annullare sia l'aberrazione di sfericità che il coma. Si deve abbandonare la forma parabolica del primario e fare calcoli molto accurati. La soluzione esiste e porta a due specchi (primario e secondario) ambedue iperbolici (o a curve anche più complesse).

Se volete che rappresenti questa geniale soluzione, che prende il nome di Ritchey-Chretien, avrete una piccola delusione. Ho ripreso tale e quale la Fig. 78 e l’ho riproposta in Fig. 82, cambiando solo S Pa in S Ip. Le curvature dei due specchi sono diverse da quelle di prima, ma la differenza è impossibile da notare sulla figura. L’aspetto complessivo è lo stesso. Tuttavia, adesso possiamo diminuire di molto la distanza focale (e quindi aumentare il campo di vista) a parità di diametro. Anche l’ingombro diventa minore. Non per niente è una delle soluzioni più usate in campo professionale.

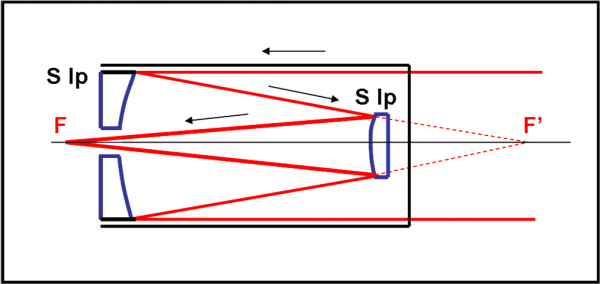
Non credete comunque che con il coma ci siamo tolte tutte le aberrazioni. Ve ne sono anche altre. Una per tutte l’astigmatismo e poi la curvatura di campo e la distorsione… Insomma il percorso verso un’immagine di diffrazione perfetta non è assolutamente facile.

Non è comunque il caso di scendere ancora di più nei dettagli. Chi usa un telescopio deve conoscerle perfettamente per non considerare, come reali variazioni topografiche di strutture planetarie, delle semplici deformazioni dovute alle aberrazioni. Quante delusioni ho dovuto dare a molti volenterosi dilettanti…

D’altra parte un ottimo Ritchey-Chretien non è certo alla portata di tutti, tranne che di qualche ricchissimo amatore giapponese. Ne ho conosciuto uno, magnate della carta di riso, che ha costruito uno strumento da 1.80 m di diametro con tanto di staff tecnico dedicato e pagato.

Attorno al telescopio un parco astronomico immenso, libero a tutti. Un sogno per l’Italia, ovviamente, ma un’esperienza bellissima. Soldi spesi bene, per la cultura e per il prossimo. A volte anche i ricchi pensano ai meno fortunati. Lo sapevate che è una cosa possibile anche oggi?

Telescopio Schmidt

Anche il Ritchey-Chretien ha comunque dei limiti di campo visivo e bisogna andare oltre se si vuole fotografare un campo ancora più grande, necessario per lavori sistematici di ricerca, in cui le aberrazioni non siano troppo importanti anche per grandi angoli di inclinazione. Per ottenere ciò bisogna tornare all’inizio di tutto: alla superficie sferica.

Sappiamo benissimo che l’aberrazione sferica va a nozze con questa superficie (si chiama così non a caso…), ma le altre, quelle fuori asse? Vale la pena fare una breve, ma fondamentale considerazione sulla sfera e sulle sue proprietà indiscusse.

Consideriamo la Fig. 83. Trascuriamo i fasci di raggi paralleli tra loro e consideriamo solo il raggio centrale di ogni fascio, ossia quello che passa per in centro C della circonferenza. Incliniamoli pure di quanto vogliamo e vediamo se le aberrazioni fuori asse, come il coma, restano importanti. Ogni raggio che passa per il centro C della sfera può essere considerato asse ottico, dato che la sfera non ha un diametro privilegiato. Sappiamo anche molto bene come calcolare il fuoco per i raggi coincidenti con l’asse ottico. La distanza focale vale proprio r/2 (lo abbiamo dimostrato poco fa).

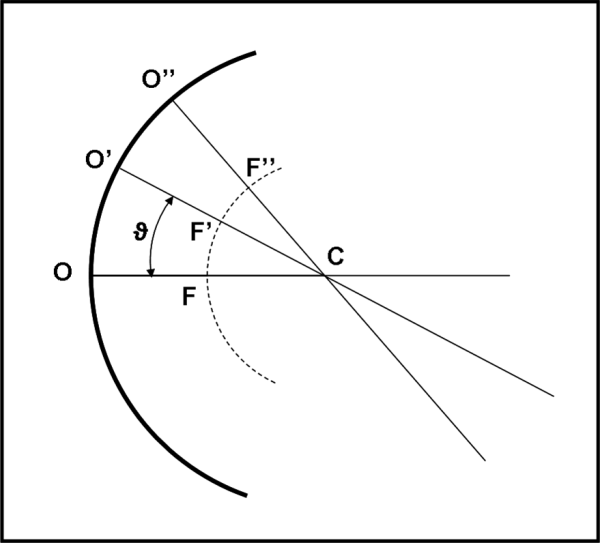
E’ ovvia la conclusione: se ogni raggio che passa per il centro è asse ottico, ogni raggio di questo tipo ha come fuoco un punto che sta su una circonferenza che ha ancora C come centro e come raggio proprio r/2. Questa circonferenza è il luogo delle immagini di tutti i raggi, anche quelli molto inclinati rispetto all’asse ottico, dato che (lo ripeto ancora) qualsiasi raggio che passi per C rappresenta perfettamente l’asso ottico.

Questo fatto vuol dire che la superficie sferica non ha aberrazioni fuori asse, dato che ogni raggio è un asse. Il coma è eliminato automaticamente. Rimangono due problemi, uno più semplice e uno più complesso.

Il più semplice è quello relativo al piano focale che non è un... piano, ma una superficie sferica. Nessun problema. Si possono modellare i ricevitori in modo che si adattino a una forma non piana. Al limite si può anche introdurre una lente che trasformi le immagini formate su una sfera in immagini su un piano (ma non si usa molto).

Il problema più importante è però quello dell’aberrazione di sfericità che resta molto importante, come abbiamo visto all’inizio dell’articolo. Tuttavia, il gioco vale la candela. Se riuscissimo a eliminarlo potremmo avere un campo visivo molto grande e telescopi compatti con lunghezze focali corte.

In realtà sappiamo come fare per correggere l’aberrazione di sfericità: interporre ai raggi paralleli incidenti una lente dalla forma strana (vedi Fig. 71) che deformi l’onda piana che arriva in un onda di forma uguale e contraria alla deformazione che causerebbe su di lei uno specchio sferico .

Vediamo la combinazione ottica nella Fig. 84. La lente “correttrice” C deforma l’onda piana verde e le dà una strana forma. Quest’ultima arriva sullo specchio sferico, viene nuovamente deformata e riesce a formare un’immagine puntiforme sul piano focale. Sul piano focale curvilineo in cui sta F si formano anche le immagini inclinate. Abbiamo ottenuto un telescopio Schmidt, fantastico per fotografare ampie zone di cielo e fondamentale, ad esempio, per scoprire asteroidi e comete. La sua focale può essere comparabile al diametro dell’obiettivo.

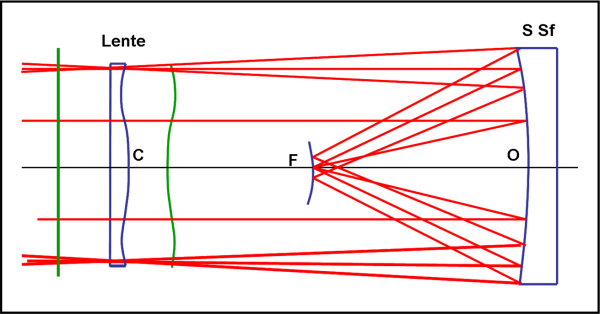
Vi sono, poi, moltissime variazioni sul tema ed esistono telescopi di tipo anche molto diverso. Alcuni sono ormai obsoleti come quelli con specchi ellittici. Teniamo anche presente che oggi gli specchi sono costituiti da tanti tasselli e che sono talmente sottili che possono essere deformati in tempo reale da un computer. Arriviamo così all’ottica adattiva, di cui avevo già scritto. In ogni modo, cambiare in tempo reale la superficie riflettente serve soprattutto per l’ultimo e non meno importante difetto che viene ad aggiungersi a tutti gli altri: il seeing atmosferico, ossia quel cerchietto confuso ed esteso dovuto all’atmosfera terrestre che devia continuamente i raggi provenienti dalla stella.

L’ottica adattiva fa proprio questo. Attraverso una sorgente simulata con un laser riesce ad anticipare la deformazione dell’onda piana in arrivo e a predisporre la superficie dell’obiettivo in modo da agire in modo uguale e contrario e produrre un’immagine decisamente migliore.

Un’altra soluzione più “drastica” è quella di andare fuori dall’atmosfera e Hubble ne è un esempio fantastico! Deve sempre scontrarsi con la diffrazione e con le aberrazioni, ma almeno ha un’immagine priva dello “sfarfallio” dovuto all’atmosfera… e non è poco.

Direi che possiamo terminare qui questo breve e semplificato discorso sull’ottica e sulla sua applicazione ai telescopi. A coloro che hanno avuto la perseveranza di arrivare fino in fondo, vorrei ribadire che la comprensione di ciò che ci può fornire un’immagine telescopica è molto più complessa di quanto comunemente non si creda. Non basta certo aggiungere marchingegni più o meno costosi, dato che quello che si guadagna da un lato si perde dall’altro. La diffrazione, prima, e le aberrazioni dopo, completate dalla turbolenza atmosferica, creano un bel problemino per chi vuole osservare  e se l’astronomo dilettante non le conosce (o spera che le aggiunte facoltative possano risolvere tutti i vari risvolti) va incontro a profonde delusioni.

L’occhio è uno straordinario sistema ottico, addirittura fornito di ottica adattiva, che ha il solo problema della limitatezza del diametro del suo obiettivo. Cercare di fornirgli un’immagine che arricchisca veramente le informazioni fisiche non è un gioco da bambini e va capito molto bene.

Conclusioni

Concludo ribadendo che il telescopio non è un cellulare che fornisce tutto e di più, schiacciando un tasto. Il telescopio vi mette in comunicazione con amici che stanno molto lontano e l’informazione che viaggia in uno spazio quasi infinito subisce pesantemente qualsiasi piccola interferenza entri in gioco, sia essa dovuta allo stesso spazio sia essa dovuta all’occhio supplementare che aggiungete al vostro.

Pensateci bene e cercate di “aprire” il vostro cellulare cosmico e capire come funziona e cosa vi può regalare. In fondo basta conoscere il teorema di Pitagora o poco di più…

Appendice: stelle quadrate, esagonali, ma anche circolari…

Abbiamo visto che per descrivere il viaggio della luce è conveniente utilizzare l’approccio legato alle onde luminose. Abbiamo anche visto che, agendo in questo modo, possiamo trattare i vari concetti (fino a un certo limite) facendoci aiutare dai raggi luminosi che in ogni momento sono perpendicolari all’onda sferica che si propaga nello spazio. Ciò vuole anche dire che la luce che esce da una stella può essere facilmente e correttamente disegnata come un insieme di raggi che escono dalla sua superficie e si dirigono ovunque nell’Universo.

Immaginiamo che lo spazio sia completamente vuoto, ossia che ci sia solo una stella in tutto l’Universo e un solo viaggiatore spaziale. Potremmo dire tranquillamente che il raggio luminoso si mantiene tale e quale per centinaia, migliaia, milioni, miliardi di anni luce. In altre parole, tutto l’Universo sarà prima o poi raggiunto da lui o da qualche suo fratello (ci vuole solo tempo perché la luce ha una velocità abbastanza... modesta).

Il punto fondamentale è proprio la DESTINAZIONE, ossia il nostro viaggiatore spaziale libero di muoversi in uno spazio quasi completamente vuoto (a parte la stella). E’ il viaggiatore che riceve più o meno luce dalla stella. Noi, normalmente, diciamo che la luminosità decresce con la distanza. E’ un modo troppo semplicistico e anche un po’ sbagliato di vedere le cose. Per il nostro scopo, è molto meglio vederla così: non è il raggio luminoso che s’indebolisce con la distanza, ma è la quantità di raggi luminosi che vengono raccolti dal viaggiatore che diminuisce con la distanza. Più è lontano l’astronauta e meno luce riceve.

Introduciamo, in Fig. 1, un semplice schema che riassuma questo concetto. Una stella S invia i suoi raggi ovunque intorno a lei. Il viaggiatore P (immaginiamo che sia proprio un pianeta) riceve una quantità di raggi luminosi che diminuisce andando più lontano dalla sorgente luminosa. Al pianeta-viaggiatore P la stella apparirà più o meno luminosa, mentre, in realtà, la luminosità della stella è sempre la stessa. Non sarebbe nemmeno difficile calcolare quanta luce arriva sul pianeta vagabondo: basterebbe fare banali calcoli sui triangoli arancioni…

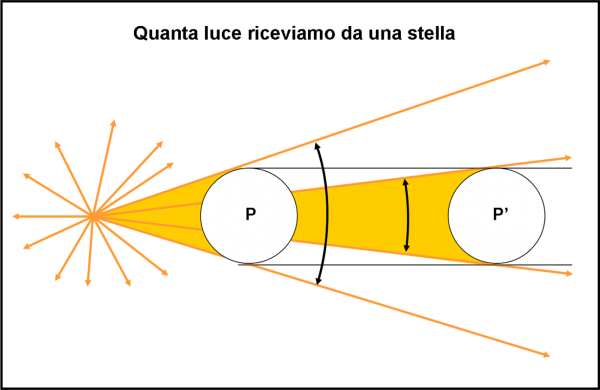
Senza usare formule, si può fare il rapporto tra l’area racchiusa dentro i triangoli e quella in cui è contenuta tutta la luce emessa dalla stella. E’ come se avessimo una bella torta rotonda e ne prendessimo delle fette di grandezza variabile. Quelle più piccole danno meno soddisfazione, così come i triangoli più piccoli (e, quindi, viaggiatore più lontano)  raccolgono meno luce. Chi volesse fare dei conti più esatti, basterebbe che considerasse la figura in tre dimensioni e confrontasse il volume di una sfera con quella di vari coni. Un giochino veramente banale.

Ovviamente, vi è anche un altro modo per ricevere meno luce. Invece di cambiare la distanza potremmo diminuire le dimensioni del pianeta-viaggiatore. Anche in questo modo, la quantità di luce raccolta diminuirebbe di conseguenza (il cono si restringerebbe comunque).

Torneremo su questo concetto FONDAMENTALE tra poco. Adesso andiamo a vedere le cose in modo più realistico.

Cerchiamo di rispondere alla prima domanda: “Come vediamo una stella dalla Terra?” Sappiamo già molto bene che la luminosità varia con la distanza della stella, ma noi vogliamo proprio sapere che forma ha la stella, indipendentemente dalla luce che riusciamo a ricevere.

Utilizziamo, allora, la Fig. 2. In essa vogliamo dimostrare che una stella può essere considerata un punto quasi perfetto nella stragrande maggioranza dei casi e soprattutto per chi vuole osservarla con il solo occhio o con una strumentazione non ultra specialistica. Ricordiamo, anche, che un punto geometricamente perfetto non ha dimensioni e quindi non ha nemmeno una forma. La stella è quasi una sfera, ma noi non riusciamo assolutamente a rendercene conto. Immaginiamo, ad esempio, di prendere una stella che abbia un diametro simile a quello del Sole, anzi un po’ di più: un milione e mezzo di chilometri.

Portiamola a una distanza piuttosto bassa da noi, ad esempio a 4 anni luce circa. Insomma, ci siamo messi in condizioni molto simili a quelle della stella più vicina (Alpha Centauri).

Dobbiamo aggiungere una piccola precisazione che è ben nota a tutti. Ogni stella invia la luce nello stesso modo. Tuttavia, a parità di dimensioni, ci sono quelle che producono più luce e altre meno. Questa circostanza è tipica del motore stellare, così come ci sono Ferrari e utilitarie di dimensioni comparabili ma di prestazioni ben diverse. Tuttavia, questa particolarità non sempre dipende dal diametro e dalla “forma”. In ogni caso, non cambia minimamente l’informazione sulle dimensioni effettive della sorgente di luce, che arriva fino alla Terra.

Torniamo alla Fig. 2. Con i numeri che abbiamo scelto risulta immediato calcolare il diametro apparente della stella vista dalla Terra, in  un qualsiasi suo punto (la distanza non cambia). Dato che stiamo lavorando con angoli molto piccoli, possiamo tranquillamente (senza commettere errori) scrivere che il diametro angolare d (ossia espresso in gradi) della stella è dato da d = D/s, dove D è il vero diametro dell’astro e s è la distanza dell’osservatore O. 4 anni luce sono circa 40 000 miliardi di chilometri, da cui segue che d = 0.007 secondi d’arco. In altre parole, l’angolo che sottende il diametro della stella è pari a 7 millesimi di secondo d’arco. Pensate che in un grado vi sono ben 3600 secondi d’arco e capirete bene quanto sia piccolo l’angolo d.

Ricordiamoci che quando si parla di dimensioni di stelle, pianeti, galassie e corpi celesti in genere, non abbiamo mai a che fare con dimensioni lineari (chilometri o metri o quello che volete). Ciò che si vede nel Cielo è solo la proiezione sulla sfera celeste e quindi non ha senso parlare di dimensioni lineari se non si conoscono le distanze. Il nostro occhio, o telescopio che sia, non è capace di misurare le distanze e quindi può solo vedere e confrontare angoli. Non per niente si dice che il Sole ha dimensioni apparenti di circa mezzo grado… Ciò vuol quindi dire che per definire le dimensioni e la forma di una stella dobbiamo solo considerare le sue dimensioni angolari.

Queste ultime sono veramente ridicole (sette millesimi di secondo d’arco) e ben al di sotto delle capacità osservative a nostra disposizione. Possiamo perciò concludere, senza alcuna incertezza, che una qualsiasi stella può essere considerata come una sorgente puntiforme. Essendo un punto non ha né forma né dimensioni percepibili da terra o dallo spazio vicino a noi. Anzi, qualsiasi strumento che ce la faccia vedere come un punto più o meno esteso è sicuramente difettoso! Sia perché ha difetti intrinseci, sia perché il raggio luminoso finisce di essere un’approssimazione valida. Riflettete bene su questo concetto!

D’ora in avanti considereremo sempre una stella come un punto perfetto e faremo partire da questo punto tutti i raggi luminosi che si propagano nello spazio. Attenzione! Rifletteteci bene: è una base di partenza FONDAMENTALE per capire cosa riusciamo a vedere con l’occhio o il telescopio. Senza aver compreso bene questo concetto fin troppo banale, e quindi spesso trascurato, non saremo mai in grado di capire cosa ci permette di fare un telescopio.

A questo punto, non ci rimane che guardare le cose dal punto di vista stellare. Anzi, meglio ancora, dal punto di vista dei raggi luminosi che stanno viaggiando nello spazio. Ognuno di loro si allontana dal suo vicino e la lontananza aumenta con la distanza. Tuttavia, dobbiamo realizzare che i raggi emessi da una stella sono praticamente infiniti. Ogni punto (reale) della stella emette un fascio di raggi e via dicendo. L’insieme di tutti questi raggi vengono poi schematizzati da quelli disegnati nella Fig. 1.

Immaginiamo quindi che i raggi che si dirigono verso la Terra siano moltissimi e formino praticamente un fascio di luce, costituito da raggi tutti a stretto contatto tra loro. Abbiamo visto che questo fascio tende ad allargarsi sempre di più allontanandosi dalla sorgente.

Tuttavia, la Terra è molto piccola e il trenino di raggi che riesce a raggiungerla è un fascio che rimane molto stretto anche a distanze enormi. Infatti, come visto nella Fig. 1, chi determina l’ampiezza del fascio di raggi è solo la distanza dalla stella e le dimensioni del ricevitore o pianeta vagabondo, come preferite chiamarlo.

Quanto sarà largo per una stella come quella trattata nella Fig. 2 e per un pianeta come il nostro?

Facilissimo a calcolarsi, utilizzando la Fig. 3 che rappresenta, in fondo, la stessa cosa della Fig. 1. A sinistra vi è la stella che può essere considerata PUNTIFORME (ricordate?), a destra vi è la Terra con le sue dimensioni reali, ossia con un diametro pari a circa 12 000 km. La distanza è sempre 40 000 miliardi di chilometri.

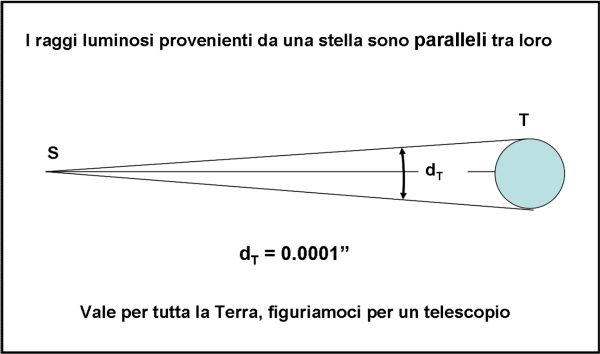
Quanto sarà, in secondi d’arco, il diametro della Terra visto dalla stella? Ormai, sappiamo benissimo come calcolarlo. Basta dividere il diametro della Terra per la distanza della stella. ossia: dT = DT/s = 0.0001 secondi d’arco: un decimillesimo di secondo d’arco.

Mamma mia, se l’angolo di Fig. 2 era piccolo, questo è ancora più ridicolo! Ma cosa ci dice questo risultato?

Immaginate di disegnare su un foglio una retta orizzontale. Adesso, sotto di lei, ne disegnate un’altra che formi con la prima un angolo pari a 0.0001”. Fatto? Bene vi sfido a dimostrarmi in qualche modo che le due rette non siano parallele tra loro. Innanzitutto, perché non vi è strumento di uso quotidiano che vi permetta di misurare un angolo così piccolo. Inoltre, anche se lo riusciste a trovare, vi sfiderei a dimostrare che le due rette non siano perfettamente parallele. Non potreste certo usare un metro o un righello qualsiasi.

Possiamo, quindi, dire che due raggi, che formino tra loro un angolo come quello che la Terra sottende vista da qualsiasi stella, possono essere considerate due rette parallele. Per vederne la differenza dovreste avere a disposizione un foglio di migliaia di chilometri di lunghezza e forse nemmeno basterebbe.

Tuttavia, nessun telescopio a vostra disposizione ha una lunghezza comparabile alle migliaia di chilometri e, di conseguenza, per un osservatore del cielo, anche con strumentazione sofisticatissima, i raggi provenienti da una stella sono tutti paralleli tra loro.

E’ talmente vera questa conclusione che si disegnano paralleli perfino i raggi che provengono da oggetti ben più vicini come il Sole e la Luna. Anche perché, forse, vi può essere sfuggito un particolare non certo trascurabile. Il valore di 0.0001 secondi d’arco si riferisce a tutta la Terra. Figuriamoci quanto diventa piccolo quando si considera solo il diametro dell’occhio o del telescopio.

Niente da fare, possiamo concludere questo discorso con una frase estremamente importante: le stelle possono essere considerate dei punti perfetti senza forma e dimensioni e i raggi che provengono da loro (e che possiamo ricevere) possono essere considerati paralleli.

Per capire ancor meglio il concetto di “ricevere” luce dalle stelle, andiamo al di fuori dell’atmosfera terrestre. In questo modo non abbiamo alcun disturbo dovuto alle goccioline d’acqua, alla polvere e ad altre porcherie del genere. Consideriamo la Fig. 4. Una certa stella (immaginiamo di nuovo che sia l’unica esistente nell’Universo) è l’unica sorgente di luce. I suoi raggi ci raggiungono. Saranno magari “pochi”, ma arrivano e illuminano gli strumenti che abbiamo portato con noi. Quali strumenti? Proprio il minimo necessario per capire e non per osservare: una cosa alla volta.

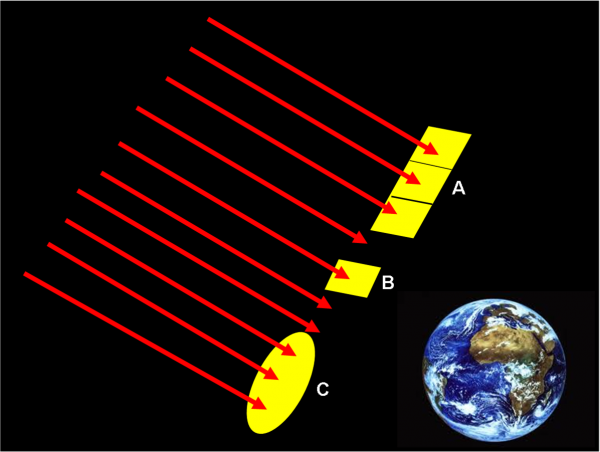
Abbiamo inventato una specie di “carta moschicida” per la luce (carta lucicida?). Ossia i raggi che ci cadono sopra lasciano un segno e non proseguono. Nella figura ho disegnato pochi raggi, ma pensate sempre che essi sono infiniti e formano un vero e proprio fascio. La carta lucicida A ha raccolto tre raggi che sono sufficienti a farla diventare luminosa. La carta lucicida B ne ha raccolto uno solo. Tuttavia, le dimensioni di B sono proprio un terzo di A. Ne deriva che la luce distribuita su A è tre volte superiore a quella distribuita su B, ma è sempre la stessa per unità di superficie, ossia carte lucicide uguali raccolgono uguali quantità di luce. Ciò vuole dire che l’illuminazione è uniforme.

Più importante è pero capire ciò che fa la carta lucicida C. Essa ha una forma diversa, circolare. Anch’essa è, però, capace di catturare luce. Ammettiamo che l’area di C sia uguale a quella di A. Ciò vuole dire che la luce raccolta da A e da C è esattamente la stessa. Entrambe ci danno tutta l’informazione possibile sulla stella in  questione, con i mezzi a nostra disposizione (non abbiamo carte lucicide più grandi).

Ci interessa molto la forma della carta lucicida? Direi proprio di no, dato che entrambe contengono la stessa quantità di luce. Possiamo tornare a casa e analizzare i risultati ottenuti. Entrando nell’atmosfera le cose cambiano di molto e quindi è bene conservare gelosamente le nostre carte lucicide. Non ci resta che studiare l’immagine che abbiamo raccolto al di fuori dell’atmosfera. La carta A viene data a uno studioso e la carta C a un altro, in modo che non si influenzino uno con l’altro.

Molti risultati sono perfettamente identici, ma su uno le conclusioni sono estremamente diverse. Il primo comunica ufficialmente ai “media” che la stella ha una forma rettangolare, il secondo che la stella ha una forma circolare. Chi ha ragione? Nessuno dei due. La stella non ha nessuna forma, ossia -meglio- la vera forma della stella non può influire minimamente su ciò che abbiamo ricevuto. L’unica forma che vediamo è quella della carta che ha intercettato il fascio luminoso.

Ciò che si vede è la forma della carta lucicida, dato che sappiamo molto bene che ogni stella è una sorgente puntiforme.

Possiamo tranquillamente buttare via le carte lucicide e ragionare in termini di strumenti di osservazione. Abbiamo sempre il nostro fascio di raggi di luce paralleli provenienti da una sorgente priva di forma individuabile (puntiforme). Invece della carta lucicida vi è adesso una “porta” molto speciale, quella che fa entrare nell’occhio o nel telescopio (Fig. 5). Non c’interessa, per adesso, cosa c’è o cosa succede dopo la porta. L’importante è che è lei e solo lei a regolare quanti raggi possono entrare e che forma ha il fascio ammesso all’interno.

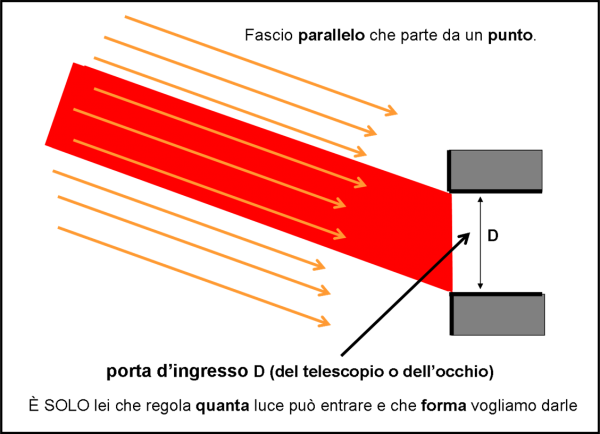
In altre parole (pensateci sopra un pochino), ciò che vediamo dopo la porta d’ingresso NON è la stella, ma la parte della sua luce che la porta ha lasciato  entrare… E’ la porta che ne regola la quantità e la  distribuzione. Non stupisce più, quindi, la forma strana del disco di Airy per aperture non circolari…