Abbiamo descritto la conica che rappresenta una curva chiusa e che ha come caso particolare la circonferenza. Manovrando il piano-coltello si arriva a un punto critico: quello in cui la curva si apre e diventa una parabola. Un caso limite anch’esso, ma altrettanto importante.

L’ellisse non si chiude più

Le cose cambiano passando alla parabola…

Prima di descriverla in termini matematici come y = f(x), torniamo un attimo al nostro cono e al piano-coltello. Abbiamo continuato a usarlo inclinato fino a che β non è diventato uguale ad α. A quel punto è nata la parabola, dato che l’ellisse si “è aperta”. Come possiamo  definire l’eccentricità che finora abbiamo visto descrivere bene l’ellisse e la sua figlia particolare, la circonferenza.  Ahi, ahi, ecco che compare di nuovo la trigonometria. Ve l’avevo detto che è molto importante! Ebbene, basta scrivere il rapporto tra la stessa funzione trigonometrica (il coseno) dei due angoli legati alla generazione delle coniche (α e β) ed ecco comparire magicamente l’eccentricità. Meraviglia della trigonometria. Non fatemi dimostrare questa semplicissima formuletta che si può ricordare benissimo, ossia:

e = cos(β)/cos(α)    ….(9)

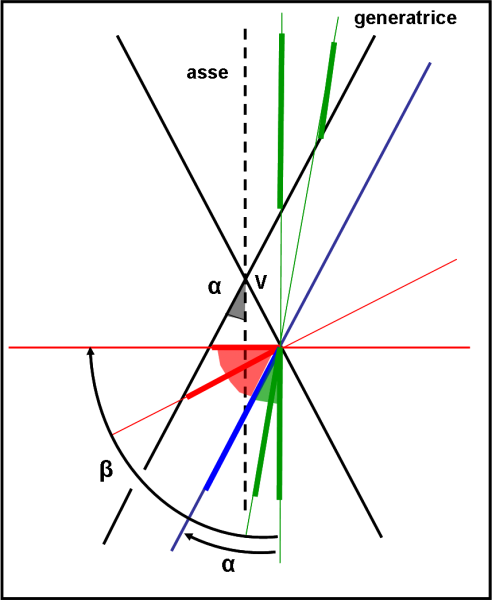
α è quello che è (costante) ed è l’angolo che definisce il cono da tagliare. β è invece l’angolo che il piano-coltello fa con l’asse del cono e che varia continuamente. Quando  iniziamo a tagliare, abbiamo un angolo β uguale a 90° (ricordate?). Il cos(90°) vale 0 e quindi il rapporto (9) deve andare a zero (il denominatore è sempre diverso da zero dato che l’angolo α non può certo essere né 0° né tantomeno  90°). Diminuendo β aumenta il suo coseno, ma sarà sempre minore di quello di α e (9) sarà maggiore di zero ma sempre minore di 1. proprio quello che ci aspettavamo. A un certo punto, il piano-coltello forma proprio un angolo β esattamente uguale ad α. Siamo nel caso particolarissimo della parabola. Quanto vale la (9) in questo caso? Facilissimo, dato che numeratore e denominatore sono uguali: esattamente 1. Basta, però, inclinare un po’ di più il piano-coltello ed ecco che β diventa più piccolo di α. Cosa succede della (9)? Il coseno di un angolo più piccolo diventa più grande e il numeratore diventa maggiore del denominatore. Ecco che l’eccentricità diventa maggiore di 1 ed entriamo nel regno delle iperboli. Quanto può diventare grande l’eccentricità? Questo dipende dal cono di partenza, ossia da α (e quindi dal suo coseno). Se esso è molto grande (coseno piccolo), il rapporto, ossia l’eccentricità, può diventare molto grande. D’altra parte il valore massimo che può ottenere il coseno è uno. Ne segue che al massimo l’eccentricità vale:

e = 1/cos(α)

Non voglio farvi del male… ma chi vuole proprio divertirsi può anche pensare di far tendere l’angolo α a 90°. Il cono tenderebbe a diventare un piano (provate), e l’iperbole tenderebbe ad avere un’eccentricità pari a: 1/cos(90°) = 1/0 = ∞. Eh sì, cari amici, volenti e nolenti siamo tornati al nostro amico infinito. Ripeto: teoricamente un’iperbole potrebbe avere un’eccentricità che tende a infinito.

Questo breve discorsetto è riassunto nella Fig. 44. Essa si riferisce a una vista di taglio del cono (ossia rappresenta un piano qualsiasi che passa per l’asse, in modo che il cono risulti un doppio triangolo, proprio come il famoso cono di luce) e mostra i vari casi descritti dall’angolo β. Ovviamente, si può fare anche cambiare l’angolo α. Divertitevi a capirla bene e magari anche a modificarla fino ai casi più estremi. La parte rossa corrisponde alle ellissi, quella verde alle iperboli e quella blu alla parabola.

Torniamo alle funzioni “normali”. C’è già abbastanza da lavorare! Non vi alterate… so di aver parlato di coseni e dei loro valori per diversi angoli. Volendo, basterebbe andare nella lezione in cui li ho definiti e potreste arrivarci da soli. Tuttavia, quando parleremo delle funzioni trigonometriche per disegnarle nel piano cartesiano, ci torneremo sopra. Per adesso, lascio a voi dedurre quanto vale il coseno (e il seno e la tangente) per angoli che vanno da 0° a 360°. Poi ci torneremo sopra con maggiore attenzione.

Quello che, adesso, c’interessa è che la parabola è il caso particolarissimo (teorico, in fondo) in cui l’eccentricità è proprio uguale ad uno. Una curva di passaggio da ellissi a iperboli, ma molto importante per la matematica e per la fisica.

Come viene definita la parabola attraverso le caratteristiche dei suoi punti? In altre parole, anche lei ha dei fuochi, dei semiassi e qualcosa che ci permetta di definirla come luogo di punti? Per l’ellisse c’eravamo riusciti con la (1) (e con due chiodi e un filo robusto). Per la parabola si può fare lo stesso? Sì, ma in modo un po’ meno semplice…

La parabola si definisce come il luogo dei punti che mantengono sempre la stessa distanza rispetto a un punto F (fuoco) e a una retta d (direttrice), ossia:

PF = Pd          (Pd è il segmento tracciato da P alla retta d, perpendicolarmente ad essa).

Non basta più uno spago e due chiodi

Riusciamo a costruirla su un foglio senza usare formule matematiche? Sì… però abbiamo bisogno di un triangolo rettangolo, se non altro per la simpatia che ormai ci lega a Pitagora. Andiamo sul foglio della Fig. 45  Disegniamo una retta orizzontale d. Poi tracciamo una sua perpendicolare. Chiamiamola y (così, alla fine avremo già l’asse delle ordinate). Consideriamo un punto qualsiasi F su y. H sia il punto dove y incontra d.

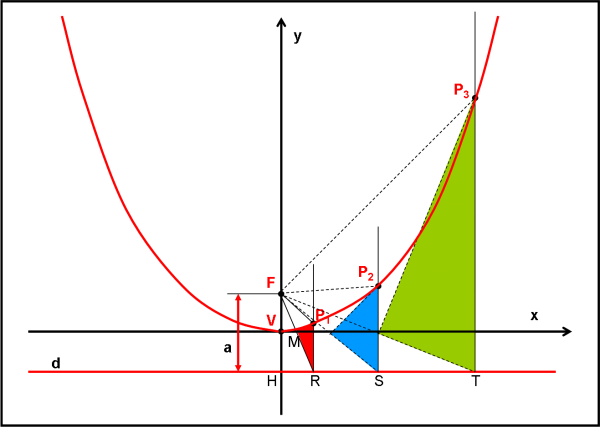
Immediatamente possiamo costruire il primo punto della parabola. Anzi, forse il più importante in assoluto: il vertice V. Dove si trova V? Esattamente a metà del segmento HF.  Perché sono così sicuro che questo punto appartenga alla parabola? Basta ricordare la definizione precedente. La sua distanza dalla retta d è uguale a quella rispetto al punto F? Beh… sì, l’ho proprio costruito così! Allora, non c’è dubbio, V appartiene alla parabola.

Finora è stato facile, ma, adesso, viene il bello.  Scegliamo un punto qualsiasi della retta d, ad esempio R. Tracciamo la perpendicolare alla retta a partire da R. Bene. Adesso congiungiamo il punto R con F e prendiamone il punto di mezzo M. Non ci resta che disegnare il triangolo, rettangolo in M, che abbia MR come cateto e l’ipotenusa lungo la perpendicolare in R a d.

Ne esiste uno e uno solo, non si può sbagliare, se no faremmo arrabbiare Pitagora! Il punto P₁ appartiene alla parabola, ne sono sicurissimo. La dimostrazione è molto facile. Per come è stato costruito il triangolino rosso, esso deve essere uguale al triangolo P₁MF. Due cateti sono uguali perché M è proprio il punto di mezzo di RF (FM = MR) e MP₁ è in comune. Due triangoli che abbiano due lati e un angolo uguali devono essere uguali (se non ci credete fate tutte le prove che volete…). Se sono uguali devono essere anche uguali le ipotenuse, ossia: P₁R = P₁F, che è proprio la condizione per essere un punto della parabola.

Ormai il gioco lo conosciamo e possiamo tranquillamente continuare con il triangolo azzurro, quello verde, ecc., ecc. Alla fine otteniamo la curva rossa. Non ci resta che scegliere, per comodità, la retta parallela a d e passante per il vertice V come asse delle x. In tal modo, il vertice V coincide con l’origine degli assi.

E’ stato piuttosto divertente, non vi sembra?  Perché non continuare, allora, e ricavare anche la funzione che rappresenta la parabola? Ne siamo sicuramente capaci e, inoltre, l’esercizio ci serve anche per prendere sempre più  dimestichezza con il piano cartesiano.

Un luogo di punti matematico

Consideriamo la Fig. 46.

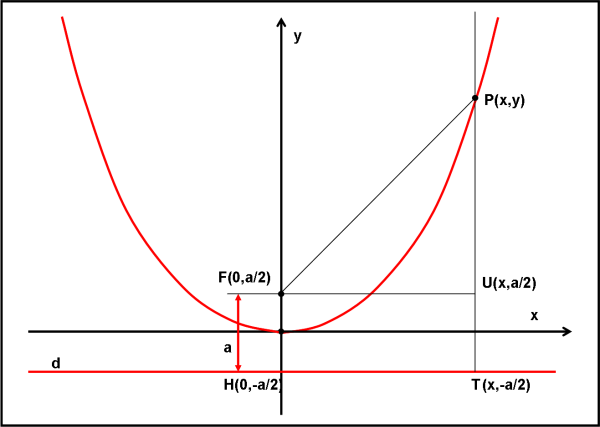
Come prima, V sia l’origine degli assi e d sia la direttrice. Chiamiamo con a la distanza tra fuoco F e retta d. Questo parametro è quello che decide la forma della nostra parabola. Il punto F ha coordinate F(0,a/2). Il punto P generico che percorre la parabola ha coordinate P(x,y). Segniamo anche i punti H(0,-a/2) , T(x,-a/2) e U(x,a/2), che serviranno per i nostri giochini. Cosa dobbiamo fare? Scrivere la condizione dei punti di una parabola sotto forma delle coordinate x e y. Ricordiamo qual è la condizione fondamentale:

PF = PT

Non ci resta che scrivere PF e PT in funzione delle coordinate x e y e poi uguagliarli tra loro.

Cominciamo con PF

PF è l’ipotenusa del triangolo rettangolo PUF di cui conosciamo le coordinate dei vertici. Potremmo anche ricordare la formula che ci permette di calcolare la distanza tra due punti di coordinate note. Comunque si faccia (tanto è la stessa identica cosa) non ci resta che scrivere:

PF² =  PU² + UF² = (y – a/2)² + (x – 0)² = y² + a²/4 - 2ay/2 + x² = y² + a²/4 - ay + x²     …. (10)

Ho considerato il quadrato per non portarmi dietro la radice quadrata (ho applicato pari pari il teorema di Pitagora) e poi ho eseguito il quadrato di un binomio (ricordate?)

Scriviamo adesso PT

PT² = (y - (- a/2))² = y² + a²/4 + 2ay/2 = y² + a²/4 + ay    …. (11)

Il segmento PT è parallelo all’asse delle y e quindi non è altro che una differenza di ordinate. Ricordiamo poi che meno per meno vale più…

Non ci resta, adesso, che uguagliare la (10) e la (11). Ovviamente uguagliare i quadrati non cambia assolutamente la relazione. Se 5 = 5, anche 25 = 25!

y² + a²/4 - ay + x² = y² + a²/4 + ay

Portiamo tutte le y da una parte e le x dall’altra insieme ai “termini noti”, ossia a quelli che sono costanti, come a. Ovviamente sapete che per spostare un termine da un lato all’altro di un’uguaglianza bisogna cambiargli di segno.

y² - ay - ay  - y² = - x² + a²/4 - a²/4

semplificando i termini tipo y² e –y², si ottiene:

- 2ay = - x²

Cambiando di segno e spostando a destra ciò che moltiplica y. Si ha infine:

y =  x²/2a

Questa è la funzione generica di una parabola che ha il vertice coincidente con l’origine degli assi cartesiani. Ovviamente, essa si allarga e si stringe in base al valore di a (la distanza tra il fuoco e la retta direttrice).

Poniamo, per semplicità, p = 1/2a e otteniamo la forma più nota della funzione parabola:

y = p x²

se p cresce, cresce anche il valore della y per un dato valore di x, ossia la parabola diventa più ripida. E’ un qualcosa di molto simile al coefficiente angolare m della retta. Ovviamente dire che p cresce vuol dire che a decresce, seguendo la relazione a = 1/2p. Quindi, per ottenere parabole sempre più strette bisogna diminuire a, ossia avvicinare fuoco e retta direttrice. Per allargarla il viceversa.

Piccola domanda: “ Se la distanza tra direttrice e fuoco diventasse sempre più piccola, tendendo a zero, come si trasformerebbe la parabola?"

La Fig. 47 vi dà tre esempi di parabola con vertice nell’origine degli assi. Per come è costruita la parabola, è ovvio che per x che tende a più infinito anche la y tende a più infinito, mentre per x che tende a meno infinito, la y continua a tendere a più infinito. Il termine x², fa sì che il risultato a partire da una x positiva 0 negativa sia sempre  una y positiva (meno per meno uguale più)

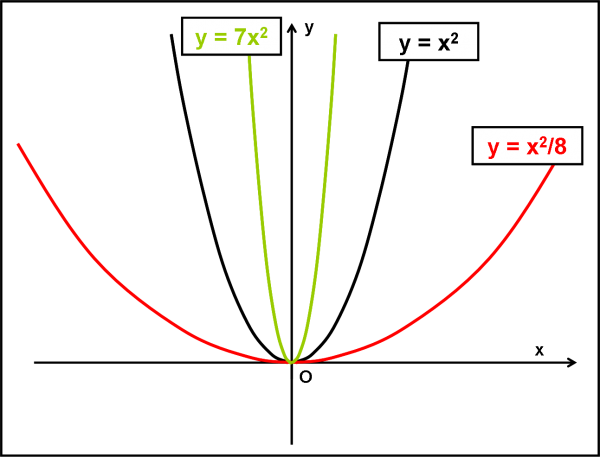
Altra domanda: “Cosa succederebbe se cambiassi di segno a p?”.

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica

 

Anche la parabola ha il suo "pi greco"? Ebbene sì! Ne parliamo QUI