E' un momento in cui la parabola domina il nostro blog... perché non continuare?
Anche la parabola ha una sua costante universale, così come il cerchio.
"Cos'è la matematica?" ovvero "si fa presto a dire genio" **
Approfondiamo il problema relativo alla strana somma dei numeri interi positivi...
In realtà, risolvere un'equazione di secondo grado non è difficile. L'unico problema può essere, per qualcuno, ricordare a memoria la formula risolutiva. Ma è veramente necessario? Rifacendosi in parte ai babilonesi, possiamo dire di NO.
Devo ammetterlo... quando il nostro carissimo amico Frank aveva detto, con la sua irresistibile sincerità intellettuale, che non capiva come, nella consueta rappresentazione della gravità generale, simile a ciò che capita attorno a una pietra posata su un lenzuolo, potesse avvenire la caduta di un oggetto inizialmente fermo, ho cercato di girare intorno al problema, evitando di mostrare apertamente come quella figura sia esageratamente approssimativa e, in realtà, del tutto fuorviante. Può darsi che essa illuda molti di aver capito facilmente lo spaziotempo einsteniano, ma, invece, cancella una parte fondamentale dell'intera faccenda, una parte che, se trascurata, ci allontana dalla vera fantastica essenza della Relatività Generale. Con questo articolo, magari non semplicissimo, ma accessibile a tutti, vedrò di rispondere nel modo più corretto a Frank e di dare al tempo il suo giusto ruolo.
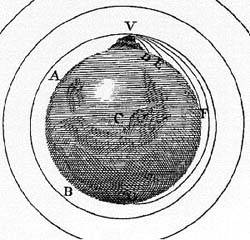
Il linguaggio usato da Galileo per descrivere la caduta dei gravi o il moto di un grave al quale è stata impartita una certa velocità è diverso dal linguaggio usato da Newton per descrivere la "sua" forza di gravità? Sì oppure no? Discutiamone giocando con proiettili, missili intercontinentali e sonde spaziali.
Nella vorticosa fucina del blog, ogni tanto succede che si producano contemporaneamente articoli gemelli, del resto anche nel mondo dei numeri esistono i “primi gemelli” e tutti ne hanno profondo rispetto. L'ultimo di questi casi riguarda la metamorfosi della catenaria in parabola, evento che è sotto i nostri occhi ogni volta che osserviamo un ponte sospeso.
Prima di affrontare la determinazione analitica della curva oggi chiamata catenaria, ricordiamo come essa sia stata trattata da Galileo Galilei nei suoi Discorsi su due Nuove Scienze, senza che il grande pisano trovasse una descrizione definitiva.
Sapete come sono fatto… ogni tanto mi sorgono dei dubbi sulle varie spiegazioni e temo che si possa creare qualche malinteso. Probabilmente è una mia paura infondata e nessuno ha bisogno di questo chiarimento. Al limite trascurate questo articolo (ne sarei, in fondo, ben lieto).
Uno dei tipi di telescopio più famosi porta il nome di uno scienziato altrettanto famoso. La sua caratteristica principale è l’obiettivo formato da uno specchio che ha una particolare forma, capace di eliminare un certo tipo di difetto che limita le prestazioni del suo compagno “sferico”. Teoricamente (ma anche praticamente), chiunque può costruire “in casa” questo tipo di obiettivo (il metodo è stato utilizzato professionalmente).
La soluzione del quiz sulla catastrofe terrestre, ha innescato una trattazione ben più articolata del previsto. Su suggerimento dell'onnipresente e onniveggente Daniela, si è convenuto di associare questo articolo a quello più vecchio sul blocco della rotazione di Papalla. Il titolo unico è diventato: Fermate il mondo, voglio scendere... L'articolo è stato scritto a quattro mani e cinque teste, dato che, anche se non compare tra gli autori, la supervisione di Umberto è stata essenziale.
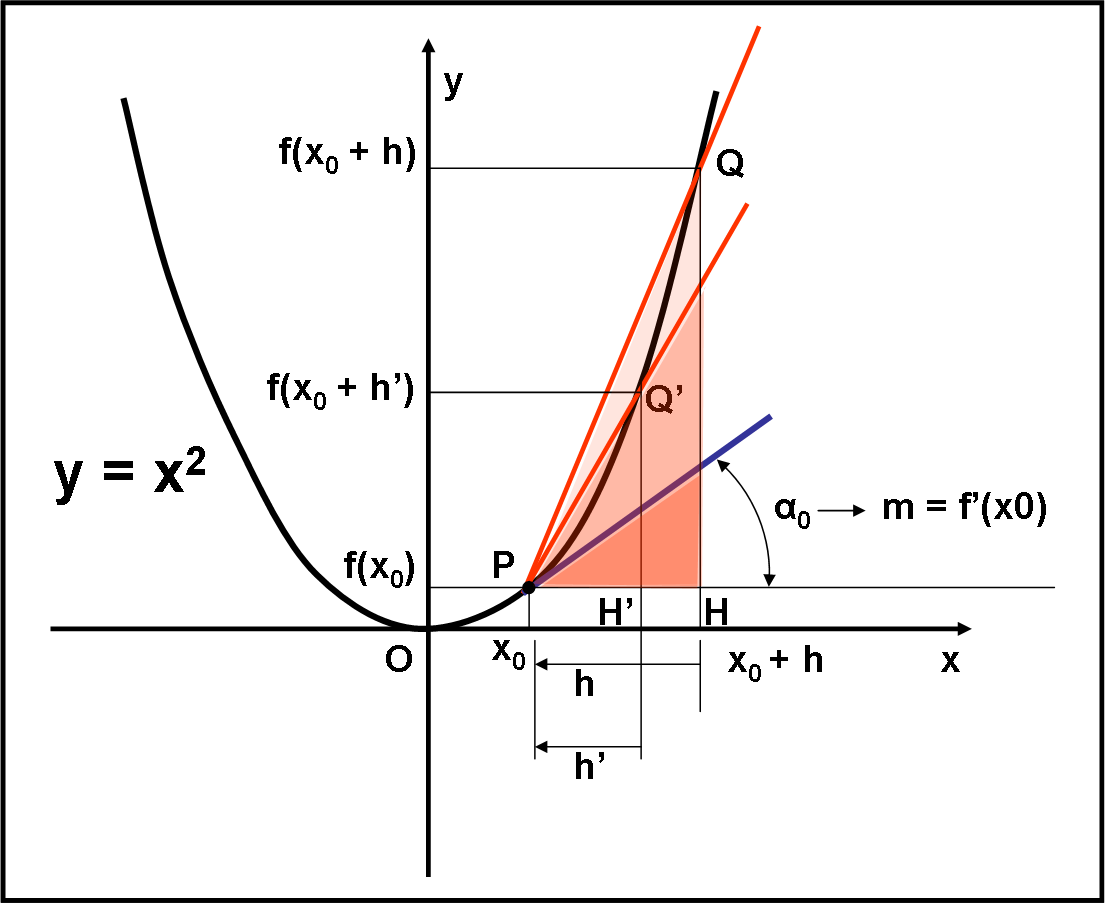
In questa parte, veramente fondamentale, calcoliamo la prima derivata di una funzione che non sia una retta e ne diamo il significato geometrico. Lo scenario si amplia sempre di più.
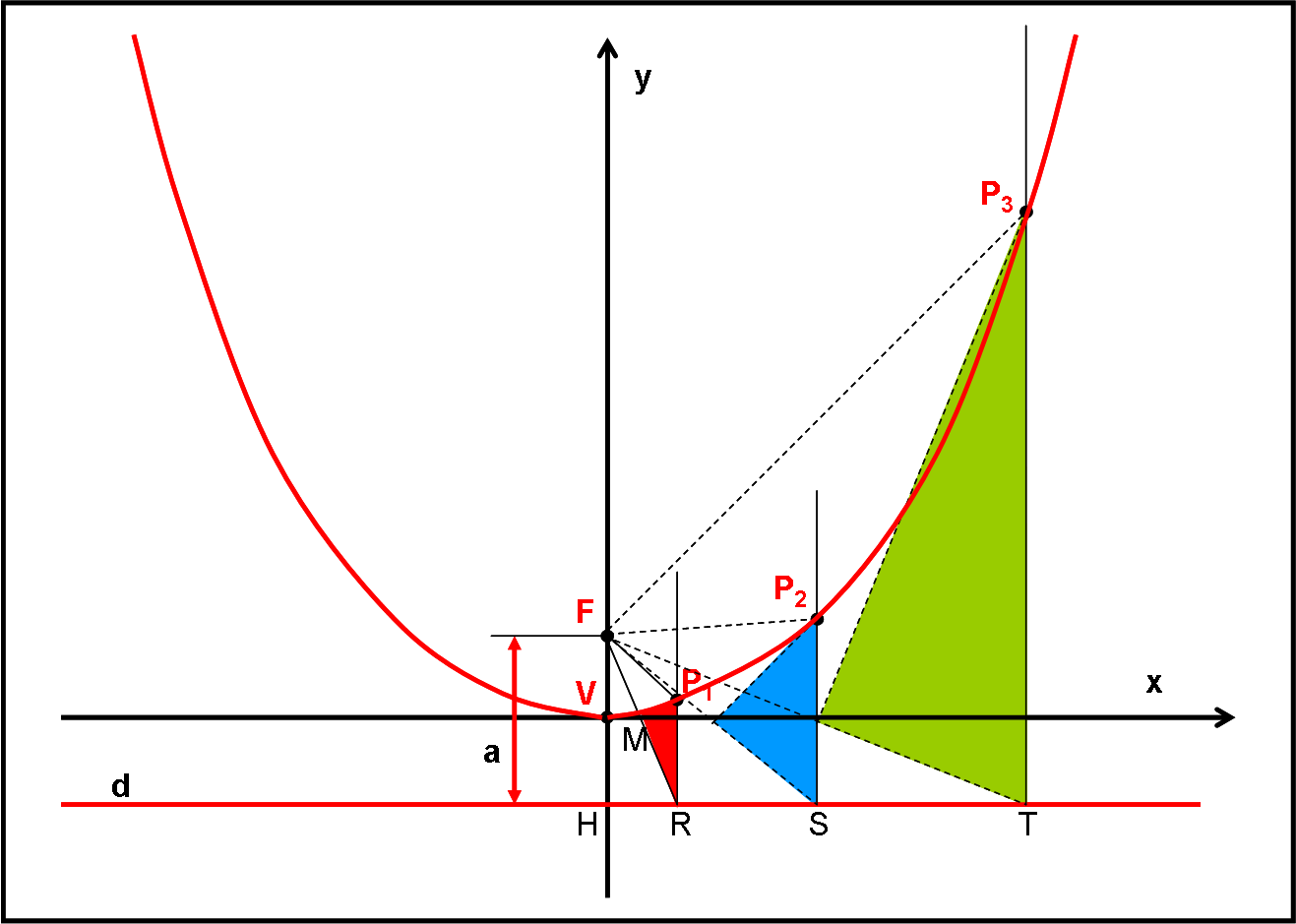
Abbiamo descritto la conica che rappresenta una curva chiusa e che ha come caso particolare la circonferenza. Manovrando il piano-coltello si arriva a un punto critico: quello in cui la curva si apre e diventa una parabola. Un caso limite anch’esso, ma altrettanto importante.
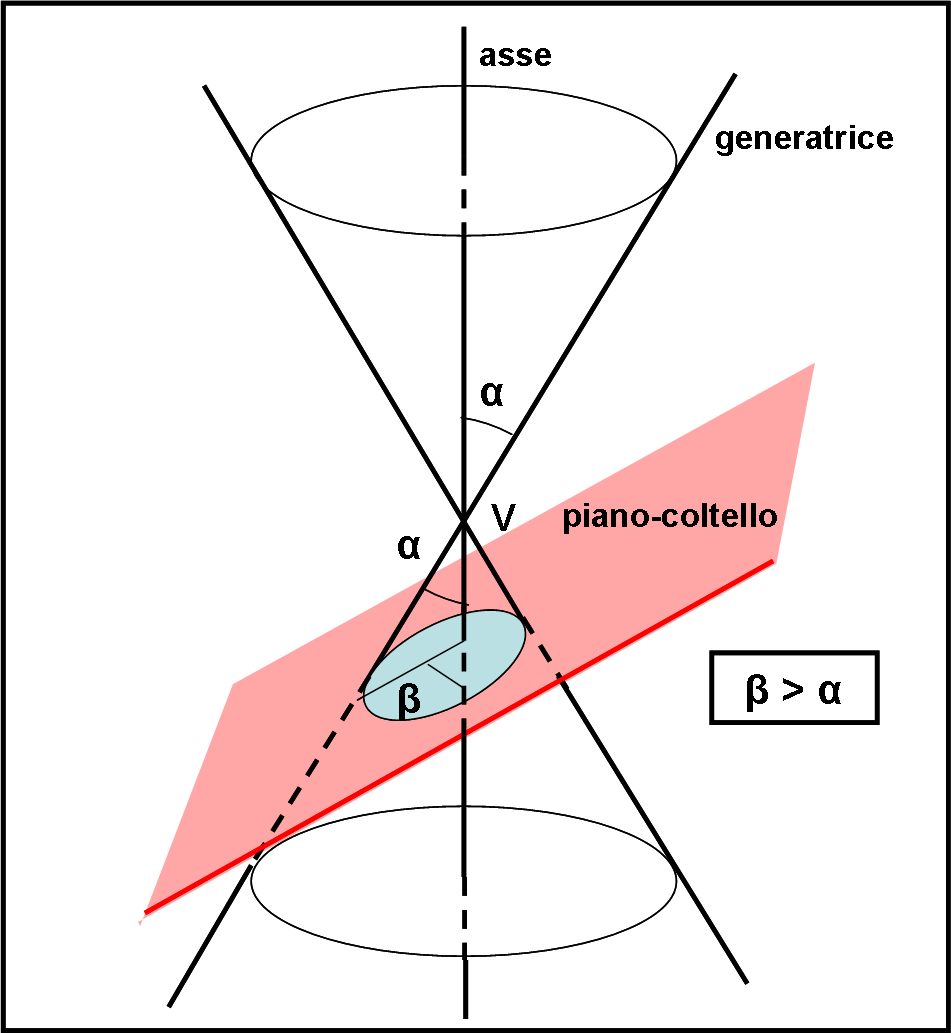
Volevo solo “sfiorare” le coniche, considerandole come altre funzioni che impareremo a studiare nei dettagli. Tuttavia, la loro enorme importanza mi ha bloccato e convinto che meritano qualcosa di più. L’articolo è diventato chilometrico, per cui lo divido in cinque parti. Non solo matematica, ma anche tanta geometria. Cominciamo… affettando un cono con un coltello molto affilato.