In realtà, risolvere un'equazione di secondo grado non è difficile. L'unico problema può essere, per qualcuno, ricordare a memoria la formula risolutiva. Ma è veramente necessario? Rifacendosi in parte ai babilonesi, possiamo dire di NO.

Come vedete è stato messo un solo asterisco. I meno esperti, perciò, non si spaventino dopo aver sbirciato nell'articolo e avere visto tante "formule". Il livello di comprensione è veramente molto basso ed è sufficiente conoscere le quattro operazioni e la radice quadrata. Qualcuno potrebbe dirmi: "Sì, va bene... ma anche la formula risolutiva da tutti usata ha solo bisogno delle quattro operazioni e della radice quadrata!". Avrebbe in parte ragione, ma bisognerebbe anche ricordare qualcosa che sembra una ricetta data da un  dottore, ossia "non la capisco ma la uso!". In questo caso, invece, eseguendo le quattro operazioni (più la radice quadrata) si svolge un processo logico e intuitivo che non ha bisogno di ricette...

Nel corso di matematica abbiamo visto come si ricava la formula per risolvere qualsiasi equazione quadratica, ossia di secondo grado. Basta memorizzarla e qualsiasi problema sparisce... Tuttavia, ci sono modi alternativi, tra cui ve n'è uno che fonda le sue basi nell'antica Mesopotamia (tanto per cambiare). Allora comportava qualche problema e veniva utilizzato in modi leggermente diversi da un caso all'altro. In qualche modo si cercava di ottenere un quadrato perfetto, ecc., ecc.

Tuttavia, fatta questa doverosa precisazione, proponiamo in questo articolo un sistema decisamente intuitivo, comprensibile e di semplicissima applicazione, anche nei casi di radici immaginarie.

Per far ciò, ricordiamo il significato geometrico di un'equazione di secondo grado. Essa si presenta , nel caso più generale, sotto la forma:

ax² + bx + c = 0                   .... (1)

Dato che conosciamo molto bene le funzioni, possiamo scrivere:

y = ax² + bx + c                   .... (2)

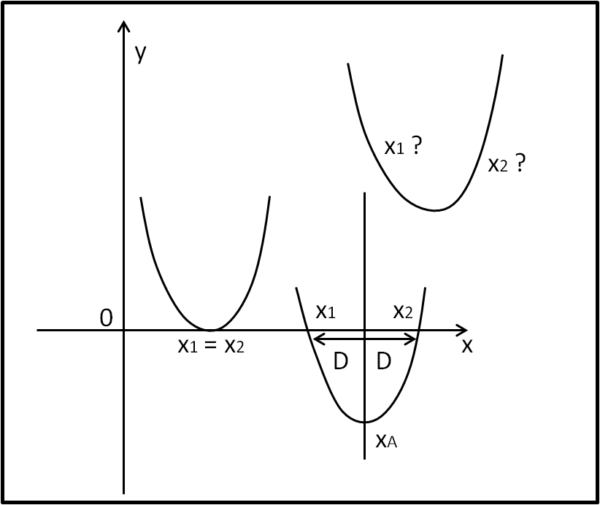
Essa, geometricamente parlando, è l'equazione di una curva molto ben conosciuta: la parabola. La parabola ha tante caratteristiche interessanti, la più importante delle quali (almeno in questo caso) è quella di essere simmetrica rispetto all'asse verticale che passa per il suo vertice (asse che è parallelo all'asse delle y). Ciò vuol dire che tutti punti che hanno la stessa y, hanno valori di x che sono equidistanti dall'asse. Disegniamo subito una figura che illustri facilmente quanto stiamo dicendo.

Bene. Cosa vuol dire risolvere l'equazione (1)? Vuole  dire geometricamente: "Trovare i punti in cui si incontrano due funzioni":

y = 0

y = ax² + bx + c

Il che comporta:

ax² + bx + c = 0

L'abbiamo fatta lunga, ma in poche parole possiamo dire che risolvere un'equazione di secondo grado vuol dire trovare i punti della parabola (2) che abbiano ordinata uguale a zero, ossia che intersechino l'asse delle x, che ha proprio equazione y = 0.

Per quanto detto prima, però, le due intersezioni devono sempre avere la stessa distanza dall'asse della parabola. Il che vuole anche dire che l'ascissa dell'asse della parabola (costante per costruzione) non è altro che la media aritmetica tra le ascisse delle due intersezioni, ossia delle due soluzioni dell'equazione. Se esse fossero x₁ e x₂, l'asse della parabola è  descritto da:

x_A = (x₁ + x₂)/2

Questo capita quando la parabola interseca l'asse delle x. ma può anche capitare che il  vertice stia proprio sull'asse x (y_A = 0). In tal caso le due soluzioni x₁ e x₂ coincidono e coincide anche la loro media x_A. Infatti:

x_A = (x₁ + x₂)/2 = 2x₁/2 = x₁ = x₂.

Scusate se sono estremamente didattico, ma lo scopo è di portare questo metodo, compresa l'applicazione alle radici immaginarie, alla portata di chiunque.

A proposito di radici immaginarie, la figura precedente mostra chiaramente anche questo caso: la parabola a destra non ci pensa nemmeno a intersecare l'asse delle x, eppure nel campo dei numeri complessi le radici esistono e come. E' un mondo a parte, "immaginario" appunto, ma che ha delle regole ben precise ed è estremamente concreto! Per poterci entrare  basta conoscere la parola d'ordine, che è estremamente facile da ricordare:

√(- 1) = i

E tutte le porte si aprono...

Torniamo a noi e lasciamo per il momento da parte questo mondo fantastico.

Dobbiamo ricordare un'altra caratteristica delle soluzioni di un equazione di secondo grado (caratteristica facilmente dimostrabile, ma che adesso prendiamo per buona). Essa ci dice che i coefficienti dell'equazione sono strettamente e facilmente legati alle soluzioni. In particolare, data la (1), abbiamo:

x₁ + x₂ = - b/a

x₁ x₂ = c/a                                    .... (3)

"Fantastico!" uno potrebbe dire: "a, b e c sono conosciuti e le due banali equazioni appena scritte permettono di trovare x₁ e x₂!" . Beh... sarebbe un serpente che si morde la coda... Vogliamo provare?

Dalla prima equazione possiamo ricavare x₂ in funzione di x₁

x₂ = - x₁ - b/a

E poi sostituirlo nella seconda

x₁ (- x₁ - b/a) = c/a

- x₁² - (b/a) x = c/a

Moltiplicando ogni termine per a, otteniamo:

- a x₁² - bx₁ - c = 0

ax₁² + bx₁ + c = 0

E ci ritroviamo con un'equazione identica a quella di partenza! No, non funziona.

Però, però... si potrebbero sfruttare le equazioni (3) in altro modo.

Consideriamo un'equazione del secondo grado scritta nel seguente modo:

x² - bx + c = 0              .... (4)

N.B.: E' sempre possibile manipolare facilmente la (1) per ottenere la (4), come vedremo tra poco.

Scriviamo le (3) per lei, notando che a = 1

x₁ + x₂ = b

x₁x₂ = c

Per quanto detto prima, ricaviamo il punto di mezzo tra x₁ e x₂, ossia la x_A dell'asse della parabola:

x_A = (x₁ + x₂)/2 = b/2

Il che vuol dire che le due soluzioni devono essere alla stessa distanza D (in valore assoluto) da b/2, ossia:

x₁ = b/2 - D

x₂ = b/2 + D              .... (5)

Moltiplichiamole tra di loro:

x₁ x₂ = (b/2 + D)(b/2 - D) = b²/4 - D² = c

D² = b²/4 - c

E immediato perciò trovare il valore di D (positivo perché è una distanza in valore assoluto) , attraverso un quadrato e una sottrazione. A questo punto le due soluzioni  si ricavano subito dalle (5) con una banale sottrazione. E' meglio fare un esempio banalissimo:

x² - 6x + 8 = 0

x_A è la metà di 6, ossia 3

Da cui:

(3 - D)(3 + D) = 8

9 - D² = 8

D² = 1

D = 1                  (non scrivo +/- 1, dato che mi interessa il valore assoluto)

x₁ = 3 - D = 3 - 1 = 2

x₂ = 3 + D = 3 + 1 = 4

Nessun problema se avessimo avuto, ad esempio:

x² - 6x + 4 = 0

x_A = 3

(3 - D)(3 + D) = 4

9 - D² = 4

D² = 5

D = √5

x₁ = 3 - √5

x₂ = 3 + √5

Non ci vuole molto a capire che attraverso queste semplici, ma comprensibili operazioni che non  necessitano memoria, abbiamo ricavato il discriminante della normale formula e via dicendo. Tuttavia, lasciatemi dire che questo metodo è basato sempre su un ragionamento e "costringe" in pratica a capire sempre ciò che si sta facendo e perché.

Qualcuno potrebbe dire: "Sì, ma hai sempre considerato a = 1 e b preceduta da un segno meno". Beh... poco male! Qualsiasi equazione può essere trasformata in questa forma: Basta dividere tutti i coefficienti per a e scrivere il coefficiente b, come -(-b). Subito un esempio:

2x² + 6x + 4 = 0

x²+ (6/2) x + 4/2 = 0

x² + 3x + 2 = 0

x² - ( - 3)x + 2 = 0

e poi agire come prima, sapendo che b è questa volta il coefficiente di x cambiato di segno e diviso per a, mentre c è se stesso diviso per a!

(x₁ + x₂)/2 = - 3/2

xA = - 3/2

(- 3/2 - D)(- 3/2 + D) = 2

D² = 9/4 - 2 = 1/4

D = 1/2

x₁ = -3/2 - 1/2 = -4/2 = - 2

x₂ = - 3/2 + 1/2 = - 1

Nessun problema nemmeno con parabole "indipendenti" e solitarie...

x2 + x + 1 = 0

x₁ + x₂ = - 1

x_A = -1/2

(-1/2 - D)(-1/2 + D) = 1

D2 = 1/4 - 1 = - 3/4 !!!

Come possiamo eseguire la radice quadrata? Nessun problema... basta scrivere:

D = 1/2√ (-3) = 1/2√3 √(-1)

E avere con noi la parola d'ordine, ossia

√(-1) = i

Da cui:

D = i√3 /2

E, infine:

x₁ = -1/2 + i√3 /2

x₂ = -1/2 -  i√3 /2

Eh sì, anche le parabole che sembrano vivere per conto loro, sono capaci di "abbracciarsi" all'asse x nel mondo immaginario!

Ancora una volta... grazie ai babilonesi!

 

Questi babilonesi non finiranno mai di stupirci: erano addirittura in grado di utilizzare le aree per calcolare lo spazio percorso da Giove! Ne abbiamo parlato QUI