Volume di un cilindro retto

Passiamo al calcolo di un volume particolare, quello del cilindro retto. Lo tratteremo, dapprima, utilizzando passo dopo passo quanto appena imparato per gli integrali doppi, accorgendoci, alla fine, che la faccenda si può sveltire molto di più, senza nessun bisogno di un integrale doppio. L'esempio, però, può servire per comprendere meglio i singoli passaggi, in un caso pratico.

(1) Integrale doppio

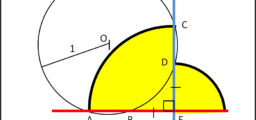
Disegniamo un cerchio, il cui centro sia posto nell'origine degli assi. A questo punto, prima di partire in quarta, è bene ragionare un poco sopra ciò che vogliamo ottenere.

La funzione z = f(x,y) non è altri che una costante h, ossia l'altezza del cilindro. Il primo passo è determinare il dominio sul piano (x,y). Ci accorgiamo che il tutto si può semplificare dato che il dominio può essere diviso in quattro parti uguali, ciascuno al di sotto della stessa superficie z = h. Basta perciò considerare un quarto di circonferenza, ad esempio quella del primo quadrante (x > 0, y > 0), come illustra la Fig. 1.

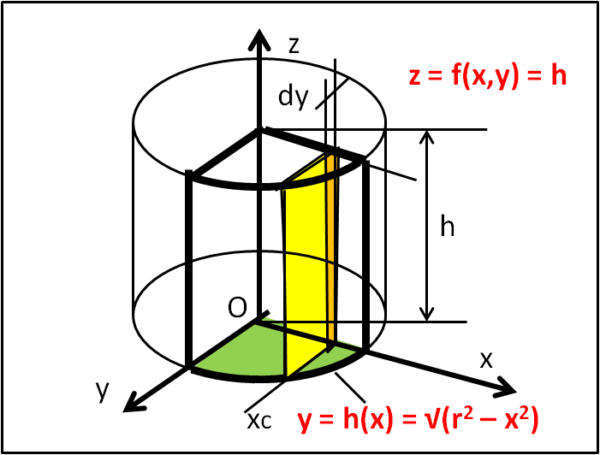
Il primo passo è assumere x = x_c = costante, ottenendo il rettangolino di base dy e altezza f(x_c,y). Per avere tutta l'area gialla basta integrare la f(x_c,y) tra h₁(x_c) e h₂(x_c). Otteniamo:

u(x_c) = ∫_h1(xc)^h2(xc)  f(x_c,y) dy

Nel nostro caso, però:

z = f(x_c, y) = f(x,y) = h

h₂ è la funzione che descrive la y in funzione della x, ossia:

y = √(r² - x²)

Che, nel caso della x_c vale proprio:

h₂(x_c) = √(r² - x_c²)

La funzione h₁ è invece l'asse delle x, per cui y = 0 per qualsiasi x

h1(x_c) = 0

u(x_c) =∫_h1(xc)^h2(xc) f(x_c,y) dy

u(x_c) = ∫₀^{√(r2 - xc2)}  h dy                          (r2 e xc2   significano r² e x_c²)

Consideriamo libera di variare anche la x e poniamo x al posto di x_c

u(x) = ∫₀^{√(r2 - x2)} h dy

Non ci resta che integrare questa funzione di x tra x1 e x2, ricordando però che x1 = 0 e x2 = r

e ottenere il volume del quarto di cilindro (Fig. 2)

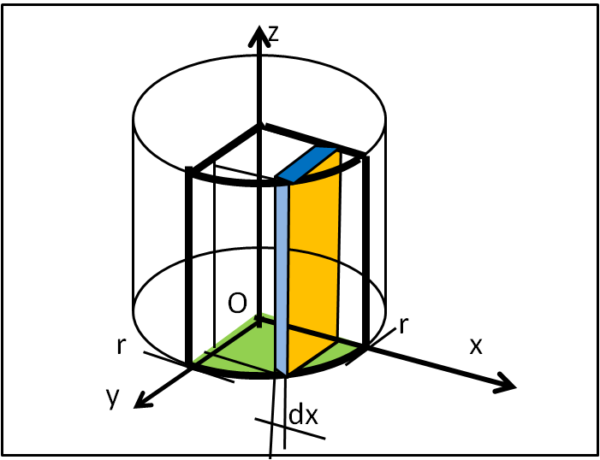
V/4 = ∫₀^ru(x) dx = ∫₀^rdx∫₀^{√r2 - x2} h dy 

L'integrale più interno vale soltanto y, dato che la funzione f(x,y) = h è una costante...

V/4 = ∫₀^r dx h [y]₀^{√(r2 - x2)}

V/4 =  h∫₀^r √(r² - x²)dx

Questo integrale semplice (in rosso) non è banalissimo, ma lo svolgiamo lo stesso per completezza.

In pratica, ci dice di calcolare l'area sottesa dal quarto di cerchio che ha equazione:

y = √(r² - x²)

cambiamo variabile, ponendo

x= r sin t

dx/dt =  r cos t

dx =  r cost dt

per cui:

I = ∫₀^r√(r² - x²) dx = ∫₀^r√(r² - r² sin²t) r cos t dt  = r² ∫₀^r√(1 - sin²t) cos t dt = r² ∫₀^r cos²t dt

cambiano, ovviamente, anche i limiti dell'integrale:

x = 0   implica t = 0

x = 1   implica  t = π/2

I = r²∫₀^π/2 cos²t dt

L'integrale di cos²t si risolve ricordando le formule di bisezione:

cos a/2 = +/-√((1 + cos a)/2)

nel nostro caso

cos t = +/-√((1 + cos 2t)/2)

cos² t = (1 + cos2t)/2

per cui:

I = (r²/2)∫₀^π/2  (1 + cos 2t) dt

L'integrale di una somma è uguale alla somma degli integrali:

I = r²(1/2∫₀^π/2 dt  + 1/2∫₀^π/2 cos 2t) dt)

La funzione che ha come derivata cos 2t vale  sin 2t/2 = , per cui:

I = r²(1/2 [t]₀^π/2 + 1/4[sin2t]₀^π/2)

I =r2(1/2 · π/2   + 1/4 [sin2t]₀^π/2)

I =r²(1/2 · π/2   + 1/4 [ 0 - 0]₀^π/2)

I =r² · π/4 = 1/4 πr²

Per avere il volume dell'intero cilindro, basta moltiplicare per h e per 4

Vtot =  πr² h

In realtà, nel caso del cilindro retto, tutto si limita al calcolo dell'integrale semplice tra o e r della funzione che descrive un quarto di circonferenza e, poi, moltiplicare per 4h. Abbiamo svolto anche gli inutili passaggi precedenti per seguire passo dopo passo quanto spiegato nel caso generale dell'articolo precedente.

Vi sarete sicuramente accorti che non è stato certo un metodo molto rapido... Normalmente si usa una diversa strategia, che si applica a tutti i solidi di rotazione.

(2a)  Solidi di rotazione

Consideriamo una qualsiasi funzione y = f(x), come mostra la Fig. 3

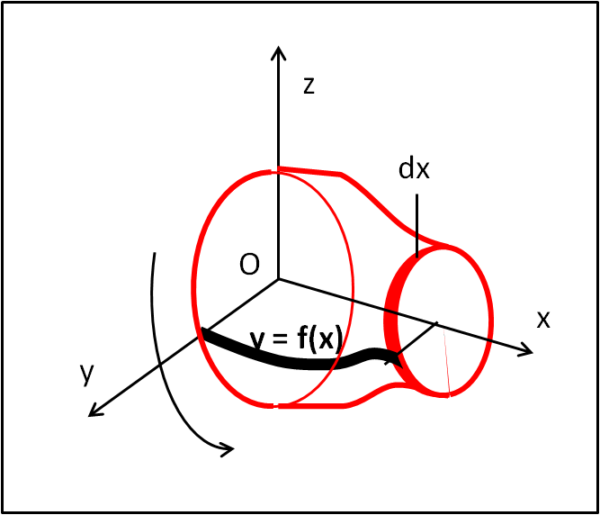
Facciamo ruotare la funzione f(x) attorno all'asse x. Otteniamo otteniamo il solido di rotazione rosso. Sezioniamolo con un piano x_c = costante ricavando un cerchio di raggio f(x_c), la cui area è:

dA = π f²(x)

Non ci resta che integrare dA per x che va da x₁ e x₂,  limiti  del dominio della funzione y = f(x);

V = π∫_x1^x2 dA dx = π∫_x1^x2 f²(x)dx               .... (1)

Nel caso del cilindro, abbiamo che

y = f(x) = r = costante

V = πr²∫_x1^x2 dx = πr²[x]_x1^x2 = πr²(x₂ - x₁)

Ma x₂ - x₁ è proprio l'altezza h del cilindro per cui

V = πr2 h

La formula (1) vale per qualsiasi solido di rotazione.

Qualcuno mi potrebbe dire che in questo caso si assume di conoscere già l'area di un cerchio...

(2b) Area di un cerchio

Bene, possiamo calcolarla una volta per tutte, come mostra la Fig. 4

Usiamo le coordinate polari r e t

Consideriamo un angolo infinitesimo dt che individua un triangolino isoscele di area

dA = 1/2  r (r dt)

Integriamola tra 0 e 2π

A = ƒ₀ ^2π (r²/2)dt =  (r²/2) 2π= π r²

Beh... veramente immediata.

A questo punto possiamo tranquillamente utilizzare la formula per i volumi dei solidi di rotazione, conoscendo l'area di un cerchio...

Insomma, vi sono svariati modi per trovare i volumi... tutto dipende dalla situazione che si ha di fronte e dalla scelta che si effettua.

Il volume di un parallelepipedo è di rapida soluzione. Provate a svolgere il problemino da soli e la prossima volta lo tratteremo assieme.