Due grandi matematici che, pur nella brevità della loro vita, hanno lasciato una profonda impronta nella storia della relatività.


Due grandi matematici che, pur nella brevità della loro vita, hanno lasciato una profonda impronta nella storia della relatività.

Einstein chiese dunque a Grossmann di aggiornarlo sui progressi da Gauss in avanti: si dice che, preso dalla disperazione, egli abbia implorato: «Grossmann, aiutami altrimenti impazzisco!».
Grossmann, rispondendo all'accorato appello, nell’agosto del 1912, comunica ad Einstein che molto probabilmente lo strumento teorico che a lui serve è il calcolo sulle varietà di Riemann e lo aggiorna sui risultati di Christoffel, Ricci e Levi-Civita.
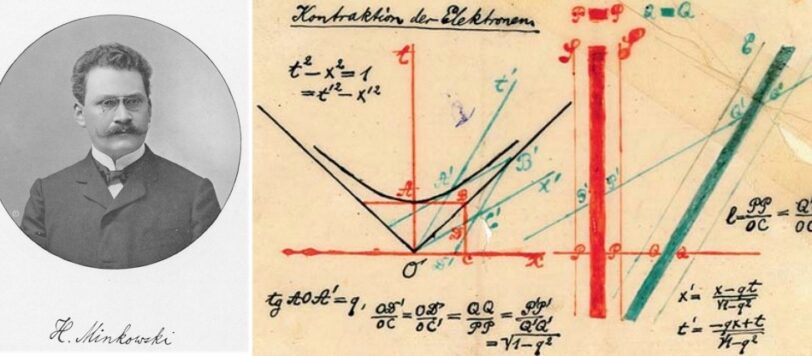
il 23 dicembre 1908, a tre anni e mezzo di distanza dall'articolo di Einstein sulla elettrodinamica dei corpi in movimento, Hermann Minkowski pubblica “spazio e tempo” un lavoro annunciato nel mese di settembre, nella sua conferenza a Colonia, alla 80a assemblea dei Naturalisti tedeschi, che inizia con queste parole..
“ Le visioni di spazio e tempo che desidero presentarvi sono scaturite dal terreno della fisica sperimentale, e in ciò sta la loro forza. Sono radicali. Per cui lo spazio, preso isolatamente e il tempo preso isolatamente, sono destinati a dissolversi in semplici ombre, e solo una specie di unione dei due conserverà una realtà indipendente .“

L’inquietante enigma dell’ Etere sullo sfondo dello sviluppo di una nuova fisica ad opera di tre grandi protagonisti della relatività

In quel secolo e mezzo o poco più che separa Newton da Einstein, molti personaggi scrivono importanti pagine nel libro della Scienza ma, tra di essi, ce n’è uno che, più degli altri, può essere considerato un vero e proprio ponte tra quei due geni assoluti, risolvendo il dubbio di Newton e ponendo le basi per le intuizioni di Einstein: nacque a Londra nel 1791, morì nel 1867, diventò il più grande fisico sperimentale dei suoi tempi e di lui bisognerebbe parlare di più.
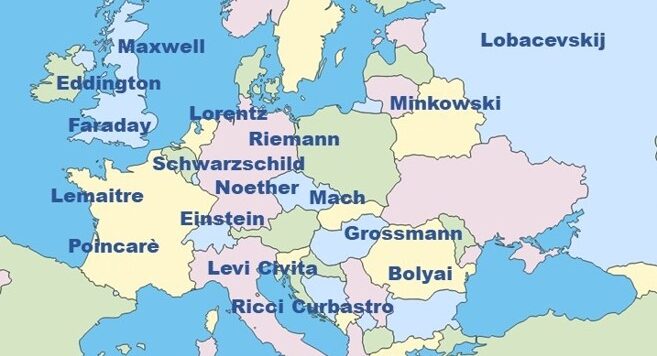
Proponiamo ai lettori, iniziando con questo articolo, il complesso percorso che ha portato alla attuale visione scientifica dello spaziotempo e della gravità, ricordando i matematici, fisici, astronomi che più hanno contribuito alla formulazione della teoria della relatività nell’arco di un secolo e l’intreccio delle loro idee, scoperte e relazioni, nel contesto dello scenario culturale in cui sono vissuti ed hanno operato.

Terza e conclusiva parte dell'articolo sui quasi-cristalli: l'impossibile diventa possibile, anzi reale.

L'intrigante argomento dei quasi-cristalli non può essere affrontato senza alcune necessarie premesse, relative alle basi teoriche della mineralogia e della cristallografia. Questo primo articolo intende illustrarne i concetti fondamentali; ad esso ne seguirà un secondo, focalizzato sulle strane peculiarità dei quasi-cristalli e sulla loro "impossibile esistenza" ed un terzo, conclusivo, che aprirà una finestra proprio su questa "impossibilità".
Non prendetevela con me se torno ancora una volta a parlare di questa tecnica tanto cara agli antichi greci. La "colpa" è del nostro amico Frank che mi ha pungolato varie volte nei commenti in questo recente articolo.