Il presente articolo è stato inserito nella sezione d'archivio Pianeta Terra

Seconda parte dell'articolo sui quasi-cristalli, centrato sul concetto di simmetria (QUI la prima parte).

Il numero delle specie minerali è decisamente limitato, in particolare se paragonato all’enorme numero di specie viventi note, vegetali o animali che siano. Ancora più sorprendente è il fatto che, delle oltre 5000 specie minerali conosciute, solo il 4% circa è considerato comune, e di questa già ridotta percentuale appena un quarto costituisce oltre il 99% delle rocce crostali.

Ciò significa che vagando sulla superficie terrestre e prestando l’occhio al variegato insieme delle rocce, tutto ciò che affiora è composto da appena una cinquantina di minerali diversi, i più abbondanti. Il restante grande insieme delle specie minerali costituisce una popolazione di peso esiguo, dispersa nell’intimo delle rocce, composte quasi esclusivamente dalla preponderante massa dei pochi minerali tipici della crosta: quarzo (SiO₂, sistema trigonale), calcite (CaCO₃, sistema trigonale), pirite (FeS₂, sistema cubico), feldspati potassici (ortoclasio, KAlSi₃O₈, sistema monoclino), sodici (albite, NaAlSi₃O₈, sistema triclino) e calcici (anortite, CaAl₂Si₂O₈, sistema triclino) e miche di vario tipo.

Da un punto di vista statistico è interessante notare che la distribuzione secondo i 7 sistemi cristallini non è omogenea, il sistema meno rappresentato è quello tetragonale, con appena il 7% circa di specie minerali, ai sistemi cubico e triclino ne competono rispettivamente il 9% e l’11% circa, il sistema monoclino predomina con un 34% circa mentre l’ortorombico segue con il 20% circa, analoga è la percentuale di minerali appartenenti alla coppia esagonale-trigonale, intorno al 19% (i 2 sistemi sono in questo caso considerati un unico sistema, essendo di fatto distinti solo dal grado di simmetria).

Parrebbe, quindi, che anche per quanto riguarda le geometrie delle celle unitarie, la natura abbia le sue preferenze, come in molti altri ambiti. La preferenza, inoltre, non sembra essere legata al grado di simmetria, crescente dal sistema triclino a quello cubico.

Ma cosa significa individuare le simmetrie possedute da una cella unitaria appartenente ad uno dei 7 sistemi cristallini? E come si stabilisce il grado di simmetria di ciascuno di essi?

SIMMETRIE ED ELEMENTI DI SIMMETRIA

Un’operazione di simmetria è una trasformazione geometrica che riproduce un oggetto in modo tale che esso venga replicato conservando tutte le sue caratteristiche. L’operazione di traslazione è un’operazione di simmetria: l’oggetto di partenza viene riprodotto applicando il medesimo spostamento ad ogni suo punto. Una volta traslato nella nuova posizione, l’oggetto è identico all’oggetto originario e pertanto indistinguibile da esso (fig. 1).

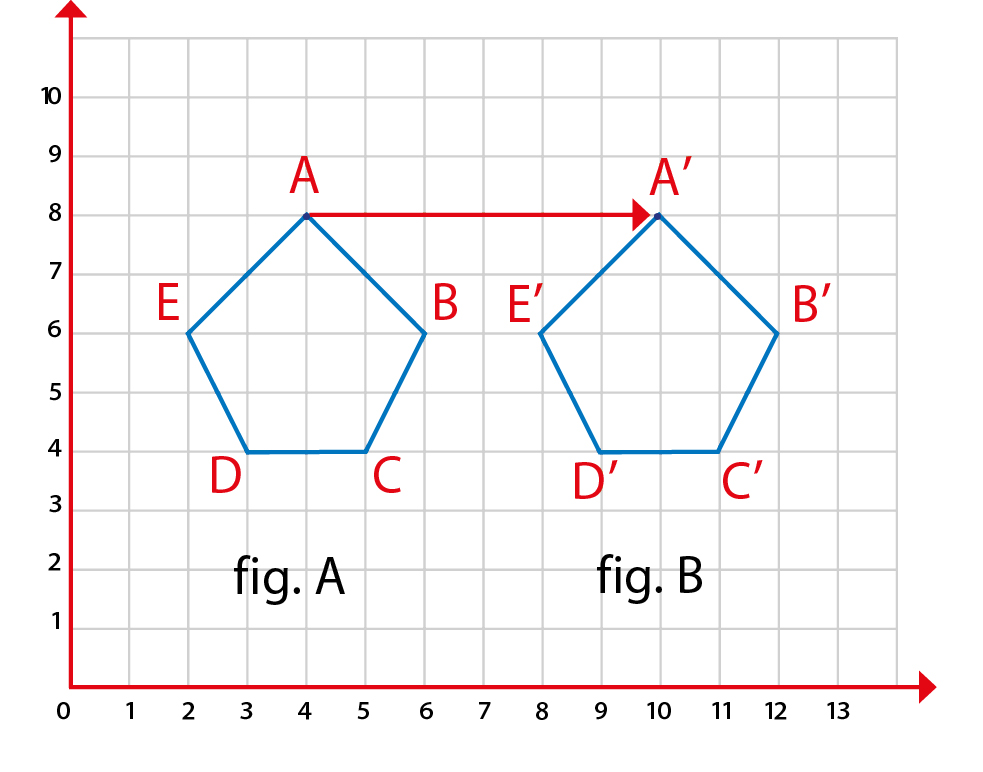
L’elemento geometrico che permette di eseguire l’operazione di simmetria è chiamato “elemento di simmetria”, esso definisce l’operazione eseguita per ottenere il nuovo oggetto. Nel caso di fig. 1, l’elemento di simmetria è il vettore rosso. E’ importante evidenziare che nella traslazione ogni punto dell’oggetto subisce il medesimo spostamento e ciò avviene per tutti i punti.

La traslazione non è il solo tipo di operazione di simmetria possibile. La rotazione è un altro tipo di operazione di simmetria, ma rispetto alla traslazione vi sono alcune differenze notevoli.

Nell’operazione di rotazione l’elemento di simmetria non è più un vettore. Nel caso della geometria piana esso è il punto rispetto al quale, effettuata la rotazione di un definito angolo θ, si ottiene un oggetto sovrapponibile a quello di partenza (fig. 2).

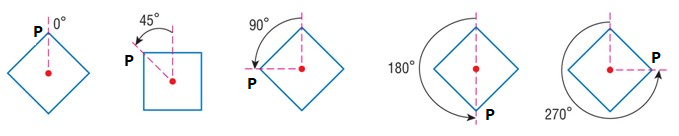
La fig. 2 evidenzia che la rotazione di un angolo θ = 90° è effettivamente un’operazione di simmetria rotazionale e che il punto rosso è l’elemento di simmetria. Nella figura il quadrato iniziale subisce per 3 volte l’operazione di simmetria (si ricordi che nell’esempio la rotazione di 45° NON è operazione di simmetria), ed è evidente che applicando all’ultimo quadrato a destra ancora una volta l’operazione, cioè ruotandolo per la quarta volta di θ = 90°, si ricade nella situazione di partenza, cioè si ottiene l’esatta corrispondenza dei vertici del quadrato, infatti il vertice P torna nella medesima posizione iniziale. Quindi l’applicazione dell’operazione di simmetria per 4 volte, cioè l’effettuazione di una rotazione complessiva pari a 4θ = 360°, riconduce alla situazione di partenza.

Generalizzando dall’esempio: se applicando p volte (con p numero naturale >1) l’operazione di simmetria rotazionale rispetto all’elemento di simmetria si ottiene la medesima situazione di partenza, p rappresenta l’ordine della simmetria. Nell’esempio la configurazione di partenza possiede simmetria rotazionale di ordine p=4.

Il più piccolo angolo di rotazione che, per una definita operazione di simmetria rotazionale, riproduce un oggetto sovrapponibile con quello originario è denominato “angolo di simmetria”. Nell’esempio l’angolo di simmetria è 90°.

Ordine di simmetria p ed angolo di simmetria θ sono legati da una semplice relazione matematica:

θ = 360°/p     [1]

Mentre nell’operazione di simmetria traslazionale tutti punti dell’oggetto di partenza, subendo l’operazione, cambiano coordinate, nell’operazione di simmetria rotazionale tutti i punti appartenenti all’elemento di simmetria e solo essi NON cambiano posizione. Nell’esempio di fig. 2 il punto rosso non si sposta, a differenza di tutti gli altri punti del quadrato.

Passando all’ambito tridimensionale cambia poco, gli stessi concetti conservano la loro validità, ma emergono ulteriori dettagli.

Considerando un cubo si nota facilmente come una retta perpendicolare ad una coppia di facce opposte e passante per i rispettivi centri sia un elemento di simmetria rotazionale di ordine p=4 (fig. 3).

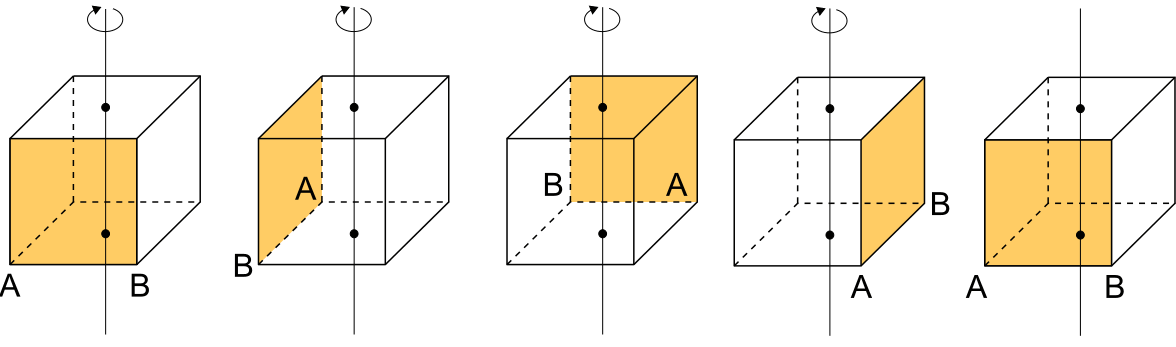
Naturalmente anche le rette perpendicolari alle restanti coppie di facce opposte del cubo sono elementi di simmetria e sempre di ordine 4, quindi il cubo ha ben 3 elementi di simmetria rotazionale (assi di simmetria) di ordine 4. Nello stringato formalismo cristallografico questa informazione si sintetizza scrivendo

3A₄

dove la prima cifra (3) esprime quanti sono gli elementi di simmetria, la lettera successiva indica il tipo di elemento di simmetria (l’asse in questo caso) e l’ultima cifra (4) esprime l’ordine di ciascun asse di simmetria.

Ma nel cubo non ci sono solo assi di simmetria di ordine 4. Con uno sforzo d’immaginazione si riesce a visualizzare che anche le 3 rette passanti ciascuna per gli spigoli opposti del cubo rispetto al suo centro sono elementi di simmetria (fig. 4, disegno a), analogamente anche le 4 rette passanti ciascuna per i punti medi degli spigoli opposti del cubo sono elementi di simmetria (fig. 4, disegno b).

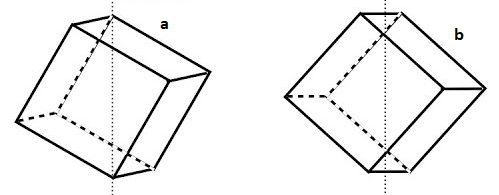
A differenza del caso di fig. 3, l’esatta situazione iniziale (cioè con le stesse facce, spigoli e vertici nelle medesime rispettive posizioni di partenza) si riproduce dopo l’applicazione dell’operazione di simmetria per 3 volte se l’asse è quello in fig. 4 disegno a) e 2 volte se l’asse è quello in fig. 4 disegno b).

Pertanto il cubo, oltre alla simmetria espressa dalla terna 3A₄, ha anche la simmetria espressa dalla terna 4A₃ (4 assi di ordine 3, uno per ogni coppia di vertici opposti, i vertici in totale sono 8 quindi 4 assi; ricordando la relazione [1] l’ordine di ciascun asse è dato da 360°/120°= 3) e anche la simmetria espressa dalla terna 6A₂ (6 assi di ordine 2, uno per ogni coppia di spigoli opposti, gli spigoli in totale sono 12 quindi 6 assi; l’ordine di ciascun asse è dato da 360°/180° = 2).

Tirando le somme nel cubo ci sono ben 3+4+6 = 13 assi di simmetria, in linguaggio cristallografico (ormai non più criptico) il tutto è riassunto nella scrittura 6A₂-4A₃-3A₄.

L’uso di una lettera nella notazione cristallografica per indicare il tipo di elemento di simmetria (“A” per l’asse, come visto) significa che quella rotazionale non è il solo tipo di simmetria non traslazionale, e infatti è così. Esiste un’operazione di simmetria eseguita tramite riflessione e l’elemento geometrico che permette di eseguire la riflessione è il piano, che nella notazione cristallografica viene indicato con “P”. La riflessione (o simmetria planare) è ottenuta replicando i punti dell’oggetto dalla parte opposta rispetto ad un piano, come se fossero specchiati (fig. 5).

 

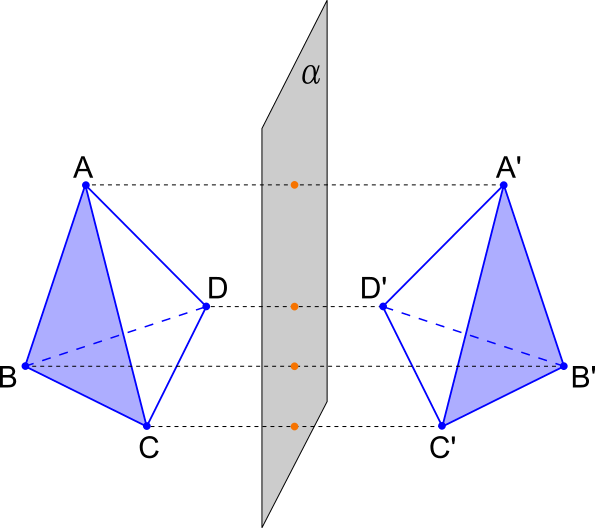
In cristallografia il piano di riflessione, se esiste, taglia il cristallo. Tutti i punti appartenenti all’elemento di simmetria (il piano) NON subiscono alcuna replicazione e pertanto sono simmetrici di se stessi. Il cubo ha ben 9 piani di simmetria (fig. 6).

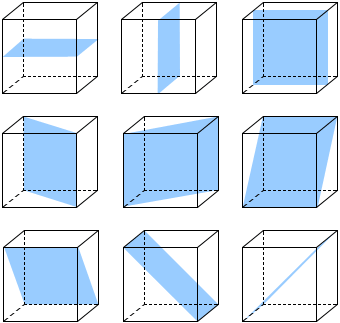
Nella simmetria planare non è possibile definire un “ordine” come nel caso degli assi di simmetria, quindi la notazione cristallografica è più semplice: il numero di piani di simmetria basta per definirla compiutamente, quindi nel cubo è 9P.

E’ possibile ora aggiornare la notazione cristallografica per il solito cubo, che diviene perciò

9P-6A₂-4A₃-3A₄

Quest’ultimo esempio indica, inoltre, che possono coesistere differenti tipologie di simmetria, nel caso specifico la simmetria rotazionale e la simmetria planare.

In 3 dimensioni, così come il piano è un elemento di simmetria anche il semplice punto può essere un elemento di simmetria. L’operazione di simmetria eseguibile tramite il punto è chiamata inversione, il punto assume la denominazione di centro di simmetria e nella notazione cristallografica viene indicato con “C”. L’operazione di inversione consiste nel replicare ogni punto dell’oggetto in modo tale che il centro di simmetria sia a metà del segmento avente per estremi il punto originario ed il punto replicato (fig. 7).

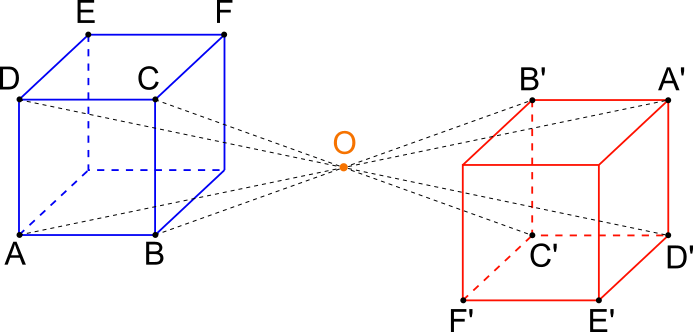
In cristallografia il centro di riflessione, se esiste, è unico ed è ubicato all’interno del cristallo nel punto d’intersezione delle diagonali (fig. 8).

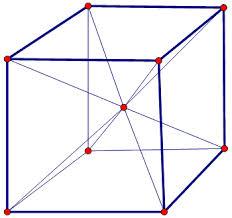
Poiché, nel caso esista, il centro di simmetria cristallografico è unico, la scrittura formale per indicarlo è ancora più semplice che nel caso dei piani di simmetria, la singola lettera C assolve totalmente il compito.

E’ possibile ora completare la notazione cristallografica indicante gli elementi di simmetria del cubo, che diviene perciò

C-9P-6A₂-4A₃-3A₄

La somma del numero di elementi di simmetria quantifica il grado di simmetria, pertanto nell’esempio del cubo esso vale 1+9+6+4+3 = 23

E’ chiaro a questo punto il metodo usato per quantificare, e quindi confrontare, i vari gradi di simmetria.

SIMMETRIE PROIBITE

E’ lecito chiedersi se possano esistere assi di simmetria rotazionale aventi qualsiasi ordine. La risposta è affermativa, con la distinzione che l’elemento di ordine p = 1 non è considerato un vero elemento di simmetria, poiché l’angolo minimo per ottenere la sovrapposizione con l’oggetto di partenza è di 360°, che coincide con il ritorno di ogni punto dell’oggetto nella medesima posizione iniziale. Per contro un cono (o oggetti di forma similare) ha un asse di simmetria di ordine infinito, infatti la retta passante per il centro della base e per il vertice è un asse attorno al quale la rotazione di qualunque angolo riproduce esattamente il cono.

Ma nel mondo della cristallografia le cose non funzionano così bene.

Va ricordato che il reticolo cristallino è una struttura, teoricamente infinita, avente una geometria precisa in cui, qualunque sia la direzione di spostamento, i nodi lungo tale direzione devono presentarsi sempre con la medesima interdistanza. Il fatto che la replicazione della cella unitaria lungo le 3 direzioni debba avvenire a distanze corrispondenti ai multipli interi delle lunghezze degli spigoli della cella implica che non vi possano essere vuoti tra una cella e quelle circostanti nè sovrapposizioni.

Il reticolo cristallino ammette le simmetrie rotazionali ma non di qualsiasi ordine, anzi ne ammette straordinariamente poche. Il motivo è legato proprio alla condizione di dover riempire tutto lo spazio con una specifica periodicità in ogni direzione. Limitandosi per semplicità alla geometria piana è immediato riscontrare che la simmetria rotazionale di ordine 5 lascia settori di piano vuoti, cioè non ne consente la “tassellatura”, a differenza delle simmetrie rotazionali di ordine 2, 3, 4, e 6. (fig. 9).

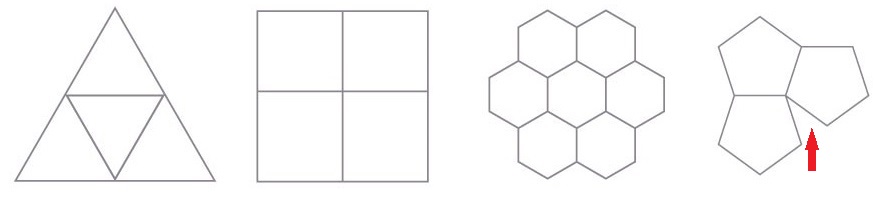
Non solo la simmetria rotazionale di ordine 5 è incompatibile con il reticolo cristallino, ma lo sono anche tutte le simmetrie rotazionali di ordine superiore a 6 (fig. 10).

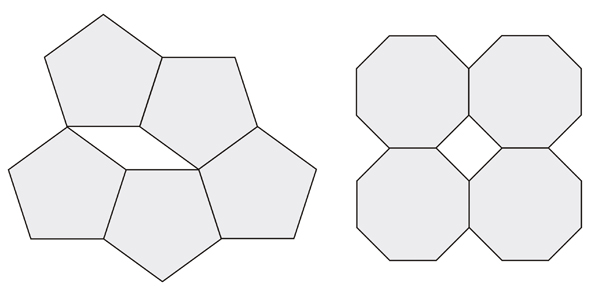
Poiché il reticolo cristallino è costruito per traslazione della cella unitaria, in termini più generali quanto appena visto si traduce nel riscontrare che in esso la simmetria rotazionale di ordine 5, 7 o superiore non è compatibile con la simmetria traslazionale, quindi per i cristalli esistono delle vere e proprie “simmetrie proibite”, che ne limitano, oltre alla geometria del reticolo, anche la forma esteriore.

La dimostrazione generale di questa proprietà è piuttosto semplice.

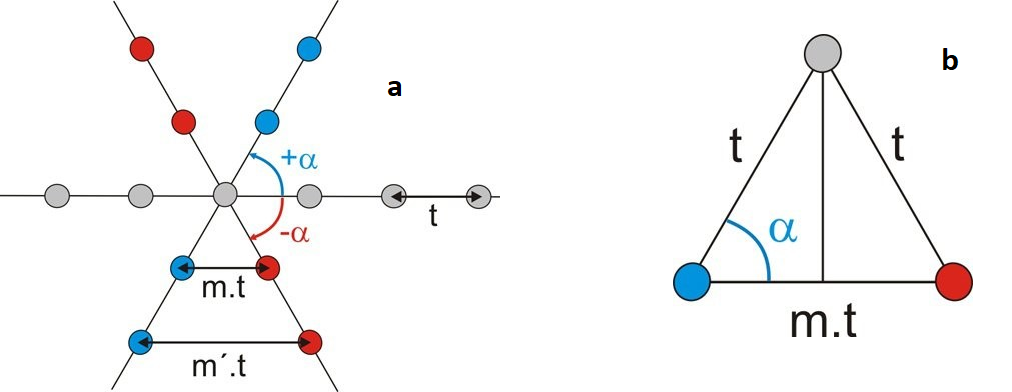
Considerata una porzione di reticolo costituita da un qualsiasi allineamento di nodi distanziati tra loro di una quantità t pari al modulo del vettore di traslazione (pallini in grigio), si applichi all’allineamento una rotazione attorno ad un asse perpendicolare al piano della figura e di ordine n qualsiasi. L’angolo di rotazione è definito da α = 360°/n e produce l’allineamento di pallini blu, allo stesso modo un angolo di rotazione di –α produce l’allineamento di pallini rossi (fig. 11 disegno a).

Se la rotazione così eseguita definisce un’operazione di simmetria reticolare, i pallini blu e quelli rossi devono essere nodi del reticolo, quindi, in ossequio alle regole geometriche che governano il reticolo stesso, tra ogni pallino rosso e ogni pallino blu deve esserci una distanza multipla intera di t (il modulo di traslazione che ha prodotto l’allineamento originario), per esempio mt o m’t. I valori m e m’ devono essere perciò interi.

Nel triangolo riportato in fig. 11, disegno b (ingrandimento di una porzione del disegno a), con angoli alla base pari ad α per costruzione, vale la relazione:

cosα = (1/2) mt/t  con m intero

da cui

cosα = m/2  con m intero

Ma la funzione coseno può assumere solo valori compresi entro l’intervallo -1 e 1, e sotto la condizione che m sia un intero, vi sono solo 5 valori di m perché ciò accada, come esplicitato in tab. 1

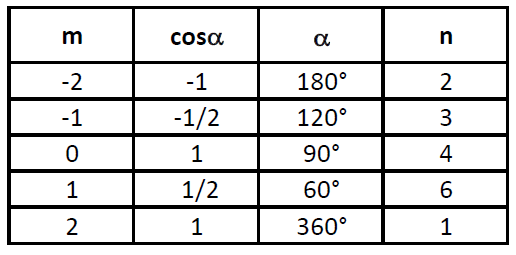
I QUASI-CRISTALLI

La condizione di compatibilità con la simmetria ottenuta per traslazione pone un limite insormontabile all’ordine della simmetria rotazionale di un reticolo cristallino e quindi all’esistenza dei cristalli, che ne sono l’espressione materiale.

Il problema della “tassellatura” del piano visualizza in modo chiaro questo limite, evidentemente noto agli artisti arabi medievali che riuscirono a coniugare la realizzazione di sbalorditivi mosaici a motivi geometrici con l’uso di tessere aventi simmetrie “proibite”. Queste opere di grande complessità e difficoltà realizzativa, oltre a presentare tassellature del piano mediante elementi di ordini vietati dalla geometria traslazionale, mostrano numerose altre intriganti particolarità (autosomiglianza, tassellatura regolare ma non-periodica, angoli interni dei poligoni sempre multipli di un valore fisso). La particolarità di più immediato impatto visivo consta nel fatto che questi mosaici, pur non possedendo simmetria traslazionale, mostrano un evidente “ordine” generale nella tassellatura (fig. 12).

Nel 1974 il matematico Roger Penrose mostrò la possibilità di tassellare il piano euclideo con due sole figure geometriche, due rombi, ottenendo una configurazione ordinata e con simmetria rotazionale di ordine 5, denominata appunto “tassellatura di Penrose”. Essa ricopre perfettamente il piano ma è aperiodica in senso stretto, quindi incompatibile con la simmetria per traslazione, e pertanto non può descrivere la geometria di un reticolo cristallino pur presentando un suo innegabile ordine ed una evidente regolarità (fig. 13).

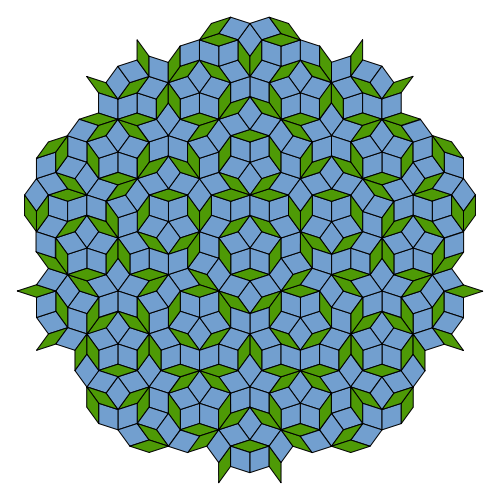
Lo studio delle tassellature ha prodotto un filone di ricerca teorica molto interessante che ha posto anche problemi di notevole difficoltà ma che per un certo tempo è rimasto confinato nell’ambito della matematica senza trovare riscontri nella realtà tridimensionale della materia. La condizione di incompatibilità di un’ipotetica cella unitaria a simmetria pentamera con la simmetria per traslazione vieta categoricamente la possibilità di una sua ripetizione periodica nello spazio e quindi mai potrà formarsi un reticolo cristallino con tali caratteristiche.

Tuttavia, alla luce delle peculiarità insite nelle soluzioni quasi-periodiche delle tassellature e delle loro proiezioni tridimensionali, è lecito chiedersi se nel mondo della mineralogia, dominio all’apparenza esclusivo dei cristalli e della loro perfetta intima architettura, possa esistere un oggetto che presenti le caratteristiche di un cristallo senza averne la periodicità reticolare richiesta dalla teoria e avvalorata da anni di analisi sperimentali cristallografiche.

L’esistenza di un simile oggetto, se da un lato si porrebbe in scomoda flagranza delle leggi cristallografiche, dall’altro potrebbe aprire un ghiotto campo di ricerca, da esplorare integralmente e dalle ricadute pratiche tutte da scoprire.

Assegnare un nome a qualcosa, pur nell’incertezza circa la sua stessa esistenza, significa iniziare già a pensarla come una possibile realtà; è un primo passo, pericoloso da un punto di vista strettamente scientifico, ma, a quanto pare, di particolare attrattiva per la fantasia umana. Ed allora, visto che non di cristalli veri e propri si tratterebbe ma di parenti ad essi molto vicini, perché non chiamarli “quasi-cristalli”?