Questo articolo è inserito in Matematica e Geometria

 

Torniamo a parlare di quel genio matematico che è stato Srinivasa Aiyangar Ramanujan, l'uomo che giocava con la matematica e che non aveva paura dell'infinito.

Della sua breve vita (morto a 32 anni) abbiamo già parlato QUI, ma ciò che egli è riuscito a dimostrare attraverso calcoli ineccepibili è veramente qualcosa di assurdo e fantastico. Questa volta tratteremo di una serie famosissima (anche grazie a Gauss):

S = 1 + 2 + 3 + 4 + 5 + ....

Una serie che sembrerebbe dar luogo a un risultato sempre più grande, tendente all'infinito. Ebbene lui ha dimostrato, giocando con i numeri come forse nessuno è mai riuscito a fare, che questa somma vale - 1/12. Non solo un numero finito, ma addirittura negativo!

Vediamo come ha fatto...

Innanzitutto ricordiamo una proprietà della somma: poco importa quali addendi si sommino insieme per primi, il risultato è sempre lo stesso. Facciamo un esempio semplicissimo:

Vogliamo sommare 1, 2, 3, 4, 5

Presto fatto: 1 + 2 + 3 + 4 + 5 = 15

Adesso vogliamo sommare questa "serie" a se stessa.

Bene, posso fare in diversi modi, ma il risultato non cambia. Mettiamoli in colonna

1 + 2 + 3 + 4 + 5   +

1 + 2 + 3 + 4 + 5  =

_________________

2 + 4 + 6 + 8 + 10   = 30

Potremmo anche sommare i primi 5 e i secondi 5 e poi sommarli assieme, ma il risultato resterebbe 30 (15 + 15 = 30)

Oltre che sommarli, potrei anche sottrarre il secondo gruppo dal primo, sempre nel modo che voglio.

1 + 2 + 3 + 4 + 5 - (1 + 2 + 3 + 4 + 5)  = 0

Ma anche, mettendoli in colonna :

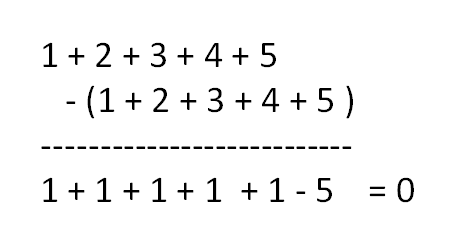
Il risultato non dipende certo dal numero di addendi, per cui potrei utilizzare due serie. Ne segue che se avessi due serie di numeri naturali crescenti potrei sommarli o sottrarli nel modo che voglio.

Bene, iniziamo a giocare...

Chiamiamo

S1 = 1 - 2 + 3 - 4 + 5 - 6 + .....

Quanto vale questa somma?

Utilizziamo un metodo un po' particolare: sommiamo 4 volte la stessa somma:

4 S1 = 1 - 2 + 3 - 4 + 5 - 6 +.... + 1 - 2 + 3 - 4 + 5 - 6 +.... + 1 - 2 + 3 - 4 + 5 - 6 + .... + 1 - 2 + 3 - 4 + 5 - 6 +....

Mettiamoli in colonna in modo un po' diverso

Ossia:

4 S1 = 1

S1 = 1/4

Non cominciate a storcere il naso. Tutto ciò è matematicamente corretto (normalmente...).

Bene adesso andiamo a fare la differenza tra

S = 1 + 2 + 3 + 4 + 5 + 6 + ...

e

S1 =  1 - 2 + 3 - 4 + 5 - 6 + ...

S - S1 = 1 + 2 + 3 + 4 + 5 + 6 + ... - (1 - 2 + 3 - 4 + 5 - 6 + ...)

Mettiamo in colonna

Ma il risultato non è altri che:

4 + 8 + 12 + ... = 4(1 + 2 + 3 + 4 + ...) = 4 S

Possiamo, perciò, scrivere:

S - S1 = 4 S

Da cui:

3S = - S1 = - 1/4

S = - 1/12

1 + 2 + 3 + 4 + 5 + 6 + ... = - 1/12

Ovviamente, Ramanujan, non aveva presentato questo risultato come corretto, ma aveva voluto mettere in evidenza come le serie infinite, che divergono, non possono essere trattate con i metodi della matematica applicabili al finito. In realtà, per determinare la somma di una serie infinita bisogna determinare prima il termine della serie e poi passare al limite per un certo numero n che tenda ad infinito.  Questo limite può benissimo essere indeterminato e si potrebbe facilmente ottenere qualsiasi risultato, come capita proprio nelle forme indeterminate.

La serie S1 è chiaramente una serie divergente e oscillante, come mostra la figura che segue.

A seconda di dove venga tagliata si ottiene un risultato diverso. Da cui il risultato uguale a 1/4 e poi il conseguente risultato per S.

Già nel 1703 Grandi aveva descritto una serie di questo tipo (che porta anche il suo nome), ma Ramanujan ha letteralmente introdotto una visione del tutto nuova della loro trattazione, una visione che porta indissolubilmente verso i numeri complessi e la matematica superiore, come quella usata nella teoria delle stringhe. Non sono cose per il nostro "Circolo", ma vale la pena vedere come la serie di Grandi possa portare a tre risultati diversi.

S2 = 1 - 1+ 1 - 1 + 1 - 1 + ...

Scriviamola così:

S2 = (1 - 1) + (1 - 1) + (1 - 1) + ...  = 0 + 0 + 0 + 0 + ... = 0

ma anche così:

S2 = 1  - (1 - 1) - (1 - 1) - (1 - 1) - .... = 1 - 0 - 0  - 0 - 0 - ... = 1

In poche parole, se essa viene troncata dopo un numero pari o dispari di termini dà come risultato o 0 o 1. Essa è chiaramente una funzione oscillante, il cui limite per n che tende a infinito è completamente indeterminato. Vi è, però, anche un terzo modo per calcolarne la somma

S2 = 1 - ( 1 - 1 + 1 - 1 + ...) = 1 - S2

da cui:

S2 = 1/2

Non stupiamoci nemmeno troppo se, in certe matematiche superiori, questo valore (in qualche modo "medio") viene abbondantemente utilizzato.

Viaggiando tra il serio e l'assurdo, è stato anche dimostrato che il valore di - 1/12 potrebbe essere considerato errato e che sarebbe molto meglio  assumere il valore -1/8. Lo vedremo nella prossima puntata (ovviamente, chi vuole provare a ottenerlo da solo è il benvenuto!).

Continua...