Introduciamo i primi limiti notevoli per evitare che il gatto si morda la coda.

Quando avevo scritto il corso di matematica avevo riportato solo le derivate delle funzioni fondamentali, evitando di dimostrare come potevano essere ottenute. Direi che è giunto il momento di farlo, dato che il Circolo e i suoi lettori sono ormai "maturi". Ringrazio, in particolare Albertone, che mi ha stimolato a fare questo passo. Consideriamola un'aggiunta alle lezioni di matematica...

Con questo articolo torniamo a uno degli scopi base del nostro Circolo: quello di rendere comprensibili a tutti coloro che hanno la volontà di conoscere, le meraviglie dell'Universo e, di conseguenza, della fisica e del suo linguaggio (la matematica). Tratteremo in modo elementare le equazioni differenziali, cardine di tutta la ricerca scientifica, non solo astronomica. Inizieremo dalle più semplici, quelle che hanno un riscontro immediato nella realtà di tutti i giorni, e poi, un po' alla volta e valutando la vostra risposta, allargheremo sempre più il discorso.

Un problema che ci avvicina al numero di Nepero (o di Eulero) "e" e che, inoltre, ci permette di richiamare lo studio di una funzione, i limiti e le derivate, nonché un po' di logaritmi naturali.

Sappiamo già che la parallasse stellare era stata prevista da quel genio assoluto che era Aristarco, che aveva anche cercato inutilmente di misurarla. Sarebbe stata la prova diretta della teoria eliocentrica. Purtroppo per avere questa “prova” si dovette aspettare il 1727 d.C. per merito dell’inglese James Bradley, ma attraverso un fenomeno del tutto inatteso. Lasciatemi colorire un po’ la “storia”.
Ritorniamo sull’integrale indefinito, definendolo ancora meglio. Ne approfittiamo per dimostrare formalmente il teorema fondamentale (facoltativo…).
E’ ora di tornare alla nostra matematica, dato che molti l’hanno seguita e vorrebbero proseguire. Abbiamo iniziato a studiare le funzioni e torniamo improvvisamente indietro a parlare di nuovo di retta, la funzione più semplice e la prima che abbiamo trattato… Sembrerebbe una cosa assurda.
Fatevi coraggio. Questo articolo è veramente noioso, devo ammetterlo. Vuole, infatti, ricavare quanto valgono le derivate di somme, differenze, prodotti e rapporti di funzioni. Potrei darvi subito il risultato e invitarvi a imparalo a memoria. In realtà, malgrado si debba fare così (come quando si memorizzano le tabelline dei vari numeri interi), mi sembra doveroso dimostrarvi il perché agiamo in un certo modo. E’ difficile trovarlo nei libri e quindi è bene tenerlo sempre in un cassetto. Oltretutto, è un perfetto esercizio di pura matematica elementare e non fa mai male.
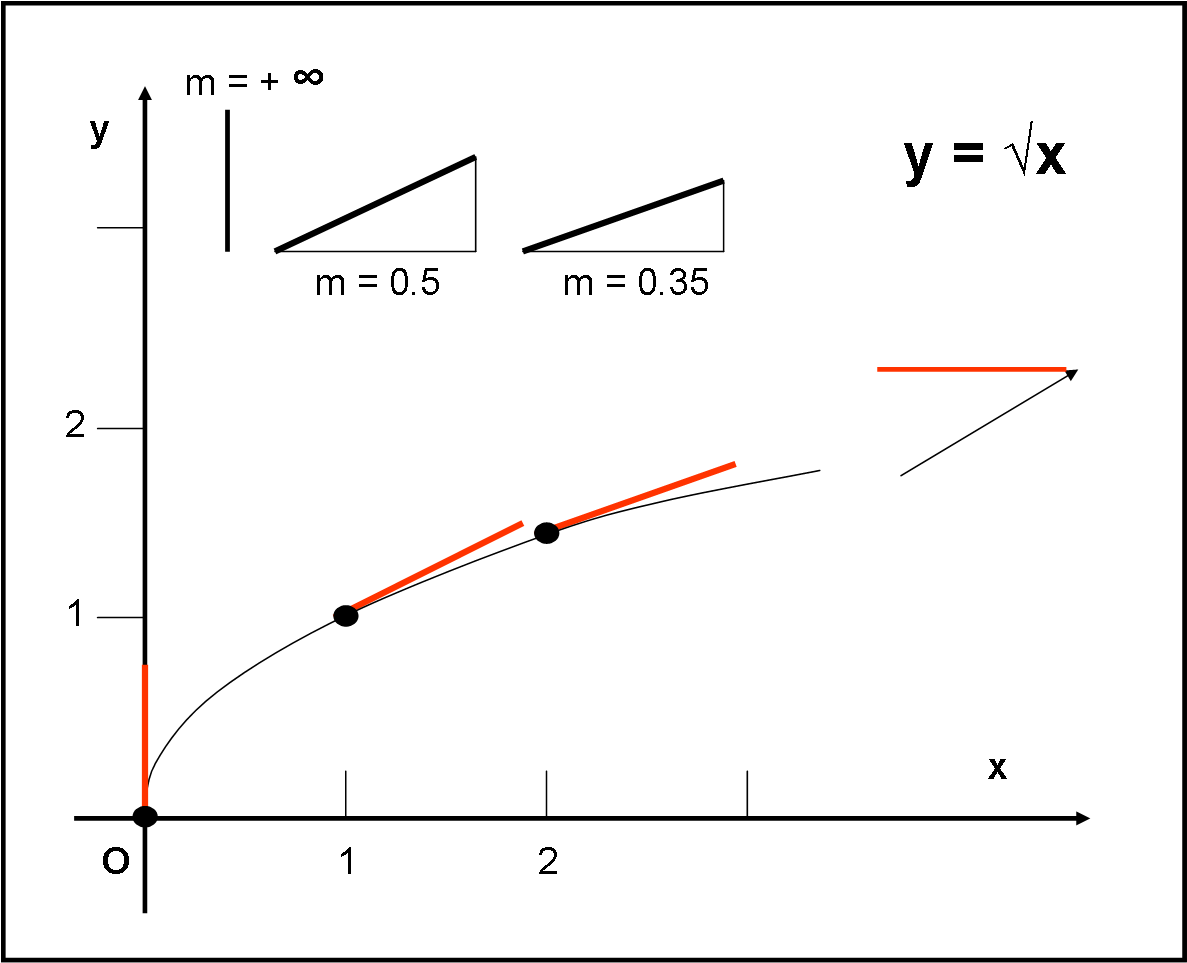
Cominciamo a calcolare alcune derivate di funzioni particolari, rappresentate dai semplici monomi. Una rapida analisi dei risultati ci insegna che esiste una facile regola generale che evita il noioso passaggio attraverso il rapporto incrementale. Segue un’appendice per i più … volenterosi.
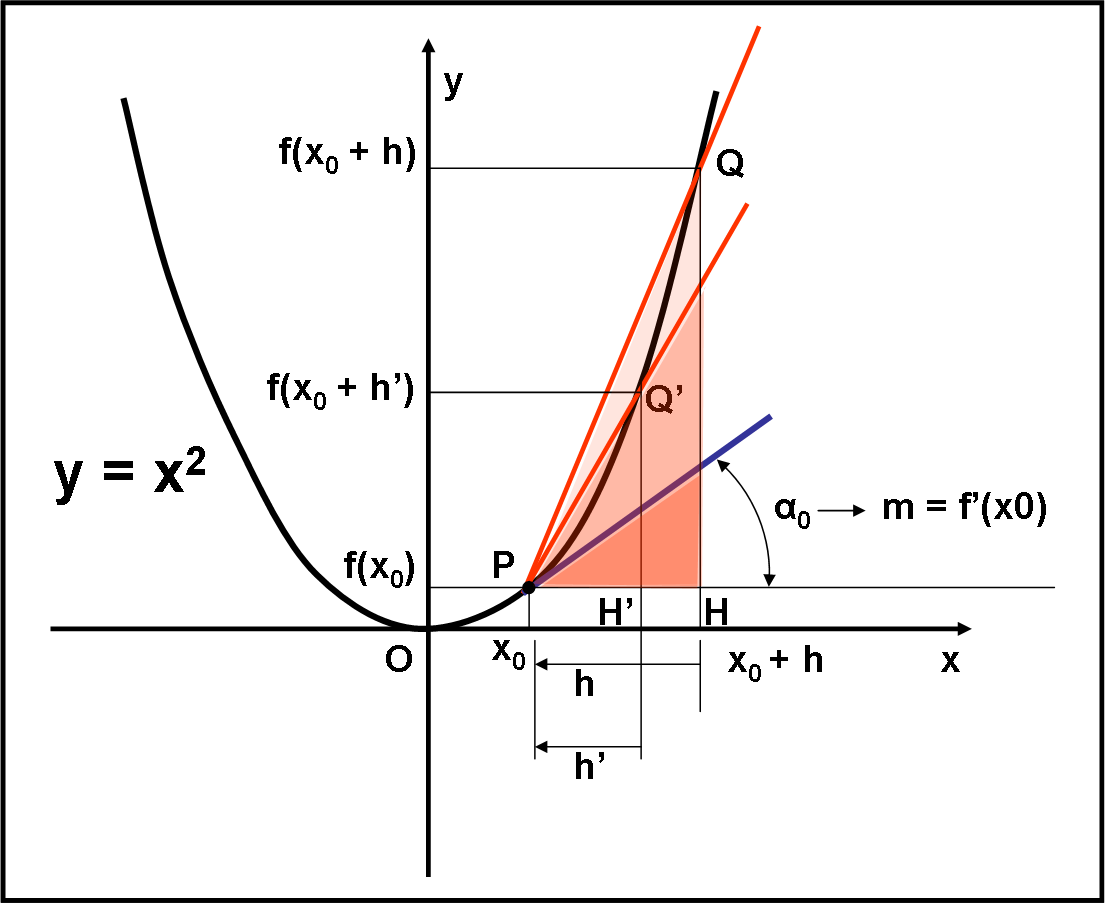
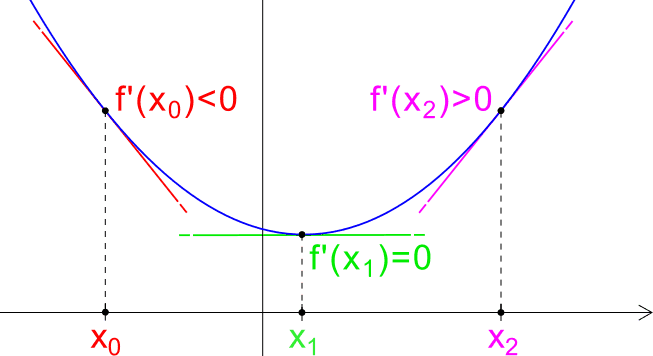
In questa parte, veramente fondamentale, calcoliamo la prima derivata di una funzione che non sia una retta e ne diamo il significato geometrico. Lo scenario si amplia sempre di più.
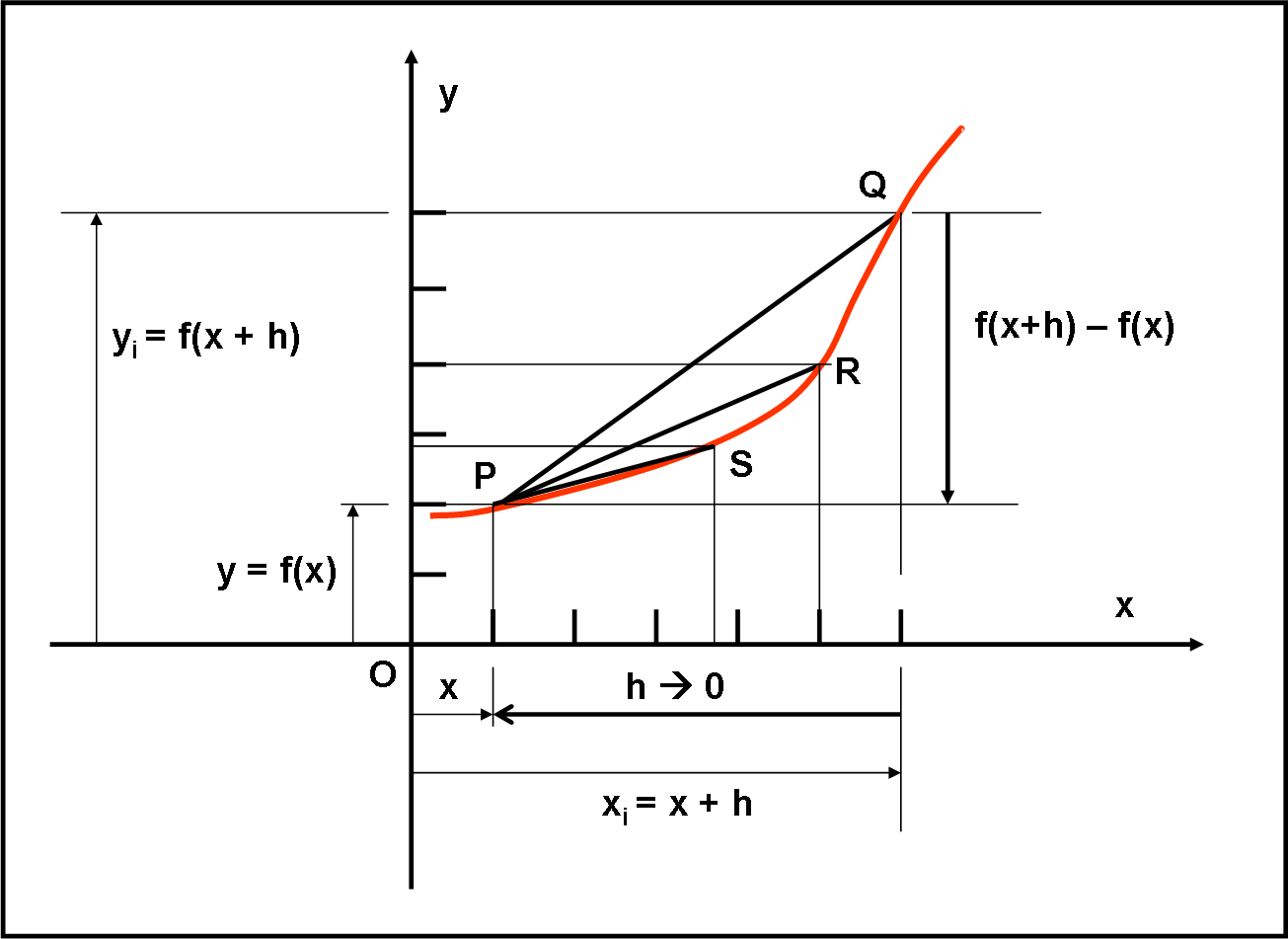
Siamo arrivati a un punto fondamentale: l’introduzione della derivata di una funzione. Iniziamo col descriverla in modo estremamente semplificato, quanto basta per afferrare il concetto base. Poi, compresa la sua ragione di esistere, vedremo di utilizzare la matematica che già conosciamo per utilizzarla al meglio. Un passo alla volta. Ho usato una strada lunga e ho girato molto attorno al problema. L’ho fatto sperando di semplificare. Tuttavia, questo è forse l’articolo più importante per entrare nel mondo della matematica “superiore” e, quindi, comunicatemi ogni pur piccolo dubbio abbiate e cercherò, se necessario, anche di cambiare la trattazione se per qualcuno risulta ancora difficile. Scrivo queste “lezioni” per voi e quindi aiutatemi a migliorarle… mi raccomando! Come al solito, ho reso l’articolo simile a un’avventura… un’avventura “matematica”, ovviamente!