Questo articolo fa parte della raccolta "Fermate il mondo, voglio scendere!" inserito nelle pagine d'archivio "Meccanica Celeste" e "Caduta libera"

 

La soluzione del quiz sulla catastrofe terrestre, ha innescato una trattazione ben più articolata  del previsto. Su suggerimento dell'onnipresente e onniveggente Daniela, si è convenuto di associare  questo articolo a quello più vecchio sul blocco della rotazione di Papalla. Il titolo unico è diventato: Fermate il mondo, voglio scendere... L'articolo è stato scritto a quattro mani e cinque teste, dato che, anche se non compare tra gli autori, la supervisione di Umberto è stata essenziale.

Questo quiz (a mio parere veramente istruttivo, soprattutto leggendo le soluzioni) ci pone davanti a due dati di fatto che forse non sono mai stati valutati attentamente.

1) un moto apparentemente semplice come quello di un corpo in caduta libera, e, quindi, con accelerazione variabile, comporta la soluzione di un’equazione differenziale che necessita il calcolo di integrali non proprio banali. Ricordiamoci quanta fatica abbiamo fatto per passare dalla semplice legge gravitazionale di Newton alle tre leggi di Keplero. L’equazione del moto è ancora banalissima (anche sfruttando gli integrali) quando l’accelerazione è costante, ma se essa inizia a variare la faccenda diventa molto più complicata e, quasi sempre, risolvibile con metodi di integrazione che noi non abbiamo mai trattato.

Immaginatevi, poi, di inserire anche corpi perturbatori, ossia passare al problema dei tre o degli n corpi. Ci vuol poco a capire come la vera meccanica celeste sia un campo di ricerca tra i più contorti e complicati, che ancora oggi non può fare a meno di approssimazioni successive e  di integrazioni numeriche e, conseguentemente, di computer sempre più potenti. E’ quindi più che divertente sentire definire come meccanica celeste l’analisi osservativa dei moti dei pianeti. L’ignoranza è sempre una brutta bestia…

2) La terza legge di Keplero (che poi non è altro che il teorema del viriale) è una legge fondamentale che permette di applicare una formuletta banalissima a tutti i corpi orbitanti, indipendentemente dalla loro eccentricità. Essa, in altre parole, ci dice che l’energia orbitale è una costante che dipende solo dal semiasse orbitale, così come il periodo di rivoluzione.

Prima di affrontare la soluzione da un solo asterisco, fatemi fare uno dei miei soliti discorsi, poco scientifici e molto fantasiosi… Attraverso la QED abbiamo capito che un raggio luminoso (chiamiamolo così) viaggia di moto rettilineo solo perché questa traiettoria è quella di massima probabilità. In realtà, niente vieta al raggio di seguire un percorso più o meno contorto anche se nettamente meno probabile. Bene, la nostra Terra che cade verso il Sole seguirà sicuramente una linea retta, ma non è un dramma se utilizziamo una traiettoria appena appena diversa, tale che, comunque, inizi dal momento di fermata della Terra e termini al momento dell’impatto con un oggetto esteso come il Sole. Questa traiettoria potrebbe proprio essere un’orbita estremamente stretta, tale da avere il fuoco (Sole) capace di contenere al suo interno il perielio.

Indovinate, infine, cosa comparirà ancora una volta, alla fine delle varie soluzioni? Sembra impossibile è invece è proprio così: l'equazione oraria della caduta libera di un grave è ben lontana dalla parabola a cui tutti (o quasi) pensano. La curva è una nostra vecchia conoscenza: la cicloide! Essa deriva, non senza difficoltà, risolvendo l'equazione del moto. La parabola non è altro che il caso particolare nel caso di accelerazione costante, ossia nei fenomeni per i quali viene considerata g come una  costante. Ci torneremo brevemente alla fine dell'articolo

Soluzione orbitale (Enzo)*

Consideriamo la Fig. 1.

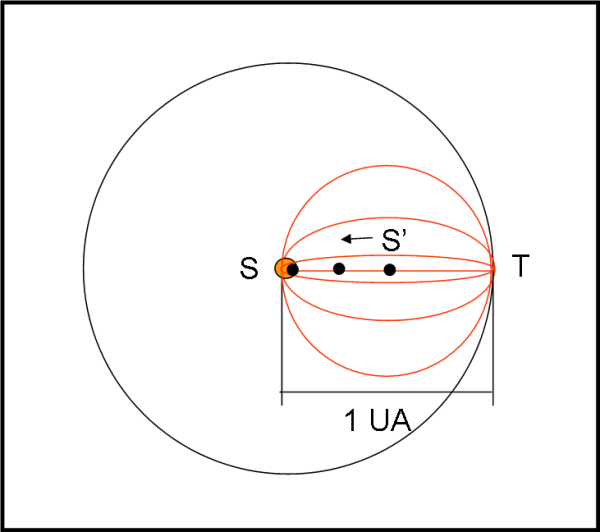
La nostra Terra si trova in T e il Sole (arancione) in S. Blocchiamo la rivoluzione del nostro pianeta e lui viene costretto a essere preda della forza centripeta che lo trascina verso il Sole. Non esiste più un forza centrifuga che le si oppone (la velocità tangenziale è andata a zero).

Costruiamo, allora un'orbita fittizia che abbia il Sole al cento della circonferenza rossa. Il suo raggio è la metà di quello originario. A noi interessa poco la traiettoria circolare rossa, dato che la Terra non può certo percorrerla, ma il fatto che ad essa si applica la terza legge di Keplero. Essa dice che il periodo orbitale è funzione solo e soltanto del semiasse maggiore.

Cosa succede se lasciamo il semiasse costante e aumentiamo l'eccentricità? Beh... il Sole S' (puntino nero) si deve spostare verso sinistra, dato che deve essere nel fuoco dell'ellisse. Più aumento l'eccentricità e e più il Sole si avvicina al bordo sinistro dell'ellisse sempre più schiacciata. Per un certo valore di e l'ellisse è così stretta che il sole S' entra all'interno del Sole vero S. Non abbiamo praticamente bisogno di andare oltre... Siamo riusciti a fare impattare la Terra vera (in caduta libera) con il Sole vero. A noi interessa il tempo impiegato e questo tempo non è altro che metà di quello necessario a percorrere qualsiasi ellissi rossa (il semiasse non è cambiato!). Conoscendo il semiasse, la terza legge di Keplero ci fornisce un tempo di impatto più che soddisfacente!

Ricapitolando:

La durata della caduta è proprio la metà del periodo di rivoluzione, dato che il Sole ingoia la Terra proprio poco prima dell’arrivo al perielio. Con questa scelta di partenza diventa poco importante che tipo di orbita descriva veramente la Terra, a noi basta calcolare metà del periodo, che è funzione solo e soltanto del semiasse maggiore e non dell’eccentricità orbitale. Tutte le orbite descritte nella Fig. 1 hanno lo stesso periodo e la stessa energia, dato che hanno lo stesso semiasse… La traiettoria non sarà quella reale, ma il tempo necessario sicuramente sì.

Non sarebbe nemmeno impossibile introdurre un’ellisse degenere, tale da avere un semiasse finito e un’eccentricità uguale a 1, ossia una vera e propria traiettoria rettilinea che si svolga tra il punto di partenza della Terra, privata della sua velocità orbitale, e un punto fuoco (Sole) che stia all’altro estremo del segmento rettilineo. Un’orbita decisamente strana che niente ha a che vedere con la parabola e che sarebbe teoricamente possibile, anche se al "perielio" si troverebbe di fronte un punto singolare (velocità infinita...)

Notiamo però che il semiasse orbitale, proprio per lo scopo finale, deve essere la metà di quello dell’orbita terrestre prima dell’incontro con la nube oscura. D’altra parte abbiamo azzerato l’energia cinetica e cambiato drasticamente l’energia dell’orbita (se così vogliamo chiamarla). Per definizione deve cambiare il semiasse…

I calcoli da fare sono veramente banali… soprattutto se si lavora in anni e Unità Astronomiche.

La terza legge di Keplero ci dice che il rapporto tra il quadrato del periodo e il cubo del semiasse è una costante, che possiamo chiamare k.

Presi due pianeti abbiamo, perciò:

P₁²/a₁³ = P₂²/a₂³

E la costante k è, ovviamente, sparita…

Ma, se il pianeta 2 fosse proprio la Terra normale, posiamo porre P₂ = 1 anno e a₂ = 1 UA.  Da cui si ha

P₁² = a₁³

con P₁ espresso in anni e a₁ in UA.

Nel nostro caso a₁ = 1/2

P₁ = 1/√8

Tempo di caduta = P₁/2 = 1/(2√8) anni

Se lo vogliamo in giorni, basta moltiplicare per il numero di giorni contenuti in un anno:

Tempo di caduta = 365. 26/(2√8) ≈ 65 giorni

L’incertezza dipende da molte cose, quali il diametro del Sole e della Terra, ma sono abbondantemente trascurabili rispetto al valore finale ottenuto, in ottimo accordo con quello ricavabile con equazioni differenziali e integrali vari. D'altra parte l'ellissi degenere porta a considerare il "mezzo periodo" un valore assolutamente corretto, dato che il Sole coincide con il perielio e il percorso effettuato è esattamente quello che si cercava.

Nel nostro piccolo, possiamo dire che spesso e volentieri è necessario riflettere e non aver paura a pensare “facile”, sempre che si resti nell’ambito della fisica scientifica. In fondo (con le dovute cautele) è un po’ quello che è successo ad Einstein con la RG e che ha fatto dire a Feynman: “Non è tanto il metodo che mi sconvolge, ma il fatto di averci pensato". Beh… Feynman non è stato da meno con la sua QED.  E noi, nel nostro piccolo abbiamo tranquillamente snobbato derivate e integrali basandoci solo sul quell’antiquato genio di nome Keplero…

Soluzione energetica (Fabrizio) ****

Si può però seguire una logica più precisa, ossia calcolare l’energia iniziale del sistema (solo potenziale) che possiamo scrivere così:

,   dove compaiono la massa del sole, la massa della terra e, a denominatore, il raggio dell'orbita terrestre.

Nella caduta appare anche l'energia cinetica K.  L'energia cinetica e quella potenziale cominciano a giocare come sulle montagne russe (scendi tu e salgo io…), ma l'energia totale rimane costante.

     che espansa diventa

dove v ed r sono la velocità e posizioni della Terra durante la caduta nel sistema di riferimento del Sole.

Ci accontentiamo della approssimazione che trascura l'energia cinetica del Sole poiché .

Dalla relazione trovata si può ricavare v.

, ma v è la derivata di r rispetto al tempo.

che è una equazione differenziale di primo grado.

Integrarla non è semplice. Ci vuole un piccolo trucco, che è spesso utilizzato nei testi di fisica, e qualche buona tabella di integrali o qualche aiuto informatico.

L'obiettivo che abbiamo è quello di trovare il tempo di caduta. Ci servirebbe avere una relazione del tipo t funzione di r, per poi calcolare il tempo che deve trascorrere per andare dal punto iniziale sull'orbita terrestre fino al sole: . Il termine a destra della equazione ottenuta sopra è effettivamente una funzione di r, ma il termine a sinistra non è quello che ci serve. C'è una derivata di r rispetto a t, cioè una r funzione di t. Qui c'è il trucco che dicevo. Una capriola della relazione che facciamo diventare:

Vista sotto-sopra appare quello che cercavamo, una t funzione di r. Il trucco è valido matematicamente. Per trovare il nostro tempo T occorre integrare questa relazione con gli estremi di integrazioni corrispondenti in termini di t ed r. Vale a dire per e per

Qui per risolvere l'integrale conviene ricorrere alle tabelle o ad altri strumenti.

Il risultato per l'integrale indefinito .

Calcolato nei due estremi di integrazione è: per e 0 per

Quindi

Attenzione all'equazione che lega tempo e spazio... potrebbe già far sollevare le sopracciglia a qualcuno molto preparato... come Umberto...

Soluzione numerica  (Maurizio, Paolo)

Non è meno interessante un approccio a piccoli passi, che mantenga costante l’accelerazione per tratti sufficientemente piccoli (il computer può farlo per intervalli infinitesimi, come nel calcolo di orbite perturbate). Benché apparentemente più approssimato, permette la derivazione della curva oraria…

Soluzione di Paolo  ***

Cosa succede alla Terra se la sua velocità orbitale si azzera?

Semplice, l’orbita della Terra è il risultato di un equilibrio tra la sua velocità tangenziale (che è la reale causa della fittizia forza centrifuga) e l’accelerazione di gravità esercitata dal Sole.

Se non ci fosse il Sole la Terra proseguirebbe dritta per la sua strada.

Ma il Sole c’è eccome, per cui il “rettilineo” movimento della Terra subisce una forza centripeta che ne modifica la traiettoria ed il nostro pianeta finisce per orbitare intorno al Sole.

Se il “rettilineo” movimento della Terra si dovesse arrestare, ossia se la sua velocità tangenziale divenisse uguale a zero, il nostro pianeta subirebbe solo ed esclusivamente la forza centripeta di gravità, esercita dal Sole, per cui la sua traiettoria sarebbe diretta verso il Sole a causa dell’accelerazione di gravità.

Insomma la Terra si comporterebbe come un sasso fermo, lasciato cadere da una certa altezza, che si dirige verso il suolo, esclusivamente accelerato dalla gravità della Terra.

Quanto tempo impiegherebbe la Terra per schiantarsi sulla superficie del Sole?

Per rispondere a questo quesito, senza imbarcarsi in complesse equazioni differenziali  e senza scomodare la terza legge di Keplero, è possibile tentare un approccio che seppur approssimativo è in grado di restituire un risultato abbastanza affidabile.

Innanzitutto è bene ricordare che la forza di attrazione gravitazionale è uguale a:

F = GMm/r²

Dove

G è la costante di gravitazione universale = 6,67 x 10^-11 m³/Kg s²

M è la massa del Sole = 1,9885 x 10^30 Kg

m è la massa della Terra = 5,972 x 10^24 Kg

r è la distanza tra Sole e Terra

Per trovare l’accelerazione di gravità a cui è sottoposta la Terra, basta ricordare il secondo principio della dinamica:

F = m a

a = F/m = GMm/mr²

a = GM/r²

Ovviamente dato che la Terra all’inizio è ferma, la distanza r dal Sole varia continuamente con lo scorrere del tempo, dato che la Terra continua a muoversi verso il Sole a causa della forza di gravità.

Ne segue che anche l’accelerazione cambia continuamente, pertanto il movimento della Terra non è assimilabile ad un moto uniformemente accelerato, poiché l’accelerazione cresce man mano che la distanza dal Sole diminuisce.

Avendo a che fare con un’accelerazione variabile, per affrontare il problema, conviene scomodare anche la legge della conservazione dell’energia.

L’Energia totale in gioco è data dalla somma tra l’energia potenziale e quella cinetica, ossia:

Etot = Epot + Ec

Epot = -GMm/r

Ec = ½ m v²

Etot = -GMm/r + ½ m v²

All’inizio, la Terra è ferma alla distanza ri di 1 UA (149 597 870 700 metri), per cui la sua velocità è zero e di conseguenza anche la sua energia cinetica è nulla:

Ec = ½ m v² = ½ m 0² = 0

Pertanto l’Energia Totale è uguale a quella inziale di potenziale:

Etot = -GMm/ri

La Fig. 2 mostra la situazione iniziale, con l’indicazione dell’accelerazione di gravità a cui è sottoposta la Terra e dell’Energia totale in gioco.

Figura 2

Ovviamente l’Energia totale si deve conservare, per cui man mano che la Terra si avvicina al Sole, acquista velocità e di conseguenza energia cinetica, sottraendola a quella di potenziale:

Etot = -GMm/rn + ½ m v²

Dove rn è la distanza Sole Terra, mentre la Terra si avvicina al Sole.

Considerato che Etot = -GMm/ri (questa è l’energia in gioco all’inizio, che si deve conservare)

-GMm/ri = -GMm/rn + ½ m v²

-GMm/ri + GMm/rn = ½ m v²

-2GMm/m ri + 2GMm/m rn = v²

-2GM/ri + 2GM/rn = v²

v² = -2GM rn + 2GM ri/(ri rn)

v² = 2GM (-rn + ri)/(ri rn)

v = √2GM (ri -rn)/(ri rn)

Ricordando quanto trovato prima, ossia a = GM/rn ² è possibile calcolare sia la velocità della Terra sia l’accelerazione mentre questa si muove verso il Sole, fissando una serie di distanze rn dal Sole.

La fig. 3 mostra velocità ed accelerazioni della Terra, dalla posizione iniziale (distanza ri = 1 UA) ad intervalli di 10 milioni di km, fino alla sua collisione con la superficie del Sole (in questo caso rn = raggio del Sole, ossia 696 000 000 metri).

Figura 3

Guardando la figura (ovviamente Terra e Sole non sono in scala) si nota che anche quando la Terra si trova a 10 milioni di Km dal Sole l’accelerazione di gravità è circa 1/7 di quella avvertita sulla superfice terrestre (a= 1,4397 m/s²), mentre quando il nostro pianeta raggiunge la superficie del Sole l’accelerazione aumenta notevolmente (a=273,79 m/s²) e la sua velocità è uguale a 615 911 m/s.

Forse qualcuno si chiederà a cosa possa servire tutto ciò, visto che in nessuna delle due formule compare il tempo.

L’accelerazione, però, non è altro che la variazione di velocità nel tempo, ossia:

a = (V-V0)/(t - t0) = ΔV/Δt

Δt = ΔV/a

Dato che l’accelerazione è variabile, per provare a risolvere il problema è possibile calcolare l’intervallo di tempo riferito a piccoli tratti del percorso di avvicinamento della Terra verso il Sole, per poi sommare tutti questi intervalli di tempo e calcolare così il tempo che rimane alla Terra prima della catastrofe.

Pertanto ho suddiviso il percorso in tratti di 1 milione di Km e per ogni tratto ho calcolato il tempo necessario per percorrerlo.

In sintesi applicando la formula V = √2GM (ri -rn)/(ri rn), si calcola la velocità ad inizio tratto (Vi) e quella a fine tratto (Vf) ricavando così la variazione di velocità del tratto di percorso:

ΔV = (Vf -Vi)

Dopodiché, considerato che l’accelerazione ad inizio tratto (ai) è diversa da quella di fine tratto (af), per ridurre l’errore si calcola l’accelerazione media:

a = (ai +af)/2

Infine è possibile ricavare per ogni tratto di percorso il tempo impiegato:

Δt = ΔV/a = (Vf -Vi)/(ai +af)/2 = 2(Vf -Vi)/(ai +af)

Ovviamente, più si considerano dei tratti brevi (anche inferiori a 1 milione di Km), più si limita l’errore, ossia l’approssimazione (usare l’accelerazione media diminuisce l’errore, ma in ogni caso non lo annulla, poiché l’accelerazione è inversamente proporzionale al quadrato della distanza ossia non ha un andamento lineare).

Una volta calcolati i tempi di percorrenza di ogni singolo tratto di percorso basta sommarli tutti per trovare il tempo totale che rimane alla Terra prima della catastrofe.

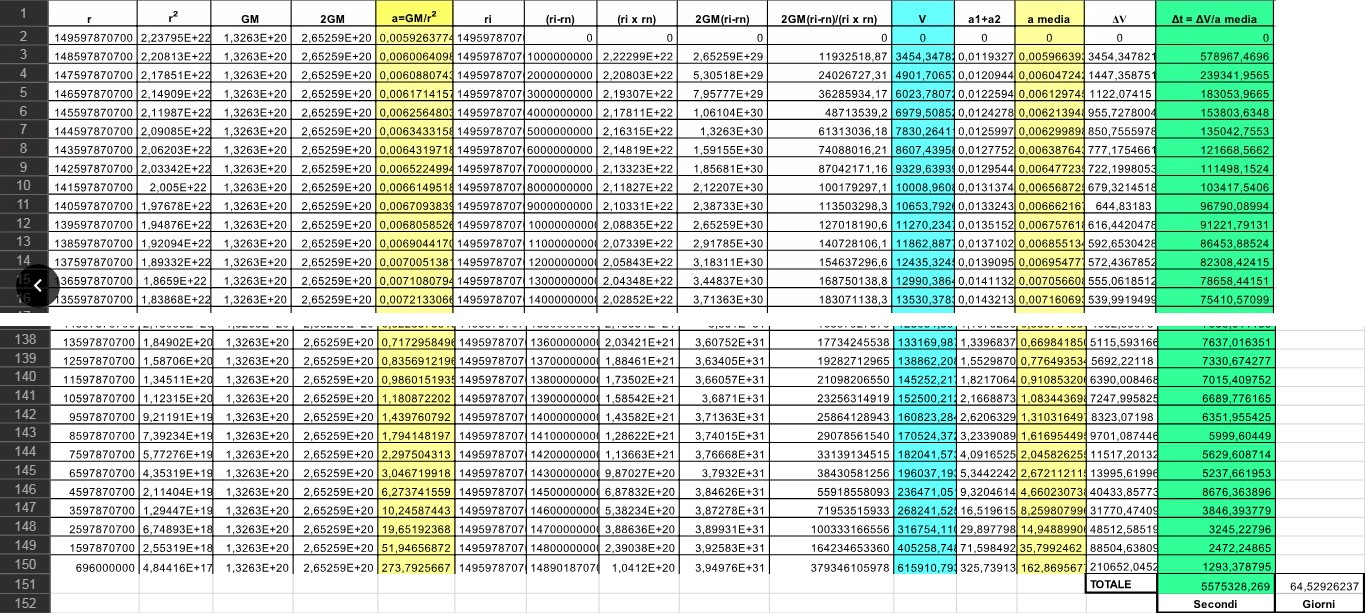
Tale tempo, così calcolato, risulta uguale a 5 575 328 secondi, che è possibile trasformare in giorni con una semplice operazione:

(5 575 328) (1/3600) (1/24) = 64,529 giorni

ecco in dettaglio, le righe di inizio e fine della simulazione ...

La Fig. 4 mostra il percorso della Terra diviso per intervalli di tempo di circa 5 giorni (il primo tratto è di 6,7 giorni e l’ultimo prima dello schianto di soli 2,2 giorni)

Figura 4

Soluzione di Maurizio ***

Non molto dissimile, nella logica, da quella di Paolo, ma con qualche considerazione addizionale su cui vale la pena di soffermarsi.

“Festina lente”, una locuzione latina attribuita ad un imperatore romano, Augusto, rappresenta bene la strategia della caduta, immaginata nel quiz, della Terra sul Sole.

La Terra si “affretta lentamente”, apparente contraddizione che si traduce in un moto iniziale quasi impercettibile che poi assume un ritmo più spedito e solo verso la fine diviene convulso.

Per la maggior parte del tempo (scopriremo alla fine che è circa il 98% ) l'accelerazione a cui è soggetta è di molto inferiore a quel 9,81 m/s² che essa esercita su di noi.

Questa visione di lentezza nell'accelerare, mi ha suggerito di calcolare, dapprima, quanto tempo sarebbe necessario per giungere sulla superficie del Sole se l'accelerazione si mantenesse costante.

Il valore di accelerazione alla distanza di 150 milioni di Km dal Sole è facilmente calcolabile: dipende linearmente dalla massa M del Sole (2*10³⁰ Kg) , dalla costante di gravitazione universale G ( 6,67 * 10^-11 N m²/Kg) e, inversamente, dal quadrato della distanza che è il raggio dell'orbita terrestre R (150 * 10⁹ m). Tutti dati approssimati, senza troppi decimali.

A conti fatti, questa accelerazione è davvero minuscola, 0,00593 m/s².

Se la Terra subisse costantemente l'accelerazione “a”, di poco meno di 6 millimetri al secondo, per secondo, il tempo di percorrenza della distanza “R” sarebbe dato dalla radice quadrata di 2R/a e varrebbe, quindi, 7.112.680 secondi , corrispondenti a 1976 ore o, se preferite, a 82 giorni e 8 ore.

Ma questo tempo non è quello vero, perché vero NON è il fatto che l'accelerazione è costante.

L'accelerazione cresce istante per istante, a causa della diminuzione della distanza , via via che il movimento di caduta procede.

Cosa rappresentano allora quei sette milioni di secondi? Sono solo un valore al di sotto del quale si colloca il tempo di caduta reale. Non possiamo sperare di avere a disposizione un tempo maggiore per fare i nostri conteggi.

Sulla base di questo limite ho pensato di simulare la caduta, iterando il calcolo ad intervalli molto ravvicinati, ovviamente in relazione al tempo complessivo. Ecco perché occorreva avere una sensazione, almeno grossolana, di questo valore.

A fronte di milioni di secondi, analizzare la situazione ogni 100 secondi potrebbe essere una ragionevole scelta per avere una fitta trama di campionamento efficace, almeno fino alla fase concitata del collasso finale.

La ripetizione del calcolo a intervalli regolari di tempo corrisponde a ipotizzare un'accelerazione costante in quell'intervallo ed una velocità crescente linearmente, da un valore iniziale, fino a raggiungere un valore finale, al termine dell'intervallo. In base al valore iniziale della velocità e alla accelerazione costante si determina lo spazio percorso. Nell'intervallo successivo la distanza sarà quindi ridotta di tale valore e l'accelerazione maggiorata in ragione dell'inverso del quadrato della attuale posizione; la velocità iniziale di questa fase coinciderà con quella finale del precedente intervallo e con questi valori si potrà procedere alla nuova iterazione.

Non è altro che l'espediente di linearizzare una curva con una spezzata poligonale, il cuore del ragionamento che ha portato Newton e Leibniz a contendersi aspramente la paternità del calcolo infinitesimale.

Passo dopo passo, giungeremo a coprire la distanza di 150 milioni di Km, fermandoci nel calcolo alla minima distanza possibile dalla superficie del Sole, il cui raggio è di 700.000 Km.

Ecco in sintesi, colonna per colonna, l'organizzazione che si può dare ad una generica riga di iterazione:

distanza residua = distanza residua precedente – distanza coperta riga precedente

accelerazione = 2*6,67 * 10^(30-11) / distanza residua²

intervallo dt = 100 secondi (costante)

velocità finale = velocità finale precedente + accelerazione* dt

distanza coperta = velocità finale precedente* dt + 0,5 accelerazione* dt²

tempo cumulato = tempo cumulato precedente + dt

spazio cumulato = spazio cumulato precedente + distanza coperta

Nella riga iniziale i dati saranno impostati come segue:

distanza residua = 150 * 10⁹

accelerazione = 2*6,67 * 10^(30-11) / distanza residua²

intervallo dt = 100 secondi (costante)

velocità finale = velocità finale precedente ( = 0) + accelerazione* dt

distanza coperta = velocità finale precedente ( = 0) * dt + 0,5 accelerazione* dt²

tempo cumulato = tempo cumulato precedente ( = 0) + dt

spazio cumulato = spazio cumulato precedente ( = 0) + distanza coperta

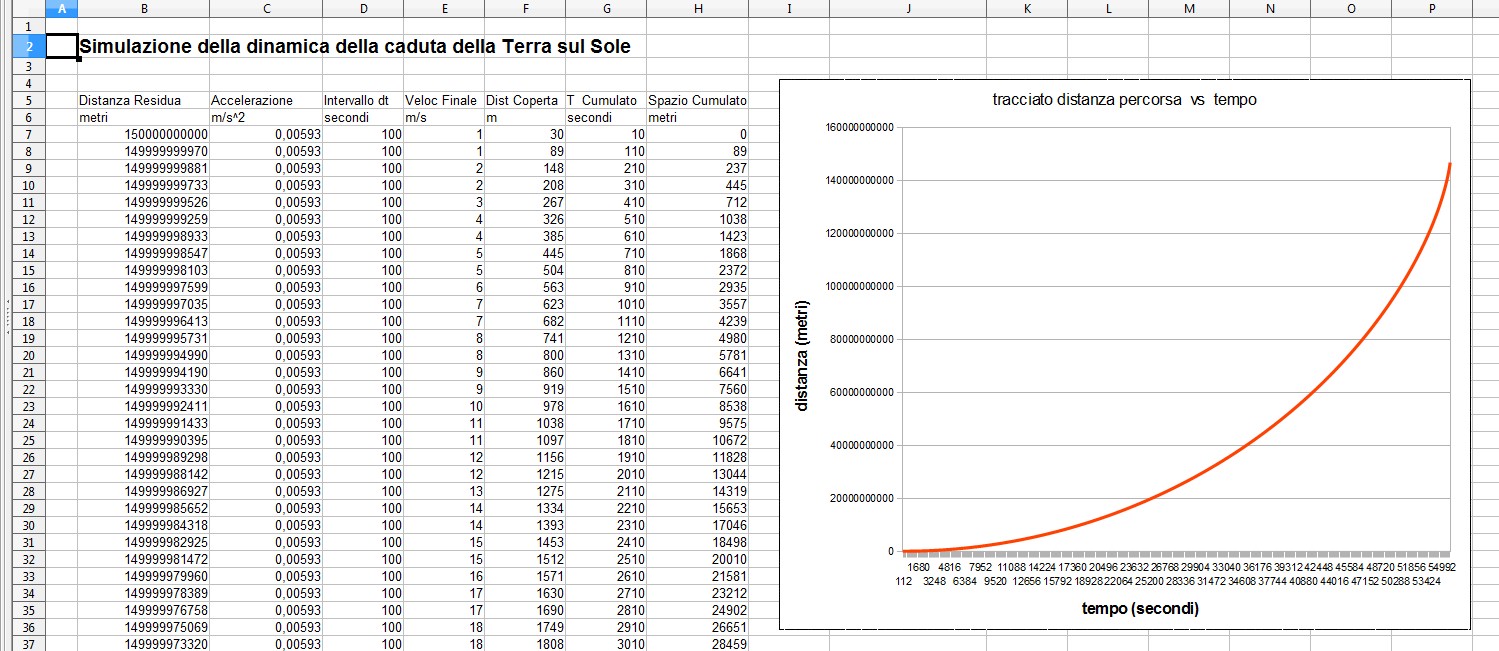
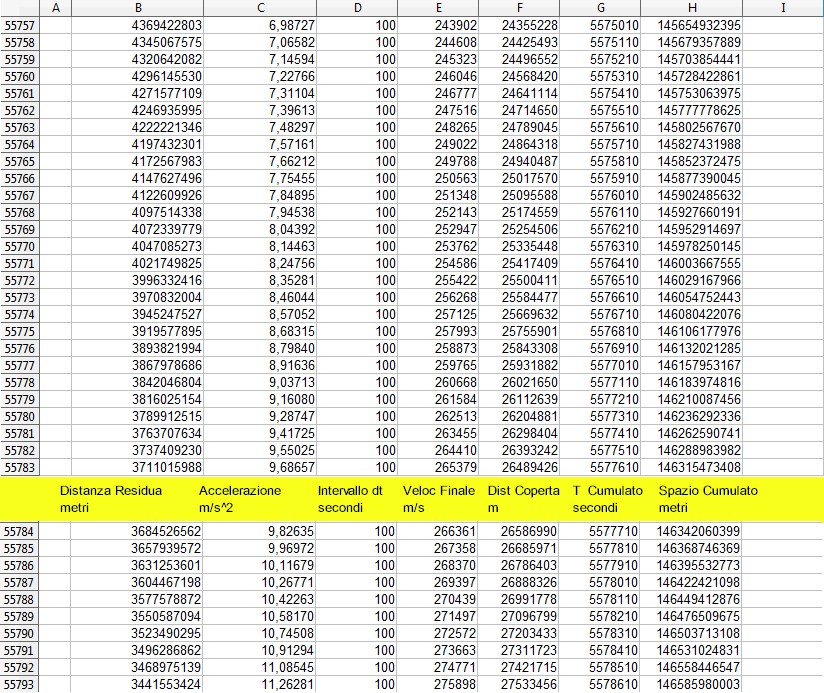
Ecco come appare l'inizio della simulazione....

E qui vediamo come si conclude...

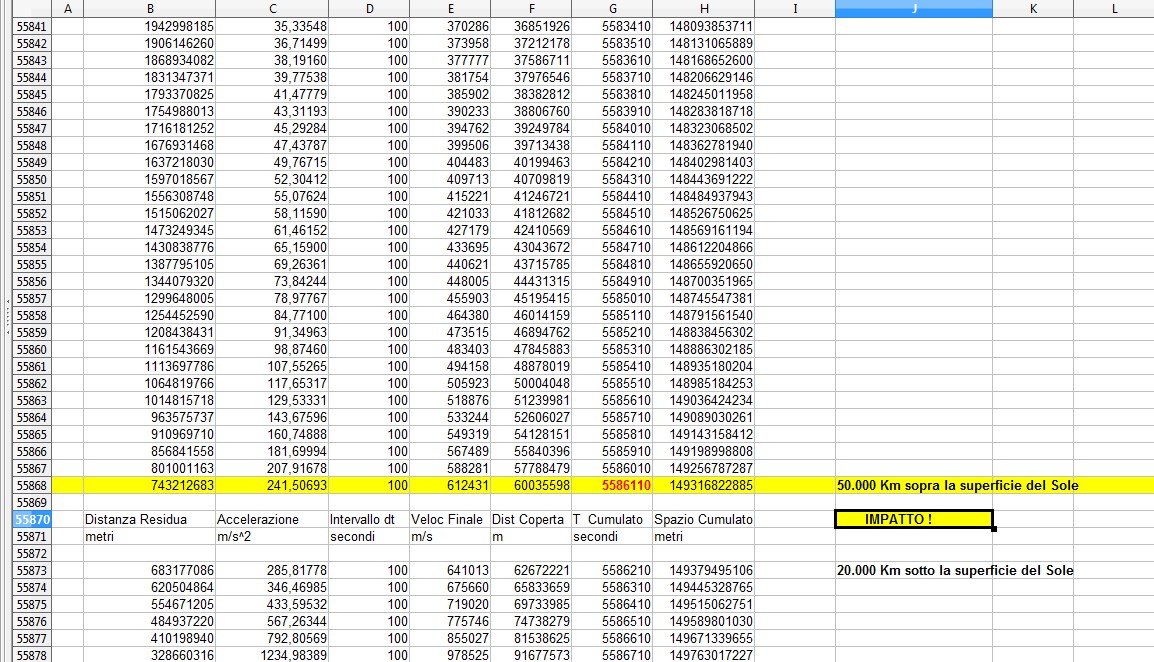
La riga scelta per la conclusione del calcolo, evidenziata in giallo, è quella in cui la distanza della Terra dalla superficie del Sole si è ridotta a 50.000 Km; la riga successiva rappresenta la situazione entro il “cratere” di profondità 20.000 Km prodotto dall'impatto della terra con il “suolo”, se cosi possiamo chiamarlo, solare.

Come si può facilmente vedere, dopo avere percorso 149.300 milioni di Km, la terra è soggetta ad una accelerazione compresa tra 241 m/s² ( a quota 50.000 km) e 285 m/s² ( a quota – 20.000 Km), quella al suolo è in realtà 274 m/s².

Per quanto riguarda la velocità finale di impatto, a 50.000 Km dal suolo è di 612,4 Km/s, non molto lontana da quella di fuga dal Sole, di 617,3 Km/s.

A questo punto il valore del tempo cumulato, ossia la durata della caduta su Sole è valutata in 5.586.110 secondi, ossia 64 giorni e 15 ore, valore ovviamente al di sotto di quella stima grossolana iniziale di 7 milioni di secondi, “sbagliata” del 27 % in più.

Scorrendo la cronaca della catastrofe annunciata, troveremmo nella riga 55.784 , corrispondente ad un tempo trascorso di 5.578.400 secondi la accelerazione 9,82 m/s² che suona tanto familiare alle nostre orecchie per essere quella del nostro pianeta.

In altre parole, dopo 64 giorni, a poche ore dall'impatto, la Terra ha percorso “lentamente”146 milioni di Km verso il Sole e, al momento, subisce una attrazione (verso il Sole) che è quella stessa che la Terra stessa esercita tutti giorni su di noi. Tutto succede nelle successive 15 ore. Se nei due mesi precedenti non si è molto affrettata nel suo avvicinamento, ora vede il traguardo a pochi milioni di Km. Questi ultimi 3 milioni di Km, questo ultimo 2% di percorso che le resta da compiere, intende coprirlo con un rush finale che in mezza giornata raddoppierà la velocità che ha acquisito nei due mesi precedenti. Un finale davvero travolgente. Il grafico della variazione della gravità si può vedere nell'articolo sulla Terra attraversata da un sasso (Fig. 10).

In poche ore l'accelerazione salirà da 9,82 m/s² a 274 m/s². Se qualcuno ha ancora voglia di fare calcoli può contare su una quindicina di ore per trarre i suoi pronostici. Poi basta.

Veniamo ora al grafico inserito nella prima figura, quello che rappresenta la curva dello spazio percorso nel tempo, insomma l'andamento della velocità di caduta.

Appena l'ha vista l'amico Pautasso ha esclamato: “non sarà mica un cicloide... neh?” Ovviamente Oreste è una persona incline a riconoscere marroni, tartufi e altre cose mangerecce, ma per le curve matematiche non è una fonte molto affidabile. Tuttavia la medesima idea, quasi una premonizione, l'hanno avuta anche altre persone ben più smaliziate come Vincenzo e Umberto.

Ma come dimostrare analiticamente che questa curva …

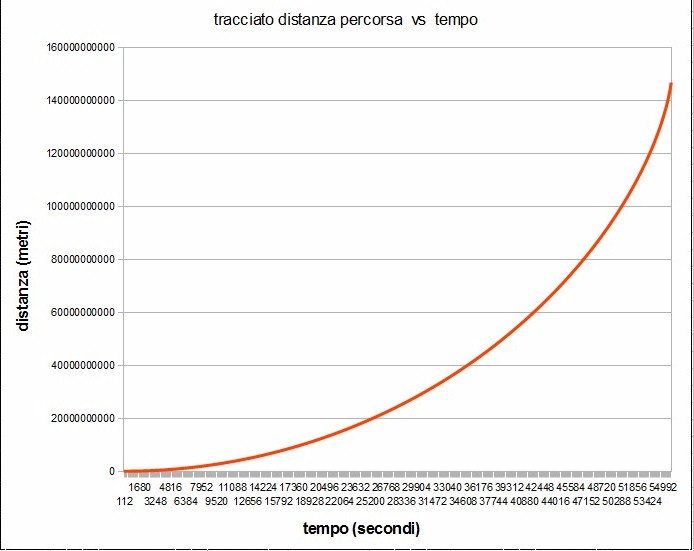
….. questa curva, così allusiva, così seducente, è proprio una cicloide?

Per dimostrarlo analiticamente occorrerebbe svolgere un lavoro piuttosto pesante, certo.

Ma con l'aiuto di macchine come quelle che sognava Leibniz, masticatrici di numeri , si potrebbe almeno provare a farsi qualche idea.

Si potrebbe, ad esempio, valutare la separazione di questa curva con una cicloide cucitale addosso.

Ecco, l'equazione cartesiana della cicloide è la seguente:

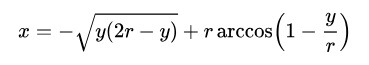
Se preferite, si può scambiare la x con la y , così …

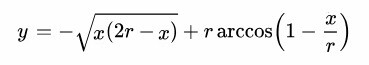
e vedere il grafico della cicloide ruotato di 90°.

Ora scriviamo una colonna per la x e una colonna per la y, poi variamo la x da zero a qualcosa, che comunque non può superare il doppio di r, e vediamo la curva che viene fuori.

Eccola qui..

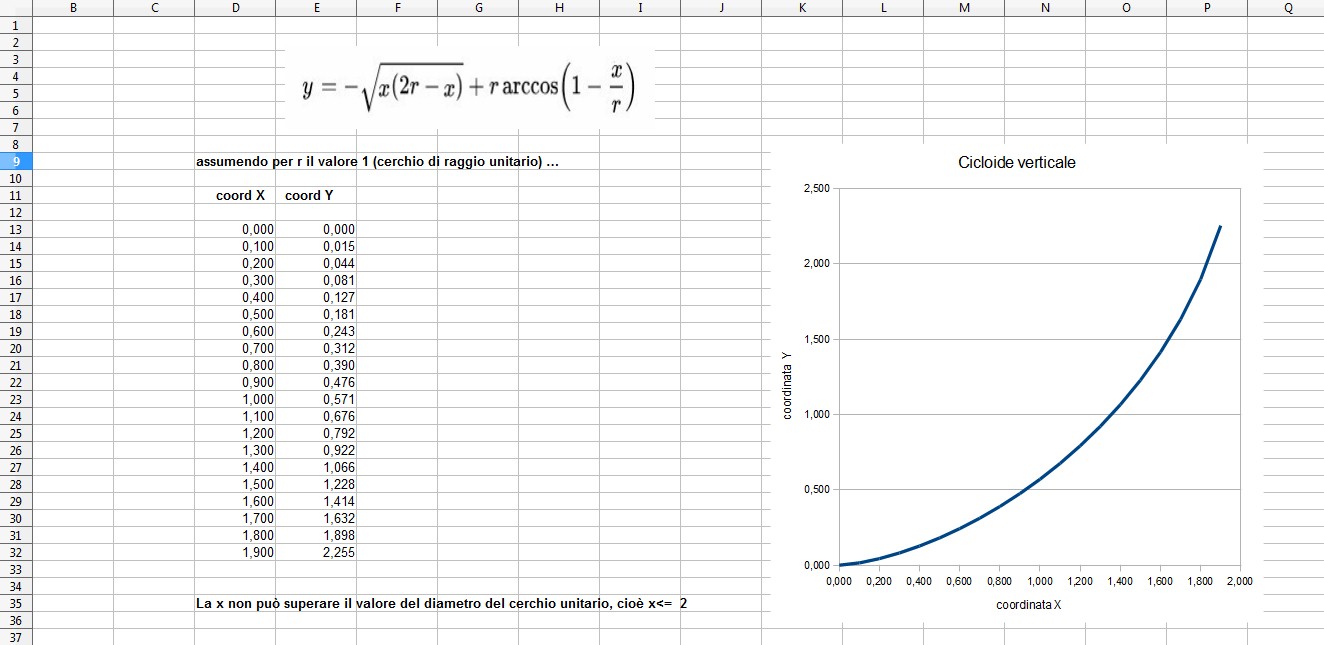
Come comparare le due curve ?

Pautasso sostiene che è sufficiente ricercare una sovrapposizione, imponendo che i punti di origine siano sovrapposti, amplificare o ridurre le scale di una figura , riallineare nuovamente i punti di origine, fino a ottenere la migliore sovrapposizione. Sarà così ?

Possiamo provare...

Questa è la sovrapposizione della cicloide (con l'aggiunta della sua costruzione grafica ) e della curva oraria relativa alla caduta del nostro pianeta sul Sole, ottenuta dalla simulazione.

Dopo avere fatto coincidere le origini delle curve nel punto Po non è stato difficile amplificare il tracciato della curva oraria fino a raggiungere l'ingrandimento opportuno per il confronto.

In trasparenza si vede che le due curve hanno un andamento del tutto compatibile.

Ancora una volta la cicloide emerge dal suo cammino carsico che attraversa vaste aree della matematica e della fisica. Riusciremo mai a comprenderla fino in fondo?

Una curva matematica che sembra assumere un ruolo fondamentale nella fisica.

Maurizio ha gettato il sasso nello stagno (e mai gettare un sasso ha avuto tanta importanza) ed è subito stato raccolto da Umberto che ha iniziato a verificare il tutto attraverso equazioni rigorose. Poi, il caro vecchio internet (utilissimo, quando viene usato correttamente), ci ha fornito la soluzione definitiva su un piatto d 'argento: la legge oraria della caduta libera dovuta alla forza di gravitazione (con tanto di accelerazione variabile, i.e. che va con l'inverso dl raggio al quadrato) è veramente una cicloide. QUI trovate il link risolutivo.

Un'attenta riflessione, che ha innescato uno scambio di idee e di ipotesi da capogiro tra gli autori di questo articolo, ha convenuto che la cicloide sia veramente una curva molto speciale, per come vanno le leggi dell'Universo e in particolare quelle legate alla gravità. Tra parentesi, sembra che anche utilizzando la Relatività Generale  e la sua curvatura spazio temporale si arrivi alla stessa conclusione (non chiedeteci di provarlo...). Una curva che non è solo una traiettoria effettiva, ma anche una curva spaziotemporale di primaria importanza.

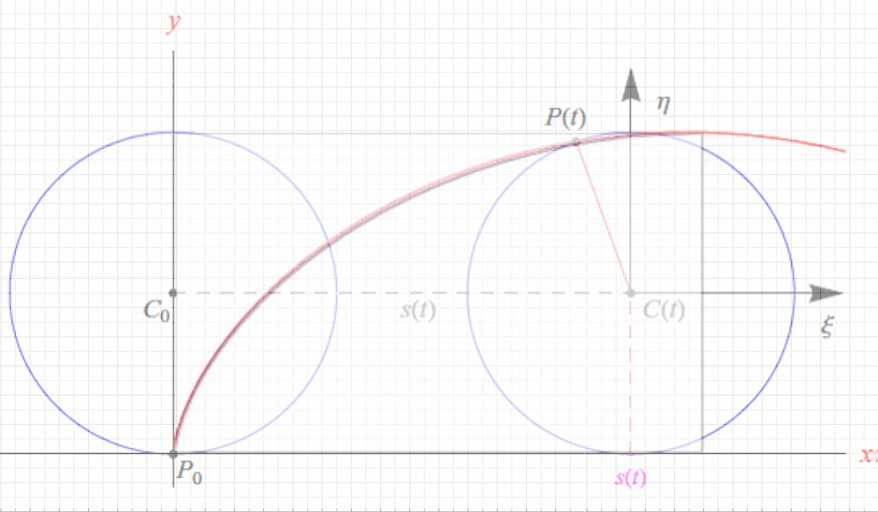
Diciamo solo qualche parola in più sulla cicloide. Essa è una traiettoria importantissima nel piano cartesiano  a causa delle sue  caratteristiche uniche. Per saperne di più, chiedete ad Achille e alla tartaruga sugli sci e all'orologio a pendolo veramente perfetto . Cose queste che mediamente sono ben conosciute. Molto meno si sa sulla curva cicloide intesa come legge oraria, ossia legata alla variazione dello spazio rispetto al tempo.

Parlando di catastrofi terrestri, abbiamo messo in luce che è proprio lei che caratterizza il moto di caduta libra. La tanto celebre parabola è una brutale approssimazione legata all'assunzione di un'accelerazione costante. Come dice Umberto, se una curva può essere approssimata da tanti piccoli trattini rettilinei, una cicloide può essere approssimata da tanti piccoli trattini "parabolici".

Dato che la gravità e i moti ad essa relativi fanno parte dell'essenza stessa dell'Universo, non pensiamo di sbagliare di molto nel dire che l'importanza della cicloide va ben oltre le sue caratteristiche geometriche e matematiche, ma diventa un'entità fisica a tutti gli effetti. Ovviamente, non è solo la gravità che è legata alla cicloide, ma tutto ciò che vede un'accelerazione che va  col'inverso del quadrato della distanza (la fisica parla sempre il linguaggio matematico...).

Non dimentichiamoci, però, del sasso che attraversa la Terra. Una legge del moto molto particolare, ma... -guarda caso-  qualsiasi sia la lunghezza del buco, il tempo impiegato a percorrerlo rimane sempre uguale... proprio quello che succede su una traiettoria a forma di cicloide (ma, in questo caso, la legge dell'accelerazione è completamente diversa).  Inoltre, si può anche pensare, senza grossi sforzi concettuali, che se considerassimo il Sole fatto di gomma perfettamente elastica tutto il moto di caduta libera sarebbe seguito da una curva oraria uguale e contraria, ossia si completerebbe la cicloide e avremmo un moto perfettamente armonico...

Fermiamoci qui... la faccenda acquista risvolti che andrebbero analizzati con molta più attenzione e riflessione (e vista la "carica" di Maurizio non è impossibile che ci si ritorni sopra, pensando a un Sole bucato al centro...). Resta il fatto che anche la cicloide sta diventando un vero prezzemolo cosmico...

Un'ultima considerazione che dovrebbe far piacere a tutti i lettori e gli autori del Circolo. Ancora una volta, un problema piuttosto ben definibile e risolvibile ha dato il via a una serie di commenti e di ragionamenti che lo hanno fatto diventare qualcosa di ben più generale. Dobbiamo esserne fieri tutti quanti! Però... che fatica!

Ora non vi resta che rimanere sintonizzati, in attesa della seconda parte di "Fermate il mondo, voglio scendere!", in cui sarà la rotazione a fermarsi... Prima, però, su richiesta di quello straordinario personaggio che è Pautasso (scarpe grosse e cervello fine)  sarebbe bene raccontare brevemente cosa succederebbe fisicamente alla Terra e ai suoi abitanti in questi terribili 65 giorni di caduta... Gli dedichiamo un articoletto separato (1bis) per non ingigantire troppo questa trattazione che sta veramente arrivando al limite dei 65 giorni!