Il presente articolo è stato inserito nelle pagine di approfondimento della Fisica classica e della Meccanica celeste.

 

Parlando di formazione stellare siamo obbligati a scontrarci con il teorema del viriale. Poi, però, ci accorgiamo che esso può essere applicato a moltissimi casi che sembrano avere poco a che fare con l'astrofisica stellare fino a utilizzarlo per trovare, con grande eleganza, la terza legge di Keplero. Noi lo applicheremo anche a un caso di moto molto particolare. Insomma, il viriale è proprio un must!

Immaginiamo di avere un numero enorme di particelle in grado di muoversi disordinatamente, in uno spazio delimitato, sotto l’effetto di una forza che vari in modo ben stabilito con la distanza. Sicuramente una situazione che l’Universo conosce molto bene a qualsiasi scala di grandezza. Bene, il Sig. Clausius, nel 1870, formulò per la prima volta un teorema estremamente semplice nella sua formulazione, chiamato del viriale, da “vis” latina, che significa forza, energia… Egli stabilì (e dimostrò) che, per ottenere l’equilibrio  del sistema, l’energia cinetica media delle particelle deve essere uguale alla metà della loro energia potenziale. A seconda della forza che agisce può comparire il segno più o il segno meno, ma la formula può essere scritta con un’espressione veramente elementare:

2K + U = 0         (K energia cinetica e U energia potenziale)

Normalmente nei fenomeni cosmici la forza che crea il campo e regala l’energia potenziale è quella gravitazionale e quindi il segno è quello che risulta nella formula appena scritta. Anche senza entrare in termodinamica e in meccanica quantistica, il teorema del viriale è, perciò, proprio come il prezzemolo e si applica alle masse collassanti verso una protostella, agli ammassi aperti e globulari, alle galassie e agli ammassi di galassie. Cambiano, di volta in volta, le particelle che vanno dagli atomi alle stelle e alle galassie.

In poche parole, il teorema del viriale stabilisce l’equilibrio che, nel caso di una stella in formazione, è dovuto al moto frenetico delle particelle che si oppongono con la loro pressione alla “caduta” gravitazionale. Proprio nella formazione stellare, il viriale trova il suo più celebre campo di applicazione, ma può essere estrapolato e mofidicato un po’ ovunque nei vari campi della fisica. Oltretutto, esso continua a valere anche se le particelle si riducono di numero, diventando anche una sola. L’importante è che si cerchi l’equilibrio tra energia cinetica ed energia potenziale quando agisce una forza conservativa (ossia il lavoro dipende solo dal punto di arrivo e di partenza).

Malgrado la semplicità della formula, la dimostrazione generale del teorema non è facilissima. Proprio perché lavora con  grandi numeri, ha bisogno di fare medie e sommatorie, sfruttando le loro proprietà. Ciò si traduce in integrali più o meno semplici. In questo articolo ci limiteremo ad affrontare il problema nel caso generale della formazione stellare e a impostarlo sufficientemente per comprendere come può essere risolto. Lo dimostreremo, invece, nel caso del moto di un pianeta attorno al Sole, trovando quasi “per miracolo” la terza legge di Keplero. Risolveremo, infine, un quiz dinamico con una sola semplicissima formula.

Iniziamo con il caso generale e cerchiamo di costruire una stella partendo da un  numero incredibile di particelle che si attraggono reciprocamente e tendono a collassare verso il centro della massa che si sta agglomerando. La gravità la fa da padrona e niente sembrerebbe in grado di fermarla, se non la resistenza stessa della materia. Ma noi vogliamo costruire stelle normali e non di materia degenere già prima di cominciare! Ci vuole qualcosa che si ribelli alla gravità e che mantenga un certo equilibrio nella massa che continua a cadere sulla stella in formazione.

La reazione viene creata dalla stessa forza che cerca il collasso. Le particelle sono costrette a muoversi in modo disordinato in questa corsa al massacro e quindi acquistano velocità elevate, creando ostacoli materiali alle particelle che continuano a precipitare. In poche parole esercitano una pressione che contrasta la gravità. La pressione è, in pratica, data dall’energia cinetica delle particelle, mentre la capacità di “spingere” verso il centro è data dall’energia potenziale della singola particella.

Non si sono ancora innescate reazioni nucleari che aiutino la pressione ed essa, per adesso, è dovuta solo e soltanto all’energia cinetica, ma la stella se la cava abbastanza bene. Non ci resta che trovare l’equilibrio e vedere come queste energie si distribuiscono. Il teorema del viriale è tutto qui…  Chi vuole saperne di più, relativamente alla nascita delle stelle e alle sue limitazioni e/o applicazioni successive, può rivolgersi al libro “Il Gioco delle Stelle”…

Impostiamo in modo molto semplice la problematica e apriamoci la strada per capire come si può giungere alla fine, nel caso più generale. In pratica, vogliamo stabilire le condizioni di equilibrio in un corpo collassante. In Fig. 1 mostriamo un cilindretto di gas soggetto alla forza gravitazionale che lo spinge e alla pressione che la fronteggia. Queste due grandezze devono essere uguali e contrarie (un  po’ come la forza centripeta e quella centrifuga… tanto per anticipare le cose…).

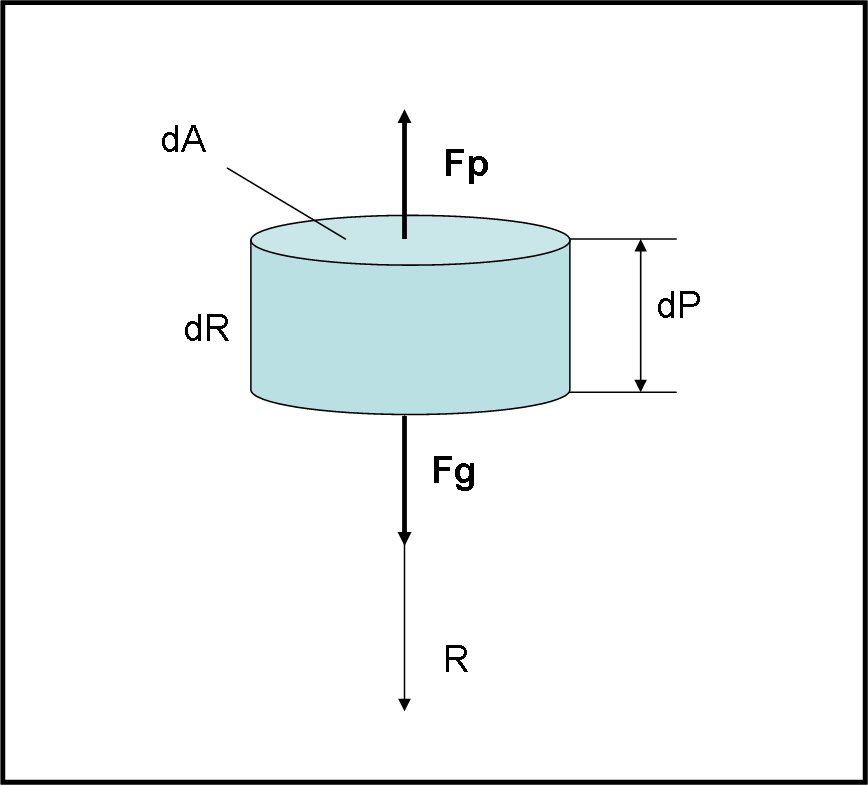
Il cilindretto ha un certo volume dA dR e quindi una massa dm = dA dr ρ, dove ρ è la densità.

La forza di gravità a cui è soggetto il cilindretto è, quindi, data da:

Fg = g dm = g dA dR ρ

La pressione esercitata dal cilindretto (scriviamola proprio come una forza, dato che contrasta quella di gravità) è legata strettamente all’energia cinetica delle particelle e si ottiene facendo la differenza tra la pressione esercitata dalla parte interna del cilindretto e da quella esterna e poi moltiplicandola per l’area della base del cilindretto. Una specie di volume che si oppone all’essere schiacciato. Ossia:

Fp = dA dP

Per ottenere l’equilibrio, le due forze devono essere uguali e contrarie, ossia:

Fp = - Fg

E ancora:

dA dP = - g ρ dA dR

ossia:

dP/dR = - g ρ

Scrivendo g per esteso (in questo caso non può certo essere considerata costante…) si ha:

dP/dR = - GM ρ/R²

Dove M è, ovviamente, la massa della nube collassante all’interno del nostro cilindretto e R è il suo raggio.

Estendendo la relazione a tutta la sfera che avvolge la nube con un po’ di integrali ed esprimendo la pressione in termini di energia cinetica delle particelle (qualche derivata e poco più) si ottiene, finalmente, quanto anticipato:

K = -1/2 U             (K energia cinetica, U energia potenziale)

Poche parole in più per toccare con mano questo equilibrio così importante per le stelle. Se non si verificasse la relazione precedente, ossia se vincesse la forza di gravità, la nube continuerebbe a collassare, mentre se vincesse l’energia cinetica la stella esploderebbe (situazioni che ritroviamo alla fine della vita stellare…).  Se applicassimo la situazione al Sole e immaginassimo che fosse violato il teorema del viriale di solo l’1%, sia a favore della contrazione che dell’espansione, vedremmo variare visivamente il diametro del Sole del 10% all’ora!

Dato che non succede (per fortuna!) siamo sicuri che la nostra stella segue perfettamente l’equilibrio del viriale, sfruttando tutte le sue capacità di trasformare l’energia potenziale in energia cinetica che la tiene a bada (almeno per il tempo necessario all'inizio della fusione del nucleo). Questa energia cinetica prende anche un altro nome e viene chiamata energia termica. In altre parole, la temperatura cresce sempre di più proprio per mantenere l’agitazione necessaria (o viceversa, ma è la stessa cosa).

Devo ammettere che avrei potuto eseguire qualche passaggio in più per mostrare il legame tra “pressione” ed energia cinetica. Bastava considerare la quantità di moto delle particelle, introdurre il lavoro, fare qualche derivata seconda, niente di impossibile per noi. Poi, però, bisognava iniziare a integrare e mostrare che il valor medio di un certo integrale vale zero e le cose ci sarebbero scappate di mano. Accontentiamoci…

Lasciamo le stelle e deduciamo il teorema del viriale nel caso semplicissimo di un pianeta che rivolve attorno al Sole. Si può fare? Direi proprio di sì, dato che esiste una forza conservativa che causa il moto della particella e che il tutto avviene in uno spazio delimitato. Inoltre il moto del pianeta-particella rappresenta proprio la condizione di equilibrio tra la forza di gravità che tende a far cadere la particella verso il Sole e la forza centrifuga che nasce dal moto circolare del pianeta. Abbiamo, perciò, sia l’energia cinetica di rivoluzione (la forza centrifuga) che la forza centripeta gravitazionale. Possiamo applicare il viriale.

Sia m la massa del pianeta che rivolve attorno al Sole di massa M a una distanza R. L’energia potenziale di questo “sistema” è una quantità ben nota a tutti noi:

U = - GMm/R

La forza centripeta che determina questa energia è la forza di gravitazione universale:

Fg = - GmM/R² (metto il segno meno considerando positivo il verso opposto alla direzione del  Sole)

Il pianeta è in equilibrio, nel suo sistema di riferimento, se questa forza eguaglia quella centrifuga. Essa è anche ben nota (ne abbiamo parlato a lungo) e dipende dalla velocità tangenziale di rivoluzione:

Fc = mv²/R

Uguagliando le forze si ha:

Fc = - Fg

ossia:

mv²/R = GmM/R²

e ancora:

mv² = GmM/R    …. (1)

Ma sappiamo anche che l’energia cinetica del sistema è data da

K = ½ mv² 

e, quindi, sostituendo, si ha:

2K = - U

e infine:

2K + U = 0

Che è proprio il teorema del viriale!

Riprendiamo la (1)

mv² = GmM/R   (teorema del viriale)

e moltiplichiamo entrambi i membri per R/m:

v²R = GM

La velocità tangenziale v è legata alla velocità angolare ω (angolo descritto nell’unità di tempo) da una semplicissima relazione che abbiamo già ricavato varie volte:

v = ω R

Sostituendo, si ottiene:

ω²R³ = GM    …. (2)

Questa relazione vale istante per istante, ma possiamo estenderla a tutta l’orbita. La velocità angolare è, allora, data all’angolo completo (2π) diviso per il tempo necessario a compiere l’orbita, ossia il periodo P. La (2) diventa:

4π² a³/P² = GM

Abbiamo sostituito R con il semiasse a, dato che abbiamo considerato l’orbita circolare (ma tutto funziona altrettanto bene con orbite ellittiche)

Tuttavia, la quantità 4π²/GM è una costante C. Da cui:

P² = C a³

Essa si legge: “Il quadrato del periodo di rivoluzione di un pianeta è proporzionale al cubo del semiasse maggiore dell’orbita”

Abbiamo, in poche parole, dimostrato, in modo elementare, che la terza legge di Keplero non è altro che il teorema del viriale applicato al sistema in equilibrio formato da un pianeta soggetto all’attrazione gravitazionale del Sole.

Cerchiamo ora di applicarla a un problemino di dinamica abbastanza interessante. Abbiamo una superficie conica di semi-apertura θ (Fig. 2).

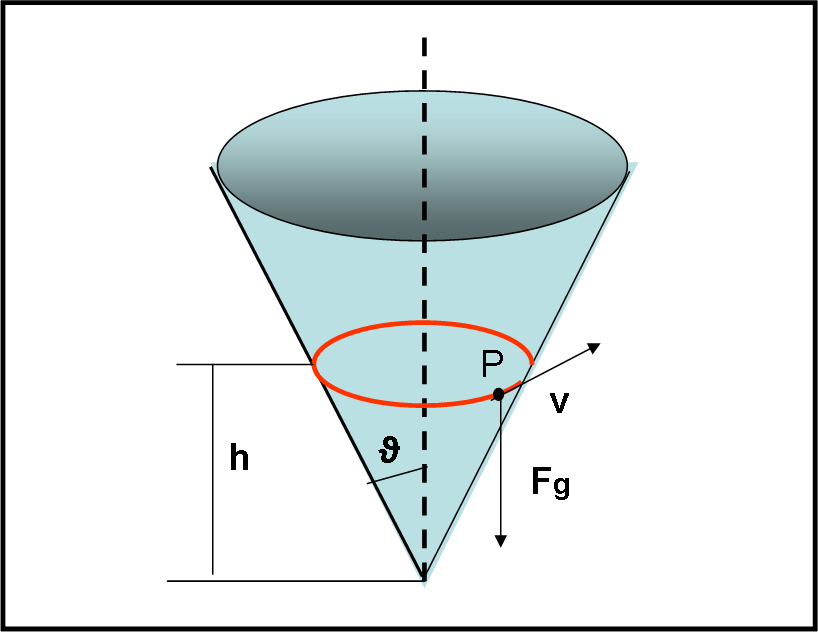
Vogliamo sapere la velocità che deve avere una pallina P per non cadere in fondo al cono e restare a un'altezza h.  La pallina  si muove con una certa velocità v in un campo gravitazionale omogeneo, ossia la forza di gravità rimane sempre la stessa dato che h è costante. Il movimento avviene in un sistema chiuso e delimitato. Possiamo, perciò, applicare il teorema del viriale al sistema pallina, cono, pianeta di massa M. L’energia cinetica del sistema è solo e soltanto quella relativa alla velocità v della pallina. L’energia potenziale corrispondente è sempre la stessa ed è quella dovuta alla gravità del pianeta di massa M.

Basta perciò scrivere il teorema del viriale:

2K = - U

Notiamo che dovremmo scrivere le medie delle energie, ma sia quella cinetica che quella potenziale sono costanti, istante per istante, e, quindi, possiamo evitare l’uso del valore medio.

Ricordando che l'energia potenziale di P vale mgh (m = massa della pallina), il viriale diventa proprio:

mv² = mgh

che dona immediatamente il risultato finale cercato:

v = (gh)^1/2

Lo stesso risultato può, ovviamente, essere trovato utilizzando le forze in gioco, con l’aiuto di un po’ di trigonometria.

La relazione ci dice subito che la velocità rimane costante al variare dell’angolo di apertura del cono, dato che dipende solo e soltanto dalla costante di gravitazione g e dall’altezza h, rispetto al suolo.