Categorie: Articoli Fisica classica Matematica Senza categoria
Tags: cicloide evolvente Huygens pendolo
Scritto da: Maurizio Bernardi
Commenti:0
Si fa presto a dire...Evolvente **/****
Si fa presto a dire Evolvente...
Tre secoli e mezzo fa, Christian Huygens pubblicava quello che può essere considerato il suo capolavoro: Horologium Oscillatorium, un'opera che assieme al Discorso sulle due nuove scienze di Galileo e ai Principa Mathematica di Newton, rientra fra i tre lavori scientifici più rilevanti del 17°secolo.
Nell'Horologium Oscillatorium si parla,tra molte altre cose, di orologi a pendolo e di cicloidi. Perché, Huygens, aveva capito che solo affidandosi al particolare profilo della cicloide si sarebbe riusciti ad ottenere una traiettoria migliore di quella circolare per il movimento del pendolo.
Occorre a questo punto introdurre il concetto di moto oscillatorio armonico ( brevemente "moto armonico") facendo riferimento a questa figura:
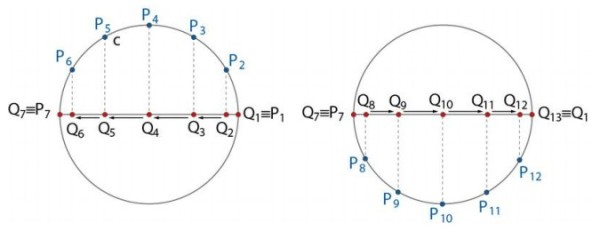

Osserviamo un punto P che percorre la circonferenza ( a sinistra) con velocità angolare costante partendo dalla posizione P1 che coincide con la posizione Q1 sul diametro. Quando il punto P si troverà in P2, la sua proiezione sul diametro sarà in Q2 e quando P passerà per P3, la sua proiezione sarà in Q3... e così via.
Se valutiamo la velocità dello spostamento dei punti Q sul diametro, al procedere del percorso di P, troveremo che per passare da Q1 a Q2 occorrerà un tempo più lungo che per passare da Q2 a Q3 per il fatto che l'inclinazione dell'arco P1P2 è maggiore di quella di P2P3. Questo è vero, in misura ancora più pronunciata nel tratto successivo: l'arco P3P4 ha una componente orizzontale, parallela al diametro, maggiore di prima e quindi la velocità di Q crescerà ancora. Superato il punto P4 , proprio al di sopra del centro della circonferenza, alla velocità massima, inizierà una fase di rallentamento negli archi successivi, fino ad azzerare la velocità nel punto P7, in cui avverrà l'inversione del senso del movimento.
Passiamo quindi alla circonferenza a destra, in cui sono raffigurati i punti da P8 a P12 e le corrispondenti proiezioni di Q fino alla sua sovrapposizione con Q1. Lungo questo percorso di "ritorno" avremo, simmetricamente, una accelerazione avvicinandoci al centro e una decelerazione allontanandocene, fino a "fermarci" per un attimo, nel punto finale, da cui riprenderà il ciclo che abbiamo descritto.
Chi si ricorda del moto oscillatorio sperimentato su di una altalena, sa bene come la velocità è massima nella posizione centrale della oscillazione e subisce un rallentamento nei punti più lontani ( più alti) in cui ci si ferma un istante e si torna indietro. La differenza sostanziale con l'esempio del punto P è che la velocità angolare di una altalena non è costante ma è smorzata dagli attriti. La posizione massima raggiunta cala progressivamente ( in assenza di spinte ulteriori) e l' energia potenziale, partendo da posizioni diverse, è inevitabilmente diversa. Questo non consente di avere una velocità angolare costante. Ergo: il moto non è armonico.
Il pendolo semplice non ha un moto oscillatorio armonico, il periodo delle oscillazioni non è indipendente dalla posizione di partenza. Solo per piccoli angoli di spostamento dalla posizione di equilibrio si può dire approssimativamente che il moto sia armonico, aumentando l'ampiezza delle oscillazioni questa caratteristica viene perduta.
Viceversa il moto che si genera su una traiettoria a forma di cicloide è sempre un moto armonico. La cicloide è Tautocrona. Non importa quanto ampie siano le oscillazioni, il periodo sarà sempre lo stesso, come ora sa bene anche Achille.
Ma come riuscire a ottenere questa traiettoria? la cosa è possibile se il filo che trattiene il peso oscillante viene costretto ad aderire a un profilo che, guarda caso, è identico alla cicloide che verrà descritta dal peso, nella sua oscillazione.
A questo punto è indispensabile chiarire il concetto di curva evolvente e di curva evoluta.
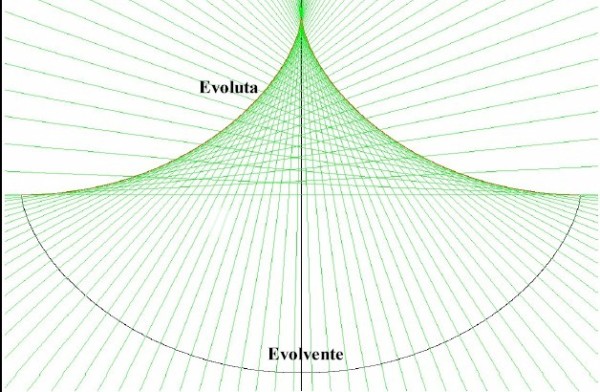
Immaginiamo che lungo il bordo di un disco sia avvolto un filo, diciamo per metà della circonferenza. Una estremità del filo verrà fissata e l'altra solo appoggiata. Ora prendiamo questo capo, mantenendo il filo in tensione, allontaniamolo progressivamente, svolgendolo. Il punto estremo descriverà una curva, via via che il filo si svolge. Questa curva si chiama evolvente, perché evolve dalla sua posizione di aderenza alla curva di origine. Quest'ultima avrà la denominazione di evoluta. Geometricamente il modo migliore per capire come viene descritta l'evolvente è quello di fare riferimento ad una semiretta tangente punto per punto all'evoluta, che, immaginata in tutte le sue possibili posizioni, genera un inviluppo come quello che appare nella figura sottostante.

In generale evoluta ed evolvente sono curve di natura e aspetto diversi. Nel caso del cerchio (evoluta) la curva che si genera (evolvente) sarà una specie di spirale (un esempio di questo genere lo trovate in questo articolo dove si parla di Coriolis).
Solo per pochissime curve, tra cui la cicloide, avremo una perfetta coincidenza di forma e dimensione (non ovviamente di posizionamento) tra evoluta ed evolvente. L'evolvente di una cicloide è una cicloide identica, semplicemente traslata ( con distanze ben determinate) in verticale e in orizzontale.
Quindi se costruisco un pendolo semplice, lascio il filo in posizione verticale e pongo ai suoi lati sinistro e destro due profili di cicloide, quando metterò in movimento il pendolo, il filo si dovrà appoggiare inevitabilmente a questi profili e, distaccandosene non farà altro che descrivere con la sua estremità, a cui è vincolata la massa, la traiettoria della evolvente della cicloide che è essa stessa una cicloide, con il risultato finale di rendere il moto oscillatorio armonico.
Un teorema geometrico che consente di realizzare facilmente questo vincolo è il seguente: “L’evoluta di una cicloide è un’altra cicloide, uguale alla prima, traslata di π lungo l’asse X e di 2r lungo l’asse Y ”.
Tutto questo lo possiamo dimostrare , a partire dalle equazioni della cicloide evolvente, fino ad arrivare a riconoscere nella sua evoluta le medesime proprietà.
In generale l'evoluta di una curva è l'inviluppo delle rette normali alla evolvente. Se pensiamo al caso del cerchio, visto in precedenza, la cosa risulta immediatamente evidente. Ma lo stesso vale anche per le altre curve, in particolare per la cicloide, come potete notare nella figura. La costruzione può essere eseguita molto semplicemente svolgendo un filo inizialmente adagiato sul profilo superiore (evoluta) e segnando, punto per punto il suo estremo libero fino a tracciare la curva evolvente.
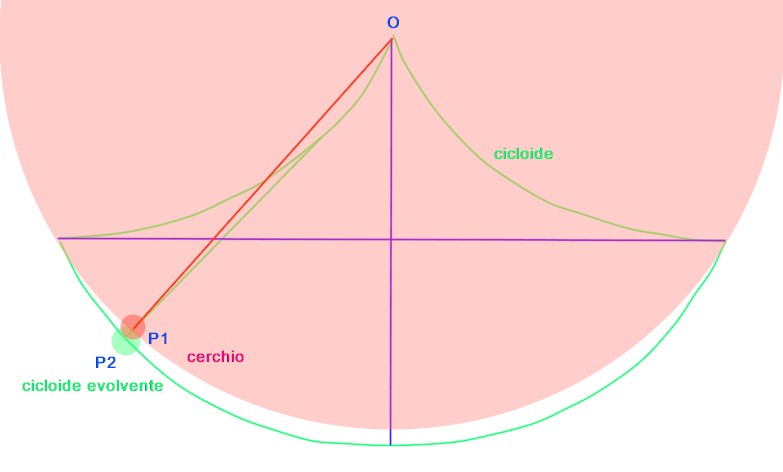
Il confronto di questa traiettoria con l'arco di cerchio percorso dall'estremo di un pendolo, realizzato in questa figura , ci permette di comprendere a livello intuitivo, come la continua variazione della distanza OP2, lunghezza del pendolo "cicloideo", corregga costantemente il periodo in modo da renderlo uniforme, rispetto a quello determinato dalla lunghezza immutabile OP1 del pendolo "circolare".
APPENDICE TECNICA
Le equazioni parametriche di una cicloide ( quella che rappresenta l' evolvente), con la concavità rivolta verso l'alto,
sono le seguenti :
Calcoliamo per queste equazioni i relativi differenziali
il loro rapporto rappresenta il coefficiente angolare della tangente alla cicloide in un generico punto
e l'inverso ed opposto non è altro che il coefficiente angolare della perpendicolare alla cicloide in un generico punto.
possiamo ora scrivere l'equazione della retta normale alla cicloide nel punto individuato dal parametro .
riscrivendo e semplificando come segue
Ora che abbiamo l'equazione della retta normale ad un generico punto della cicloide, ci resta solo da descrivere la collettività di tutte le rette di questo insieme, lungo tutta la cicloide.
Vediamo come si ragiona, in generale, poi torneremo al caso specifico della nostra cicloide.
Supponiamo di avere l'equazione delle rette che formano l'inviluppo in funzione di un parametro "t"
Le funzioni che descrivono le rette devono essere derivabili, il che implica che siano continue e biunivoche: ad ogni valore del parametro t deve corrispondere una retta diversa.
È evidente che ogni retta è tangente all’inviluppo in un punto, ma non sapendo quale punto della retta appartiene all’inviluppo non possiamo ricostruire l’inviluppo.
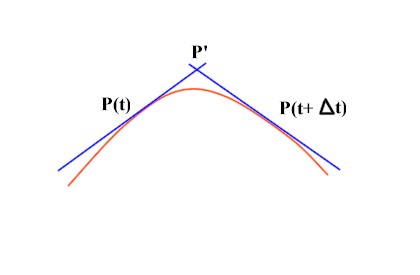
Allo scopo di determinare questo punto sulla retta consideriamo due rette che differiscono di Δt nel valore del parametro t, come nella figura soprastante.
Non sappiamo dove si trovano P(t) e P(t+Δt), ma l’intersezione fra le due
rette nel punto P’ deve essere fra i due punti, e al tendere di Δt a zero P’ deve tendere a P(t).
Scriviamo quindi il sistema fra le equazioni delle rette r(t) e r(t+Δt), che determinerà il punto P’,
Alla seconda equazione di questo sistema sottraiamo la prima e dividiamo per
Facendo ora il limite per , il punto
, mentre la seconda equazione tende alla derivata prima.
Il sistema diventa pertanto il seguente:
La soluzione di questo sistema costituisce il luogo dei punti cercato
Applichiamo ora il metodo appena visto al caso della cicloide:
per ricavare l’equazione dell’evoluta, cioè l’inviluppo dell rette normali all'evolvente che ci consente di costruire l'evoluta, al variare di α, deriviamo la sua equazione rispetto ad α e mettiamola a sistema con se stessa
Proseguiamo ricavando facilmente l'equazione parametrica di x eliminando y.
Moltiplichiamo la prima equazione per e la seconda per
poi sottraiamo membro a membro.
Con analoga procedura a quella seguita per x, potremo ottenere y.
L'equazione della curva generata dall'inviluppo è quindi la seguente
In essa si riconosce l' equazione di una cicloide, identica alla prima , ma traslata di in direzione Y e di
in direzione X.
Solo la cicloide e la spirale logaritmica presentano questa proprietà, per cui l'evoluta della curva è identica alla curva madre, l'evolvente.
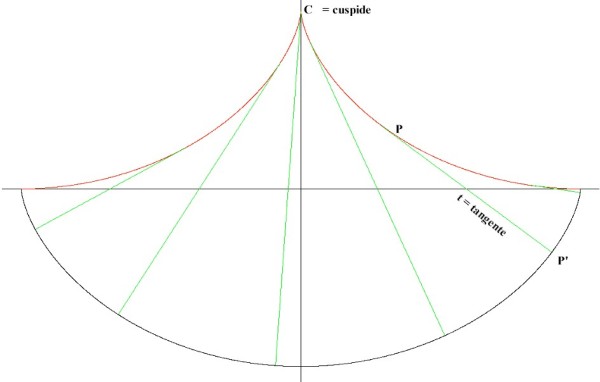
Questa peculiarità è proprio quella che consente di realizzare il pendolo armonico.
Consideriamo il fatto che ciascuna retta è perpendicolare alla cicloide evolvente nel punto P' ed è tangente alla cicloide evoluta nel punto P.
Conosciamo le coordinate di questi punti, che sono funzioni del parametro
La distanza tra questi due punti è facilmente calcolabile operando sui due sistemi che rappresentano x e y di ciascuna evolvente.
coordinate P' coordinate P
ora non ci resta che calcolare la lunghezza dell'arco di evoluta tra la cuspide C e il punto di tangenza P.
Sommando i due tratti , rettilineo e curvilineo possiamo verificare che
CP +PP' =
Pertanto, se appendiamo una massa m ad una corda sottile lunga 4r , vincolata alla cuspide dell’evoluta, e la facciamo oscillare, durante il moto oscillatorio la corda si distende sull’evoluta e poi da lì parte tangenzialmente fino alla massa oscillante. Dalle proprietà suddette discende che la traiettoria che la massa descrive è una cicloide, esattamente è l’evolvente della cicloide soprastante.
Abbiamo quindi realizzato con facilità un pendolo cicloidale, perfettamente isocrono per qualunque ampiezza del moto. Nell'ultima figura si possono notare alcune posizioni del filo del pendolo per diversi valori del parametro .
Scarica l'articolo in formato PDF





