Ecco perché la Tartaruga era certa di vincere la scommessa

Sostanzialmente il quiz richiedeva di trovare l' equazione che rappresenta il profilo di un curva sulla quale, indipendentemente dalla posizione di partenza, il periodo delle oscillazioni di oggetti in movimento è costante.

Premessa

Se la pista avesse il profilo di un piano inclinato, non si verificherebbe alcuna oscillazione: vincerebbe sempre chi parte avvantaggiato, più vicino al traguardo.

Questo perché ambedue gli sciatori partono da fermi e la componente di accelerazione lungo la traiettoria è costante in ogni punto della pista.

Se invece la pista avesse un profilo circolare ci troveremmo nella stessa situazione di un pendolo in cui la traiettoria del peso segue appunto una circonferenza.

In questo caso la componente di accelerazione lungo la traiettoria sarebbe proporzionale allo spostamento dalla posizione di equilibrio solo per piccole oscillazioni. Aumentando la distanza iniziale dalla posizione di equilibrio, le oscillazioni avrebbero un periodo maggiore. Questo implica che i due concorrenti non arriverebbero al traguardo insieme, vincerebbe anche in questo caso chi parte in vantaggio e oscilla con un periodo più breve .

Insomma, il moto sarebbe periodico ma non armonico, cioè il periodo  non sarebbe indipendente dalla ampiezza delle oscillazioni , ossia dalla posizione scelta per la partenza.

Il risultato di avere oscillazioni con periodo indipendente dalla posizione di partenza si ottiene solo con un particolare profilo della curva, ed è proprio questa funzione che si deve individuare.

Svolgimento del calcolo

La forza a cui sono soggetti i due concorrenti è proporzionale alla componente del peso (F=mg) che agisce nella direzione del moto, ossia lungo la tangente al profilo della curva.

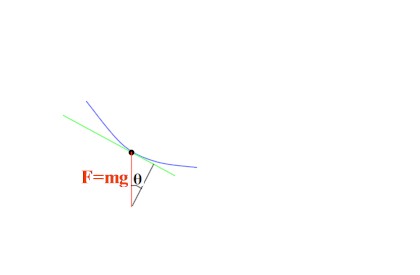
Questa componente, osservando la figura, vale mg senθ.

All'arrivo la traiettoria sarà orizzontale e l'angolo θ varrà zero: non ci sarà alcuna componente di accelerazione che agisca sul corpo in movimento.

A causa dello spostamento prodotto dal moto, varia la distanza dalla posizione di equilibrio e l'azione del peso si manifesta con la forza di richiamo ks che è proporzionale alla posizione raggiunta s . Questo è esattamente il meccanismo di un moto periodico armonico.

L'angolo  θ dovrà variare in funzione di s in modo tale che sia sempre vera la seguente uguaglianza:

          da cui

        e quindi, sulle componenti x e y...

           

Procediamo ora esprimendo diversamente i prodotti delle funzioni sinusoidali  che compaiono in queste formule.

Nel primo caso  (dx), ricordando la formula di duplicazione del coseno ,            possiamo scrivere

Nel secondo caso (dy), ricordando la formula di duplicazione del seno ,           possiamo scrivere

Ora si tratta di eseguire, con qualche passaggio, le due integrazioni per trovare le equazioni di x e y in funzione dell'angolo  θ

per la coordinata x

e per la coordinata y

               ricordando che             sostituisco

     ricordando che                ricavo         e sostituisco

 

In definitiva il profilo cercato è descritto da queste  due equazioni:

Come indicato nel testo del quiz, l'origine del sistema di riferimento è  nel punto corrispondente al traguardo:

    per        risulta quindi   

Infine definiamo     e         sostituendo, otteniamo

che rappresentano proprio le equazioni di una cicloide.

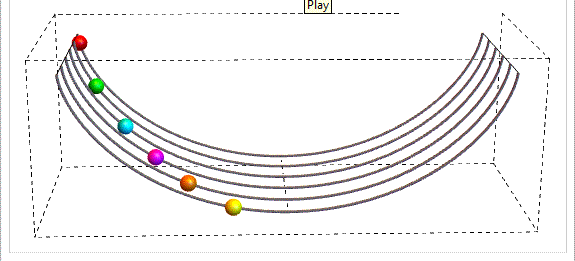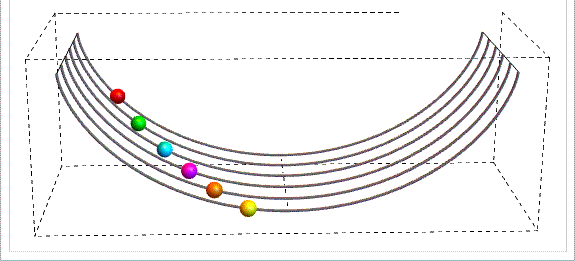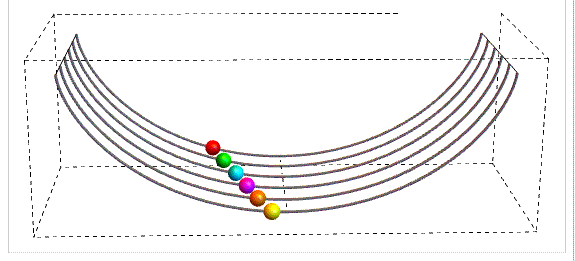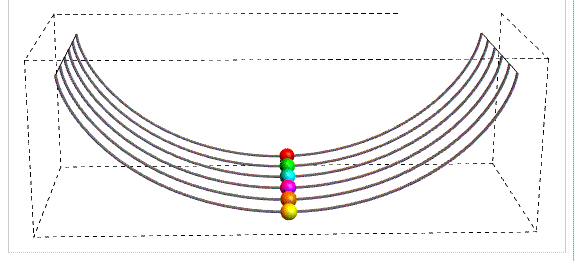
Ecco cosa succede, come possiamo vedere in questa  animazione del movimento degli atleti lungo la discesa.

https://ggbm.at/pSpgBc3Y

E con maggiori dettagli sulla geometria del moto in questa seconda animazione

https://ggbm.at/Qqu2Qke8

Capite che Achille non aveva alcuna possibilità di vincere, di non essere raggiunto, nemmeno se si fosse posizionato a una piccolissima distanza dal traguardo, nemmeno alla distanza di Planck !

 

QUI la rivincita di Achille

QUI tutti i quiz dei Maghi

QUI tutti i quiz del blog

Vi è piaciuto calcolare questo percorso? QUI ne troverete altri!