Questo articolo fa parte della raccolta "Fermate il mondo, voglio scendere!" inserito nelle pagine d'archivio "Meccanica Celeste" e "Caduta libera"

 

Abbiamo visto (QUI) cosa succederebbe alla Terra se essa decidesse di fermarsi e non girare più attorno al Sole. Potremmo continuare con il nostro pianeta che, però, si è un po' arrabbiato di essere sempre messo in mezzo e allora ci trasferiamo su Papalla che, come sappiamo bene, ha tutte le caratteristiche di massa e di orbita uguali alla Terra. Ma, soprattutto, i papalli sono meno irascibili dei terricoli (tranne uno che - ahimé - conosciamo fin troppo bene e ci tocca sopportarlo perché non se ne vuole più andare!).

Ma parliamo di cose serie... la situazione è questa: due papalli (uno abita all'equatore e uno al polo nord) si incontrano durante una gita scolastica ai tropici e fanno subito amicizia. Ridendo e scherzando, prima o poi fanno lavorare la loro mente (come tutti i papalli) e si pongono un problemino fantascientifico. Si domandano: “Cosa succederebbe a noi due (e a molte altre cose) se il pianeta smettesse improvvisamente di ruotare attorno al suo asse?”.

CASO 1 - Uno dei due dice subito: “Mamma mia, saremmo lanciati verso l’alto dalla nostra forza centrifuga, come fossimo sparati da un cannone!”.

CASO 2 - L’altro invece si mette a ridere: “Ma no, cosa dici… staremmo tranquilli a casa nostra. La gravità di Papalla non ci farebbe certo scappare!”

Ricordando che Papalla è un pianeta che ha le stesse caratteristiche della Terra (non gli abitanti, però…), chi dei due ha ragione e chi ha torto?

Il quiz sull’improvvisa fermata della rotazione di Papalla merita qualche parola in più. Innanzitutto, evitiamo qualsiasi confusione tra la rotazione dell’intero pianeta e l’immissione in orbita di un oggetto attorno al pianeta.

Nel secondo caso è decisamente importante la massa del pianeta e il suo campo gravitazionale, dato che è proprio lui che regola la velocità orbitale.

Nel primo caso, poco importa che la Terra abbia una massa oppure no: quello che conta è che tutta la sua superficie ruoti attorno a un asse.

Usiamo altre parole. Nel secondo caso, il fatto che Papalla ruoti oppure no attorno al suo asse non ha alcuna importanza, dato che interessa soltanto inserire qualcosa in orbita attorno a lei. Per altezze diverse si avranno velocità diverse o -se preferite- oggetti che provengono con una certa velocità di crociera uniforme si inseriscono in orbita a diverse altezze.

In questo caso la forza centripeta è solo e soltanto la forza di gravitazione papalliana. Si può avere il caso limite di entrata in orbita ad un’altezza, rispetto alla superficie di Papalla, uguale a zero (sempre che non vi siano atmosfera, montagne, alberi o altri ostacoli…), ma questa orbita non ha niente a che fare con l'eventuale rotazione del pianeta.

Nel primo caso abbiamo, invece, un’enorme giostra sferica che ruota. Teoricamente potrebbe non avere alcuna massa al suo interno. Tutti gli oggetti che le sono posati sopra ruotano con lei. Possiamo anche vederla come una giostra in cui vi è un asse verticale (asse di rotazione) che ha una serie di corde di lunghezza decrescente dal centro verso l’alto e verso il basso a cui sono attaccati i vari oggetti che ruotano. Tutte le corde ruotano con la stessa velocità angolare. Ne consegue che più la corda è lunga e maggiore è la velocità tangenziale, che diventa zero quando si è ai due poli. In questo caso, ogni corda definisce una differente forza centripeta. Qualcosa di simile alla creazione di  una gravità artificiale su una "ruota" spaziale.

La Fig. 1 illustra i due casi. In alto Papalla con la sua massa e con un satellite che orbita attorno a lei a un’altezza uguale a zero lungo un’orbita equatoriale (prima vista da un polo e poi  equatorialmente). In basso, la giostra papalliana che ruota attorno all’asse di rotazione AR, anch’essa vista prima da un polo e poi lungo l’equatore.

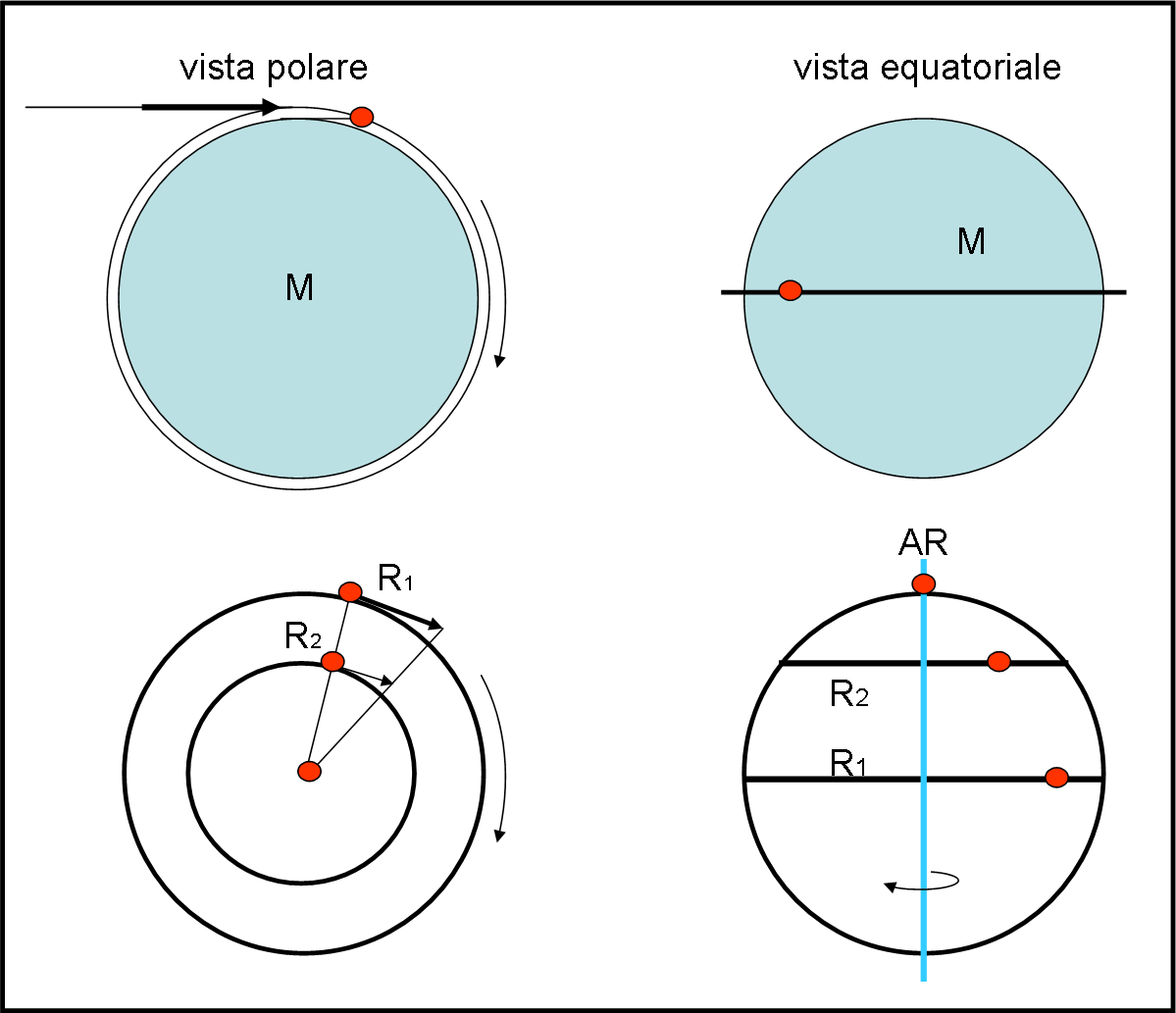
Abbiamo separato nettamente i due fenomeni per meglio discutere gli effetti di una "fermata".

Cosa vuol dire fermare la rotazione di Papalla? Beh… nel primo caso assolutamente niente, dato che il satellite percorre la sua orbita, bassissima, indipendentemente da cosa faccia il pianeta Papalla. Se fosse l’unico abitante di Papalla, non si accorgerebbe di niente.

Nel secondo caso, invece, fermare Papalla vorrebbe dire fermare la giostra o, se preferite, tagliare tutte le corde che legano i papalli all’asse di rotazione. Che ci sia o non ci sia un pianeta al centro della giostra, interessa relativamente poco.

TUTTI gli oggetti posati sulla giostra sferica viaggiano con una velocità, indipendentemente dalla loro massa, che varia passando dall’equatore (massima) verso i poli (zero). Fermando la giostra si elimina l’unica forza agente sui papalli, ossia quella centripeta; il primo principio della dinamica ci dice, allora, che i corpi continuano nel loro stato di quiete o di moto rettilineo uniforme. Quelli posizionati all’equatore continuano a muoversi lungo la tangente con un valore massimo della velocità, mentre quelli ai poli stanno perfettamente fermi.

A questo punto, però, entra in gioco la massa di Papalla e il suo campo gravitazionale. Ogni corpo in movimento lungo la tangente risente dell’accelerazione di gravità e tende a cadere verso il suolo. Esattamente ciò che capita a un proiettile sparato da un cannone (come già Newton aveva compreso).

La velocità tangenziale equatoriale, pur essendo molto grande, non riesce a mettere in orbita gli oggetti come nel primo caso. Siamo, infatti, ormai passati al primo caso, avendo oggetti che viaggiano a una certa velocità sotto l’effetto di un campo gravitazionale (che, se ruota o no, non importa più a nessuno).

Prima di proseguire, possiamo dire subito che, tra i due papallini, chi è stato più esatto nella risposta è stato il secondo (anche se si è riferito a “casa sua”).

Il primo papallino ha fatto un po’ di confusione… Se si ferma la rotazione, viene a mancare la forza centripeta (è come se si fosse tagliata la corda) e di conseguenza anche la centrifuga che gli era necessaria per sentirsi fermo nel suo sistema rotante. Ora, in balia del suo moto rettilineo uniforme, si sta semplicemente muovendo lungo una tangente alla sfera ormai immobile. In poche parole non esiste più il sistema solidale con la giostra rotante che lo vede andare in senso radiale. Ciò non toglie, tuttavia, che, esistendo un pianeta con la sua massa, anche se fermo, il moto rettilineo uniforme dura ben poco, in quanto viene subito deformato dall'accelerazione di gravità.

Il secondo papallino, invece, abita al polo per cui lui non ha mai subito alcuna velocità tangenziale (al limite girava su se stesso come l’asse di rotazione). Se l’asse di rotazione si ferma lui non acquista assolutamente una velocità tangenziale e non cambia posizione.

Potremmo fermarci qui… ma il quiz merita qualche parola in più relativamente alle conseguenze a breve e lungo termine. Anzi, ci sarebbe da scrivere un libro, anche se di scarso interesse fisico.

Un vero scienziato direbbe: “E’ un  problema del tutto fantasioso che non può mai capitare e, quindi, è inutile parlarne. Al limite, si potrebbero studiare gli effetti di una rotazione che tende a zero su tempi lunghissimi, per effetti mareali…”.

Uno scienziato un po’ papalliano, come me, invece, accetta anche l’intervento di un PapalScherzone qualsiasi, aiutato da un PapalErcole, capace di bloccare la rotazione di Papalla, magari anche solo per un minuto.

Il primo scienziato avrebbe ragione, dato che per poter fermare bruscamente la rotazione di un pianeta come Papalla ci vorrebbe quasi sicuramente l’urto contro un oggetto di massa non molto diversa (è questione di annullare un momento angolare). Un tale urto non solo fermerebbe la rotazione, ma distruggerebbe l’intero pianeta… per cui la questione si chiude prima di iniziare.

Il secondo "scienziato" (?), pur accettando la situazione fantascientifica, è, comunque, costretto a farsi una domanda: “Dove finisce il pianeta e dove cominciano i papalli?”. In altre parole, quando si dice fermare il pianeta vuole dire fermare tutto ciò che è in qualche modo legato al pianeta o solo la parte fatta di roccia e terra. O ancora: un albero che è legato al pianeta attraverso le sue radici o un edificio che è ancorato saldamente attraverso le sue fondamenta alla roccia sottostante vanno considerati pianeta che si blocca o corpi che proseguono nel loro moto?

Pensiamo a una macchina che si ferma improvvisamente. Il guidatore (se non avesse la cintura) sfonderebbe il vetro (non fa parte della macchina). Ma se fosse un robot costruito insieme alla macchina si fermerebbe anche lui.

Ovviamente, a seconda dei limiti “teorici” dati al pianeta che si ferma, le conseguenze sono più o meno disastrose. Se alberi ed edifici restassero fermi, i papalli nel loro volo a grande velocità finirebbero sicuramente contro qualcuno di loro, prima di fermarsi grazie alla gravità papalliana.

Se, invece, gli edifici e gli alberi non si “fermassero”, riuscirebbero a sradicarsi e a crollare e le cose non sarebbero migliori…

Ovviamente, un discorso più serio dovrebbe tener conto degli attriti e dell’atmosfera (su Papalla non c’è, ma…). L’atmosfera viaggerebbe a grande velocità e si possono immaginare  i suoi “impatti” contro le montagne e via dicendo. Per non parlare del mare che se ne andrebbe a zonzo. Insomma, uno scenario, comunque, terrificante. Chi vuole, può anche divertirsi a fare conti, ma anche uno scienziato un po’ papalliano deve limitarsi nel fare fantascienza catastrofica gratuita…

Ancora un accenno a un effetto sicuramente notevole che darebbe un brutto colpo al nostro papallino “polare”. La rotazione di Papalla fa sì che essa si “gonfi” verso l’equatore, ossia assuma la forma di un ellissoide schiacciato ai poli e allungato all’equatore.

Se si fermasse la rotazione, Papalla tenderebbe a diventare perfettamente sferica. Tuttavia, lungo la zona equatoriale gli oceani odierni si "prolungano" di qualche chilometro rispetto a una sfera perfetta. Quest’acqua tenderebbe, perciò, a ridistribuirsi sulla superficie e si creerebbe una zona emersa equatoriale simile a un unico enorme continente. I poli verrebbero sommersi e anche il nostro papallino finirebbe male…

Questa conseguenza è decisamente più “fisica”, perché si verificherebbe anche se Papalla si fermasse lentamente. QUI potete trovare informazioni più accurate.

Non dimentichiamo, infine, che anche il campo magnetico potrebbe fermarsi, ossia sparire, se il nucleo non ruotasse. Niente campo magnetico, niente difesa contro i raggi cosmici…

Povera Papalla… continua a ruotare, non ti fermare!!!!!

P.S.: Non ne ho parlato apposta… potete calcolare da soli la velocità tangenziale all’equatore e la velocità necessaria per inserirsi in orbita a zero metri d’altezza. Vedrete che la differenza è piuttosto notevole. (Per chi fosse proprio in crisi, consiglio di andare a sfogliare questo articolo)

 

QUI l'approfondimento sulla forza centrifuga, la centripeta e la gravità newtoniana

QUI e QUI le spiegazioni semplici e divertenti (arrivate direttamente da Papalla!) della forza centrifuga e di quella centripeta, adatte a bambini di tutte le età!

NEWS! Potrebbe esistere vita su un pianeta che mostra sempre la stessa faccia al proprio sole? QUI una risposta seria, QUI una un po' meno...