Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.

 

Mettiamo subito in chiaro una cosa: la forza di marea non è altro che un effetto del secondo ordine della forza gravitazionale. In altre parole, nasce la marea solo se vi è una forza gravitazionale che agisce tra due corpi celesti. Ne segue che la marea agisce su tutte le scale, dai grossi “sassi”, o poco più, fino alle galassie.

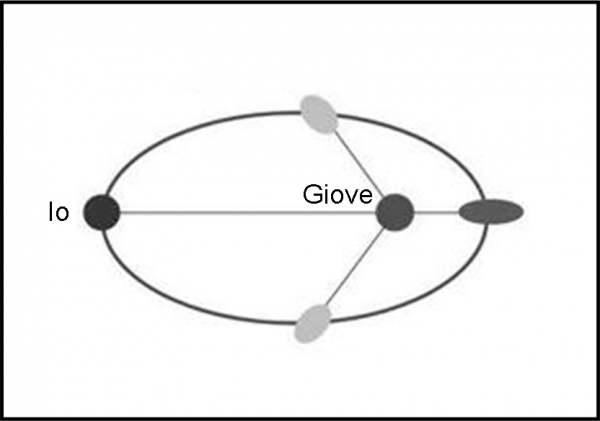
Spieghiamola in modo molto semplificato. Se un oggetto di dimensioni non trascurabili rispetto alla distanza che lo separa da un altro oggetto massiccio, subisce la forza gravitazionale di quest’ultimo, ne consegue un fatto molto importante: la parte del primo oggetto che sta più vicina al secondo oggetto (A) risente maggiormente della sua gravità rispetto a quella più lontana (B). E’ solo e soltanto un questione di distanza e sappiamo bene che la forza gravitazionale viaggia con l’inverso del quadrato della distanza. La Fig. 1 mostra uno schema veramente semplificato della situazione.

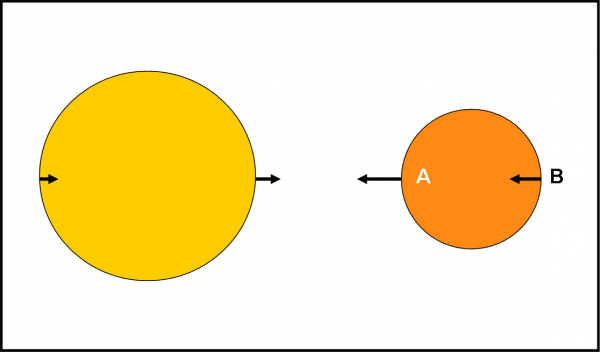
Questo fatto comporta, in parole molto povere, che una parte dell’oggetto (A) è attirata di più della parte opposta (B). Si capisce, immediatamente, che se i due oggetti celesti hanno masse comparabili, questo fenomeno diventa uno “scambio” di favori ed entrambi i corpi subiscono la marea del vicino di casa. Non è assolutamente detto che gli oggetti debbano essere solidi o compatti. L’importante è che abbiano una certa massa totale e che si possa, perciò, calcolare la mutua attrazione gravitazionale e la sua variazione con la distanza della zona considerata.

Ciò vuol dire che gli effetti mareali si vedono molto bene, ad esempio, negli incontri tra galassie, dando luogo a quelle bellissime figure che abbiamo imparato a conoscere, come mostrato dalla Fig. 2.

Se un oggetto è decisamente più massiccio di un altro, e quest’ultimo, di dimensioni non trascurabili, gli passa molto vicino, succede una cosa analoga e l’oggetto risente di questa forza variabile con la distanza. Se è solo composto di gas viene stirato, allungato  e deformato in relazione al suo moto e alla distanza delle sue varie parti rispetto all’oggetto più massiccio. Se, invece, è un corpo compatto, come una stella, può venire completamente disgregato. L’importante è che la differenza tra la forza gravitazionale agente su un estremo e quella agente sull’altro sia superiore all’autogravitazione che tiene unita la stella. Ovviamente, perché possa capitare questa piccola-grande tragedia ci vuole un oggetto massiccio che sia realmente massiccio, come, ad esempio, un buco nero.

Come abbiamo visto il fenomeno della marea è qualcosa che lavora principalmente sulle strutture più grandi e potenti del nostro Universo e le situazioni che causa sono ben più numerose e variegate. Qualcosa che sembra ben lontana dall’innalzamento del livello del mare sulla Terra. E’ come confrontare un elefante con una pulce…

In questo articolo, scenderemo su scale più piccole di quelle galattiche e ci limiteremo al Sistema Solare. Ci permetteremo anche di calcolare la forza di marea (una parte dedicata a chi ama un po’ la matematica), ma -soprattutto- l’applicheremo a situazioni che sembrano abbastanza diverse tra loro. In particolare, la creazione di un anello planetario, la frammentazione della cometa Shoemaker Levy 9,  il riscaldamento di un satellite, l’uguaglianza tra periodo di rotazione e di rivoluzione di un satellite e, infine, anche la marea terrestre…

Di tutto e di più, ma sempre riconducibile alla stessa legge fisica.

Il limite di Roche

Cominciamo con gli effetti distruttivi. Distruttivi sia per chi subisce la marea, ma anche per chi legge questa parte, dato che do via libera alla matematica (semplicissima, ve lo assicuro!). Tuttavia, potete anche limitarvi alle conclusioni e poi passare agli altri effetti. Io, come sempre, consiglio di comprendere, anche se con un po’ di fatica, la parte fisica dato che poi tutto apparirà, più facilmente, nel suo giusto contesto.

Roche è un nome che risuona spesso in astronomia. E’ legato a molte cose, ma,  in particolare, può creare confusione il concetto di lobo di Roche e di limite di Roche. Il primo è qualcosa che si riferisce ai sistemi binari e ai famosi punti lagrangiani. Il secondo, invece è quello che interessa a noi per la marea.

Due parole sul lobo prima di lanciarci verso la marea, tanto per chiarire le idee. Esso è ormai un vecchio amico che abbiamo incontrato varie volte quando si è parlato di stelle doppie quasi a contatto. Ci ha permesso di definire il celeberrimo punto lagrangiano L1, l’unica porta sempre aperta per lo scambio di materia tra due stelle vicine. Come nascano i lobi e come si identifichino nel contesto di due campi gravitazionali è stato lungamente esposto nei vari libri divulgativi. Al momento, possiamo soprassedere.

Consideriamo la Fig. 3 che ci mostra la situazione in cui lavoriamo. A sinistra vi è un grande pianeta (come, ad esempio, Saturno) e a sinistra vi è un piccolo satellite (ma non “troppo” piccolo, come vedremo più in là). Il pianeta ha raggio R e massa M, mentre il satellite ha raggio r e massa m. La loro distanza è D. Per potere giungere fino in fondo dobbiamo assumere che r sia molto più piccolo della distanza D. Ma questa è una situazione più che normale.

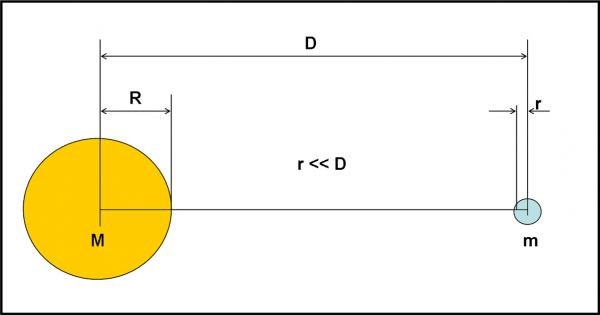
La domanda che ci facciamo è la seguente: “A che distanza D dal pianeta può avvicinarsi  il satellite prima che la forza di marea lo frantumi completamente trasformandolo in una nuvola di frammenti?”  Questo limite di sopravvivenza prende il nome di limite di Roche.

Per essere più semplici nella trattazione, consideriamo il nostro satellite formato da due sfere uguali  di raggio r e di massa m. Le cose non cambiano di certo rispetto alla Fig. 3, ma ci permettono un calcolo molto più intuitivo. Dobbiamo assumere un’altra ipotesi di partenza (che alla fine discuteremo): le due sfere stanno attaccate SOLO per la forza gravitazionale reciproca. Non vi sono quindi forze di coesione della materia che complicherebbero la trattazione in modo terribile. In realtà, questa ipotesi non è poi così strana, se pensiamo che gli asteroidi e probabilmente molti satelliti medio-piccoli non sono altro che ammassi di blocchi di pietra o di ghiaccio tenuti insieme dall’autogravitazione.

Ne abbiamo già parlato riguardo alla vita collisionale degli asteroidi e anche a riguardo della vita avventurosa dei satelliti di Saturno, che, probabilmente, si sono frantumati più di una volta nella loro vita a causa di impatti catastrofici con comete di passaggio. Essendo più lontani del limite di Roche sono riusciti a ricostruirsi (vedi Mimas, ad esempio), come ha fatto la Luna attraverso i frammenti dell’impatto contro la nostra Terra.

Torniamo al nostro satellite, “diviso” in due parti a stretto contatto, e disegniamo la Fig. 4.

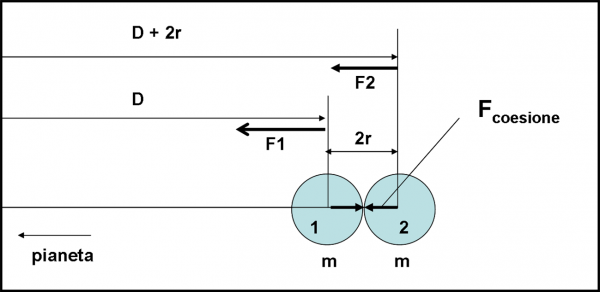
Calcoliamo, innanzitutto, la forza di gravità che tiene unite le sue sferette di raggio r e di massa m (il nostro “speciale” satellite).  Basta richiamare la legge di gravitazione universale di Newton che ci dice che la forza gravitazionale è data dal prodotto delle masse in gioco, diviso per il quadrato della distanza tra i rispettivi baricentri (in caso di sfere il baricentro è il loro centro). Il tutto è moltiplicato per una costante G, il cui significato possiamo tranquillamente tralasciare. Scritta “matematicamente”, e in modo generale, diventa:

F = Gm1m2/d²               ….  (1)

Nel nostro caso, con due sfere di massa m e di raggio r (a contatto), si scrive:

F_coesione = Gmm/(2r)² = Gm²/4r²             ….  (2)

L’abbiamo chiamata forza di coesione (un nome non proprio azzeccato) dato che è quella che tiene attaccate le due sfere (ma si basa solo sulla reciproca gravità). La distanza tra i due centri è ovviamente 2r, mentre m è la stessa per entrambe.

Vediamo, adesso, quale forza gravitazionale subiscono le due sfere per effetto del pianeta di massa M, posto a distanza D. La sfera più vicina a lui subisce una forza di gravitazione pari a:

F1 = GMm/D²                     ….  (3)

Mentre la sfera più lontana subisce una forza

F2 = GMm/(D+2r)²            ….  (4)

Cosa ci dicono queste due forze? Una cosa molto semplice: il pianeta attira verso di sé in modo maggiore la sfera 1 che non la 2, dato che quest’ultima si trova leggermente più distante. Questo fatto lo vediamo confrontando la (3) con la (4). La seconda è una forza più piccola dato che è uguale a quella precedente a parte il denominatore. Anche se di poco, esso è più grande e quindi la forza che ne deriva è più piccola. Questa differenza di forze tra la sfera più vicina e quella più lontana, tende a separare le due sfere (una è attirata di più dell’altra). In altre parole, possiamo dire tranquillamente che la differenza tra le forze si comporta come una forza unica che tende a “stirare” l’oggetto formato dalle due sfere e, se possibile, separarle, ossia distruggere il satellite.

Questa forza non è altro che la forza di Marea, dovuta proprio alla differenza di gravità che subiscono i due estremi di un unico corpo solido (nel nostro caso tenuto insieme solo dall’autogravitazione).

Per scriverla matematicamente, ci basta fare la differenza tra F1 e F2. Quello che troveremo sarà proprio la forza di marea, indotta dal pianeta di massa M a distanza D su un satellite formato da due masse m a contatto. Capite bene che il discorso semplificato non sarebbe cambiato assolutamente se avessi preso, come satellite, una sfera unica. Avrei, comunque, avuto un emisfero più vicino e uno più lontano. Il discorso non si sarebbe modificato, ma la trattazione sarebbe stato molto più complicata.

F1 – F2 = GMm [1/D² – 1/(D+2r)²] = GMm A        ….  (5)

Per meglio seguire i passaggi successivi (ridondanti) ho chiamato A  la parte dentro alla parentesi quadra, dopo aver messo in evidenza la parte comune alle due espressioni delle forze.

A = 1/D² – 1/(D+2r)² = [(D + 2r)² – D²]/ [D² (D+2r)²]

A = (D² + 4r² + 4Dr – D²)/ [D² (D+2r)²] = (4r² + 4Dr)/ [D² (D+2r)²] = 4r (r + D)/ [D² (D+2r)²]

Ossia abbiamo

A = 4r (r + D)/ [D² (D+2r)²]            ….  (6)

Fin qui ho solo usato passaggi di aritmetica elementare (massimo comun divisore, quadrato di un binomio e cosucce del genere) … è vero oppure no? Non per niente avete a disposizione il corso di matematica negli “approfondimenti”.

A questo punto dobbiamo fare una piccola approssimazione, tenendo conto dell’ipotesi fatta fin dall’inizio, quando abbiamo detto che il raggio r delle sfere deve essere molto più piccolo della distanza D dal pianeta. Possiamo quindi scrivere in modo “simbolico”:

r << D, ma anche

2r << D.

Se r è molto piccolo, lo è anche 2r. In queste condizioni, si può anche dire che r è trascurabile rispetto a D e quindi:

r + D ~ D            …. (7)

D + 2r ~ D

Attenzione: si può scrivere D + r = D, ma non D r = D

Verifichiamolo con numeri “veri”. Poniamo che D sia uguale a 100 000 e che r sia solo 3. Bene, aggiungendo a 100 000 il numero 3 o il numero 2 ∙ 3 = 6, il risultato cambia di poco. 100 003 o 100 006 possono essere considerati ancora 100 000. Ben diversa sarebbe la situazione se avessimo 100 000 ∙ 3 o 100 000 ∙ 6.  In questo caso, 300 000 e 600 000 sono ben diversi da 100 000.

Sostituiamo allora le approssimazioni  (7) nella  (6), ottenendo:

A ~ 4rD/D⁴ = 4r/D³

Sostituendo A nella (5), si ha

F1 – F2 = 4GMmr/D³     ….  (8)

Questa è la formula (lievemente approssimata) che  descrive matematicamente la forza di marea. Notate un fatto importante (che spesso si sente dire): la forza di marea decresce con il cubo della distanza (e non con il quadrato come fa la forza gravitazionale). Inoltre, oltre a dipendere direttamente dalle masse in gioco, dipende anche dal raggio del satellite che la subisce. In più compare anche un fattore 4 (ma quello è molto meno importante). La dipendenza dal raggio r è abbastanza ovvia, dato che a parità degli altri parametri, più il corpo è allungato e più la differenza tra la parte vicina e quella lontana aumenta. Riscriviamo la (8) chiamandola proprio forza di marea:

F_marea = 4GMmr/D³      ….  (9)

Beh, ragazze e  ragazzi, abbiamo già ottenuto un risultato niente male. Siamo riusciti a ricavare la formula che descrive la forza di marea senza nemmeno bisogno di fare una derivata che sarebbe stata la più ovvia decisione.

Torniamo al nostro satellite che è soggetto a due forze contrastanti: una è quella gravitazionale tra le due sfere che tende a farlo stare unito. L’altra è quella di marea che tende a separare le due sfere e a distruggerlo.

Per sapere a che distanza riesce a vincere quella di marea, basta scrivere la diseguaglianza:

F_marea > F_coesione

Ossia:

4GMmr/D³ > Gm²/4r²          …. (10)

Ricordiamo che le semplificazioni nelle diseguaglianze seguono le stesse regole delle uguaglianze e si possono portare termini da un lato all’altro senza problemi. Possiamo, allora scrivere:

4 Mr/D³ > m/4r²

16 M/D³ > m/r³

16 M > D³ m/r³

16 Mr³/m > D³

E infine isolare D, che compare al cubo

D³ < 16M r³/m         …. (11)

A questo punto, notiamo che conosciamo sia il raggio del pianeta R che il raggio della sfera r, per cui possiamo scrivere la massa come volume moltiplicato per la densità ρ dell’oggetto celeste. Ricordiamo, infatti, che si definisce densità il rapporto tra la massa e il volume del corpo. Essa ci dice che tipo di materia vi è all’interno. Se fosse composto d’acqua avremmo una densità uguale a 1. Se fosse composto di ferro, la massa, a parità di volume, sarebbe ben maggior e quindi la densità sarebbe molto più grande. Se invece fosse di panna montata la densità scenderebbe sotto all’unità. E via dicendo.

Ricordando che il volume V di una sfera di raggio r è dato da 4/3πr³, le masse diventano:

M = V_P ρ_P = 4πR³ ρ_P /3

e

m = V_S ρ_S = 4πr³ ρ_S /3

Sostituendole nella (11), la diseguaglianza diventa, con qualche semplificazione:

D³ < 16 (4πR³ ρ_P /3) r³/ (4πr³ ρ_S /3) = 16 R³ ρ_P/ ρ_S

ossia:

D³ < 16 R³ ρ_P/ρ_S         …. (12)

Uffa! Abbiamo ancora il cubo che ci dà un po’ fastidio. Nessun problema. Basta eseguire la radice cubica di entrambi i membri della diseguaglianza. Per i meno preparati, ricordiamo che la radice cubica di un numero N  è il numero m che bisogna elevare al cubo (ossia moltiplicare per se stesso tre volte) per ottenere il numero N. Invece di usare il solito simbolo di radice, non ben definito nella scrittura al PC, usiamo la notazione di frazione. La radice quadrata si indica con l’elevazione a 1/2, quella cubica a 1/3 e via dicendo.  Si ottiene:

D < (16)^1/3 R (ρ_P/ρ_S)^1/3

e, infine:

D < 2.5 R (ρ_P/ρ_S)^1/3       …. (13)

Il numero esatto sarebbe un po’ più piccolo (2.46 circa), ma possiamo tranquillamente usare 2.5 viste le incertezze in gioco e la maggiore facilità mnemonica di 2.5. Ovviamente, se il pianeta e il satellite hanno la stessa densità, la formula si semplifica ancora di più e diventa:

D < 2.5 R       …. (14)

Il valore di D definisce il limite di Roche relativo a un pianeta di raggio R. Visto? Ce l’abbiamo fatta alla grande!

E’ necessario fare qualche piccola considerazione. Abbiamo considerato il satellite tenuto insieme solo dall’autogravitazione. In realtà, la materia si lega anche attraverso altre forze, quelle di stato solido, ad esempio. Pensiamo, infatti, che gli atomi e le molecole si abbracciano con grande passione e per separarli ci vuole un po’ più di fatica. Tuttavia, in molti casi possiamo tranquillamente pensare a corpi celesti formati da blocchi separati che stanno uniti tra loro proprio grazie all’autogravitazione. In fondo, fanno così anche le stelle… Quindi, il limite di Roche è normalmente utilizzabile, ad esempio, nel sistema di Saturno, dove i satelliti medio-piccoli hanno sicuramente subito qualche distruzione catastrofica e la susseguente ricostruzione. Per loro il modello basato sull’autogravitazione è più che realistico.

Potremmo anche pensare di utilizzare la formula pensando al sistema Terra-Luna. Fortunatamente, il gioco di rotazione e rivoluzione e di marea sta allontanando la Luna. Ma in altri casi potrebbe capitare proprio il contrario. A che distanza si distruggerebbe la Luna per effetto della forza di marea? Sarebbe facilissimo calcolarlo dalla (14), assumendo che le densità possano essere considerate uguali (in realtà non è affatto vero). Avremmo:

D < 2.5 ∙ 6000 = 15 000 km

Sarebbe uno spettacolo affascinante e terribile. La Luna, però, non è tenuta assieme solo dall’autogravitazione e, inoltre, ricordiamoci che la formula è valida solo se il raggio del satellite è molto più piccolo della distanza tra lui e il pianeta. E questo non è certo il caso della Luna. Il suo raggio di 1700 km è comparabile con 15 000 km. Niente da fare, la Luna ci piomberebbe addosso senza sgretolarsi, se non in maniera molto superficiale.

Ben diverso è stato il destino subito dalla cometa Shoemaker-Levy 9 che nel 1993 si è frantumata completamente per effetto della marea di Giove. Essa è stata sgretolata (Fig. 5) quando è giunta troppo vicina al gigante gassoso e poi i vari frammenti sono caduti su di lui. Pensate che proprio in quei giorni Shoemaker in persona aveva annunciato al congresso internazionale ACM 93,  organizzato a Belgirate, sul Lago Maggiore, (e di cui mi onoro di essere stato il presidente scientifico) l’avvenuta frammentazione e aveva mostrato le prime immagini. Che bei ricordi e che uomo Eugene!

Concludiamo questa parte con Saturno, il Signore degli anelli. Prendiamo un bel satellite ghiacciato (un po’ come Mimas) e avviciniamolo al pianeta. Quando si distruggerà dando luogo a una miriade di frammenti, che poi si trasformeranno nell’anello (o anelli, dato che sono separati da risonanze che vietano la presenza di frammenti a certe distanze particolari)? Ce lo dice il limite di Roche. Basta calcolarlo, tenendo presente che il raggio di Saturno è di circa 60 000 km. La densità del pianeta è circa 0.7, mentre per il satellite possiamo considerarla uguale a 1 (quella dell’acqua, dato che molte lune di Saturno sono, in realtà, enormi sfere di ghiaccio).

Sostituendo nella (13), si ottiene:

D < 2.5 ∙ 60 000 ∙ (0.7/1)^1/3 = 133 000 km

Le osservazioni ci dicono che gli anelli (principali) arrivano fino a circa 140.000 km. Con le approssimazioni fatte, direi che possiamo considerarci più che soddisfatti. Il limite di Roche funziona davvero!

Qualcuno potrebbe dirmi (e tra di voi ce ne sono di certo ... furbacchioni!): “Eppure quello che dici non è vero! Innanzitutto perché i blocchi di ghiaccio degli anelli non si distruggono fino a diventare polvere. Inoltre, sappiamo benissimo che ci sono almeno un paio di satelliti che si nascondono tra gli anelli”.  Avrebbero sicuramente ragione, ma non terrebbero conto che in un corpo molto piccolo chi tiene insieme la materia non è più la gravità, ma le già citate forze di coesione della materia, ben più resistenti della gravità. Se lanciamo un  sasso da un altezza di 15000 km verso la Terra non si disintegrerebbe certo per la forza di marea, ma solo per l’attrito con l’atmosfera. Insomma, il limite di Roche è applicabile solo per oggetti abbastanza grandi, tali che l’autogravitazione abbia il ruolo più importante nel tenerli insieme. Teniamo anche conto che se l’oggetto è molto piccolo e sempre più piccola anche la distanza tra le due sferette e quindi la forza di marea.

Abbiamo parlato di satelliti, ma il discorso vale anche per un pianeta e una stella: guai ad avvicinarsi troppo. Come già detto all’inizio, un buco nero galattico distrugge le stelle utilizzando la sua forza di marea. Ed è l’intera galassia, con la sua massa, che deforma e frantuma una galassia più piccola. Essa è proprio tenuta insieme solo dalla gravità mutua e i “blocchi” che si separano sono proprio le stelle e/o i loro ammassi e/o le nubi di gas.

La prossima volta che guarderete Saturno, con un binocolo o con un telescopio di alta tecnologia, penserete a quel disco attorno al pianeta come a un qualcosa di ben più affascinante. Rifletterete sulla sua vita avventurosa, sulla sua creazione; vi sembrerà di poter vedere il limite di Roche; capirete la fortuna dei satelliti che guardano il tutto al di là del limite di sicurezza.  Scorgerete gli enormi blocchi di ghiaccio che ricordano i tempi antichi, comprenderete perché ci sono delle strisce vuote e immaginerete gli scontri continui tra quegli “iceberg” cosmici. Vi accorgerete che state vedendo Saturno così da vicino che sembra quasi di poterlo toccare e che non c’è oculare che tenga.

Avrete un vostro oculare potentissimo, quello della mente, della conoscenza e della fantasia.

Riscaldamento

Ricapitoliamo ancora una volta che cosa si intende per forza di marea. Per far ciò immaginiamo di portare un satellite abbastanza vicino al suo pianeta (di dimensioni decisamente più grandi). Il punto del satellite più vicino al pianeta subisce un’attrazione gravitazionale da parte di quest’ultimo maggiore di quella che si riscontra nel punto più lontano.

Questo fatto risulta ovviamente non trascurabile se le dimensioni del satellite non sono irrisorie rispetto alla distanza dal pianeta. La differenza di forza gravitazionale tende ad “allungare” la forma della luna sempre di più, mano a mano che ci portiamo in prossimità del pianeta. In altre parole, se l’orbita è perfettamente circolare, la forma di un satellite dipende solo dalla sua distanza dal pianeta (Fig. 6).

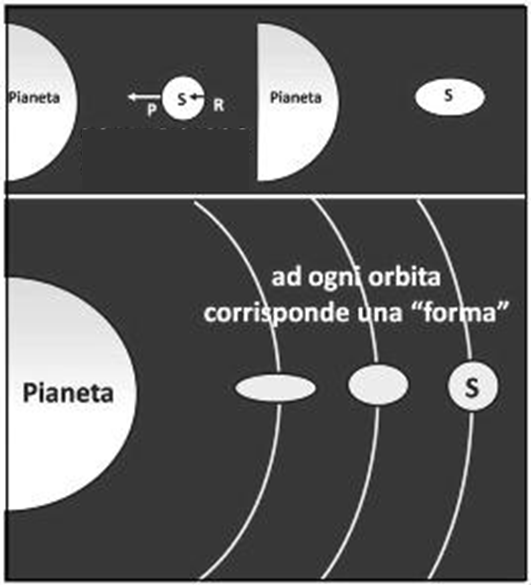
Se dovessimo esagerare, però, le cose diventerebbero critiche. Andando troppo vicini, la forza di marea (ossia la differenza tra le forze gravitazionali applicate ai due estremi) potrebbe diventare così forte da superare la forza di coesione della materia ed il satellite potrebbe disintegrarsi. Ma questo lo abbiamo appena studiato calcolando il limite di Roche.

Lasciamo Saturno e andiamo vicini a Giove e vediamo cosa succede sul primo dei grandi satelliti galileiani. Se Io descrivesse un’orbita perfettamente circolare, assumerebbe una forma abbastanza allungata (ovviamente tutto va inteso in modo relativo e le varie figure ingigantiscono tutto per comodità di spiegazione), ma questa sarebbe sempre la stessa, non cambiando la distanza dal gigante gassoso. Il problema è che Io non è solo, ma accompagnato nel suo continuo viaggio attorno a Giove dai suoi fratelli più esterni, soprattutto Europa e Ganimede (i più vicini).

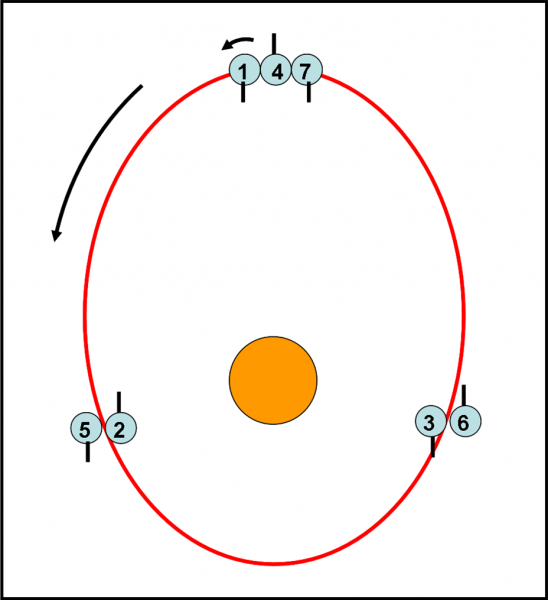
I periodi orbitali dei tre oggetti sono tali da far assumere la stessa posizione geometrica al sistema con periodicità costante (Fig. 7), dato che  tra i primi tre esistono risonanze di moto medio. Questo fatto comporta che a volte Io viene leggermente allontanato da Giove e a volte viene avvicinato. Le masse dei suoi fratelli, infatti, sono piccole, ma non del tutto trascurabili. La loro gravità può attirarlo verso l’esterno o verso l’interno a seconda delle reciproche posizioni. Questo gioco gravitazionale costringe Io a rivolvere lungo un’orbita che non è mai perfettamente circolare, ma leggermente eccentrica. Il che però vuole anche dire che la sua distanza da Giove varia in modo continuo, da un valore massimo a uno minimo.

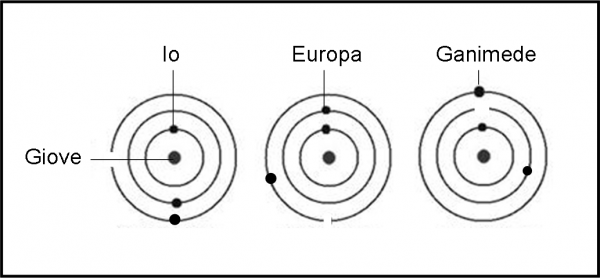
Come si era detto precedentemente, a seconda della distanza dal pianeta varia anche la forma per effetto mareale. Ne consegue che la forma di Io passa da essere quasi sferica ad essere più allungata (Fig. 8). E’ come se il satellite continuasse a comprimersi ed a stirarsi. Questo “tiramolla” causa dei forti attriti interni che portano al riscaldamento della materia. E’ come quando ci si strofina le mani una con l’altra e si sente subito caldo. Per concludere, l’interno di Io rimane fuso per gli effetti della forza di marea (continuamente variabile).

Anche Europa subisce un riscaldamento analogo, anche se di minore entità, essendo più lontano da Giove, ed è per questo che ha un interno abbastanza caldo, tale da mantenere probabilmente un oceano di acqua liquida sotto la crosta ghiacciata. A volte basta poco per riscaldarsi …

Blocco mareale

Affrontiamo adesso il problema della sincronizzazione del periodo di rotazione di un  satellite con quello di rivoluzione attorno al pianeta. Ciò ci porta molto vicini alla marea terrestre, conosciuta da tutti. In parole povere vogliamo rispondere alla domanda: “Perché la Luna ci mostra sempre la stessa faccia?” Vedremo che ciò non capita solo per il nostro satellite, ma per tutti i satelliti di dimensioni abbastanza considerevoli.

Consideriamo, allora, un pianeta e un suo satellite. Immaginiamo che ognuno dei due ruoti con un periodo diverso e che diverso sia anche il periodo di rivoluzione. Sappiamo molto bene che il moto orbitale di un corpo attorno a un altro deriva dalla legge di gravitazione universale di Newton e che le possibili traiettorie sono descritte sufficientemente bene dalle leggi di Keplero. Per quello che ci interessa non vi è bisogno di introdurre argomentazioni relativistiche (per adesso almeno).

Tutto sembrerebbe essere in perfetto equilibrio a parte le perturbazioni causate sul sistema pianeta-satellite dagli altri pianeti. Ammettiamo, però, che queste siano trascurabili. Niente dovrebbe cambiare la configurazione raggiunta. Ed ecco, invece, comparire la marea.

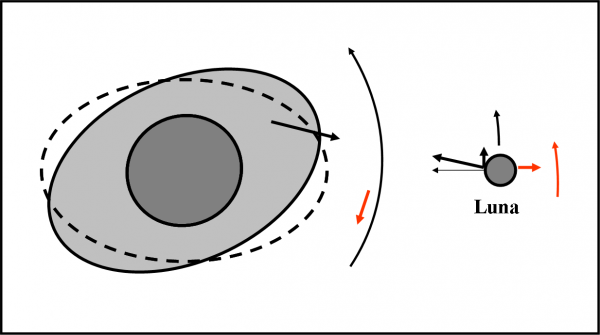
Un satellite di forma sferica rivolve attorno a un pianeta anch’esso sferico. La sua rotazione è, per esempio, più veloce della rivoluzione. Per il momento non interessiamoci della rotazione del pianeta. Immaginiamo inoltre, per semplificare l’approccio, che con una bacchetta magica si riesca a congelare la configurazione del sistema pianeta-satellite a un certo istante. La Fig.9a ci mostra questa situazione.

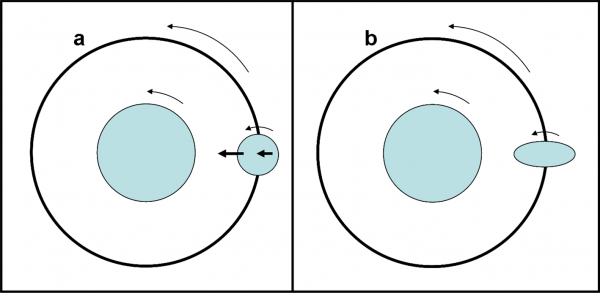
Cosa succede? Il solito fatto che ormai conosciamo a menadito. La gravità che il pianeta esercita sul satellite è più forte sul lato del satellite che guarda il pianeta ed è, invece, più debole sul lato opposto. Ovviamente, questo effetto è importante solo se le dimensioni del satellite non sono trascurabili rispetto alla distanza pianeta-satellite, come già abbiamo molte volte accennato.

La parte del satellite più vicina al pianeta tende ad allungarsi verso di lui, lungo la linea che congiunge i loro centri di massa. Il risultato è una cambiamento della forma del satellite che si deforma assumendo una struttura a ellissoide (Fig. 9b). A questo punto, usiamo di nuovo la bacchetta magica e rimettiamo in moto il sistema. Se il satellite fosse perfettamente deformabile, indipendentemente dal suo periodo di rotazione, dovrebbe assumere istante per istante, durante la sua rivoluzione, una forma allungata diretta verso il centro del pianeta.

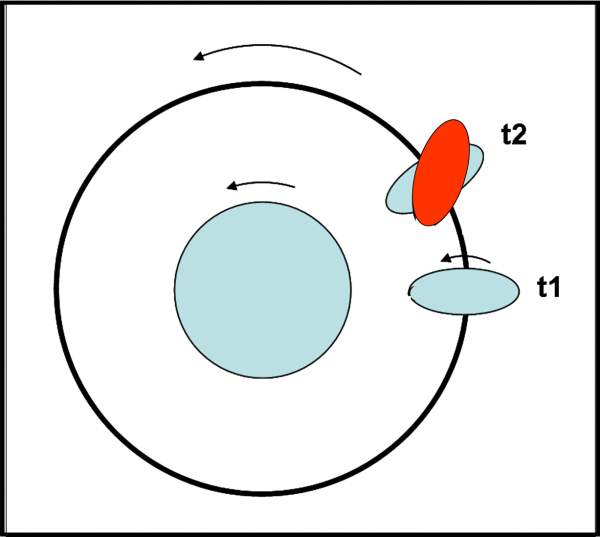
ATTENZIONE! questo non vuole dire che mostrerebbe sempre la stessa faccia al pianeta, ma solo che la sua forma istantanea sarebbe un ellissoide diretto verso il centro del compagno più massiccio. Una montagna o un cratere si muoverebbero molto più velocemente e sparirebbe presto alla vista del pianeta. Se, all’istante t1, una certa caratteristica superficiale A si trovasse proprio di fronte al pianeta, sulla punta dell’ellissoide, all’istante successivo t2 si sarebbe già spostata verso una zona molto meno deformata dalla marea (ossia in una parte meno curva dell’ellissoide) come indicato nella Fig. 10.

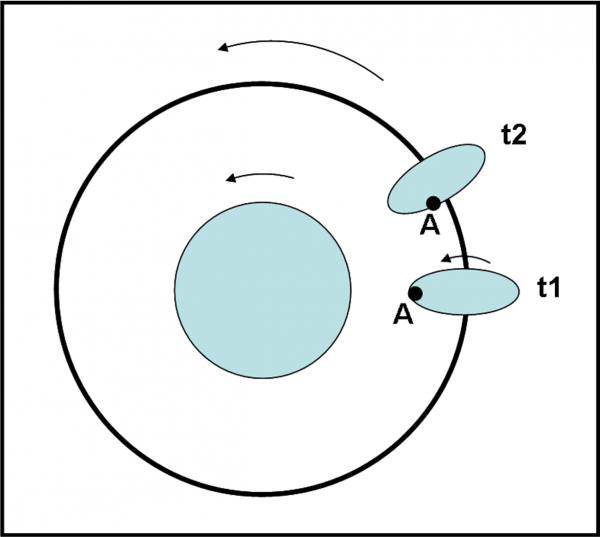
Tuttavia, i corpi planetari non si deformano a piacimento senza cercare di ribellarsi. Le forze che tengono unite tra loro le varie parti del satellite (forze di stato solido o di coesione della materia) si oppongono come possono a questo “stiramento” dovuto alla marea. Alla fine sono costrette a cedere, ma ciò comporta un “ritardo” nella deformazione dominata dalla marea. In altre parole, la deformazione avviene un po’ dopo che l’oggetto ha subito la marea. Nel frattempo, però, la rotazione attorno all’asse trascina con sé una forma deformata che non è più diretta verso il centro del pianeta. La situazione è, allora, quella della Fig. 11, con la configurazione reale al tempo t2  indicata dall’ellissoide rosso, dove, come già detto, il rigonfiamento viene trascinato avanti dalla rotazione del satellite.

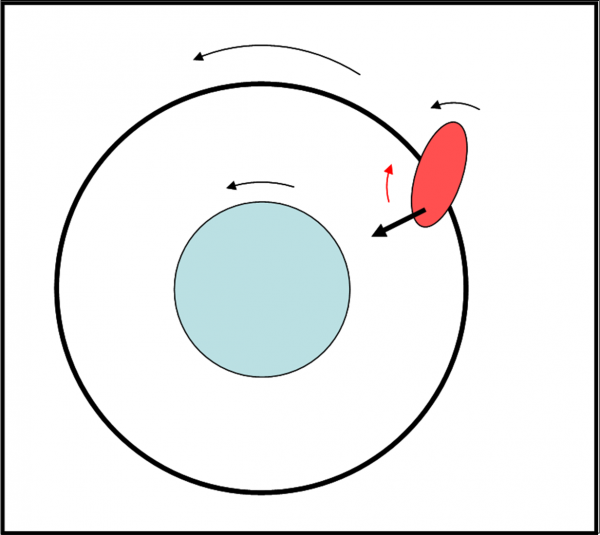
Adesso però le cose cambiano… e come! La forza di gravità del pianeta che agisce sul rigonfiamento del satellite non passa più lungo la congiungente i due centri, ma è fuori asse rispetto a essa. Si crea un “momento”, ossia la forza tende a far ruotare il corpo che la subisce. E’ come quando si dà un colpo “di taglio” a un oggetto e questo si mette a ruotare. Lo potete verificare con qualsiasi cosa abbiate vicino a voi sul tavolo. Dato che il rigonfiamento è più avanti della posizione teorica, la rotazione impartita dal momento va in verso opposto a quello delle rotazione iniziale (Fig. 12).

La velocità di rotazione  diminuisce, ossia il periodo di rotazione si allunga. Questo fenomeno continua ad agire fino a che…

Potete facilmente rispondere voi! Fino a che il periodo di rotazione del satellite diventa proprio uguale al suo periodo di rivoluzione. In questo caso, la parte allungata rimane sempre la stessa, anche fisicamente, e il satellite mostra sempre la stessa faccia al pianeta.

Ciò è successo per la Luna e per i satelliti maggiori di Giove, Saturno, Nettuno e Urano. Ossia, per tutti gli oggetti che siano abbastanza grandi e vicini al proprio pianeta.

Quanto detto vale per un periodo di rotazione inizialmente più rapido di quello di rivoluzione. Tuttavia, il meccanismo funziona, ovviamente, anche per il viceversa. In questo caso, il momento causa un aumento della velocità di rotazione (lascio a voi la figura esplicativa di questa configurazione. Sarà una prova per confermarvi di aver capito il meccanismo).

Per satelliti lontani, la configurazione finale ha bisogno di molto più tempo per realizzarsi, così come per quelli molto piccoli. Inoltre, nel secondo caso, la forma sarebbe facilmente diversa da una sfera e complicherebbe ulteriormente le cose.

Si potrebbero, con relativa facilità, derivare le formule che descrivono compiutamente il meccanismo, ma penso che non sia necessario scendere troppo nei dettagli. Basta solo riportare la relazione (approssimativa e semplificata) che ci dice in quanto tempo avviene la sincronizzazione del periodo orbitale del satellite e del suo periodo di rotazione, in funzione delle masse del pianeta (m_P) e del satellite (m_S), del raggio del satellite (R_S) e, soprattutto, della distanza tra di loro (d):

t = 6 k 10¹⁰ d⁶ R_S/(m_S m_P²) anni

k è un parametro che dipende dalla rigidità del satellite e varia a seconda che il corpo sia ghiacciato o roccioso. Come vedete, chi comanda veramente è la distanza che compare alla sesta potenza.

Se ci fermassimo qui, però, commetteremmo un grave errore di fisica. Abbiamo cambiato una rotazione, senza cambiare l’altra e nemmeno la rivoluzione. In questo modo, abbiamo ottenuto una diminuzione (o un aumento) del momento angolare totale, senza fare intervenire forze esterne a quelle del sistema (la gravità e la marea risultante esistono all’interno dello stesso sistema fisico).

Questo, però, è impossibile, perché si sa benissimo che il momento angolare totale del sistema DEVE rimanere costante (leggetevi le lezioni sul momento angolare…).

Come si fa, allora, a cancellare questa mostruosità? Presto detto: si trasferisce ciò che si è guadagnato (o si è perso) nel momento angolare di rivoluzione. In altre parole, se il momento angolare di rotazione diminuisce (o aumenta) si deve aumentare (o diminuire) quello di rivoluzione, allargando l’orbita del satellite (oppure il viceversa), in modo che la somma rimanga costante. Ciò è quello che è capitato alla Luna che, nata molto vicina a noi, ha raggiunto la sincronizzazione a scapito della distanza dalla Terra. Oggi la sua orbita è molto più larga di qualche miliardo di anni fa.

Però, però… sappiamo anche che essa continua ad allontanarsi. Qui le cose sembrano complicarsi. In realtà non è così. Tutto ciò che abbiamo detto per il satellite vale anche per il pianeta, anche se in forma ridotta. Il pianeta subisce le conseguenze della marea del satellite e si deforma in modo simile anche se meno violentemente. Tende, perciò, a rallentare (o a velocizzare) la sua rotazione. Anche la Terra lo sta facendo, benché sia troppo grande per arrivare a una sincronizzazione completa (tutti e tre i periodi perfettamente uguali tra loro). Come conseguenza, la Luna continua ad allontanarsi.

Nel Sistema Solare (a parte alcuni asteroidi) il meccanismo completo di sincronizzazione è giunto alla fine solo per Plutone e Caronte (probabilmente lo troveremo anche su altri KBO). Per loro sono uguali sia le due rotazioni che la rivoluzione. Ciò è stato possibile perché gli oggetti hanno una massa comparabile e, quindi, i tempi necessari per la sincronizzazione dei due periodi di rotazione con quello di rivoluzione sono molto simili.

Non sempre le configurazioni finali che abbiamo descritto sono quelle che si ottengono in natura. Si possono trovare altre soluzioni di equilibrio. Una ce la mostra il piccolo Mercurio.

Quando l’orbita è eccentrica (proprio il caso del primo pianeta del Sistema Solare) e l’effetto mareale non eccessivo, si può giungere a una situazione che potremmo dire “intermedia”. Invece di una sincronizzazione, si ottiene una più complicata risonanza orbitale, chiamata risonanza spin-orbita, ossia una risonanza tra periodo di rotazione e periodo di rivoluzione. Il loro rapporto, come per le risonanze di moto medio, di cui abbiamo parlato a lungo per gli asteroidi, deve essere formato da numeri piccoli e interi. La sincronizzazione, discussa precedentemente, diventa un caso particolare di questo tipo di risonanza, quello che si ottiene per il rapporto 1:1.

Nel caso di Mercurio la risonanza è la 3:2, cioè il pianeta ruota tre volte intorno al suo asse nel tempo in cui compie due rivoluzioni intorno al Sole. Ciò implica che il giorno solare (intervallo tra due passaggi del Sole al meridiano) è uguale esattamente a due rivoluzioni attorno al Sole. Quindi il pianeta mostra la stessa faccia al Sole ogni due anni mercuriani, come rappresentato in Fig. 13.

Ricordiamo che questa scoperta è stata fatta solo nel 1965, attraverso osservazioni radar. Vi sembra strano? In realtà no.  Prima si pensava che Mercurio fosse sincronizzato col Sole. Così almeno mostravano le osservazioni. Invece era solo colpa del caso, dato che il periodo di rotazione di Mercurio è esattamente la metà del suo periodo sinodico rispetto alla Terra. Ne consegue che ogni volta che il pianeta si trova nelle giuste condizioni di visibilità appare sempre nella stessa configurazione rispetto al Sole. Accidenti, veramente una bella sfortuna! Mercurio non è nuovo a insegnarci concetti molto importanti. Pur se così piccolo è stato fondamentale per verificare la teoria della relatività. Ma questo è un altro discorso.

Le rotazioni della Luna

Visto che stiamo per parlare di Luna, anche se il discorso c’entra poco con la marea, possiamo chiederci: “Siamo sicuri di conoscere tutto sulla sua rotazione?”

Sembra una domanda banale e forse tutti voi siete capaci di dare una risposta. Tuttavia, le modalità di rotazione del nostro satellite sono descritte raramente anche se hanno risvolti importanti come quello relativo all’esistenza di ghiaccio d’acqua nei suoi poli. Vale la pena parlarne un poco e fare chiarezza. Anche perché ne è stato studioso fondamentale un grande astronomo italiano: Gian Domenico Cassini.

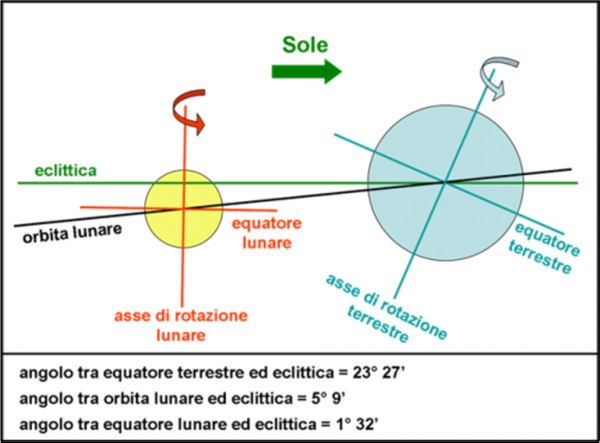
Si sa benissimo che l’equatore della Terra è inclinato di 23° e 28’ rispetto al piano dell’eclittica, ossia il piano dove avviene la rivoluzione intorno al Sole del sistema Terra-Luna. Proprio questo fatto dà origine alle stagioni, estremamente importanti per la vita sul nostro pianeta. Si sa anche abbastanza bene che il piano orbitale della Luna intorno alla Terra forma un angolo di 5° e 9’ rispetto al piano dell’eclittica. Si sa anche che la Luna ci rivolge sempre la stessa faccia (abbiamo appena dimostrato il perché). Abbiamo, quindi, automaticamente risposto a una parte della domanda: “La Luna ruota intorno a un asse e il suo periodo è esattamente uguale a quello di rivoluzione attorno alla Terra”.

Tuttavia, quanti sanno la direzione dell’asse di rotazione lunare? Forse tanti, forse pochi, ma sicuramente è un dato poco conosciuto. Eppure è proprio a causa della direzione dell’asse se esiste ghiaccio d’acqua sul nostro satellite.

Si è già discusso del fatto che esistono crateri lunari, in prossimità dei poli, che non ricevono mai la luce solare. In quei luoghi, costantemente al freddo, si ipotizzava da tempo che potessero essersi conservati depositi di ghiaccio d’acqua trasportato da comete cadute sulla superficie del nostro satellite. Una missione della NASA ha anche provato direttamente la verità di questa ipotesi.

E’ facile sollevare, allora, un’altra domanda: “Perché esistono zone in cui la luce del Sole non riesce mai ad arrivare? I crateri non sono così profondi da nascondere il loro fondo se non ci fosse una geometria generale favorevole”.

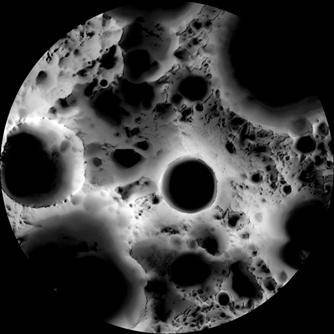
Guardate l’immagine del polo sud della Luna  riportata in Fig. 14. Essa è stata ottenuta attraverso il Lunar Reconnaissance Orbiter della NASA, la navicella che nella sua orbita attorno alla Luna ha il compito di fotografare continuamente il suolo del satellite per pianificare al meglio le future missioni. Ogni foto scattata al polo sud, per un periodo di sei mesi, è stata convertita in un’immagine binaria in modo che a ogni pixel illuminato dal Sole è stato assegnato il valore di 1, mentre a quelli in ombra il valore 0. Le foto così elaborate sono state poi sovrapposte  determinando per ogni pixel la percentuale di tempo in cui ha ricevuto luce. Il risultato è stata una “mappa d’illuminamento”, in cui si notano chiaramente le zone rimaste sempre in ombra e quelle poche (creste vulcaniche o picchi) rimaste sempre alla luce. Le scale di grigi riflettono invece zone che hanno subito periodi sia di oscuramento che di illuminamento. Veramente suggestiva e istruttiva.

Torniamo, però, alla nostra domanda. Per ottenere questo risultato e avere buio completo in zone molto estese è necessario che l’asse di rotazione lunare sia diretto nel verso giusto rispetto al Sole. In particolare, che esso sia praticamente perpendicolare all’eclittica. E così è infatti.

L’equatore lunare è inclinato rispetto all’eclittica di solo 1° e 32’. Un’inezia, che permette di avere grandi zone d’ombra e di conservare l’acqua piovuta dal… cielo. Ovviamente, una situazione simile avviene anche al polo nord.

Questa conformazione geometrica era già stata studiata e tradotta in leggi dal grande astronomo ligure Gian Domenico Cassini nel 1693, durante le sue ricerche sulle maree e sulle loro influenze sui satelliti. Riferite alla Luna, esse dicono:

1)      Il periodo di rotazione della Luna è sincronizzato con il periodo orbitale attorno alla Terra.

2)      L’asse di rotazione della Luna mantiene una inclinazione fissa rispetto al piano dell’eclittica.

3)      L’asse di rotazione, la normale all’orbita e la normale all’eclittica sono complanari.

Dopo tre secoli, queste leggi sono state recentemente verificate attraverso i metodi più sofisticati della meccanica celeste, che hanno confermato la loro quasi perfetta esattezza. La Fig. 15 ci mostra la conformazione geometrica del Sistema Terra-Luna.

Siamo arrivati finalmente alla marea terrestre: poca cosa se non ci toccasse così da vicino e se la Terra non fosse coperta di grandi distese di acqua.

La marea oceanica

Va subito detto che una descrizione accurata del fenomeno delle maree oceaniche è tutt’altro che semplice, dato che concorrono un numero incredibile di fattori non solo astronomici ma anche collegati ai fondali oceanici e a quelli costieri e a molte altre cose. Ne do quindi una trattazione veramente elementare.

Per semplicità consideriamo la Terra come una sfera circondata completamente dalle acque (come se non ci fossero terre emerse). Nella Fig. 16, la parte solida della Terra è rappresentata dal cerchio più scuro, mentre l’oceano che la circonda ha uno sfondo più chiaro. La distanza e le dimensioni della Luna non sono in scala, per meglio apprezzare la configurazione generale.

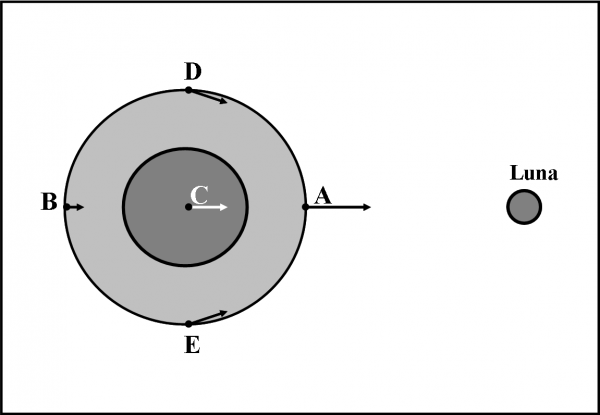
Consideriamo 5 punti particolari sul nostro pianeta: A è il punto più vicino alla Luna, B il più lontano, D ed E due punti intermedi,  C è il centro della Terra. Il punto A, più vicino, subisce una certa forza gravitazionale da parte della Luna. Il punto B subisce anch’esso una forza, che è però più piccola in quanto B è più lontano dal nostro satellite.  Il centro della Terra ( C ) si trova a una distanza intermedia e quindi subisce una forza intermedia. Analogamente i punti D ed E subiscono una forza anch’essa diretta verso la Luna. Le frecce riportate in figura indicano l’intensità e la direzione delle forze in accordo con quanto detto precedentemente: frecce più corte si riferiscono a forze minori.

In altre parole A è più attratto dalla Luna di quanto non lo sia B (tanto per cambiare…). A causa di queste forze agenti sulla Terra, si potrebbe pensare che l’intero pianeta si sposti verso la Luna. Questo però non può accadere in quanto la Luna orbita attorno alla Terra ed il centro della Terra mantiene sempre la sua posizione rispetto alla Luna. Per mantenere questa configurazione non dobbiamo allora considerare le forze che sono riportate in figura, ma le forze che si ottengono sottraendo a queste una forza uguale e contraria a quella esercitata sul centro C. Ne segue che il centro C rimane fermo (perché la forza finale che ne risulta è uguale a zero), mentre A si sposta verso la Luna e B in verso opposto. In altre parole, dobbiamo considerare solo gli spostamenti dei vari punti rispetto al centro della Terra che è costretto a rimanere fermo.

Come risultato finale si ottiene la configurazione illustrata in Fig. 17, dove le frecce più marcate sono quelle realmente esercitate sui singoli punti e ottenute dopo aver sottratto a quelle iniziali (riportate con tratto più leggero) la forza uguale e contraria esercitata sul centro della Terra, mentre A’, B’, D’ ed E’ rappresentano le posizioni finali dei punti A,B,D ed E dopo aver subito l’attrazione della Luna.  Ne consegue che l’intera massa oceanica subisce una deformazione  che  tende  ad allungarsi  nelle direzioni della Luna e in quella opposta, mentre tende a schiacciarsi in direzione perpendicolare.

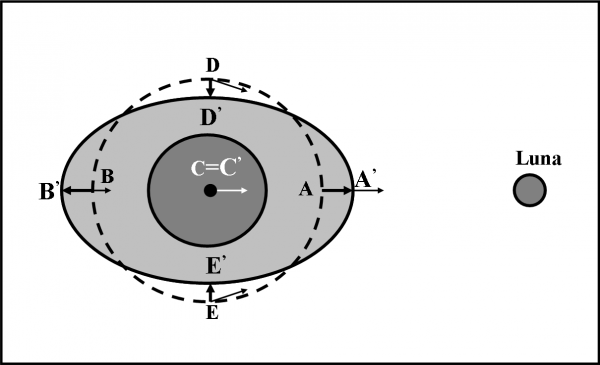
La nuova Terra è quella che passa per i punti A’, D’, B’ ed E’ (grigio chiaro), mentre quella originaria è rappresentata dalla linea tratteggiata. Il sollevamento subito da A (e da B) e l’abbassamento subito da D (ed E) causano uno scorrimento delle acque da A’ e B’ verso D’ ed E’. Questo scorrimento origina la corrente di marea, che in prossimità delle coste può dar luogo a fenomeni anche molto appariscenti. Come si può notare la corrente di marea si ottiene solo perché i punti A’ (e B’) sono molto distanti da D’ (e E’). Se questi punti fossero molto vicini (come in un lago, o in una tinozza, o all’interno del corpo umano) non ci sarebbe spostamento relativo importante e gli effetti mareali sarebbero del tutto insignificanti.

Dato che la Terra ruota intorno al proprio asse (24 ore) molto più velocemente di quanto la Luna rivolva attorno al nostro pianeta (circa 29 giorni), la deformazione, che è sempre diretta verso la Luna, va ad interessare punti sempre diversi del globo. Un certo punto della Terra subirà un’alta marea quando si trova in A’, una bassa marea quando si trova in D’, un’altra alta marea quando passa per B’ ed un’altra bassa marea quando coincide con E’. In poco più di un giorno una data località subirà due alte maree e due basse maree, distanziate di circa 6 ore una dall’altra.

Ho detto poco più di un giorno in quanto anche la Luna si è spostata un poco rispetto alla Terra, per effetto del suo moto attorno al nostro pianeta, e quindi occorrerà un po’ più di tempo perché ci si allinei di nuovo con essa.

Come si è visto, le maree lunari si susseguono costantemente ogni giorno del mese. Come mai allora si pone particolare attenzione a quelle che capitano quando c’è la Luna Piena o la Luna Nuova ?  In queste due configurazioni particolari, il Sole (che esercita anch’esso una forza di marea sulla Terra, anche se minore di quella lunare) si trova nella stessa direzione della Luna rispetto alla Terra (Luna Nuova) o in direzione opposta (Luna Piena). In entrambi i casi la marea lunare si somma a quella solare e quindi maggiori sono gli effetti sul nostro pianeta.

Gli effetti saranno invece minori al Primo ed all’Ultimo Quarto, quando il Sole è in posizione perpendicolare rispetto a quella della Luna. La Fig. 18 illustra le quattro configurazioni descritte.

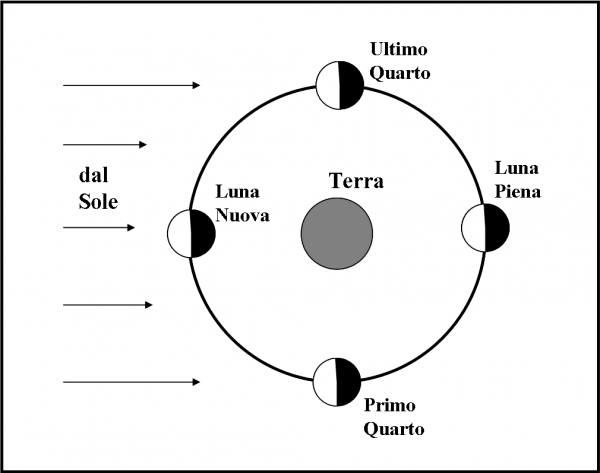
Ciò dimostra che gli effetti mareali della Luna, sono del tutto uguali quando c’è la Luna Piena e quando c’è la Luna Nuova. Favorire una situazione rispetto all’altra non ha quindi significato. Inoltre, al Primo e Ultimo quarto la marea è minore, ma non poi di tanto, dato che quella solare è meno della metà di quella lunare.

Per essere più esatti va detto che quanto descritto corrisponderebbe alla realtà dei fatti solo nel caso di una struttura oceanica perfettamente elastica e se non ci fossero attriti. Dato che le masse d’acqua non sono perfettamente elastiche, esse rispondono con un certo ritardo all’azione mareale della Luna. Inoltre la Terra gira su se stessa molto più rapidamente di quanto non si muova la Luna sulla sua orbita. Ne consegue che la deformazione dalla massa liquida non avviene quando la Luna è perfettamente allineata  (come illustrato in Fig. 17),  ma un  poco più tardi, ossia quando la Terra è già avanti rispetto alla Luna a causa della sua rotazione più veloce. La deformazione avviene quindi come rappresentato nella Fig. 19, dove la Terra “reale” è la figura grigia, mentre quella perfettamente “elastica” è quella tratteggiata.

La situazione è poi ancora più complessa in quanto bisogna anche tener conto della posizione del Sole. Tuttavia, quanto riportato è più che sufficiente per avere un’idea generale delle forze mareali. La configurazione non simmetrica di Fig. 19 causa però un altro effetto mutuo tra Terra e Luna di cui si era già fatto cenno precedentemente: il rallentamento della Terra e l’allontanamento della Luna. Infatti, l’azione gravitazionale della Luna sui rigonfiamenti dovuti alla marea tende a frenare la rotazione terrestre (freccia rossa in verso opposto alla rotazione terrestre). Come reazione a questa forza la Luna tende a ruotare più velocemente e, quindi, a portarsi su un orbita più lontana.

Qualcosa di molto simile a quanto capita negli anelli di Saturno per effetto di satelliti che li confinano. A titolo di esempio si stima che il giorno terrestre fosse di poco inferiore alle 22 ore circa 350 milioni di anni fa. Più in generale si può dire che la Terra rallenta di 0.0016 secondi al secolo e la Luna si allontana di 3-4 centimetri all’anno.

La Luna se ne andrà? Molto difficile, in quanto allontanandosi  diminuiranno gli effetti mareali e la Luna dovrebbe riavvicinarsi alla Terra in un continuo gioco di conservazione del momento angolare del sistema.