Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Questo articolo propone un problema di meccanica classica ben conosciuto e lo affronta a livelli di difficoltà diversi. Dal moto di un sasso lungo un buco che attraversi l'intero pianeta si giunge a conoscere sempre meglio il grande genio di Newton e ci si avvicina alla curvatura dello spaziotempo. Come al solito, l'articolo finirà nell'archivio, sempre più ricco...

Personaggi molto influenti dei passati governi italiani non hanno avuto problemi a ideare  (e dicono anche a realizzare?) “buchi” attraverso la Terra in modo da farci transitare i poveri neutrini che si sarebbero altrimenti trovati a dover superare tonnellate e tonnellate di dura roccia. Utilizziamo uno di questi tunnel, che congiunge in linea retta due punti della superficie terrestre. Poco importa se questi punti sono o non sono diametralmente opposti. Anzi potete provare a farne uno che passi per il centro della Terra e uno che vada solo da Ginevra al Gran Sasso. Il risultato è lo stesso.

Consideriamo la Terra perfettamente sferica, di densità costante, senza rotazione e, ovviamente, omogenea e fredda.  Non sono nemmeno ammesse frizioni e/o attriti.  A questo punto non ci resta che far “cadere” un oggetto all’interno del tunnel perfettamente liscio (state tranquilli che cade…). Le domande sono: “Quanto tempo impiega a raggiungere l’altra uscita del tunnel? Ma è sicuro che la raggiunga? E cosa fa se non viene fermato?”

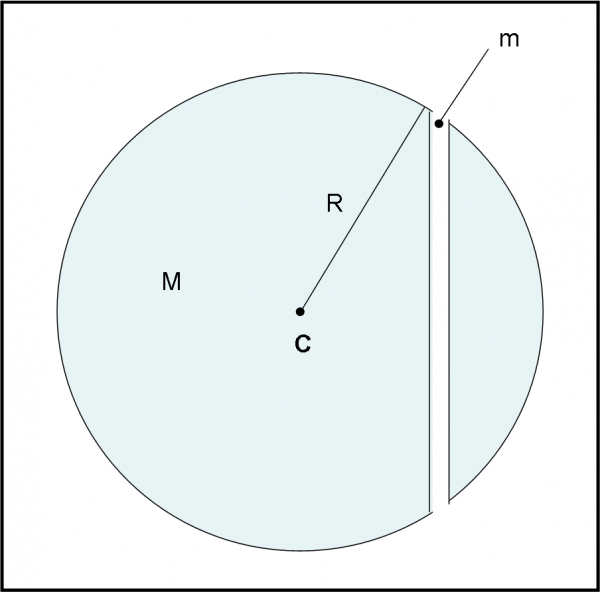
La figura da cui partire è quella che segue.

La massa dell’oggetto è m

La massa della Terra è M = 5.98 · 10²⁴ kg

La costante G vale 6.67 · 10⁻¹¹  m³/kg · s²

Il raggio della Terra  è R = 6.38 · 10⁶ m

Notate che ho fatto il tunnel in senso verticale per facilitare l’idea di una “caduta”, ma potevo disegnarlo anche orizzontale: non sarebbe cambiato niente.

Il problema è un “classico”, spesso legato alla vecchia barzelletta del verdone mangiasassi (il famoso uccello che viaggia pochi metri sotto la superficie terrestre e si ciba di sassi...) .

Piano d’azione

Per i meno preparati daremo una soluzione estremamente “occhiometrica”, che dovrebbe già far capire il succo dell’intera faccenda. Passeremo poi a una soluzione matematicamente completa che regalerà la descrizione del moto. Per questa fase leggermente più complicata accetteremo, momentaneamente, per buona una soluzione trovata da quel grande genio che è Newton. Poi ci spingeremo un po’ oltre e ricaveremo “rozzamente”, senza integrali, proprio questa soluzione. Non sentiamoci limitati, però. Lo stesso Newton l’aveva trovata in questo modo e la matematica più accurata aveva dimostrato l’esattezza della sua descrizione.

Senza entrare nei dettagli, vedremo anche come Newton era arrivato a concentrare tutta la massa di un corpo esteso nel suo baricentro. Un risultato ormai del tutto ovvio e accettato senza problemi, ma ben più complesso di quanto possa sembrare.

Concluderemo l’articolo con la descrizione completa della variazione del campo di gravità creato da una massa sferica come la Terra e con una rappresentazione spaziotemporale che sfrutta proprio il “buco” della Terra per avvicinarci sempre più alla comprensione della curvatura legata alla relatività generale.

Un programma davvero ambizioso, ma che rimane sempre a un livello abbastanza semplice per tutti, da cui i due soli asterischi.

Non si ferma più

Diciamo subito ciò che capita: il sasso cade nel buco e la attraversa arrivando dall'altra parte del foro con una velocità nulla ed è quindi pronto a tornare indietro e ripetere questo continuo tira e molla che non avrebbe fine se non ci fossero attriti.

Utilizziamo la Fig. 1, dove in alto disegniamo sette istanti successivi della caduta della massa m dentro al buco. A parole, il problema è abbastanza semplice. La massa m viene attratta dalla massa che sta sotto di lui (o sopra, insomma tra lui e il centro), ma il buco le permette di muoversi in una sola direzione.

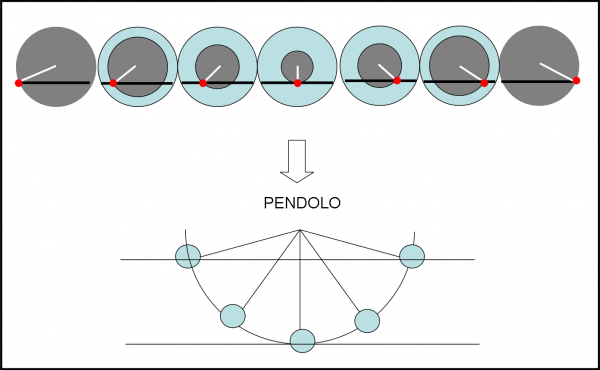
Energeticamente parlando la nostra massa m, alla partenza, ha una certa energia potenziale, ma una energia cinetica uguale a zero. Lasciamola libera di muoversi, sotto l’azione dell’unica forza che agisce su di lei, quella di gravità. A mano a mano che si sposta diminuisce la sua energia potenziale e aumenta quella cinetica. Quest’ultima raggiunge un massimo proprio nel punto di minima distanza dal centro della Terra, dove possiamo considerare nulla quella potenziale (la massa che l’attrae è la minima possibile per il tragitto scelto). La massa m, quindi, non può fermarsi e prosegue nella sua corsa, perdendo energia cinetica e riguadagnando energia potenziale. Si ferma quando ha raggiunto quella iniziale. Se non la fermassimo con una mano, tornerebbe indietro ripetendo il giochino.

A nessuno è certamente sfuggita l’estrema somiglianza con le “montagne russe” dei Luna Park. Il trenino parte dall’alto con energia cinetica zero e energia potenziale massima. Al fondo della discesa si annulla l’energia potenziale che, trasformatasi interamente in energia cinetica, permette al trenino di risalire fino a un’altezza uguale a quella iniziale, ristabilendo le due energie di partenza. Insomma, il solito vecchio concetto della conservazione dell’energia! L’unica vera differenza è che, nel caso del “buco”, l’accelerazione gravitazionale varia durante il viaggio.

In questo modo siamo già in grado di capire ciò che succede e si potrebbe anche calcolare la velocità acquisita dalla massa m nei vari punti del “buco”.

Un’analogia ancora migliore si ha, forse, con il moto di un pendolo, rappresentato nella parte bassa della figura. La distanza tra centro della Terra e massa m (punto rosso) sembra muoversi proprio come la corda del pendolo… La Fig. 2 aiuta già a capire che niente cambia se il “tunnel” passa dal centro della Terra. La cosa non deve certo stupire. Se prendete un pendolo e lo fate partire più in alto o più in basso, il tempo che impiega a completare un’intera oscillazione è sempre lo stesso (per piccole oscillazioni) e dipende solo dalla lunghezza della corda e dall’accelerazione di gravità. Nel caso attuale, le analogie finiscono qui, dato che l’accelerazione di gravità è una variabile così come lo è la distanza dal centro della massa attraente.

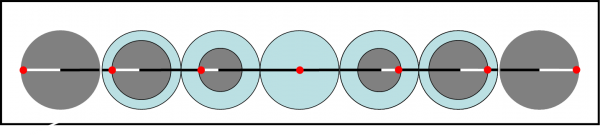
In modo molto qualitativo possiamo già intuire che qualsiasi sia la corda che attraversa la Terra, la massa m impiega sempre lo stesso tempo a passare da una parte all’altra. Vedremo che questo tempo è più breve di quanto si possa pensare: solo 42 minuti per attraversare l’intero pianeta. Risulterà anche ovvio che se la massa partisse all’interno della Terra (lungo il buco) essa arriverebbe solo fino a una distanza, rispetto al centro della Terra, uguale a quella di andata. Ancora una volta, però, il tempo impiegato rimarrebbe lo stesso. In poche parole, il tempo di oscillazione è indipendente dal tragitto scelto e dalla lunghezza percorsa.

Per provare quanto detto dobbiamo fare comparire qualche formuletta in più, cosa che faremo tra non molto.

Riflettiamo ancora un attimo sul risultato “preliminare” della situazione. Beh… se la Terra fosse davvero omogenea, senza calore interno e senza rotazione e il buco fosse perfettamente liscio si potrebbe andare dall’Italia alla Nuova Zelanda in soli 42 minuti, con una fermata (istantanea) turistica al centro della Terra, dove si sarebbe senza peso dato che si annulla la gravità. Vale la pena, infatti, riguardare bene le due figure precedenti. A mano a mano che la massa m si avvicina al centro della Terra, la massa che fa sentire la propria gravità è solo quella della parte interna del pianeta (cerchio grigio scuro).  Non preoccupatevi se la cosa vi sembra un po’ strana: è proprio quello che vogliamo dimostrare nella terza fase della spiegazione, facendoci aiutare da Newton. Nel caso del tunnel che passa proprio per il centro, la massa interna si annullerebbe: niente accelerazione di gravità e, quindi, niente peso!

Una massa variabile e un moto speciale

Risolviamo il problema da un punto di vista più fisico e matematico. Ci basta e avanza, però, la forza di gravitazione. Continuiamo ad accettare, come atto di fede, per adesso, quanto detto poco fa: la massa della Terra che agisce gravitazionalmente sulla massa m è solo quella relativa alla sfera che ha come raggio proprio la distanza (variabile) r, dal centro della Terra, della massa m. Insomma, su P agisce solo la parte della Terra compresa al suo “interno”. Chiamiamo P il punto di massa m e passiamo alla Fig. 3.

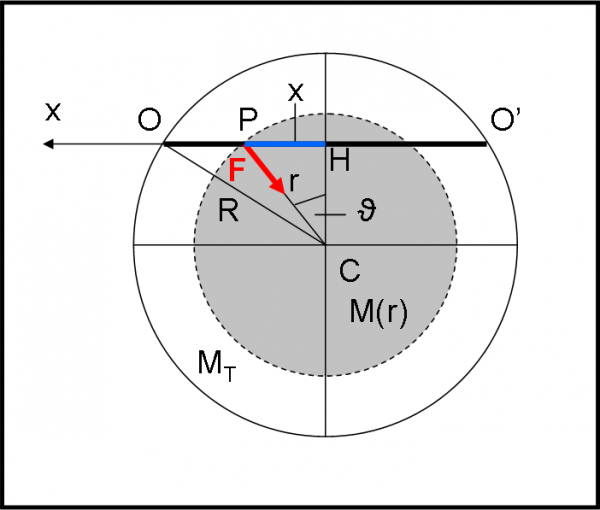
Prendiamo come asse dello spostamento x di P la retta orizzontale, lungo il buco, diretta verso sinistra (ossia le x si misurano a partire da CH). La linea tratteggiata indica proprio la sfera la cui massa è quella che agisce su P. r è il raggio istantaneo di questa sfera “attiva”. Su P agisce, perciò, una forza F variabile diretta verso C. Attenzione: anche questa asserzione, ossia considerare il centro della Terra C come il punto in cui viene applicata la massa, è un atto di fede, dato che bisognerebbe dimostrarlo, come vedremo tra non molto.

La forza nel punto O vale qualcosa di ben conosciuto (tutta la Terra è sotto il punto O):

F = GmM_T/R²

Appena il punto P si muove, varia r e di conseguenza varia la massa contenuta all’interno della sfera istantanea. In parole matematiche, la massa M è una funzione di r, ossia M = M(r).

Come detto fin dall’inizio, assumiamo che le densità sia costante per tutta la Terra. Possiamo allora scrivere che essa vale:

ρ = M/V = M/(4πr³/3)

da cui

M = ρ 4πr³/3    …. (1)

Questa è proprio la massa M(r) di cui abbiamo bisogno. Tuttavia, la densità della Terra è quella che è, e vale:

ρ = M_T/V_T = M_T/(4πR³/3)

sostituendo nella (1) si ottiene:

M = M_T (4πr³/3)/(4πR³/3) =  M_T r³/R³

La forza di gravità che agisce su P, vale, perciò:

F = GMm/r² = GmM_T r³/(R³ r²) = GM_T m r /R³

Questo è già un risultato interessantissimo: la forza varia linearmente con il raggio r

Tuttavia, a noi interessa solo la componente della forza diretta lungo il buco. Risulta subito dalla Fig. 3 che:

F_x = - F sin(ϑ)                (va in verso opposto all’asse x)

Ma:

sin(ϑ) = x/r

e si ottiene subito:

F_x = - (x/r) (GM_Tm r/R³) = - (GM_Tm/R³) x         …. (2)

La componente “attiva” della forza dipende linearmente solo dall’ascissa del punto P. Non compare assolutamente la distanza dal centro e quindi il moto è indipendente dal percorso del “buco”. L’unica variabile, infatti, è l’ascissa x. Oltretutto, per la stessa ragione, la massa può partire da qualsiasi punto del buco e la forza non cambia. Notate che abbiamo avuto bisogno di far comparire l’ascissa, dato che per studiare il moto di P dobbiamo proprio studiare la variazione di x nel tempo.

F_x è, comunque, una forza e il secondo principio della dinamica dice che essa vale:

F_x = m a = m d²x/dt²     …. (3)

Dalle lezioni di matematica sappiamo, infatti, che l’accelerazione non è altro che la derivata seconda della x fatta rispetto al tempo (la velocità è la derivata prima, ma l’accelerazione è la derivata della velocità e quindi l’accelerazione e la derivata della derivata…).

Uguagliando la (2) e la (3) si ottiene:

- (GM_Tm/R³) x = m d²x/dt²

E, infine:

d²x/dt²  = - (GM_T/R³) x       …. (4)

La (4) è l’equazione del moto del punto P, dato che ci dice come varia la sua ascissa in funzione del tempo. Essa è una equazione ben nota, del tipo:

d²x/dt² = - kx

dove k = GM_T/R³  è una costante.

Beh…. Adesso la somiglianza con il moto del pendolo è perfetto. Potrei dirvi, facendolo cadere dall’alto, che l’equazione (4) rappresenta il moto armonico semplice (ossia la variazione, istante per istante, dell’ascissa di un pendolo rispetto a un punto fisso). Si potrebbe anche risolvere l’equazione (differenziale) e usare gli integrali, ma posiamo benissimo limitarci alle derivate e ragionarci un po' sopra…

Il pendolo sotterraneo

Cerchiamo, allora, di ragionare con la nostra testa. Cosa dice “esattamente” un relazione come la (4)? Leggiamola passo a passo: “Prendiamo una x(t) ed eseguiamo la sua derivata seconda. Dopo aver fatto ciò otteniamo che il risultato non è altro che la stessa x cambiata di segno, moltiplicata per una costante”. In poche parole la x deve essere una funzione la cui derivata seconda vale ancora x, moltiplicata per una certa costante e cambiata di segno.

Beh… pensandoci un po’, non è difficile trovare una funzione la cui derivata seconda sia nuovamente la funzione di partenza. Basta pensare alle funzioni trigonometriche.  Ad esempio, prendiamo x = cos (t), immaginando per un attimo che t sia l’angolo variabile. La sua derivata prima è dx/dt = - sin (t); la derivata seconda è d²x/dt² = - cos(t). Perfetto, abbiamo trovato la funzione adatta! Rimane, però, da lavorare un po’ con quella costante k che moltiplica la x.

Innanzitutto, non usiamo più t come angolo, ma un vero angolo che vari con t. Basta moltiplicare t per 2π/P, dove P è il periodo della funzione coseno. Moltiplicando 2π/P per t, otteniamo, al variare di t, l’angolo (in radianti) corrispondente.

Chiamiamo, per semplicità, ω = 2π/P (non è altro che la frequenza dell’oscillazione) e scriviamo:

x = cos (ωt)

La derivata prima diventa:

dx/dt = - ω sin (ωt)     …. (5)                              (ricordate… funzione di funzione)

la derivata seconda è:

d²x/dt² = - ω² cos (ωt) =  - ω² x                            (ricordate… derivata di un  prodotto)

Accidenti… è esattamente la (4), con:

ω = (GM_T/R³)^1/2

La frequenza è legata al periodo completo (da O a O’ e ritorno) da:

P = 2π/ω = 2π (R³/GM_T)^1/2

Con i valori che abbiamo, si ottiene finalmente:

P = 84.5 minuti

Dalla  (5) si possono ricavare le velocità istante per istante (la derivata prima è proprio la velocità!)

Ribadiamo ancora che l’equazione del moto è del tutto indipendente dalla lunghezza della corda e dalla massa m. Dovunque bucassimo la Terra, il tempo di attraversamento di una qualsiasi massa sarebbe sempre uguale, come nel pendolo.

A questo punto, volendo, si possono anche calcolare l’energia potenziale e cinetica e trovare l’energia totale del sistema istante per istante (comunque il problema è completamente risolto)…

Piccolo QUIZ (tanto per non perdere l’abitudine)

Voglio farvi una domandina semplice semplice: “Se ci mettessimo in orbita attorno alla Terra, esattamente al livello del suolo (Terra liscia e senza atmosfera, ovviamente), quale sarebbe il periodo di rivoluzione?”. Sembra qualcosa di completamente diverso? In un certo senso sì, ma in un altro no. Oltretutto, cambiando adeguatamente l’unità di misura, ci richiama alla mente un famoso “giro del mondo” letterario.

Il problema si può risolvere applicando il bilanciamento tra forza centripeta (gravità) e centrifuga.

GMm/(R²) = mω²R
dove :
R è il raggio della terra: 6,38*10^6 m
M è la massa della Terra: 5,98*10^24 kg
G è la costante di gravitazione: 6,67*10^-11 m3/kg*s^2
ω è la velocità angolare, da determinare, misurata in rad/s.

Svolti i calcoli si ottiene che:
ω = 0,001239 rad/s.

Ora, per compiere un giro completo si dovranno completare i 360° della circonferenza, che corrispondono a 2π radianti.

Quindi: 2π /0,001239 = 5.068 s = 85  min
Insomma, il giro del mondo in ottanta…cinque minuti!

Si poteva arrivare alla stessa conclusione ragionando sulle energie (potenziale e cinetica).

Il teorema della “shell”

Finora, abbiamo evitato di affrontare il punto, apparentemente, più complicato: perché la massa attiva sul punto P è sempre e soltanto quella relativa alla sfera di raggio uguale alla distanza, istante per istante, di P dal centro della Terra? A prima vista sembrerebbe un assurdo. Dove mettiamo la massa che sta sopra e di lato della nostra massa m che sta viaggiando dentro al “buco”? Potremmo chiederlo ai nostri esperti governativi che tutto sanno sui tunnel, ma noi preferiamo richiamare il Sig. Newton che aveva già risolto “brillantemente” il problema attraverso il suo teorema della “shell”, ossia del “guscio sferico”.

Cominciamo, cercando una soluzione puramente geometrica. P è in una certa posizione lungo il suo viaggio attraverso il buco (un punto qualsiasi, ovviamente). In Fig. 4 dividiamo il nostro cerchio (a parte quello grigio all’interno del punto) in zone che siano simmetriche rispetto alla direzione PC. Può darsi che si riesca a scoprire qualcosa…

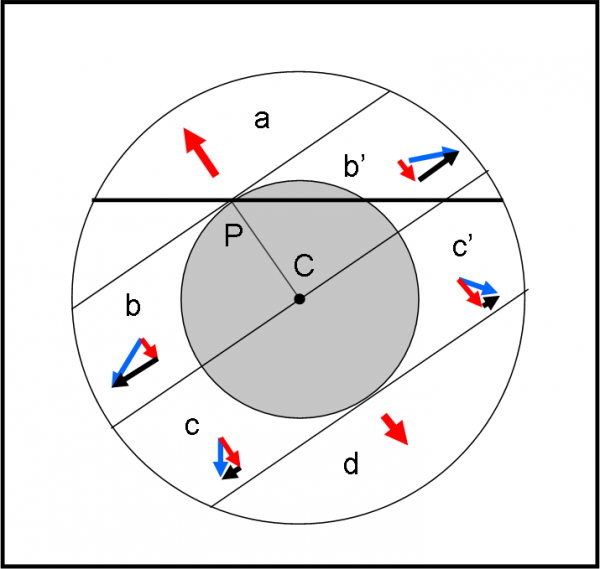
Le zone sono a, b, b’, c, c’, d. Potevamo anche sceglierle in modo diverso, ma poco importa. Ogni zona ha un suo centro di massa in cui possiamo applicare la forza esercitata su P (attenzione che stiamo ammettendo che la massa può essere concentrata nel baricentro… vedremo che non è cosa così ovvia).

Di tutte le zone considerate solo la (a) mostra una forza che cerca di trascinare P in direzione opposta a C. Analogamente, solo la zona (d) ha una forza diretta in senso opposto, ossia nel verso da P verso C. Non possiamo sapere quale sia il modulo delle forze, ma queste due non possono certo annullarsi a vicenda, dato che la massa deve essere uguale (la forma geometrica è la stessa), mentre la distanza è sicuramente diversa.

Andiamo avanti… (b) e (b’) agiscono con la forza azzurra. Essa può essere scomposta in una direzione perpendicolare e una parallela a PC. Quelle perpendicolari (nere) sono uguali e opposte e quindi si annullano (è già qualcosa). Rimangono, però, le due componenti rosse, entrambe dirette da P verso C.

Ci restano ancora le zone (c) e (c’). Tutto risulta simile a quelle precedenti. Dopo la scomposizione ci rimangono le due componenti rosse, ancora una volta dirette nel verso da P a C.

Un bel pasticcio. Noi vorremmo dimostrare che la somma di tutte queste forze è uguale a ZERO, ossia che tutta la parte esterna al cerchio grigio non agisce sul nostro punto P. A prima vista sembrerebbe assurdo. Tuttavia, non abbiamo calcolato i moduli delle varie forze e nemmeno il baricentro delle zone, per cui la nostra figura è solo MOLTO qualitativa… Possiamo passare ai numeri giusti? Beh… provateci voi… io non ci penso nemmeno!

Dovremmo calcolare la massa contenuta in ogni zona (dalla forma molto strana), trovare il baricentro e applicare la forza risultante che dipende anche dalla distanza tra punto P e baricentro di ciascuna zona. Insomma, è meglio abbandonare questa idea. O, quantomeno, Newton ha semplificato di molto la trattazione, conoscendo benissimo il calcolo infinitesimale. Facciamo come lui e tutto sarà semplicissimo e non dovremo nemmeno usare i tanto temuti integrali.

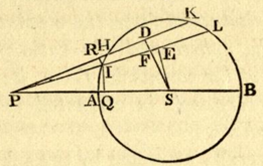
Partendo da P disegniamo un cono o una piramide quadrangolare (triangolo nel piano del foglio) di apertura φ, estremamente piccola (non abbiamo problemi matematici nel considerare angoli di questo genere). Consideriamo un guscio sferico sottilissimo e l’intersezione di esso col cono tracciato da P. Otteniamo la semplicissima Fig. 5.

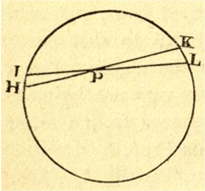
Notate che è proprio la figura disegnata da Newton! Risulta subito chiaro che i due triangoli PIH e PKL sono simili, dato che IH e KL possono tranquillamente essere approssimati con i segmenti corrispondenti. La Fig. 6 mostra come si possono trovare nei due casi (cono e piramide) le aree date dall’intersezione con il guscio sferico sottile.

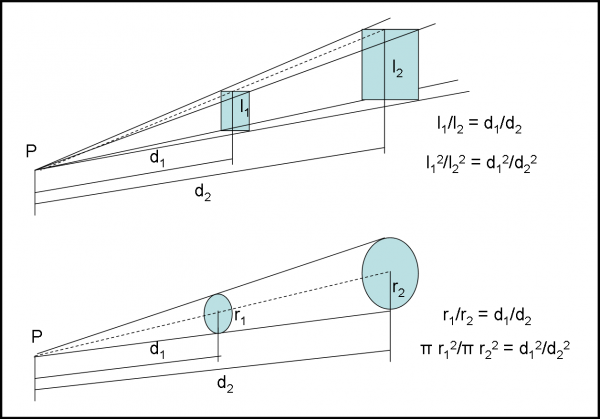
Abbiamo messo dalla stessa parte le piramidi e i coni delle intersezioni opposte rispetto a P, dato che i triangoli sono simili. Dalla similitudine risulta subito che, nel primo caso, si ha:

r₁/r₂ = d₁/d₂

facendo il quadrato e moltiplicando per π si ottiene subito:

π r₁²/ π r₂² = d₁²/d₂² = A₁/A₂      (rapporto tra le due aree)

Nel secondo caso:

l₁/l₂ = d₁/d₂

Facendo il quadrato:

l₁²/l₂² = d₁²/d₂² = A₁/A₂

I rapporti delle aree sono uguali ai rapporti delle distanze al quadrato. Le aree possono essere considerate dei volumi (lo spessore è piccolo, ma esiste) e anche delle masse (la densità è la stessa ovunque). In parole povere, abbiamo trovato che le masse aumentano con il quadrato della distanza. Tuttavia, sappiamo che la forza gravitazionale applicata a P va con l’inverso del quadrato della distanza.

F₁ = GmM₁/d₁²

F₂ = GmM₂/d₂²

Ma, abbiamo appena trovato che:

M₁/M₂ = d₁²/d₂²

Ossia:

M₁/d₁² = M₂/d₂²

E, quindi:

F₁ = F₂

Il modulo è lo stesso, ma il verso è opposto e quindi le due forze s’annullano.

Il giochino che abbiamo fatto è indipendente dalla posizione del punto P, dalla direzione del cono o piramide e dal guscio considerato. Quindi, possiamo concludere che confrontando tutti i “volumetti” costruiti in questo modo otteniamo sempre forze che si annullano. Tutta la massa esterna alla sfera centrale (variabile da punto a punto) non dà alcun contributo alla gravitazione subita dal punto P durante il suo viaggio attraverso la Terra.

Ovviamente, questo modo di ottenere il risultato è estremamente rozzo e abbastanza qualitativo (abbiamo fatto delle piccole approssimazioni). Potremmo usare qualcosa di più ambizioso, considerando la Fig. 7, dove vi è sempre il cono e lo spessore del guscio è posto uguale a dr. Un po’ di trigonometria aiuterebbe a ottenere un risultato più accurato, ma del tutto analogo a quanto fatto precedentemente (potete tranquillamente trovare il risultato che già conosciamo andando avanti con quanto impostato nella figura).

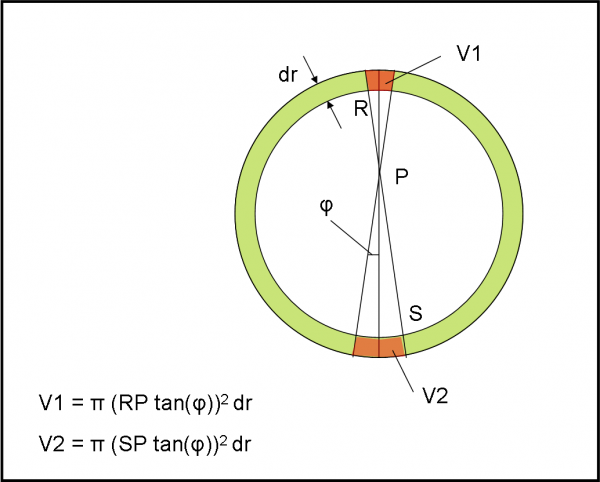
Se volessimo essere estremamente precisi dovremmo introdurre gli integrali e avremmo una soluzione perfetta (ma sempre la stessa, ovviamente).

Possiamo concludere che il punto P, durante il suo viaggio, risente solo della gravità della parte sferica di Terra che ha come raggio la distanza istantanea del punto P dal centro del pianeta. Tutto ciò che lo circonda si può trascurare dato che la forza gravitazionale risultante è nulla.

Guardiamo la Terra da fuori

Se questa dimostrazione è stata abbastanza semplice, non dobbiamo dimenticare il problema che abbiamo, ancora, lasciato da parte. A prima vista sembra ben più facile, ma, in realtà, è molto più complesso. Stiamo parlando del fatto che le forze agenti su di un punto esterno alla Terra possono essere considerate come un’unica forza applicata nel baricentro, dove è concentrata l’intera massa terrestre. Una cosa talmente utilizzata che non ci si pensa più.

La situazione è quella di Fig. 8.

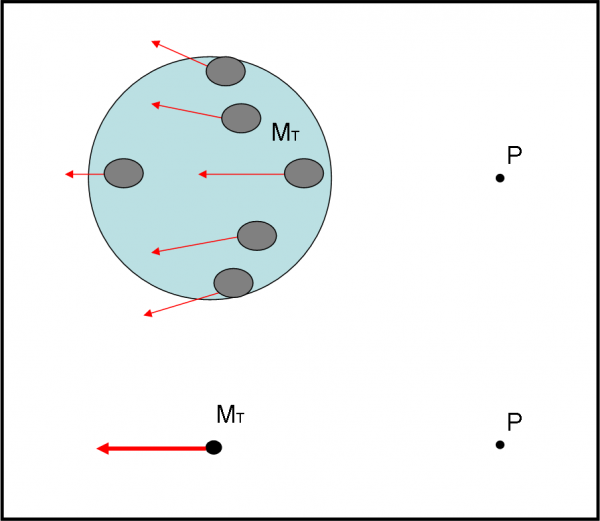
Come si vede, dovremmo valutare la forza di gravità relativa a ogni zona della Terra che ha una sua massa e una sua distanza. Un qualcosa di molto simile a quanto fatto prima per un punto interno alla Terra. La faccenda è, però, molto più complicata, anche se Newton l’aveva schematizzata con la Fig. 9. Ancora una volta, è questione di triangoli simili e cose del genere. Tutto risulta più preciso e “semplice” considerando anelli di Terra ed eseguendo i necessari integrali. Tuttavia, come possiamo intuire, non è cosa da prendere come procedimento “banale”… tutt’altro!

Questa dimostrazione sarebbe necessaria anche per quanto abbiamo fatto noi con i nostri volumetti piccoli piccoli. Anche per loro abbiamo assunto che la massa fosse concentrata nel baricentro. Se pensiamo che, una volta scritta la legge di gravitazione universale, tutto sia diventato semplice per Newton, ci sbagliamo di grosso. I teoremi e le dimostrazioni che ha dovuto affrontare sono stati tanti e anche complicati. Non basta una mela in testa, ma ci vuole anche la … testa! E poi qualcuno dice che la meccanica classica non è affascinante e piena di sorprese…

Le risposte sono state date, ma vale la pena introdurre brevemente due concetti molto importanti. Uno riguarda sempre la meccanica newtoniana, l’altro un ulteriore stimolo per la curvatura dello spazio.

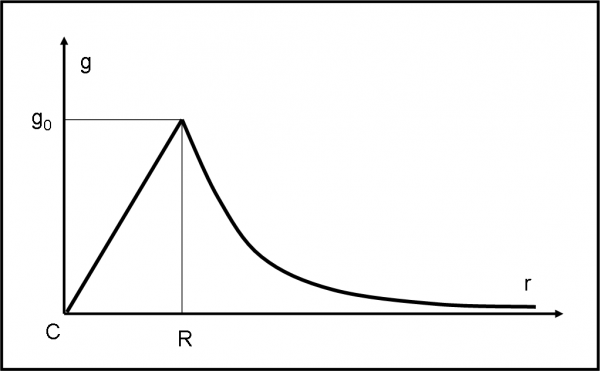
L’andamento di g

Normalmente viene chiamata  g₀ l’accelerazione di gravità della Terra. Essa viene considerata costante, dato che il nostro "mondo" normale opera e vive a una distanza dal centro della Terra (dove si può concentrare la massa, ormai lo sappiamo bene) che è praticamente sempre uguale: cosa sono pochi chilometri rispetto alle migliaia di chilometri che ci separano da quel punto misterioso? Questa accelerazione è data da:

g₀ = GM_T/R²

La formula generale è, però:

g = GM_T/r²

g è, in realtà, variabile, dato che dipende dalla distanza r. Non abbiamo, però, problemi a disegnare la sua variazione andando verso lo spazio (capite perché è importante lo studio delle funzioni?). La massa M_T della Terra è sempre la stessa e quindi l’unica variabile è la distanza r. La funzione è del tipo:

y = c/x²                     (potete studiarla voi)

Nella Fig.10, riportiamo in ordinata l’accelerazione g(r) e in ascissa la distanza r dal centro della Terra. A partire da un punto della superficie terrestre, la curva tende a zero andando verso l’infinito (sempre che non ci siano altri pianeti, stelle o galassie rompiscatole). Questo andamento della “efficacia” della nostra “ragnatela” (ricordate) lo conosciamo già molto bene. Adesso, però, possiamo anche disegnare l’andamento “interno” alla Terra. Lo abbiamo determinato risolvendo il problema del buco…

La forza agente, punto a punto, è:

F = (GM_Tm r /R³)

quindi, l’accelerazione g è:

g = K r

dove K è una costante.

La funzione è una retta che ha l’origine nel centro della Terra e che vale g₀ sulla superficie, collegandosi al tratto “esterno”. In questo modo, abbiamo completato la famosa ragnatela del campo gravitazionale terrestre, penetrando anche nel suo interno fino a raggiungerne il centro. Per la seconda volta ci colleghiamo a un romanzo di Giulio Verne…

Un buco rettilineo ci mostra la curvatura

Bene, adesso ci resta la parte più “difficile”, anche se non presenta nessuna formula. Potevamo anche tralasciarla, ma la voglio inserire per far notare come un discorso puramente dinamico newtoniano ci serva per capire come agisce la curvatura di uno spazio e come si evidenzino bene i movimenti spaziali e quelli spaziotemporali in uno spaziotempo curvo (può anche servire per lo spazio piatto di Minkowski…).

Ormai sappiamo riconoscere una superficie curva. E’ molto facile se la vediamo in modo estrinseco, aggiungendo una dimensione in più, ma è anche calcolabile vivendoci sopra.  A sinistra di Fig. 11 vediamo quattro abitanti che partono dall’equatore di una sfera e vanno verso il polo.

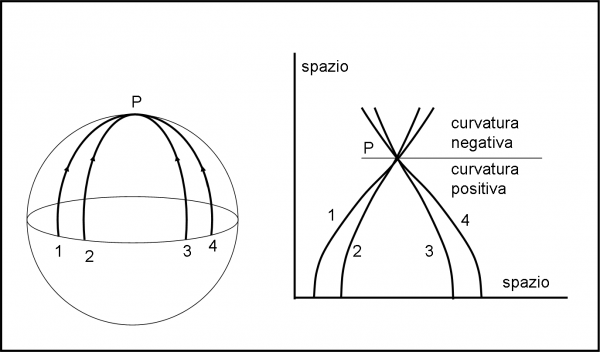
In questa visione estrinseca il fatto che convergano verso il polo P è una conseguenza ovvia. Cosa provano, però, gli abitanti di questa superficie. Partono lungo traiettorie che formano un angolo di 90° con l’equatore e quindi, nella nostra tradizione euclidea, “dovrebbero” percorrere delle rette parallele. Tuttavia, la superficie sferica non è euclidea. Dopo un certo tempo, camminando alla stessa velocità, si incontrano al polo P. Si rendono conto di essere su una superficie curva (sempre che siano istruiti…) e, dato che le loro traiettorie si incontrano, sono di fronte a una curvatura positiva. Se non fossero “istruiti”, potrebbero non stupirsi affatto: per loro “non-euclidei” le rette parallele si incontrano “normalmente” in un punto. Se proseguissero lungo le loro strade si allontanerebbero nuovamente e arriverebbero in punti dell’equatore del tutto simili a quelli di partenza. Direbbero che la curvatura è diventata negativa.

Attenzione: abbiamo realizzato una curvatura intrinseca nello spazio, per l’esattezza in uno spazio curvo a due dimensioni.

L’esempio appena fatto può essere realizzato nello spaziotempo? Se ci riuscissimo, potremmo dire che esiste una curvatura spaziotemporale. Nel primo caso si tratterebbe solo di geometria dello spazio, nel secondo caso di geometria spaziotemporale. In entrambi i casi saremmo di fronte a una curvatura intrinseca, esistente nello spazio o spaziotempo e non visibile soltanto da un punto di vista estrinseco (come il cilindro che ha intrinsecamente una geometria piana euclidea, ma che risulta curvo aggiungendo una dimensione).

Ed ecco come ci aiuta perfettamente il buco terrestre. Usiamo la Fig. 12.

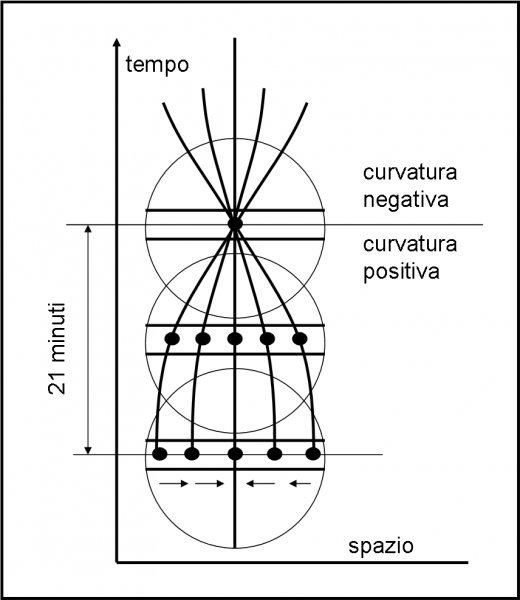
Nella visione estrinseca possiamo disegnare la Terra sferica con le nostre palline che vengono lasciate libere (in caduta libera, ossia sotto l’effetto della sola accelerazione di gravità). Sappiamo esattamente come si muovono nello spazio del buco: dovunque partano arrivano nello stesso istante nel punto centrale, proprio come hanno fatto i viaggiatori dello spazio sferico.

Adesso, però, vogliamo rappresentare questo moto nello spaziotempo, dove lo spazio è solo e soltanto la traiettoria percorsa nel foro (ascissa). L’ordinata diventa il tempo. Non ci resta che disegnare le cinque palline al variare del tempo (la Terra è stata disegnata, ma non c’era un bisogno reale, dato che bastavano le posizioni delle palline nel loro spazio). Dopo un certo tempo (21 minuti) tutte le palline arrivano nel punto centrale e le loro traiettorie nello spaziotempo sono le linee curve che congiungono le varie posizioni.

Abbiamo ottenuto la stessa figura di prima, lavorando, però, in uno spaziotempo. Possiamo concludere che esso ha mostrato le caratteristiche perfette della curvatura e, quindi, che esso è uno spaziotempo intrinsecamente curvo. Mentre le palline convergono la curvatura è positiva. Se continuassero il loro moto “libero” sentirebbero una curvatura negativa (dal centro verso i loro estremi laterali).

Nella Teoria di Newton questo risultato  dice solo che il l moto è dovuto alla gravità che agisce su di loro. Tuttavia, il risultato così simile alla curvatura di uno spazio, può anche dire una cosa completamente diversa: il moto delle palline in caduta libera è dovuto solo e soltanto a una curvatura intrinseca dello spaziotempo. Le traiettorie descritte non sono altro che le linee “rette” di questo spaziotempo curvo a due dimensioni (tale e quale al caso dei viaggiatori sulla sfera).

Notiamo una cosa fondamentale: la “grandezza” della curvatura non dipende dalla massa, ma solo dalla densità, come abbiamo ampiamente dimostrato risolvendo il problema del buco…

In conclusione: l’accelerazione di gravità non è altro che una manifestazione della curvatura intrinseca dello spazio tempo.

Basta… mi fermo, se no questo articolo diventa veramente un "volume" che abbraccia la gravità newtoniana, lo studio della curvatura delle superfici, la relatività generale e il modo di viaggiare senza consumare energia dall’Italia alla Nuova Zelanda!

Basterebbe fare un bel foro, rivestirlo di materiale che non conduca calore, rimescolare bene l’interno della Terra in modo da ottenere una densità costante, eliminare tutta l’aria dal tunnel, fare in modo che non crolli per la pressione, lisciarlo perfettamente e altre cosucce del genere, come eliminare del tutto i “verdoni mangia sassi”... Ammortizzate le spese di costruzione, il viaggio non costerebbe niente e poco importa se il merito è di Newton o della curvatura di Einstein. Ricordiamoci solo che all’arrivo bisogna saltare velocemente a Terra, per non tornare "tristemente"  al punto di partenza.

Se la Terra non è, forse, il pianeta adatto, chissà che un giorno  il treno “a gravità” (o è meglio chiamarlo pendolino come il treno ad alta velocità di tanti anni fa?) non sia realizzabile su un satellite di Saturno in cui non vi è atmosfera e la densità è abbastanza costante?

Utilizzando l'ormai ben nota formula:

P = 2π(R³/GM_T)^1/2

È facilissimo calcolare la durata del viaggio completo in tutti i corpi del Sistema Solare (Sole compreso) e non solo…