Continuiamo con i nostri esercizi sul baricentro, per poi passare al momento d'inerzia e al momento angolare. Visto il silenzio, dalla prossima volta inserirò subito la soluzione. Chi vuole esercitarsi può sempre fare a meno di leggerla.
D'ora in poi aggiungerò ai quiz la risposta in modo da dare maggiore sicurezza a chi cercherà di risolverli. Un paio di giorni di attesa e poi riporterò la soluzione particolareggiata.
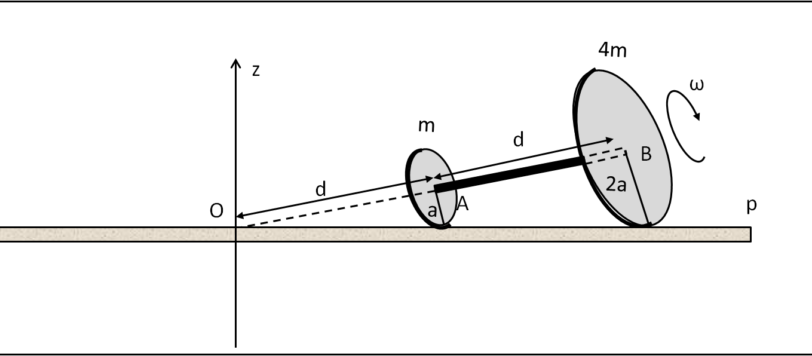
Ho trasformato il quiz sul carrello in un problema risolto passo dopo passo. Quello che è necessario sapere è stato trattato con tutti i particolari nel nostro Circolo (vedi archivio).
E' iniziato l'esodo estivo in massa (ma non erano tutti poveri in Italia?) e cerchiamo di divertirci un po'.
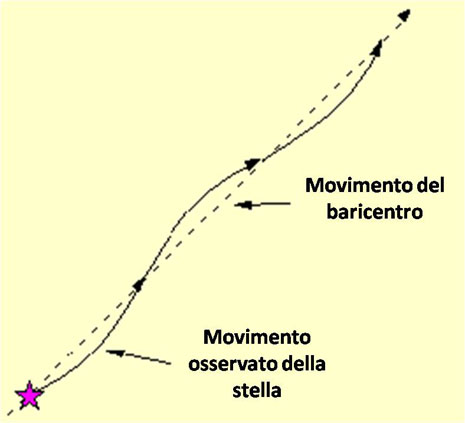
Andando ad analizzare una vecchia lastra fotografica del 1917, eseguita per determinare lo spettro della stella di van Maanen (una nana bianca molto vicina), ci si è accorti che vi era già la prova dell’esistenza di un sistema planetario attorno a questo residuo di stella di tipo solare. Quanti ricordi personali…
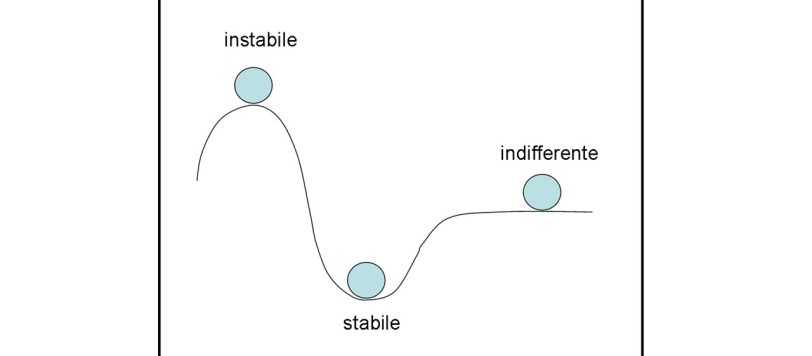
Approfondiamo l'argomento della stabilità dell'equilibrio che abbiamo trattato parlando del galleggiamento nell'ambito del teorema (o "principio") di Archimede, riproponendo un articolo che qualche anno fa abbiamo proposto sotto forma di quiz.
Vedo che i quattro amici non hanno riscontrato grande interesse... Poco male, dato che lo scopo del quiz era quello di introdurre una delle tante scoperte di Eulero uno dei più grandi matematici della storia, già noto attraverso la matematica superiore di Umberto e per la più bella formula matematica in assoluto (come diceva il grande Feynman). Noi tratteremo il tutto in modo estremamente elementare.
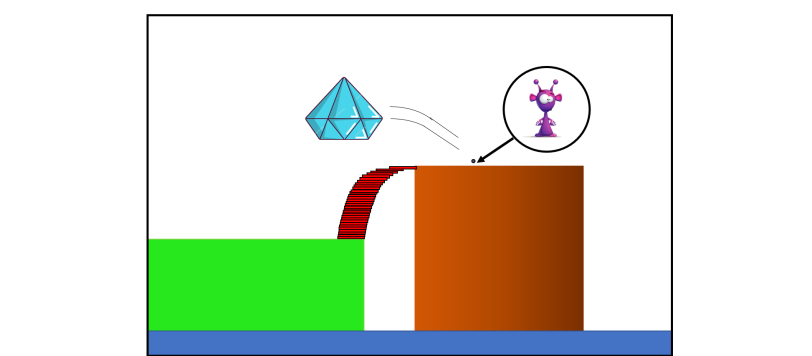
Andiamo a vedere come la nostra formica viola ha risolto il problema dello scoglio e si è impossessata del magnifico diamante.
Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica. Centinaia di barche a vela si sfidano per vincere la regata più celebre del mondo. Essa si svolge su un lago e la variazione del vento è la dominatrice della gara, unita all'abilità nel saperla sfruttare. Dopo ore e ore […]
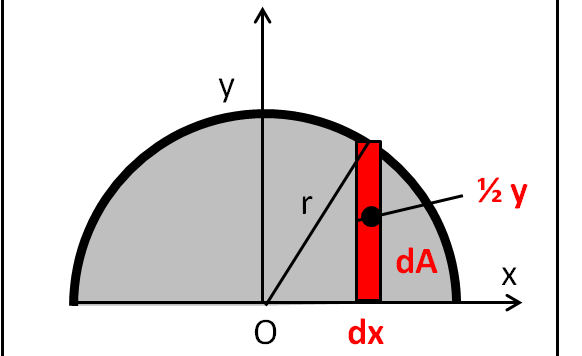
Come anticipato, il problema è decisamente facile e ha il solo scopo di richiamare la differenza che esiste tra baricentro geometrico e centro di massa.
Questo quiz è decisamente semplice, ma, come sempre, deve essere impostato correttamente. Il suo interesse sta nel richiamare un concetto fondamentale della geometria e della fisica.
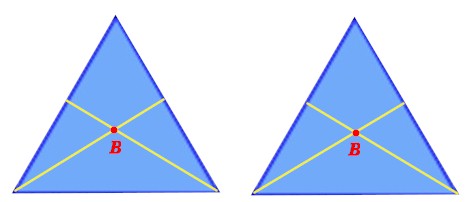
Abbiamo visto come un triangolo equilatero, appeso per un vertice, possa funzionare da bilancia. Ma se la volessimo davvero realizzare fisicamente, per pesare oggetti di pochi grammi, dovremmo dotare questa bilancia di una scala di lettura che indichi i grammi da zero alla portata massima, che possiamo fissare a 10 grammi. Possiamo decidere che questo sia anche il peso del nostro triangolo equilatero che fungerà da bilancia.
Dopo i consigli baricentrici per una sana alimentazione anche a Natale, non potevano mancare i consigli per trascorrere un Santo Stefano in perfetto stile Art-Attack. E poi non dite che non pensiamo a voi, cari lettori.
Buon divertimento a grandi e piccini di tutte le età!
Questo articolo propone un problema di meccanica classica ben conosciuto e lo affronta a livelli di difficoltà diversi. Dal moto di un sasso lungo un buco che attraversi l'intero pianeta si giunge a conoscere sempre meglio il grande genio di Newton e ci si avvicina alla curvatura dello spaziotempo. Come al solito, l'articolo finirà nell'archivio, sempre più ricco...
Questo quiz era passato nel dimenticatoio e grazie a Daniela è tornato alla memoria (mia per prima…). Ne diamo la soluzione che è veramente semplice e che vede la Luna come “rompiscatole” di turno.
Non si può parlare solo di matematica, di geometria e di giochi numerici ed ecco, allora, un quiz di fisica (meccanica classica), con un piccolo punto chiave. E’ ambientato su Papalla, dove sanno fare cose ancora impensabili per noi.
- 1
- 2