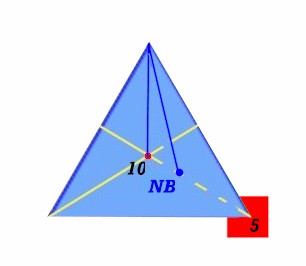
Abbiamo visto come un triangolo equilatero, appeso per un vertice, possa funzionare da bilancia. Ma se la volessimo davvero realizzare fisicamente, per pesare oggetti di pochi grammi, dovremmo dotare questa bilancia di una scala di lettura che indichi i grammi da zero alla portata massima, che possiamo fissare a 10 grammi. Possiamo decidere che questo sia anche il peso del nostro triangolo equilatero che fungerà da bilancia.

Pronti ?
Occorre investire un piccolo capitale (circa  5 Euro)  per acquistare in un centro di Bricolage una lastra di alluminio (non di ferro, perché useremo un magnete) di spessore 0,5 millimetri. Il formato che si trova facilmente è di 40x50 cm ed è sovrabbondante per il nostro utilizzo. Vuol dire che potrete realizzare diverse bilance da regalare agli amici. Farete un figurone! Oppure potrete usarle per fare scambio con qualcosa che vi piacerebbe avere, non farete un figurone ma porterete a casa una parte del capitale speso, o anche di più.

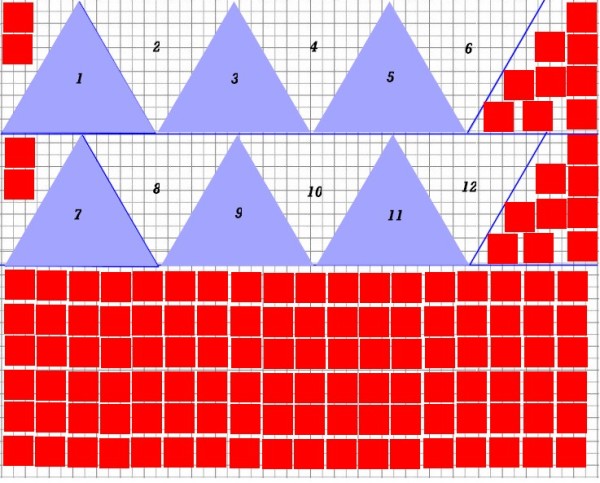
Seguendo questo schema potrete comodamente realizzare ben 12 bilance (triangoli equilateri) dotate ciascuna di 10 piccoli pesi  da un grammo, e vi avanzeranno 10 pesi di scorta, con uno spreco di materiale ridottissimo.

Ecco tutto quello che vi serve per la realizzazione: materiali e attrezzi.

Si tratta di cose di uso comune che potrete trovare in casa, tranne il foglio di lamiera di alluminio e, forse,  il magnete.  Vediamole in dettaglio:

1. foglio lamiera alluminio 40 x 50 cm spessa 0,5 mm       su cui compaiono .....
2. punta per tracciare segni sul metallo
3. gabbietta per tappo spumante
4. pinza
5. lima a grana fine
6. cesoie
7. martello leggero
8. asse di legno per proteggere ripiano tagliere
9. filo rosso da cucito
10. magnete toroidale piatto
11. chiodino in acciaio
12. spillo
13. due o tre fogli di carta                su cui compaiono .....
14. compasso
15. matita
16. nastro da mascheratura (leggermente adesivo)
17. gomma
18. super-colla Attak
19. forbici
20. righello

La radiolina non è obbligatoria, ma se vi piace ascoltare un po' di musica mentre lavorate, può servire.
Una raccomandazione da non sottovalutare è di sbordare con la lima dolce a taglio fine, subito dopo il taglio con le cesoie, tutto il perimetro del ritaglio, per rimuovere le sbavature che inevitabilmente si saranno formate a causa delle caratteristiche meccaniche dell'alluminio. E' opportuno anche dare una leggerissima smussatura agli angoli più acuminati.

Cominciamo a realizzare il corpo della bilancia: un triangolo equilatero di 12,8 cm di lato.  Se volete sapere perché deve avere proprio questa misura aprite il testo nascosto.

Potete fare la costruzione del triangolo equilatero di 12,8 cm di lato su carta, usando riga e compasso. Ovviamente i due  cerchi hanno raggio 12,8 cm

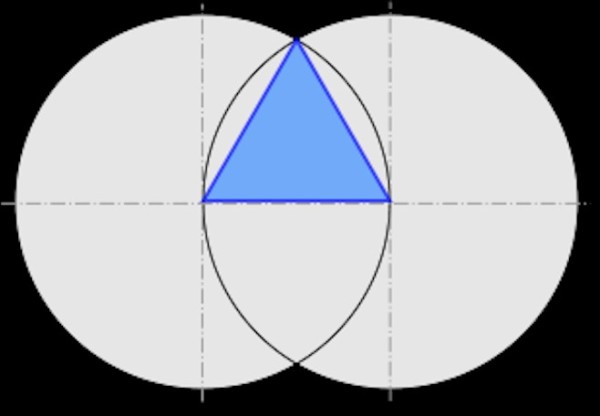
Ritagliamo il triangolo e posiamolo sulla lastra di metallo su cui andiamo a disegnare il perimetro, seguendo i bordi con la matita. Se invece preferite disegnare il triangolo direttamente sulla lastra con matita e compasso, sceglietevi un angolo di lastra, prendete la misura di 12,8 cm lungo il lato che sarà la base e tracciate dai suoi estremi due archi di cerchio di raggio 12,8 in modo che si intersechino. Tracciate quindi le due linee dei lati.

Ritagliate (o meglio fate ritagliare dal papà) con una cesoia da giardinaggio (senza farvi vedere dalla mamma) il triangolo equilatero.

Osservate questa foto che mostra il triangolo appena tagliato.

Come vedete, presenta sbavature molto pericolose. Occorre provvedere immediatamente a lisciare bene i lati con la lima. Dovrete anche appiattire la figura, in particolare i vertici che si saranno un po' incurvati a fine taglio. Agite con calma e attenzione, senza fretta, evitando di passare le dita lungo i lati finché non avranno un aspetto liscio e regolare. Non dovete "affilare" i bordi , al contrario, dovete far scorrere la lima di piatto lungo i lati.  Al termine avrete un triangolo che, oltre ad essere sicuro avrà  anche un look professionale.

Tagliate con le forbici un pezzo di filo da cucito di 3 cm, piegatelo a metà posatelo vicinissimo al vertice superiore facendo spuntare appena la piegatura e incollatelo con una goccia di super-colla Attak, in modo da ottenere un minuscolo anellino appena sopra la punta del triangolo come nella figura:

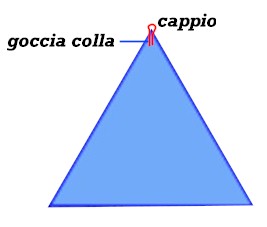
Dalla gabbietta metallica (recuperata dal tappo di bottiglia di spumante), liberate l'anello di base, non intrecciato. raddrizzatelo bene con le pinze e tagliate due pezzetti di filo di ferro di 2 cm ciascuno, e un terzo pezzo di circa 4 cm. Per il taglio potete usare le cesoie, ma dovrebbe essere più facile con il tronchesino delle pinze o piegando più volte il filo su e giù, fino a spezzarlo nel punto voluto.

Accostate un pezzo di filo da 2 cm al lato sinistro del triangolo, in modo che si appoggi al bordo per 0,5 cm e sporga per 1,5 cm prolungando la direzione del lato. Fissatelo alla costa della lamiera con una goccia di Attak. Questo sarà l'indice di lettura. Posate l'altro filo da 2 cm, per 1 cm lungo la bisettrice dell'angolo di base destro, facendo sporgere il centimetro rimanente oltre la lamiera. Fissate il tratto  a contatto con il triangolo con Attak e quando è ben saldato, con le pinze, piegate delicatamente il tratto sporgente  in perpendicolare verso l'alto.

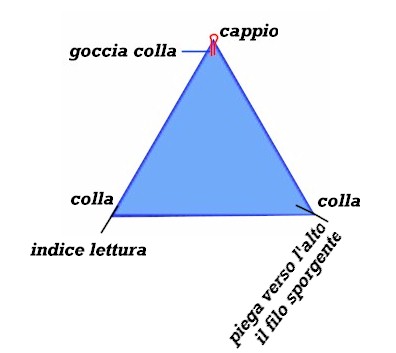
Ecco la foto del risultato ottenuto

Prepariamo ora i nostri pesi "campione" da 1 grammo. Saranno dei quadratini di lamiera di misura opportuna. Sì ma quanto dovrà valere questa "misura opportuna"? Che lato avranno?  Il lato dovrà essere esattamente di 2,67 cm, se volete sapere perché devono avere proprio questa misura, aprite il testo nascosto.

Disegniamo una striscia lunga 26,7 cm e dividiamola in dieci quadretti di 2,67 cm di lato. Ritagliamoli con cura perché questi saranno proprio i nostri pesi-campione da 1 g.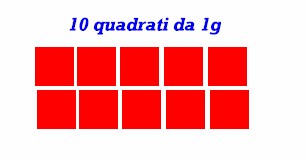
Segniamo il loro baricentro, all'incrocio delle diagonali, con un puntino usando il punteruolo e pratichiamo un piccolo foro, utilizzando la punta di un chiodino e il martello leggero, con cui daremo una serie di piccoli colpi, non sul tavolo del salotto, per piacere, ma sulla assicella di legno che avremo posato sul tagliere della cucina. Questo è proprio il momento di alzare il volume della radio per coprire il rumore del martello ed evitare domande tipo "cosa stai facendo in cucina? cos'è questo martellamento? " con possibili incursioni inquisitorie mammesche.

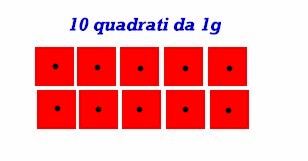
Ecco una immagine di quattro dei nostri pesi-campione, non vi  sembrano di Platino - Iridio?

 

Adesso arriva la parte più scientifica... dobbiamo costruire la scala graduata su cui leggere i valori, di grammo in grammo.
Su un foglio di carta bianca, disegniamo il solito triangolo equilatero, con la base orizzontale.  Tracciamo la sua altezza e congiungiamo il vertice di destra della base con il punto medio del lato opposto. Troviamo così, alla intersezione con la linea della altezza, il baricentro P.

Da questo punto, che non è altro che il centro del triangolo, segno  lungo il segmento che lo collega al vertice di base destro, una serie di punti di riferimento, ciascuno ad una certa distanza che ora vi dico.

Ecco i dati delle misure (in mm)  che userete per segnare i   dieci  punti lungo la linea che va da P al vertice destro :

 6,7        12,3       17       21,1       24,6       27,7       30,4       32,8       35       36,9

Per capire il ragionamento alla base di questo procedimento, basta aprire il seguente testo nascosto.

Adesso con lo spillo facciamo un buchino in ciascuno dei punti che abbiamo disegnato. Ritagliamo la metà di destra del triangolo equilatero, ottenendo un triangolo rettangolo. Disponiamolo in modo che il suo cateto più lungo (l'altezza del triangolo equilatero) sia sovrapposto al lato dell'altra metà-triangolo, a sinistra. Ribaltiamo ora il mezzo triangolo ritagliato attorno a questo lato in modo da vederne il rovescio e fissiamolo al foglio con un po' di nastro adesivo senza premere troppo, per poterlo poi distaccare facilmente ( notate nella figura qui sotto che in questa fase le linee rosse appaiono sbiadite perché viste in trasparenza). Ora tracciamo dal vertice superiore del triangolo equilatero le linee che passano per i buchini praticati con lo spillo, per una lunghezza di 15 cm ciascuna. Ecco, in quattro passaggi, illustrato in modo qualitativo, il procedimento: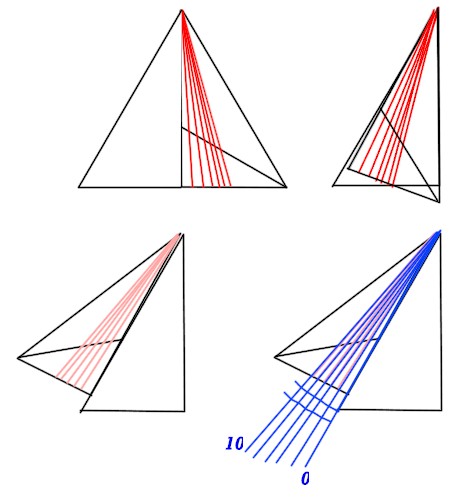

E  questa è la foto corrispondente.

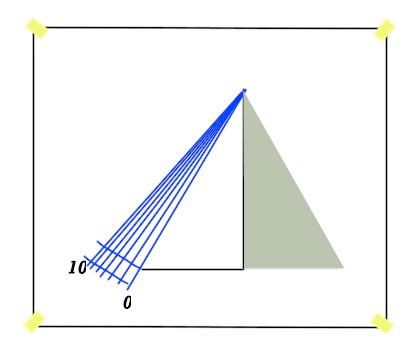
Togliamo delicatamente il nastro adesivo e rimuoviamo il triangolo rettangolo che non serve più. Con il compasso centrato sul vertice superiore, disegniamo un arco di cerchio di raggio 12,8 cm che intersechi tutte le linee appena disegnate. Scrivete 10 vicino alla linea più in alto e, a scalare, numerate tutte le linee, terminando con lo 0 in corrispondenza del lato del triangolo.
Ecco fatta la nostra scala di lettura!  Facciamone subito una fotocopia (così da poter conservare l'originale), collochiamola sulla porta del frigorifero in modo che la base del mezzo triangolo equilatero sia perfettamente orizzontale e l'altezza perfettamente verticale e fissiamola con il nastro adesivo.

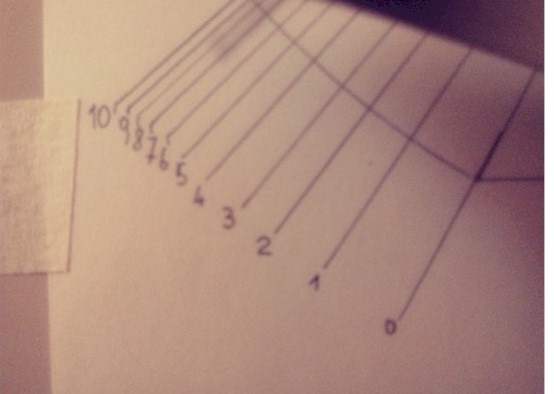
Particolare della numerazione delle linee della scala d lettura dopo la numerazione.

 

Prima di posizionare il magnete riprendiamo quel filo di ferro di 4 cm e pieghiamolo a metà, di 90°, formando una L. Inseriamolo nel buco del magnete in modo che una parte sia adagiata e allineata come un raggio e l'altra spunti perpendicolarmente dal buco.  Ora con le pinze eseguiamo un piegatura del filo adagiato in modo che la sua estremità sia ripiegata come nella foto, e fissiamolo solidamente con del nastro adesivo trasparente, in modo che non si sposti più. Notate che l'anello magnetico è sollevato a causa del  ferretto che sporge perpendicolarmente e che costituirà il supporto a cui appendere il triangolo equilatero.

Applicate il  magnete alla porta del frigo, con il ferretto di supporto che fuoriesce verso l'esterno, in modo che il vertice da cui partono le linee di lettura si veda spuntare nel punto più basso del buco dell'anello magnetizzato, così:

Infilate il perno che esce dal magnete nell'anellino di supporto del triangolo...

Notate che , non essendoci alcun peso agganciato al vertice destro, il triangolo è in equilibrio e  l'indicatore nel vertice sinistro segna 0.

Applicate ora un quadratino-peso con il suo baricentro coincidente con il vertice destro (piatto della bilancia) e leggete il valore indicato sulla scala. Se tutto è OK deve essere proprio 1.

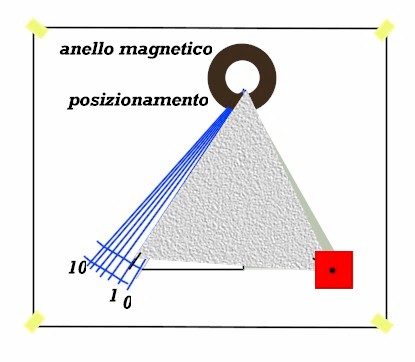
Nella foto notate anche l'ombra dell'indice, posizionato proprio su 1 grammo, che è il peso del quadratino agganciato al vertice destro.

Proseguite aggiungendo pesi e verificando la precisione di ciascuna lettura.   Ecco le foto per  2g   3g   4g  ....

Ai fini pratici le prime divisioni consentono di valutare bene anche i pesi intermedi, dato che all'inizio sono abbastanza spaziate. Oltre i 4 o 5 grammi, però le linee sono più ravvicinate e, verso fondo scala, ci sono solo un paio di millimetri di spaziatura. Naturalmente se applicate, invece dei quadratini, un peso sconosciuto è probabile che l'indice si fermi "tra una linea e l'altra" e dovrete fare una valutazione a occhio per decidere i decimali di grammo. Se l'indicazione è esattamente a metà tra 3 e 4 il peso sarà di 3,5 grammi, se è più verso il 3 sarà meno di 3,5 se è più verso il 4 sara più di 3,5. Sta a voi valutare.

Se, dopo avere realizzato il tutto, farete una bella foto e la pubblicherete in un commento, ne saremo lieti. In alternativa, se preferite una comunicazione privata, potrete allegarla ad una mail con il vostro nickname e i vostri commenti e inviarla a infinitoteatrocosmo@gmail.com specificando anche se potremo eventualmente pubblicarla in forma anonima.

 

Appendice applicativa
Ora che abbiamo la bilancia non ci resta che utilizzarla. Molti pensano che con una bilancia che pesa solo pochi grammi non si possa fare nulla di interessante. Non è affatto vero. Riusciremo a scoprire una importante relazione tra le aree di due  fondamentali figure geometriche.

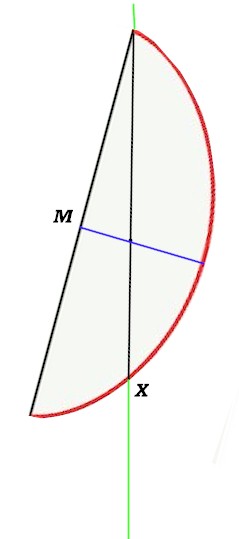
Osservate il cerchio che rotola senza alcun slittamento sulla retta orizzontale. Seguiamo il punto segnato sulla circonferenza durante il movimento e notiamo che da quando si stacca a quando si posa nuovamente sulla retta di contatto, descrive quella elegante curva rossa, il cui nome è Cicloide.
Questa curva ha moltissime proprietà di cui abbiamo parlato in altre occasioni (ha addirittura una sezione dedicata nell'archivio del blog). Ma in questa circostanza desideriamo solo capire qual è il rapporto tra la sua area e l'area del cerchio che l'ha generata.
La curva è un'onda periodica, una sequenza di infiniti archi. Fissiamo la nostra attenzione sul primo arco.

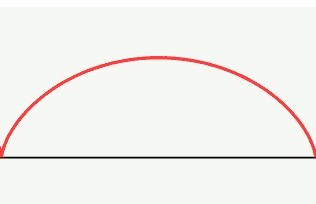
Questa cicloide è stata generata da un cerchio di 3 cm di diametro e la sua altezza, nel punto centrale, è quindi di 3 cm. Per quanto riguarda la base è facile capire che, essendo della esatta lunghezza della circonferenza che rotola senza slittamenti, sarà lunga cm
Verificate con il righello se queste sono esattamente le misure della figura sullo schermo.
Se è così, e dovrebbe essere così, non vi resta che appoggiare allo sullo schermo un foglio di carte bianco e ricopiare il disegno.

Viceversa potete scaricare l'immagine e lavorarci sopra ingrandendola o rimpicciolendola fino a ottenere quelle esatte proporzioni. Poi potrete copiarla su carta come già detto.

Occorre ritagliare il disegno con le forbici per usarlo come modello da riportare sulla lastra di alluminio che  abbiamo già utilizzato e ritagliare il metallo (papaà....!). Con il compasso costruite anche un cerchio di raggio 1,5 cm, direttamente sul metallo  di lamiera di diametro 3 cm e ritagliatelo.

Il baricentro del disco è ovviamente il suo centro, ma dove sarà mai il baricentro della cicloide? Ebbene, si trova a metà della base, sulla verticale, a distanza di  1,25 mm.

Se vi interessa sapere perché.... aprite il testo nascosto e leggetevelo. Altrimenti...

Alzate il volume della radio e praticate il consueto forellino nel baricentro del disco e in quello della cicloide.

Eccoli qui, tutti e due...

Ed ora... alla Bilancia !
Prima infiliamo nel porta-pesi il disco. Cosa segnerà l'indice? possiamo saperlo in anticipo perché il volume del disco è:

Moltiplicando per il peso specifico dell'alluminio che è 2,8 otteniamo un valore vicinissimo a 1 grammo. Vediamo se è vero...

Verificato che il disco pesa effettivamente 1g , lo togliamo e passiamo a pesare la cicloide. In questo caso non abbiamo idea di quale potrà essere il peso, perché non è cosi semplice calcolare l'area di questa figura. Allora... pesiamola!

Sorpresa! l'indice si ferma su 3g. Secondo la nostra bilancia la cicloide pesa il triplo del disco che l'ha generata. Dato che il materiale è omogeneo e lo spessore della lamiera è costante possiamo dedurre che l'area della cicloide è il triplo di quella del cerchio.

Ed è proprio così, è stato dimostrato matematicamente molti anni fa da un allievo di Galileo Galilei, Torricelli, dopo la morte del Maestro.
Galileo, però, lo aveva intuito e, per averne la conferma empirica, fece proprio la pesatura che abbiamo fatto con la nostra piccola bilancia. Visto che serve ?

Questa idea , molto furba ,  era già venuta molto tempo prima ad  Archimede, che aveva anche le idee molto chiare sulle leve e sulle bilance. Non perdetevi questa interessante storia che è stata ampiamente raccontata in questo articolo

Ora, invece, vediamo una applicazione molto pratica e utile.