Ho inserito tre asterischi in questo articolo (o lezione). Non spaventatevi, però. Esso non contiene formule difficili o passaggi acrobatici. Il fatto è che richiede concentrazione per capire esattamente il concetto di limite e le sue applicazioni. Non leggetelo, perciò, velocemente, ma cercate di entrare dentro il mondo di Achille e della tartaruga, facendolo veramente vostro.

Il paradosso di Zenone, ci ha aiutato a trovare un giusto compromesso tra fisica e matematica. In poche parole, abbiamo sostituito al concetto di punto puramente matematico (senza dimensioni) il concetto fisico di intervallo che ha dimensioni finite e misurabili. Per passare da intervallo a punto basta solo eseguire una strategia operativa: fare tendere a zero l’intervallo che lo contiene. Questa strategia l’abbiamo anche descritta in termini rigorosi (la matematica non accetta niente che vada “a spanne”): dato un numero piccolo finché si vuole, è sempre possibile trovare un intervallo che abbia dimensioni più piccole di quel numero e che contenga il punto. Il punto matematico viene quindi definito come un intervallo le cui dimensioni tendono a zero.

Sembrerebbero solo parole fini a se stesse, un “escamotage” che cerca solo di girare intorno all’ostacolo, ma senza arrivare veramente al … punto del problema. Questa è la matematica più difficile, non quella delle formule complicatissime e intricate con simboli apparentemente assurdi.  No, quella matematica sembra difficile solo perché usa parole che non conosciamo, come se leggessimo un libro scritto in cirillico. Basterebbe imparare la lingua straniera e ci accorgeremmo che non dice niente di strano o incomprensibile.

La matematica veramente difficile è invece quella che definisce le sue regole logiche fondamentali. Capire la differenza “enorme”, che esiste tra punto matematico e punto inteso come intervallo fisico che tende a zero, vuol dire risolvere uno dei concetti più ostici della matematica. Compreso lui, tutto il resto diventa molto più semplice.

Potremmo anche chiederci: “Perché sprecare tante parole e fare tanta fatica mentale per definire un punto? Basterebbe non pretendere troppo e accontentarsi di un qualcosa che gli assomigli, come il segno lasciato dalla punta di una matita”. Non avremmo torto, in prima approssimazione. Tutto sta in quello che vogliamo studiare attraverso la matematica e sua sorella, la geometria. Se volessimo rappresentare le strategie di gioco per una partita di calcio potrebbe sicuramente bastare. Sarebbe sufficiente anche per un grande artista che dipinge la Gioconda. Le cose cambiano, invece, se vogliamo studiare le funzioni matematiche, quelle strane macchine che legano una x a una y in modo indissolubile. Sono realmente importanti? Beh… lo abbiamo già detto e ridetto. Senza l’introduzione delle funzioni la fisica rimane empirica e non riesce ad avere una descrizione rigorosa e generale. Non riuscirebbe a esprimere le leggi universali e i vari fenomeni sarebbero descritti ma non capiti fino al punto di poterli prevedere e ricostruire in laboratorio. Insomma, Galileo Galilei e la sua ricerca scientifica perderebbero di senso.

Come appassionati di Universo, non potremmo certo chiudere gli occhi e abbandonare al loro destino le funzioni matematiche applicate agli attori del grande Teatro del Cosmo. Ci dovremmo accontentare di assistere a fenomeni, magari entusiasmanti, trascurando tutte le loro interazioni e i loro legami. E’ un po’ come osservare senza capire  oppure osservare dopo aver capito. Nel primo caso, la macchia rossa di Giove, una nebulosa planetaria, una galassia a spirale o ellittica, sarebbero solo dei simboli; nel secondo caso diventano, invece, fenomeni meravigliosi, naturali, legati tra loro attraverso una intricata catena formata da molte o poche leggi fisiche (ossia funzioni).

Il momento angolare che determina la macchia rossa del pianeta gigante è lo stesso parametro che domina le caratteristiche di una stella di neutroni o che introduce nel mondo quasi assurdo dello spazio rotante attorno a un buco nero galattico. Diventa, quindi, ovvio che, per cercare di capire, non ci si può limitare a immagini “personali” e limitate, ma bisogna pretendere di vedere il meglio del meglio, quello che la tecnologia dei telescopi odierni riesce a regalarci giorno dopo giorno. Senza essere degli esperti, ma anche solo degli appassionati, solo così potremmo avvicinarci veramente alle leggi fondamentali e all’importanza altrettanto fondamentale delle funzioni matematiche. Senza un’applicazione fisica, la matematica perde gran parte del suo significato e della sua piacevolezza estetica.

Scusate questa digressione, che però è sempre utile per sapere in che campo cerchiamo di muoverci. Torniamo alle funzioni e al nostro punto-intervallo. Esso diventa essenziale se vogliamo addentarci nell’affascinate mondo delle funzioni (ossia delle leggi fisiche).

Per quanto conosciamo finora delle funzioni (solo la retta), la frase di prima sembrerebbe fin troppo categorica. In fondo, senza bisogno di tanti giri di parole potremmo determinare la posizione di un punto senza andare troppo nel sottile, anche se Zenone ci ha dimostrato che è sempre molto rischioso non essere rigorosi fin dall’inizio. Ma noi proviamo a non dargli retta e applichiamo quanto sappiamo per trovare e definire un punto su una retta che altro non è che una funzione, magari semplice, ma sempre una funzione.

Facciamoci aiutare dalla banalissima Fig. 29.

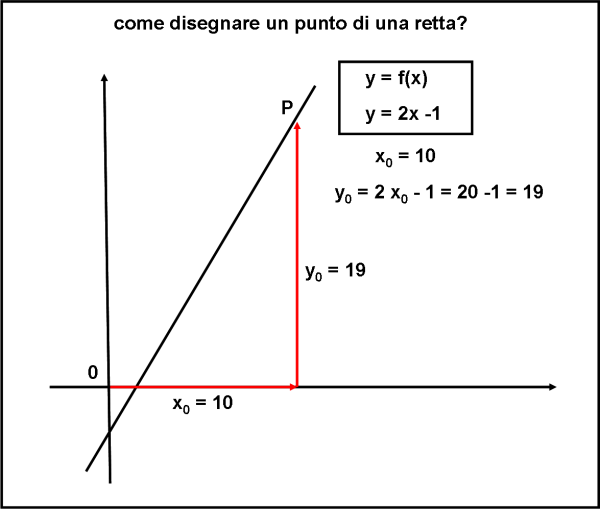
Conosciamo la funzione y = f(x), essa è, ad esempio, la retta y = 2x – 1 (2 è il coefficiente angolare m della retta e 1 è la costante n). La domanda che vi faccio è: “ Siete capaci a determinare il punto P della retta che ha per ascissa x₀ = 10?”. La risposta sarà (spero proprio) immediata: “Basta inserire il valore di x₀ all’interno della macchina f e aspettare che faccia le sue operazioni. Il risultato sarà l’ordinata y₀ del punto della retta P che ha come ascissa x₀”. In parole matematiche:

x₀ = 10

y₀ = 2 ∙10 – 1 = 19

Il punto P è P(10,19).

Tutto fatto, senza bisogno di intervalli e di verbi come “tendere a”.

Fermi, fermi, sarebbe troppo bello. Lo possiamo fare solo perché la nostra funzione è veramente semplice e riesce a mascherare molto bene i problemi legati a un punto matematico. Abbiamo usato la matita e abbiamo troncato tutti i possibili decimali che esistono (sempre e comunque) dietro a un numero. Se misuraste l’ascissa 10 con un righello da pochi soldi sareste anche contenti. Ma se la misuraste con un microscopio che legge anche i millesimi di millimetro vi accorgereste che il vostro 10 non è assolutamente 10, ma 10.002 o -magari- 9,997.

Non stupitevi, quindi, se anche in questo caso, apparentemente senza problemi grafici o concettuali, abbia deciso di inserire il concetto di limite di una funzione. Finalmente, direte! Eh sì, lo so, ve l’ho fatto desiderare a lungo, ma la sua importanza è tale che dovevo preparargli un ingresso teatrale.

Invece di inserire “rozzamente” l’ascissa x₀ nella funzione f(x) e ottenere y₀, devo definire un’operazione molto più elaborata. Considero un intervallo intorno all’ascissa x₀ e lo faccio tendere a zero (con la solita frase : “Dato un numero ε piccolo a piacere esiste sempre un intervallo x -x₀ più piccolo di ε”). Se contemporaneamente la differenza f(x) – y₀ tende anch’essa a zero, ossia esiste un numero ρ piccolo a piacere, legato a ε, tale che … ecc., ecc., posso dire che

lim _{x → x0}  f(x) = y₀           …. (1)

a parole: y₀ è il limite della funzione f(x) per x che tende a x₀.

Proviamo ad applicare questa espressione al caso della retta precedente. Non stupitevi se non cambia assolutamente niente rispetto a prima…

lim _{x → x0} (2x – 1) = 19

Non ho fatto altro che sostituire x₀ al posto di x…  Non arrabbiatevi, non vi ho preso in giro… Per funzioni come la retta, l’introduzione del limite sembra proprio una cosa assurda e inutile, ma per altre funzioni sarà ben più importante.  In pratica, cosa ho fatto nel passaggio al limite di una funzione? Consideriamo la Fig. 30.

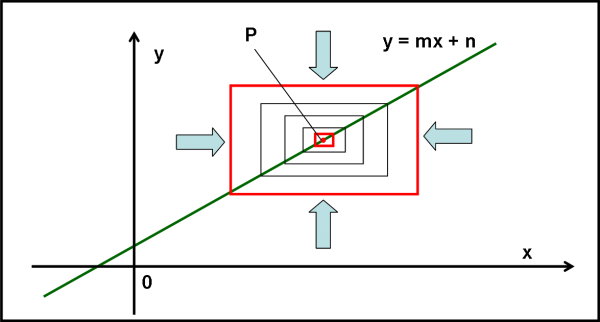
Abbiamo una certa retta y = mx + n. Cosa ci dice di fare l’operazione “limite”? Praticamente uno “zoom”. Prendiamo un rettangolino che ha come lati le differenze di ascissa e ordinata dei suoi estremi e poi rendiamolo sempre più piccolo, fino a farlo tendere a zero. Il rettangolino coinciderà, al suo limite, con il punto P.

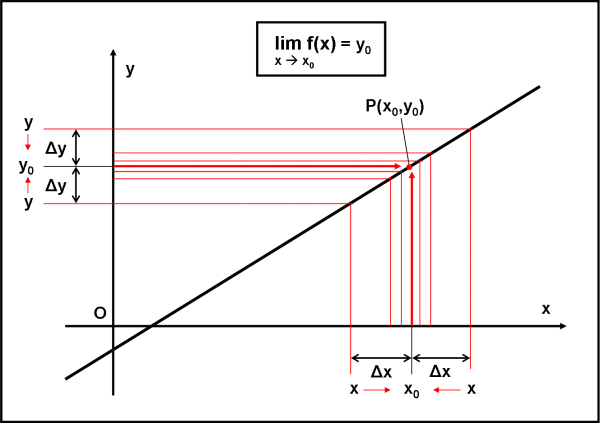
Più rigorosamente, rivediamo il procedimento in Fig. 31.  Consideriamo intervalli di y e x attorno alle coordinate y₀ e x₀ del punto. Facendo tendere a zero l’intervallo delle x vediamo se tende a zero anche l’intervallo delle y (solitamente si enuncia il viceversa, ossia si fa tendere a zero l’intervallo delle y e si vede se fa lo stesso anche l’intervallo delle x, ma poco importa per noi…). Se questo succede vuole dire che y₀ è il limite della funzione f(x) per x che tende a x₀.

In realtà dovremo essere ancora più precisi (vedremo che sarà spesso molto utile) e definire sia il limite sinistro che il limite destro di una funzione in un punto. In poche parole definiamo il limite della funzione separando l’intervallo delle x in due intervalli separati, quello delle x più grandi e quello delle x più piccole. Infatti, x può tendere a x₀ sia arrivando da sinistra che da destra. Basta considerare l’intervallo che deve tendere a zero compreso tra il valore x e il valore x₀. Nel caso si arrivi da sinistra si scrive:

lim _{x → x0}^-  f(x)

e si definisce come il  limite della funzione f(x) per x che tende a x₀ provenendo da valori più piccoli (da sinistra). Si scrive, invece:

lim _{x → x0}⁺  f(x)

e si definisce come limite della funzione f(x) per x che tende a x₀  provenendo da valori più grandi (da destra).

Attenzione a quello che sto per dire e che forse fa già capire alcuni problemi delle funzioni più complicate.

Una funzione è continua in un punto, se in quel punto esistono sia il suo limite sinistro che il suo limite destro e se essi sono uguali tra loro e finiti.

Due parole da comprendere bene: “continua” e “finiti”.

Dire che una funzione è continua in un punto (a parte la definizione appena data) vuol dire, in modo un po’ semplicistico, che ogni punto della funzione “dà la mano” sia al punto adiacente di destra che a quello di sinistra. Esiste, insomma, una catena indistruttibile. Non arrabbiatevi se illustro la situazione con una figura sciocca come quella di Fig. 32. Più seriamente, un funzione che non è continua ammette limiti diversi arrivando da destra o da sinistra. Più “sottile” è la parola “finiti”. Il contrario di finito è il solito caro amico infinito. Il che vuol dire che un punto infinito non può essere contato come un punto vero di una funzione, a meno che non appaia ai suoi limiti estremi.

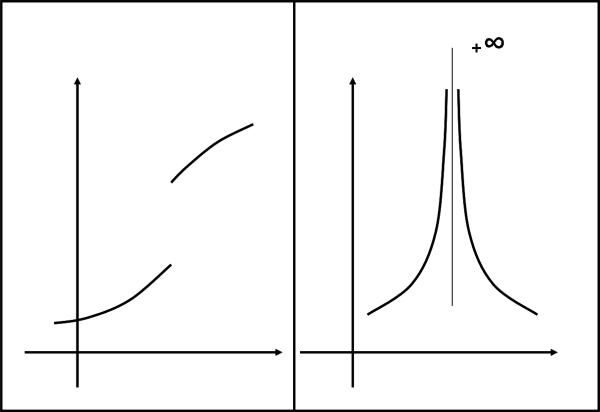
A questo punto, dobbiamo proprio convincerci che infinito è un simbolo, un concetto, ma non qualcosa di veramente rappresentabile. Scusatemi se anticipo cose che tratteremo più in là, ma voglio farvi vedere, in Fig. 33, due casi “veri” di funzione non continua. A sinistra, abbiamo proprio una rottura della catena; a destra la catena si unisce solo nel punto infinito, ma non può comunque essere considerata continua.

Lasciamo subito da parte queste strane funzioni, dato che abbiamo ancora parecchia strada da fare per poterle analizzare in dettaglio. Torniamo al nostro limite e alla sua definizione che sembra molto astratta e forse poco comprensibile. Vi faccio presente che ho cercato di renderla più leggera rispetto a quella usata normalmente nei libri. Potremo anche ritornarci sopra, ma per non creare confusioni su definizioni esageratamente corrette in senso matematico, possiamo limitarci a una definizione un po’ semplificata (e anche non propriamente perfetta…), ma più che sufficiente per il lavoro che vogliamo svolgere.

Posso solo dirvi che il concetto di limite ci farà finalmente lavorare tranquillamente con quel maledetto “infinito” che passa da punto concreto a entità sfuggente, con grande disinvoltura. Inoltre, ci permetterà di risolvere molti casi indeterminati nelle operazioni tra infinito e zero. E questo non è certo un piccolo risultato.

Tuttavia, vedremo anche che il limite di un funzione è solo una “stazione intermedia”. La sua importanza non è tanto pratica quanto concettuale. In particolare, permette di poter trattare infinito e zero in modo molto più matematico e secondo regole ben delineate, ma ha comunque dei … limiti. Esso lavora solo in un punto o -al massimo- in un intorno del punto e si disinteressa di tutto ciò che capita più lontano. Una ferrovia, però, non deve essere controllata solo nei passaggi a livello, ma lungo tutto il suo percorso. Cominciamo, quindi, a pensare il limite di una funzione in un punto solo come un preparativo per qualcosa di molto più pratico e generale. Non vado oltre, ma teniamo presente di non pretendere troppo da un concetto che ha già svolto un ruolo molto importante nel legare la matematica con la fisica.

Vediamo alcune sue applicazioni.

Abbiamo visto che se applichiamo la definizione di limite a un punto “tranquillo” della funzione, la sua entrata in campo sembra essere del tutto inutile. Sì, ha introdotto l’intervallo fisico che lega fisica e matematica, ma ha fatto ben poco dal punto di vista pratico. Data una y = f(x) è, in fondo, un’operazione inutile cercare il limite della funzione y  per x che tende a x₀ attraverso l’intervallino che decresce, e cose del genere. Basta sostituire x₀ al posto della x nella funzione e un facile calcoletto aritmetico mi dà la y₀ corrispondente. Parliamoci chiaro, il limite in questi casi non serve proprio a niente.  E’ solo servito alla tartaruga per cercare di “fregare” matematicamente Achille! E a noi per fare i raffinati e voler dare al punto un’importanza che praticamente interessa ben poco.

Accidenti, tanta attesa per un’operazione matematica fine a se stessa, quasi narcisistica. No, no, non abbiate paura. Se il limite di un punto “normale” ha risvolti solo “tecnici”, ben diversa è la sua applicazione ai famosi punti zero e infinito.

Forza diamoci dentro!

Consideriamo per primo l’ormai celebre (e un po’ antipatico) punto all’infinito. Abbiamo già accennato al fatto che il concetto di limite può estendersi facilmente anche a un intervallo che, invece di diventare sempre più piccolo,  diventa sempre più grande. E questo è proprio il caso di infinito. Un esempio immediato: qual è il limite dell’ordinata della nostra solita e banalissima retta y = mx + n per x che tende a infinito? La scrittura di limite prende la forma:

lim _{x → ∞}  f(x) = lim _{x → ∞} (mx + n) … (2)

Beh… la cosa si fa interessante. Finalmente il nostro treno sta proprio viaggiando verso quel punto un po’ simbolo e un po’ realtà. Ripetiamo cosa dice il limite in questo caso. Se considero un  numero grande a piacere, troverò sempre un valore di x che sia più grande di quel numero. E’ uno strano intervallo, ma proprio l’unico che ci definisce il tendere all’infinito. Cosa capita a y in questa situazione che è tenuta, in qualche modo, sotto controllo? Nel caso della retta, anche la y tende ad essere sempre più grande e anche per lei si può dire che dato qualsiasi numero grande a piacere si troverà una y maggiore di quel numero.

Uffa… di nuovo parole, solo parole. Beh… allora passiamo ai fatti e calcoliamo il limite  (2). Per far questo dobbiamo, innanzitutto, saper fare qualche operazione con i limiti. Ad esempio, quanto vale il limite di una costante e -ancora di più- quanto vale il limite di una variabile (x) moltiplicato per una costante. Il primo problema è facilissimo da risolvere: il limite di una costante è del tutto indipendente da quello che fa la x (non compare per niente). Ne segue che scrivere:

lim _{x → ∞} n

non porta nessun cambiamento a n. Lei non dipende da x e quindi continua a essere n per qualsiasi valore di x. Ne segue:

lim _{x → ∞} n = n    …. (3)

Per il secondo problema, basta ricordare che valgono le quattro operazioni aritmetiche anche per i limiti, ossia: il limite di una somma è uguale alla somma dei limiti; il limite di una differenza è uguale alla differenza dei limiti; il limite di un prodotto è uguale al prodotto dei limiti; il limite di una divisione è uguale alla divisione dei limiti.

Sembra che abbia detto un’enorme banalità. Tuttavia, vi devo chiedere di credere a queste costatazioni. La loro dimostrazione matematica non è assolutamente facile. Sappiate, però, che si possono dimostrare.

A noi, al momento, interessano la somma e il prodotto.

lim _{x → ∞} (mx + n) = lim _{x → ∞} (mx) + lim _{x → ∞} n

Ho solo applicato la regola che dice che il limite di una somma è uguale alla somma dei limiti! Posso ancora scrivere:

lim _{x → ∞} (mx) + lim _{x → ∞} n = lim _{x → ∞} m ∙ lim _{x → ∞} x + lim _{x → ∞} n

Ho solo applicato la regola che il limite del prodotto è uguale al prodotto dei limiti

Ricordando che il limite di una costante è una costante (3), possiamo scrivere:

lim _{x → ∞} (mx + n) = m ∙ lim _{x → ∞} x + n    ….(4)

Vi sembra che abbia ottenuto poco. E invece no. Posso dire che il limite della mia funzione y  per x che tende a infinito si riduce solo a calcolare il limite di x per x che tende a infinito. Ma, la risposta è ovvia: se x tende a infinito, il limite di se stesso è ovviamente infinito! La (4) diventa allora:

lim _{x → ∞} y = lim _{x → ∞} (mx + n) = m ∙ ∞ + n = ∞

Sembra di essere tornati ai primi articoli, quando avevamo bisogno di rette parallele che si incontravano e di cose molto ambigue e astratte. E, invece, no. Adesso possiamo dare il risultato senza problemi concettuali. Moltiplicare  infinito per una costante, così come sommargli un’altra costante, non possono certo cambiare le caratteristiche di x che tende a infinito. Ricordiamo che se x tende a infinito vuol dire che non esiste alcun numero grandissimo, scelto a piacere, che non possa risultare più piccolo di x. Che si moltiplichi o si sommi x a qualcosa,  questa caratteristica non cambia di certo. Anche con queste aggiunte la variabile tende comunque a infinito. Posso anche esprimerlo matematicamente.

Ripeto, se x tende a infinito vuol dire che scelto un numero N grande a piacere  vi sarà sempre una x più grande di N, ossia

x > N

Se aggiungo e moltiplico x per delle costanti, trovo che anche mx + n (che è proprio y) deve essere maggiore di un numero grande a piacere. Basta prendere il numero un po’ diverso, ossia P = mN + n.

Infatti, posso scrivere senza problemi:

mx + n > mN + n = P

quindi se x > N anche mx + n > P, con P grande a piacere.

Il risultato è che per una retta qualsiasi, se x tende a infinito, anche la y tende a infinito. Ne segue che il risultato del limite è proprio infinito e non indica solo una “tendenza a”. Quest’ultima frase fa già parte della definizione di limite.  Non abbiamo più bisogno di eseguire operazioni simboliche come m + ∞ = ∞, senz’altro vere ma basate su disquisizioni più filosofiche che matematiche. Il simbolo ∞ resta un simbolo, ma definisce un’operazione matematica perfettamente controllabile ed eseguibile.

Capisco di aver creato un po’ di confusione. Tuttavia, come già detto molte volte, dimostrare le cose ovvie è molto più difficile che dimostrare le cose complicate. Il succo di quanto fatto è l’essenza profonda della matematica: sostituire a concetti apparentemente accettabili, ma non realmente quantificabili, nuovi concetti descrivibili rigorosamente.

Adesso, possiamo dire con molta più tranquillità che al tendere di x a infinito, anche la y, legata a x da una funzione matematica come la retta, tende a infinito. Possiamo, perciò, dimenticarci le scritte relative al punto all’infinito di una retta e tutte le visioni più o meno astratte. Il limite ci ha dato un metodo rigoroso per descrivere la retta fino ai suoi estremi, benché irraggiungibili. La cosa diventa ancora più chiara per funzioni più complicate.

Facciamone un esempio veloce. Prendiamo un “ramo”, quello positivo, della funzione y = 1/x (vedremo tra non molto che funzione importante essa sia).

Qual è il limite di questa funzione quando x tende a infinito? Ossia, calcoliamo:

lim _{x → ∞} (1/x)     …. (5)

lim _{x → ∞} (1/x) = lim _{x → ∞} (1)/ lim _{x → ∞} (x) = 1/ lim _{x → ∞} (x)

Ma ormai sappiamo molto bene quanto vale il lim _{x → ∞} (x). Esso è infinito (l’abbiamo appena definito). Risulta, perciò, che il limite della nostra nuova funzione tende al rapporto tra 1 e qualcosa che tende a infinito. Detto in parole matematiche se x diventa sempre più grande (maggiore di qualsiasi numero a piacere N), il suo inverso non può che diventare sempre più piccolo, ossia si troverà sempre un numero ε piccolo a piacere tale che 1/x < ε o, analogamente, che (1/x – ε) < 0. Il che vuole anche dire che 1/x tende a zero! In poche parole:

lim _{x → ∞} (1/x) = 0

Questa volta il risultato è proprio zero, dato che la tendenza è già insita nel limite.

Avete visto che la celeberrima asserzione 1/∞ = 0 ( e viceversa)  acquista un significato ben più rigoroso e matematico. La rappresentazione geometrica di quanto abbiamo appena detto è riportata nella Fig. 34.

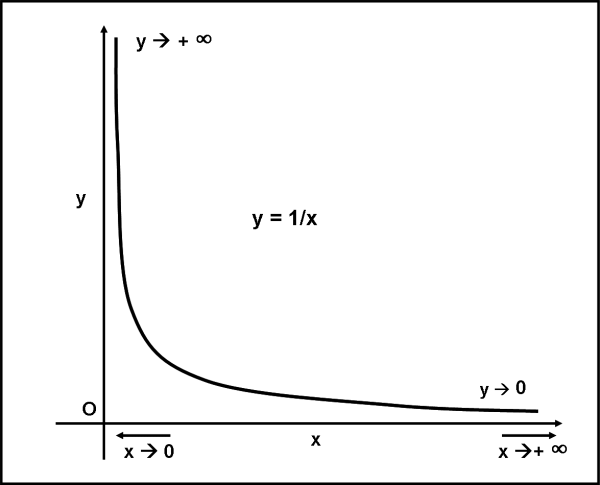
Facciamo un altro esempio, dove x non tende a infinito, ma a un punto finito. Per esempio proprio lo zero. La funzione è la stessa di prima: y = 1/x.

Scriviamo

lim _{x → 0} (1/x)

Ormai non abbiamo più bisogno di tante parole e sappiamo come eseguire le operazioni:

lim _{x → 0} (1/x) = lim _{x → 0} (1) / lim _{x → 0} (x)

Il numeratore è il limite di una costante e quindi rimane la costante. Il denominatore è invece il limite di x per x che tende a zero. Ovviamente è zero e quindi:

lim _{x → 0} (1/x) = 1/0 = ∞

Quello che abbiamo fatto è stato di rendere il denominatore sempre più piccolo, ossia abbiamo fatto diventare sempre più piccola la differenza (x – 0). Ne segue che il numero 1 diviso qualcosa che diventa sempre più piccola (0.1, 00000.1, 0.00000000000001, ecc. ecc.) non può che tendere a infinito, ossia essere sempre più grande di qualsiasi numero grande a piacere volessimo scegliere. Ossia il limite è infinito.

Sì lo so, eravamo capaci a ottenere gli stessi risultati sostituendo a x il valore 0 o ∞, ma adesso, lavorando con gli intervalli, abbiamo eseguito un’operazione fisicamente corretta.

Concludiamo questo articolo con un piccolo esercizio. Quanto vale:

lim _{x → ∞} (1/x + n)

Concludo ripetendo una constatazione già fatta, ma che sembra talmente banale da creare , forse, problemi interpretativi e logici. Essa, invece, è di estrema importanza matematica e non solo.

D’ora in poi per determinare il limite di una qualche funzione in un punto non avremo più bisogno di fare tutti quei discorsi su numeri piccoli e grandi a piacere e nemmeno parlare di “tendenza a” (tutte cose che sono già implicite nella definizione di limite). Basterà sostituire il valore limite di x e vedere se la y assume un valore determinato. In altre parole, possiamo trattare tutti i punti nello stesso modo e inserire l’ascissa nella funzione e calcolare l’ordinata. Esattamente ciò che avevamo cercato di fare all’inizio di tutta la “nostra” matematica. Tante lezioni per tornare al punto di inizio? A prima vista sì, ma da un punto di vista logico e concettuale abbiamo fatto passi da gigante e i punti zero e infinito, pur rimanendo simboli, hanno acquistato una loro definizione perfettamente corretta e descrivibile.

Non ci resta desso che riprendere in mano le forme indeterminate e vedere se il concetto di limite ci permette , finalmente, di risolverle… Ce la faremo, ma capiremo anche che il concetto di limite di una funzione in un punto è solo l’inizio di un discorso ben più ampio ed efficiente.

Se siete riusciti a seguirmi fin qui, posso dirvi che avete superato le difficoltà maggiori. Tutto ciò che verrà adesso (studio di funzioni, derivate, asintoti, ecc., ecc.) sembrerà più complicato, ma avrà bisogno di uno sforzo interpretativo decisamente minore. Fidatevi…

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica