Un’appendice alla gara di Achille e della tartaruga. Cerchiamo, infatti, di risolvere la questione in modo puramente matematico (nonché geometrico) in modo da rendere giustizia alla visione fisica che Zenone aveva cercato di nascondere sapientemente.

Questa specie di appendice è destinata solo ai più “esperti”, dato che tratta di funzioni come se già le conoscessimo molto bene. In realtà, la funzione che viene considerata è poi soltanto una retta, niente di più. E, ormai, la dovremmo conoscere... Tuttavia, alcuni passaggi un po’ “azzardati” la rendono, per adesso, un po’ ostica. Ovviamente, chiunque può provare a seguirla e confrontarsi fin da subito  con ciò che tra un po’ diventerà il nostro pane. Chi non riuscirà a seguire, però, non si preoccupi. Tra qualche lezione, tornando indietro, si accorgerà della sua semplicità. Consiglio, però, a tutti di leggere le ultime frasi. Capirete che questo esempio vale più delle tante parole che ho cercato di usare per spiegarvi l’importanza della funzione nel descrivere la fisica.

Cosa voglio fare in questa appendice? Beh… la storia di Achille e della tartaruga è stata mostrata in due modi opposti. Il primo ha portato a un concetto completamente errato, ma ben costruito dal grande Zenone. L’altro a una soluzione fisicamente inoppugnabile, ma decisamente “rozza” dal punto di vista matematico. Permettetemi, allora, di usare un terzo metodo, fondato sulla matematica esprimibile con una semplice funzione. In altre parole, vorrei trovare senza troppi giri di parole o di concetti qual è il punto (matematico o fisico, come volete) in cui Achille raggiunge la tartaruga.

Vi sono sicuramente vari metodi matematici per ottenere il risultato. La matematica ha spesso una grande fantasia. Noi useremo due metodi (che i più preparati capiranno essere in fondo la stessa cosa) che si rifanno all’esempio applicativo di una retta speciale che abbiamo già trattato: il movimento rettilineo uniforme, dove la x diventa il tempo e la y lo spazio percorso.

In questo caso quale sarà l’equazione del moto di Achille? Lui parte dall’origine degli assi e descrive una retta che ha velocità (ossia coefficiente angolare) uguale, ad esempio, a 10 metri al secondo, ossia:

s =  m_A t =  v_A∙ t = 10/1  t = 10 t      …. (1)

che è, ovviamente, una retta passante per l’origine

La tartaruga parte invece lungo l’asse delle ordinate, ossia in s = 100 metri (n) , ma poi si muove con una velocità (m_T) pari a v_T = 1 m/sec. La funzione che la esprime è quindi:

s = m_T t +  n = v_T t + 100 = 1/1 t + 100 = t + 100   …. (2)

A questo punto non resta che disegnare le due curve nel diagramma cartesiano di Fig. 27.

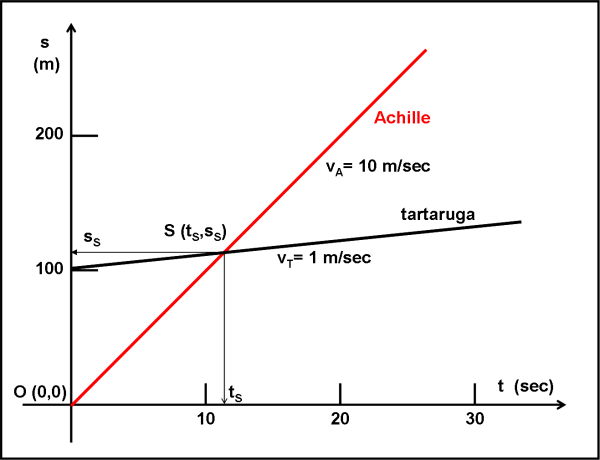
Come si può notare facilmente, le due rette che descrivono i moti di Achille e della tartaruga si incontrano in un punto. Esso indica proprio il punto del sorpasso. Dopo di lui l’ordinata di Achille (lo spazio percorso) è sempre più grande di quella della tartaruga. L’ascissa di quel punto ci dà il tempo in cui avviene il sorpasso, mentre l’ordinata la distanza dall’origine in cui Achille affianca la furba, ma lenta, bestiola. Proprio quello che cercavamo e che dà pienamente ragione alla fisica, esprimendolo, però, in termini matematici e geometrici. La figura potrebbe anche bastare per misurare le coordinate di cui abbiamo bisogno, ma ci conviene ricavarle matematicamente.

Le due rette sono:

s = 10 t         (Achille)

e

s = t + 100           (tartaruga)

Per trovare t_S (ossia il tempo del sorpasso) basta eguagliare le due relazioni (vogliamo proprio il punto in cui la s è uguale per i due avversari):

10 t_S = t_S+ 100

10 t_S – t_S  = 100

t_S (10 – 1) = 100

t_S = 100/9 = 11.1111111…. secondi

Per trovare la distanza dall’origine s_S relativa al punto di sorpasso, basta inserire il tempo t_S in una delle due rette di prima (una o l’altra è lo stesso, dato che il punto deve appartenere a entrambe le rette).

Si ha, da quella di Achille:

s_S = 10 t_S = 10 ∙ 11.11111111… = 111.11111111111…   metri

Da quella della tartaruga (tanto per controllare…):

s_S = 100 + t_S = 100 + 11.111111111… = 111.11111111… metri   (ovviamente, uguale a prima).

Il punto S di sorpasso è quindi S(t_S,s_S) = S(11.111111…., 111.11111111…).

Le rette della Fig. 27 ci permettono non solo di dimostrare che la tartaruga viene “matematicamente” superata, ma anche di sapere dove e quando. Anche di più, però. Potremmo, infatti, sapere anche le distanze tra i due avversari per ogni istante della gara. Basta scegliere un t qualsiasi e vedere di quanto differiscono le s dei due avversari.

Potrei anche trovare lo stesso risultato con una manovra più “azzardata”. Per fare ciò chiamerò con y i punti descritti dalla tartaruga e con x quelli descritti da Achille.  Per come si svolge la gara e per come differisce la velocità di Achille da quella della tartaruga (una è dieci volte più veloce dell’altra) è ovvio pensare che la y sia legata alla x. Ossia, il percorso della tartaruga deve essere strettamente collegato a quello di Achille. Questo concetto si esprime (ormai dovremmo saperlo abbastanza bene) con la frase: “y deve essere funzione di x”. Tutto sta a trovare quale “macchina” riesca a trasformare la x in y. In altre parole possiamo scrivere:

y = f (x)

ma dobbiamo esprimere matematicamente le operazioni che sono eseguite da f.

Facciamo una piccola tabella che ci mostri empiricamente quali valori assume la y per alcuni valori di x. Ci riferiamo perciò alla Fig. 25 (quella di Zenone).

La Tabella 1 ci mostra il risultato per valori numerici già trovati precedentemente.

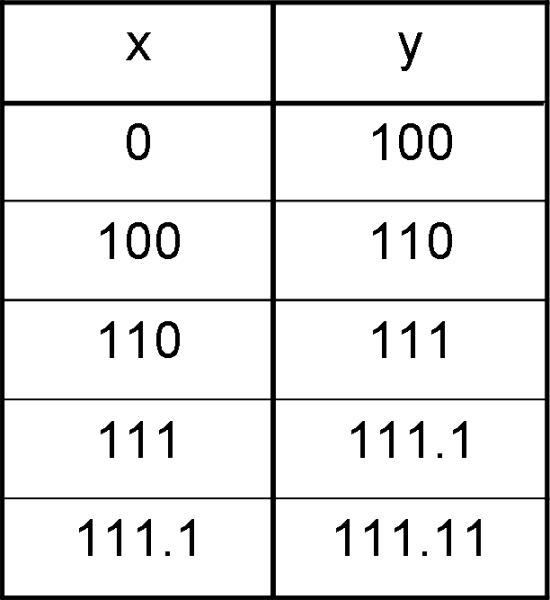
Vediamo se l’equazione di una retta qualsiasi può soddisfare le nostre necessità.

Come ormai sappiamo bene, la sua equazione è:

y = mx + n.

Il coefficiente angolare m può trovarsi facilmente dal rapporto tra la differenza delle y di due punti della retta e la corrispondente differenza delle x.  Ossia:

m = (y2-y1)/(x2-x1) 

Non ho fatto niente di speciale… ho solo eseguito un rapporto tra due cateti e questo deve essere proprio tan(α) che, a sua volta, è il coefficiente angolare m della retta.

Nel nostro caso abbiamo, ad esempio:

m =  (110 - 100)/(100 - 0) = 10/100 = 1/10

per conferma, eseguiamo l’operazione usando altri due punti:

m = (111 -  110)/(110 – 100) = 1/10

Beh… non c’è da stupirsi… la matematica non è un’opinione!

La retta diventa allora:

y = x/10 + n

Per trovare n, basta sostituire alla x e alla y, un punto reale della retta (qualsiasi esso sia).

Ad esempio, so che per x = 0, la y deve valere 100. Posso, quindi, scrivere:

100 = 0/10 + n,   ossia:

n = 100

Cambiando punto trovo, ovviamente, la stessa cosa:

111 = 110/10 + n,  ossia  111 = 11 + n, e ancora  n = 111 - 11 = 100

La retta che cercavamo ha, allora, l’equazione:

y = x/10 + 100     …. (1)

Come detto all’inizio, la y descrive il percorso della tartaruga in funzione del percorso x di Achille.

Siamo sicuri che Achille superi la tartaruga? I punti della tabella (quelli usati da Zenone) sembrano indicarci che la y rimane sempre più grande della x. Adesso, però, possiamo utilizzare la (1) anche per determinare la y in corrispondenza di valori di x diversi da quelli “scelti” dal grande e furbo scienziato greco. Ad esempio, se inserisco x = 200, ottengo:

y = 200/10 + 100 = 20 + 100 = 120

y è già minore del valore di x, 120 contro 200. Questo vuol dire che Achille è già molto più avanti della tartaruga. Sì, quello di Zenone era proprio un paradosso studiato molto bene.

Tuttavia, noi vogliamo anche determinare il valore di x in cui avviene il sorpasso. Non come intervallo, ma proprio come punto matematico. In questo caso e per questa funzione così semplice, si può fare tranquillamente. Cosa dobbiamo imporre per trovare questo punto, che chiamiamo S(x_S, y_S)? Beh… facilissimo, basta considerare che y_S sia uguale a x_S. Questo è proprio il punto (e anche l’unico) in cui Achille e tartaruga sono perfettamente appaiati. L’equazione della retta (1) diventa , allora:

x_S = x_S/10 + 100

x_S (1 - 1/10) = 100

x_S (1 - 0.1) = 100

x_S = 100/0.9 = 111.111111111111111111111111….    metri

e, quindi, anche:

y_S =  111.111111111111111111111111….    metri

Un numero periodico (ossia vi sono infiniti 1 dopo la virgola). Cera proprio d’aspettarselo... Zenone aveva scelto bene i parametri giusti per il suo paradosso.

Il punto cercato è quindi, nuovamente, S (111.111111111…., 111.111111111…) e il procedimento usato è riassunto graficamente nella Fig. 28.

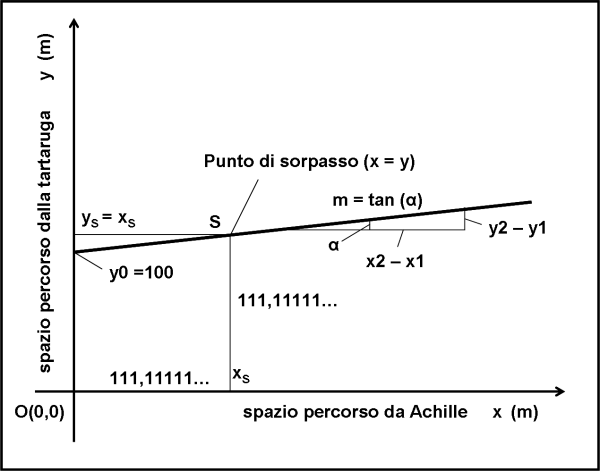
Ovviamente, il risultato finale è lo stesso per entrambi i metodi usati (ci mancherebbe altro… la matematica non è un’opinione!). Qual’é la loro differenza? Nel primo caso ho usato due funzioni; nel secondo caso una sola. In ogni modo, rette, soltanto rette, niente di speciale.

Il primo metodo è senz’altro più intuitivo e permette di calcolare anche il tempo del sorpasso, ma ha bisogno di sapere la velocità dei due avversari. Il secondo è -forse- più rapido e ha solo bisogno del rapporto tra le velocità. Tuttavia, ci regala solo la distanza del punto di sorpasso dall’origine. Insomma, sono del tutto equivalenti ed è immediato passare da uno all’altro. Sono, in pratica, la stessa cosa… Chi ha voglia di provare se ne accorgerà rapidamente.

Oltretutto, gli esempi fatti sono solo casi particolari. Cambiando la pendenza della retta, ossia la velocità relativa di Achille rispetto alla tartaruga, si hanno risultati sempre diversi. Se avete voglia, potere divertirvi a cambiare le condizioni della gara e/o la velocità degli avversari (un ghepardo invece di una tartaruga, ecc., ecc.).

In ogni caso, come previsto, S è un punto non realmente quantificabile, dato che il suo valore cambia sempre a seconda della precisione che vogliamo, ossia di quante cifre dopo la virgola abbiamo “fisicamente” bisogno. In concetto di limite è quanto mai azzeccato per questo punto. E’ infatti impossibile attribuirgli un numero esatto, a meno di non considerare infiniti 1 dopo la virgola. Possiamo perciò giustamente dire che esso è compreso nell’intervallo 111 e 112, ma anche in quello 111.111 e 111.112,  111.11111111111 e 111. 11111111112 e via dicendo.

In altre parole possiamo trovare sempre un numero ε, piccolo a piacere, tale che esista un intervallo, più piccolo del numero, che contenga il punto cercato. Prendete pure ε con diecimila zeri dopo la virgola e poi 1 (più piccolo, quindi, di qualsiasi grandezza fisica) ed esiste sempre un intervallo ancora più piccolo che contiene il nostro punto S.

S è allora proprio il limite a cui tende un certo intervallo, quando questo intervallo tende a zero. Ma, sul concetto di limite di una funzione, parleremo diffusamente la prossima volta. Se non altro dovremo imparare a descriverlo sinteticamente e non sempre con un “sacco” di parole.

In generale, chi è riuscito a seguire questa appendice (non è difficile ve lo assicuro…), ha compreso un concetto fondamentale che avevamo già spiegato “sprecando” molte frasi.

Siamo di fronte a un fenomeno fisico, ossia la corsa di Achille e della tartaruga. Lo potremmo descrivere in tanti modi, farne la radiocronaca, riprenderlo con una cinepresa, ripeterlo cento volte e segnare più o meno empiricamente il momento in cui ci “sembra” che Achille effettui il sorpasso. Probabilmente, alla fine arriveremo a determinare un valore del punto abbastanza esatto. La fisica può dirci solo questo.

Tuttavia, chiedendo aiuto alla matematica e basandosi sulle condizioni di partenza e sulle modalità della gara (la tartaruga parte più avanti di Achille di un certo valore ben conosciuto; la velocità è costante per entrambi; quella di Achille è dieci volte quella della tartaruga) è stato possibile descrivere il fenomeno fisico con un semplice legame tra il percorso di Achille e quello della tartaruga. Abbiamo avuto bisogno solo e soltanto di due o addirittura di una retta. Ossia di una funzione matematica. Essa è sempre valida, pur cambiando le condizioni di partenza e le modalità di gara. Basta inserire la m (velocità) e la n (differenza di spazio tra i due punti iniziali) corrispondenti.

In una sola frase: abbiamo verificato come un fenomeno fisico possa essere espresso rigorosamente e semplicemente attraverso una funzione matematica. La geometria ci regala la sua rappresentazione grafica. Che bel gruppo di amici!

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica