Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Approfondiamo l'argomento della stabilità dell'equilibrio che abbiamo trattato parlando del galleggiamento nell'ambito del teorema (o "principio") di Archimede, riproponendo un articolo che qualche anno fa abbiamo proposto sotto forma di quiz.

 

Un corpo lasciato libero, vicino al suolo, tende a cadere. Al di là della legge di Newton, possiamo concludere che esso tende a raggiungere la sua posizione più stabile. In parole fisiche, cerca di assumere la minima energia potenziale gravitazionale.

Ricordiamo che l'energia potenziale è quella posseduta un corpo solo in relazione alla sua posizione e va pienamente d’accordo con l’energia cinetica, adattandosi alla legge che stabilisce la costanza dell'energia totale : quando cresce una deve diminuire l’altra (pensiamo alle montagne russe).

Abbiamo anche conosciuto il baricentro di un corpo, quel punto che può diventare il “riassunto” dell’intero corpo: basta concentrare su di lui l’intera massa.

Questi due concetti si riuniscono facilmente, quando si parla di equilibrio stabile, instabile e indifferente. Si possono facilmente definire basandosi solo sul movimento che segue un corpo quando viene spostato anche solo leggermente da una certa posizione. Se tende a ritornare da dove è partito, l’equilibrio è stabile, se tende a discostarsi sempre di più, l’equilibrio è instabile. Se niente cambia, l’equilibrio è indifferente. Facciamo in Fig. 1, l’esempio classico della pallina lungo un tracciato a saliscendi (che sono poi le montagne russe…).

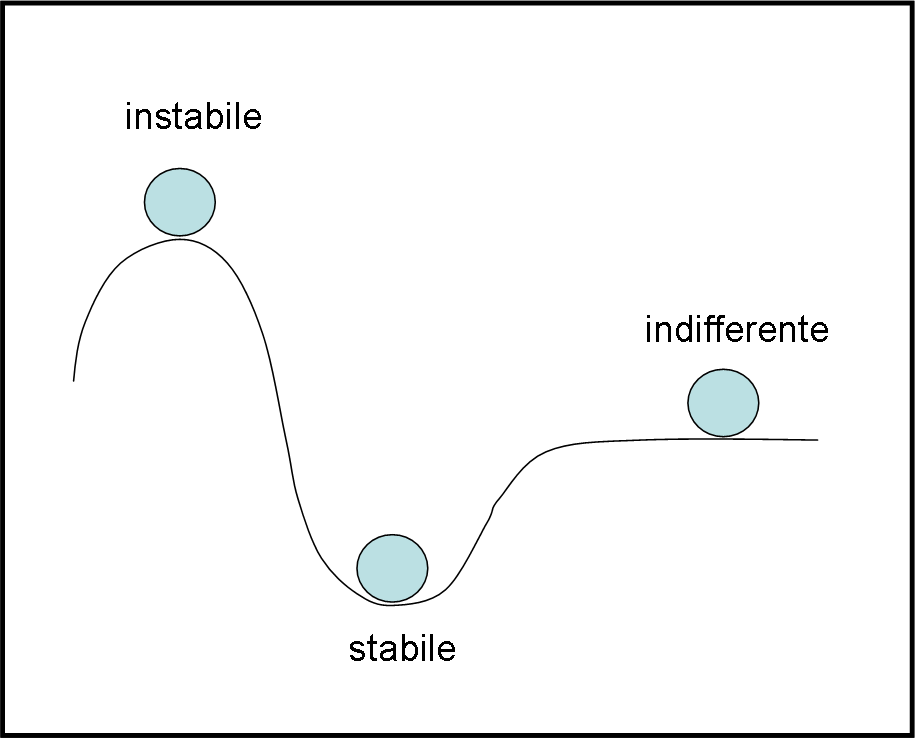
Un altro esempio è quello del cono appoggiato. Se viene appoggiato sulla base, un piccolo spostamento lo fa tornare al punto iniziale, se viene appoggiato sulla punta, il cono cade al suolo. Se lo poggiamo secondo la sua superficie laterale qualsiasi posizione comporta l’equilibrio. Ancora una volta l’oggetto in questione cerca di ridurre la sua energia potenziale. D’altra parte, l’Universo deve pur risparmiare energia e i suoi attori cercano di aiutarlo in questo “risparmio”.

Un ulteriore caso è quello della barra di ferro che può girare attorno a un chiodo: se la barra è sospesa in un punto più alto del suo baricentro, qualsiasi movimento tende a far tornare l’asta nella posizione iniziale. Se il chiodo è posto nella parte bassa, sotto il baricentro, l’asta inizia a cadere e si fermerà solo perché trattenuta dal chiodo.

Non parliamo, poi, della Torre di Pisa. Essa non crolla se la verticale tracciata dal baricentro cade all’interno della base, mentre può crollare se la stessa verticale cade fuori dalla base. Gli esempi sull’equilibrio sono tanti e anche se non sembra si riferiscono sempre all’energia potenziale.

In poche parole, e per dare un aiuto in più, possiamo dire che il baricentro sta nella posizione più bassa (minima energia potenziale) nei casi di equilibrio stabile e viceversa nei casi di equilibrio instabile. Lo studio del moto del baricentro è quindi fondamentale per stabilire la stabilità…

Ricordiamo, tra parentesi, che l’energia potenziale non è solo quella gravitazionale… anche i sistemi del microcosmo (atomi, nuclei) sono stabili quando l’energia è minima, mentre diventano instabili se acquistano energia, riemettendola per tornare in condizioni di stabilità.

Fatti nostri questi dovuti richiami e scegliendo il caso che più è vicino al nostro problema, portiamoci su una situazione ben più divertente e legata a un celebre classico della letteratura, non solo per bambini: Pinocchio.

Ormai Geppetto ha quasi finito la sua opera e misura la testa del suo burattino. Una sfera di raggio uguale a 15 cm. Tutto perfetto… manca solo un bel cappellino di forma conica. Usa un materiale che può renderlo estremamente sottile (mollica di pane?) e quindi leggero. Il cappellino serve per proteggere Pinocchio dal Sole, ma, vivendo in un posto ventoso, dove  il vento spira anche violentemente in senso orizzontale, è bene che il capellino abbia un equilibrio stabile…

Geppetto fa quello che può (non è un genio in fisica…), basandosi sulla sua esperienza di falegname. Alla fine costruisce un bellissimo e sottile cappellino, di sezione uguale a un triangolo isoscele, il cui  angolo al vertice superiore è 60°, mentre l’altezza, tra questo vertice e la base, è di 20 cm.

La domanda è: il cappellino costruito da Geppetto è in equilibrio stabile oppure no?

Prima di rispondere sul cappellino di Pinocchio, vediamo di inquadrarlo per bene nel problema generale dell’equilibrio stabile e instabile, di cui abbiamo parlato all'inizio dell'articolo. Abbiamo fatto parecchi esempi, ma quello che più si avvicina al nostro caso è la barra sospesa a un chiodo. Facciamo qualche foro nella barra in modo da poterla appendere in modi diversi (sostanzialmente due). Innanzitutto determiniamo il baricentro della barra che, essendo perfettamente simmetrica, coincide con il suo punto di mezzo, ossia con il foro centrale.

Portiamoci sulla Fig. 1. A sinistra infiliamo la barra nel chiodo nel suo punto più basso. Se facciamo molta attenzione riusciamo anche a far rimanere in equilibrio la barra, ma… basta un leggero colpo di vento (o anche meno) e la barra di ferro cade verso il basso senza più tornare nella posizione iniziale. L’equilibrio è instabile. Traduciamo lo stesso discorso in altre parole: il baricentro G si sposta verso il BASSO, ossia diminuisce la sua energia potenziale. Proprio quello che desidera e niente lo può convincere a tornare indietro.

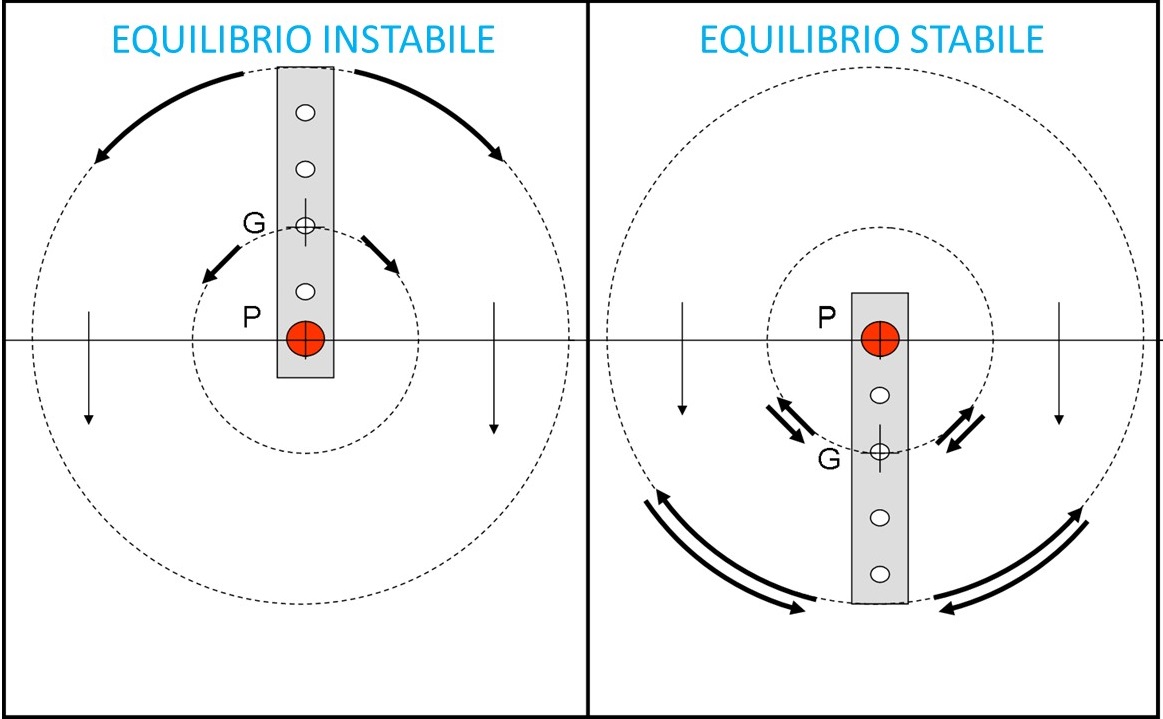
Vediamo, adesso, la parte di destra. La barra è appesa al chiodo nella sua parte alta. La barra è in equilibrio. Impartiamo dei movimenti ad essa in modo da farla ruotare attorno al chiodo. Questa volta, però, il baricentro G si sposta verso l’ALTO, ossia acquista energia potenziale. No, questa soluzione non gli piace per niente e appena lasciamo libera la barra, questa tende a riacquistare la posizione iniziale, quella di energia minima. L’equilibrio è stabile.

Qual è il modo più semplice per vedere in quale caso ci troviamo? Presto detto: basta vedere se il baricentro G è più alto o più basso del chiodo, ossia del punto di rotazione della barra. Se è più alto, l’equilibrio è instabile; se è più basso l’equilibrio è stabile.

Possiamo passare ora al nostro Pinocchio e al suo cappellino. Dato che sia la testa del burattino (sfera) che il capellino (cono con sezione triangolare isoscele) sono solidi simmetrici  (solidi di rotazione) possiamo benissimo raffigurare il problema su un piano, riducendo la sfera a un cerchio e il cono a un triangolo isoscele. Anzi, il triangolo è addirittura equilatero, dato che ha un angolo di 60° e, quindi, deve averli tutti e tre.

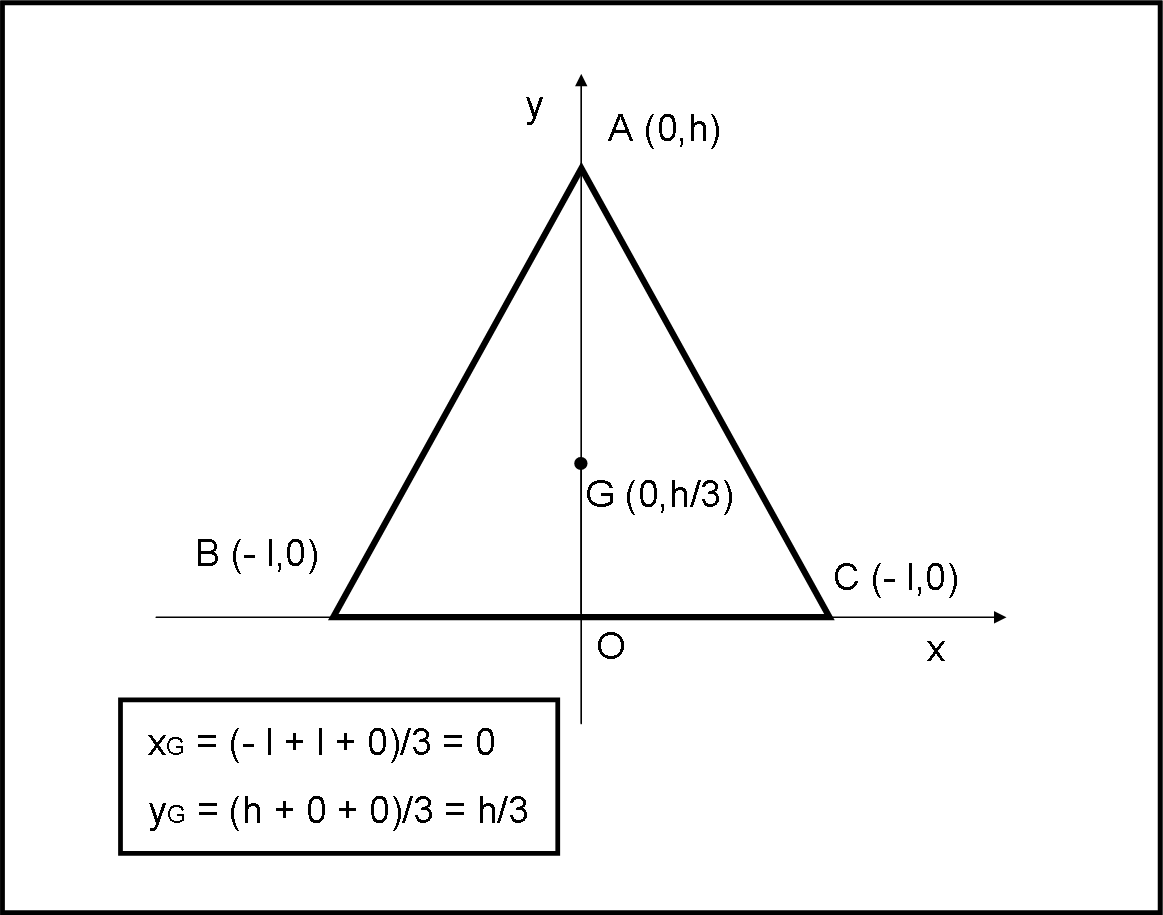
La prima cosa che dobbiamo fare è trovare il baricentro del cappellino, ossia del triangolo ABC. Possiamo agire in vari modi, ma basta ricordarsi il baricentro geometrico di tre punti, cioè i vertici del triangolo. Le coordinate del baricentro si ottengono sommando le coordinate dei tre punti e dividendo per tre (numero di punti). Se non vi piace, potete anche considerare il baricentro dei tre lati (punto di mezzo) e poi trovare il baricentro finale (il risultato non cambia). Si può addirittura calcolare il baricentro attraverso l’integrale esteso a tutto il triangolo, ma direi che non è proprio il caso…

In ogni modo, come si vede in Fig. 2, il baricentro G si trova esattamente sul segmento AO del triangolo a un’altezza dal lato inferiore uguale ad h/3.

Bene ora possiamo inserire il cappellino sulla testa (perfettamente liscia) del burattino. Facciamo prima il caso generale di Fig. 3. Il triangolo è poggiato sul cerchio ed è libero di ruotare attorno al suo centro P, sia a destra che a sinistra, come mostra la figura. Il triangolo ha sempre due lati tangenti al cerchio.

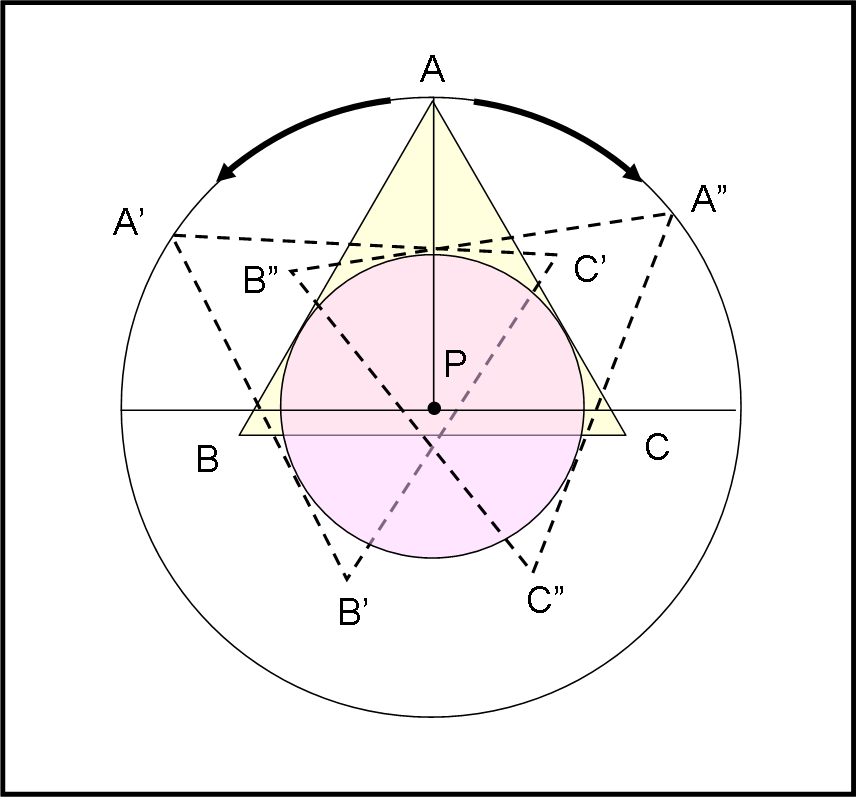
Introduciamo, adesso, il baricentro G del triangolo. Anch’esso ruota attorno al centro del cerchio P, sotto l’azione del vento orizzontale, descrivendo un cerchio di raggio GP, come mostrato in Fig. 4. Tuttavia, è facile notare che il baricentro G, al pari di quello della barra di ferro, tende a scendere verso il basso. Per quanto detto precedentemente abbiamo un equilibrio instabile. E’ facile notare che G risulta più in ALTO di P.

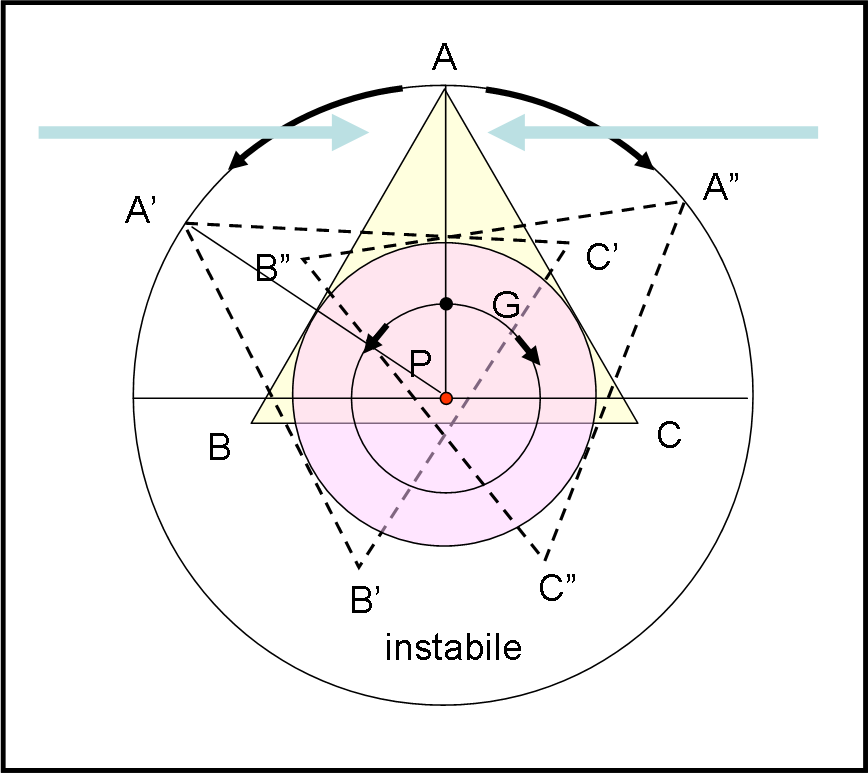
Passiamo alla Fig. 5 in cui abbiamo ingrandito il cappellino. Di conseguenza è anche cambiata la posizione del baricentro G rispetto alla testa su cui è poggiato. Si nota molto bene che, adesso, sotto l’azione del vento, A si sposta nuovamente o verso sinistra o verso destra, ma il baricentro G tende a ruotare attorno a P verso l’alto. Ne segue che appena cessa il vento, il cappellino torna nella posizione iniziale. Ovviamente, questa situazione dipende, come per la barra, dal fatto che il baricentro G è in posizione più BASSA di O.

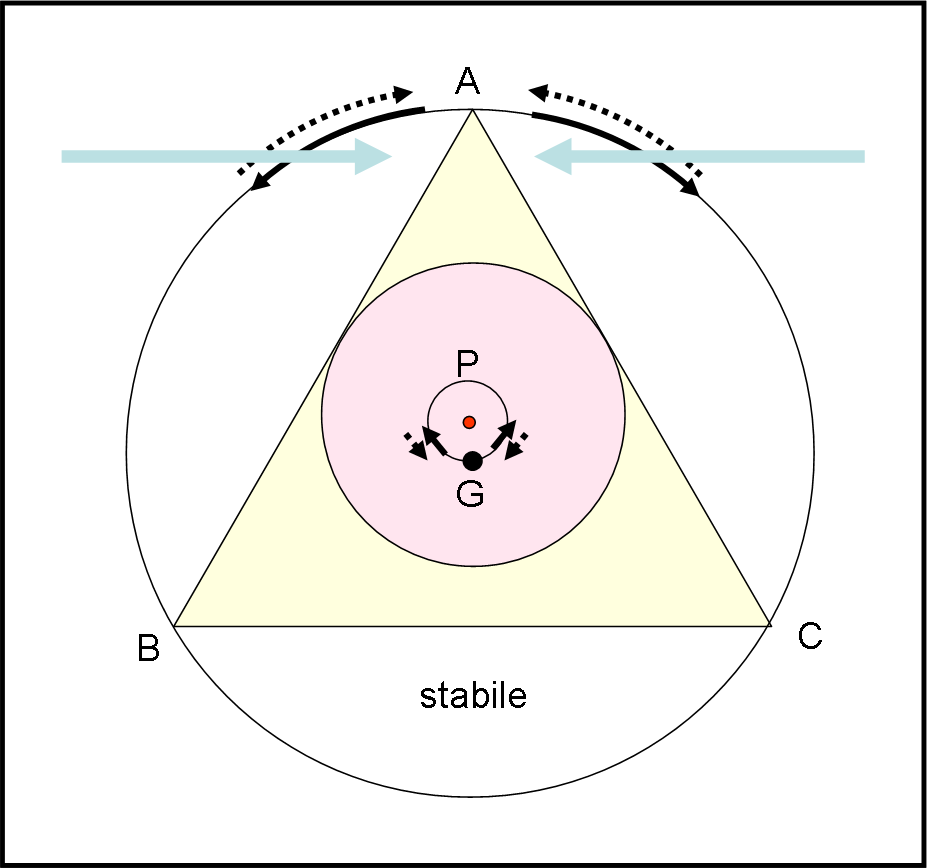
Per sapere, allora, se Geppetto ha fatto un buon lavoro non dobbiamo fare altro che controllare se il baricentro del cappellino è più alto o più basso del centro della testa P del burattino. La Fig. 6 non dà una buona notizia al falegname: il baricentro G è nettamente più alto di P.

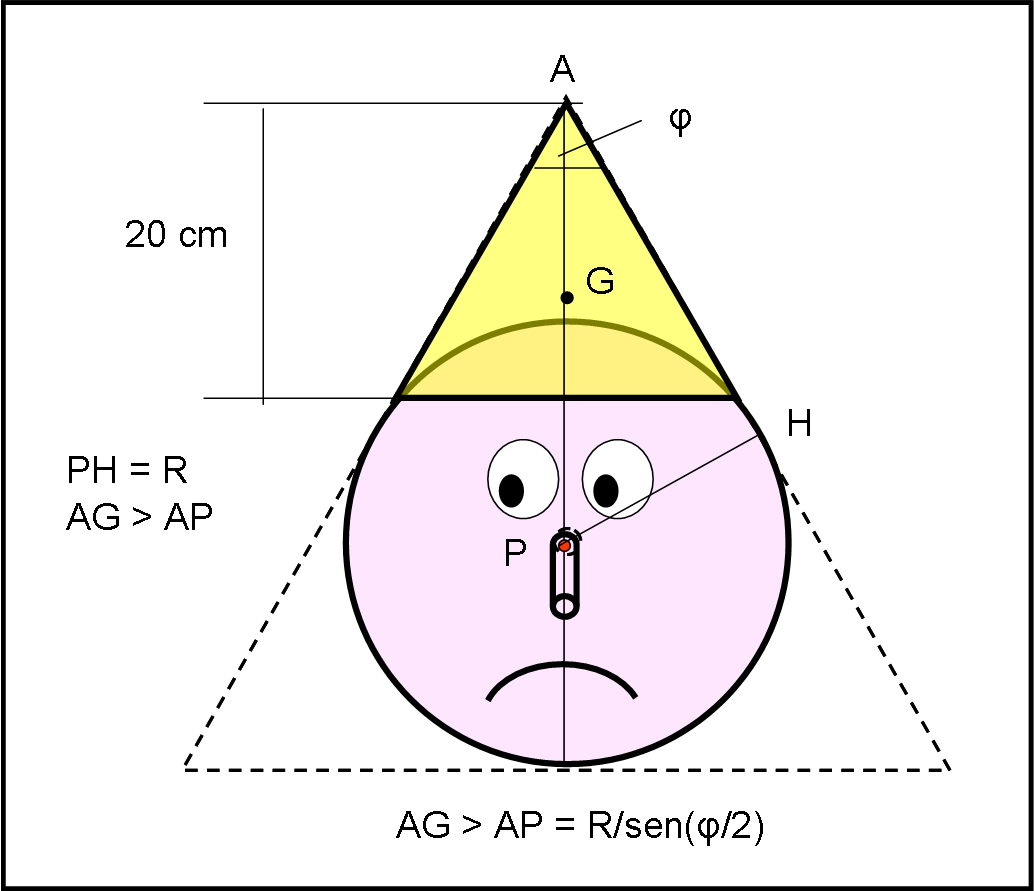
Per potere avere un equilibrio stabile bisogna che:

AG > AP

Dal triangolo APH si ha che:

AP = R/sen (φ/2)

Per cui si ha un cappellino in equilibrio stabile solo se:

AG > R/sen (φ/2)

O, ancora:

2/3 h > R/sen (φ/2)

h > 3R/(2 sen (φ/2))

Questa è la condizione perché vi sia equilibrio statico.

Nel nostro caso

sen (φ/2) = sen (30°) = 1/2

Per cui si dovrebbe avere

h > 3R

Ma R è uguale a 15 cm e quindi h dovrebbe essere maggiore di 45 cm

Il povero Geppetto ha cercato di risparmiare un po’ troppo con i suoi 20 cm…

La parte tratteggiata di Fig. 6 raffigura le minime dimensioni del cappello. Sarà anche stabile, ma Pinocchio non vedrebbe niente… Fare dei fori o ritagliare il cono in modo da lasciare visibilità? Forse è meglio fare intervenire direttamente Collodi!