Categorie: Fisica classica
Tags: angolo di rotazione equilibrio stabile galleggiamento principio di Archimede teorema di Archimede tronco a sezione quadrata
Scritto da: Vincenzo Zappalà
Commenti:14
Il Teorema di Archimede. 4: il galleggiamento e l'equilibrio **/***
Dopo la discussione sulle densità, siamo pronti ad affrontare la parte più interessante legata alla spinta di Archimede, ossia il galleggiamento. D'altra parte se si riescono ad attraversare gli oceani con una nave è fondamentale che la nave non vada a fondo! Non perdetevi questo articolo, dato che -forse- scoprirete un fenomeno poco conosciuto, che può dare il via a varie simulazioni "casalinghe".
Abbiamo visto che il galleggiamento dipende essenzialmente dalla densità del corpo che viene immerso nel fluido (d'ora in poi possiamo anche chiamarlo acqua dato che ci interessano, alla fin fine, proprio le navi). Ripetiamo quanto detto precedentemente:
Se la densità del corpo è minore di quella del fluido il corpo galleggia, ma può rimanere sia parzialmente immerso sia del tutto al di fuori del fluido. Quando rimane una parte sommersa, vuol solo dire che si è raggiunto l'equilibrio, ossia la parte sommersa è sufficiente a creare una spinta che è uguale al peso di tutto il corpo.
Possiamo anche trascurare i due casi limite in cui la densità è proprio uguale a quella dell'acqua (interessa relativamente poco galleggiare completamente immersi) oppure quella in cui si resta al pelo dell'acqua (come se la densità fosse zero). Occupiamoci quindi del vero e proprio galleggiamento, in cui solo una parte del corpo immerso subisce la spinta di Archimede, ma la subisce a sufficienza per non farlo sprofondare. Banalmente, possiamo dire che maggiore è la densità del corpo (ma sempre minore di quella dell'acqua) e più il corpo scende verso il basso (e viceversa).
Un tronco alla deriva
Prima di passare alle barche o alle navi, continuiamo a considerare il nostro corpo con sezione quadrata. Anzi, possiamo immaginarlo molto lungo, in modo che la sezione decida veramente le condizioni di equilibrio, senza bisogno di passare alle tre dimensioni. Insomma, prendiamo un bel tronco di legno che abbia sezione quadrata e immergiamolo nell'acqua. Ciò che ci aspettiamo è che venga raggiunto l'equilibrio, Con una sezione quadrata sembra cosa ovvia: basta immergerlo in modo che il lato del quadrato sia parallelo al bordo dell'acqua. Ma ne siamo sicuri?
Cominciamo a pensare che non sempre l'equilibrio è stabile (ossia che un leggero spostamento faccia tornare il corpo nelle condizioni iniziali) e che il volume della parte immersa non è detto che abbia il suo baricentro A sempre in linea verticale perfetta con il centro di gravità del corpo G. La cosa sembra ovvia utilizzando le figure dei capitoli precedenti, ma vediamo un po' meglio cosa succede se immergiamo il corpo in maniera inclinata.
Utilizziamo la Fig. 4
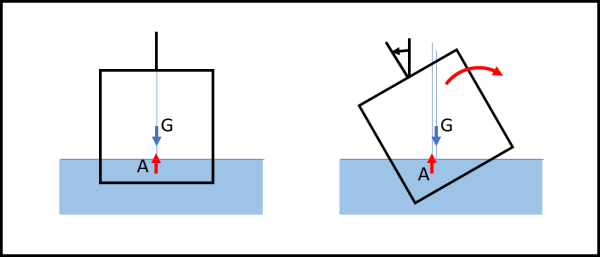
A sinistra abbiamo il nostro solito corpo immerso con il lato parallelo all'acqua e tutto sembra andare in modo perfetto. A destra, invece, immergiamo il corpo "di traverso". Cosa succede? La parte del corpo immerso nell'acqua assume un baricentro A che non giace sulla verticale della forza peso dell'intero corpo dove agisce la forza di gravità. La spinta di Archimede è diretta sempre verso verso l'alto, ma si trova spostata rispetto alla verticale che passa per G. In poche parole, mentre il baricentro del corpo G resta sempre lo stesso, la spinta di Archimede viene applicata in un punto A che si sposta lateralmente. Questo fatto causa due forze non allineate e quindi origina una coppia che fa ruotare il nostro tronco.
Sì, ma come lo fa girare? Siamo sicuri di saperlo? Assolutamente no. Il parametro fondamentale per analizzare questa situazione, forse non molto conosciuta è, ovviamente, la densità del corpo. E' lei, infatti che decide la parte immersa, da cui il suo baricentro e quindi il verso della coppia di forze.
Consideriamo un rapporto di densità tra corpo e acqua che sia pari a 0.2. Il corpo galleggia poco e, immergendolo leggermente inclinato, il volume (ma noi possiamo considerare l'area che si vede in figura) occupa una forma triangolare. Sia piegandolo a destra che a sinistra rispetto alle condizioni in cui il lato è parallelo al bordo dell'acqua, la coppia tende a farlo ruotare verso questa posizione. Nella Fig. 5 abbiamo piegato il lato di 30° (a titolo di esempio) e lasciandolo andare il tronco si sistema con il lato a 0°. I gradi sono contati attraverso una rotazione attorno a G verso sinistra.
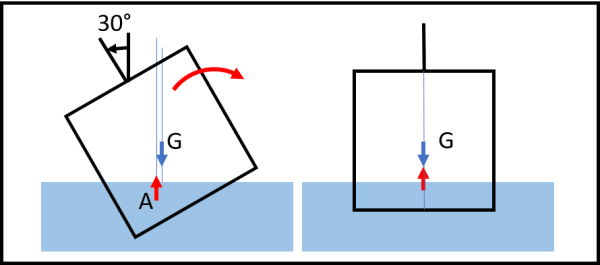
Consideriamo, adesso, un corpo pesante, con un densità pari a 0.8 quella dell'acqua. Il baricentro del corpo immerso è quello di una forma che può anche diventare pentagonale. Tuttavia, calcolandolo, abbiamo di nuovo una coppia che tende a farlo tornare nella posizione considerata di riposo. Nella Fig. 6 abbiamo nuovamente il lato piegato di 30°, ma, alla fine, torna a 0°.

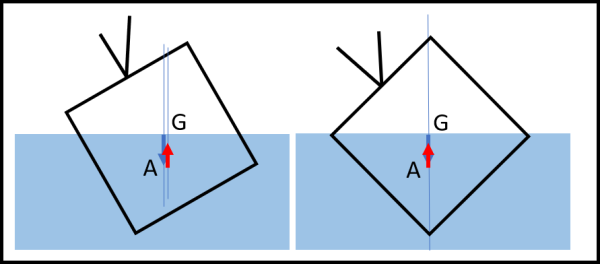
No, non vi sto prendendo in giro... Facciamo, adesso, l'esempio di una densità pari a 0.5 quella dell'acqua. Proviamo a metterlo inclinato e ci accorgiamo che la coppia lo trascina verso la posizione in cui la diagonale del quadrato è verticale. Se, addirittura, provassimo a metterlo col lato parallelo ci accorgeremmo che anche un solo lievissimo spostamento lo farebbe tornare nella posizione con il lato posto a 45° rispetto al bordo dell'acqua. In poche parole, per una densità media l'equilibrio è raggiunto con una configurazione che certo non ci aspettavamo. Nella Fig. 7 abbiamo di nuovo messo il lato a 30°, ma questa volta si è sistemato a 45°!
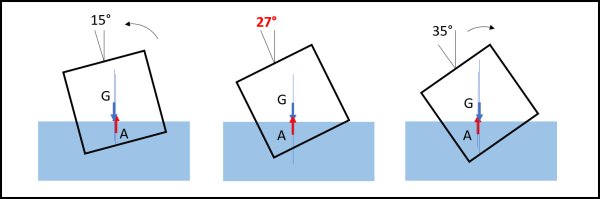
La faccenda diventa ancora più strana se scegliessimo una densità di 0.25. Proviamo, in Fig. 8, a mettere il lato prima a 15° e poi a 35°. In entrambi i casi il tronco si sposta verso una nuova condizione di equilibrio che corrisponde a un angolo di circa 27°! Ma se andassimo poco oltre i 35° ecco che la situazione cambierebbe di nuovo e ci troveremmo con un equilibrio intorno ai 63°.
No, non sto sparando numeri a caso... La coppia di forze che si crea gioca proprio questi strani scherzi. Ovviamente, come già puntualizzato, chi comanda il tutto è la densità che costringe la parte immersa ad assumere una forma il cui baricentro A si sposta rispetto a quello sempre costante del baricentro G di tutto il corpo. Insomma, non abbiamo solo una spinta, ma anche una coppia che tende a fare assumere la più vicina condizione di equilibrio "stabile", dove non solo le verticali tracciate dal baricentro G e dal baricentro sommerso A coincidono, ma dove anche un piccolo spostamento laterale fa riprendere questa configurazione.
Direi che è giunta l'ora di rappresentare graficamente e in modo generale cosa capita al nostro tronco a base quadrata. Mettiamo in ascissa la densità del tronco e in ordinata i valori dell'angolo di rotazione del tronco. Le linee rosse più marcate sono quelle che indicano l'equilibrio stabile. In realtà basterebbe far ruotare il nostro tronco tra 0° e 45°, ma per avere un quadro completo eseguiamo una rotazione completa di 360°, come mostra la Fig. 9.
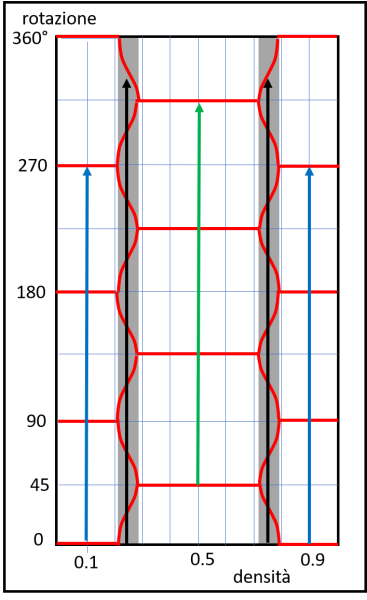
Fissiamo la nostra densità a 0.1. A questo punto facciamo ruotare il tronco (ossia ci spostiamo lungo la linea blu verticale) e ci accorgiamo che i punti di equilibrio (segnati con le linee rosse) sono proprio quelli pari a 0°, 90°, 180°, 270° (e nuovamente a 360° = 0°), ossia con i lati paralleli al pelo dell'acqua. Estremamente più interessante è il caso in cui la densità è intorno a 0.25. La linea verticale nera, che corrisponde a questa densità, interseca molte più volte la linea rossa ondulata: proprio per i valori di 27° e 63°, che poi si ripetono tra 90° e 180° e via dicendo. Invece di 4 punti di stabilità ne abbiamo 8.
Completamente diversa la situazione per una densità pari a 0.5. In questo caso, i punti di equilibrio (linea verticale verde) sono a 45°, 135°, 225° e 315°, ossia con le diagonali del quadrato messe in verticale. Poi, nuovamente, nella zona ristretta intorno a 0.70, ricompaiono gli 8 casi, per finire in bellezza con i quattro casi più "classici".
Per essere più precisi, la prima zona -con otto soluzioni per ogni giro- è compresa tra una densità di 0.21 e 0.28, mentre la seconda tra 0.72 e 0.79.
Cosa succede realmente lo possiamo vedere nella Fig. 10, dove il primo cerchio riporta le soluzioni a 0°, 90°, 180° e 270°. Entrando nello stretto intervallo di densità prima citate, è come se le soluzioni si sdoppiassero partendo dai segmenti verticali e orizzontali, andando verso la linea dei 45° e dei 135°. A metà la configurazione è nuovamente simmetrica con 8 soluzioni equidistanti; infine riprende la strada verso i segmenti a 45° e 135° fino a coincidere per densità maggiore di o.28. Identica soluzione per l'altro intervallo "critico".
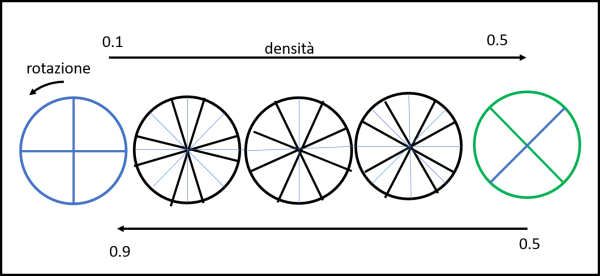
Per ancora maggiore chiarezza vediamo in Fig. 11, la nostra sezione di tronco, il cui lato rosso descrive 90° (variando la densità). Si notano bene le soluzioni di equilibrio, di cui due corrispondono a 0.25.
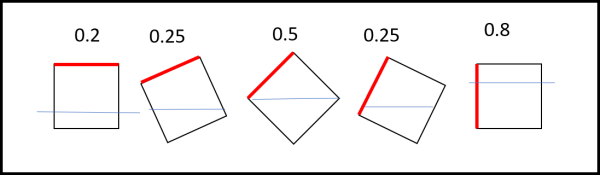
Per concludere, possiamo dire che le configurazioni di equilibrio per densità minori di 0.5 si ripetono specularmente per densità maggiori di 0.5. L'unica differenza è che il tronco è meno o più immerso nell'acqua.
Volendo si potrebbe anche calcolare il baricentro caso per caso o, addirittura, teoricamente. Io penso che basti così, ma non sarebbe male che qualche "uomo pratico d'assalto" facesse veramente la prova con tronchi di diversa densità e una bella vasca d'acqua (vero Arturo?).
Penso che quanto descritto in questo articolo sia una cosa abbastanza poco conosciuta e non scapperà a molti che in fondo vi è sempre una ricerca continua di minima energia potenziale del sistema...
Nella prossima (e ultima) puntata ci occuperemo delle navi che sembrano così pesanti e che invece galleggiano perfettamente e tendono a rimettersi sempre in orizzontale.
QUI Approfondiamo l'argomento della stabilità dell'equilibrio
Gli altri articoli dedicati al Teorema di Archimede li trovate QUI






14 commenti
proprio in queste settimane sto seguendo un progetto che tende a sfruttare il moto ondoso.. quindi energia dalle onde del mare.. la ricerca in questo campo vuole trovare la strada migliore per sfruttare questo tipo di energia praticamente inesauribile .. nel mio caso, l'azienda interessata a questo progetto, noto che si dedica molto a tarare il generatore elettrico in base al carico applicato.. e questo va bene..ma, vedo che trascura il "trasduttore" dell energia primaria, quello che trasforma la forza dell onda in forza peso,di tiro.. ossia la boa.. ci si accontenta delle boe standard.. senza progettarne nessuna appositamente per questa funzione.. le boe.. devono galleggiare.. e ok.. ma nel caso di una boa che deve "seguire" un onda nella sua verticale, quale forma sarebbe ideale? guardando questo post mi son venuti dei dubbi sul concetto che qualsiasi boa vada bene basta che galleggi..
nel nostro caso.. serve una boa che ancorata sul fondo con una fune(la spiego semplice) avvolta su una carrucola, quando l 'onda sale, tirando, fa girare la carrucola, la quale fa ruotare a sua volta il generatore.. ( ci sono allo studio anche generatori lineari che evitano la carrucola e quindi la trasformazione del moto alternato in rotatorio) la domanda che mi pongo è : metto due boe DELLO STESSO VOLUME, ma di forma differente.. una, la classica boa a rombo o doppio cono, e l'altra un semplice cubo galleggiante con la presa al centro.. quando l'onda sale.. tutte e due le boe danno lo stesso risultato come forza x spostamento?
Caro Ale,
assodato che la boa abbia sempre lo stesso peso, quello che conta è la parte sommersa e questa dipende sicuramente dalla densità e dalla forma. In particolare il suo baricentro e la spinta da applicargli. Ci sono due parametri fondamentali: la spinta che dipende solo dal volume e il baricentro del volume immerso che dà origine alla coppia. Inoltre, molto dipende anche dalla distanza verticale tra i due baricentri, Nel caso delle barche, per farle tornare in equilibrio si calcola il metacentro, di cui parleremo la prossima volta. Per chiarirci meglio la situazione, sarebbe veramente interessante che tu preparassi una riassunto divulgativo dell'intera apparecchiatura. Cosa ne dici? Qui tra noi ci sono molti ingegneri che potrebbero essere molto utili (più di me che sono un povero teorico) a riguardo...
Aggiungo qualcosa a livello veramente... infantile, in attesa di commenti più tecnici.
Teoricamente, se l'onda facesse solo alzare e abbassare il livello dell'acqua niente cambierebbe nell'equilibrio e la boa ripeterebbe tale e quale lo spostamento dell'acqua. Purtroppo, il moto dell'onda è turbolento, da cui ci si può aspettare che la quantità d'acqua che viene a coprire la boa vari rapidamente comportando una variazione del volume sommerso. Inoltre, lo stesso movimento laterale causa uno spostamento del baricentro della parte sommersa. Per ottenere una maggiore stabilità, ossia il ritorno alle condizioni di equilibrio iniziali, è importante che il baricentro della boa sia più basso del baricentro della parte sommersa. Non per niente nelle barche molto strette, che possono inclinarsi di molto, si mette un peso al fondo della chiglia. In tal modo la coppia tende a far riassumere l'equilibrio. La boa a doppio cono tende proprio a dare uno spostamento tra le verticali ai baricentri molto grande e quindi la coppia che rimette in equilibrio è molto forte.
Se, invece, si cerca di imporre una minore possibilità di variazione sono preferibili le imbarcazioni larghe e piatte che permettono coppie minori, tipo zattera.
La presenza del peso viene sicuramente sostituita dall'ancoraggio della boa al fondo. La realtà pratica è ben diversa da quella teorica e bisognerebbe vedere come giocano i vari fattori di disturbo, tenendo presente che la turbolenza delle onde è un fenomeno di tipo caotico e dipende da molte condizioni al contorno.
Forza Mau... chiedi aiuto a Oreste, che scenda dall'albero e risolva la questione!!!
Tirava vento dal mare, ricordo, e si muovevano le foglie. Oreste disse: Ho detto che non voglio e non voglio! Mai s'era vista disubbidienza più grave.
L'argomento è piuttosto tosto, anche per il nostro Oreste. Visto che fa le bizze comincerei a proporre qualche breve filmato illustrativo della tecnologia di cui stiamo parlando.
La boa progettata dall'ENEA
https://www.youtube.com/watch?v=PY9iqY6znx8&list=PLQ6GP8fdPtKK4BGcPJLNPXhBKRmFWrBiS&index=3&t=0s
Particolare del movimento della boa
https://www.youtube.com/watch?v=MUaxS3tHsCc
Qui si trova una dissertazione tecnica del modello matematico del comportamento del dispositivo
https://www.worldscientific.com/doi/pdfplus/10.1142/S1758825117500247
http://www.dimeas.polito.it/content/download/1483/10957/file/Pozzi_XXX%20ciclo.pdf
Come per la maggior parte dei fenomeni complessi quello che succede nella realtà va indagato con strumenti di simulazione computerizzata che consentono di verificare l'impatto di molte variabili concomitanti.
La pubblicità della Alfa Romeo Giulia, un mito della fine degli anni 50, recitava ..."l'ha disegnata il vento" facendo riferimento all'impiego in progettazione della galleria del vento, un ambiente all’interno del quale si soffia aria sulla vettura, mentre appositi sensori raccolgono i dati per controllare la resistenza aerodinamica delle varie parti alla forza dell’aria.
http://www.maranello.it/cosa-fare/la-galleria-del-vento/
Oggi la galleria del vento è anche virtuale .... https://netbikers.eu/language/it/con-airshaper-la-galleria-del-vento-diventa-virtuale/
Chissà se la boa migliore non dovremmo farla disegnare dal mare.
purtroppo Enzo, non essendo una mia idea non posso rivelare molti particolari su tutto l'insieme, il mio compito è tecnico, ed è quello di preparare un banco prova in lab per delle simulazioni.. quello che invece chiedevo appunto di argomentare (ma vedo che già lo state facendo) è proprio quella parte del progetto che per me è stata trascurata, che è appunto la boa.
Maurizio ha dato un ottimo consiglio se fosse fattibile.. ( ma forse lo è?) una boa che si modifica in forma e volume nel sito in cui è immersa.. sarebbe l ideale..
Enzo,tu dici giustamente:
"se l'onda facesse solo alzare e abbassare il livello dell'acqua niente cambierebbe nell'equilibrio e la boa ripeterebbe tale e quale lo spostamento dell'acqua. Purtroppo, il moto dell'onda è turbolento, da cui ci si può aspettare che la quantità d'acqua che viene a coprire la boa vari rapidamente comportando una variazione del volume sommerso. Inoltre, lo stesso movimento laterale causa uno spostamento del baricentro della parte sommersa. Per ottenere una maggiore stabilità, ossia il ritorno alle condizioni di equilibrio iniziali, è importante che il baricentro della boa sia più basso del baricentro della parte sommersa."
e i miei dubbi ora sono chiariti.. nel senso che nel progetto, di tutto questo non se ne parla..
che senso ha fare in modo che il generatore elettrico trasformi il moto meccanico in energia elettrica nella maniera più efficiente possibile se la boa non riesce a tirare fuori dall'onda la percentuale più alta possibile della sua energia potenziale?
Caro Alessandro la tua obiezione è più che giusta. Ottimizzare il rendimento a valle non compensa le carenze a monte.
L'efficienza della boa, la sua forma, sono intuitivamente legate al regime delle onde, variabile da luogo a luogo.
Inoltre si deve considerare che il comportamento di prototipi in scala non garantisce uguali risultati quando si passa alle dimensioni reali del sistema.
Un cenno semiserio a questo notevole problema lo trovi in questo articolo:
http://www.infinitoteatrodelcosmo.it/2019/05/10/poincare-da-incubo/
caro Ale,
per quello che possiamo ti aiutiamo, ma ci vorrebbero un ingegnere navale e delle prove sul campo in regime turbolento.
caro Ale,
ho trovato questa tesi di laurea sullo sfruttamento delle onde. Magari potresti trovare qualche spunto...
http://tesi.cab.unipd.it/25081/1/tesi.pdf
In pochi post mi avete già aiutato a confermare quelli che erano i miei dubbi..proporrò uno studio aggiuntivo sulla boa.. Grazie Enzo x la tesi che è anche molto chiara. . E il post di Maurizio che mi ha linkato illuminante su dei sospetti che già avevo..visto che di prototipi in scala per altri progetti ne ho fatti non pochi..ed empiricamente ero arrivato alla conclusione che non è possibile fare lo zoom 10x aspettandosi poi prestazioni aumentate di un ordine di grandezza. .. con questo circolo bastano pochi scambi x accendere lampadine

grazie a te, Ale, per seguirci e stare con noi appena hai un po' di tempo!
Grazie a te Ale, e buon lavoro!
Ringrazio sempre per la chiarezza.
Quando ho da chiarirmi un problema fisico cerco sempre prima in queste pagine.
Ora ne ho uno: una bolla d'aria in acqua è necessariamente sferica?
Secondo me: no.
Non ho argomenti forti ma penso che l'equilibrio fra la pressione interna del gas, che è praticamente indipendente dalla quota, e la pressione esterna idrostatica, che dipende dalla quota, porti ad un appiattimento della bolla o addirittura alla sua rottura.
Direi che hai ragione, caro Giovanni.
La pressione della parte inferiore è maggiore di quella della parte superiore, ne segue che la bolla tende a essere schiacciata. Ovviamente, molto dipende dalle dimensioni della bolla, ossia da quanto vari la pressione sopra e sotto e quindi quanto sia capace l'acqua di averla vita sulla densità dell'aria che sono separate solo dalla superficie della bolla. Il discorso si fa, comunque, interessante, coinvolgendo altri fattori come la tensione superficiale e altro ancora. Un bel problemino!
Grazie Giovanni... condivisione e collaborazione, sono le nostre parole d'ordine!!
D'altra parte se si va troppo a fondo si viene letteralmente schiacciati dalla pressione...