Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Centinaia di barche a vela si sfidano per  vincere la regata  più celebre del mondo. Essa si svolge su un lago e la variazione del vento è la dominatrice della gara, unita all'abilità nel saperla sfruttare. Dopo ore e ore di duelli e di colpi di scena, due barche si avvantaggiano su tutte le altre e si giocano la vittoria.

Sono esattamente sulla stessa linea quando, improvvisamente, il vento cessa del tutto. Le vele si afflosciano e le due barche si fermano nel lago, diventato piatto come un tavolo di biliardo. Malgrado tutti gli sforzi dei due avversari, le barche restano immobili. E pensare che il traguardo è solo a 99 cm dalla loro prua.

Ovviamente non hanno né remi né altri utensili adatti a spingerli in avanti per quei pochi centimetri che mancano all’agognato trionfo. I due sfidanti, A e  B,  sono entrambi a prua e guardano con occhi disperati il traguardo così vicino e così irraggiungibile. Il regolamento, inoltre, vieta ai contendenti di toccare l’acqua con qualsiasi parte del corpo o materiale vario. Che fare?

A decide di usare l’intelligenza al posto del vento. Si mette a riflettere e, alla fine, trova la soluzione. Agisce immediatamente e la sua barca percorre il tragitto mancante.Può alzare le braccia al cielo, mentre B lo guarda sconsolato, non capendo ancora come ha fatto a muovere la barca. Sicuramente ha usato qualche strana magia, ma la giuria conferma che tutto è stato regolare: la prestigiosa coppa finisce nelle mani di A.

Qualche dato tecnico… Le due barche, da sole, hanno entrambe una massa di 100 kg e sono lunghe esattamente tre metri. I due partecipanti hanno la stessa massa di 50 kg, come prescritto dal regolamento.

Come ha fatto A a vincere? Facile... si è ricordato delle proprietà del centro di massa di un sistema.

Per semplificare il tutto non teniamo in conto dell'albero e della vela, tanto sono ormai inutili e disegniamo la situazione  nella figura che segue:

Per essere estremamente didattici, iniziamo proprio con la definizione di baricentro di un insieme di punti.

Consideriamo il caso più semplice (Fig. 1, in alto), ossia i punti stanno tutti su una stessa retta che viene scelta come asse delle ascisse. Scegliamo anche un punto qualsiasi della retta come origine. Limitiamoci al caso di DUE soli punti (ma non cambierebbe niente se i punti fossero in numero ben più grande…).

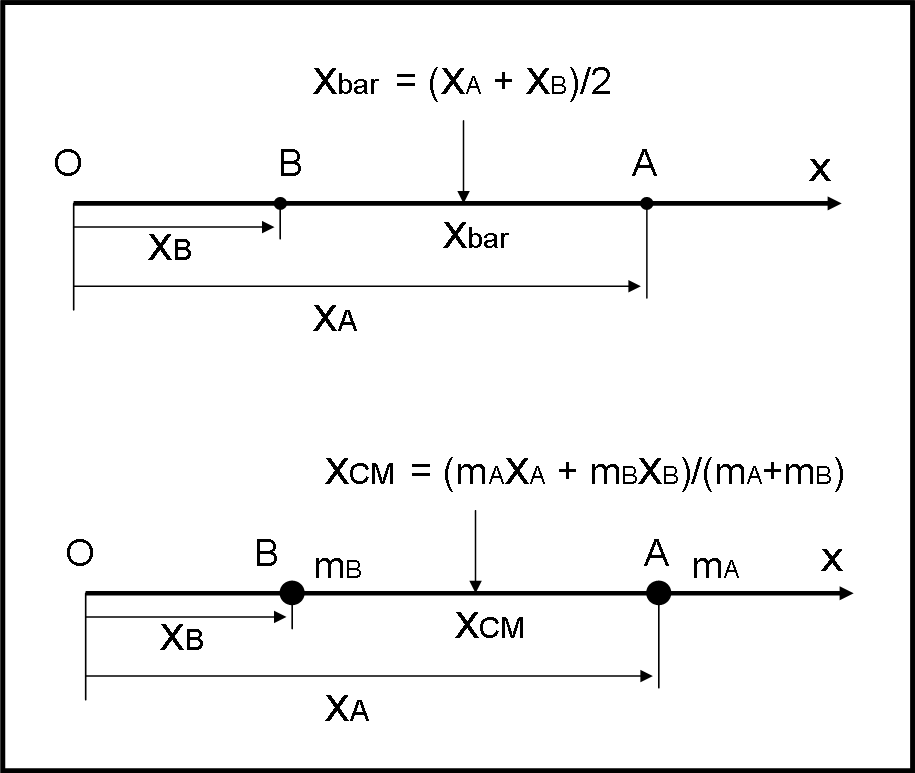
Rispetto all’origine O i due punti A e B hanno ascissa  x_A e x_B. Il baricentro dei due punti è dato dalla somma delle due ascisse divisa per due, ossia:

x_bar = (x_A + x_B)/2     …. (1)

In poche parole, non è altro che il valor medio delle ascisse dei due punti. Si otterrebbe una formula simile se considerassimo punti su di un piano (x,y): avremmo una formula come la (1) per le ascisse e una del tutto simile per le ordinate. Se, invece, i punti fossero N, la formula diventerebbe:

x_bar = (x_A + x_B + …. + x_N)/N        …. (2)

Beh… queste sono formule conosciute fin dalle scuole medie.

La faccenda cambia di poco se facciamo diventare i punti A e B dei corpi dotati di una certa massa (Fig.1, in basso). Possiamo comunque definire la posizione del loro baricentro con una formula come la (1), solo che, adesso, bisogna moltiplicare ogni ascissa per la massa del punto-corpo corrispondente . La (1) diventa:

x_CM = (x_Am_A + x_Bm_B)/(m_A + m_B)   …. (3)

Invece di baricentro si preferisce chiamarlo centro di massa, ma il significato è praticamente lo stesso (vedi QUI) . Notiamo, infatti, che la (3) diventa la (1) se le masse sono tutte uguali e unitarie…

Il centro di massa o baricentro di un sistema di corpi è estremamente importante dato che sappiamo bene come si possa sostituire l’intero corpo con un punto posizionato nel centro di massa che abbia come massa la somma di tutte le masse del sistema. Ricordiamo, ad esempio, il centro di massa di un sistema stellare binario. Ogni stella rivolve attorno al centro di massa del sistema, mentre quest’ultimo si muove di moto rettilineo uniforme.

Se considerassimo “fermo” il sistema, rispetto a un sistema di riferimento esterno, avremmo che le stelle continuano a rivolvere, mentre il baricentro sta fermo. E’ un punto estremamente importante perché può fare le veci dell’intero sistema e può agire solo lui in problemi di dinamica ben più complicati. In altre parole, i corpi che compongono il sistema possono muoversi come vogliono al suo interno, ma se non agiscono forze esterne, il centro di massa deve restare immobile.

Questo concetto è fondamentale e può anche dedursi tenendo conto della conservazione della quantità di moto del sistema e che, se la sua velocità è ZERO, tale deve rimanere senza l’intervento di forze esterne. In poche parole, le singole masse possono divertirsi a muoversi e a cambiare la posizione relativa del centro di massa del sistema, ma esso non può assolutamente muoversi rispetto a un sistema esterno e quindi la sua posizione x_CM deve rimanere costante.

Fatte queste premesse, oltremodo semplici e ben conosciute, possiamo cominciare a risolvere il nostro problema di... vele senza vento.

Il nostro sistema è composto da due sole masse: la barca di 100 kg e A di 50 kg. Come ben noto, possiamo benissimo sostituire i due corpi con i loro rispettivi baricentri, in cui sia concentrata l’intera massa del corpo. In Fig. 2 (a), disegniamo il sistema barca + A in modo schematico, inserendo i loro baricentri. Prendiamo come origine la poppa della barca O e, come asse, l’asse della barca. Il baricentro della barca sia B e quello del concorrente A sia proprio A.

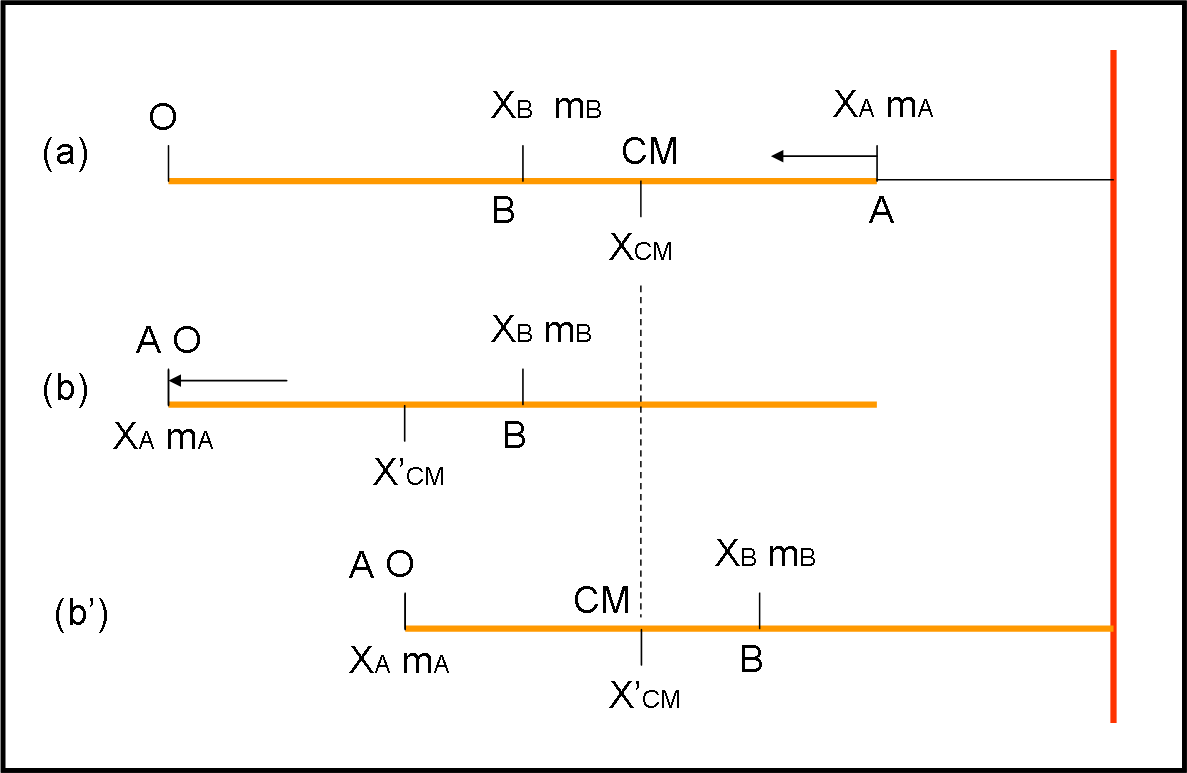
Ovviamente, dato che la barca è simmetrica lungo l’asse x, il baricentro x_B (o centro di massa) della barca si trova a 3/2 = 1.5 m rispetto a O. Il baricentro di A si trova, invece, a una distanza x_A = 3 m. Conosciamo anche la loro massa e, quindi, è immediato scrivere l’ascissa x_CM del centro di massa dell’intero sistema, attraverso la (3):

x_CM = (x_Bm_B + x_Am_A)/(m_B + m_A) = (1.5 x 100 + 3 x 50)/(100 + 50) = 2 m

Il centro di massa del sistema ha un ascissa x_CM = 2m, ossia si trova a 2 metri dalla poppa della barca. Ricordiamo che il sistema deve stare fermo dato che non esistono forze esterne. In altre parole x_CM deve rimanere sempre lo stesso, rispetto al lago, comunque si divertano a muoversi le masse che formano il sistema.

La barca non può muoversi, ma il concorrente A sì. Ed ecco, allora, che si sposta senza fretta (a parte quella di sollevare al più presto la coppa di campione…) verso la poppa O (Fig 2 (b)). In poche parole, A  cambia la sua ascissa da 3 a 0. Cosa succede facendo questa operazione? Beh… deve cambiare la posizione relativa del centro di massa del sistema, ma non certo la sua posizione rispetto al lago, allo stesso modo di un sistema binario di stelle che non abbia velocità propria.

Calcoliamo allora la posizione del nuovo centro di massa x’_CM, rispetto all’origine O (la poppa) che fa parte del sistema.

x’_CM = (x_Bm_B + x_Am_A)/(m_B + m_A) = (1.5 x 100 + 0 x 50)/(100 + 50) = 1 m

Il centro di massa si è spostato di un metro verso sinistra nel sistema di riferimento interno. Tuttavia, il centro di massa deve rimanere fermo rispetto al lago e quindi tutto il sistema barca + A  deve spostarsi verso destra in modo da far coincidere la posizione del nuovo baricentro x’_CM con la posizione di quello vecchio x_CM. In altre parole, ancora, la distanza tra centro di massa e traguardo (sistema di riferimento esterno) deve rimanere uguale (Fig. 2 (b'))!

Notate che l'azione (b) e (b') avvengono contemporaneamente.

Attenzione: se avete problemi a immaginare questa azione, pensate di stare su una stella di un sistema binario. Per voi il baricentro del sistema si sposta in continuazione (un po’ lo vedete a destra e un po’ a sinistra), ma lui in realtà resta sempre fermo in un  sistema di riferimento esterno (come il lago, le sue sponde e il traguardo).

La conclusione della “passeggiata” del concorrente A costringe la barca a spostarsi di un metro verso destra. Non un centimetro di più, però… I tre metri della barca, e quindi la variazione possibile del nuovo baricentro, non permettono uno spostamento maggiore. Quanto basta ad A per toccare il traguardo e sollevare la coppa del vincitore!

Come si vede chiaramente, la soluzione può ottenersi facendo un calcolo a mente e trovando solo e soltanto la differenza tra la posizione del centro di massa iniziale e finale. Questa differenza è uguale e contraria allo spostamento del sistema rispetto al lago

Chi vuole può anche fare un breve studio di funzione per generalizzare la situazione allungando la barca e/o cambiando le masse in gioco. Oppure, vedere come varia lo spostamento del sistema verso destra per tragitti diversi del concorrente A. Funzioni veramente elementari…

 

Ma le meraviglie del baricentro non finiscono qui... guardate QUI come riesce a "distruggere" (apparentemente) la gravità!