Categorie: Fisica classica
Tags: baricentro centro di massa quiz soluzione statica
Scritto da: Vincenzo Zappalà
Commenti:8
Soluzione della Luna strana: baricentro o centro di massa ? *
Come anticipato, il problema è decisamente facile e ha il solo scopo di richiamare la differenza che esiste tra baricentro geometrico e centro di massa.
Spesso si legge che i due concetti sono del tutto equivalenti. Tuttavia ciò non è assolutamente vero. Il baricentro è qualcosa di puramente matematico definito come il punto di una certa figura geometrica tale da avere come coordinate la media aritmetica delle coordinate dei punti della figura. Per saperne di più potete andare QUI. Il centro di massa, invece è qualcosa di fisico e rappresenta una proprietà intrinseca di qualsiasi corpo e può essere definito come quel punto in cui è possibile concentrare tutta la massa ai fini del suo comportamento dinamico. Quando, però, il corpo in questione ha una densità costante, le due definizioni coincidono. In particolare la massa può essere sostituita dal volume.
Il problema sollevato dal quiz chiede il baricentro di una figura geometrica ottenuta eliminando una parte di essa. Tuttavia, si fa, fin da subito, riferimento a un cartoncino, da cui si ritaglia qualcosa. Queste poche parole fanno subito capire che siamo di fronte a un corpo fisico che possiede una caratteristica ben definita. La densità è la stessa in ogni parte del corpo e la massa non può solo essere sostituita dal volume, ma addirittura dalla superficie dei corpi in questione, dato che il suo spessore rimane costante (oltre a essere decisamente piccolo).
Conviene perciò risolverlo cercando il suo centro di massa che coinciderà perfettamente con il baricentro geometrico della figura, supposta bidimensionale. In poche parole, possiamo lavorare tranquillamente sul piano del foglio.
Ricordiamo la formula che ci regala il centro di massa:
rCM = ∑miri/Mtot .... (1)
Nella formula, Mtot è la massa totale, mi le masse delle varie parti in cui si può considerare diviso il corpo in esame e ri la distanza di ogni singolo centro di massa da un punto qualsiasi scelto come origine degli assi. Il risultato ci fornisce il valore della distanza del centro di massa dall’origine.
Nel nostro caso, le masse sono sostituite dalle aree dei corpi in esame e possiamo tranquillamente chiamarlo baricentro B… Consideriamo la Fig. 1
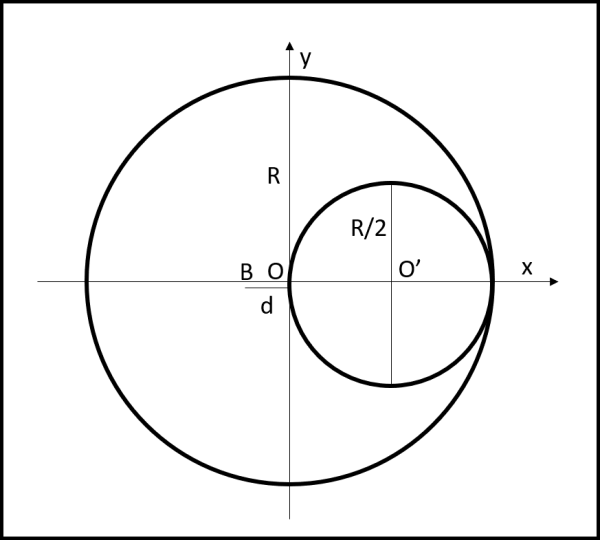
Noi conosciamo perfettamente dove stanno i baricentri (o centri di massa) del cerchio grande e del cerchio piccolo: esattamente nel loro centro O e O’. Eliminando il cerchio piccolo è ovvio che il baricentro della nuova figura deve trovarsi, per simmetria, lungo l’asse x, dalla parte sinistra rispetto al centro del cerchio maggiore. Chiamiamo questa distanza d. Essa non è altro che la posizione del baricentro rispetto all’origine delle coordinate che abbiamo scelto.
Scriviamo, allora la relazione (1), inserendo le aree al posto delle masse e le distanze dai baricentri delle due figure considerate, ossia il cerchio piccolo e la strana falce di Luna. In pratica, abbiamo ricostruito il cerchio iniziale, rimettendo al suo posto il cerchio ritagliato.
Ricordiamo, prima, anche le aree (masse) che andiamo a utilizzare:
ACP = πR2/4 (area cerchio piccolo)
AL = πR2 - πR2/4 = 3πR2/4 (area "mezza luna")
ATOT = πR2 (area cerchio grande)
xO = (R/2 ACP + d AL)/ATOT
xO = (πR3/8 + d 3πR2/4)/ πR2 = R/8 + 3/4 x
Nel nostro sistema di coordinate cartesiane xO è proprio l’origine degli assi, ossia xO = 0. Per cui
R/8 + 3/4 d = 0
d = - 4R/(8∙3) = - R/6
Come previsto, il valore è negativo.
Come piccolo esercizio supplementare, possiamo anche cambiare sistema di riferimento, spostandolo sia in x che in y rispetto al centro del cerchio più grande.
Rifacciamo la Fig.1 con gli assi spostati (Fig. 2).
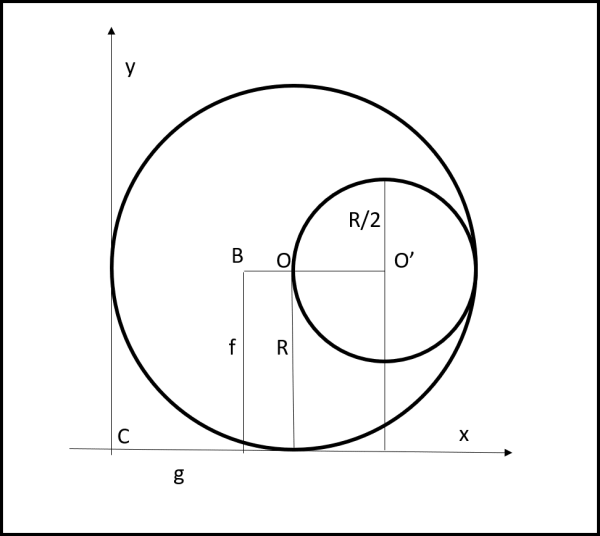
Ovviamente, cambiano le coordinate dei tre baricentri, che diventano O(R,R), O’(3R/2, R), B(g,f)
Calcoliamo prima l'ascissa (eliminiamo subito π e R2 che si semplificano tra numeratore e denominatore)
xB = R = 3R/8+ 3g/4
3g/4 = R – 3R/8 = 5R/8
g = 5∙4 R/(8∙3)
g = 5/6 R
e poi l’ordinata
yB = R = R/4 + 3f/4
3f/4 = R - R/4 = 3∙4R
f = R
Abbiamo, ovviamente, ottenuto lo stesso punto B di prima.
Era anche possibile lavorare direttamente con le distanze tra i baricentri e l'origine...






8 commenti
Centro di massa e baricentro fisico coincidono solo se il corpo ha una densità costante in tutti i suoi punti e il corpo è in un campo gravitazionale uniforme
infatti...
Forse tra gli esempi più semplici (almeno per me) si possono considerare due punti aventi la stessa massa m ed uguale distanza dal centro della Terra il loro centro di massa coincide col baricentro fisico ed è situato a metà del segmento avente per estremi i due punti. Se spostiamo uno dei due punti ad una distanza maggiore dell'altro il centro di massa sarà situato sempre a metà del segmento che li unisce ma il baricentro fisico NO: le forze peso che agiscono su i due punti non sono uguali (in modulo) ma sul punto più lontano è minore (secondo Newton).
Il baricentro fisico si trova su un punto interno al segmento di unione e tale che i momenti delle due forze peso rispetto ad esso siano opposti
vuoi dire spostare un punto mettendolo più lontano dal centro della Terra? Beh... ovviamente. Ma quello diventa il baricentro fisico e non il centro di massa. Baricentro geometrico e centro di massa restano uguali...
Insomma ci sono tre punti che possono coincidere oppure no: baricentro geometrico, centro di massa e baricentro fisico. Nel quiz si parla solo dei primi due.
Grazie .. Vincenzo e Michele, ho trovato questo mentre cercavo qualcosa sui baricentri,.
Vincenzo mi consocie perche' scrivo in Astronomia, sono quello del foglio di calcolo in excel, che ora e' un programma fatto in VB.NET e che calcola la posizione dei pianeti.
Stavo cercando l'algoritmo per il calcolo del Baricentro Pianeta - Pianeta.
Se quello tra Pianeta Sole e'
X = Dist.Sole Pianeta UA:
m1 = massa pianeta inferiore
m2 = Massa pianeta + grande)
(X* ua)*(m1/(m1+m2)) = Baricentro Sole-Pianeta.
--------------------------------------------------------
In teoria doveva funzionare anche tra Pianeta e Pianeta, al posto del Sole ci metto la massa del pianeta maggiore.
Ma qualcosa mi sfugge. Esempio.
MT = massa Terra = 5,972186297153e+24
MS = Massa Giove = 1.898523324710e+27
DTua = distanza pianeta in UA.
=((DTua*149597870,7)*(Massa T/(MassaT+Massa Giove)))
mi esce ., 2.167.541,87 .-
Che non riesco a capire come il baricentro sia fuori la terra , ma sarebbe anche assurdo fuori giove...........
Diametro Terra.... 12.756,273 km
Diametro Giove ... 142984 km
Mi manca qualcosa che mi sta sfuggendo ...............???
cordiali.. LucianoB al Prof. Vincenzo e l'altro che non conosco.
caro Luciano B,
che un baricentro cada fuori dai due corpi considerati è cosa normalissima. Non ho fatto i calcoli, ma la formula deve sempre valere, ovviamente. Che il baricentro tra Giove e Terra sia fuori dalla Terra è cosa molto ovvia, vista la differenza di massa... Così come lo è tra Sole e Terra.
Per saperne di più sul baricentro, puoi andare qui:
http://www.infinitoteatrodelcosmo.it/2016/10/01/la-doppia-ragnatela-dal-baricentro-ai-punti-lagrangiani-e-ai-lobi-di-roche/
dove si capisce che la soluzione per qualsiasi oggetto del sistema solare è ben diversa da quella kepleriana senza perturbazioni. Il problema dei tre corpi non si può risolvere analiticamente se non per i punti lagrangiani.
Sai Luciano,
il tuo lavoro è sicuramente encomiabile... ma per avere le posizioni ultra precise dei pianeti (e non solo) vi sono canali tenuti da grandi istituti che le danno per qualsiasi posizione e per qualsiasi tempo. E usano programmi che noi non possiamo permetterci di far girare... Una cosa è capire bene come funzionano le cose e un'altra è guadagnare tempo per eseguire calcoli ultra complessi. Li avesse avuti Gauss...! Questo è il grande problema di astronomia.com: la gente parla di tutto, ma non ha le basi per farlo... un vero facebook pseudo-scientifico (parola troppo grossa). Non per niente me ne ero andato... io voglio fare vera divulgazione, non ripetere le stesse risposte mille volte con personaggi che pur non conoscendo RR, RG e MQ vogliono stravolgere i modelli attuali.
Gentile Prof Vincenzo, ti ringrazio e ti porgo i miei Saluti.
Leggero' sicuramente quello che mi hai linkato.
Ho conoscenza dei punti di Lagrange L1/L2/L3/L4 .. dove per'altro in alcuni punti ci sono le sonde di controllo per il Sole. Gia' inseriti nel foglio calcolo e poi da inserire all'interno del programma più avanti.
Parti della Meccanica Lagrangiana.
Si' mi sono accorto infatti che non e' all'interno del pianeta ma esce fuori. !
Perché la logica mi pareva corretta, al posto del Sole cambiava corpo e ovviamente il R-vettore istantaneo era considerato per i corpi in questione a far data e momento..
Devo mettermi un po' a leggere, visto che nel programma ho gia' messo i Baricentri tra corpi verso il Sole e di quanto influisce in esso. (Pross. vers.1.0.8.4) -------- So' che e' un lavoro immane e mi pare di avere fatto un qualcosa di decente.
So' che e' un lavoro immane e mi pare di avere fatto un qualcosa di decente.
Ma volevo anche capire l'influenza dei Pianeti ----(visto che esistono le perturbazioni planetarie, considerate per i vari movimenti orbita, menzionati da J.Meeus e sui libri, del quale il mio programma tiene in considerazione per aumentare la precisione e migliorare il calcolo.) ----
Tieni conto gli aggiornamenti nei prossimi mesi sulla pagina dove usualmente usata per il programma.
Dove cerco sempre di controllare che i risultati siano corretti e precisi.
Comunque il problema e' come risolvere il problema, quando programmi come SolarMotion, vedi dove e' il baricentro del Sistema Solare verso il sole.
Mi servono i calcoli e capire.. circa la sommatoria e l'equilibrio delle forze che in tal caso diventa complessissimo.
Ad esempio leggo anche qui http://www.matemania.it/matematica/article/baricentro-e-centro-di-massa-definizione-ed-esempi-di-calcolo
Va bene, si' quelli che vogliono stravolgere senza conoscere la Mnewtoniana classica. E neppure Keplero !
Cordiali Saluti e grazie per la risposta.
Gentile Prof. Vincenzo.
Luciano B