Categorie: Fisica classica Matematica
Tags: baricentro figura piana geometria meccanica quiz
Scritto da: Vincenzo Zappalà
Commenti:26
Quiz: una Luna un po' strana */**
Dopo il fiocco di neve di Koch, dedichiamoci a un quiz decisamente più semplice, ma che, come sempre, deve essere impostato correttamente. Il suo interesse sta nel richiamare un concetto fondamentale della geometria e della fisica.
Disegniamo e ritagliamo un bel cerchio di raggio R su un cartoncino. Su di lui disegniamo un altro cerchio di raggio R/2 che sia tangente internamente al primo cerchio e ritagliamo anche lui. Quello che ci rimane è una specie di Luna in fase, con le due punte che si toccano. Dove si troverà il baricentro di questa strana figura?
Scegliete liberamente l'origine da cui misurare la posizione del baricentro...
26 commenti
Prima di tutto, vista l'esistenza di un altro Guido, ben più ferrato di me... mi firmo da ora in poi GuidoD...
Se non sbaglio, il baricentro di un cerchio è il proprio centro C. Levandone però un pezzo, il baricentro dovrebbe spostarsi lungo l'asse di simmetria della figura (quale, dipende dal punto della circonferenza il cui il cerchio interno tange il maggiore) ma finire all'esterno della stessa. Credo...
Saluti
Stavolta voglio fare il birbantello...
Rispondo con una domanda: ipotizzando di restare nel piano del cartoncino, che l'oggetto sia immerso in un campo gravitazionale e di sospenderlo esattamente nel suo centro, una volta praticato il taglio richiesto, come si disporrà ?
e bravo Artù... un quiz alla seconda...
La figura ottenuta "luna in fase con le due punte che si toccano può essere riferita ad un sistema di assi cartesiani ove Y passa per le due punte e il centro del cerchio di raggio R, X è perpendicolare ad Y e tangente al cerchio di raggio R sul punto in basso al centro stesso.
La figura è simmetrica rispetto all'asse Y quindi il suo baricentro si troverà sullo stesso.
Utilizzo il metodo dei momenti statici delle figure in questo caso rispetto all'asse X:
yG =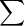
Si * yi / 
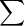Si
la superficie del cerchio di raggio R è positiva quella del cerchio con raggio R/2 negativa
yG = [
R2* R - 
R2/4 (R+ R/2)] / 
R2 - 
R2/4 = (
R3 - 
R2/4 * 3/2R) / 3/4
R2 =
= 5/8
R3 / 3/4 
R2 = 5/6 R
Le coordinate del baricentro G nel riferimento considerato sono
xG = 0 ; yG = 5/6 R
aspetto a rispondere, ovviamente... Però, Michele, dovresti fare una figurina o far capire meglio dove si trova l'origine degli assi rispetto al cerchio più piccolo. Io penso di aver capito capito, ma è meglio, per i lettori essere più chiari. Tu dici "in basso", ma rispetto a cosa? Grazie!
Artù... scommetto che hai anche fatto il modellino
Va beh... questa era molto facile...
caro GuidoD... dovresti essere più preciso e dare un po' di ... numeri!
Il cerchio più piccolo si trova rispetto all'origine degli assi sul 1° quadrante (x pos y pos).
Ho un po' di difficoltà ad inserire la figura
Correggo:
I centri dei due cerchi sono sull'asse y
L'asse x è tangente al cerchio grande nel punto sull'asse y (unione due punte "Luna") al centro circonferenza raggio R
"L'asse x è tangente al cerchio grande nel punto sull'asse y (unione due punte "Luna") al centro circonferenza raggio R. " (???)
Scusa, ma continuo a non capire... D'accordo sull'asse y. Ma l'asse x è tangente alla circonferenza grande in quale punto? Quello opposto al cerchio piccolo o dove è anche tangente al cerchio piccolo
Come la prima figura a sinistra, il verso positivo della Y è verso dx, quello positivo della X verso il basso.
Purtroppo una figura vale più di mille descrizioni, ma con gli strumenti a disposizione della sezione commenti non riesco a inserire figure/disegni. Probabilmente la procedura è banale ma non sono un "mago" del Web.
Grazie Vincenzo
Purtroppo anch'io non sono un mago del web... ma so che si può fare ed è stato già spiegato tempo fa (ma non mi ricordo dove e quando). Faccio una richiesta a Umberto e/o Arturo che di queste faccende sono ben più esperti. Potete descriverlo ancora una volta per il nostro amico MIchele.
Sai, io me la cavo perché posso entrare negli articoli o nei commenti e inserire facilmente le figure...
Comunque la tua scelta è proprio quella che pensavo...
Ti ringrazio Vincenzo, ora mi debbo assentare dal PC per andare a gestire l'orto e la vigna. Come pensionato ho anche queste "necessità".
Buona giornata
caro Michele, nel mio piccolo ti capisco... Tra mezz'ora inizio a tagliare l'erba nel prato...
buon lavoro!!!
per prima cosa bisogna avere a disposizione l'immagine nel PC: mettiamo sia questa:
questa immagine dobbiamo trasferirla nel web. Come? con un sito tipo IMGUR:
Seguendo le istruzioni( semplici) si carica l'immagine. Io ho scelto imgur ma esistono altri siti.
adesso l'immagine può essere individuata tramite un indirizzo internet, nel nostro caso :
https://i.imgur.com/gCIcL77.gif
basta ora aprire lo strumento immagine che trovate nella testata dei commenti:
(quello selezionato in giallo)
e appare la finestra di dialogo:
nel campo "sergente" evidenziato mettiamo l'indirizzo della nostra immagine, https://i.imgur.com/gCIcL77.gif
ed eccola qua.
grazie Umberto!!!!
speriamo.. uno scoglio potrebbe essere la scelta del programma web. Io userei imgur.
l'indirizzo è questo:
https://imgur.com/
registrarsi (in alto a destra il link di registrazione)
e dopo di che autentificarsi.
Per aggiungere una immagine:
si apre la finestra:
con varie possibilità di inserimento. Scegliere sfoglia.Una volta inserita l'immagine, bisogna trovarne l'indirizzo che poi dobbiamo aggiungere nei nostri commenti.
andare su nome utente-->immagini
cliccate sull'immagine: vi apparirà un'altra finestra a destra:
il link che a noi serve è quello scritto in "collegamento diretto"
"Artù... scommetto che hai anche fatto il modellino"
toh: , per adesso solo virtuale... ;-)
(mg è la forza peso della lunula nera, A è la reazione del punto di sospensione)
E' solo questione di ... massa e di momento!!!
grande Artù!!!!
Se hai voglia, Arturo, scrivi due righe sull'esperimento e poi le inserisco nella soluzione...
E se non ci fossero attriti... sai quante cose si potrebbero dire... C'è niente da fare, la fisica, anche quando è apparentemente "statica", ci mette un niente a diventare "dinamica". Basta un po' di fantasia...
Grazie Artù a nome di tutti i lettori!
Grazie Umberto mi hai dato gli strumenti per inserire immagini nei commenti. Proverò certamente ad utilizzarli sperando d riuscire.... altrimenti chiederò delucidazioni
caro Artù
ne sai una più del diavolo !
Nell'animazione riportata qualche commento più sopra si vede come si dispone la lunula nera sospesa nel centro del cerchio grande originario, una volta espulso il cerchio minore. Ma quale è la situazione prima di togliere quest'ultimo ? Cioè, considerando il cerchio grande immerso in un campo gravitazione nel suo piano e sospeso nel suo centro, cosa succede prima di tagliare e togliere il cerchio minore ? Ovviamente nulla, tutto è in equilibrio . In particolare, essendo l'oggetto sospeso nel suo centro, essendo cioè "vincolato", pur sotto l'azione del campo gravitazionale, non può traslare. Inoltre, esso non ruota neppure, attorno al vincolo, perché, per la simmetria della sua forma (cerchio) e nell'ipotesi di densità costante del materiale di cui è fatto (...), la sua metà destra tende a farlo ruotare in senso orario nella stessa misura in cui fa la sua metà sinistra in senso antiorario. In termini fisici, il momento (forza*braccio) della metà destra è uguale e contrario al momento della metà sinistra. Ora , però, anziché considerare le due mezzelune destra e sinistra, considero il cerchio minore, che sta a destra, e il resto del cerchio grande, che sta a sinistra ma si propende anche verso destra. Il cerchio minore, considerato a sè stante, è soggetto alla forza peso m*g. Tale forza si traduce, tornando al cerchio grande originario, in una coppia (o momento) pari a m*g*R/2 (centro di rotazione è il centro del cerchio grande originario) che tende a ruotare il cerchio grande originario in senso orario. La parte restante del cerchio grande originario, invece, considerata a sè stante, è soggetta alla forza peso M*g. Tale forza si traduce, tornando al cerchio grande originario, in una coppia pari a M*g*x, dove x è la distanza, incognita, dal centro del cerchio grande.
All'inizio, si è detto, il tutto è in equilibrio alla rotazione, per cui i due suddetti momenti , o coppie, devono farsi equilibrio:
M*g*x=m*g*R/2
da cui, dividendo tutto per g ed esplicitando rispetto alla x:
x = m*R / (2 M) (1)
A questo punto, calcolo
M =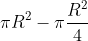
sostituisco nella (1) ottenendo:
x=R/6 (distanza tra il centro del cerchio grande originario e baricentro della lunula nera. Se l'origine del sistema di riferimento è il centro del cerchio grande originario, allora x, col segno meno davanti, è anche l'ascissa del baricentro della lunula nera).
P.S.: nel calcolo delle masse ho considerato una densità del materiale pari a 1 e uno spessore dell'oggetto pari a 1.
Tutta la massa della lunula nera può essere concentrata nel suo baricentro. Appena tolgo il cerchio piccolo, la figura mostra chiaramente che il nuovo baricentro si trova a sinistra di O sullo stessa retta. Il che da luogo a un moto pendolare del baricentro attorno ad O. Siamo un po' come nelle montagne russe o nel pendolo... l'energia potenziale persa dal baricentro acquista in energia cinetica che lo fa proseguire fino alla stessa altezza di prima. Perché dovrebbe fermarsi nella posizione finale?
Qualcosa del genere...