Categorie: Matematica
Tags: baricentro circocentro ortocento quiz retta di Eulero tre amici triangolo qualsiasi
Scritto da: Vincenzo Zappalà
Commenti:2
I primi tre amici (in attesa del quarto): la retta di Eulero **
Vedo che i quattro amici non hanno riscontrato grande interesse... Poco male, dato che lo scopo del quiz era quello di introdurre una delle tante scoperte di Eulero uno dei più grandi matematici della storia, già noto attraverso la matematica superiore di Umberto e per la più bella formula matematica in assoluto (come diceva il grande Feynman). Noi tratteremo il tutto in modo estremamente elementare... non perdetevi questo articolo e il prossimo!
La cosa migliore da fare è dare direttamente la parola ai nostri amici che spigheranno chi sono, come possono essere trovati e quali sono le loro caratteristiche. In particolare, dimostreranno che sono sempre allineati e mantengono le distanze in modo a dir poco perfetto!
Il primo amico
Buon giorno, io mi chiamo centroide, ma c’è chi mi chiama baricentro o centro di massa o addirittura medicentro (da medicenter inglese). Anche se poco usato, l’ultimo nome spiega molto bene come si fa a costruirmi facilmente ed è proprio questo metodo che uso adesso per presentarmi ufficialmente e per darvi modo di sapere sempre dove mi trovo.
Prendiamo un triangolo qualsiasi ABC (Fig. 1) e indichiamo sui suoi lati i rispettivi punti di mezzo L, M, N. A questo punto basta tracciare i segmenti che uniscono i vertici del triangolo con il punto di mezzo del lato opposto (in altre parole, le mediane) ed ecco che il punto dove si incontrano sono proprio io, G.
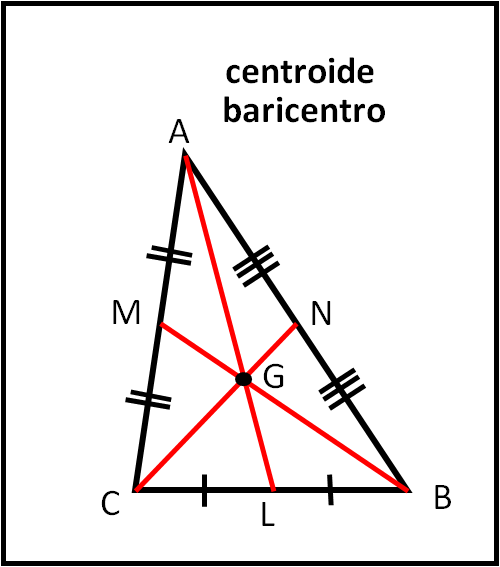
Prima di cedere la parola, permettetemi di enunciare una mia proprietà che ci sarà molto utile in seguito: io taglio ogni mediana in due parti, una doppia dell’altra. E posso anche dimostrarvi che è proprio così!
Uniamo tra loro i punti medi M e N. Come per miracolo ecco nascere, in Fig. 2, un nuovo triangolo AMN che assomiglia molto (in piccolo) a quello di partenza. Anzi non solo gli assomiglia ma gli è anche simile.
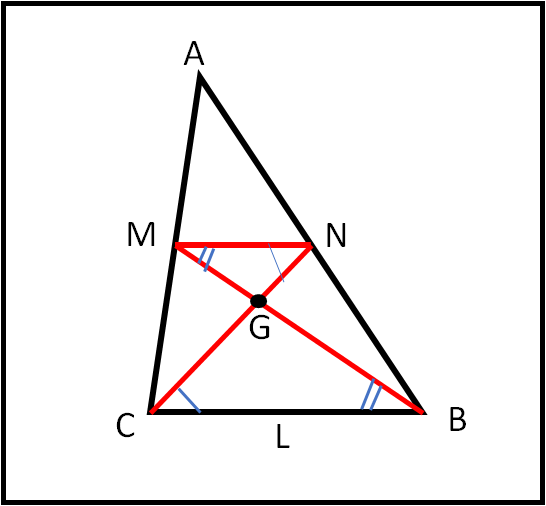
Infatti, ABC e AMN hanno lo stesso angolo in A e i lati AM e AC e AN e AB sono tra loro proporzionali con lo stesso rapporto 1 a 2 (ricordiamoci che AM e AN sono stati proprio costruiti in modo che AM = ½ AB e AN = ½ AC). Quanto basta per dire che i due triangoli sono simili. Ma allora ne seguono due fatti molto importanti: MN deve anche essere la metà di BC e gli angoli AMN e ANM devono essere uguali agli angoli ACB e ABC, rispettivamente. Ma se capita questo, allora, ricordandoci Talete, possiamo dire che MN è parallelo ad AB.
Bene, ora non ci resta che considerare i due triangoli MNG e GBC. Essi hanno gli angoli in G (ossia me medesimo) uguali perché opposti al vertice e gli altre due angoli uguali perché alterni interni di due rette parallele tagliate da una trasversale. I due triangoli sono, perciò, simili. Ma, allora, è anche vero che i loro lati corrispondenti devono stare tutti nello stesso rapporto. Ma noi un rapporto lo conosciamo ed è quello tra MN e BC: esso vale proprio 1/2. Lo stesso rapporto deve esistere tra GN e GC, così come tra GM e GB, ossia gli altri due lati corrispondenti dei due triangoli simili. In altre parole io (G) divido le due mediane BN e CM in due parti che stanno tra di loro come uno sta a due. Possiamo scrivere il tutto con una semplice formuletta:
NG = ½ NB
MG = ½ MC
Ovviamente, procedendo in modo simile, cambiando i vertici, possiamo dimostrare che la stessa cosa succede anche per la terza mediana, ossia AL. Vale perciò anche che:
LG = ½ AL.
In altre parole: presa una mediana, possiamo dividerla in tre parti uguali attraverso due punti equidistanti e io (G) mi troverò sempre in uno di questi due punti, quello più lontano dal vertice del triangolo.
Il secondo amico
Buon giorno, io vengo solitamente chiamato circocentro e tra poco capirete perché. Per costruirmi non ci vuole molta fatica, in quanto abbiamo già segnato i punti di mezzo di ogni lato. Adesso, però, invece di tracciare le congiungenti con i vertici (mediane) tracciamo le perpendicolari ai lati. Queste tre perpendicolari si incontrano in un punto e questo punto sono proprio io, O. Le perpendicolari non sono altro che gli assi dei lati.
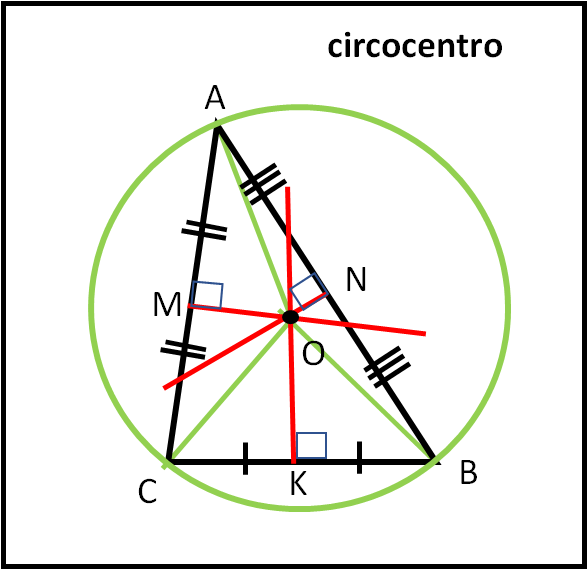
Anch’io ho una caratteristica molto speciale che andiamo subito a descrivere. Ogni punto delle perpendicolari, tracciate dai punti medi dei lati, mantiene sempre la stessa distanza dai vertici, dato che appartiene proprio all’asse del lato. Ma io, O, che appartengo a tutte e tre queste perpendicolari, devo avere la stessa distanza da tutti e tre i vertici! Ma se AO, BO e CO sono uguali, essi non sono altro che il raggio del cerchio (unico) che passa per i tre punti A,B e C. E io, O, ne sono proprio il centro. Ed ecco l’origine del mio nome, circocentro, ossia centro del cerchio (o se volete del … circolo, non per niente mi sento il più importante, ma non ditelo agli altri!).
Il terzo amico
Buon giorno, io vengo chiamato normalmente ortocentro e indicato con la lettera H. Anch’io sono molto facile da determinare: basta tracciare da ogni vertice la perpendicolare al lato opposto (l’altezza). Il punto in cui si incontrano queste tre altezze sono proprio io, H.
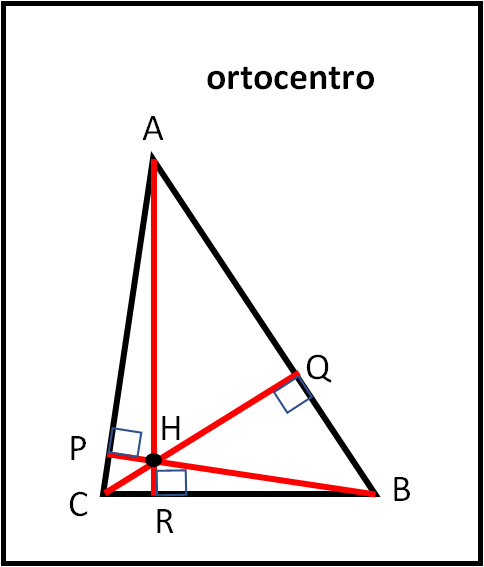
La mia caratteristica, più “utile” per il nostro scopo, è un pochino più complicata delle altre, ma non è certo difficile: basta costruire un bel triangolo simile a quello di partenza. Simile ma più piccolo, tale che abbia i lati proprio uguali alla metà di quello originario. Per costruirlo torniamo ai punti medi M, N e L e uniamoli tra loro, M con N , N con L e L con M.
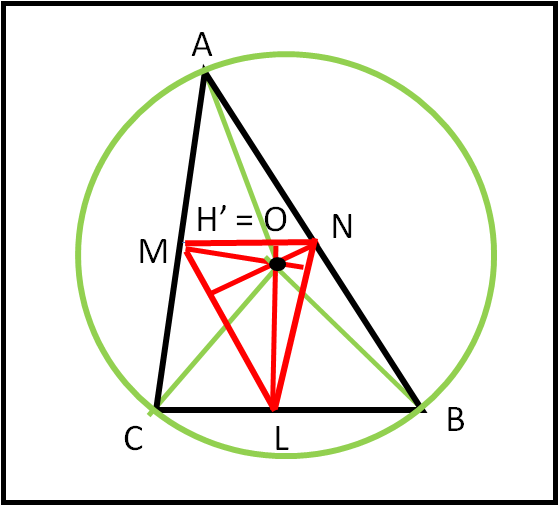
Anzi, facendo in questo modo, abbiamo addirittura costruito 4 triangoli tutti uguali fra loro e tutti simili, quindi, al triangolo di partenza. Dimostrare che MNL è simile ad ABC è un gioco da ragazzi, ricordando che ogni lato del triangolo piccolo è parallelo al corrispondente lato del triangolo grande. Come mai? Beh … abbiamo già visto che se una retta passa per i punti medi dei lati di un triangolo essa è parallela al terzo lato. E questo fatto capita per tutti e tre i lati.
Se i lati sono paralleli, è anche vero che tutti gli angoli risultano uguali, ma a noi basterebbe anche ricordare che i tre lati piccoli sono tutti proporzionali ai tra lati grandi nel rapporto ½ (ricordiamoci la costruzione del mio amico baricentro). Insomma, ci sono un “sacco” di ragioni per dire che i due triangoli sono simili.
Vi devo dire una cosa … ma non prendetevela con me. Non c’era affatto bisogno di dimostrare che i due triangoli sono simili, ma l’ho fatto per portarmi avanti nel lavoro futuro.
A noi basta aver dimostrato che i lati dei due triangoli sono paralleli … Infatti, andiamo a costruire il punto H’, ossia me stesso, per il triangolo piccolo. Esso, per costruzione, si trova all’incrocio delle altezze del triangolo piccolo. Ma le altezze del triangolo piccolo non sono altro che gli assi dei lati del triangolo grande, dato che se sono perpendicolari ai lati di quello piccolo devono essere anche perpendicolari ai lati di quello grande, essendo i lati paralleli. Inoltre i punti M, N e L sono proprio i punti di mezzo dei lati AB, BC e CA. Ma, allora io, H’, coincido con il circocentro O del triangolo grande. Che bello! E quanto ci verrà utile in seguito …
Le regole vanno rispettate
Il seguito è già adesso, però! Infatti, abbiamo già in mano tutte le condizioni per dimostrare la nostra unione e la nostra regolarità nel mantenere le posizioni. Riprendiamo la Fig. 5 e riportiamola nella Fig. 6
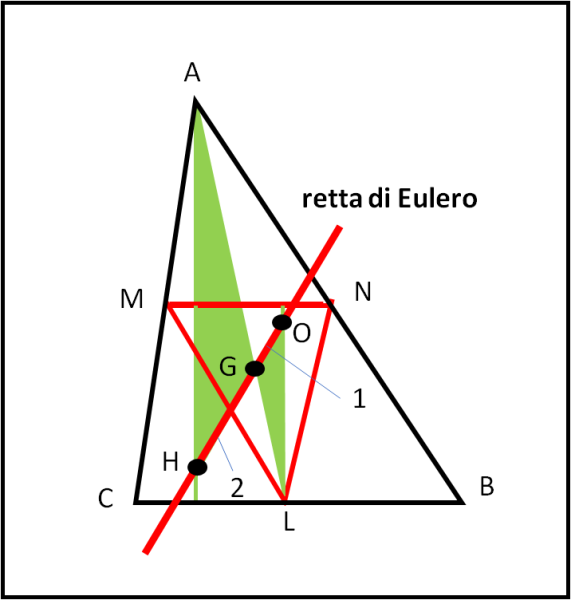
Abbiamo nuovamente i nostri due triangoli, quello grande e quello piccolo che sono simili e le cui lunghezze corrispondenti stanno nel rapporto 2 a 1. Bene, tracciamo da A la perpendicolare al suo lato opposto BC e da L la perpendicolare al lato opposto MN, del triangolo piccolo. Per quanto già visto precedentemente, queste due rette sono parallele, dato che sono perpendicolari a rette parallele. Nella prima retta deve trovarsi l’ortocentro H del triangolo grande e nella seconda retta l’ortocentro H’ del triangolo piccolo, che però non è altro che il circocentro O del triangolo grande. Tuttavia, sappiamo benissimo che le distanze AH e LH’ = LO devono stare nel rapporto 2 a 1, dato che sono lunghezze corrispondenti di due triangoli simili che hanno il rapporto 2/1 tra tutte le loro lunghezze.
Potremmo segnarli pure a caso, ma l’importante e che le distanze dai vertici siano nel giusto rapporto. E’giunto il momento di fare conoscenza con due nuovi triangoli, AHG e GOL, ottenuti sfruttando anche il baricentro G del triangolo grande. Essi hanno gli angoli in A e in L uguali perché alterni interni di rette parallele (AH e LO) tagliate da una trasversale. I lati devono AH e LO stanno nel rapporto 2 a 1, ma lo stesso vale anche per i lati AG e GL dato che G è il baricentro del triangolo grande e divide la mediana (AL) in una parte che è doppia dell’altra.
Accidenti, ma allora i nostri due triangoli sono simili veramente e se lo sono devono avere uguali anche gli angoli in G (AGH e OGL). Consideriamo la congiungente H e O, che potrebbe anche non essere un segmento rettilineo. Tuttavia, la linea AL è sicuramente un segmento rettilineo e quindi l’angolo AGO più l’angolo OGL devono dare come somma 180°. Ma quanto vale la somma di HGA e AGO? Facile a dirsi, dato che HGA è uguale a OGL:
AGO + OGL = 180°
ma
OGL = HGA
quindi
AGO + HGA = 180 °
La loro somma è uguale a 180°, il che vuol dire che la congiungente H O è un segmento rettilineo. Non solo però, la distanza HG deve essere doppia della distanza GO, essendo due lati dei triangoli simili appena studiati.
Prima conclusione
Abbiamo così dimostrato che noi, ortocentro H, baricentro G e circocentro O del triangolo grande, quello di partenza, siamo sempre situati lungo una linea retta e che la distanza tra il baricentro e il circocentro è la metà della distanza tra il baricentro e l’ortocentro.
E’ vero o no che viaggiamo sempre assieme? E non è anche vero che G mantiene perfettamente le distanze dagli altri due amici?
In parole più “scientifiche” abbiamo introdotto la linea di Eulero o -meglio- retta di Eulero, quella retta che ci contiene sempre qualsiasi sia il triangolo.
Dicevamo che ogni tanto riusciamo a riunirci … ed è vero! Lo facciamo quando il triangolo è equilatero! Che bel momento quello … possiamo trovarci tutti esattamente nello stesso punto e siamo indistinguibili uno dall’altro!
Un minimo di storia
Ricordiamoci che Eulero (1707 -1783, in realtà, Euler, di nazionalità svizzera) è stato, forse, il più grande matematico del settecento. Alcuni pensano, addirittura, … di tutti tempi. Lo stesso nostro caro amico Richard Feynman (autore di quello che è giudicato il più bell’esperimento della fisica, ossia la doppia fenditura) disse che l’identità di Eulero, che collega con estrema semplicità il numero e con l’immaginario i e con pi greco (eiπ + 1 = 0), era probabilmente la più bella formula della matematica.
Il teorema di Eulero riguardante la collinearità dei tre punti del triangolo è stato enunciato nel 1765.






2 commenti
Baricentro, circoncentro e ortocentro sono stati sempre argomenti che vengono fatti studiare nelle scuole ma che esista la retta di Eulero che li congiunge sempre in qualsiasi triangolo è una bellissima novità.
Grazie Vincenzo
in questo blog non si finisce mai di imparare e con la tua "magia" gli argomenti vengono sempre esposti in maniera facile e soprattutto esaustiva
grazie Michele, troppo buono