Introduzione alla meccanica quantistica ***
Questo articolo è stato inserito nella pagina d'archivio dedicata alla Meccanica Quantistica, nella quale troverete articoli che, pur rimanendo sempre ad un livello semplice e divulgativo, trattano l'argomento a livelli diversi di difficoltà, a partire da quelli adatti anche ai bambini.
Stiamo per affrontare la Meccanica Quantistica (da adesso in poi MQ) e la cosa potrebbe spaventare. A differenza di altri argomenti, però, la vera difficoltà non sta nel capire, ma nell’accettare qualcosa di completamente insensato, proprio nel giusto significato del termine: non sensato, ossia contrario alla percezione dei nostri sensi. E’ necessario allora fare prima un accurato lavaggio del cervello e prepararlo a fenomeni apparentemente inaccettabili
L’inizio sarà, quindi, dedicato proprio a questa fase di resettaggio. Come diceva Gilmore, stiamo entrando nel fantastico Paese di Alice, quello meraviglioso dei quanti. Tuttavia, vi accorgerete che la meccanica quantistica è molto più “facile” della teoria della relatività. Anzi, potreste farvi aiutare da un bambino nel digerire certi concetti. La grande difficoltà, infatti, non sta nella loro complessità, ma nello loro assurdità in termini di logica acquisita dopo molti anni di esistenza in un mondo che segue costantemente certe regole. Più il cervello è libero da preconcetti e da nozioni ormai radicate e meglio è.
Resettiamo il nostro cervello
Nell’antica Grecia nacque una disputa molto accesa riguardo alla natura della luce. Tolomeo e altri studiosi pensavano che essa fosse una specie di raggio che viaggiava dall’occhio verso l’oggetto che si osservava. Sembra, ovviamente, un enorme errore interpretativo e tale fu dimostrato solo qualche secolo dopo. Tuttavia, con l’avvento della MQ, questa conclusione è diventata molto meno assurda e ingenua, se non altro per le ricadute di tipo soggettivo dei fenomeni che riguardano l’infinitamente piccolo e, quindi, anche la luce stessa.
Ho usato questo inizio un po’ ambiguo e misterioso per affrontare i fondamentali della MQ proprio per avvicinarmi il più possibile allo sbalordimento e al senso di incertezza e di incapacità che subisce una mente umana, anche di altissimo livello, quando si avvicina alle regole/non-regole che governano le particelle elementari e al loro mondo assurdo, simile veramente al Paese delle Meraviglie di Alice.
L’importante è allora riuscire a non stupirsi di niente e accettare e cercare di descrivere anche ciò che la nostra logica quotidiana tenderebbe a rifiutare. Non dobbiamo, però, pretendere di capire ciò che succede nella MQ. Essa è per definizione non comprensibile, come diceva lo stesso Premio Nobel per la fisica del 1965, Richard Feynman, proprio colui che può essere considerato il massimo illustratore e divulgatore della problematica della MQ nei suoi punti più essenziali e fondamentali.
Il suo esperimento della doppia fenditura è considerato da molti il più bello ed elegante esperimento di fisica mai realizzato. Eppure, la conclusione è quanto di meno scientifico si possa pensare, se si rimane ancorati alla fisica che regola la realtà macroscopica dell’Universo.
Per introdurre la MQ e renderla meno assurda di quello che possa sembrare se paragonata alla realtà macroscopica quotidiana, è conveniente partire proprio dalla luce e dalla sua storia. Una storia che, infatti, tutto sembra meno che scientifica. Un continuo cambiamento di idee e di prove inconfutabili che si scontrano tra loro, annullando -apparentemente- le conclusioni precedenti.
Essa fu considerata a lungo come una pioggia di particelle o di corpuscoli, simili, in qualche modo, ai proiettili sparati da un fucile (lo stesso immenso Newton ne era più che convinto). Dopo secoli di lunghe ricerche e di esperimenti divenne chiaro che la situazione non doveva essere quella: la luce si comportava, fuori da ogni ragionevole dubbio, come le onde del mare. Il fenomeno dell’interferenza luminosa e l’esperimento di Young, in particolare, ne fornirono una prova inconfutabile.
Nel ventesimo secolo, dopo altre lunghe ricerche, la luce apparve, però, nuovamente composta da particelle, chiamate fotoni e, attraverso l’effetto fotoelettrico, fu, addirittura, possibile contarli (il Nobel preso da Einstein non gli fu dato per la sua teoria della relatività, ma proprio per i suoi studi sull’effetto fotoelettrico). Il gioco, però, non era finito. Altre ricerche dimostrarono, rapidamente, che la natura ondulatoria non poteva essere assolutamente cancellata. Anche se stiamo parlando di idee e deduzioni formulate dai più grandi scienziati dell’umanità ciò che si ottenne fu una terribile confusione. Una confusione così ovvia ed evidente da essere compresa da chiunque.
Permettetemi, allora, di accompagnarvi verso un ragionamento che penso importantissimo per rendere più semplice un argomento che deve apparire non tanto complicato quanto veramente assurdo. Noi siamo abituati a vivere in un mondo in cui tutto ciò che percepiamo è composto da eventi macroscopici e da sistemi complessi. La fisica classica ha sempre cercato di descrivere e di spiegare questi fenomeni, riuscendoci egregiamente. Sono state scritte leggi e sono stati fatti esperimenti per provarle. Tutto sembrava quasi perfetto. In realtà, non tutto era (ed è) spiegato perfettamente, ma -forse- basterebbe continuare in quella direzione e prima o poi le leggi della fisica potrebbero descrivere tutto l’Universo. D’altra parte ciò che non si capisce ancora è essenzialmente legato a fenomeni e a oggetti sempre più giganteschi. Basterebbe proseguire con perseveranza secondo binari di logica e di esperienza ben consolidati. E, invece, le cose non stanno assolutamente così.
Per accorgersene bisogna guardare nel telescopio dalla parte apparentemente sbagliata. In altre parole, per spiegare le cose più grandi si deve guardare verso le cose più piccole. Non solo, però. Non è sufficiente un microscopio. Si devono anche accettare situazioni che appaiono completamente insensate nella realtà macroscopica percepita quotidianamente. E questa è senza dubbio la parte più semplice, e nello stesso tempo, difficile dell’intera impresa. Lo stesso tempo assume una caratteristica ambigua e incredibile. Noi sappiamo benissimo descrivere la differenza tra passato e futuro. Conosciamo per esperienza diretta la freccia del tempo. Eppure, le leggi che regolano l’essenza dell’Universo sono tutte reversibili, ossia non hanno alcun problema a sostituire passato con futuro e viceversa. Come è allora possibile che la vita macroscopica segua un verso irreversibile? Non è, in fondo, composta da micro strutture, governate da leggi reversibili?
Il vero punto chiave di tutta la MQ è, quindi, proprio la confusione. Lungo tutta la sua storia, l’uomo ha trasmesso, attraverso fenomeni percepibili con i sensi, informazioni al cervello che potevano essere spiegate con la creazione di teorie che, a loro volta, potevano essere verificate direttamente con i sensi. In altre parole, ha seguito il metodo scientifico galileiano. Cercando di andare verso l’infinitamente piccolo, ci si è invece scontrati contro qualcosa del tutto nuova. I sensi hanno assistito a fenomeni assurdi e hanno trasmesso al cervello informazioni prive di logica e buonsenso. Povero cervello! E’ entrato in crisi profonda. Come poteva spiegare qualcosa che era poi impossibile verificare? L’unica possibilità era di immaginare una realtà del tutto inaspettata, senza l’aiuto dei sensi. Doveva costruire teorie basate solo sulla matematica, senza poter vedere direttamente gli attori dei fenomeni. La luce è stata proprio una delle assurdità più “visibili” e più assurde.
Oggi sappiamo come si comportano la luce, i suoi fotoni e gli elettroni, pedine fondamentali dell’Universo. Tuttavia, è ben difficile poter dire cosa sono. Se dico che sono particelle potrei darne un’impressione sbagliata; la stessa cosa capiterebbe, però, se dicessi che sono onde. Il modo esatto di rispondere è dire che essi sono qualcosa che può essere descritto solo attraverso la MQ, l’unica in grado di abbattere le barriere che la nostra esperienza quotidiana ci obbliga a costruire. I fotoni e gli elettroni si comportano in un modo che nessuno è mai riuscito a vedere. Addirittura, sappiamo giù utilizzarlo per scopi quotidiani, ma non riusciamo assolutamente a percepirne la natura, senza fare intervenire una visione puramente matematica.
Per rimanere semplici, dovremo perciò limitarci ai concetti base. Qualsiasi tentativo di descrizione approfondita abbisogna di una matematica prettamente intellettuale, frutto del nostro cervello e non dell’esperienza ripetitiva dei fenomeni normali.
L’atomo può continuare a essere paragonato a un sistema planetario in miniatura, sapendo, però, molto bene che è solo un’artificiosa e parziale rappresentazione di una realtà assolutamente non rappresentabile. Purtroppo, non si può nemmeno cercare di girare attorno all’ostacolo ed evitare il comportamento bizzarro dei fotoni e degli elettroni: tutte le particelle che formano l’Universo seguono le stesse regole. Se vogliamo comprendere completamente qualsiasi legge fisica che ci circonda dobbiamo attraversare questo mondo assurdo. Come dire che per uscire da casa ed entrare nella realtà bisognerebbe sempre attraversare il Paese di Alice. Potremmo farne a meno, come si è fatto per secoli e secoli, ma, una volta saputo che ciò che pensiamo di capire con i sensi è solo una visione parziale di ogni cosa, com’è possibile far finta di niente?
Teniamo, inoltre, presente che le difficoltà della MQ sono essenzialmente di tipo psicologico. Si possono quasi escludere del tutto le formule ma i concetti restano assurdi. La prima ovvia risposta sarebbe: “E’ possibile che si sia fatti proprio così?”. Il cervello tende subito a cercare una descrizione legata alle esperienze quotidiane. E questo tentativo va subito combattuto ed eliminato. Sarebbe inutile e dannoso cercare di descrivere le “cose” della MQ attraverso una serie di eventi e di collegamenti legati alla nostra portata sensoriale. Sarebbe assolutamente impossibile. Si può solo descriverle per come sono, cercando di liberarsi da ogni remora e da ogni luogo comune.
Immaginiamo di “resettare” il nostro cervello e di immergerci in un mondo che non possiamo ancora conoscere e che forse non potremo conoscere mai, per le sue stesse caratteristiche.
Non creiamoci, però, degli alibi. Quando comparve la teoria della relatività si diceva che solo un numero limitatissimo di persone l’avesse capita. In realtà, non era così. Il numero limitatissimo era relativo a chi aveva letto qualcosa sulla teoria. Quando si iniziò a farlo, improvvisamente divenne una materia a portata degli alunni delle scuole medie superiori e anche meno. Lo stesso vale per la MQ, anche se lo sforzo intellettuale non è aiutato da rappresentazioni visive altrettanto esplicative. Ed è un vero peccato che nelle scuole non si cerchi ancora di “allevare” i cervelli a ragionare su una realtà apparentemente irreale, ma assolutamente concreta.
Ricordiamo ancora una volta che la MQ e le sue implicazioni e previsioni sono ormai normalmente usate nella tecnologia quotidiana.
Mi ricorda un po’ la Storia che si studiava ai “miei tempi”. Si fermava sempre e comunque alla Prima Guerra Mondiale. Non si voleva nemmeno parlare ufficialmente di quello che era successo dopo: era meglio far finta di niente. La scarsissima conoscenza della MQ da parte di molti professori fa sì che si preferisca escluderla dai programmi di fisica. Eppure, non è un qualcosa di puramente teorico, tutto da confermare, ma una realtà irreale talmente vera che le sue leggi e le sue previsioni vengono usate quotidianamente. Sembra proprio un controsenso.
Come già accennato all’inizio, il grande Feynman, riferimento essenziale per la descrizione della MQ, diceva: “Nessuno capisce la meccanica quantistica”. Ed è la sacrosanta verità. Nessuno può capirla proprio perché nessuno conosce qualcosa che le assomigli. Gli stessi scienziati che la descrivono, illustrano, in fondo, una visione personale di una realtà irraggiungibile per definizione dai nostri sensi. In altre parole, ognuno cerca di esprimere concetti, ormai consolidati, secondo la propria immaginazione. La forza della matematica è proprio questa: permette di unificare infinite visioni soggettive in una forma intellegibile a tutti.
Quindi, cari ragazzi, siamo in buona compagnia. Non capire la MQ è già un bel punto di partenza. Riuscire a descriverla sarà l’unico vero impegno del nostro cervello, pulito delle nozioni immagazzinate finora.
Scusate le frasi un po’ ripetitive e i concetti ridondanti, ma è essenziale partire col piede giusto sia per capire le descrizioni sia per assaporare appieno il senso di mistero e di bellezza del mondo microscopico. Altro che UFO e fenomeni paranormali. Qui si va ben oltre!
Feynman ha usato un metodo descrittivo che è entusiasmante e semplice pur rimanendo perfettamente concreto. Esso si basa su analogie e contrasti con la realtà di tutti i giorni. Io cercherò di seguire il suo approccio, sempre che ci riesca. Prima però è bene ricordare cosa sia il fenomeno dell’interferenza delle onde e l’esperimento risolutivo di Young. Digerite bene queste due nozioni, tutto il resto scorrerà semplice verso… l’assurdità più imprevista. Non preoccupiamoci, però, di non riuscire a capire la conclusione dell’esperimento di Feynman, dato che lui stesso diceva che è impossibile capirlo. Potremo quindi sentirci anche noi dei grandi scienziati, dato che anche noi riusciremo facilmente a capire ben poco. Come già detto, questo risultato è già un passo fondamentale per una descrizione più accurata della MQ. Se dicessimo di aver capito, sfruttando le nozioni della fisica classica, avremmo sicuramente imboccato una strada sbagliata.
Noterete, tra poco, che descriverò due volte il fenomeno dell’interferenza. Un’inutile ripetizione? Forse sì, ma a volte leggere due volte la stessa trattazione, espressa con parole leggermente diverse, può aiutare moltissimo nella comprensione. Inoltre, non volevo modificare più di tanto l’esperimento di Feynman, pur descrivendo già prima l’interferenza. Come vedremo tra non molto uno più uno non è detto che faccia sempre due.
L’interferenza delle onde
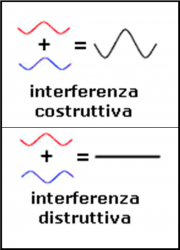
Vi sono moltissimi esempi pratici che descrivono perfettamente il fenomeno dell’interferenza tra onde. Consideriamo quelle del mare, ad esempio. E’ noto a tutti che se vi sono due sorgenti di onde (due sassi tirati in acqua) quando queste si incontrano possono sommarsi o annullarsi a vicenda. Le onde interferiscono tra loro. Si dice che l’interferenza è costruttiva quando si incontrano le “creste” delle onde, dando luogo a un’ampiezza d’onda più grande, mentre si dice distruttiva quando si sovrappongono una “cresta” e un “ventre”. Le celebri onde anomale sono proprio date da saltuari e occasionali incontri di onde di ampiezza normale.
Riassumiamo questo fenomeno ben noto a tutti attraverso la Fig. 1.

Se tiriamo due sassi nell’acqua, si originano due onde che si incontrano sommandosi e annullandosi. In Fig. 2, vediamo in dettaglio come due onde di uguale ampiezza, che si sommano mentre sono entrambe al massimo, diano luogo a un’onda di ampiezza doppia. L’interferenza tra loro è costruttiva. Ovviamente, se si incontrano “fuori fase”, ossia quando al massimo di una corrisponde il minimo dell’altra, l’onda risultante si annulla, ossia l’ampiezza è zero. L’interferenza è distruttiva. Anche nel caso in cui i due sistemi d’onda abbiano ampiezza diversa, si continua a eseguire la loro somma, considerando negativa l’ampiezza di un “ventre”, ossia l’onda risultante ha ampiezza minima ma non uguale a zero. D’ora in poi, però, considereremo sempre onde di uguale lunghezza e ampiezza.
Ai tempi di Young si conosceva già questo fenomeno, anche se in modo molto empirico e non generalizzato. Sicuramente si conoscevano le onde, ma esse erano associate a fenomeni macroscopici come appunto il mare o il suono. In qualche modo le onde erano un “qualcosa” in grado di aggirare gli ostacoli. Se veniva inserito un muro davanti a un mare agitato, era ovvio che l’acqua riuscisse a girargli intorno e a propagarsi anche dall’altra parte. Lo stesso faceva il suono che si sentiva anche se tra noi e la sorgente del rumore si interponeva una montagna. Sicuramente la luce non poteva farlo, dato che si propagava solo in linea retta. La prova decisiva si aveva nel cielo: se un pianeta passava davanti a una stella la luce della stella scompariva e non riusciva certo a raggirare l’ostacolo. E, inoltre, mentre nelle onde marine c’era il mare e nelle onde sonore c’era l’aria, ossia due sostanze che servivano a propagare le onde, nel vuoto cosmico non c’era assolutamente niente. Chi cercava di pensare alle onde della luce si scontrava per forza con il concetto di “etere”, ossia un qualcosa che potesse far propagare le onde luminose.
Young sapeva benissimo che l’impresa di dimostrare che anche la luce si propagava per onde non era semplice e ci voleva un esperimento veramente inattaccabile. Anche se passò un po’ sottotono, soprattutto per il suo carattere schivo, Young realizzò un vero capolavoro: l’esperimento delle due fenditure, che sarà poi ripreso e modificato proprio da Feynman.
Un fascio di raggi luminosi (continuiamo a chiamarli così, per adesso, dato che vanno bene sia per le particelle che per le onde) colpisce uno schermo in cui sono presenti due fori, o fenditure, molto piccoli, che possono essere considerati l’origine di due nuovi fasci di raggi.
I due fori o fenditure diventano, in effetti, due sorgenti luminose, indipendenti, ma perfettamente omogenee, dato che si sono create da un unico fascio omogeneo. A questo punto mettiamo uno schermo che raccolga la luce proveniente dai due fori. Con un certo sbalordimento (per l’epoca in cui era stato effettuato) si vedono nettamente delle frange chiare e scure, molto simili alle onde del mare provenienti da due sorgenti diverse. L’unica differenza è che, nel caso dell’acqua, l’osservatore guarda le figure d’interferenza dall’alto, vedendo due serie di cerchi che si sovrappongono o si annullano, mentre nell’esperimento con la luce deve osservare la figura d’interferenza che si forma su uno schermo. L’esperimento è schematizzato in Fig.3 (visto dall’alto).
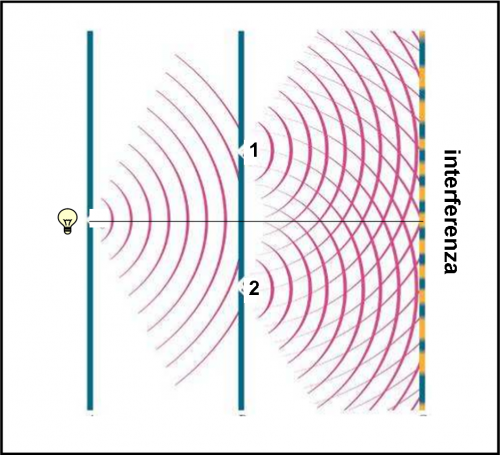
La Fig. 4 lo riprende visto “di taglio”, ossia evidenziando la sovrapposizione e l’annullamento delle onde.
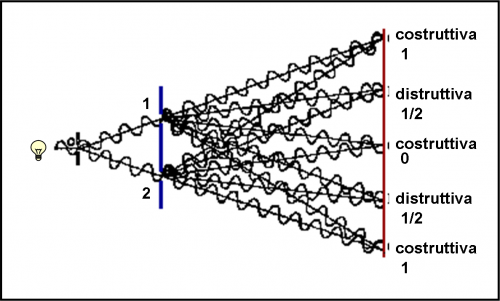
La Fig. 5, è una fotografia che illustra perfettamente il fenomeno nella sua interezza.
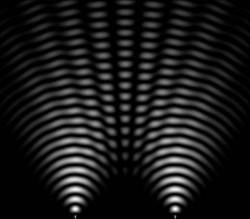
Le frange di interferenza consistono in strisce parallele di luce: le bande chiare sono le aree in cui le onde luminose si sommano reciprocamente, mentre le bande scure sono le aree in cui esse agiscono in modo distruttivo l’una sull’altra. La luce si vede in base alla sua intensità. La Fig. 6 mostra le frange di interferenza che si originano sullo schermo finale.

Ciò che le frange dimostrano senza alcun dubbio è che la luce si propaga per onde e non per corpuscoli. L’interferenza lo prova in modo inconfutabile. Se non altro, per il semplice fatto che le bande luminose non si trovano solo in corrispondenza dei fori, ma sia al loro interno che all’esterno. Solo un’onda può raggiungere questi punti, raggirando gli ostacoli, e interferire con un’altra. Questo punto essenziale lo rivedremo tra poco.
Il fenomeno dell’interferenza luminosa permette, oltretutto, di misurare facilmente la lunghezza dell’onda, dato che le distanze dalle sorgenti (fori) al punto di arrivo sullo schermo sono strettamente legate a lei. Si devono, infatti, considerare le distanze dalla sorgente al punto di arrivo per sapere se vi è interferenza costruttiva o distruttiva. Se i percorsi della luce dai fori alla parete di fondo differiscono di un numero intero di lunghezze d’onda (0,1,2,3) si sovrappongono due massimi di ampiezza e si ha una frangia chiara (Fig. 7). Se, invece, le distanze differiscono di mezza lunghezza d’onda si ha un massimo in corrispondenza del minimo e l’ampiezza totale si annulla. Non per niente il massimo più luminoso sta proprio sulla parete di fondo, a metà esatta tra i due fori. In quella posizione le distanze dalle due fenditure sono perfettamente uguali, ossia il numero intero definito prima è zero.
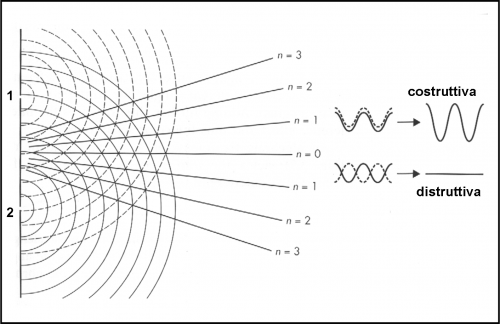
Ripeto ancora che il fatto stesso che la massima luce si ha non in corrispondenza dei fori, ma addirittura nel punto intermedio tra loro, ci dice in modo molto semplice che la luce riesce a raggirare gli ostacoli e quindi non può che propagarsi attraverso onde, come nel mare. Tanto per non farci mancare niente, inseriamo anche la Fig. 8 che riassume l’esperimento con una visione tridimensionale.
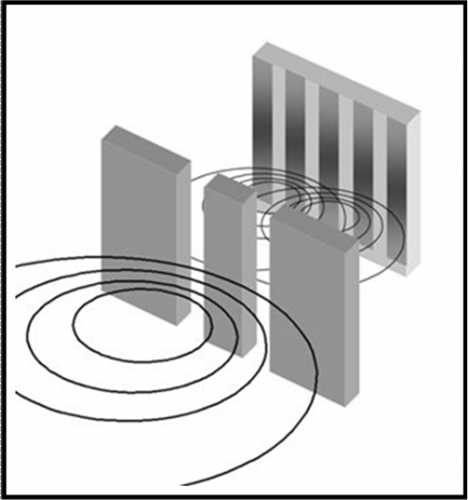
Per adesso lasciamo da parte la luce, anche se sull’interferenza torneremo molto presto.
Fino a qui vi sarete accorti che ho descritto i fenomeni utilizzando la fisica classica. Tutto il fenomeno non solo si dimostra, ma è verificabile facilmente. Young ha fatto un capolavoro rimanendo nei binari del pensiero scientifico galileiano. Proprio per questo, la sua conclusione è fantastica, ma non è completamente vera, dato che in realtà si basa sul comportamento di particelle come i fotoni che seguono le assurde regole della MQ.
Lo so, siete un po’ delusi. Tanta attesa e ancora di MQ nemmeno l’ombra. Abbiate pazienza. L’importante è capire molto bene il fenomeno dell’interferenza nella sua generalità. Solo comprendendo bene ciò che la logica ci mostra, in modo chiaro e inconfutabile, saremo in grado di rivelare appieno l’assurdità di certi comportamenti che se ne discostano. Prima di affrontarla, le onde e le loro caratteristiche devono diventare un’ovvietà, un fenomeno abituale come vedere cadere sempre per terra una qualsiasi cosa che abbia un minimo peso.
Iniziamo, allora, l’esperimento di Feynman, uno dei più grandi capolavori dellamente umana. Attenzione a ogni singolo passaggio dell’esperimento, solo così ne capirete la meravigliosa lucidità ed essenzialità. Ci fermeremo al punto dove la fisica classica riesce ancora a fornire spiegazioni esaurienti e soddisfacenti, prima del balzo conclusivo verso l’assurdo. Tutto sarà facilmente comprensibile (Feynman usa la semplicità, l’arma migliore per descrivere i grandi problemi), dopo aver già digerito l’interferenza delle onde. Tuttavia, leggete con molta calma, senza dare niente per ovvio e scontato.
L’idea base di Feynman era di paragonare il comportamento seguito da particelle singole e da onde, nelle stesse condizioni dell’esperimento di Young. Banale no? E’ sempre così: le idee geniali sembrano sempre ovvie … a posteriori. Il confronto avrebbe chiarito le differenze e le caratteristiche di entrambe le situazioni. La logica normale avrebbe accettato con piacere questo risultato, ma sarebbe rimasta sbalordita e incredula davanti alla terza fase dell’esperimento, quando come particelle singole sarebbero entrati in azione “oggetti” molto diversi.
Complichiamo, quindi, un po’ l’esperimento di Young, lasciando libero il cervello di staccarsi, al momento giusto, dalla realtà di tutti i giorni.
Un soldato ubriaco
La prima parte dell’esperimento utilizza un soldato, un fucile mitragliatore e i suoi proiettili, riprendendo pari pari lo schema delle due fenditure di Young. Il fucile è posto dietro a un foro fatto in una parete. L’arma, però, spara a casaccio in tutte le direzioni e non solo davanti a sé, lungo una linea fissa e determinata. Probabilmente è un’arma vecchia e sgangherata oppure il soldato è un po’ ubriaco. Meglio così, fa proprio al caso nostro. A una certa distanza davanti alla prima parete ne inseriamo un’altra, sempre di metallo e capace di fermare i proiettili che vi piombano addosso. In questa pratichiamo i due fori o -meglio- fenditure, 1 e 2. Esse permetteranno di proseguire solo ai proiettili che le attraversano. Infine, a distanza ancora maggiore, poniamo un’altra parete di metallo, coperta con qualche materiale simile alla sabbia che intrappoli il proiettile che vi giunge. Questa permette di raccogliere i proiettili che l’hanno colpita e contarli, dopo aver sparato una raffica.
Ovviamente, i proiettili escono dal fucile uno alla volta e quindi non possono urtarsi tra di loro, durante il viaggio, e nemmeno rompersi o dividersi in più pezzi. Conseguentemente, i proiettili che arrivano sulla sabbia lo fanno uno alla volta e sono perfettamente integri. Sembra una cosa ovvia, ma tenetela bene a mente. La Fig. 9 rappresenta la configurazione del nostro esperimento. Questa figura e la 12 e la 14 che seguiranno sono piuttosto approssimative, anche se più che sufficienti per definire il problema. Le uso perché sono proprio gli schizzi di Feynman. Alla meraviglia si aggiunge anche un po’ di emozione.
Diamo il via al soldato. Immaginiamo che la raffica sia stata lunghissima e che quindi abbia sparato un numero molto alto di proiettili (i grandi numeri sono fondamentali per parlare di probabilità). Contiamo i proiettili finiti nella sabbia in funzione della posizione che hanno. Anzi, facciamo qualcosa di ancora più raffinato matematicamente. Calcoliamo la percentuale di proiettili arrivati nelle diverse posizioni. In tal modo si ha immediatamente la probabilità che ha una certa posizione della lastra di essere raggiunta da un proiettile. Potevamo fare lo stesso in modo ancora più preciso. Mettere una “scatola” o un “barattolo” pieno di sabbia in posizioni sempre diverse della parete finale e sparare ogni volta 100 o 1000 o 10000 proiettili. Contare quanti ne giungevano nella scatola e stabilire la probabilità per la scatola in quella posizione. Poi facevamo scorrere la scatola in un altro punto (in modo continuativo e completo) e via con altri 100 o 1000 o 10000 colpi. Alla fine avevamo nuovamente la probabilità di ogni punto della parete di essere colpito a parità di colpi sparati. Insomma, la scatola può essere considerata un rivelatore di proiettili e quindi di probabilità.
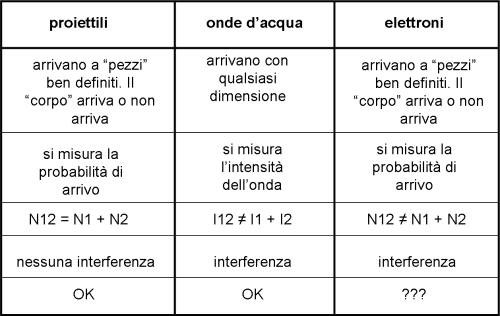
In un modo o nell’altro possiamo facilmente disegnare la curva della probabilità in funzione di una certa coordinata x, che indica la posizione lungo la piastra di raccolta. Comunque, proiettili o probabilità che siano, la parete finale assomiglierebbe alla Fig. 10, dove le strisce scure sono le due zone maggiormente colpite. Al massimo due e non più di due.

Qualcuno potrebbe dirmi: “Perché non contare i proiettili, senza fare troppi passaggi matematici?” La risposta sarà ovvia tra non molto. Abbiamo bisogno di parlare in termini di probabilità, dato che i proiettili che useremo dopo hanno un comportamento assai più strano di quello delle pallottole.
La curva di probabilità ha una forma simile a quella segnata come N12. Ovviamente, se il soldato mirasse con precisione, i proiettili si troverebbero quasi esattamente dietro alle due fenditure. Invece è ubriaco, spara a casaccio e i proiettili entrano inclinati o toccano le pareti delle fenditure e rimbalzano. In altre parole, possono cadere nella scatola anche quando è spostata rispetto alle fenditure, pur se in numero minore. Ne segue che la linea della probabilità descrive una curva che ha due picchi in corrispondenza delle due fenditure (più o meno) e poi si smorza. Questa curva dipende molto dalla distanza tra le due fenditure, come vedremo tra poco.
Cosa rappresenta la curva della probabilità N12? Sicuramente è la somma dei proiettili entrati attraverso 1 e quelli entrati attraverso 2, espressa come probabilità. E’ una cosa ovvia, pensando che ogni proiettile è un singolo oggetto perfettamente definito. In altre parole, il proiettile è visibile e localizzabile lungo tutto il suo percorso. Tenete bene a mente questa frase, mi raccomando.
Per averne la certezza, però, basta fare una prova semplicissima (è meglio essere sicuri di ciò che facciamo perché tra poco l’apparenza ingannerà e come!).
Chiudiamo la fenditura 2 e rifacciamo tutto l’esperimento. Otterremo la curva di probabilità N1. Poi chiudiamo la fenditura 1 e ricominciamo tutto da capo. Si avrà la curva N2. Se il numero di colpi è sufficientemente alto, la statistica ci assicura che N12 è esattamente la somma di N1 più N2. Come già detto, ogni proiettile è un singolo oggetto e quindi il loro numero totale si ottiene sommando i proiettili che arrivano sulla scatola, indipendentemente dal fatto che provengano da 1 o da 2. Questo fatto si ripercuote pari pari sulla probabilità.
Meglio essere ancora più semplici. Se spariamo cento colpi con solo la fenditura 1 aperta e poniamo la scatola con la sabbia in una certa posizione, verifichiamo, ad esempio, che soltanto 10 proiettili l’hanno centrata. La probabilità è quindi data da 10/100. Chiudiamo 1 e apriamo 2, mantenendo, però, la scatola di sabbia sempre nella stessa posizione. Questa volta attraverso 2 arriveranno sulla scatola solo 4 proiettili su 100 sparati. Il che vuol dire una probabilità del 4/100. Possiamo quindi dire che la probabilità di avere un proiettile nella scatola è il 10% attraverso la fenditura 1 e il 4% attraverso la fenditura due. Apriamole ora entrambe e spariamo nuovamente 100 colpi con la scatola (svuotata) sempre nella stessa posizione. E’ ovvio che 10 proiettili arriveranno sulla scatola attraverso 1 e soltanto 4 attraverso 2. In totale avremo 14 proiettili, su 100 sparati, finiti nella scatola. La probabilità è allora del 14%, proprio uguale alla somma delle probabilità ottenute aprendo singolarmente le due fenditure.
Ricapitolando, la probabilità relativa ai proiettili che provengono da entrambe le fenditure è uguale alla somma delle probabilità relative a ogni singola fenditura. Ne deriva, quindi, che il valore massimo della somma delle probabilità delle singole fenditure (ossia la massima probabilità con entrambe le fenditure aperte) può verificarsi anche nel punto medio tra di loro, se queste sono molto vicine. Lo vediamo nella Fig. 11, per varie posizioni.
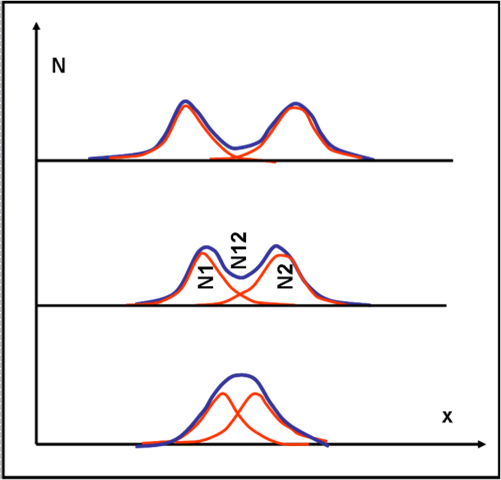
Comunque, questo è un problema decisamente secondario che ho toccato solo per non creare una confusione del tutto inutile e spiegabilissima: ce ne saranno di ben più importanti. I massimi di probabilità possono essere due o diventare uno solo, ma questo dipende solo dalla distanza tra le fenditure e non dal comportamento dei proiettili. Attenzione, quindi a non confondere questo risultato con la frangia d’interferenza luminosa che è sempre al centro delle due fenditure. La cosa veramente importante nel caso dei proiettili è che la curva somma rimane sempre uguale alla somma delle curve singole.
Questo risultato appare ovvio e addirittura “stupido” a tutti noi abituati a vivere la realtà quotidiana. Tuttavia, descrive un fenomeno che diventerà ben più importante tra poco: non vi è stata interferenza, ossia i proiettili non si sono disturbati reciprocamente (d’altra parte non potevano farlo, secondo la nostra logica). Nell’esperimento appena fatto, i proiettili escono, infatti, uno alla volta e non si possono urtare tra loro. Chi arriva arriva, e il suo destino è indipendente da quello che fanno gli altri. Quanto è importante la parola “indipendente”! E quanto è legata alla nostra visione logica del mondo.
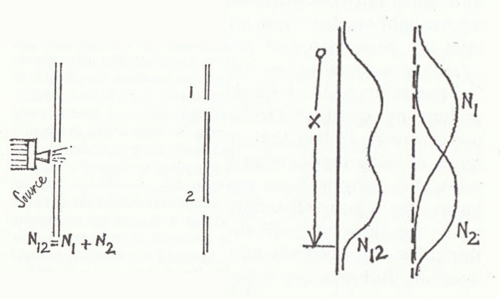
Fatemi scrivere una banale formula, che ci sarà utile per confrontarla con quelle (pochissime) successive.
N12 = N1 + N2 nessuna interferenza
Passiamo adesso alle onde marine o qualcosa del genere. Abbiamo già parlato di questa situazione, ma non è male ripeterla sia per non interrompere la sequenza logica ideata da Feynman, sia perché tornare su certi concetti non fa mai male.
Una piscina bucata
La sorgente adesso non è più il fucile, ma una grande massa d’acqua, che preme dietro la prima parete. In quella parete c’è un foro, da cui l’acqua riesce a passare e si riversa al di là del muro. Lo fa producendo un’onda composta di creste e depressioni (massimi e minimi). Per causare un’onda, basta che si agiti l’acqua prima della parete: più viene agitata e più l’onda aumenta. Per essere più esatti, si origina un treno di onde, una dietro l’altra, separate tra loro da quella che viene chiamata lunghezza d’onda (distanza tra due creste o tra due depressioni).
Ad un certa distanza poniamo nuovamente la parete con le due strette fenditure, come nel caso dei proiettili. L’onda che si è formata dopo la prima apertura colpisce la seconda parete e riesce ad attraversarla solo dove ci sono le due fenditure. Cosa succede a questo punto? L’onda, passando dalle fenditure, si divide in due nuove onde che mantengono la stessa lunghezza di quella originaria. In altre parole, è come dire che, se l’apertura è abbastanza piccola, essa dà origine a una nuova onda che si propaga da lei, come se si fosse scagliato un sasso proprio in quel punto. Di questo comportamento avevamo già parlato a proposito della luce. In realtà, al posto dell’acqua potremmo considerare onde luminose (come ha fatto Young) e otterremmo lo stesso risultato, almeno apparentemente e a una prima visione sommaria.
Torniamo alle due onde originatesi nelle due fenditure. Esse proseguono verso la terza parete dove prima avevamo messo la sabbia per i proiettili. Adesso, dobbiamo cambiare rivelatore. Scegliamo, ad esempio un tappo di sughero. Quando l’onda arriva sull’ultima parete lui si alza e si abbassa seguendo le creste e le depressioni. L’esperimento si vede in Fig. 12. Come abbiamo fatto prima, con la scatola piena di sabbia, spostiamo il tappo lungo tutta la parete e vediamo come varia l’altezza che riesce a raggiungere. In realtà, ciò che a noi interessa è l’energia che viene rilasciata dall’onda al tappo o -se preferite- la sua intensità.
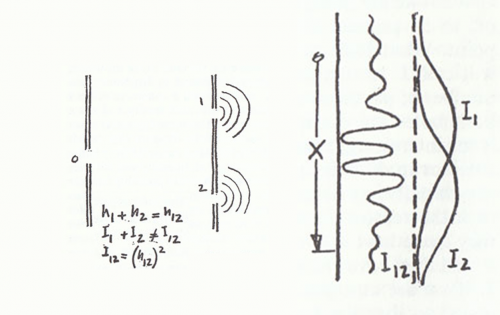
Stiamo attenti a non confondere l’ampiezza di un onda con la sua intensità. Nel caso del fucile, energia rilasciata e proiettile erano praticamente la stessa cosa, dato che ogni proiettile rilasciava la stessa energia. Per le onde, la situazione è leggermente più complicata. Si può dimostrare (non lo facciamo perché bisognerebbe eseguire parecchi calcoli matematici, però credeteci!) che l’intensità è proporzionale al quadrato dell’altezza. D’altra parte a noi interessa proprio l’intensità o energia rilasciata, per confrontarla, ad esempio, con quella della luce o dei proiettili.
La curva finale, in funzione della posizione del tappo lungo la parete, è ben più strana della N12 del caso precedente. Ciò che si vede è una figura che sembra anch’essa un’onda, un continuo sali e scendi, senza nessuna relazione con la posizione delle due fenditure. O -meglio- dipendente dalla distanza tra loro, nel senso che l’oscillazione che si nota sulla parete può stringersi o allargarsi. La struttura a strisce, però, non cambia. Il risultato (lo conosciamo bene) non è altro che il fenomeno dell’interferenza delle onde. E’ estremamente simile a quello ottenuto da Young con la luce. D’altra parte Young aveva detto che la luce si propagava per onde proprio perché il suo comportamento era uguale a quello delle onde marine. Anche questa seconda fase dell’esperimento è di una banalità quasi sconcertante e nuovamente ovvia. Ma… Feyman è davvero un genio? Aspettate, aspettate…
Ricordiamo ancora che nel caso dei proiettili vi erano poche scelte: o arrivava o non arrivava. Nel caso dell’onda, l’energia o intensità dell’onda può assumere tutti i valori compresi tra un massimo e lo zero (acqua piatta).
Chiamiamo la curva finale, che descrive la figura d’interferenza, I12. Questa volta, però, per ottenere la curva I12, non possiamo sommare le energie rilasciate al tappo con l’acqua che passa da una sola fenditura aperta, come succedeva nel caso dei proiettili. Per provarlo basta tappare prima 2 e poi 1. Si ottengono separatamente le curve I1 e I2, curve che assomigliano a quelle dei proiettili sparati dal fucile attraverso una sola apertura. Questo è ovvio (rimanendo nella fisica classica) dato che se l’onda passa da una sola fenditura non può interferire con un’altra e quindi ha un comportamento apparentemente simile a quello dei proiettili: un picco che si smorza, allontanandosi dalla direzione centrale, in quanto l’onda perde di intensità. La massima intensità la mostra proprio dove “sbatte” per la prima volta contro la parete. Nel caso dell’interferenza, abbiamo, invece, diversi massimi e minimi (basta considerare una qualsiasi linea parallela alla parete e si vede chiaramente che i massimi e i minimi sono molteplici). La Fig. 13 illustra abbastanza bene la situazione.
L’unica differenza sostanziale tra proiettili passanti da una singola fenditura e onda proveniente anch’essa da una sola apertura è che i proiettili, o -meglio- l’energia rilasciata o, se volete, l’intensità dei proiettili, è praticamente il loro numero, nel caso dell’onda l’intensità è proporzionale al quadrato dell’altezza, ossia I1 = h12 e I2 = h22. Dobbiamo paragonare altezze e numero di proiettili, dato che sono le grandezze che rileviamo e che indicano la probabilità finale.
Sappiamo però che le altezze delle onde si sommano e vale la relazione: h1 + h2 = h12. Per l’intensità, ossia per l’energia data al tappo, con entrambe le fenditure aperte, si ha quindi (l’intensità va con il quadrato dell’altezza):
I12 = h122 = (h1 + h2)2 e, sicuramente:
I12 ≠ I1 + I2 à interferenza
Bisogna riflettere bene su questa conclusione che, in pratica, fornisce la migliore descrizione della differenza tra onde e particelle. Queste ultime non mostrano alcun fenomeno di interferenza e la probabilità di trovare una particella in un certo punto, con entrambe le fenditure aperte, è esattamente la somma delle probabilità di trovare una particella in quello stesso punto chiudendo una fenditura alla volta (N12 = N1 + N2). Le onde mostrano invece un risultato finale diverso. L’intensità dell’onda risultante, a fenditure aperte, non è la somma delle intensità a fenditure alternativamente chiuse. Non è difficile considerare l’intensità come la probabilità del tappo di alzarsi di più o di meno. Rifletteteci un attimo e la cosa diventerà ovvia.
Questo esperimento, che abbiamo fatto con l’acqua, è praticamente lo stesso che Young aveva fatto con la luce. Egli aveva trovato le frange di interferenza e aveva potuto concludere che la luce non poteva essere trasmessa attraverso particelle (proiettili) dato che causava interferenza. Feynam, per adesso, ha solo dato una definizione “matematica” e concettuale della differenza tra onde e particelle che colpiscono un muro. Per adesso, niente di speciale … sembrerebbe.
Si entra, ora, nella parte fondamentale dell’esperimento di Feynman e, quindi, cercherò di descriverla sotto vari aspetti per prepararci convenientemente alla speculazioni filosofiche che ne conseguono. Sarò molto ridondante e ripetitivo, ma ogni frase va digerita con calma ed estrema attenzione. Fatevi aiutare dai bambini, mi raccomando… Alla fine, però, ci rimarrà ancora un dubbio, che cercheremo, comunque, di risolvere.
Un fucile molto speciale
Eccoci finalmente alla terza parte dell’esperimento di Feynman, quella che apre la porta alla MQ e fa vacillare (anzi distrugge) la nostra capacità di comprensione. Per varcare questa porta dobbiamo rifare l’esperimento delle due fenditure con dei proiettili speciali, gli elettroni. Su di essi possiamo essere sicuri: sono particelle che “girano” attorno al nucleo atomico, ma, soprattutto, posseggono una massa misurabile. Proiettili a tutti gli effetti anche se piccolissimi. La sorgente è un filamento, le pareti sono di tungsteno e il rivelatore è un sistema elettrico che riesce a segnalare ogni elettrone che arriva. In realtà, (udite, udite!) si potrebbero anche usare i fotoni, ma ai tempi di Feynman non era facilissimo costruire l’apparecchiatura adatta. No, non stupitevi se ho parlato di fotoni dopo aver appena dichiarato che la luce si propaga attraverso onde. Fa parte del gioco e dovete accettare una prima apparente assurdità. In ogni modo, andiamo avanti con gli elettroni che pongono minori problemi pratici.
Innanzitutto, ribadiamo ancora una volta che ciò che riceviamo nell’ultima parete sono indiscutibilmente segnali singoli dovuti a masse singole. Ogni segnale, una specie di “clic”, ha una certa dimensione (o intensità), sempre uguale. Se la sorgente s’indebolisce non si fa altro che rallentare la produzione dei “clic”, ma la singola intensità rimane sempre uguale, proprio come i proiettili del fucile. Impostiamo le cose in modo da essere sicuri che gli elettroni partano, arrivino e vengano rilevati uno alla volta. A questo punto possiamo ripetere tale e quale l’esperimento fatto con i proiettili e misurare la probabilità di arrivo nelle varie posizioni della parete finale, come rappresentato nella Fig. 14.
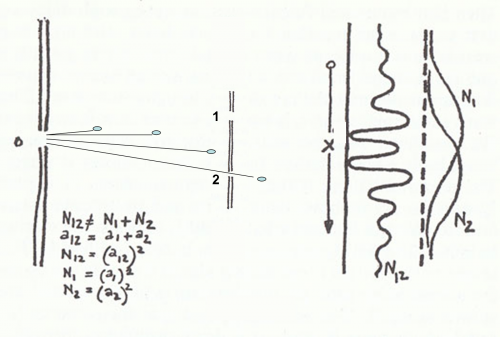
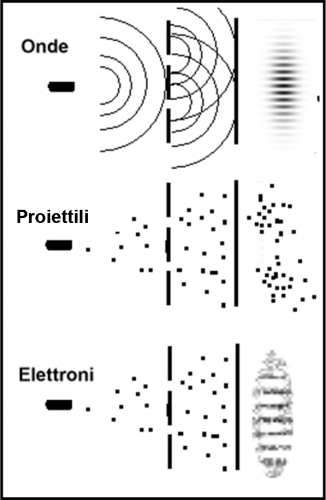
Cosa si ottiene alla fine? Ovviamente ci aspetteremmo la stessa cosa ottenuta con il fucile mitragliatore, ossia una curva come la N12 (ricordate?). E invece no, assolutamente no. Ciò che si ottiene è una serie di massimi e minimi del tutto simili a quelli dovuti all’interferenza delle onde prodotte sull’acqua. L’unica differenza è che la curva a sali e scendi non rappresenta l’energia o l’intensità dell’onda, ma la probabilità che ha un elettrone di colpire la parete in un certo punto di essa, in modo perfettamente analogo ai proiettili.
La matematica che descrive la curva è molto semplice e differisce completamente da quella dei proiettili. Assomiglia, invece, perfettamente a quella delle onde. Basta cambiare la I scritta nel caso delle onde con N. Sappiamo però che I è uguale al quadrato dell’ampiezza h delle onde che interferiscono. Adesso, che cosa rappresenta h? Non lo sappiamo assolutamente e indichiamola per il momento con una a minuscola. Possiamo anche chiamarla, per analogia, ampiezza della probabilità, ma il suo vero significato resta un mistero. Così come un vero mistero è l’intera figura di interferenza ottenuta sparando proiettili “concreti” uno alla volta.
Abbiamo fatto vera scienza (in senso tradizionale)? In realtà no: abbiamo solo imitato il comportamento delle onde dato che il risultato è uguale. Stesso aspetto e stessa matematica. In ogni modo, per essere sicuri di non commettere errori interpretativi, proviamo a chiudere, uno alla volta, i fori 1 e 2, in modo da ottenere le vere distribuzioni N1 e N2. Un tentativo perfettamente logico, dato che è sicuro che se un elettrone passa da 1 non può certo passare anche da 2. Una alla volta, per carità! O, almeno, eseguiamo i due esperimenti, a singolo foro aperto, ammettendo questa ovvia deduzione (il nostro cervello può solo operare così). Chiudiamo il foro 2 e misuriamo quanti elettroni mandano il loro segnale sulla parete finale. Essi sono solo quelli che sono passati dal foro 1 per definizione e la curva che descrive la loro probabilità è N1. Poi chiudiamo 1 e disegniamo N2. Non potevamo che aspettarcelo: la somma di N1 e N2 non è uguale a N12. Accidenti! Benché le due curve singole N1 e N2 siano perfettamente analoghe a quelle ottenute con i proiettili del fucile, quella totale è decisamente diversa, identica a quella delle onde. Dobbiamo essere forti e accettare il risultato.
Dato che N12 ≠ N1 + N2 vi è stata interferenza. Sì, ma di cosa? Siamo più che sicuri di avere usato proiettili, anche se piccoli, e invece il risultato sembra proprio quello delle onde. Non possiamo fare altro che concludere che vi è interferenza e che la probabilità che un elettrone arrivi in un certo punto della piastra è data da N12 = (a1 + a2)2, dove a1 e a2 sono due ampiezze. Sì ma ampiezze che non hanno alcun senso dato che non sono collegate a N1 e N2, a meno di non imporre, sempre per analogia, che N1 = a12 e N2 = a22.
Ribadiamo ancora il concetto. La cosa inconcepibile è che sappiamo benissimo cosa fanno gli elettroni che passano dal foro 1 (si distribuiscono secondo N1) e quelli che passano dal foro 2 (si distribuiscono secondo N2). Questa evidenza estremamente logica ci farebbe dedurre una conclusione altrettanto logica: la distribuzione N12, con entrambi i fori aperti, non potrebbe essere altro che N1 + N2 come per i proiettili, dato che non vi sono alternative: o un elettrone passa da 1 o passa da 2. Su questo la nostra mente non ha alcun dubbio. E invece si ha che N12 ≠ N1 + N2 , ossia si ha interferenza.
Ragioniamoci ancora un po’ sopra e ripetiamo l’esperimento in modo veramente semplificato, può darsi che si stia facendo un errore e non ne accorgiamo. Usiamo anche la Fig. 15 che è un po’ meno “approssimativa” della Fig. 14. Mettiamo il nostro rivelatore di elettroni in un certo punto P della parete. Lasciamo aperto il foro 1 e spariamo gli elettroni. Niente, la probabilità finale di avere un qualche elettrone in quel punto è praticamente nulla. Facciamo lo stesso con 2. Il risultato non cambia. Proviamo adesso, con un po’ di tremarella ad aprire entrambi i fori. Niente, ancora poco o niente. Meno male, è andata, avevamo proprio commesso un errore!
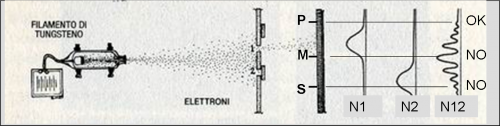
Per esserne proprio sicuri poniamo adesso il rilevatore in M, proprio nel centro della parete a metà strada tra 1 e 2. Ancora niente con 1 aperto e 2 chiuso; niente anche con 2 aperto e uno chiuso. In altre parole nessun elettrone riesce ad arrivare in M, sia che sia passato da 1 che da 2. Un lungo respiro e apriamo entrambi i fori. Porca miseria! Il numero di elettroni arrivati in M è diventato enorme. Siamo proprio in uno dei massimi di probabilità. Altro che errore, è il nostro cervello che non funziona più o sono i nostri sensi che ci tradiscono.
Proviamo ancora con S. Dovremmo trovare una probabilità abbastanza alta e, invece, quella totale è relativamente modesta. Per avere un’idea ancora più chiara di quello che è successo usiamo la Fig. 16.
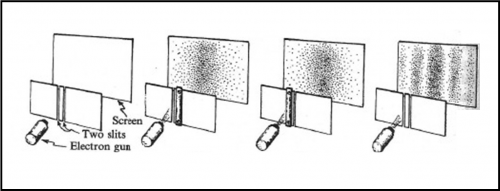
Si vede chiaramente che con entrambe le fenditure aperte sono arrivati molti elettroni dove ne erano giunti ben pochi sia con una che con l’altra fenditura aperta (insomma, 2 + 2 non fa 4!). Ancora peggio, però, ne sono arrivati pochissimi dove anche solo una fenditura aperta ne aveva fatti passare moltissimi. Se non è assurdo tutto ciò…
Un attimo, un attimo. Qui sotto c’è qualche trucco e probabilmente gli elettroni sono passati da un buco che non avevamo visto o, meglio ancora, sono andati avanti e indietro. Qualcosa di simile al gioco delle tre carte: sembra impossibile, ma una volta scoperto il trucco tutto diventa banale.
Illusione! Potremmo girare tutta l’apparecchiatura e vedremmo che l’esperimento non è stato viziato da nessun trucco. Non ci resta che pensare che per qualche motivo (ancora sconosciuto) l’elettrone si sia spezzato in due e sia passato da entrambi i fori contemporaneamente. No, niente da fare, nemmeno in questo caso (almeno secondo il nostro modo di ragionare consueto).
Non esiste, in effetti, nessuna spiegazione scientificamente valida che spieghi il risultato finale. Dobbiamo accettare una verità assurda e descriverla come tale. Attenzione. E’ proprio adesso il momento di NON usare il cervello nel modo consueto. Non cerchiamo assolutamente di spiegare il fenomeno o di trovare errori logici nella trattazione. Accettiamo la conclusione senza fare inutili sforzi cerebrali.
Tuttavia, sappiamo benissimo predire il risultato finale, sebbene privo di senso. Ciò vuol dire che, anche senza capirlo, potremmo usarlo per scopi pratici. Per esempio, mettendo qualcosa che ha “fame” di elettroni in M, della Fig. 15, saremmo sicuri di dargli il cibo che desidera, anche se la nostra logica si rifiuterebbe di accettarlo. In realtà ciò capita ormai quotidianamente con i risultati incompresi ma prevedibili della MQ.
Prima di proseguire fatemi riassumere ancora una volta ciò che abbiamo ottenuto.
Gli elettroni giungono sulla parete finale sicuramente uno alla volta e sono costretti a passare o da uno o dall’altro foro. Agiscono proprio come i proiettili del fucile. Questo risultato è confermato quando si chiudono alternativamente i due fori e si calcola la probabilità di arrivo sulla parete. Tuttavia, la probabilità che hanno gli elettroni di arrivare in un punto della stessa parete, quando i fori sono entrambi aperti, segue la stessa regola delle onde. La probabilità è simile all’intensità delle onde e si determina elevando a quadrato l’ampiezza di un “qualcosa” che deve essere l’ampiezza di un’onda, ma che non sappiamo assolutamente cosa sia. L’abbiamo chiamata “ampiezza della probabilità”.
Non ci resta che accettare un dato di fatto che non può che metterci in imbarazzo e sconvolgere la nostra mente: gli elettroni sono oggetti misteriosi e assurdi, a volte si comportano come particelle e a volte come onde. Tuttavia, stiamo molto attenti a questa frase che sembrerebbe risolvere in parte il mal di testa che c’è venuto. Ricordiamoci che stiamo mandando gli elettroni uno alla volta e non a coppie e quindi non abbiamo contemporaneamente due onde che si originano nei due fori come nel caso dell’acqua. Siamo costretti a tenerci il mal di testa e usare la descrizione precedente anche se è sicuramente artificiosa e semplicistica. Riassumo matematicamente il tutto (si fa per dire) anche con la tabella di Fig. 17 che potrà servirci in futuro.
Dobbiamo anche accettare un ulteriore assurdità a cui avevamo già accennato all’inizio della terza parte dell’esperimento di Feynman: la stessa identica cosa si può ottenere con i fotoni, proprio quelle particelle che Young sembrava aver cancellato dalla fisica. Se sono così bizzarri i comportamenti degli elettroni e dei fotoni, cosa succede alle altre particelle elementari? Purtroppo la stessa identica cosa. Accidenti, noi siamo fatti proprio di queste particelle, ma non dobbiamo seguire stranezze del genere. Quando passiamo da una porta passiamo da quella e arriviamo sempre in un solo punto camminando o correndo. Non riusciamo assolutamente a diventare onde o restare particelle più o meno solide ma ben concrete. Beh… questa è l’apparente fortuna dei sistemi complessi… come vedremo meglio più in là.
L’esperimento finirebbe qui ed è riassunto globalmente nella Fig. 18. Si potrebbero anche scrivere molte formule che descrivano il comportamento degli elettroni e la probabilità di giungere in un certo punto sotto diverse circostanze. Potremmo anche farlo e non pensare più a quelle stupide onde-particelle o particelle-onde. Sappiamo cosa si ottiene, lo possiamo quantificare con la “nostra” matematica e addirittura applicarlo alle nostre macchine e necessità quotidiane. Pensate che lo fa addirittura il Sole quando riesce a fondere l’idrogeno e ottenere l’elio. L’uomo, però, non è (o forse non lo era…) capace di subire e accettare ciò che non è logico. Ed ecco che da queste assurdità è nata la MQ, o, meglio ancora, l’esperimento di Feynman ne racchiude, per la prima volta, tutti i punti essenziali.
A questo punto non ci resterebbe che commentare l’esperimento facendo filosofia scientifica e richiamare anche alcuni esperimenti molto più recenti e sofisticati che hanno ulteriormente confermato le assurdità e le loro descrizioni. Non solo, essi hanno anche portato prove di un qualcosa, che potremmo chiamare “informazione”, che pervade l’Universo e che potrebbe viaggiare a velocità ben superiore a quella della luce.
Poi passeremmo, finalmente, alla descrizione di tutte le leggi e regole (sempre che siano tali) della MQ, sapendo ormai con chi abbiamo a che fare.
Era meglio non voler sapere…
Tuttavia, vorrei fare qualcosa di speciale, per rendere ancora più semplice e chiaro il risultato ottenuto. Comportiamoci, allora, da “testoni” , come quelli che se non toccano con mano non vogliono credere. Tempo perso, vedrete, però può aiutarci a entrare meglio nella nuova Scienza. Chiediamoci, quindi: “Siamo veramente sicuri di tutto ciò che abbiamo ottenuto e delle frasi molto strane che ci siamo inventati?” Mah… è meglio provare ancora una volta, cercando di non farci ingannare dalle apparenze. Che ne dite?
Per cercare di descrivere tutti risvolti che si nascondono nell’esperimento di Feynman bisogna muoversi per gradi e senza dare niente per scontato. Arriveremo alla fine e poi torneremo indietro senza aver paura di annoiarci o di sentirci degli idioti. Ogni volta cercheremo di vedere le cose sotto angolazioni leggermente diverse. Abbiamo detto che il nostro cervello deve abituarsi gradatamente a non rifiutare situazioni fuori da ogni logica “normale”, ma prima vuole essere veramente sicuro.
Ad esempio, potremmo dire, secondo la logica corrente, che la proposizione: “Un elettrone o passa dal primo foro o passa dal secondo” è un dato di fatto, che non si può contestare. Non possiamo pensare che succeda qualcosa di diverso dato che gli elettroni si comportano esattamente come i proiettili e lo abbiamo provato sentendo i loro “clic” sulla piastra.. Questa proposizione la possiamo chiamare evidenza A. Cerchiamo allora di discuterla a fondo, dato che è proprio ciò che sembra logico che deve sollevare i nostri dubbi. Poiché il risultato finale è illogico, il salto dalla conoscenza comune alla realtà assurda si può avere in un qualsiasi punto. Niente deve essere, quindi, giudicato sicuro.
L’evidenza A porterebbe a dire che la somma finale deve proprio essere la somma degli elettroni che passano dai singoli fori. La logica scientifica impone questa deduzione. Tuttavia, l’esperimento con i due fori aperti contraddice il risultato atteso e dobbiamo fare uno sforzo e ammettere che la proposizione A è falsa. E’ una scelta durissima e contro ogni nostra capacità deduttiva.
A questo punto, non ci resta che ammettere che non è vero che un elettrone debba passare per forza o dal foro 1 o dal foro 2. Vi deve essere un’altra possibilità. Forse Alice non si sarebbe stupita tanto come stiamo facendo noi. Per non abbandonare una logica che è dura a morire non ci resta che dimostrare, in qualche modo sensato, che gli elettroni passano contemporaneamente attraverso entrambi i fori. Insomma, stiamo cercando di trovare una logica in un’evidenza completamente illogica. Il cervello potrebbe anche riuscirci, ma gli esperimenti sono quelli che sono e non possono inventarsi cose che non avvengono. Dobbiamo affidarci a loro. Non ci resta che osservare direttamente se un elettrone passa da 1 o da 2 o da entrambi. In altre parole, dobbiamo guardarli mentre attraversano i fori. Così saremo veramente sicuri di quello che fanno.
La realtà dell’esperimento non potrà essere confutata, qualunque sia il risultato.
Insomma, vogliamo controllare ancora una volta l’esperimento di Feynman, andando più a fondo. La speranza è l’ultima a morire e saremmo ben contenti di dire che i discorsi fatti precedentemente sono una “bufala”, uno scherzo dell’immaginazione o un trucco da Premio Nobel. In fondo, chi ci ha garantito che gli elettroni, una volta in volo, passino realmente da un solo foro?
Per potere vedere qualcosa, però, è necessario illuminarla. Siamo quindi costretti a mettere dietro ai fori una sorgente di luce. Se essa è sufficientemente intensa la luce viene dispersa dall’elettrone e la parte che rimbalza verso di noi ci permette di localizzare il “proiettile” microscopico. In queste condizioni possiamo verificare tranquillamente cosa succede prima del ‘clic” sulla parete. Vi sono tre possibilità: o l’elettrone passa da 1, o passa da 2 o si divide in qualche modo e passa sia da 1 che da 2. La sorgente luminosa ci permette di verificare quale evento sia quello vero.
Con una certa ansia iniziamo l’esperimento. Anche se niente sembra poterci più sorprendere, dobbiamo ammettere, alla fine, che tutti gli elettroni che hanno fatto ‘clic’ sono stati visti passare o dal foro 1 o dal foro 2. In altre parole, ogni elettrone ha mostrato il 100% di probabilità di passare da un certo foro piuttosto che dall’altro. In nessun caso si è visto un elettrone passare contemporaneamente sia da 1 che da 2.
Impossibile! E’ necessario rifare l’esperimento comportandoci come potrebbe fare un bambino. Forse proprio i bambini sono i più vicini alla MQ, dato che ancora non sono stati plagiati dalla fenomenologia quotidiana che è ormai troppo radicata in tutti noi.
Prendiamo un quaderno e prepariamo due colonne. Nella prima segniamo gli elettroni che sono passati da 1 e nella seconda quelli che sono passati da 2. Controlliamo, adesso, la loro distribuzione sulla parete. Quelli che sono passati dal foro 1 descrivono esattamente la curva N1, mentre quelli che sono passati da 2 descrivono esattamente la curva N2. Accidenti, questo sì che è un risultato logico. Abbiamo, infatti, provato che gli elettroni, con entrambi i fori aperti, passano sempre o da uno o dall’altro foro e che quando giungono sulla parete seguono esattamente le distribuzioni che avevamo ottenuto chiudendo un foro alla volta.
Ma, allora, sia lavorando con un foro alla volta che con tutti e due il risultato finale è uguale. Ma dov’è finita quella strana curva d’interferenza? Sparita nel nulla. Forse avevamo bevuto anche noi come il soldato…
Proviamo addirittura (anche se sembrerebbe una fatica del tutto inutile) a disegnare la distribuzione degli elettroni sulla parete senza far differenza tra quelli provenienti da 1 e da 2. La solita logica ci direbbe che devono per forza seguire la curva N1 + N2. E’ un momento molto critico, dato che è quello che abbiamo fatto nell’articolo precedente con entrambi i fori aperti e che ci aveva portato a quella assurda figura di interferenza. Meraviglia delle meraviglie! La curva che vediamo è proprio N1 + N2. Altro che interferenza… Avevamo davvero bevuto troppo, possiamo scrivere che N12 = N1 + N2, proprio come per i proiettili del fucile.
Scusate, buttiamo via tutto quanto avevamo scritto precedentemente: era solo un’illusione. Forse anche Feynman aveva bevuto e con lui tutti gli scienziati che si sono fatti influenzare dalla sua sbornia.
Un attimo, un attimo. Prima di passare all’azione, facciamo un veloce riassunto di quello ottenuto prima e di quello ottenuto poco fa.
Prima avevamo chiuso 2, obbligato gli elettroni a passare dal foro 1 e trovato N1. Poi avevamo chiuso 2, fatto passare gli elettroni solo da 2 e la curva era risultata N2. Poi avevamo aperto entrambi i fori e avevamo sorprendente trovato una curva N12 ben diversa da N1 + N2, una tipica curva di interferenza. Non contenti di questo risultato assurdo, adesso abbiamo ripetuto l’esperimento, lasciando entrambi i fori aperti, ma controllando, direttamente in “volo”, da dove sono passati i singoli elettroni. Abbiamo visto che tutti, proprio tutti, sono passati da 1 o da 2. Risultato confermato dalle distribuzioni N1 e N2 sulla parete. Infine, abbiamo trovato, con rinnovata speranza nella nostra logica normale, che N12 = N1 + N2. Due risultati opposti. L’ultimo però è logico, il primo assurdo. Sarebbe facile concludere che il primo era stato ottenuto sotto i fumi dell’alcol.
Potremmo dimenticare l’esperimento precedente e dire che tutto è perfetto: gli elettroni, giustamente, si comportano come i proiettili del fucile. Però, però, a me sembrava di essere perfettamente lucido e non ubriaco. Feynman amava il buon vino, ma, per fare quello che ha fatto nella sua vita, non doveva certo essere un alcolizzato. Che ne dite di rifare l’esperimento dell’altra volta, tanto per essere sicuri che non poteva essere vero? Ci vuole un attimo. Apriamo entrambi i fori e spariamo gli elettroni senza più guardarli in “volo”, tanto abbiamo verificato direttamente che o passano da 1 o passano da 2. Con un mezzo sorriso di soddisfazione tracciamo subito la curva N12 risultante.
No, no! Ci sentiamo davvero girare la testa: ecco di nuovo la ben nota figura d’interferenza! Misuriamo per sicurezza, ma già sappiamo il risultato: N12 ≠ N1 + N2. La MQ esiste o non esiste? Abbiamo solo verificato che ogni volta otteniamo risultati diversi, a volte logici e a volte illogici.
Stiamo per buttare tutto all’aria e maledire Feynman che ci ha fatto fare questo “stupido” esperimento. Dov’è il trucco? Calma e sangue freddo.
Basta non guardare
In realtà qualcosa di diverso c’è stato tra il classico esperimento di Feynman e quello fatto da noi poco tempo fa. Nel primo caso non abbiamo guardato gli elettroni subito dopo essere passati dal foro, la seconda volta invece sì. Nel terzo tentativo abbiamo di nuovo evitato di guardare gli elettroni e l’interferenza è tornata a mostrarsi.
L’assurdo diventa quasi ovvio nella sua assurdità e mi vergogno quasi a scrivere la conclusione: “La differenza trovata non può che dipendere dal fatto che abbiamo accesa la luce per guardare gli elettroni, mentre erano in volo. Se la luce è accesa N12 = N1 + N2, se la luce è spenta N12 ≠ N1 + N2. In parole un po’ più tecniche possiamo dire che la luce influisce sulle caratteristiche degli elettroni”.
Veniamo per un attimo catturati nuovamente dalla nostra consueta logica e continuiamo: la luce ha alterato leggermente il moto degli elettroni e invece di fare arrivare l’elettrone nel massimo della curva di probabilità lo ha fatto arrivare nel minimo, distruggendo la figura d’interferenza. Non risolviamo certo l’assurdità delle frange d’interferenza ottenute a luce spenta, ma, almeno abbiamo risolto logicamente, la differenza dei risultati ottenuti a luce accesa e luce spenta.
Cerchiamo di convincerci sempre di più: gli elettroni sono corpuscoli delicati e non sono robusti come i proiettili di un fucile. Loro sono sensibili anche alla radiazione luminosa, mentre i proiettili nemmeno se ne accorgono. In questa conclusione, che non è certo la soluzione finale, troviamo però già una verità di importanza fondamentale: non possiamo usare le stesse leggi per i corpi macroscopici e per quelli microscopici. Teniamolo bene a mente.
Supponiamo adesso di abbassare sempre più la luce che illumina gli elettroni. Prima o poi sarà così debole da non potere deviare tutti gli elettroni a tal punto da annullare tutte le frange d’interferenza. Abbassando la luce dovremmo avvicinarci lentamente al caso in cui N12 diventa diversa da N1 + N2. Purtroppo, la luce (dobbiamo accettarlo perché l’esperimento della doppia fenditura può anche essere fatto con i fotoni al posto degli elettroni, ricordate?) non viaggia come le onde del mare, anch’essa si muove attraverso particelle come gli elettroni.
A mano a mano che abbasso la luce non faccio altro che inviare sempre meno fotoni verso gli elettroni. Questa situazione è molto a rischio: qualche elettrone potrebbe passare indisturbato dal foro senza essere colpito da un fotone e non lo vedremmo.
Quell’elettrone non sarebbe deviato, ma il nostro esperimento fallirebbe. In altre parole, meno luce non vuol dire disturbo minore agli elettroni ma non vederli tutti mentre passano dai fori.
Dovremmo aggiungere una terza colonna nel nostro quaderno in cui scrivere: “Non l’ho visto”, ogni volta che a un “clic” sulla parete non corrisponde una visione diretta dell’elettrone attraverso il foro. Più la luce diventa debole, e quindi meno fotoni sono sparati e meno elettroni sono colpiti, e più la terza colonna diventa ricca di casi. Potete facilmente immaginarvi il risultato finale: se sommo gli elettroni della prima e della seconda colonna essi sono distribuiti proprio secondo N1 + N2. Quelli della terza colonna sono invece distribuiti secondo la strana curva N12 che mostra interferenza.
A questo punto sembrerebbe che la questione sia risolta. La luce disturba gli elettroni e distrugge la curva di interferenza. Non so ancora come si costruisce realmente, ma so molto bene come distruggerla. Un’ovvia conclusione, però, che sembra già molto interessante, e la ripeto un’altra volta: “Non posso osservare direttamente un fenomeno legato a particelle microscopiche senza stravolgere lo stesso fenomeno”. In qualche modo sembra che si sia riusciti a dare un risvolto parzialmente logico all’intero esperimento.
A parte il fatto che questa conclusione “raffazzonata” non spiega comunque la figura di interferenza a luce spenta, anche a luce accesa dà una visione distorta della realtà. Dopo Feynman, come lui aveva previsto, sono stati fatti esperimenti ben più sofisticati per vedere gli elettroni senza disturbarli. Tuttavia, il risultato è sempre stato lo stesso. Il fatto stesso di sapere dove passa un elettrone disturba il suo movimento. Questa è una frase molto più sensata nella sua insensatezza.
In pratica basta solo la “minaccia” di una misura a far cambiare stato al sistema! Questa “buffa” parola, “minaccia”, è stata provata e confermata da molti esperimenti successivi, veramente strabilianti, a cui accenneremo in seguito.
Fatemi, finalmente, scrivere poche frasi che potrebbero descrivere ciò che avviene e che sono ormai abbastanza accettabili dal nostro cervello, che inizia ad adattarsi all’assurdo. Ripeteremo il concetto varie volte, con piccole sfumature di differenza. Mai come adesso il ripetere serve a … non capire e quindi a entrare nel mondo della MQ.
Siamo noi a decidere la realtà?
Immaginiamo, anche se non sappiamo ancora come sia possibile, che un elettrone (o un fotone) passi dai due fori come un’onda e che quindi possa fare interferenza con se stesso quando colpisce la parete ed essere rivelato come particella. Tuttavia, se osserviamo lo stesso elettrone subito dopo i fori riusciamo a localizzarlo prima dell’impatto finale ed esso diventa immediatamente una particella annullando l’interferenza. Questo risultato non si deve al disturbo fisico effettuato sull’elettrone, ma al fatto stesso che abbiamo determinato la sua reale posizione nello spazio. Avendo provato o scoperto (o quello che volete) che esso è passato dal foro 1 o 2 abbiamo annullato la sua possibilità di comportarsi come un’onda ed esso diventa a tutti gli effetti una particella con le conseguenze del caso.
In altre parole, possiamo “decidere” se osservare l’elettrone come particella o se permettergli di fare la figura di interferenza come un’onda.
Ma come può succedere tutto questo? Siamo davvero entrati nel paese delle Meraviglie?
In realtà, finché l’elettrone non viene rivelato sul bersaglio, esso non si trova mai in un punto preciso dello spazio, ma esiste in uno stato potenziale probabilistico, descritto da una funzione d’onda, che si propaga appunto come un’onda e non secondo una traiettoria definita. La famosa onda di probabilità, ricordate? Adesso capite perché l’avevamo già introdotta.
Niente da dire. Veramente affascinante anche se sempre più assurdo.
Un momento, non picchiatemi… Tutto sembra finalmente chiaro nella sua incomprensibilità, ma vi invito a ripetere ancora una volta l’esperimento cambiando un po’ le regole del gioco in modo da verificare meglio quest’ipotesi da mal di testa. Ricordiamoci, infatti, che il nostro corpo (e anche il cervello) sono strapieni di elettroni (accidenti!), eppure sono ben lontani dall’essere un po’ onde e un po’ particelle.
Fratelli gemelli
Abbiamo detto che riveliamo l’elettrone “subito dopo” che è transitato dal primo foro. “Subito dopo” significa che è passato pochissimo tempo dal transito nel foro. Ma per quanto piccolo sia il tempo trascorso, l’elettrone, comunque, ha già oltrepassato il foro; inoltre fino a questo momento esso è rimasto un’onda perché non l’abbiamo ancora rivelato. Perciò, nel frattempo, l’onda ha già attraversato anche l’altro foro e lo ha oltrepassato. Giusto no? E allora come fa l’elettrone a essere rivelato “tutto intero” vicino al primo foro? Che fine fa l’onda che ha appena oltrepassato il secondo foro? Scompare nel nulla? Sembra proprio di sì, ma com’è possibile?
Per chiarire questo punto, il fisico Wheeler utilizzò i fotoni e non gli elettroni (sappiamo ormai bene che il risultato non cambia) e propose di lasciare che il fotone passasse sicuramente attraverso entrambi i fori, come onda. In che modo? Molto semplice: inserendo un rivelatore non troppo lontano dal primo foro, ma neanche troppo vicino, insomma quanto bastava perché si fosse veramente sicuri che nel frattempo tutto il fronte d’onda fosse già transitato dai fori. In pratica, si voleva effettuare l’osservazione del fotone come particella, sicuramente dopo che esso era transitato da entrambi i fori come onda. Non per niente l’esperimento venne chiamato “a scelta ritardata”.
Non illudetevi, se proviamo a rifarlo anche noi, il risultato non cambia. L’onda scompare nel nulla, poiché il fotone viene rivelato come particella “intera”, senza alcun dubbio. Eppure l’onda è transitata sicuramente anche dal secondo foro: infatti, se non si inserisce il rivelatore, si forma la figura di interferenza (che può formarsi solo se l’onda transita da entrambi i fori). E allora com’è possibile?! Non possiamo che concludere che l’informazione del fotone “colto sul fatto” è stata immediatamente trasmessa all’onda transitata dall’altro foro ed essa è sparita.
Insomma, gli elettroni, i fotoni e tutte le particelle si scambiano informazioni in tempo reale, altro che alla velocità “lentissima” della luce.
Le cose non stanno proprio così, ma l’esempio è oltremodo calzante. La realtà è che ancora una volta stiamo cercando di fornire un’immagine oggettiva di ciò che accade. Purtroppo, dobbiamo convincerci che un’immagine di tipo oggettivo non è adeguata alla realtà. Non ha senso dire che “l’onda è già passata”, perché solo all’atto della misura possiamo dire che qualcosa è avvenuto. Prima della misura il fotone rimane in uno stato indefinito di potenzialità o di non-oggettività (o, meglio ancora, irrealtà).
Indietro nel tempo…
Quando poi inseriamo il rivelatore, allora possiamo dire con certezza che il fotone è passato solo dal primo foro e non dal secondo foro, e infatti non c’è interferenza. Se, invece, non inseriamo il rivelatore e aspettiamo di scorgere i fotoni solo al loro arrivo sul bersaglio (con la relativa figura di interferenza), allora possiamo dire che ciascun fotone ha fatto interferenza come se fosse un’onda transitata da entrambi i fori; ma questo lo possiamo dire solo dopo che il fotone viene rivelato sul bersaglio, anche in un punto raggiungibile solo da un’onda e non da una particella, cioè dopo la misura.
La cosa che a noi appare incredibile è che ciò che il fotone ha deciso di fare (passare da un solo foro o da entrambi) dipende da una scelta successiva al transito stesso! Infatti il rivelatore viene inserito dopo che il fronte d’onda è transitato da entrambi i fori. Come dice Wheeler, la “scelta” di far passare il fotone da un solo foro o da entrambi è “ritardata”, cioè avviene dopo che il fotone è passato! Se non è follia questa! Una particella cambia il suo “stato” di adesso se le capita qualcosa dopo! Anche il concetto di tempo, di prima e di dopo, sembra perdere ogni sicurezza.
Torniamo nuovamente all’esperimento di Feynman ed esprimiamo la conclusione in modo più matematico e meno empirico. Ormai lo possiamo fare, anche perché la matematica è estremamente semplice. La probabilità che si verifichi un qualsiasi evento in un esperimento ideale (un esperimento in cui tutto è perfettamente specificato) è sempre il quadrato di qualcosa. Noi avevamo chiamato questo qualcosa a, ampiezza della probabilità. Quando un evento può compiersi in diversi modi alternativi (nel caso precedente, attraverso un foro o attraverso l’altro) possiamo dire che le varie ampiezze a di ogni alternativa si sommano. La probabilità finale sarà poi il quadrato di questa somma (interferenza, N12 = (a1 + a2)2 ≠ N1 + N2 = a12+ a22). Se, invece, l’esperimento è eseguito in modo da determinare esattamente quale alternativa è stata scelta, allora la probabilità finale diventa semplicemente la somma delle probabilità di ciascuna alternativa (N12 = N1 + N2 = a12 + a22).
Questa è una regola generale che possiamo estendere a tutti i fenomeni della Natura ed è anche la prima formula matematica che associamo alla MQ.
La domanda che tutti ci stiamo facendo è, a questo punto: “Sì, va bene, accettiamo pure questa conclusione. Ma, qual è la “macchina” in grado di produrre questa realtà indiscutibilmente illogica?” Nessuno la conosce, siamo in buona compagnia. Possiamo, al pari dei più grandi scienziati, limitarci a descrivere i risultati.
Gli studiosi vi possono dare una spiegazione molto ampia e dettagliata, ossia vi possono mostrare molti esempi in cui quando si sa la posizione degli elettroni si distrugge immediatamente la figura di interferenza, non solo attraverso l’esperimento dei due fori. La matematica che descrive gli esperimenti e le conclusioni può diventare sempre più sofisticata fino a permettere predizioni e applicazioni. Può anche introdurre i numeri complessi e qualsiasi altra diavoleria, ma il succo del discorso non cambia: il mistero del come (e del perché) rimane un mistero ancora oggi, un mistero per il nostro cervello abituato alle leggi della fisica macroscopica.
Un regno del tutto casuale
Fatemi dire una frase estremamente strana, ma molto illuminante: “La Natura stessa non sa mai da quale parte passa l’elettrone”. Nel momento in cui qualcuno o qualcosa riesce a identificarlo, immediatamente si rompe la situazione originaria e l’interferenza si annulla. La Natura è costretta a prendere una decisione.
Ricordiamoci un’altra constatazione che fa parte ormai -e da tanto tempo- del nostro pensiero comune: “Le stesse condizioni di partenza devono produrre sempre lo stesso risultato finale”. Bene, essa non è più vera, nella MQ (in parte era già stata messa in dubbio dal caos).
Noi potremmo riprodurre le stesse condizioni di partenza e compiere tutte le azioni nello stesso identico modo, ma non potremmo mai sapere dove l’elettrone passerà. Forse non lo sa nemmeno lui, dato che produce due onde di probabilità che creano interferenza, ossia riesce a trovarsi in due posti contemporaneamente (anzi … ovunque possa andare).
Un elettrone e una guerra mondiale
Le ripercussioni di questa realtà assurda della Natura ha dei risvolti pratici che potrebbero essere terribili. Immaginiamo di costruire un apparecchiatura come quella precedente in cui però se un elettrone passasse dal foro 1 innescherebbe un contatto che farebbe scoppiare una bomba atomica e inizierebbe la III guerra mondiale. Se invece passasse dal foro 2 la pace si manterrebbe (sempre che si possa chiamare pace quella odierna). Il futuro del mondo sarebbe legato solo e soltanto dalla decisione di un elettrone o -meglio ancora- dal fatto di avere voluto sapere da che parte è passato. Avremmo il 50% di probabilità di far finire l’Umanità. Cosa posso dirvi? : “Non guardate l’elettrone e lasciatelo passare come onda! Causerebbe interferenza su qualche muro, ma non farebbe esplodere un conflitto terrificante”. Un esempio questo che ci ricorda il gatto di Schrodinger, su cui torneremo più avanti.
Siamo proprio entrati nella filosofia ed è meglio tornare indietro e concludere qualcosa di più preciso per descrivere (solo descrivere, di più non possiamo fare) ciò che capita ai nostri elettroni.
Gli elettroni sono realmente corpuscoli quando viaggiano e lo riusciamo a provare guardandoli direttamente o rivelandoli in modo anche non invasivo. Tuttavia, essi hanno una libertà di scelta innata nel dove poter stare in un certo momento e quindi anche alla fine della loro traiettoria. Ne consegue che essi possono essere rappresentati molto bene attraverso la probabilità che hanno nell’essere in un certo punto (e, quindi, di passare da una o dall’altra fenditura).
Più correttamente possiamo parlare di onda di probabilità ad essi associata, nel senso che descrive in termini probabilistici quali futuri sono possibili per un certo elettrone.
Se preferiamo, gli stessi elettroni possono essere considerati una vera e propria onda (nel senso probabilistico del termine, però… attenzione a non volerlo pensare come un’onda formata da qualcosa, se no rientreremmo nella fisica classica e addio alla MQ).
Conosciamo, però, bene le caratteristiche delle onde (che siano di probabilità o di acqua poco importa): esse danno luogo a interferenza ed ecco che le frange viste sullo schermo colpito dagli elettroni mostrano proprio le zone dove le onde di probabilità si sommano e si sottraggono. La probabilità associata a un elettrone ha, infatti, sempre il 50% di passare da una fenditura o dall’altra. Queste onde di probabilità sono quelle che causano l’interferenza. Tuttavia, dobbiamo lasciare libera la probabilità associata a un elettrone. Se riusciamo a localizzarlo, si distrugge immediatamente la sua onda di probabilità (sappiamo esattamente dove si trova), l’elettrone si trasforma immediatamente in una particella e addio all’interferenza.
Se, invece, abbiamo un solo foro, non permettiamo comunque il passaggio da una fenditura e l’onda di probabilità, che continua a esistere, non può comunque dar luogo alle frange dato che non esiste una sorella che interferisce con lei. Sia che la guardiamo e la trasformiamo in particella, sia che la lasciamo viaggiare come onda fino alla parete finale, non si può creare l’interferenza. Sulla parete finale, in ogni caso, l’onda diventa particella è fa “clic”. In fondo, è ovvio: la parete è servita a rilevarla. La probabilità finale di colpire un certo punto è identica sia per le particelle che per le onde, come ormai sappiamo molto bene.
In parole ancora più semplici e generali: all’atto dell’osservazione, una particella che ha insita in sé la probabilità di trovarsi in molti posti (come ad esempio in 1 o in 2), viene ad occupare una sola delle sue possibilità e inizia a vivere un’esistenza concreta. Il suo “stato” è completamente cambiato.
La sua libertà è stata distrutta, dato che si è scoperto dove si trova, come quando si scopre un assassino che potrebbe nascondersi in mille luoghi della città. Quando, finalmente, si riesce a catturarlo, tutte gli altri possibili rifugi perdono di significato. Più tecnicamente, la probabilità di essere nella posizione rivelata è il 100%. E’ impossibile che si formi un’interferenza con un’altra onda di probabilità. L’altra onda avrebbe una probabilità uguale a zero. L’onda si è trasformata in un proiettile ben definito per “colpa nostra” (o per qualcosa o qualcuno che ha svelato il suo segreto…). L’aspetto sconvolgente ma anche illuminante di queste scoperte è che tutto l’Universo -e noi stessi- siamo formati da particelle; le stesse particelle che esistono come materia quando le osserviamo ed esistono come onde di possibilità quando non le osserviamo.
Fatemi fare un altro esempio legato alla vita di tutti i giorni. Attenzione però, non è un’esperienza concreta, ma un’esperienza puramente mentale. Supponiamo che l’umore di una persona sia cattivo (C) o buono (B) e che la probabilità di trovarla in uno di questi due stati sia del 50 %. La MQ che abbiamo appena imparato a conoscere ci dice allora che l’umore della persona in oggetto, in un momento qualunque della giornata, è rappresentato dalla sovrapposizione degli stati C e B, ma che la probabilità P di trovarla di cattivo o di buon umore sta nel rapporto 0.5 a 0.5. Indichiamo con P(C) e P(B) le probabilità di trovarsi nei due casi C e B.
Questa condizione si può scrivere simbolicamente con la formula banalissima: P = 0.5 P(C) + 0.5 P(B). Si può quindi anche dire che l’umore della persona oscilla (proprio come un’onda) dallo stato C allo stato B. Per saperne di più dobbiamo incontrarla (“osservarla”) e verificare quale sia realmente il suo umore. La potremo, ad esempio, trovare nello stato B, che ci permette automaticamente di dire che al momento dell’incontro abbiamo ridotto la sua funzione d’onda (onda di probabilità) al solo stato P = P(B). Semplicissimo, no? Questo discorso ci sembra più che logico quando parliamo di stati d’animo, ossia di pensieri astratti. Lo accettiamo molto meno quando ci riferiamo a particelle solide e concrete.
La differenza fondamentale, rispetto all’analisi dei fenomeni, tra fisica classica e fisica quantistica, è che nella prima l’interazione tra gli oggetti e gli apparati di misura può venire trascurata o eliminata, mentre nella seconda questa interazione è parte integrante del fenomeno. Non è l’interazione con la particella (fisica classica), ma è la determinazione dell’esatta posizione che distrugge l’onda di probabilità che possiede il 50% di passare da 1 e il 50% di passare da 2. Appena si sa dov’è, quella posizione possiede il 100% di essere vera e in tutto il resto dello spazio la probabilità diventa esattamente lo 0%, ossia nulla.
Un qualsiasi “microsistema” (fotone, elettrone, ecc.) non è obbligato da leggi deterministiche a percorrere traiettorie precise. Il “probabilismo” vieta esplicitamente a qualsiasi particella elementare di possedere una traiettoria definita. Nel caso dell’esperimento a due fenditure, anche un solo elettrone, o fotone che sia, percorre tutte le possibili traiettorie comprese tra la sorgente e la parete di arrivo. Percorrendo tutte le possibili traiettorie, la particella inevitabilmente incontra anche le due fenditure, riuscendo, dopo averle oltrepassate (e avendo quindi interferito con sé stessa), a produrre sullo schermo le bande chiare a scure tipiche dell’interferenza costruttiva e distruttiva.
Quando la particella passa attraverso la fenditura 1 ciò determina un certo mondo possibile (che chiameremo mondo 1); quando passa attraverso la fenditura 2, abbiamo invece il mondo 2. Nel nostro caso significa che entrambi questi mondi coesistono in qualche modo, l’uno sovrapposto all’altro.
Beh… ho pronunciato diverse frasi tutte molto simili, ma che potrebbero rifinire meglio il pensiero e il concetto relativo (astratto per definizione).
Per ora può bastare e proseguiamo con qualcosa di più tecnologico, ma davvero stupefacente. Dovremmo già aspettarcelo, ma la meraviglia dell’esperimento che segue è sempre indescrivibile. Uno di quelli che preferisco in assoluto per farmi accompagnare verso le pazzie del Paese di Alice.
Abbracciati e attorcigliati
In realtà ve ne presento due, in qualche modo simili. Scegliete voi quello che preferite…
Consideriamo, per primo, l’esperimento di Aspect del 1982. Esso si basa su due fotoni correlati (ossia con caratteristiche simmetriche, dato che pure loro hanno un “carattere”, come vedremo più in là) sparati contemporaneamente lungo direzioni diverse. Anch’essi, alla fine, arrivano su un rivelatore in grado di contarli. Lungo il percorso di uno dei due, però, può essere inserito un filtro in grado di modificarne la direzione.
Il risultato fantastico è che quando devia il primo elettrone, devia immediatamente anche l’altro benché si trovi a più di tredici metri di distanza. Il fatto straordinario, già previsto e temuto da Einstein sin dal 1935, dà una chiara evidenza di una reazione, a seguito di una certa azione, che avviene praticamente “in tempo reale”, quasi ci fosse tra le particelle correlate una trasmissione di informazione istantanea che se ne infischia della insuperabilità della velocità della luce (immaginate le ricadute sul principio di simultaneità). Due fotoni gemelli che “sentono” lo stesso problema contemporaneamente. Non è che i gemelli monozigoti abbiano proprio questo tipo di particelle correlate nel loro neuroni?
Per chi volesse saperne un po’ di più, la Fig. 19 raffigura lo schema di massima dell’apparecchiatura utilizzata da Aspect. Al centro abbiamo un atomo di Calcio eccitato, che produce una coppia di fotoni correlati che si muovono lungo percorsi opposti. Lungo uno di questi percorsi, di tanto in tanto e in maniera del tutto casuale, viene inserito un “filtro” (un cristallo birifrangente CB) che, una volta che un fotone interagisce con esso, può, con una probabilità del 50 %, deviarlo oppure lasciarlo proseguire indisturbato per la sua strada facendosi attraversare. Agli estremi di ogni tragitto previsto è posto un rivelatore di fotoni.
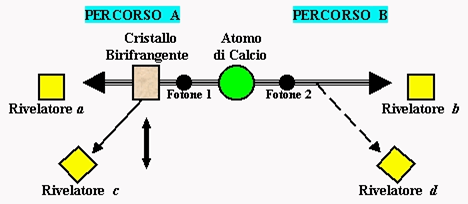
Ora, la cosa straordinaria verificata da Aspect è che nel momento in cui viene inserito il cristallo birifrangente CB e si produce una deviazione del fotone 1 verso il rivelatore c, anche il fotone 2 (senza “ostacoli” davanti), “spontaneamente” e istantaneamente, devia verso il rivelatore d. Praticamente, l’atto di inserire CB, con la conseguente deviazione del fotone 1, fa istantaneamente e a distanza deviare il fotone 2. Se non sono gemelli siamesi…
Cosa ci dice questo inspiegabile e sbalorditivo esperimento? Che bisogna abbandonare l’idea che le particelle correlate, situate in luoghi distanti, rappresentino enti distinti. Contemporaneamente, scompaiono anche buona parte degli ostacoli concettuali (e di fatto) che impediscono una comunicazione o un’azione non locale. Se agiamo su qualcosa otteniamo un’altra cosa anche se la loro interconnessione fa parte di una situazione descrivibile ma illogica. Possiamo fare succedere qualcosa in un luogo A, agendo sul luogo B, senza che vi sia nessun rapporto concreto tra i due luoghi e tra i fenomeni che vi avvengono. Ubiquità? Gemelli monozigoti? Velocità infinita? No, solo MQ! Come diceva il Premio Nobel per la Fisica Brian Josephson: “L’universo non è una collezione di oggetti, ma un’inseparabile rete di modelli di energia vibrante nei quali nessun componente ha realtà indipendente dal tutto: includendo nel tutto l’osservatore”.
Abbiamo fatto la nostra conoscenza con le particelle “entangled”, ossia “attorcigliate”, in un abbraccio che non può mai essere dimenticato
Attenzione: chi avesse voglia di riflettere un po’, capirebbe che questo esperimento ha già risolto uno dei problemi legati all’inflazione. Abbiamo particelle (e quindi anche oggetti macroscopici che sono composti da loro) troppo distanti per avere avuto scambio di informazioni, eppure si comportano nello stesso modo. La soluzione è ovvia… non vi pare? Niente paura, ci torneremo sopra e come!
Le particelle ci leggono nella mente?
L’esperimento, compiuto all’inizio degli anni ’90 da Mandel, fa ancora un passo in avanti rispetto a quello di Aspect anche se in qualche modo gli assomiglia. Esso rappresenta senza dubbio un gioco di prestigio fantastico, ma perfettamente riproducibile. Pur non sapendo cosa in realtà succede fisicamente, sappiamo benissimo come utilizzarlo per scopi tecnologici.
Innanzitutto, ricreiamo una situazione simile a quella del fotone che transita attraverso le due fenditure, ma per mezzo di un dispositivo diverso, cioè uno specchio semi-riflettente (detto anche divisore): esso trasmette la luce al 50%, ovvero solo metà dell’intensità luminosa riesce ad attraversare lo specchio, mentre l’altra metà viene riflessa. Insomma, qualcosa di molto simile al CB di prima.
Analizzando i singoli fotoni, in una descrizione tradizionale, diremmo che la probabilità che un fotone attraversi lo specchio (invece di essere riflesso) è del 50%. Se consideriamo 100 fotoni, secondo la logica convenzionale, ci aspettiamo statisticamente che 50 fotoni attraversino lo specchio, mentre gli altri 50 vengano riflessi: il fascio iniziale di 100 fotoni sarà, quindi, diviso in due fasci diversi che percorrono cammini diversi. Questo però è vero solo se abbiamo modo di rivelare i singoli fotoni, altrimenti dobbiamo ammettere che ciascun fotone si trova in uno strano “stato di sovrapposizione”, cioè al 50% attraversa lo specchio e al 50% viene riflesso.
In altre parole, il percorso di ciascun fotone sarà indefinito, poiché “per metà” passa attraverso lo specchio e “per l’altra metà” viene riflesso, sebbene esso sia indivisibile. Ma queste cose le sappiamo già abbastanza bene.
Se noi non misuriamo esplicitamente il percorso seguito dal fotone e facciamo incidere i due percorsi potenziali su uno schermo, otteniamo la solita figura di interferenza, ovvero il fotone (pur rimanendo una particella singola) è passata da entrambi i percorsi e alla fine produce interferenza con se stesso. Fin qui avviene ciò che abbiamo già descritto fin troppe volte. La differenza fondamentale è che stavolta il misterioso sdoppiamento del singolo fotone non è causato dalle due fenditure bensì dallo specchio semi-riflettente.
Come si vede nella Fig. 20, il laser 1 emette un fotone, lo specchio semi-riflettente 2 “divide” il fotone in due parti “fantasma”, ciascuna delle quali percorre un percorso diverso, 3 e 4. Gli specchi nei punti 3 e 4 sono “normali” e servono solo a indirizzare in maniera opportuna i due percorsi: le onde rimangono onde.
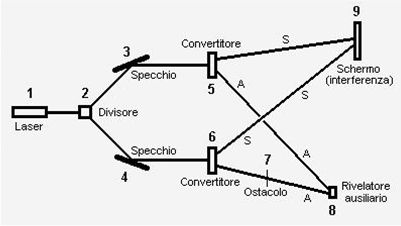
Su ciascun percorso vi è un “convertitore “. Non entriamo nei dettagli e fidatevi della perfezione dell’esperimento: garantisco al 100%. Ciascun convertitore, 5 e 6, divide il proprio fotone fantasma in due fotoni “gemelli” di energia dimezzata. Uno viene chiamato “fotone segnale” ed è indicato con S, mentre l’altro viene chiamato “fotone ausiliario” ed è indicato con A. Infine, i due percorsi S vengono rivelati sullo schermo 9, mentre i due percorsi A vengono indirizzati sul rivelatore ausiliario 8.
Vediamo come funziona l’intero sistema: il laser 1 spara un singolo fotone alla volta che incide sullo specchio semi-riflettente 2. Poiché noi non misuriamo quale percorso viene effettuato dal fotone, esso passa come onda da entrambi i percorsi 3 e 4, e nei convertitori 5 e 6 viene diviso in due onde gemelle di energia dimezzata. Alla fine, i due percorsi “segnale” (indicati con S) incidono sullo schermo 9 dove il fotone S farà interferenza con se stesso (cioè con l’altra parte di se stesso passato dall’altro percorso) e diventerà finalmente particella (è stato rilevato).
In seguito dal laser spareremo altri fotoni, uno alla volta, e alla fine come risultato vedremo una chiara figura di interferenza sullo schermo 9. Fin qui tutto come sempre. Ormai abbiamo capito il succo dell’esperimento. Tuttavia, non dimentichiamoci i fotoni ausiliari A. Anch’essi si incontrano in 8, con le ovvie conseguenze del caso. Anche lì sentiamo un “clic” ben noto, come quello che si verifica in 9.
Siamo stati molto bravi, ma non abbiamo fatto niente di speciale. Siamo riusciti a ottenere il solito esperimento moltiplicato per due, attraverso l’uso di specchi che non alterano per definizione lo stato probabilistico di onda. Benissimo: ora viene il bello. Vediamo che cosa succede se si inserisce un ostacolo nel punto 7.
I percorsi di S e A sono ormai divisi e ci aspettiamo che essi siano indipendenti: l’ostacolo nel punto 7 non dovrebbe alterare la figura di interferenza nello schermo 9, poiché il punto 7 si trova su un altro percorso, anche molto distante, che porta al rivelatore ausiliario 8 e non allo schermo 9. In altre parole, si dovrebbe distrugge solo la figura di interferenza di 8.
E invece no! Se inseriamo l’ostacolo nel punto 7, interrompendo così il percorso di un fascio ausiliario, anche la figura di interferenza dei fasci “segnale” S nello schermo 9 scompare! Eppure non abbiamo effettuato misure sui fasci “segnale” (che finiscono sullo schermo 9), ma solo su un fascio ausiliario (che finisce nel rivelatore 8). Anche se allontaniamo moltissimo i due fasci, A e S, tra di loro, quando operiamo sui fasci A incredibilmente influenziamo anche i fasci S.
Com’è possibile? Che cos’è cambiato rispetto al caso precedente quando non vi era un ostacolo nel punto 7? State bene attenti a quanto sto per dire, mi raccomando! È cambiata la “conoscenza potenziale” che abbiamo sui fasci “segnale”. Poiché il percorso che passa dall’ostacolo 7 è interrotto, quando riveliamo un fotone sul rivelatore ausiliario 8, esso deve provenire necessariamente dal percorso che passa per lo specchio 3 (non può provenire dal percorso dello specchio 4, dato che è interrotto nel punto 7). Perciò, misurando la sua interazione col fotone segnale sullo schermo 9 noi saremmo in grado di dire con certezza che quel fotone “segnale” deve provenire dal percorso dello specchio 3, cioè sapremmo o -meglio ancora- dedurremmo che il fotone è passato “interamente” da questo percorso e conseguentemente non può essere passato dal percorso dello specchio 4 (ormai è diventato una particella dato che abbiamo scoperto la sua traiettoria attraverso la semplice deduzione).
E’ ovvio, quindi, che non può fare interferenza (come nel caso delle due fenditure). Questo spiega perché la figura di interferenza nello schermo 9 viene distrutta se inseriamo un ostacolo 7 sul fascio ausiliario.
Un esempio “concreto”? Non vi è bisogno di cogliere un ladro con le mani nel sacco per arrestarlo. Basta che le indagini fatte in una stanza chiusa della Polizia abbiano dimostrato la sua colpevolezza, attraverso prove inconfutabili. Magari il ladro è ormai scappato all’estero, ma la sua sorte è segnata (sempre che valga l’estradizione): per tutti è ormai un ladro a tutti gli effetti.
Il fatto notevole è che si tratta di una sconcertante “azione a distanza”: agendo sul punto 7 alteriamo lo stato fisico in un luogo diverso, cioè sullo schermo 9, dove la figura di interferenza viene distrutta, e questo è dovuto solo al fatto che noi possiamo dedurre quale percorso ha seguito il fotone che incide sullo schermo 9. Non è necessaria una conoscenza diretta, ma basta un’informazione, o, se preferite, un atto di consapevolezza.
Questa conoscenza potenziale è sufficiente ad alterare lo stato fisico sul rivelatore dei segnali, distruggendo la figura di interferenza. Qualcuno potrebbe dirmi: “Sì, ma lo scienziato o l’ispettore di polizia potrebbero non essere abbastanza intelligenti da fare il ragionamento deduttivo che inchioda il ladro”. No, la Natura ci considera tutti ugualmente “intelligenti”, proprio perché siamo fatti con le stesse particelle. Per le leggi dell’Universo non esistono ignoranti o luminari, esistono solo creature, le creature che ha costruito nei primi istanti di vita. Speriamo di non farle capire che purtroppo non è sempre vero… magari distruggerebbe tutto ciò che ha creato finora.
Sto scherzando ovviamente, ma non ne sono completamente sicuro. In fondo, anche l’incapacità di comprendere può essere considerata un’interferenza, un difetto anomalo e non sappiamo ancora come le particelle-onde si comportino in questi casi. Per chi ha voglia di pensare, non è difficile immaginarsi, allora, Universi paralleli o scelte casuali o quello che preferite. Dio forse gioca proprio a dadi. Anche Einstein può sbagliare…
In effetti, sembra che la meccanica quantistica dia un messaggio nuovo sulla struttura della realtà, e che sancisca la fine dell’oggettività materialistica, a favore di una concezione “idealistica”, in cui gli oggetti esistono in uno stato “astratto” e “ideale” che rimane teorico finché la percezione di un soggetto cosciente non lo rende reale. Oppure, senza farla tanto grossa, possiamo limitarci a notare che il classico modello materialistico è inadeguato a descrivere la realtà quantistica ed occorre rivolgersi a modelli che concepiscono l’Universo in termini di “informazione” piuttosto che di “materia”. Chiedetevi: “La Luna esiste anche quando non la guardiamo?”. Sembra ed è una domanda sciocca, ma per la MQ non è proprio così…
La QED…
Mi lancio un po’ avanti solo per costruire una specie di ponte. L’esplorazione del mondo subatomico ha rivelato la natura intrinsecamente dinamica della materia; ha mostrato che i costituenti dell’atomo, le particelle subatomiche, sono configurazioni dinamiche che non esistono in quanto entità isolate, ma in quanto parti integranti di una inestricabile rete di interazioni. Queste interazioni comportano un flusso incessante di energia che si manifesta come scambio di particelle; un’azione reciproca dinamica in cui le particelle sono create e distrutte in un processo senza fine, in una continua variazione di configurazioni di energia. Le interazioni tra particelle (presa di coscienza o certezza di un evento o ciò che volete) danno origine alle strutture stabili che formano il mondo materiale, il quale a sua volta non rimane statico, ma oscilla in movimenti ritmici. L’intero Universo è quindi impegnato in un movimento e in un’attività senza fine, in una incessante danza cosmica di energia (QUI e QUI).
Questa danza comporta un’enorme varietà di configurazioni ma, sorprendentemente, queste rientrano in poche categorie distinte. Lo studio delle particelle subatomiche e delle loro interazioni rivela quindi l’esistenza di un ordine perfetto. Il Paese di Alice non è poi così pazzo come sembrerebbe. Siamo solo noi che non riusciamo a capire le sue regole precise e addirittura semplici.
Vedremo che tutto ciò che riguarda la MQ è già completamente “sbocciata” attraverso l’esperimento di Feynman. Il suo esperimento, e le naturali implicazioni, rimangono uno dei punti più alti di tutta la Scienza, non solo degli ultimi due secoli, ma di tutta la storia umana. Un sommario semplice e meraviglioso di un mondo che nessuno, lui per primo, è stato ancora capace di capire. Forse ci vorrà una bambina, magari di nome Alice, a spiegarci (e non solo a descriverci) la nuova logica. Magari è già a casa vostra … datele un bacione da parte mia!
Riflessioni
La parte che segue potete saltarla a piedi uniti, essendo frutto solo e soltanto della mia mente contorta. Permettetemi, però, una riflessione molto personale (ma esiste ancora l’oggettività nel Paese della MQ?). Il mondo macroscopico che ci circonda sembra seguire la regola fondamentale di causa-effetto. In altre parole, tutto ciò che capita è legato a una causa più o meno macroscopica. Addirittura il caos è in qualche modo legato a una variazione infinitesima delle condizioni iniziali. In maniera veramente “rozza”, niente al mondo sembra in grado di scegliere il proprio futuro. Anche gli animali, in fondo, attraverso l’istinto, seguono regole analoghe.
L’unica “cosa” che sembra andare contro questa legge universale, dettata dalla freccia del tempo, è il cervello umano (quello “vero”, però, merce ormai rarissima). Possiamo chiamarla razionalità, libertà, intelligenza o come preferite. Attraverso l’esperimento di Feynman, però, ci siamo accorti che non è così. Le particelle elementari (e non solo l’elettrone e il fotone) hanno davanti a loro (ma per loro anche il tempo assume una valenza diversa, come vedremo attraverso la reversibilità delle leggi fondamentali) una situazione estremamente libera. Sono ovunque e hanno infinite possibilità di agire.
Cosa fa il cervello umano? Anch’esso ha teoricamente davanti infinite (o quasi) scelte e solo l’interazione con qualcosa che accade lo costringe a fare una scelta. Esiste una vera differenza tra le possibilità della mente e quelle delle particelle elementari. Direi proprio di no. L’entità “mente” è in fondo una particella elementare, proprio quella che noi associamo alla diversità tra l’essere umano senziente e tutto il resto. Cosa potrei allora concludere? Che gli alieni, ossia i personaggi dotati di una ragione e di una capacità di pensiero, sono già tra noi, anzi noi stessi siamo fatti di loro.
Pensate a quello che chiamiamo “carattere” di una persona. Cosa vuol significare? In parole semplici, la differenza di azione e/o reazione, a parità di libertà o di possibilità, tra un cervello e un altro. Una combinazione tale da far reagire in modo diverso alle stesse sollecitudini. Un’onda e nient’altro. Ebbene, per le particelle elementari capita lo stesso. Anch’esse hanno un loro “carattere”, un certo “spin”, un certo “profumo”, ecc. Cervelli in libertà, onde di probabilità o di possibilità? Senz’altro, ma legate tra loro da un legame ancora negato a noi esseri pensanti (molto rozzi): la capacità di informarsi in tempo reale, di agire a distanza, di adeguarsi a ciò che i fratelli e le sorelle hanno “deciso” di fare. Non illudiamoci troppo a pensare che siamo noi con i nostri esperimenti e le nostre azioni a modificare il comportamento delle particelle elementari. Pensateci bene… sono proprio loro che ci comandano. Vi è veramente bisogno della nostra presa di coscienza per far cambiare stato a una particella? O non è solo uno dei nostri soliti moti di orgoglio?
Va beh… scusate… ho fatto filosofia spicciola che può o non può interessare la descrizione della MQ. Io, nel mio piccolo, la ritengo estremamente utile per poter dire -seguendo le parole di Feynman- : “Ho capito di non aver capito”. Nessuna paura, però… le particelle elementari ce lo insegneranno… prima o poi!
Riprenderemo comunque questi concetti tra non molto.
In ogni modo, la MQ che abbiamo appena cominciato a conoscere, risolve già il problema “storico” sulla natura della luce. Essa, quando non è rivelata si comporta come un’onda (l’interferenza lo prova in modo inconfutabile). Quando viene osservata, o anche solo dedotta, diventa immediatamente una particella, il fotone. E non c’è da meravigliarsi, dato che la sua possibilità di essere ovunque viene annullata. Questa doppia “natura”, nascosta accuratamente dal microcosmo, è stata dimostrata in modo meraviglioso dall’esperimento di Feynman. A questo punto, siamo veramente in grado di apprezzarne la genialità.
Vedremo che la costante di Planck, il principio d’indeterminazione, gli orbitali atomici, il “carattere” delle particelle, la simmetria e la sua rottura, la formazione della materia, le transizioni di fase, il vuoto quantico, ecc., ecc. “aleggiano” più o meno nascoste tra le due fantastiche fenditure.
Un esperimento famoso, ma poco calzante: il gatto di Schrodinger
Quando si parla di particelle attorcigliate (entangled) e di stati sovrapposti di una stessa particella si fa spesso e volentieri riferimento al paradosso o esperimento mentale del gatto di Schrodinger. Il grande fisico riuscì a descrivere un esperimento mentale (non lo eseguì mai veramente, se no… povero gattino!) che trasferisse la sovrapposizione di due stati di una particella (in questo caso un atomo) a un oggetto macroscopico, ossia a un gatto. In tal modo metteva di fronte i suoi colleghi a un assurdità verificabile nella realtà di tutti i giorni.
In realtà, Schrodinger l’aveva proposto solo per provocare e dimostrare come l’estendere il concetto di “stati sovrapposti” richiedeva molta attenzione e portava a soluzioni inaccettabili. In altre parole, lui che aveva ricavato la funzione d’onda, base di tutta la MQ, aveva molti dubbi su una visione completamente probabilistica e non deterministica del mondo (era, insomma dalla parte di Einstein).
Spesso, invece, il suo “gatto”viene presentato come un esperimento atto a dimostrare proprio l’opposto di quanto pensasse lo stesso autore. Problemi comuni nella divulgazione di ciò che non è ben compreso da chi divulga…
Vale, comunque, la pena di descriverlo e utilizzarlo per riassumere molte idee e cercare di capire come possa essere “smontato” in vari modi, pur senza ledere le regole base della MQ.
Riprendiamo le esatte parole del fisico austriaco, che ci chiariscono perfettamente le sue motivazioni : “… Uno può anche costruire casi veramente ridicoli. Un gatto è sistemato all’interno di una camera d’acciaio, insieme a una strumentazione molto particolare (che non può essere raggiunta dal gatto). In un contatore Geiger vi è una piccolissima quantità di una sostanza radioattiva. Così piccola che FORSE, nel corso di un’ora, uno dei suoi atomi decadrà, ma, con la stessa probabilità, potrebbe invece non decadere. Se dovesse decadere il contatore azionerebbe un martello che romperebbe una fiala di cianuro, sufficiente a uccidere immediatamente il gatto. Tuttavia, se la camera non si aprisse per un’ora, uno potrebbe tranquillamente continuare a dire che il gatto potrebbe esser vivo, senza nessun decadimento dell’atomo. La funzione d’onda dell’intero sistema (atomo - contatore - martello - fiala - gatto) direbbe che il gatto si trova in una sovrapposizione di stato (come l’atomo di partenza), ossia sarebbe mezzo vivo e mezzo morto (scusate l’espressione…). Questo è uno dei casi tipici in cui un’indeterminazione ristretta, all’inizio, a un sistema microscopico viene trasferita a un sistema macroscopico che può essere osservato direttamente. Questo fatto deve metterci bene in guardia dall’estendere all’intera realtà le regole d’indeterminazione a cui sono soggette le particelle. Vi è una grande differenza tra una fotografia fuori fuoco e una fotografia di una nuvola o di un banco di nebbia".
Prima di andare avanti, permettetemi una piccola e insignificante modifica, dato che sono uno sviscerato amante dei gatti e degli animali in genere. Io preferirei sostituire la fialetta di cianuro con un bell’anestetico (giustamente dosato, però…) che faccia SICURAMENTE dormire profondamente il gatto per almeno un’ora… Accordato? OK… proseguiamo…

In realtà, il caso del gatto è facilmente attaccabile e “smontabile”. Si sono usati vari modi. Ad esempio, si può dire che la sovrapposizione di stato può avvenire solo in un sistema chiuso (in qualche modo come se la camera rappresentasse un Universo separato dal nostro), mentre invece ciò non è vero e attraverso qualsiasi tipo di radiazione o di sottilissime interrelazioni tra camera e mondo esterno questo non succede e quindi la funzione d’onda collassa immediatamente e il gatto è veramente o vivo o morto anche se noi non possiamo “apparentemente” appurarlo.
Oppure, dire che il gatto non si trova mai nella sovrapposizione di stati perché essa viene rotta già dal contatore geiger, posto tra l'atomo radioattivo e il veleno, che serve appunto a rilasciare il veleno: questa è a tutti gli effetti un'osservazione.
Non dimentichiamo, però, che ancora oggi si pensa a una soluzione ben più affascinante: il gatto è veramente in due strati sovrapposti che esistono entrambi in due Universi separati. In uno il gatto è vivo e in uno il gatto è morto.
Insomma, le implicazioni e le discussioni, non volute dalle stesso Schrodinger, continuano ancora oggi e portano a visioni e teorie veramente straordinarie anche se puramente teoriche e non verificabili con esperimenti “ad hoc”. Ricordiamo, infatti, che le stranezze del microcosmo sono ormai perfettamente verificabili (come abbiamo già visto parzialmente) e usate nella tecnologia più avanzata in tutti i campi della Scienza. Non solo però. Fenomeni come la fusione nucleare all’interno della stella Sole (e delle sue numerosissime sorelle) può avvenire solo e soltanto se certi principi della MQ si verificano. In particolare, l’effetto tunnel, di cui discuteremo senz’altro e che si collegano al principio d’indeterminazione di Heisenberg (QUI), che veramente comanda tutte le danze “microscopiche”.
Resta, però, un dubbio profondo ancora irrisolto. Qual è, e dove e come si stabilisce il confine tra mondo microscopico e macroscopico? L’applicazione del principio d’indeterminazione riesce a risolvere gran parte di questo problema. Ancora più forte è il dubbio sulla effettiva necessità di avere una verifica cosciente della posizione della particella. Basta il contatore geiger (privo di intelligenza) a trasformare l’onda in particella e/o un’apparecchiatura che non ci avverta in alcun modo da che fenditura è passato il fotone, oppure è proprio necessaria una effettiva presa di coscienza del fenomeno? Su questa problematica ancora aperta ci torneremo tra breve nelle conclusioni (preliminari).
Non dimentichiamoci, infine, che la visione non deterministica della realtà è tutt’altro che risolta. Il problema delle variabili mancanti sollevata da Einstein e colleghi sembra riacquistare vigore e un recente esperimento macroscopico sembra aprire nuove visioni della realtà, riportandoci alla celebre onda pilota di de Broglie. Una specie di compromesso deterministico in cui tutta la descrizione della MQ rimarrebbe inalterata, ma sarebbe comandata da una specie di onda materiale che guida le particelle, che non acquisterebbero mai effettivamente lo “stato” di onde ma si adatterebbero all’onda pilota.. Ci torneremo sicuramente sopra… Un esempio molto preliminare? Pensate di avere un liquido che non ha vibrazioni evidenti, ma che è percorso da onde al di sotto della soglia di rivelazione. Fategli cadere una goccia dello stesso liquido. Vedrete la goccia disgregarsi e spostarsi nel liquido spinta solo dall’onda che ha causato. La goccia resta goccia, ma assume le caratteristiche di un’onda.
Prima di passare alle conclusioni preliminari, che riassumono e generalizzano quanto abbiamo visto finora, permettetemi di raccomandare ai più volenterosi un vero e proprio gioco mentale che necessita un grande sforzo logico e interpretativo. Ricordate i famosi giochi di società in cui si prospettavano situazioni del tipo: “Una porta conduce all’Inferno e una al Paradiso. Davanti a ogni porta vi è un guardiano: uno, però, dice sempre la verità e l’altro sempre una bugia. Non sappiamo, ovviamente, chi dei due è il bugiardo e chi è l’onesto. Quale domanda dobbiamo fare a uno qualsiasi dei due guardiani per essere sicuri di andare in Paradiso?” Bene, elevate il gioco mentale a un livello un po’ superiore e potete leggere questo articolo che dimostra che per fare collassare l’onda del gatto non vi è bisogno di avere una diretta coscienza dello stato. Sembra un puro gioco, ma la sua conclusione è di grande interesse…
Conclusioni molto preliminari, ovvero “A ruota libera con la MQ” o ancora “All the MQ you can eat”
Forse, anzi… sicuramente, mi ripeterò un poco, ma, come ormai sapete, questa è una delle mie “strategie” di divulgazione, che molti apprezzano e, quindi, la continuo…
Innanzitutto, fatemi fare una constatazione che non vi è certo nuova. La MQ è nata negli stessi anni della teoria della relatività ed è stata, in modo del tutto analogo, una teoria di riferimento per l’intero XX secolo. Tuttavia, non è mai riuscita a uscire veramente dall’ambito ristretto degli addetti ai lavori. Si potrebbe pensare che ciò sia dovuto alle difficoltà matematiche delle espressioni che governano la funziona d’onda e non solo (piano complesso e cose simili). No, non è sufficiente a spiegare la sua “ghettizzazione”.
Vi deve essere dell’altro che sembra precludere la sua divulgazione. La relatività non è da meno, però è entrata prepotentemente nel linguaggio comune. Oltretutto, la MQ sta alla base di tutte le innovazioni tecnologiche dei giorni nostri, dall’energia atomica alla microelettronica dei computer, dagli orologi digitali ai laser, ai sistemi semiconduttori, alle celle fotoelettriche, alle apparecchiature diagnostiche e di cura di molte malattie. Insomma, oggi riusciamo a “vivere” in modo “moderno” (?) proprio grazie alla MQ e alle sue applicazioni.
La nostra stessa mente, come già avevo accennato prima, sembra basarsi su processi quantistici, comprese le sovrapposizioni di stato, i collassi d’onda e le situazioni di “entanglement”. La vera difficoltà sta nei suoi postulati “controinutitivi” riguardo alla realtà della Natura. Un vero e proprio disagio nell’entrare in un mondo sconosciuto e assurdo come quello di Alice. Non sentiamoci troppo inferiori, però… Gli stessi padri fondatori vivevano questa situazione al limite dell’assurdo. Si poteva veramente credere che la Natura seguisse regole del tutto casuali o, invece, era tutta un’apparenza dovuta alla mancanza di informazioni, di tipo deterministico, ancora mancanti?
Proprio l’ideatore del generalissimo e ultra confermato principio d’indeterminazione (Heisenberg, appunto), diceva: “Ricordo le lunghe discussioni con Bohr, che ci facevano stare svegli fino a tarda notte e ci lasciavano in uno stato di profonda depressione, per non dire effettiva disperazione. Continuavo a girare da solo nel parco e continuavo a pensare che era impossibile che la Natura fosse così assurda come ci appariva dagli esperimenti”. In poche parole, non esiste una realtà definita e descrivibile, ma una realtà oggettivamente indistinta, composta di stati sovrapposti.
Riprendiamone due punti essenziali che abbiamo imparato a conoscere (si fa per dire), ma non certo a capire:
(1) Ogni azione della struttura più fine della materia è caratterizzata solo e soltanto dalla sua probabilità di accadere. Fenomeni del tutto acausali, non deterministici. Ma, soprattutto, dalla indistinta separazione tra l’oggetto osservato, lo strumento di misura e l’osservatore.
(2) E’ possibile che, sotto certe condizioni, ciò che avviene in un certo luogo possa influenzare drasticamente ciò che avviene in un luogo completamente diverso, in modo istantaneo. Ciò porta al fenomeno dell’entanglement”, dell’attorcigliamento di particelle che abbiano avuto un’interazione nel loro passato (ma, ricerche recenti sembrano anche addirittura ammettere “contatti” nel futuro) o che siano nate “assieme”. Esse, benché completamente separate, rappresentano sempre e comunque una stessa entità. Un’azione eseguita su una ha un effetto istantaneo anche sull’altra.
Forse avete già notato il vero problema della MQ. Da un lato la difficoltà di affrontare concetti troppo lontani dalla realtà di tutti i giorni, dall’altro la difficoltà di usare un linguaggio adeguato a spiegare questo mondo così assurdo. La matematica può anche descriverlo, ma mancano le lettere e le parole di questo strano alfabeto. Eccezionale, a questo riguardo, è stato il lavoro di Feynamn con i suoi diagrammi applicati alla QED (che ormai conosciamo abbastanza bene).
E’ interessante riportare un frase di Max Born a riguardo: “La vera difficoltà sta nel fatto che siamo costretti a usare parole del linguaggio comune quando vogliamo descrivere un fenomeno quantistico. Il nostro linguaggio si è formato e si è evoluto attraverso la realtà quotidiana e non può superare certi limiti. La Fisica Classica si è lentamente adattata all’uso di questi concetti. Analizzando i movimenti “visibili” ha definito due “modi” di rappresentazione: particelle e onde. Non conosciamo altro modo per caratterizzare il movimento attraverso immagini concrete. Tutto ciò comporta che si continui a cercare di applicare le stesse descrizioni anche ai processi sub-atomici, dove la Fisica Classica non ha più senso.” In poche parole, la stessa descrizione della MQ potrebbe essere pesantemente influenzata dai nostri limiti descrittivi di tipo “classico”.
Spesso, perciò, gli stessi padri fondatori hanno utilizzano analogie e similitudini per esprimere concetti puramente matematici. Esse, tuttavia, devono esser considerate per quello che sono e non bisogna darle una validità effettiva e concreta. Questo è un problema veramente enorme per il nostro cervello (soprattutto odierno) anche se – forse – avrebbe tutte le basi per usare un linguaggio più adeguato, ma ancora troppo indistinto per essere formulato correttamente: i diagrammi di Feynman, ripeto, sono un tentativo meraviglioso in tale direzione.
Lo stesso Niels Bohr utilizzava analogie grafiche per cercare di sostenere teorie così assurde per il nostro linguaggio classico. Celebre è il famoso vaso bianco che rappresenta contemporaneamente due profili umani neri.

Uno stato di sovrapposizione tra due realtà esistenti istantaneamente (due stati o -magari- due Universi?). Questo tipo di analogia ha influenzato parecchi giochi di illusione ottica e addirittura correnti artistiche…In fondo, lo stesso Picasso, non cercava di inserire anche ciò che non vedeva nell’immagine visibile di una figura.
E’ un vero peccato che questi sforzi interpretativi, unti a quelli più completi e raffinati di Feynman non trovino sbocco nelle scuole in modo da preparare adeguatamente i giovani a “balbettare” le prime parole quantistiche e a iniziare un linguaggio primitivo che gli permetterebbe, oggi, di capire, almeno parzialmente la realtà di Alice. E non solo subire passivamente le più meravigliose applicazioni tecnologiche che ormai sono parte integrante del loro corpo fisico. Vere e proprie “appendici” che, però, agiscono inconsciamente, indipendentemente da qualsiasi comando mentale. Riflessi incondizionati e nulla più…
In fondo, de Broglie avanzò la sua ardita ipotesi proprio seguendo le simmetrie della Natura visibile. Non fece che associare alla materia in genere ciò che capitava alla luce. In breve: se la luce si manifesta sotto un duplice aspetto, ondulatorio e corpuscolare, perché non pensare che anche la materia segua la stessa regola? Basta associare a ogni corpuscolo di materia un’onda di determinata lunghezza, cioè un fenomeno esteso allo spazio che circonda la particella. La natura dualistica (particella-onda) si applica a tutte le particelle, come elettroni, atomi e altre entità in movimento.
Resta, però, aperto il problema di fondo (ancora oggi tema di discussione e di interpretazione) di cui abbiamo accennato. L’onda di materia che comanda la particella può essere deterministica, e quindi ancora sconosciuta nella sua reale struttura (in linea con l’idea di Einstein) o, invece, una rappresentazione diversa della stessa particella e quindi seguire le regole della completa acausalità (scuola di Copenhagen).
In un modo o nell’altro, si deve comunque concludere che la luce o un fascio di elettroni, non sono altro che un “treno” di onde elettromagnetiche, ma anche un getto di “proiettili” come nell’esperimento della doppia fenditura.
Pur rimanendo in questa ambiguità di fondo, Schrodinger formulava l’equazione che descrive perfettamente ogni proprietà ondulatoria della materia, attraverso la sua funzione d’onda. Essa permette di descrivere ogni singolo comportamento e, soprattutto, di calcolare la distribuzione di probabilità di trovare una particella all’interno dell’onda associata. Una matematica sopraffina che però non annulla il fatto che lo stesso Schrodinger non credesse alla effettiva concretezza di questa rappresentazione. Tutto e il contrario di tutto (concettualmente), ma descritto nello stesso identico modo.
Tuttavia, la sua equazione conferma chiaramente quanto illustrato precedentemente dall’esperimento di Feynman: una particella può occupare TUTTE le possibili posizioni all’interno dell’onda associata. Occupando tutte le possibili posizioni non ha più un luogo effettivo di esistenza e nemmeno una direzione. Annulla, automaticamente, qualsiasi possibile previsione sul suo futuro se non in termini puramente probabilistici (la QED è sempre più comprensibile… non vi pare?). L’onda pilota o una variabile nascosta non cambia l’azione della Natura e la sua descrizione probabilistica.
Ancora una volta si ricade nel principio di Heisenberg… In meccanica classica, l’essenza deterministica permette automaticamente di prevedere il futuro se si hanno informazioni esatte della posizione e della velocità di una particella. Ricordiamo, a riguardo, che i primi metodi matematici che hanno permesso il calcolo di un’orbita di una particella “planetaria” si basavano (e si basano ancora) sulla conoscenza di almeno tre posizioni e tre velocità, tali da permettere la soluzione di un’orbita caratterizzata proprio da sei incognite. Troppo facile per le particelle microscopiche.
La concezione probabilistica porta inesorabilmente al principio d’indeterminazione, insito in tutto il microcosmo: o si conosce la posizione o si conosce la velocità. Conoscere entrambe con accuratezza è impossibile, altrimenti si localizzerebbe la particella e l’onda collasserebbe. E torniamo nuovamente al punto di partenza. Che vi sia una causalità iniziale (del tutto incognita) o non vi sia per niente. In poche parole, l’esperimento della doppia fenditura illustra perfettamente tutte le problematiche della MQ.
Vale la pena riflettere sulla drammatica situazione emotiva di Einstein. Lui che stava dando alla realtà fisica una rappresentazione perfettamente deterministica, si è trovato coinvolto in una rappresentazione che portava alla completa acausalità della Natura. Egli stesso diceva: “Le teorie quantistiche sulla radiazione mi interessano (QUI e QUI) moltissimo, tuttavia non vorrei essere costretto ad abbandonare la causalità stretta senza cercare di difenderla fino allo stremo. Trovo del tutto intollerabile che un elettrone esposto a una radiazione SCELGA di sua spontanea volontà non solo il momento di “saltare”, ma anche la direzione del “salto”. In questo caso preferirei fare il croupier in un casinò piuttosto che il fisico!”.
Eppure, nessun fisico ha contribuito come Einstein alla creazione della Fisica Quantistica… Ciò che lui ha dimostrato su di lei (e per lei) bastava e avanzava per una carriera scientifica di altissimo livello (non per niente gli è valso il Nobel). E’ quindi facilmente comprensibile il suo dramma esistenziale, che non l’ ha mai abbandonato fino alla morte. Un misto di rabbia, di orgoglio ferito, di fiducia incrollabile e di disperazione nel non riuscire a dimostrare le proprie certezze.
Mi ricorda molto uno dei grandi ciclisti dei miei tempi: Felice Gimondi. Ha vinto un Tour de France al primo anno di professionismo. Era bravo in salita, a cronometro, e in ogni situazione. Davanti a lui si prospettava un futuro straordinario, da campione indiscusso. Una specie di Einstein con la sua teoria della relatività. Dopo un anno o due, però, ecco comparire la figura, quasi assurda come la MQ, di Eddy Merckx. Un vero alieno, capace di fare nel ciclismo ciò che nessuno aveva mai fatto e forse non riuscirà mai a fare nemmeno in futuro. Era apparsa davanti a Gimondi la sua MQ. Sebbene fosse bravissimo in tutti i campi, era sempre e comunque superato dal “mostro” belga. A volte, raramente, Gimondi vinceva anche, ma non faceva che rendere ancora più grande la figura del rivale inarrivabile.
Questo mix di frustrazione, esaltazione, speranza e delusione, innovazione e conservatorismo, ha permeato tutte le grandi menti che hanno fatto nascere la MQ. Un’opera quanto mai corale e non certo un puzzle di idee singole. Ognuno, quasi senza volere (a volte addirittura contro i suoi stessi scopi) non faceva che mettere un mattone in più a una costruzione che stava diventando un incredibile grattacielo dalle basi sempre più solide, inattaccabili.
Forse, proprio questo modo veramente unico nella storia della Scienza di formulare una teoria sempre più completa e raffinata, da parte di molte menti superiori, potrebbe far capire che la MQ è qualcosa di veramente insita nella mente umana, ma che ha una difficoltà estrema nell’ uscire allo scoperto. Sicuramente, la conoscenza del linguaggio della Fisica Classica ha fatto fare enormi passi in avanti, ma non così lontani dalle intuizioni quasi inconsce di Democrito ed Epicuro. In poche parole, la mente deve essere addestrata ad assecondare una realtà solo storicamente e culturalmente assurda.
Quanto più entriamo nell’essenza stessa della MQ e dei suoi principi, tanto più l’esperimento della doppia fenditura acquista un’importanza fondamentale e completa. Un vero capolavoro scientifico, manifesto stesso del futuro dell’intelletto umano.
Richiamiamone il concetto base sotto una visione ancora più generale. La visone probabilistica, il principio di sovrapposizione degli “stati”, quello d’indeterminazione, non possono che vietare a qualsiasi entità microscopica di avere una traiettoria definita. E’ una “ovvia” conseguenza che non può più essere smentita. Nell’esperimento delle due fenditure tutto ciò è rappresentato perfettamente. Il singolo fotone (o elettrone o entità microscopica o -se preferiamo- qualcosa di comparabile alla grandezza di Planck) percorre TUTTE le possibili traiettorie comprese tra la sorgente e il rivelatore (ricordiamoci sempre la QED e il suo linguaggio).
Percorrendo tutte le possibili traiettorie, il fotone incontra anche le due fenditure e, dopo essere passato da entrambe, interferisce con se stesso producendo le bande chiare e scure dell’interferenza (la QED ce l’ha spiegata benissimo con le ampiezze di probabilità). Come diceva Bohr: “Quando il fotone passa attraverso la fenditura A, ciò determina un certo mondo possibile: il mondo A; quando passa attraverso B costruisce il mondo B. Nel caso della doppia fenditura il concetto base è che entrambi questi mondi coesistono, uno sovrapposto all’altro”. Chiudendo un fenditura distruggiamo un intero mondo… So, benissimo, che risulta quasi impossibile credere che un unico oggetto possa avere la capacità di essere nello STESSO momento in due luoghi diversi (simultaneità, povero Einstein…), ma questo è proprio ciò che avviene e gli esperimenti lo dimostrano senza ombra di dubbio!
A questo punto, si ricade sul dubbio che già abbiamo formulato e che è stato evidenziato nel caso del povero gatto di Schrodinger. La realtà obiettiva del microcosmo ( che è pur sempre ciò che compone l’Universo) dipende oppure no dalle “scelte” effettuate da chi osserva un esperimento? La visione più “semplice”, da un certo punto di vista, sembra dimostrare che se l’osservatore decide di rivelare la posizione di una particella, questa cessa istantaneamente di esistere nella sua dimensione velocità e viceversa. Tutto si riduce, quindi, alla definizione di osservatore e su questo siamo ancora in alto mare, anche se Feynman ne dà una spiegazione abbastanza ambigua ma condivisibile: cambia soltanto l’evento. Un modo, però, di girare furbescamente intorno al vero problema di fondo.
Tuttavia, la faccenda si può affrontare in vari modi. Primo fra tutti quello relativo alla scuola di Copenaghen. Il ruolo dell’osservatore è qualcosa che non può esser scollegato da ciò che si osserva. In altre parole, colui che osserva e ciò che si osserva fanno parte dello stesso sistema. Le scelte del primo determinano le caratteristiche del secondo. Ciò significa che la materia, prima di essere misurata, vive in uno stato sovrapposto. Solo l’intervento dell’osservatore produce la cosiddetta “riduzione della funziona d’onda” o collasso che dir si voglia. Solo così lo stato sovrapposto si presenta come entità materiale con determinate caratteristiche.
Questo paradigma, ancora del tutto aperto alle speculazioni sia sperimentali che teoriche (esperimento ben difficile da eseguire dato che qualsiasi esperimento comporta l’intervento, prima o poi, di un osservatore) ci fa capire meglio perché Schrodinger, proprio il “papà” della funzione d’onda, abbia formulato il paradosso- non paradosso del suo gatto.
Come abbiamo più volte notato, chi gioca un ruolo fondamentale è sempre il principio di Heisenberg, sempre e soltanto lui, il vero pilastro centrale dell’intera costruzione.
Vale, quindi la pena accennare alla sua estrapolazione più sconvolgente per l’intero Universo. Esso non vale solo per velocità (meglio dire “quantità di moto”, dato che la massa non è poi così costante come sembra. La relatività di Einstein deve convivere con la MQ, ricordiamocelo sempre), ma anche per altre grandezze, ancora più decisive: l’energia e il tempo. In parole povere, ciò comporta che per tempi brevissimi (e ci riferiamo sempre a grandezze di Planck, in questo caso il suo tempo) la legge di conservazione dell’energia può essere violata. Qualcosa di veramente assurdo (nuovamente), dato che tutti sappiamo bene che nel “nostro” mondo niente si crea e niente si distrugge. Quante volte lo abbiamo ripetuto!?.
Ancora, una volta, però, le cose, su scala microscopica, non funzionano così semplicemente. Lo stato di indeterminazione che esiste tra energia e tempo può provocare (anzi provoca sicuramente) fluttuazioni di energia di un certo sistema in intervalli brevissimi. Intervalli di miliardesimi di trilionesimi di secondo, in cui un elettrone e il suo amico-nemico positrone possono comparire improvvisamente dal nulla (anche questo la QED ce lo ha mostrato abbastanza chiaramente), unirsi e svanire. Anche le leggi più certe diventano indeterminate.
Non crediamo che sia solo teoria, dato che ormai gli esperimenti di laboratorio l’hanno confermato senza ombra di dubbio. Qualcuno potrebbe dire: “Sì, va bene, ma sono fluttuazioni così piccole e brevi che non possono certo influire sulla realtà dell’Universo”. E, invece, com’è facilmente prevedibile, influiscono e come! Basterebbe pensare solo all’effetto tunnel (che tratteremo a parte), capace di far vivere una stella.
Il vuoto è come un enorme oceano che, visto da grande altezza, sembra essere perfettamente calmo e uniforme. Ma se scendessimo su una barchetta ci accorgeremmo che è solcato da onde continue e anche violentissime. Lì, le particelle quantistiche possono comparire e scomparire dal nulla e nel nulla. Siamo tornati alle fluttuazioni del vuoto, al mare di Dirac, all’esistenza dei positroni, alle asimmetrie, alla nascita dell’Universo e all’inflazione. La MQ è un serpente che si morde la coda, continuamente. Sì, possiamo davvero concludere che proprio lo spazio che sembra vuoto è il luogo dove avvengono i fenomeni fisici più violenti! Proprio le sue caratteristiche potrebbero costringere i buchi neri a restituirci l’energia apparentemente ingoiata e cancellata.
Direi che possiamo terminare qui queste considerazioni sparate un po’ a raffica, come gli elettroni-proiettili della doppia fenditura. Hanno solo cercato di dare un quadro concettuale il più generale possibile e costruire “ponti” abbastanza stabili con quanto abbiamo descritto in altri articoli e, in particolare, nell’esposizione della QED. Spero di aver fornito un piccolo aiuto in tal senso, anche se potremmo parlare e scrivere per ore e ore e gireremmo sempre attorno ai punti e ai dubbi fondamentali.
Ciò che chiedo a chi comincia a socchiudere la porta in cui è passata Alice è di comunicare le sue sensazioni e le sue emozioni ai più giovani. Il mondo futuro è sempre più nelle mani della MQ ed è giusto che i giovani si formino con questi concetti, in modo analogo a ciò che fanno con quelli di forza, velocità, accelerazione, momento angolare, ecc. ecc. della fisica classica e della relatività.
Se non vuole (o non può) più farlo la scuola, cerchiamo di farlo noi. Inoltre, cosa ancora più importante, facciamo in modo, nel nostro piccolo, che i giovani riescano finalmente a capire che esistono indipendentemente dal fatto che si siano ripresi con il loro stesso cellulare. Facciamo parte della Natura, governata dal microcosmo e dalla MQ, esistiamo comunque. Il cellulare ci regala una realtà virtuale, utile e straordinaria proprio perché sarà sempre più legata alla MQ e -forse- alle regole e al linguaggio ancora nascosti nel nostro cervello. Ma è un’imperfetta e parziale rappresentazione semplicistica della Natura. Non è la Natura e nemmeno la realtà! E’ solo un’esecuzione di giochi privi di qualsiasi sforzo mentale. Un modo di rappresentarla che può essere utile a chi comprende la Natura, ma che mai potrà essere la Natura. In questo contesto, credetemi, è molto meno assurda la MQ…
Se smettiamo di esistere, ma diventiamo anche noi solo una rappresentazione virtuale, che senso avrebbe mai comprendere ciò che esiste attorno a noi. Ma anche, e soprattutto, potremo mai conoscerlo? Probabilmente smetterà di esistere anch’esso. Almeno per il nostro avanzo di cervello rattrappito e incapace di agire in modo autonomo. La scuola di Copenaghen dice proprio che siamo un tutt’uno con la materia e, se manca l’osservatore-attore, crolla l’intero sistema.
Insomma, la MQ non solo come Scienza ma come scuola di vita!
QUI una semplice storia della Meccanica Quantistica raccontata da Einstein e Bohr, attraverso le interazioni umane e professionali di alcuni dei grandi scienziati che l'hanno fatta nascere e crescere.
QUI la dualità onda-particella spiegata dal nostro amico Curiuss grazie ad un ornitorinco e un'attrice svizzera


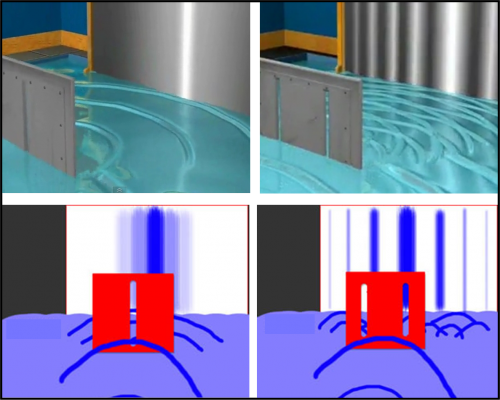




37 commenti
bello questo manuale, da incorniciare
"Bisogna riflettere bene su questa conclusione che, in pratica, fornisce la migliore descrizione della differenza tra onde e particelle. Queste ultime non mostrano alcun fenomeno di interferenza e la probabilità di trovare una particella in un certo punto, con entrambe le fenditure aperte, è esattamente la somma delle probabilità di trovare una particella in quello stesso punto chiudendo una fenditura alla volta (N12 = N1 + N2)"
Ciao Enzo non mi torna molto questo pezzo, visto che le particelle (ad esempio gli elettroni) con entrambe le fenditure aperte provocano interferenza.
caro SMA,
fa parte del modo molto descrittivo che ho usato: fino a questo punto non so ancora come si comportino gli elettroni... e tra proiettili e onde quella descritta è proprio la differenza più LOGICAMENTE decisiva.
Questa è la differenza concettuale che sarebbe ovvio aspettarsi tra comportamento di particelle e onde... Prosegui e vedrai...
Bellissimo questo articolo, sopratutto molto chiaro per la mia mente ottusa! Grazie, aspetto il seguito.
grazie Adriano!!!!
Grazie Enzo. Inutile che ti dica come si chiaro nelle spiegazioni.Del resto lo sai già.
Me lo sto gustando piano piano....
Complimenti Enzo davvero un bel lavoro un'articolo che conservero e rileggero spesso volentieri aprofitto per rinnovare la stima e ammirazione che ho nei tuoi confronti.
Grazie!
Caro Enzo, davvero uno splendido manuale per chi vuole avvicinarsi alla MQ.
Un articolone che suscita un sacco di riflessioni e domande.
Mi limito a porne una sola, riguardo all'esperimento “Aspect”, mi chiedevo se una simile situazione possa verificarsi spontaneamente in natura.
In pratica, se la sorgente è una stella e il fascio luminoso in una certe direzione subisce una certa deviazione (al di là del fenomeno che genera tale variazione.... per esempio un forte campo magnetico), è possibile che tale deviazione interessi istantaneamente anche la luce emessa in altre direzioni, oppure il fenomeno è limitato solo ai fotoni emessi dallo stesso atomo?
Paolo
Chiaro e meticoloso come sempre...
caro Paolo,
dici molto bene... L'importante è però che le due particelle siano entangled... Due qualsiasi fotoni non è detto che lo siano. L'esperimento li costruisce, ma la Natura non ce lo dice quando lo fa.. Resta, però, il fatto che la luce di una stella che viene separata da una lente gravitazionale potrebbe essere osservata come nel caso delle due fenditure. E, quindi, guardando ciò che è successo miliardi di anni fa (vicino alla stella) potremmo influire su quello che vediamo oggi. Purtroppo il lungo percorso rende difficile l'interferenza, ma teoricamente si potrebbe rilevare... Ogni singolo fotone è collegato a se stesso... la doppia fenditura è un fenomeno universale e su tutte le scale. Se ricordi, la stessa inflazione impone che vi sia un entanglement tra particelle che non potrebbero mai avere un contatto. L'hanno avuto alla loro origine e si sono comportate nello stesso modo ai due estremi dell'universo, da cui l'omogeneità dell'Universo su grande scala.
Perfetto, caro Prof. ! Grazie per la cortese attenzione.
caro Iginio,
sei riuscito a vederlo tutto? Si vede che basta che ogni tanto lo rinfreschi... (forse è troppo lungo...). Buona lettura
Grazie ancora! Ma come fai ad esserecosì chiaro?!!
ma dai Iginio!


La verità è che è la fisica è chiara, ma certe persone non la amano abbastanza e la complicano... Basta farsi trasportare da lei con umiltà e semplicità... senza cercare di usarla per mettersi in mostra
Comunque sono veramente contento che ti parli con semplicità... si vede che ti considera un amico!!!
Grazie e complimenti, davvero un articolo emozionante!
Ciao Vincenzo,
Ci sono bollicine piccolissime,che scorrono veloci come quelle dentro un bicchiere di spumante,sono tutti gli attimi della vita che si rincorrono e spariscono subito dopo.
Ce ne sono di più grandi che ne contengono altre più piccole,di grandissime che ne contengono di grandi.Tutte hanno il proprio tempo ,poi scoppiano e spariscono.Quel che rimane è l'acqua e il sapone,dove nasce tutto.Io spaziotempo è l'acqua e sapone.Pure noi che abbiamo una struttura materiale,siamo un modo diverso di essere spazio. Lo spazio è la grande madre di tutto ciò che esiste,è lui che crea/genera l'energia e la trasforma in entità multiformi.Quello che secondo me si dovrebbe considerare, nel guardare alla MQ,è che a livello fondamentale il tempo non ha direzione,perché proprio non esiste.Se guardiamo la cosa in maniera alternativa,i dualismi posizione/velocità -tempo/ energia ed altri ancora vanno considerati in maniera diversa.Lo spazio è come il fondo del mare,da dove nascono le bollicine,ma lui è temporalmente immobile,generando eventi genera anche il tempo che accompagna l'evento,a meno che l'infinito non prosegua verso un infinitamente piccolo. Gli eventi non sono ancora definiti,il fenomeno è ancora in itinere,a volte si trova questo pezzo a volte l'altro,per misurare il movimento abbiamo bisogno del tempo,se manca il tempo non c'è movimento,il tempo da solo è una chimera,non ha senso.Proviamo a fare una capriola,la particella può essre ovunque,ma è la funzione d'onda che ci permetterà di individuarla con precisione,come pescare un pesce che passava di là o che si materializza là?.Il mio interesse per la scienza è nato molto tardi,e da qualcosa di poco scientifico, mi chiedevo:"Perché a me capita di fare dei sogni dove "vedo"qualcosa che capiterà poi,e che non ha nessun rapporto di conseguenza logica su ciò che ho vissuto?Tempo,grande sconosciuto.Il cevello è quantistico?Si,hai ragione,il figlio non può che assomigliare al padre.Un modo per pensare alla simultaneità?Semplice,levagli il tempo,e i conti tornano.(Se soffri d'insonnia mi ringrazierai).Ciao,
Gianni Bolzonella
caro Gianni,
non soffro d'insonnia, ma mi sveglio prestissimo (ma di sera vado anche a letto molto presto...).... sempre che esista il presto e il tardi... Le tue parole mi toccano abbastanza e le sento vicine. In ogni caso ti ringrazio per l'interesse...!!!!
Ho una domanda il bosone di higs si stima sia grande come 5 fotoni come andrebbe a interagire, e possibile che non interagisca se meno di 5?grazie
caro Efisio,
ammetto che non capisco bene la tua domanda. Il fotone non ha massa e questo fatto implica proprio che non abbia interazioni con il bosone di Higgs o quantomeno non riceva massa da lui. Il discorso delle 5 volte il fotone non capisco cosa voglia dire (il fotone ha solo massa dinamica, ma essa è nulla in quiete). Inoltre, non abbiamo mai discusso del modello standard e quindi questo argomento è ancora lontano dal nostro corso divulgativo...
Grazie per questo bellissimo e interessantissimo articolo letto di mattina presto
grazie a te Fabio per dedicare il tuo tempo (mattutino) alla scienza. Ogni commento di questo tipo è una boccata d'aria fresca!
Grande sei riuscito a far assimilare a una come me tutto questo.
Scusa l'ignoranza ma vorrei sapere se hai scritto altre cose. Sto cominciando a leggere il libro di Lanza sul biocentrismo e le tue spiegazioni mi sono state di un utilità indescrivibile.
P.S. Sono una sessantenne mooooolto ignorante
Sonia
cara Sonia,
tu non sai quanto ci hai allietato con il tuo commento! Per me, poi, tu sei una ragazzina (sto toccando i 72...) e ho deciso di dedicare quello che mi resta (fino a che il cervello funziona) a divulgare ciò che ho avuto la fortuna di toccare con mano dopo 40 anni di ricerca astrofisica. Sono aiutato da amici validissimi che toccano svariati temi della ricerca e amiamo spesso condire il tutto con molta ironia (una parola ormai scomparsa), come puoi vedere nei quasi 2000 articoli pubblicati. Ultimamente abbiamo "rivisto" le vite di Colombo e Napoleone, mischiando la realtà con la fantasia. Attraverso la meraviglia che è l'Universo (il Tutto) si sconfina facilmente nell'arte, nella letteratura, nella biologia e via dicendo. Non ultima (due giorni fa) una rivisitazione del 5 maggio, scritta da un altro giovincello, assecondando la "nuova" storia di Napoleone.
Tornando a cose più serie, negli approfondimenti, riga in alto della homepage, puoi trovare argomenti tra i più caldi e attuali, tra cui ancora la meccanica quantistica, la relatività generale e ristretta, l'ottica, la meccanica classica, e molto altro... Non perderti, anche, storie di vita e di scienza nei racconti di Astericcio e nella fisica di Papalla (tasto "rubriche" sempre in alto). Insomma di tutto e di più...
Cara ragazzina, speriamo proprio che non ci lascerai più...

Un caloroso benvenuto anche da parte mia, cara Sonia, e da parte di tutti gli altri autori!
Aggiungo solo un paio di informazioni importanti all'ottima panoramica che ti ha fatto il nostro Enzone (sai, è talmente preso dalla sua vulcanica attività divulgatrice che va un pochino aiutato a ricordarsi tutto )...
)...
la prima è che puoi chiedere aiuto a me per avere informazioni sui temi trattati (ma vedo che lo sai già perché ricevo in questo momento la tua mail e tra poco ti rispondo), la seconda è che, tra gli argomenti da non perdere, Enzo ha finto di dimenticarsi di segnalarti la vera storia di Vin-Census, che sto pubblicando io, assumendomene tutte le responsabilità, nonostante il suo parere contrario!
Buona lettura e buon divertimento!
Eh sì, cara Sonia, senza l'aiuto di veri ragazzini (?) a volte mi perdo...
Da molto tempo leggo libri e articoli divulgativi su questi argomenti ma mai finora avevo trovato una esposizione tanto chiara di questi fenomeni. Apprezzo in particolare la tua tecnica di ripetizione, di riproposizione dei concetti secondo angolazioni diverse, di prendere in considerazione tutte le interpretazioni e "fraintendimenti" che si generano nel discutere di questi concetti. Grazie veramente per aver messo a disposizione di tutti questo bellissimo lavoro.
Benvenuto Luigi!
Se hai un debole per la MQ spiegata in modo semplice, nel caso tu non lo abbia ancora scoperto, in QUESTA PAGINA degli approfondimenti troverai di tutto di più.
Buon divertimento!
caro Luigi,
già ieri ti avevo scritto un commento, ma poi si vede che non l'ho spedito... Ti dicevo un GRAZIE enorme e sono proprio commenti come questo che mi danno la forza e la volontà di proseguire nella mia modesta ma sincera opera divulgativa. Continua a seguirci, il nostro Circolo ha bisogno di persone che ancora hanno voglia di pnsare e di imparare!!!
Ho letto con vero interesse l'introduzione alla meccanica quantistica e mi è sorta almeno una domanda che mi vergogno un po' a dire per quanto potrebbe essere stupida.
Se le particelle sub atomiche fanno cose "impossibili" al di fuori di ogni logica razionale, sarebbe in teoria possibile "indirizzarle" a compiere azioni altrettanto impossibili come ad esempio trasferire oggetti da un posto ad un altro?
Mi rendo conto che la domanda sia poco intelligente ma visto che stiamo parlando di cose impossibili e del mondo di Alice......
Alessandro
caro Alessandro,
la domanda non è affatto stupida e gli studi si stanno già facendo con risultati promettenti...
caro Vincenzo,
sono un settantacinquenne, ignorante all'ennesima potenza e anche poco intelligente, tanto che ho un po' di timore ad intromettermi in un discorso di questo genere, scusa la doverosa premessa.
Ho letto il tuo, pregevole, articolo di "introduzione alla meccanica quantistica". Ho iniziato a leggere per curiosità, l'argomento mi ha sempre affascinato ma mi sono sempre tenuto rispettosamente alla larga.
Ho iniziato a leggere per curiosità, convinto di non capirci niente, poi ne sono stato catturato e non ho smesso fino in fondo affascinato come da un thriller. Lo strano è che mi sembra di averci capito qualcosa. merito sicuramente del tuo linguaggio.
Quello che più mi affascina di questo argomento non è tanto la possibilità di usare questo "entanglement" a fini pratici (cosa molto importante) ma la possibilità di capire meglio come funziona il nostro universo e come esso possa essere un "organismo unico" dove tutto e collegato istantaneamente; anche per trarne insegnamenti morali. Inoltre tutto ciò rafforza la mia speranza che noi possiamo fare parte di un unico grande disegno.
Scusa la mia ingenuità e, comunque, grazie.
caro Lido,
il tuo commento mi riempie di gioia e di forza! Sono io che ringrazio te per aver provato, aver voluto continuare e soprattutto per essere riuscito a superare la paura "mediatica" del sapere. Oggi sembra che imparare ragionando sia un peccato o un gesto inutile. Forza caro coetaneo (anch'io ho 75 anni!) e che il 2020 possa riservarci ancora tante possibilità di aprire quel paracadute che è il nostro cervello.
Buon anno e fatti sentire!!!
Magnifica trattazione sulla MQ!
Leggo poi nelle Sue risposte un paragone veramente interessante: paracadute e cervello.
Grazie per avermi dato emozioni!
In questo difficile periodo le emozioni non bastano mai.
Le auguro tutto il bene!
Un caro saluto
Eliana
cara Eliana,
intanto diamoci del tu... in questo gruppo di persone con la voglia di pensare e riflettere non ci sono livelli diversi. E poi sono io che ti ringrazio per la passione dimostrata... tu, come tanti ormai, date un senso al mio lavoro!
Caro Vincenzo
Penso che per alcune persone colte come te non dovrebbe passare il tempo.
Bisognerebbe poter aggiungere giorni ai giorni perché possano scrivere ed esercitare la loro gentilezza a lungo!
Buon pomeriggio
Eliana
Dai Eliana, non mettermi in imbarazzo Io penso di fare solo il mio dovere, dopo che la Scienza mi ha dato tante possibilità di conoscere fatti, persone e luoghi. Non posso che cercare di ricambiare... e, inoltre, di tenere attivo il cervello (finché riesco...).
Io penso di fare solo il mio dovere, dopo che la Scienza mi ha dato tante possibilità di conoscere fatti, persone e luoghi. Non posso che cercare di ricambiare... e, inoltre, di tenere attivo il cervello (finché riesco...).
Sto leggendo il libro di Feynman sulla QED ma senza le Sue lezioni ci avrei capito sicuramente molto meno. Feynman sarà anche bravo a spiegare ma ci vuole Lei per capirci qualcosa di più.
Una domanda... il fatto che la probabilità di trovare l'elettrone in un determinato punto dello spazio vari secondo un'onda significa che mettendomi di fronte ad una lampada accesa e tenendo gli occhi chiusi (in modo da non funzionare io stesso come il rilevatore che rompe le uova nel paniere...) la probabilità che un fotone mi tocchi il naso varia con continuità da un valore minimo e un valore massimo, ovvero che in determinati istanti è maggiore e in altri è minore?
La frequenza di quest'onda di probabilità coincide con la frequenza legata al "colore" del fotone che viene emesso dalla lampada accesa, per cui la frequenza con cui varia l'onda di probabilità della luce rossa è minore di quella con cui varia l'onda di probabilità della luce blu?
Cordiali saluti,
Massimiliano