Categorie: Matematica Relatività
Tags: compasso da campo la vera storia Mascheroni Napoleone Problema di Napoleone strategia teorema di Napoleone
Scritto da: Vincenzo Zappalà
Commenti:15
La vera storia di Napoleone, un grande matematico che adorava la geometria ** (con tanti bei quiz facoltativi…)
Questo articolo è inserito nella sezione d'archivio "La Vera Storia di..."
Un dittatore? un tiranno? Un guerrafondaio? Un uomo assetato di potere? E se, invece, fosse stato solo un grande matematico assetato di sapere e con il sogno, mai raggiunto completamente, di mettere in pratica le sue figure geometriche e le costruzioni che ne derivavano? Ricordiamo che la sua opera è stata apprezzata disinteressatamente da scienziati come Laplace e de La Grangia. Svariati sono stati i suoi quiz, così come fondamentale è stato il suo problema e il suo teorema. Quest’ultimo permette di individuare graficamente e velocemente il punto di Torricelli-Fermat (e dico poco…). Insomma, attraverso documenti segreti e ricerche mirate, esce fuori un personaggio ben diverso da ciò che si pensa di conoscere. Sembra, addirittura, che Einstein sia andato spesso ad Austerlitz durante la stesura della sua Relatività Ristretta… La storia è proprio un telefono senza fili… la verità fa in fretta a confondersi…
Io pur vidi coll’invitta mano,
Che parte i regni e a Vienna intimò pace,
Meco divider con attento guardo
Il curvo giro del fedel compasso.
Lorenzo Mascheroni
Piccolo, di carattere introverso e dalla volontà di ferro, nascosta dietro un ingannevole velo di timidezza, Napoleone capi fin da subito di avere due grandi sogni nella vita: la matematica (la geometria in particolare) e la possibilità di dimostrare i suoi teoremi in campo aperto, senza restrizioni di spazio.
Il foglio di carta e la matita o la penna, gli andavano stretti, dato che le sue ardite costruzioni erano estremamente complesse e intricate. Solo lo spazio aperto e senza confini, poteva mostrare l’eleganza e la genialità delle sue visioni innovative.
Per sopravvivere, dando sfogo al suo ingegno, dovette trovarsi un lavoro sicuro, che gli permettesse di guadagnare qualcosa e di avere, nel contempo, anche molto tempo a disposizione. L’ideale era entrare nell’esercito. Ogni tanto doveva anche combattere, ma con i vari trucchi che la sua intelligenza sapeva scovare in ogni frangente, riusciva facilmente a ritagliarsi lunghi tempi in cui dare via libera al suo pensiero, sparendo dalla circolazione e rifugiandosi in luoghi particolarmente tranquilli e sicuri.
Per non rischiare di essere scoperto e di passare per le armi come disertore, era riuscito a diventare indispensabile nelle operazioni di tiro. Come sapeva puntare il cannone lui non lo sapeva fare nessuno (in fondo bastavano poche nozioni di trigonometria sferica), per non parlare delle traiettorie curvilinee che imprimeva ai proiettili che riuscivano a entrare nelle case senza nemmeno bussare alla porta.
Ciò gli permise di non avere mai incarichi di prima linea e di godere dell’appoggio dei suoi diretti superiori. Era diventato indispensabile e si cercava di non sprecarlo per azioni rischiose o troppo faticose. Insomma, poteva dare sfogo al suo sogno in relativa pace e libertà.
Una delle sue fissazioni giovanili era quella riguardante il compasso. Era convinto che tutta la geometria euclidea si potesse descrivere attraverso questo semplice strumento, senza l’aiuto di alcun righello. Nelle varie campagne militari, che cominciò anche a guidare in prima persona, proprio per avere la massima libertà, conobbe illustri scienziati nei vari paesi che andava conquistando. Con loro poteva, finalmente, discutere dei suoi problemi più importanti (l’ambiente militare non era proprio l’ideale per quello scopo).
In Italia, trovò un matematico, poco considerato e a prima vista un po’ “schizzato”, che aveva a disposizione tutto il materiale necessario e anche nozioni, accurate e quasi segrete, riguardo agli studi antichi (ricordiamo che Napoleone era praticamente un autodidatta nelle questioni di matematica superiore).
Trattavasi di un certo Lorenzo Mascheroni, insegnante di algebra in quel di Pavia: l’uomo giusto al momento giusto. Napoleone, senza nemmeno volerlo, aveva acquistato potere e il tempo libero poteva ormai prenderselo apertamente senza rischiosi stratagemmi. Mascheroni aveva amore puro per il compasso e Napoleone non ebbe difficoltà a spingerlo ancora di più verso quel modo eccezionale di descrivere le più diverse costruzioni geometriche.
Il compasso era per Napoleone anche un’arma fondamentale per finire in fretta le guerre e tornare ai suoi studi. In fondo bastavano due fanti ben addestrati, uno con una corda legata a un picchetto da poter fissare per bene, in qualche punto scelto adeguatamente, e un altro che potesse distenderla fino alla lunghezza desiderata. Di soldati adatti allo scopo ne aveva a iosa. La coppia con la corda venne quasi subito chiamata “compasso da campo” e le strategie che ne facevano uso erano quasi fantascientifiche per un ambiente, quello militare, che non brillava per avversari alla sua altezza “geometrica”.

Passò quasi inosservato il primo problema che Napoleone pose a Mascheroni per tastarne le capacità. L’ormai generale fu sorpreso da quanto rapidamente il suo “collega” riuscisse a risolverlo. Un perfetto collaboratore (e se lo portò anche a Parigi).
Desideriamo proporvelo, dato che è alla portata di qualsiasi ragazzo (e adulto) di buona volontà.
Il problema è: dati due punti A e B qualsiasi, determinare il loro punto di mezzo attraverso l’uso del solo compasso. Potrete provare a risolverlo (e a dimostrarne la validità), in modo da capire se siete sulla strada buona per diventare il prossimo Imperatore d’Europa o anche solo per puro divertimento. Vi posso solo dire che il vero scopo è ridurre "strategicamente" al minimo il numero di passaggi… provate, chissà che un novello Bonaparte non si annidi tra di voi. La descrizione (ma senza dimostrazione, per adesso) la trovate nell’Appendice 1.
Come si può notare ho già usato la parola chiave “strategia”: il futuro del grande matematico, militare per necessità e per bisogno di tempo libero, si stava costruendo…
Un altro problemino ideato dal nostro Napo (noi possiamo permettercelo, essendo uno dei “nostri”) è quello di trovare i quattro punti di un quadrato inscritto in un cerchio. Questo quiz ha bisogno di pochi passaggi per trovare la soluzione. Anche lui è riportato nell’Appendice 2.
Tuttavia, il più importante problema, proposto da Napo a Lorenzo, prende proprio il suo nome (problema di Napoleone). L’enunciato è decisamente semplice e in fondo lo è anche la costruzione (Appendice 3): data una qualsiasi circonferenza (costruita da qualcuno che non ha reso visibile il centro), determinare con il solo compasso il centro di tale circonferenza. Problema di facile applicazione sui campi di battaglia, per cui è facile immaginare tutta una serie di “compassi da campo” che scorazzano per dare a Napo una posizione costantemente e perfettamente centrale (vedremo che questo schema ha portato al poco conosciuto Teorema di Austerlitz)
“Generale tutto ci potevamo aspettare da voi, fuorché lezioni di geometria”: con questa frase, Laplace e de La Grangia avevano accolto stupiti e ammirati le spiegazioni di Napoleone.
La storia proseguì per il suo verso e Napo si trovò, quasi senza volerlo, Imperatore dei francesi e padrone di gran parte dell’Europa. Innumerevoli le sue battaglie vinte contro eserciti anche più numerosi e preparati dei suoi. La spiegazione è ormai abbastanza semplice: Napo utilizzava strategie geometriche eccezionali, con le quali riusciva a scompaginare eserciti legati a manovre ripetitive, ormai prevedibili e monotone.
Famosi i suoi accerchiamenti e le sue azioni rapidissime. La realtà appare, quindi, piuttosto chiara e Napo l’ebbe a dire ad alcuni suoi fedeli allievi che presto divennero celebri scienziati: “I miei problemi geometrici hanno bisogno di grandi spazi e di migliaia di comparse per rappresentare certe figure geometriche. Come avrei mai potuto avere a disposizione entrambe le cose senza diventare Imperatore e scendere in battaglia?”.
Provate voi, anche se di alto livello militare, a chiedere alla gente di un intero paese o città di schierarsi secondo strane e incomprensibili linee e poi muoversi in sintonia secondo precise regole geometriche? Anche un famoso generale avrebbe subito una punizione corporale durissima, tenendo conto che la maggior parte dei soldati francesi erano rudi agricoltori e, quindi, piuttosto rozzi, ma anche molto robusti.
Creare un impero era quindi un obbligo per il sogno geometrico-matematico di Napoleone. Le battaglie sarebbero state le sue dimostrazioni più lampanti. Teniamo inoltre in conto che Napo, insieme a Mascheroni, gettarono le basi della geometria “proiettiva”. Non per niente era necessario che le sue figure geometriche (ops… armate) si proiettassero velocemente nelle direzioni pensate dal suo genio.
Uno dei punti più alti della visione cinematica dell’opera di Napo, si può vedere nella ricostruzione, rivista in versione geometrica, della battaglia di Austerlitz, uno dei capolavori di Napoleone, chiamato dai dotti del tempo “il teorema di Austerlitz”.
Lo schema segue quello della “presa alle spalle” in cui si riesce ad attrarre l’armata avversaria verso un luogo apparentemente dominante, per poi bloccarle ogni via d’uscita e stringerla in una morsa ferrea e insuperabile. La Fig. 1a mostra la classica rappresentazione degli storici militari, con i movimenti delle truppe. La Fig. 1b mostra invece il teorema di Austerlitz, ossia la versione geometrico proiettiva dell’intera dinamica.
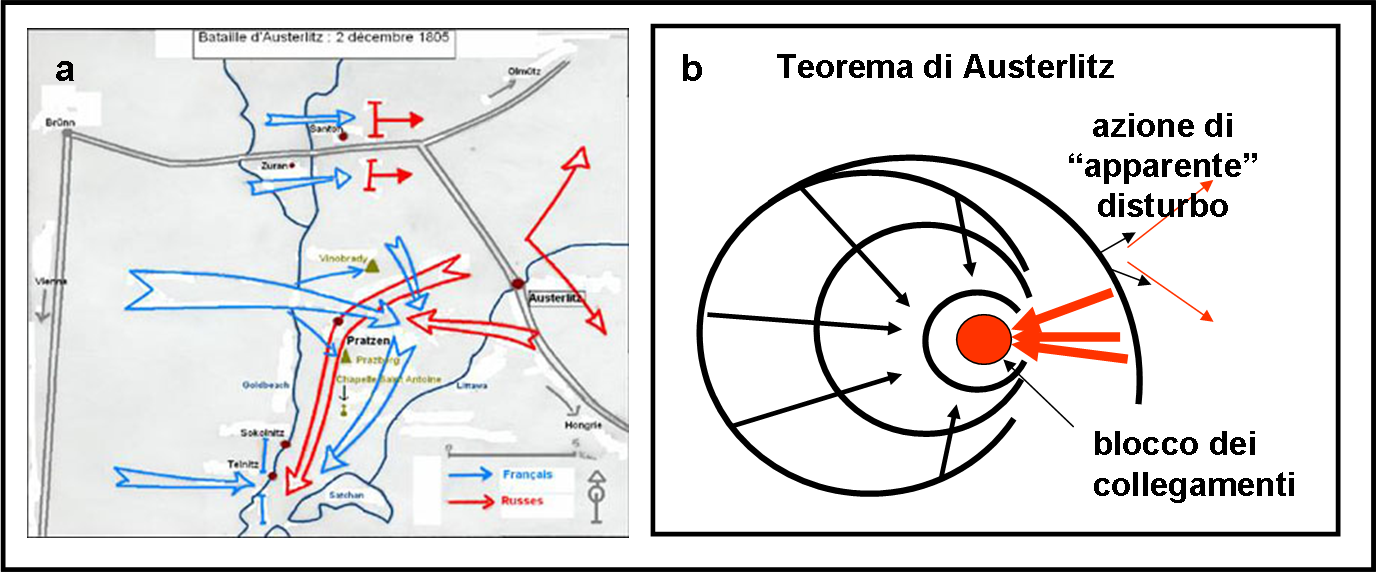
Il meccanismo, in funzione del tempo, prevedeva una circonferenza aperta verso il nemico che si stringeva sempre di più chiudendolo dove e come il generale voleva (notate l’applicazione continua del problema di Napoleone).
Data la velocità di esecuzione esiste anche una versione relativistica della manovra (Fig. 2), in cui si può intuire il rallentamento del tempo dei francesi, come appariva ai russi (sistema fermo), che sbagliarono completamente i tempi di risposta al fuoco.
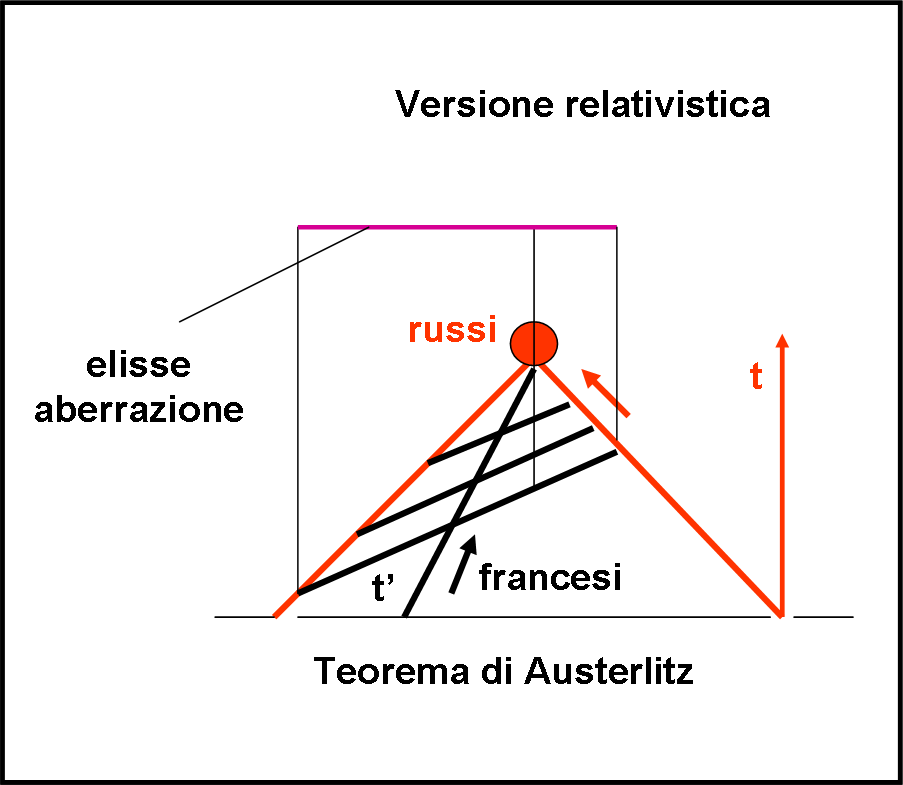
Ai più attenti lettori non può sfuggire l’analogia con l’ellisse di aberrazione (QUI). Il colle che viene scalato rapidamente dai francesi appare come il cono di luce che termina con la concentrazione delle truppe russe. La sezione del colle-cono di luce con un piano di simultaneità nel riferimento dei francesi, porta i russi ad avere le traveggole sia temporali che “colorate” (effetto doppler relativistico). Non solo furono sconfitti per l’errata percezione del tempo, ma anche per avere scambiato le divise avversarie per quelle degli amici austriaci. Si dice (documenti segretissimi trovati nella cuccia del cane di Albert) che Einstein, ancora giovinetto, si recasse ripetutamente presso la località di Austerlitz (l’attuale Slavkov u Brna nella Repubblica Ceca).
La tecnica semplificata di “presa alle spalle” si aggiungeva ad altre due tecniche geometriche spesso utilizzate da Napo: la “posizione centrale” e il suo opposto, ossia, la “concentrazione”. Le tre tecniche sono schematicamente riportate nelle Figure 3, 4 e 5 (il nemico è sempre rappresentato in rosso).
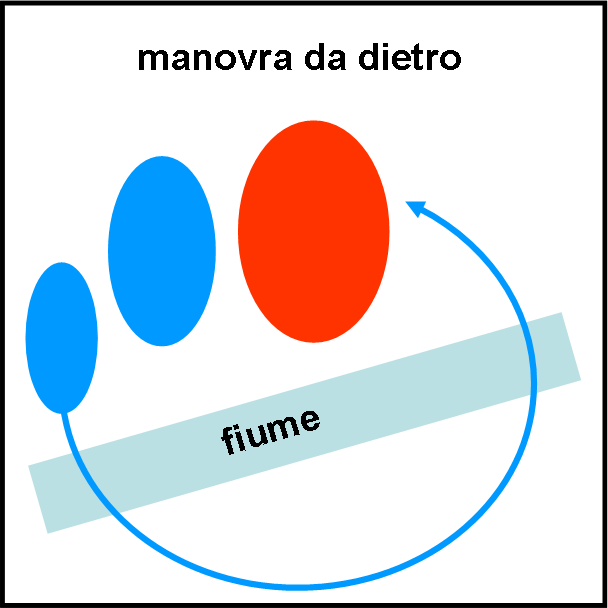
Nel primo caso, un gruppo sostanzioso di francesi si portava alle spalle delle armate avversarie attraversando un fiume o girando attorno una qualsiasi formazione geologica che bloccasse la vista della manovra circolare, esterna al campo di battaglia.
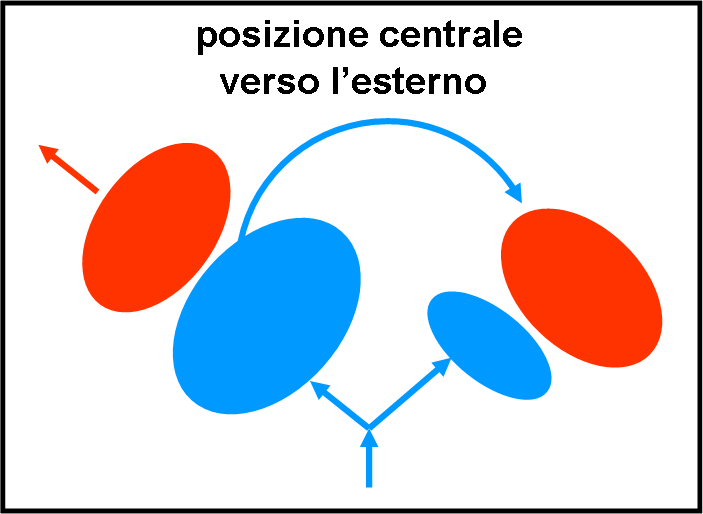
Nel secondo caso, si incuneavano all’interno dell’armata nemica, spezzandola in due parti circa uguali, lasciando la loro parte più debole di fronte a una parte del nemico che pensava di avere partita vinta e si concentrava su questa operazione apparentemente facile. La parte principale dell’armata francese aveva, nel frattempo, facile e rapida ragione della seconda parte degli avversari e riusciva a riversarsi, a sorpresa, lateralmente, sulla seconda parte creando scompiglio e confusione indicibile. La geometria veniva aiutata dalla componente psicologica. Inoltre, manovrando all’interno del loro sistema di riferimento, i francesi erano aiutati, nello scambio di informazioni, dalla relativa vicinanza delle due parti in lotta. Questa tecnica fa già presagire quello che sarà il capolavoro assoluto di Napoleone, gettato purtroppo al vento dall’incapacità matematica di alcuni suoi generali
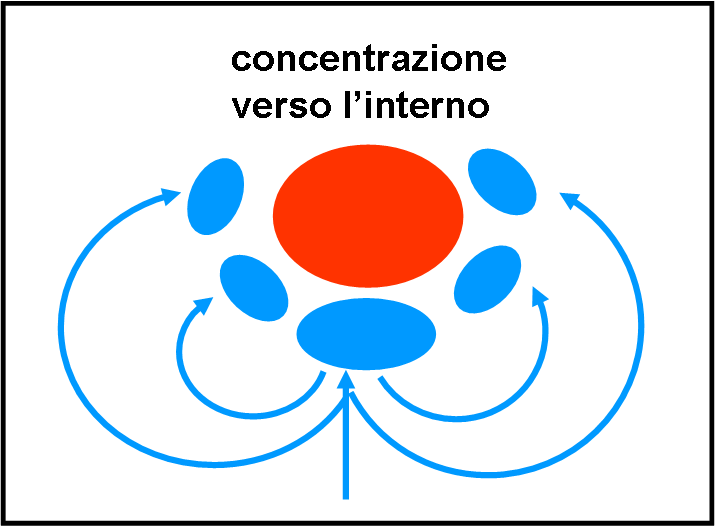
Nel terzo caso, l’azione era contraria: l’amata francese si spezzava in piccole sotto-unità che attiravano in varie direzioni l’armata nemica, deformandola ed espandendone le dimensioni (alcuni pensano che lo studio di questa tattica abbia dato il via all’ipotesi della relatività generale, prima, e dell’espansione dell’Universo, dopo). A quel punto gli spezzoni francesi si concentravano rapidamente verso il centro (sapientemente calcolato attraverso i “compassi da campo”) colpendo in modo inatteso le milizie nemiche, ormai in gran parte disperse.
La determinazione di un punto centrale, dotato anche di un’altra fondamentale caratteristica, scaturisce quasi banalmente dal celeberrimo Teorema di Napoleone. Nato quasi soltanto per mettere in difficoltà i suoi colleghi matematici, non è di facile soluzione, ma porta quasi automaticamente alla determinazione rapida e sicura del punto di Torricelli-Fermat. Se trovare questo punto fondamentale poteva essere impossibile attraverso complessi calcoli angolari, durante una battaglia in corso, non era assolutamente difficile ottenerlo graficamente partendo dal Teorema di Napoleone e affidandola ai soliti indispensabili “compassi da campo”.
Ricordiamo che il punto di Torricelli-Fermat è quello che rende minima la somma delle distanze dai tre vertici di un triangolo qualsiasi. Si riuscì a dimostrare che, se tutti gli angoli di un triangolo ABC sono minori di 120°, allora il punto di Torricelli-Fermat F è il punto tale che FA, FB, FC si incontrano formando angoli di 120°; altrimenti coincide con il vertice relativo all’angolo più grande. Napoleone ne fece uno dei suoi capisaldi, in quanto quello era proprio il punto di riferimento di tutte le azioni belliche, da dove far partire gli ordini e ricevere le notizie.
Ovviamente, Napoleone riuscì a costruirlo con il semplice uso del compasso o poco più. Tralasciamo, per adesso le dimostrazioni (non banali) e vediamo come il Teorema di Napoleone possa banalmente ricavare il punto così ambito e utile.
Il Teorema di Napoleone dice che i baricentri dei triangoli equilateri costruiti sui lati di un triangolo qualsiasi sono i vertici di un triangolo equilatero (i triangoli possono essere sia esterni che interni). Le ripercussioni, le applicazioni e le generalizzazioni meritano sicuramente un articolo a lui dedicato (e lo faremo senz’altro). Accontentiamoci, per adesso, dell’Appendice 4 e del fatto che i cerchi circoscritti ai tre triangoli equilateri napoleonici di partenza si incontrano nel punto di Torricelli-Femat: eccezionale!
E’ ovvio come l’uso dei “compassi da campo” sia fondamentale. Tuttavia, il punto tanto ambito si può anche trovare tracciando le tre rette che uniscono l’angolo lontano dei tre triangoli equilateri (esterni, ad esempio) con il vertice opposto del triangolo di partenza.
Ma torniamo alla storia… Napoleone non vedeva l’ora di applicare sul campo la sua ultima “strategia”, basata essenzialmente sul punto di Torricelli-Fermat e sulla semplice costruzione ottenibile con il suo teorema. Il problema era, però, che per una costruzione adeguata aveva bisogno di spazi enormi, liberi da impedimenti che potessero bloccare i suoi “compassi” umani.
L’Europa conquistata gli stava troppo stretta ed era obbligato a spingersi in quella che viene erroneamente chiamata la campagna di Russia. Lui aveva chiesto gentilmente un po’ di spazio allo zar, ma il dispettoso regnante, dopo averglielo concesso, non faceva che spezzargli i cerchi necessari. Insomma, per colpa di mille e uno motivi, compresi generali non altezza della situazione, l’inverno arrivò prima della conclusione dell’opera di Napo. Lavorare sul ghiaccio era impossibile e fu costretto a tornare. Purtroppo in condizioni inadeguate e con quel pensiero che non lo faceva dormire, subì una tragica sconfitta a Lipsia.
Aveva cercato di applicare le sue teorie più moderne, ma senza la prova sul campo il risultato voluto non era arrivato: anche i grandi scienziati devono lavorare in “pace”, qualche volta…
Si ritirò (si dice anche gentilmente accompagnato da galanti nemici) sull’isola d’Elba, ma essa non risultò all’altezza delle ambizioni di Napo: troppa poca pianura, troppe coste scoscese, insomma una vera “ciofeca” per le sue rappresentazioni geometriche proiettive.
Il punto di arrivo, la sua fissazione, era ormai uno e uno solo: il punto di Torricelli-Fermat! Se ne andò, perciò, dall’Elba e decise di racimolare più gente possibile per fare un ultimo tentativo in Belgio, nei pressi di Waterloo. Diede il massimo di se stesso e riuscì quasi a ottenere il risultato voluto. Non rimaneva che una sola circonferenza, che fu affidata a un generale di nome, ma non di fatto. Quello fu il più grande errore della vita di Napo. Al suo ordine di non dimenticarsi del pi greco, lo stolto generale iniziò una furibonda quanto inefficace ricerca tra le sue truppe di un soldato di nome “pi” che avesse almeno qualche lontana origine egea.
La circonferenza non venne mai chiusa e un capolavoro assoluto non ebbe il compimento ormai a portata di mano. Inutilmente Napo impose con una ferrea legge che tutti i generali dovessero conoscere i rudimenti della matematica; ormai era troppo stanco e stufo di dovere fare guerra per potere raggiungere i suoi sogni scientifici. Si fece rinchiudere sull’isola di Sant’Elena, abbastanza pianeggiante, ma si rese tristemente conto che gli abitanti, comprese pecore, montoni e conigli selvatici introdotti anni prima, non potevano certo formare le figure meravigliose di cui aveva bisogno.
Si spense sognando il punto di Torricelli-Fermat, tra il pianto dei pochi seguaci che lo avevano seguito, la completa indifferenza degli ovini e il sorriso soddisfatto dei conigli che non aspettavano altro per poter tornare alla loro più divertente occupazione principale, senza bisogno di imparare cos’era quello strano e antipatico pi greco.
E fu con encomiabile
opra di pali e filo
e di possente logica,
segno di tanto spiro,
che con paziente ingegno
il mondo conquistò.......
QUI potete leggere tutta l'ode dedicata al Nostro dal grande scritttore e poeta Alessandro Maurizioni
Note dell’autore.
Il sottoscritto ammette di aver utilizzato qualche fonte abbastanza incerta, ma conferma la veridicità di (quasi) tutte le opere scientifiche del sommo matematico, descritte nel presente articolo. Anima inquieta e dal pensiero lanciato verso un futuro ancora troppo precoce, Napoleone non è forse stato capito appieno da molti. Spero che queste righe servano a illuminarlo sotto una luce ben più risplendente.
A proposito di storie vere, QUI potete conoscere quella su Colombo e la scoperta dell'America e QUI quella della rivoluzione copernicana
Appendice 1
Dati due punti A e B qualsiasi, determinare il loro punto di mezzo attraverso l’uso del solo compasso
I passi da eseguire sono i seguenti (Fig. 6):
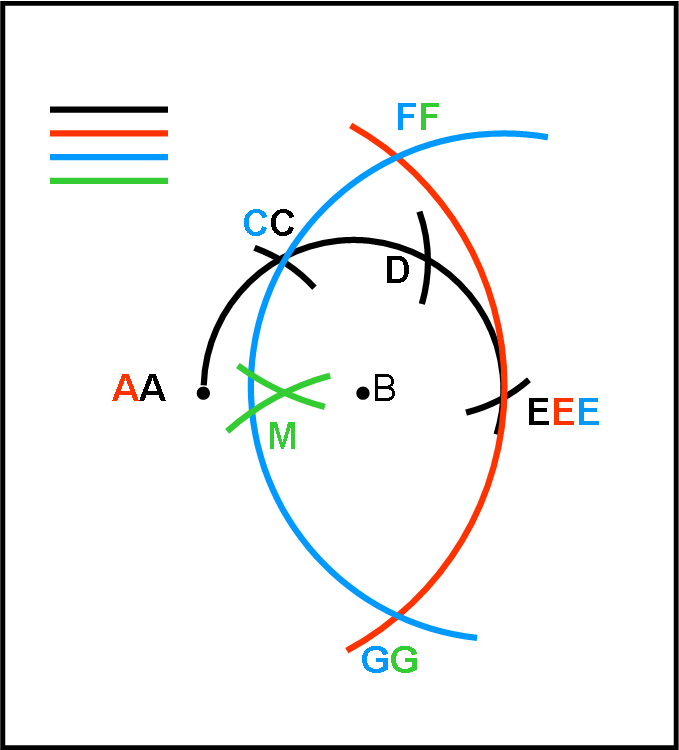
1) Con centro in B descrivere il cerchio di raggio AB
2) Con raggio AB, tracciare da A l’arco di cerchio che intersechi il cerchio originario (nero) in C e ripetere altre due volte l’operazione, trovando D ed E.
3) Con centro in A tracciare il cerchio rosso di raggio AE.
4) Con centro in E tracciare il cerchio azzurro di raggio EC che incontri il cerchio rosso in F e G
5) Con centro in F tracciare il cerchio verde di raggio EC e fare lo stesso con centro in G.
Il punto intersezione dei due cerchi verdi è il punto di mezzo M tra A e B
Appendice 2
Trovare i quattro punti di un quadrato inscritto in un cerchio.
I passi da eseguire sono i seguenti (Fig. 7):
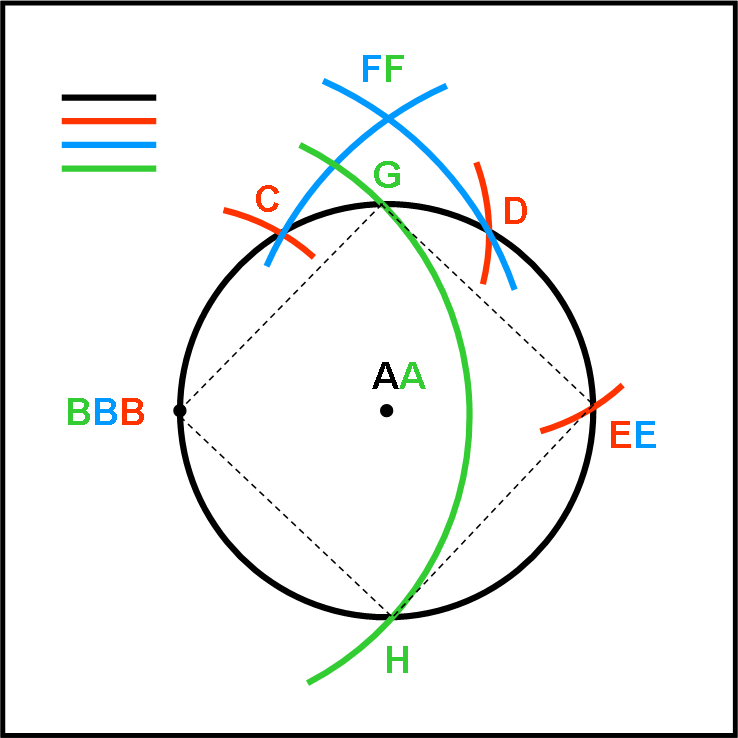
1) Tracciare una circonferenza nera di raggio qualsiasi e centro in A
2) Da un punto B qualsiasi della circonferenza, con il suo stesso raggio, tracciare un cerchio rosso che tagli la circonferenza di partenza in C ed eseguire altre due volte la stessa operazione, trovando D ed E.
3) Con centro in E e in B tracciare i cerchi azzurri di raggio CE (uguale a BD) che si intersechino nel punto F.
4) Con raggio AF, fare centro in B e tracciare la circonferenza verde che incontri la circonferenza
di partenza nei punti G e H
I punti BGEH sono i vertici del quadrato inscritto
Appendice 3
Il problema di Napoleone
Data una qualsiasi circonferenza, determinare con il solo compasso il centro di tale circonferenza.
La circonferenza nera di partenza sia un già stata costruita senza aver lasciato segno del suo centro. Le operazioni da svolgere (Fig. ![]() sono le seguenti:
sono le seguenti:

1) Da un punto A qualsiasi della circonferenza tracciare una circonferenza rossa di raggio qualsiasi che tagli quella di partenza in B e C.
2) Con lo stesso raggio tracciare due circonferenze azzurre che si incontrino nel punto D.
3) Dal punto D tracciare la circonferenza verde di raggio DA che incontri la circonferenza rossa in E e in F.
4) Dai punti E ed F tracciare i cerchi viola di raggio EA. Essi si incontrano nel punto O, centro della circonferenza di partenza.
Di tutte tre queste descrizioni potete facilmente trovare una dimostrazione più o meno ovvia, che lascio a voi, così come strategie alternative
Appendice 4
Il punto di Torricelli-Fermat
Dato un triangolo qualsiasi A, B e C, il punto di Torricelli-Fermat è quel punto che minimizza la somma delle distanze dai vertici A, B e C.
Ciò vale solo per angoli del triangolo minori o uguali a 120°. Nel caso che un angolo sia maggiore di 120° il punto coincide con il vertice dell’angolo maggiore di 120°.
Occupiamoci solo del caso più “normale”, ossia di un triangolo senza angoli maggiori di 120°, situazione conforme agli schemi delle battaglie di Napoleone.
Notiamo subito che questo punto non coincide con il baricentro del triangolo (sarebbe troppo facile).
Il Teorema di Napoleone
I baricentri dei triangoli equilateri costruiti sui lati di un triangolo qualsiasi sono i vertici di un triangolo equilatero.
La Fig. 9 illustra la situazione nel caso di triangoli esterni. Le soluzioni sono molteplici e le tratteremo a parte, anche se siete tutti invitati a provarci già da adesso.
Ciò che ci interessa di più, in questo articolo storico-scientifico, è la semplice costruzione che si può ottenere unendo gli angoli lontani dei triangoli equilateri con l’angolo opposto del triangolo di partenza. Il punto di intersezione delle tre linee è proprio il punto di Torrricelli-Fermat.
Se vogliamo usare solo il compasso, basta tracciare le circonferenze circoscritte ai tre triangoli equilateri. Il loro punto d’incontro è ancora il punto di Torricelli-Fermat (Fig. 10).

Il Teorema di Napoleone porta anche a un altro punto particolare, il punto detto proprio di Napoleone, ossia quello che si ottiene dall’intersezione dei segmenti che uniscono i vertici del triangolo equilatero finale con gli angoli opposti del triangolo di partenza (Fig. 11). Un punto ancora tutto da studiare, ma che sembra che Napo abbia usato o cercato di usare nelle sue ultime battaglie.







15 commenti
E bravo professore! Quando competenza tecnica, genio e fantasia vanno a braccetto, riescono a far diventare meno antipatico anche quell'Hitler del XIX secolo che è sempre stato - almeno per me - Napoleone!
Non ho ancora letto l'appendice perchè prima voglio provare ad "annodarmi" col compasso, chissà se riuscirò perlomeno a trovare il punto medio di un segmento... ne dubito, ma ci proverò!
Per il momento, dovrai accontentarti di questo:
E ripensò i mobili
Compassi, e i percossi angoli,
E il lampo de’ baricentri,
E l’onda dei triangoli,
E il concitato teorema,
E il celere dimostrar.
Chissà se un certo sig. Mauritius, magari aiutato dall'inseparabile Pautasso, riuscirebbe a fare di meglio, offrendoci una rielaborazione de "Il cinque maggio" in chiave geometrico-matematica. Del resto, da uno che è capace di fare una cosa come questa, ci si può aspettare di tutto...
Sì, sì, un 5 maggio geometrico-matematico-relativistico!
Una cosa tipo questa?
E fu...
E fu con encomiabile
opra di pali e filo
e di possente logica,
segno di tanto spiro,
che con paziente ingegno
il mondo conquistò.
Che dir di quella testa
di luce circonfusa,
sapiente tra i sapienti,
la mente mai confusa,
incontestabil centro
di un fulgido avvenir.
Dall'Alpi alle Piramidi,
dal Manzanarre al Reno,
veloce più del fulmine,
veloce più di un treno,
d'immensi cerchi magici
demiurgo e creator.
Fu vera gloria?
dubiti?
Credi sia facil prassi
muover cotali eserciti
solo con i compassi?
Ebben, postero incredulo,
prova solo a pensare,
senza calcolatori,
cosa lui seppe fare.
Quali lampi di genio
al mondo rivelò.
Ben poca cosa, postero,
ciò che di lui si sa.
Ma la giustizia storica
la prova ci darà,
grazie ad un Professore:
Vincenzo Zappalà.
Cateti e ipotenuse,
circonferenza e raggio
tracciati e misurati,
con gesti da gran saggio,
furono gli alleati
del grande condottier.
E immaginò il corrusco
baleno dei compassi,
e delle squadre il palpito,
delle figure gli assi,
e il concitato imperio,
e il rapido eseguir.
Fu l'intuizione fulgida
che penetrò il mistero
di magici triangoli,
svelando al mondo intero
il celebre teorema
che il nome suo portò.
Onore quindi all'uomo,
al generale e al genio
che con cipiglio indomito
tracciò il suo gran disegno,
su lande sconfinate
dall'uno all'altro mar.
Uao!
Sono senza parole... conoscendo il personaggio, mi aspettavo una grande prova, ma questa supera le mie più rosee aspettative! Dico sul serio, Mau, complimenti infiniti come il teatro del cosmo! Grande, davvero grande!!
Che ne dici, Enzone, questo piccolo capolavoro merita un posto di primo piano nell'articolo?
Il primo dovere del principe è quello senza dubbio di fare ciò che vuole il popolo, ma il popolo non sa quasi mai ciò che vuole.
A fare le cose a mezzo si perde sempre.
Lo disse Lui stesso:"fui bravissimo a mandare a morire milioni di uomini per un nastrino."
È matematico,l'essere umano non crede alle cose reali.In compenso è disposto a morire e far morire per dei fumetti ben disegnati.Questo lo dico io ovviamente!
Io direi di inserire questo capolavoro assoluto della scienza poetica o se preferite della poesia scientifica in un articolo a se stante legato a quello precedente... Un binomio che non si può staccare... Tolgo il piccolo accenno al misero 5 maggio e preparo il saggio lettore a questa stupenda ode... che deve sparire dai commenti...
Che ne dite?
Dico che mi sembra un'ottima idea!
Grande Enzo.
Grazie Mariolino... ma il merito è soltanto del grande Napo!!!!

Un blog fantastico, intelligente, stimolante, che trasmette conoscenze ed elabora lezioni e spiegazioni mai banali e scontate, ma con la rigorosità del vero matematico e scienziato. Divulgare non è facile e per farlo bisogna essere ben preparati e avere molta esperienza alle spalle, nonché un pensiero lucido, chiaro, razionale. Onore al dottor Vincenzo Zappalà, che mette a disposizione degli altri la sua lunga esperienza di astronomo e matematico con un'umiltà e una passione encomiabili, da vero maestro e uomo di pensiero!
Grazie!
Angela Delgrosso
Grazie a te Angela! Mi fai arrossire...
Devo dire, però, che gran parte del merito va a un gruppo di fantastici colleghi-amici che sono entrati perfettamente nello spirito del Circolo e sanno arricchirlo di infinite sfumature. Ovviamente, tu sarai sempre la benvenuta...
ci vediamo presto....
Dati due punti A e B qualsiasi, determinare il loro punto di mezzo attraverso l’uso del solo compasso
poniamo il segmento AB di lunghezza unitaria.
passo 1) Il punto C , insieme a A e B costituisce un triangolo equilatero di lato 1.
passo 2) si costruiscono i triangoli equilatero di lato 1 : CBD e DEB.
passo 3) si costruisce un triangolo isoscele AFE con lati due lati lunghi 2.
passo4) si chiude il triangolo con la base lunga .
.
si dimostra osservando che EC è il doppio dell'altezza del triangolo equilatero unitario e che quindi corrisponde a .
.
passo5) si costruisce il triangolo isoscele FME con base minore pari a 1+x ove x è il punto incognito cercato tra A e B.
Ora si osserva che l'angolo FEM = MFE (triangolo isoscele di lato )
)
e che AFE = AEF (riangolo isoscele di lato 2).
Quindi i due triangoli FAE e MFE sono simili.
Varranno quindi le proporzioni sui lati
FA : FE = FE : (1+x)
cioè
2: =
=  : (1+x)
: (1+x)
che risolta fornisce l'asserto
2 ( 1+x) = 3 ===> x= 1/2
caro Leandro,
finalmente uno che comprende il grande Napoleone! Hai sbagliato secolo... magari l'avresti convinto a non fare la campagna di Russia
Bravo!
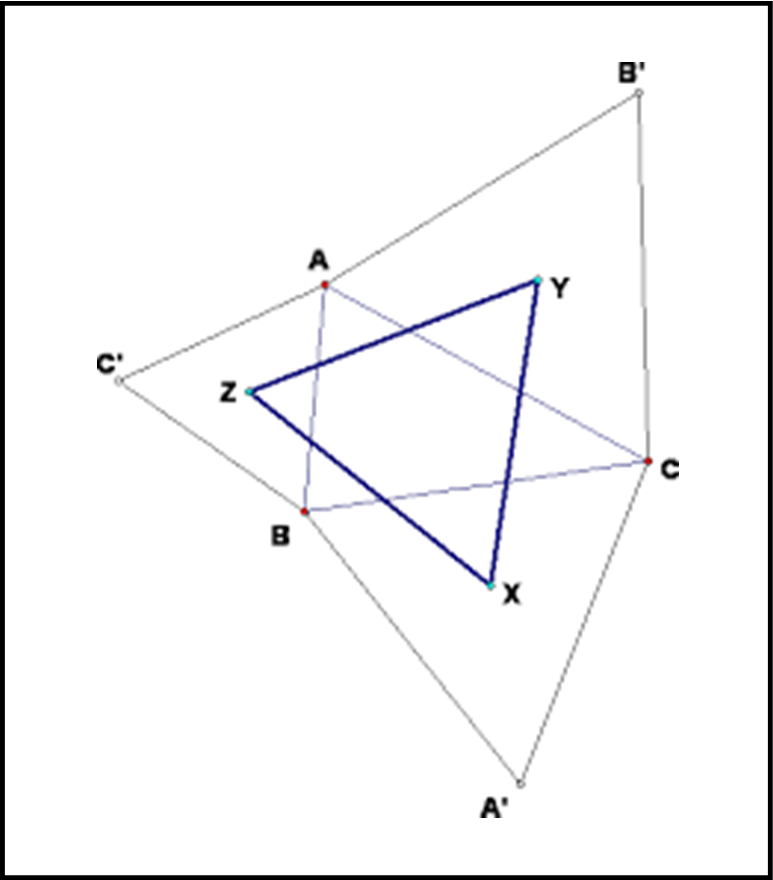
Questa mattina, prima di andare a scuola, è venuto a trovarmi il nipote Oreste junior.
Dato che è un grande ammiratore di Napoleone gli ho fatto vedere quel bel triangolo equilatero con i vertici nei baricentri... e gli ho detto: Oreste, studia, che quando saprai la trigonometria e la geometria analitica potrai dimostrare questo teorema del grande Napoleone.
Orestino ha guardato ben bene la figura, che metto qui sotto...
e con la biro rossa ha disegnato l'esagono irregolare AZBXC dicendo: "la somma dei suoi angoli interni è 720°"
Poi ha aggiunto:"Per costruzione la somma degli angoli AZB, BXC, XCY è 3*120° = 360°. Quindi la somma degli angoli YAZ, ZBX, XCY è 720°-360° = 360°"
"Bene, Oreste, e adesso?"
"Guarda qui a destra, nonno, vedi il triangolo ABC e quest'altro XYZ che ho ricopiato dalla figura di sinistra...?"
"Vedo..."
"Adesso, osserva questo triangolo verde YAZ: faccio ruotare attorno al punto Z il triangolo rosso ZBX
e, attorno al punto Y, il triangolo giallo YCX."
E ha colorato con i pastelli tutti i triangoli mentre me li indicava.
"La somma degli angoli giallo+verde+rosso nel punto A è 360° . Nota che ZA=ZB YA=YC AX'=BX=CX (perché derivano da triangoli isosceli).
Si forma così il triangolo ZX'Y che ha base comune ZY con ZXY."
Sembrava soddisfatto di questo ragionamento, così non ho fatto commenti e ho lasciato che continuasse.
"Ora, è chiaro che il lato XY=X'Y e il lato XZ=X'Z. Quindi ZXYX' è un parallelogramma e l'angolo ZX'Y = ZXY. Valgono anche queste uguaglianze: ZX'A= ZXB e YX'A= YXC"
Si capiva che mancava poco alla conclusione.
"Ecco, nonno, adesso basta ricordarsi che BXC è = 120° per costruzione e quindi (2 ZXB + 2 YXC) = 120°, da cui ZXB+YXC = 60°, nel vertice X.
Analogamente posso fare il medesimo ragionamento negli altri 2 vertici Y e Z.
Quindi...il triangolo XYZ è equilatero"
A questo punto gli ho detto: "Adesso vai a scuola, Oreste,studia. Sentirò cosa ne pensa il Professor Vincenzo e poi te lo dico"
"Eh sì, nonno devo proprio scappare se no arrivo tardi, ciao!"
Si è messo il cappello in testa, è saltato in sella e via! Come il fulmine. Ho fatto appena appena in tempo a fargli questa foto...
grande Oreste! Sono convinto che tuo nipote farà strada (convincilo a non andare in Russia, però...)