Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Cominciamo, nuovamente, l’avventura con una trattazione sul piano (x,y), ma poi passeremo immediatamente nello spaziotempo. Alla fine, troveremo nuovamente l’ellisse, lavorando con la geometria di Minkowski (vedi questo quiz).

Questa volta non ci facciamo mancare niente e riprendiamo la nostra circonferenza riflettente, introducendo il cono di luce relativo al momento della partenza da un certa origine O. Il cono di luce non è altro che l’espansione dell’onda luminosa della lampadina fino a incontrare i bordi della circonferenza. A quel punto la luce inverte il percorso e torna nell’origine che, intanto, si è spostata lungo l’asse del tempo. Guardiamo l’esperimento dall’alto (ossia nel piano (x,y)), con il tempo che punta verso di noi, in Fig. 42.

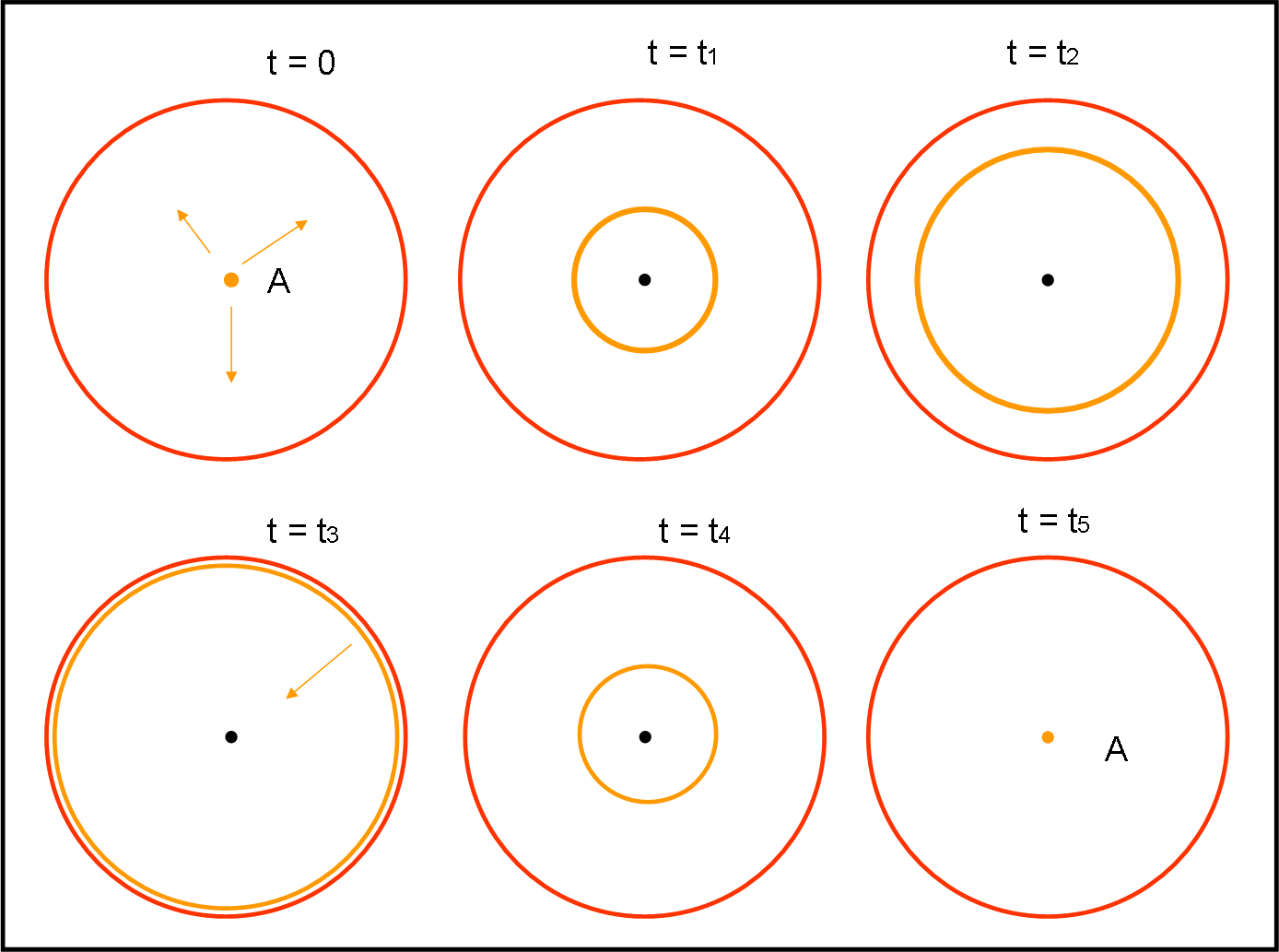
Cosa succede? (scusate se sono quasi infantile, ma è meglio partire non lasciando niente al caso).

La circonferenza rossa rimane sempre al suo posto, dato che si muove solo nel tempo. Dal centro A parte la luce che viene rappresentata dalla circonferenza arancione che si allarga fino a incontrare la circonferenza in t₃. In quel momento, viene riflessa e torna indietro fino a tornare nel punto A in t₅. Banale, ma non sentitevi presi in giro…

Vediamo la stessa situazione nella Fig. 43. A sinistra abbiamo lo stesso esperimento visto nel piano (t,x) con l’asse y che punta verso di noi. A destra vi è una visione tridimensionale che dovrebbe essere chiara a tutti.

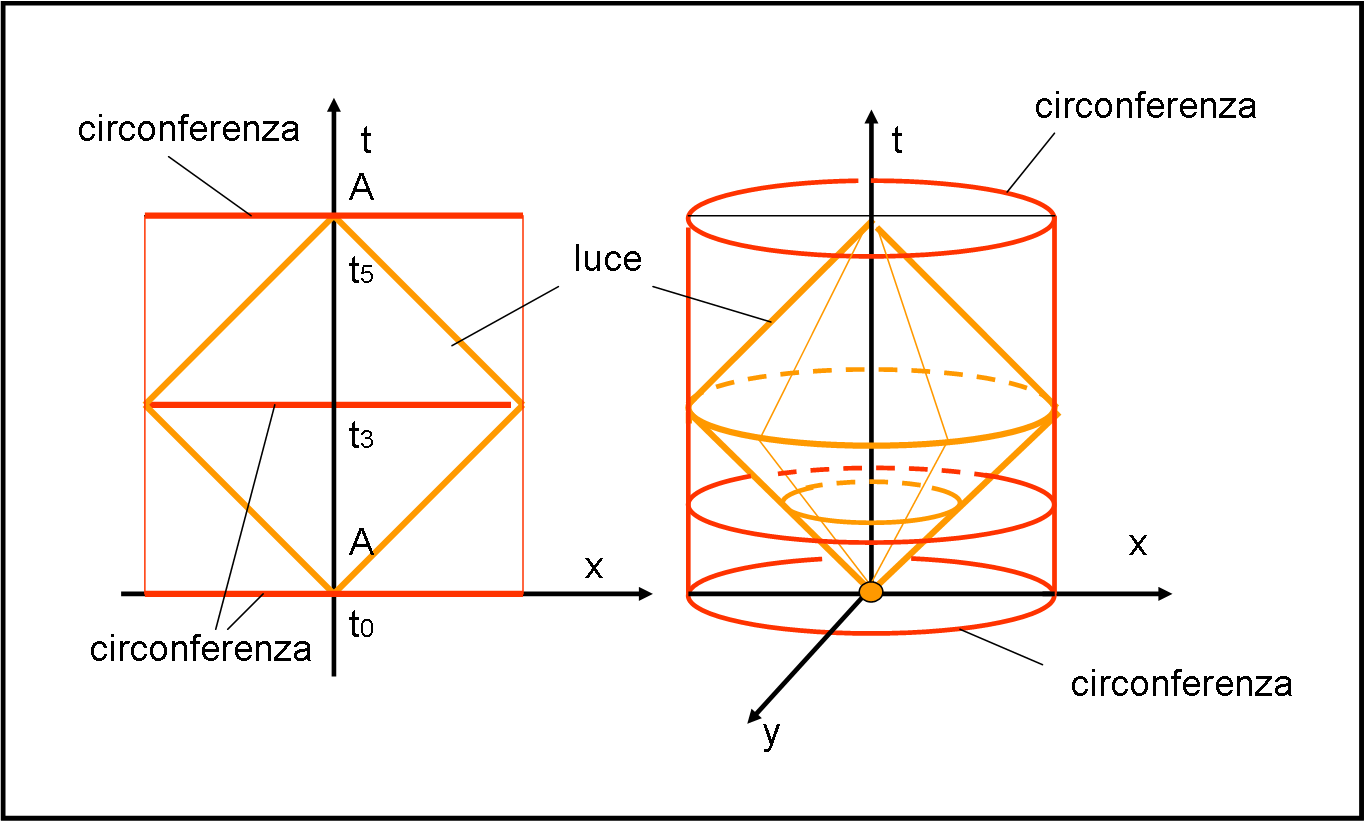
Abbiamo descritto il caso in cui A non si muove. Avete anche notato che la luce si muove a 45°, secondo quanto utilizzato nel diagramma di Minkowski. Anche se non sembra, siano già entrati al suo interno.

Ora complichiamo le cose… e facciamo muovere la sorgente di luce A verso destra. Nel diagramma di Minkowski (Fig. 44) si individuano subito i nuovi assi x’ e t’. L’asse y’ resta, invece, quello che è (y), essendo normale al movimento. Guardiamo il tutto con l’asse delle y diretto verso di noi, ossia il piano del foglio è quello che contiene sia (x,t) che (x’,t’).

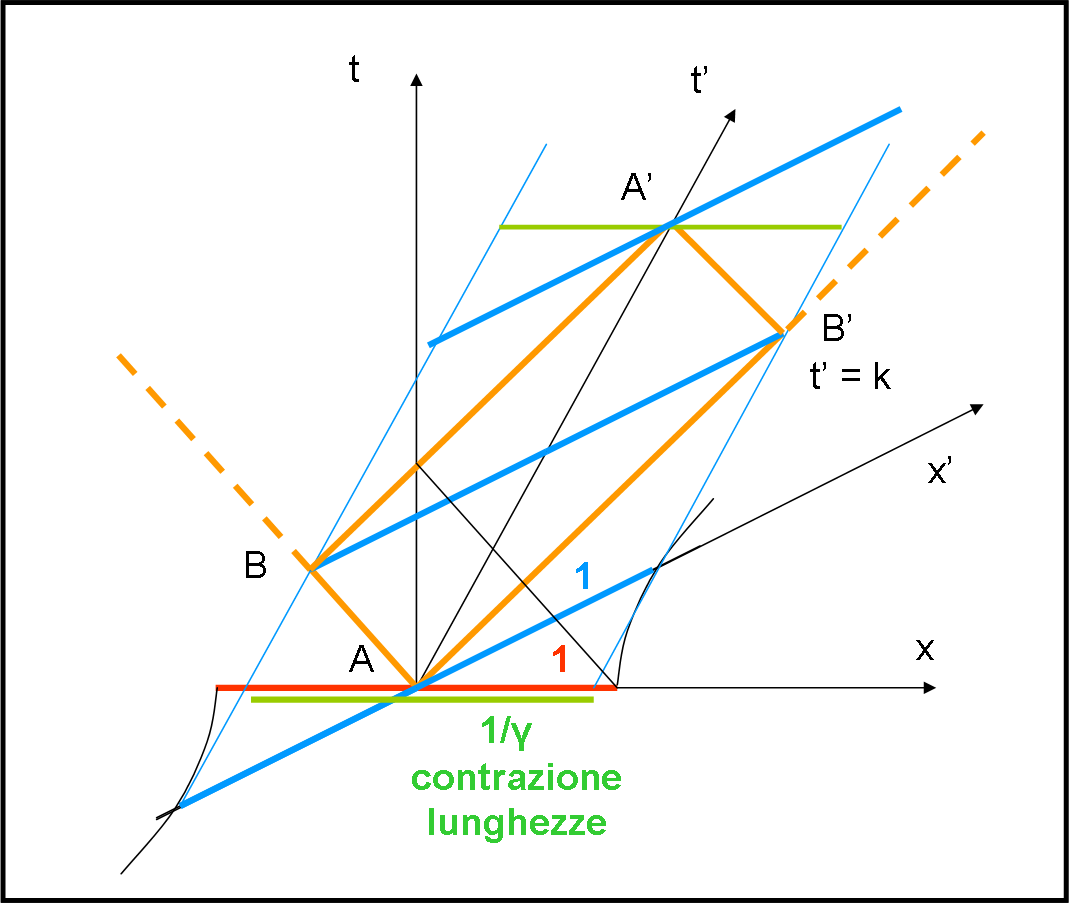
La nostra circonferenza riflettente di partenza (rossa) si trasforma nel segmento inclinato azzurro. Esso individua l’asse di simultaneità per il sistema (x’, t’) ossia t’ = cost. Notiamo che per costruire il segmento azzurro dobbiamo utilizzare l’iperbole di calibrazione in modo da trovare ciò che corrisponde in x’ a un valore di x (nella figura li abbiamo indicati entrambi con 1 per vedere bene come avviene la trasformazione). E poi immediato trovare la distanza contratta sull’asse x (segmento verde). Guardando dall’alto (ossia lungo l’asse t) il segmento verde si trasforma in un’ellisse che ha per semiasse maggiore la lunghezza lungo y (che non è cambiata) e per semi asse minore 1/γ (per maggiori informazioni andate QUI e QUI).

Per ripetere quanto fatto con l’orologio di luce, non ci resta altro che vedere il movimento di questa ellisse verde (circonferenza contratta) e seguire i raggi di luce che corrispondono sempre al cono di luce di prima, dato che esso non cambia, cambiando sistema di riferimento. Notiamo anche che il segmento azzurro, se visto dall’asse t, dà luogo anch’esso a un’ellisse, ma con semiasse maggiore allungato verso la direzione del moto e il semiasse minore sempre uguale a y. Questa ellisse ci interessa per trovare quali sono i punti in cui si ha la riflessione della luce. Ovviamente, essi devono avvenire nello stesso istante relativamente al viaggiatore A, ossia lungo l’intersezione tra il piano t’ = k e il cono di luce. A quel punto la luce torna indietro e converge nuovamente in A’, che intanto si è mosso lungo t’. La forma “quadrata” della Fig. 43 (viaggiatore fermo) si trasforma in una strana figura (un rettangolo,) che abbiamo spesso usato nella RR per spiegare la relatività della simultaneità nel diagramma di Minkowski.

In poche parole ciò che è simultaneo nel sistema in moto (x’, y, t’) non lo è più nel sistema (x, y, t) proprio quello in cui vogliamo eseguire le osservazioni del nostro esperimento.

La Fig. 44 può sembrare complicata, ma ci torneremo ancora sopra. Per adesso consideriamo l’ellisse verde che tiene già conto della contrazione delle lunghezze e vediamo cosa succede mentre si muove lungo x. guardando tutto dalla direzione t, come fatto nell’orologio di luce. Torniamo, quindi a lavorare nel piano (x,y) con una circonferenza contratta riflettente, che si muove verso destra (Fig. 45)

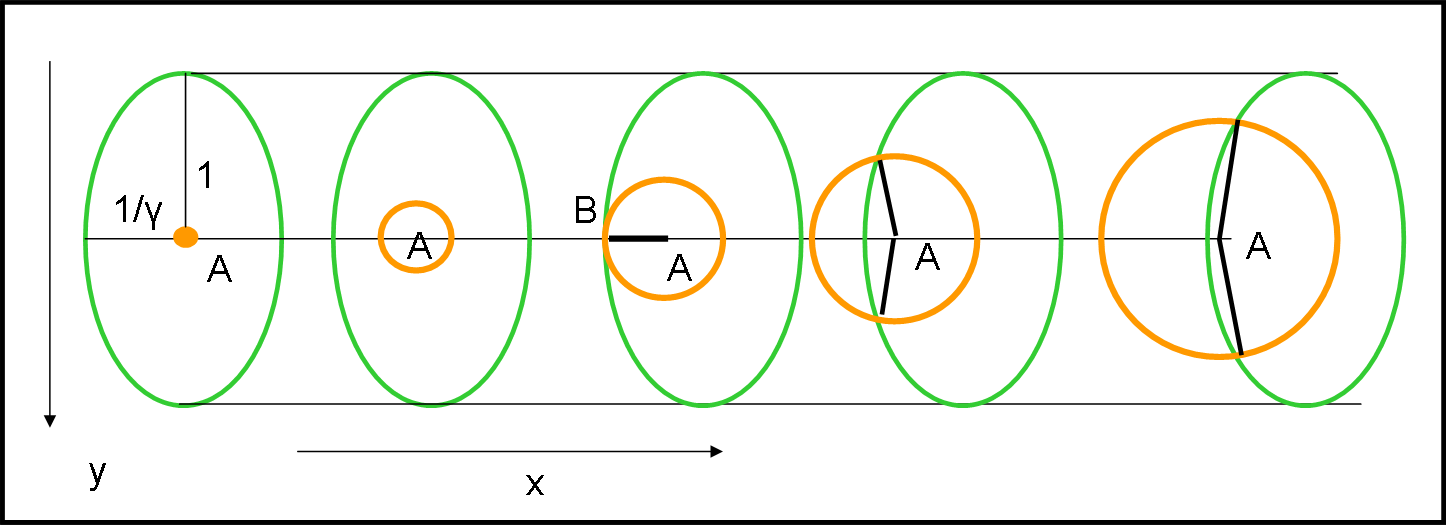
Al tempo t = 0 la lampadina viene accesa e la circonferenza si muove ormai contratta dal fattore di Lorentz, diventando un’ellisse, come detto precedentemente. Nell’istante successivo, l’onda luminosa (il cono di luce) si è già allargata, ma ancora non tocca la parete riflettente. Siamo nel tratto in cui la luce passa da A a B (vedi Fig. 44). La luce ovviamente non riesce a raggiungere tutto il bordo nello stesso tempo (lo farebbe solo nel sistema x’,t’). Il primo punto della circonferenza-ellisse verde che viene toccata dalla luce è proprio B.

Il cono di luce continua ad allargarsi e poco interessa che esca fuori dalla parte sinistra. A noi interessa quali sono i punti dell’ellisse verde che vengono toccati dalla luce prima di riflettersi.  Altre due posizioni sono disegnate in tempi successivi. Stiamo sperimentando una cosa interessantissima che è in pratica il succo stesso della Relatività Ristretta: la luce continua a toccare punti diversi dell’ellisse verde in tempi diversi, mentre nel sistema di riferimento della circonferenza originaria (rossa) in movimento (ellisse azzurra) questi contatti avvengono simultaneamente (t’ = cost.).

L’intero discorso si riduce al concetto di  relatività della simultaneità: ciò che è simultaneo in un sistema (x’,t’) NON è simultaneo in un altro (t,x). La y continua a disinteressarsi e rimane sempre la stessa dato che non è influenzata dal movimento e dal cambiamento di sistema.

Torniamo alla Fig. 44. Tutto il tragitto tra B e B’  comporta contatti continui con l’ellisse contratta verde, mentre per il sistema in movimento tutti questi contatti avvengono nello stesso istante (mi ripeto per cercare di non far perdere qualche concetto per strada). L’ultimo contatto avviene in B’.

Notiamo bene che stiamo guardando l’ellisse verde mentre si muove lungo il suo asse x, ragione per cui si riescono a evidenziare abbastanza bene solo i punti di contatto iniziale e finale nel sistema (x,t). Quelli relativi a y diverse si intuiscono soltanto. E’ fondamentale riuscire a capire che mentre la luce raggiunge contemporaneamente il segmento (ellisse) rosso, essa tocca l’ellisse verde in tempi diversi che obbligano la luce a fare percorsi sempre diversi, descritti perfettamente dal legame che esiste tra t’ e t, che si ripercuote pari pari su x. Comunque, più di tante parole, vale un’attenta lettura della figura…

Diciamo le cose in altro modo: l’orologio del sistema in movimento non gira tra B e B’ (i due punti sono raggiunti simultaneamente) mentre si muove tranquillamente nel sistema di partenza, fisso..

Quando arriviamo in B’ le cose cambiano drasticamente. Tutti punti dell’ellisse verde sono stati colpiti dalla luce, malgrado i contatti siano avvenuti in tempi diversi. I raggi che ormai hanno colpito l’ellisse verde in tempi t diversi devono convergere simultaneamente in A’. Infatti, il fenomeno fisico deve essere lo stesso in entrambi i sistemi di riferimento.

Ovviamente, il punto A’ ha dovuto spostarsi rispetto ad A, in accordo con la velocità β.

L’esperimento sarebbe finito, ma noi lo analizziamo ancora, non dubitate… Innanzitutto fatemi inserire di nuovo la figura precedente, in cui ho aggiunto un segmento viola (Fig. 46), che corrisponde ai due estremi, in x, in cui abbiamo visto la luce arrivare per toccare l’ellisse verde. E’ un segmento interessante dato che si individuano molto bene i due estremi C e D (la luce tocca per la prima volta l’ellisse e la tocca per l’ultima volta) e la proiezione dei due puti A e A’ di partenza e di arrivo della lampadina.

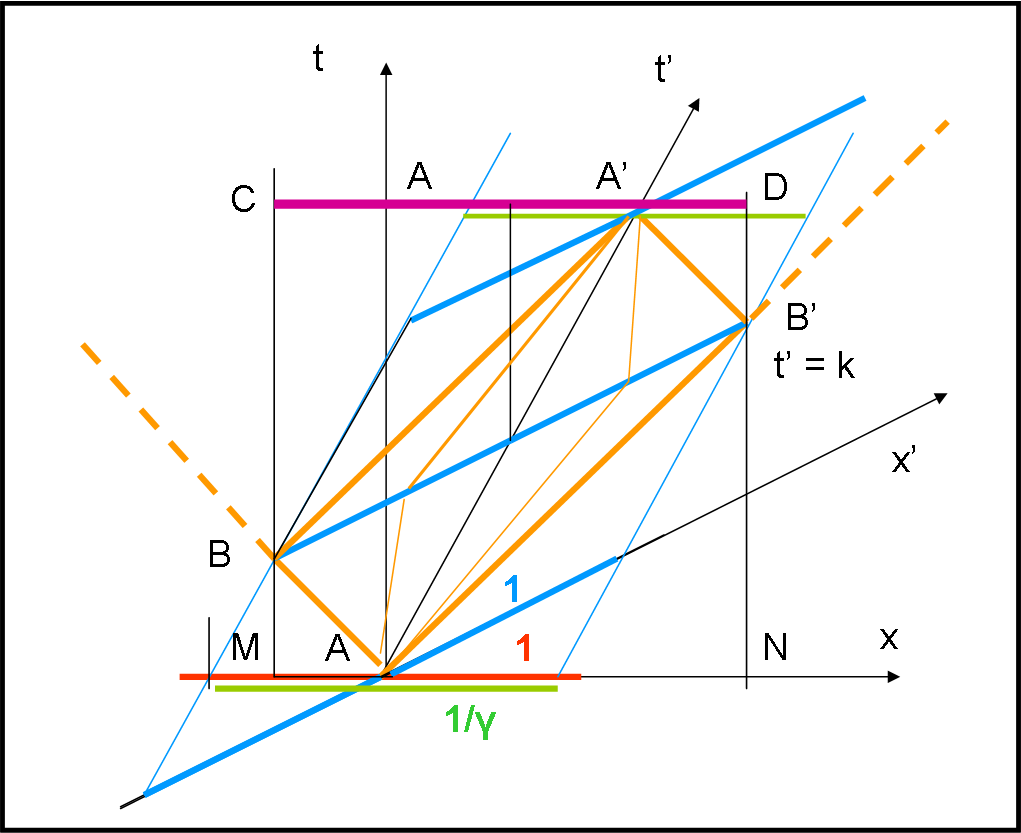
Notiamo anche che, per costruzione, il poligono CMND deve essere un quadrato (la luce va a 45°). Ciò comporta che ciò che capita nei tempi (dilatazione) si rispecchia perfettamente nelle x che misuriamo alla fine. D’altra parte i segmenti sono dati da ct e c è uguale 1. Ma questo è una banalità che abbiamo già affrontato nel diagramma di Minkowski e anche nell’orologio di luce.

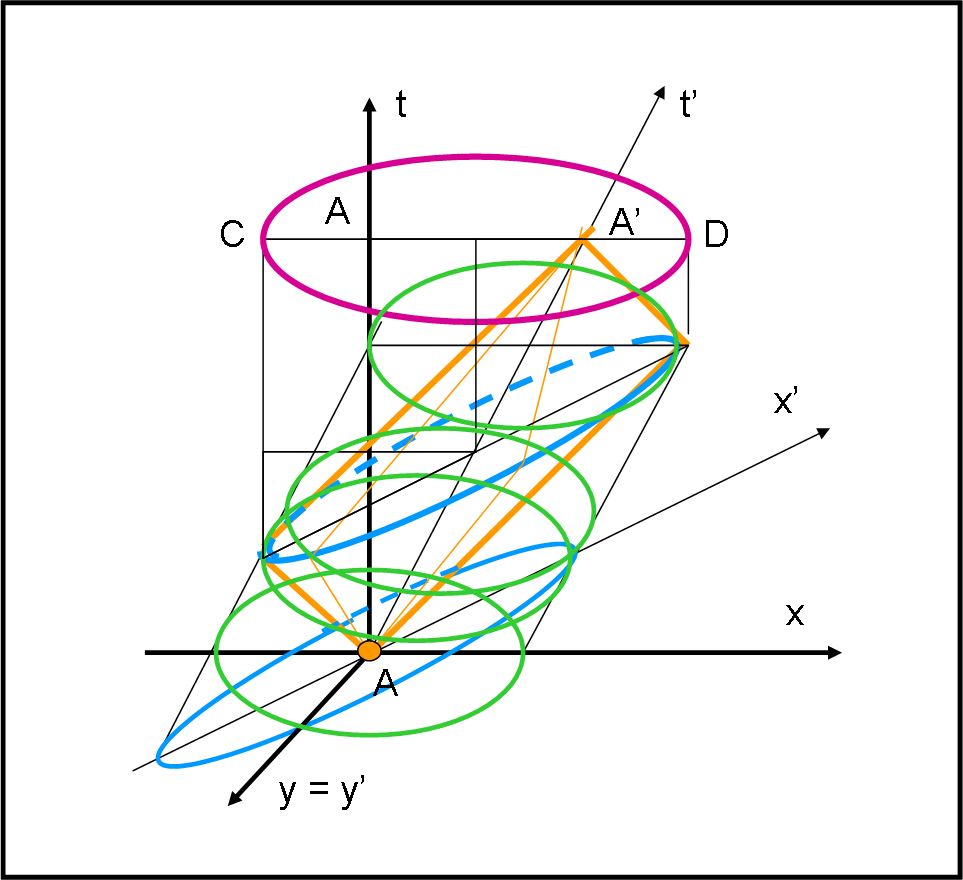
Cerchiamo di disegnare in tre dimensioni (due di spazio e una di tempo) quanto descritto finora, usando la Fig. 47 Divertitevi pure, ma dato che siamo in ballo,continuiamo a ballare. Intanto facciamo una scommessa: “Volete vedere che quel segmento viola, se visto dall’asse delle t, diventa proprio l’ellisse di aberrazione?”. I più bravi diranno: “Certo, è ovvio…”, ma forse per qualcuno non è ancora del tutto ovvio.

Per cui riprendiamo la Fig. 45 e costruiamola in modo regolare e preciso nella Fig. 48.

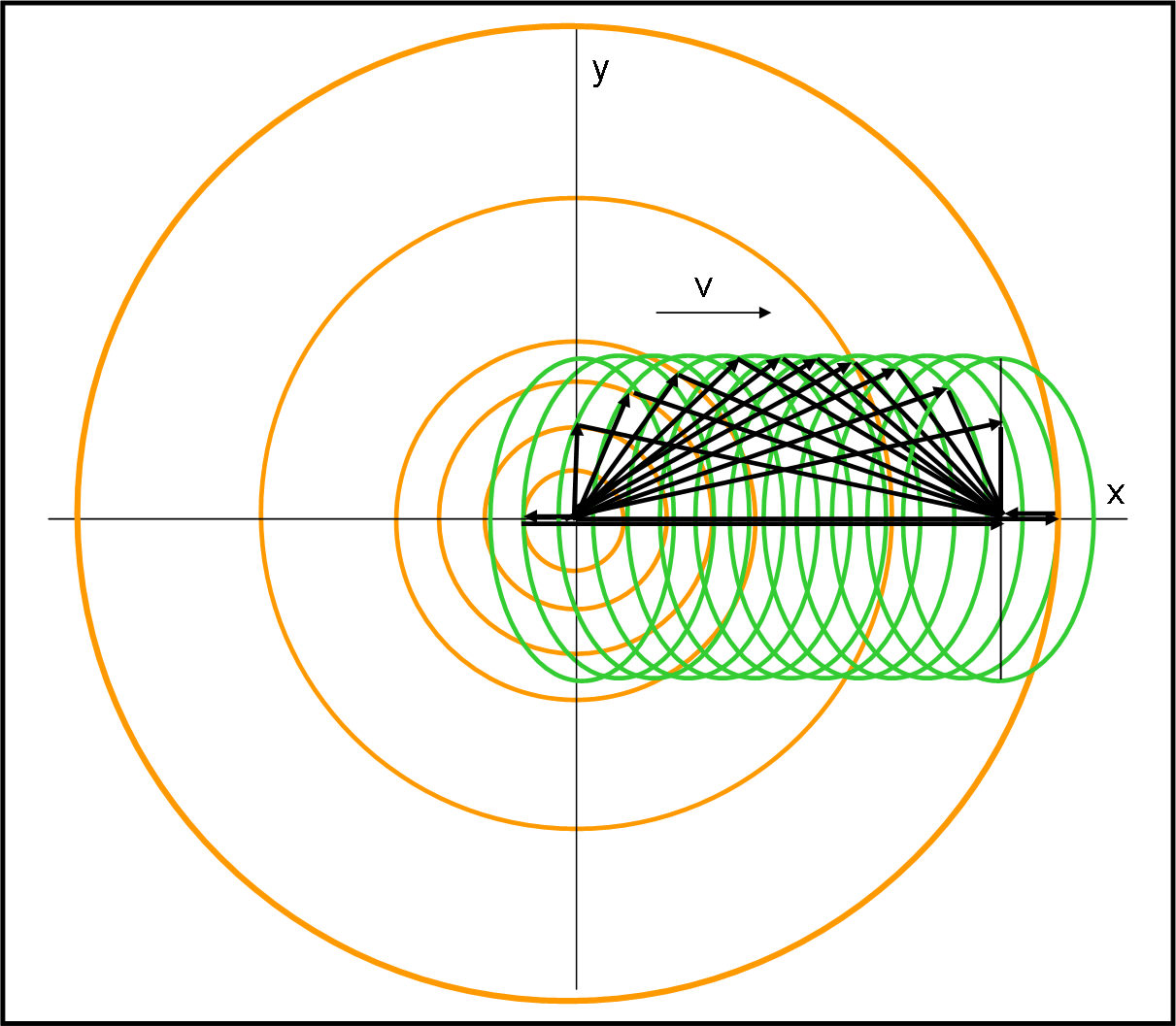
Ci portiamo decisamente nel piano (x,y), lo stesso che avevamo usato per l’orologio di luce (ma in fondo anche la nostra circonferenza è un orologio di luce generalizzato). Lungo l’asse x disegniamo le varie posizioni assunte dall’ellisse verde a intervalli di tempo costanti. La prima ellisse è quella centrata in A e l’ultima è quella centrata in A’. Ho anche inserito alcune visioni del cono di luce tanto per ricordare che i punti di contatto sono sempre quelli tra ellisse verde e cerchi di luce (il cono visto dall’alto).  In questa figura, solo apparentemente intricata, siamo nel piano x, y e il segmento viola della Fig. 47 è esattamente quello che unisce il primo e l’ultimo contatto, ossia i punti di contatto che stanno sull’asse delle x.

Per non esasperare la figura abbiamo solo disegnato la parte superiore, ma la stessa identica cosa capita anche in basso.

Per ogni posizione dell’ellisse verde si determina il relativo punto di contatto con il cono di luce (e l’analogo nella parte sotto). Le righe nere sono il percorso della luce partita da A che si riflette sull’ellisse verde e poi continua per raggiungere A’. Tutte le linee devono, perciò, partire da uno stesso punto (A) fisso (la luce è inviata solo in quel punto e all’istante t = 0), riflettersi e raggiungere tutti lo stesso punto A’ nello spesso istante t = t_F. Come abbiamo già detto parlare di tempi è come parlare di x, per cui le varie righe possono essere considerati legate nello stesso modo sia ai tempi che ai percorsi.

A noi cosa interessa disegnare? Beh… abbastanza semplice: tutti punti di contatto (da un estremo all’altro) che nel sistema in movimento devono essere simultanei, oltre che i due punti A e A’ . La y non  può ovviamente superare il semiasse maggiore dell’ellisse verde, dato che non è influenzata dal movimento. Non ci resta che unire tutti questi punti, come fatto in Fug. 49.

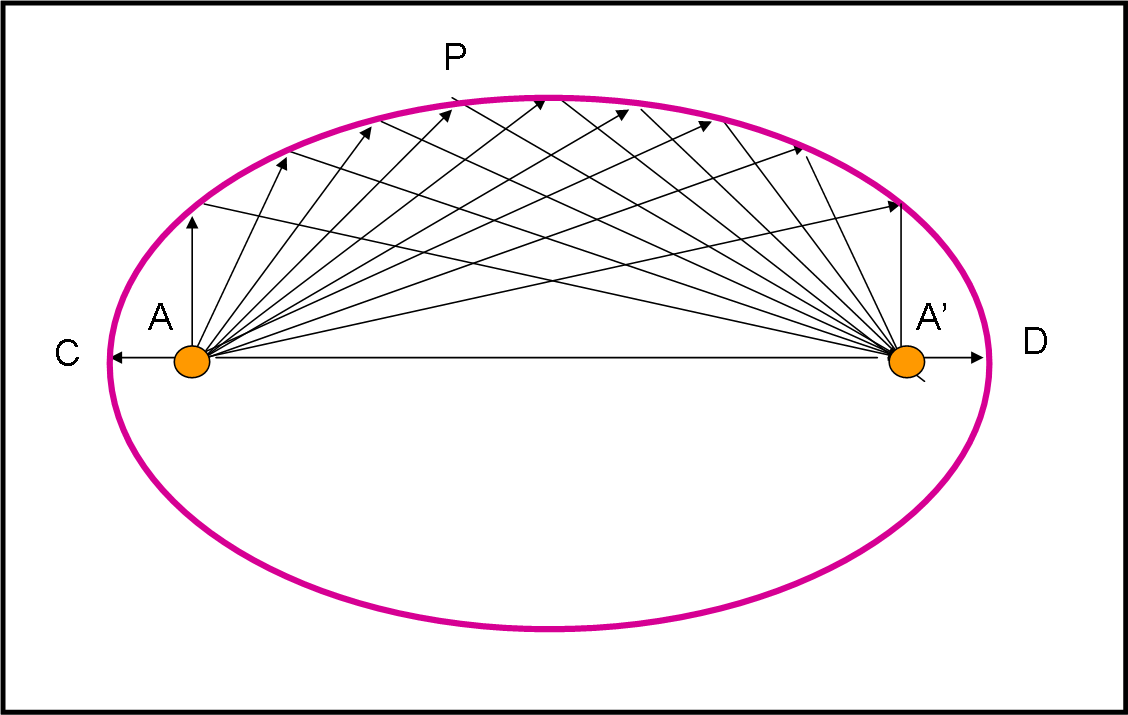
Essi, però, sono quei punti P tali che il percorso da A fino a loro e da loro fino ad A’ deve essere sempre uguale (il fenomeno deve essere lo stesso in ogni sistema). Ovviamente, i percorsi parziali da A al punto di contatto e da questo ad A’ devono essere diversi nel sistema x,y (non lo sarebbero nel sistema x’,y), ma la loro somma deve essere uguale.

Dalle nozioni più spicciole di geometria analitica, sappiamo benissimo che la curva luogo dei punti la cui distanza da due punti fissi è costante non è altro che un’ellisse di cui A e A’ sono i fuochi. Il semiasse minore dell’ellisse finale è sempre uguale all’unità, se tale abbiamo posto il raggio della circonferenza iniziale. Quanto vale il semiasse maggiore dell’ellisse e la distanza focale?

Non sarebbe un problema arrivarci attraverso la RR e le sue trasformazioni. Noi però ci vogliamo divertire a calcolare l’equazione dell’ellisse attraverso le condizioni con cui è stata creata: proiezione sul piano (x,y) dell’intersezione tra il piano di simultaneità t’ = cost, e il cono di luce. Insomma, proprio il quiz che avevamo proposto QUI e che era stato risolto da alcuni di voi (vedi commenti).

Questa volta vorremmo calcolare la sua equazione in modo analitico. In realtà, l'ellisse viola non è altro che la proiezione nel piano x, y della ellisse azzurra, la quale a sua volta è l'intersezione tra cono di luce e un piano (x', y'=y).

In poche parole, basta trovare la soluzione del sistema:

 

x² + y² = t²

t' = γ(t – βx)

La prima è l’equazione del cono di luce (una circonferenza che assume raggi crescenti e/o decrescenti descrive proprio un cono), la seconda è la relazione che lega  t’ con t e x (trasformata di Lorentz) e quindi descrive proprio il piano di simultaneità del sistema x’,y’,t’ nelle coordinate x,y, t.

Basta allora invertire la seconda e ricavare t:

t = t’/γ + βx

Tuttavia, t’ è una costante (simultaneità) e per semplicità possiamo prenderlo uguale a 1.

Sostituiamo t ricavato dalla seconda nella prima equazione e otteniamo la relazione:

(1/γ + βx)² = x² + y²

Che è proprio la curva desiderata che già sappiamo essere un’ellisse. Dobbiamo, però, cercare di scriverla nella forma canonica…

Elevando a quadrato il primo membro si ha:

1/γ² + β²x² + 2 βx/γ = x² + y²

Portiamo tutto al secondo membro e otteniamo:

x² + y² - β²x² - 2 βx/γ - 1/γ²  = 0

Raccogliamo x²

x²(1 - β²) + y² - 1/γ² - 2 βx/γ = 0

Ma…

(1 - β²) = 1/γ²

Da cui:

x²/γ² - 1/γ² - 2 βx/γ + y² = 0

Moltiplichiamo e dividiamo per γ il terzo fattore e raccogliamo 1/γ²:

(x² - 1 - 2 βγx)/γ² + y² = 0

Accidenti… vorremmo un bel quadrato a, numeratore, ma non sembra proprio possibile… a meno di scrivere l’unità in modo un po’ strano…

Ricordiamo che:

1/γ² = 1 – β²

1 = γ² – β² γ²

Andiamo a sostituire questa espressione al posto di -1 al numeratore dell’equazione:

(x² - γ² + β² γ² - 2 βxγ)/γ² + y² = 0

Magnifico, possiamo estrarre dalla parentesi - γ² che diviso per γ² è uguale a -1. L’equazione diventa:

(x² + β² γ² - 2 βxγ)/γ² + y² = 1

Finalmente, abbiamo costruito il quadrato che volevamo e possiamo scrivere:

(x - βγ)²/γ² + y² = 1

Abbiamo ritrovato l’ellisse della volta scorsa (ci mancava altro…) con semiassi  γ e 1 (QUI, Fig. 41).

Ovviamente, ho usato un metodo del tutto personale e probabilmente si può fare meglio e più rapidamente.

Notiamo che l’ellisse costruita è veramente fondamentale. Innanzitutto le direzioni dei raggi che partono da A sono proprio quelle che risultano combinando la velocità della luce e la velocità del viaggiatore, ossia sono le direzioni che hanno subito l’aberrazione luminosa. Inoltre, la lunghezza dei percorsi è sempre diversa e, data l’uguaglianza tra x e t, ci dice direttamente di quanto il tempo si è dilatato passando da un sistema fermo a un sistema in moto. Una variazione dei tempi indica anche una variazione di frequenza nella luce (un moto di allontanamento o di avvicinamento) e quindi comporta un effetto doppler che ci permette di colorare ogni direzione, ammettendo che la luce originaria sia bianca o quello che volete. Ne risulta che una lettura diretta delle grandezze dell’ellisse ci permette di ottenere ben quattro dimensioni: x, y, tempo, frequenza, con un righello e un goniometro.

Andiamo con calma e torniamo alla nostra ellisse di aberrazione (o di simultaneità - ormai abbiamo capito bene il significato del suo nome) e alla sua equazione e dedichiamoci all'effetto doppler.