Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Ci siamo divertiti un po’ con gli dei greci e siamo arrivati a vedere cosa succede alla luce che proviene dall’esterno mentre un cosmonauta viaggia nella sua astronave. Come già dovevamo immaginare, per effetto dell’aberrazione luminosa, il fascio luminoso si stringe verso la direzione del moto. Stiamo per entrare in un campo decisamente più generale, che comporta, nella seconda parte almeno, una conoscenza più che discreta della RR e del diagramma di Minkowski. Cercheremo, perciò di andare avanti con piedi di piombo e fare tante figure esplicative.

Dal quiz precedente (QUI e QUI) sappiamo già che l’aberrazione è un fenomeno relativistico che può essere risolto compiutamente solo entrando nella RR. In poche parole, se l’astronave viaggia molto velocemente l’inclinazione dei raggi è data dalla formula relativistica. Si ricade nel caso classico solo se la velocità è decisamente bassa (come quella dell’astronave Terra).

Ci tengo a precisare un punto fondamentale che è sicuramente ovvio per tutti, ma che preferisco mettere in evidenza. Finora abbiamo sempre lavorato su uno spazio a due dimensioni. I raggi che entrano o escono dal viaggiatore, in moto o fermo, sono descritti in un piano. Il tempo scorre sicuramente, ma non è ancora stato preso in considerazione nel suo giusto valore. Ricordiamo sempre che passando da un sistema di riferimento fermo a uno in moto valgono le formule di Lorentz e il tempo e lo spazio sono strettamente collegati.

Con l’articolo precedente potremmo anche accontentarci e dire di aver finito. Potremmo, infatti, già immaginarci scenari fantastici come quello visto andando verso Orione. Ormai sappiamo calcolare le deviazioni dei raggi e valutare quanto un  fascio di luce si stringa o si allarghi. Tuttavia, facendo così, perderemmo molta informazione portata dai nostri amici fotoni. Innanzitutto non sapremmo che energia trasferiscono all’astronauta. Energia trasferita vuole dire frequenza del fotone che lo colpisce. Siamo, inoltre, nelle condizioni in cui vi è un movimento rispetto alla sorgente di luce, ossia un effetto doppler. Ne segue che a seconda della direzione del moto e della direzione della luce, si ha un cambiamento di frequenza e quindi del colore visto dall’astronauta. Basterebbe calcolare l’effetto doppler relativistico e si potrebbe costruire ciò che vede l’astronauta in tutte le direzioni. Insomma ce la caveremmo con le formule dell’aberrazione e dell’effetto doppler relativistico, legati strettamente tra di loro.

Tuttavia, l’effetto doppler è legato al tempo e il tempo scorre in modo diverso per chi sta fermo e per chi si muove. Se non vogliamo prendere per buone le formule del caso e desideriamo capire bene come i vari parametri escono allo scoperto, non possiamo rinunziare al solito vecchio orologio di luce (per darne una visione semplicistica) e infilarci nello spazio di Minkowski (per entrare nei dettagli). Pensate che la costruzione di quanto andremo a fare viene usata anche per spiegare “in toto” la cinematica della RR e il diagramma di Minkowski. Un metodo alternativo…

Concentriamoci, perciò, e cerchiamo di seguire molto attentamente i vari passaggi. Alla fine otterremo la cosiddetta elisse di aberrazione o di simultaneità (si capirà molto bene il secondo nome).

Ci costruiremo un grafico a… quattro dimensioni. In cui si potranno leggere la deviazione della luce (due dimensioni), la frequenza dei fotoni in arrivo e la dilatazione del tempo lungo ogni direzione. Un’ellisse straricca di informazioni, che sintetizza una bellissima avventura effettuata nello spaziotempo di Minkowski.

Immaginiamo il nostro viaggiatore, munito del vecchio e sempre utile orologio di luce. Vediamo subito cosa c’entri con l’aberrazione. Beh… la risposta è molto semplice e immediata (Fig. 35). Riprendiamo una figura che conosciamo molto bene, dove vi è una lampadina e uno specchietto posto esattamente sopra di lei (il piano della figura è il piano dello spazio x e y).  Accendiamo la lampadina e vediamo la luce colpire lo specchio a 90° e tornare indietro.  Il sistema è fermo è la luce colpisce lo specchietto dopo un certo tempo t e poi torna indietro nello stesso tempo t.

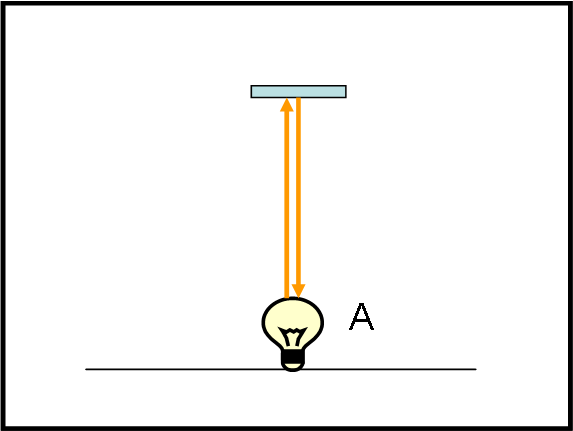
Immaginiamo, adesso, di muoverci verso sinistra con velocità - v e di osservare cosa capita all’orologio di luce (potremmo anche far muovere il viaggiatore e noi rimanere fermi, il succo non cambierebbe). Per il viaggiatore tutto funziona esattamente come prima, ma non certo per noi che ci consideriamo fermi (Fig.  36).

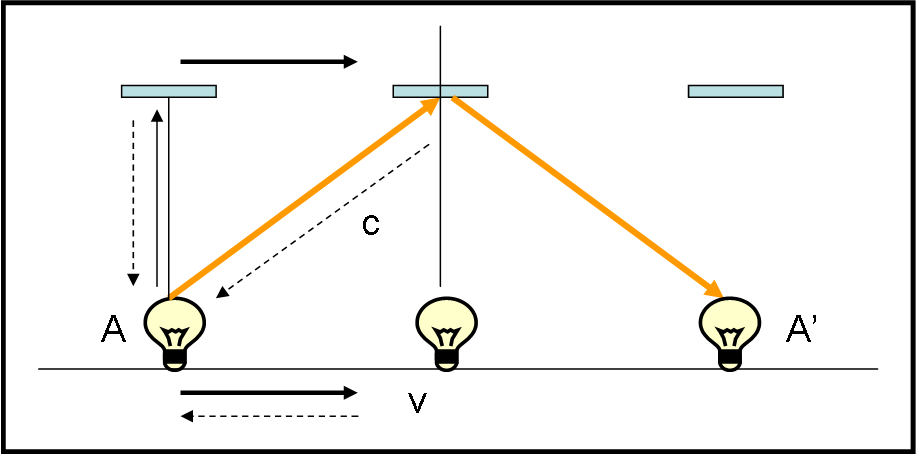
La luce che invia l’astronauta non va certamente lungo la direzione perpendicolare, dato che quando colpisce lo specchietto, lo strumento si è spostato verso destra. La traiettoria della luce è inclinata rispetto a quando l’orologio era fermo. Tuttavia, la luce si riflette comunque (anche se con un angolo diverso da 90°) e si muove in avanti fino a incontrare di nuovo la lampadina. A noi, per adesso, interessa solo la prima parte. Cosa possiamo concludere? Che la luce della lampadina è costretta a piegarsi rispetto alla verticale di un certo angolo per riuscire a raggiungere lo specchio. I vettori coinvolti sono sempre gli stessi e l’inclinazione non è altro che quella che abbiamo imparato a conoscere attraverso l’aberrazione annua.

In questo caso abbiamo inviato della luce, ma la faccenda è del tutto simile: basta invertire il verso della luce e della velocità per ottenere il caso relativo all’osservatore che si muove verso destra e che deve inclinare il suo telescopio per catturare la luce. Per lui è la stella che si muove verso di lui e tutto resta perfettamente uguale, come mostrano le frecce tratteggiate. In poche parole, la prima parte dell’esperienza dell’orologio di luce ci permette di calcolare l’aberrazione della luce da parte di chi si muove verso di lei.

Ricordiamo anche che l’orologio di luce ci aveva permesso di ricavare il tempo t’, relativo a chi si muove, rispetto al tempo t proprio di chi si considera fermo. I due tempi erano legati dal celeberrimo fattore di Lorentz γ, capace di misurare di quanto rallenta un orologio che si muove se visto da chi sta fermo (la famosa dilatazione dei tempi).

Andiamo avanti per gradi e vediamo se è stato solo un caso, oppure se l’orologio di luce può veramente descrivere l’aberrazione per ogni direzione della stella. Basta considerare uno specchietto posto in una posizione avanzata rispetto alla lampadina (ma che sia sempre alla stessa distanza) e mettere “in moto” il viaggiatore (ossia ci muoviamo verso sinistra), come in Fig. 37.

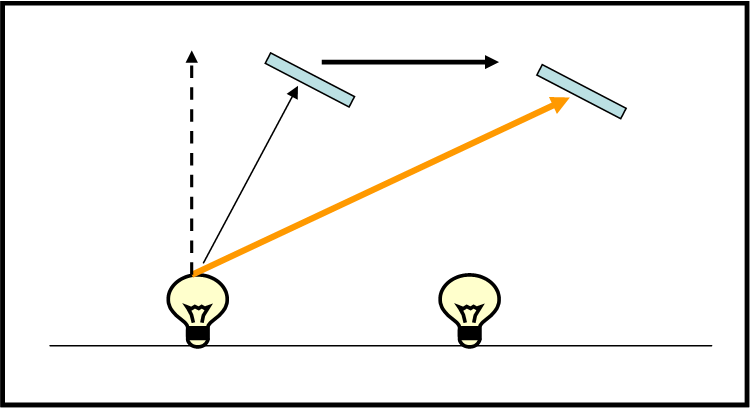
Ancora una volta la luce è costretta a puntare verso destra per poter raggiungere lo specchio e la traiettoria finale è più inclinata di quella vista a vagone fermo. Lo specchio sarà comunque colpito e la luce tornerà sulla lampada ancora più avanti (questa conclusione è obbligatoria, dato che quello che capita nel sistema in moto deve capitare anche se viene visto da fuori; il fenomeno: luce che esce, si riflette e torna da dove è partita, deve SEMPRE capitare).

In modo molto qualitativo abbiamo ritrovato quanto avevamo descritto con i tre dei greci (QUI).

Chi si muove appare inviare luce più concentrata in avanti o -se preferite- ricevere luce più concentrata (basta cambiare sistema di riferimento)

E’ giunta l’ora di generalizzare l’intera faccenda. Invece di un semplice orologio a luce consideriamo una circonferenza riflettente con la lampadina al centro.

La nostra circonferenza-astronave è ferma, con il centro-astronauta in A. Lui accende la sua lampada e vede che tutto torna perfettamente: la luce parte, tocca le pareti nello stesso istante (percorrendo uno stesso spazio uguale al raggio della sfera) e torna indietro nello stesso identico tempo. In altre parole, la differenza tra tempo iniziale e tempo finale è proprio quella necessario alla luce per percorrere due volte il raggio della circonferenza.

Il tutto è rappresentato in Fig. 38 Stabiliamo i tre eventi: (a) partenza della luce da A; (b) arrivo della luce sulla superficie sferica; (c) ritorno della luce in A. (a) , (b) e (c) di ogni raggio luminoso sono simultanei, ossi (a) è uguale per tutti; (b) è simultaneo per tutti, così come (c).

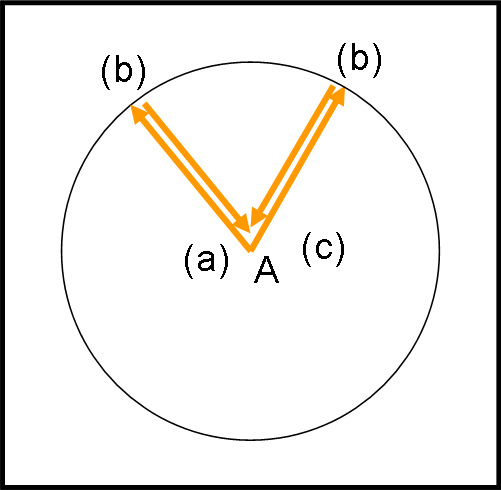
Cominciamo, commettendo un errore madornale che dimostra come questo quiz aveva una sua ragione d’essere.

A questo punto mettiamo in moto la circonferenza verso destra, con un po’ di leggerezza (e spero che tutti voi gridiate allo scandalo), muovendoci verso sinistra con una velocità v =  βc. L’astronauta continua a usare la sua “torcia” e tutto continua a funzionare perfettamente per lui. L’osservatore esterno, invece, vede un orologio di luce esteso a tutta la circonferenza-astronave. E’ inutile complicarci troppo la vita e consideriamo solo due direzioni luminose: quella verticale (la solita che usiamo sempre) e una orizzontale, ad esempio verso sinistra. Vediamo cosa viene fuori, utilizzando la Fig. 39 Per semplificare, consideriamo uguale a 1 il raggio della circonferenza, che vuole anche dire porre t = 1 e c = 1. La velocità orizzontale dell’astronave è, perciò, β = v/c = v.

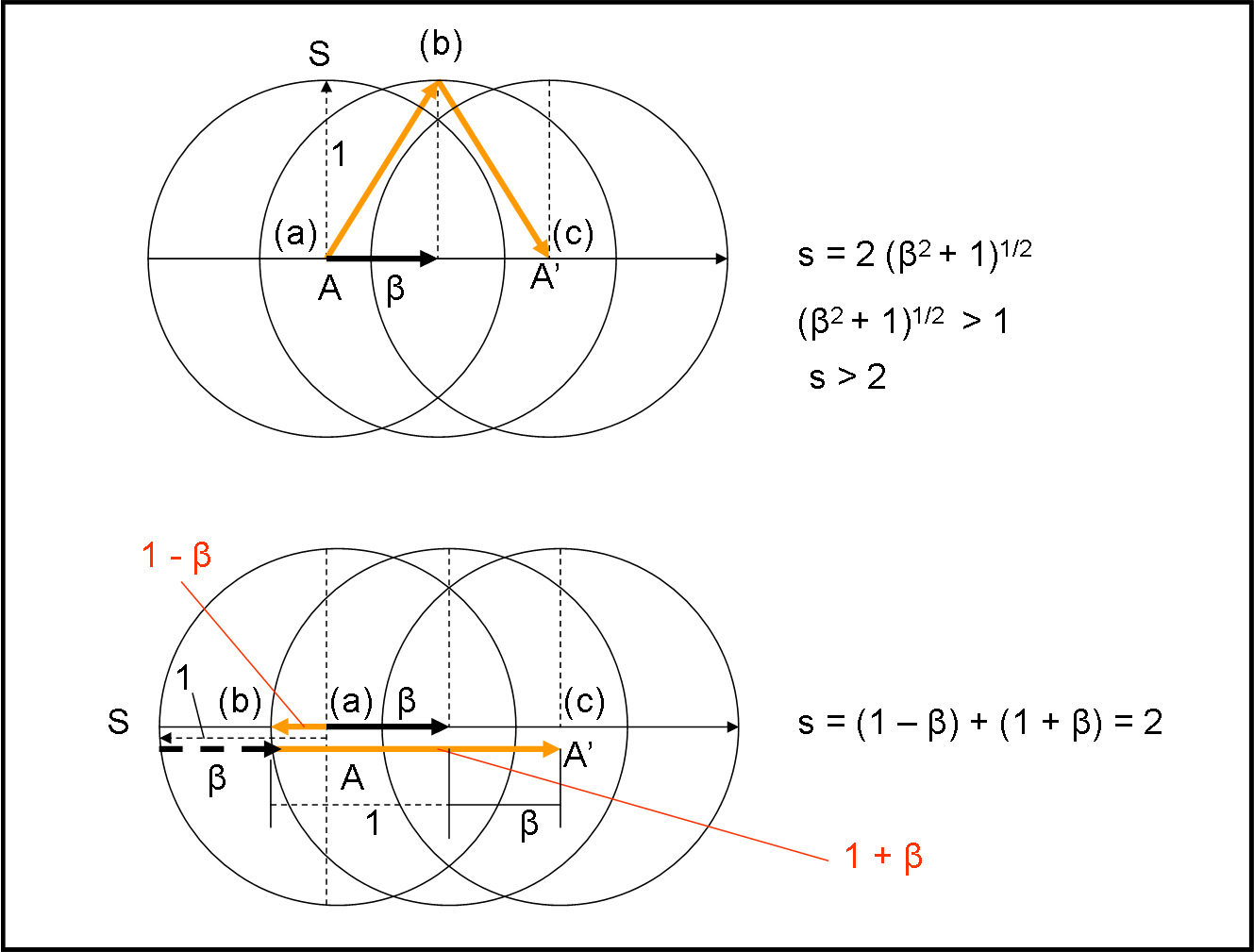
Cominciamo con la parte alta della figura che conosciamo molto bene e calcoliamo il percorso s arancione della luce. Possiamo scrivere, senza porci grandi problemi:

s = 2 (β² + 1)^1/2

Adesso, facciamo lo stesso, nella parte bassa, considerando però un raggio orizzontale. La luce parte da A e va verso sinistra. Nel frattempo, però, la circonferenza si muove verso di lei e la raggiunge in (b), dove avviene la riflessione. A questo punto, per concludere l’esperimento, basta arrivare di nuovo nel centro A’ , in accordo con quanto successo nel caso precedente. Abbiamo già detto che per qualsiasi raggio il tempo trascorso tra inizio e fine deve essere lo stesso. Se il tempo è lo stesso deve essere lo stesso anche il percorso totale s.

Calcoliamolo…

Da (a) a (b) si ha un percorso s₁ uguale a (1 – β) e un percorso s₂ da (b) a (c) uguale a (1 + β). Beh… sicuramente sono percorsi diversi, ma possiamo anche accettarlo, dato che la sfera si muove, ma sulla somma dei percorsi non ci si può sbagliare: s₁ + s₂ deve essere uguale a s del caso precedente!

Proviamo a fare la somma tra s₁ e s₂

s₁ + s₂ = 1 - β  + 1 +  β = 2

esattamente il diametro della circonferenza. Controlliamo s trovato prima:

s = 2(β² + 1)^1/2

Accidenti… (β² + 1) è una quantità sempre maggiore di 1 e tale deve essere anche la sua radice quadrata. Il che comporta che s deve essere  sempre maggiore di 2. Per essere uguale a 2 dovrebbe essere β = 0, ossia astronave ferma!

Insomma, niente da fare… abbiamo sicuramente commesso un errore, e anche piuttosto grave. Ormai lo conosciamo bene: abbiamo considerato uguali i tempi t e t’. Il tempo t funziona solo per chi è solidale con l’astronave, ma è t’ che va considerato per chi guarda da fuori. E’ sempre e soltanto un problema di simultaneità relativa. Ecco che allora possiamo andare a prendere il grafico che avevamo giustamente evidenziato nella risposta al quiz (QUI) e applicarlo alla nostra astronave in movimento, in Fig. 40 (abbiamo eliminato la circonferenza per non "pasticciare" troppo la figura)..

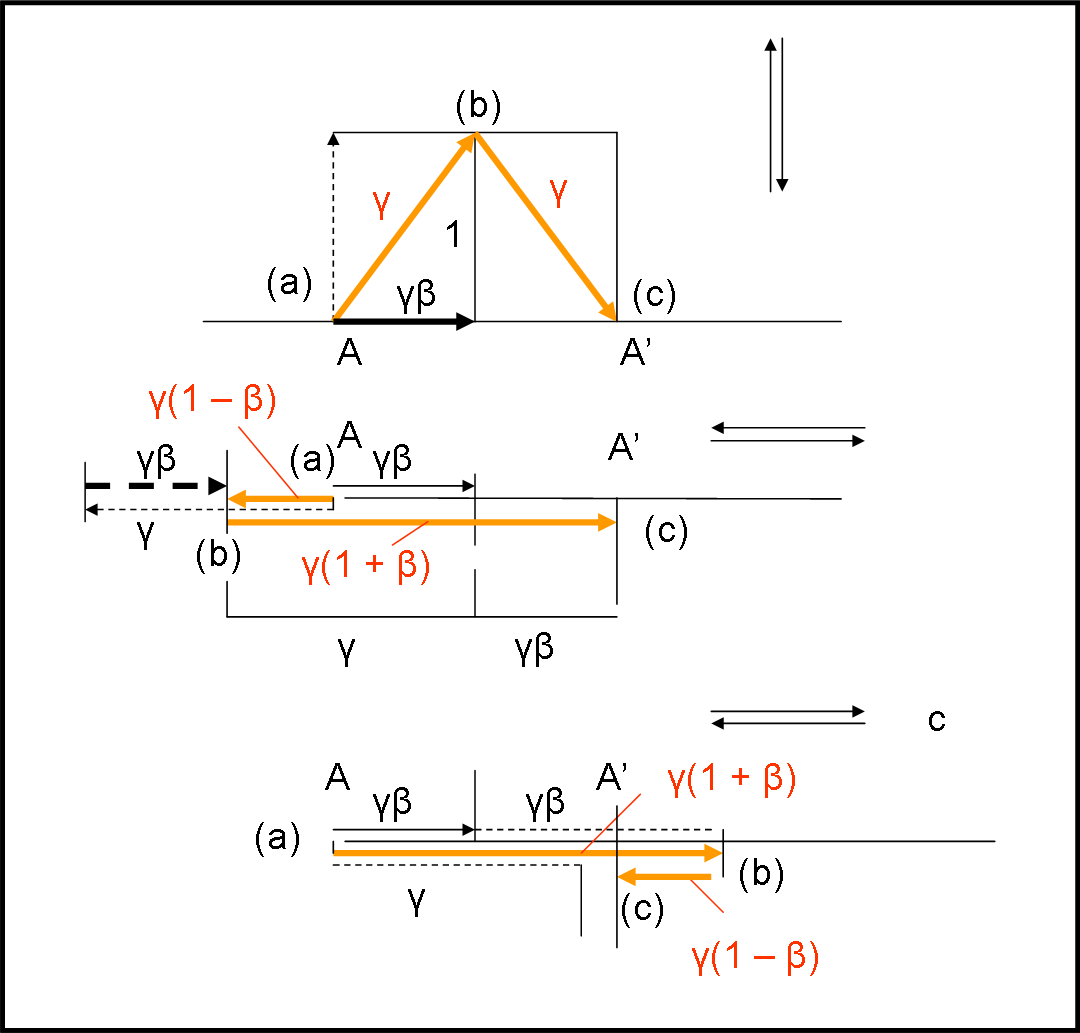
Come si vede chiaramente tutto ciò che è visto da chi sta fuori deve usare un tempo t’ che è legato a t da γ, ossia t’ = γ t. La figura precedente cambia completamente. In particolare, tutte le grandezze lungo l’asse orizzontale, quelle del moto, devono essere moltiplicate per γ.

Rifacciamo, adesso, i nostri calcoli di prima…

Cominciamo con  la luce mandata verticalmente, che ripropone perfettamente il caso classico dell’orologio di luce.

Il percorso della luce dall’inizio alla fine è adesso data da:

s = 2γ

Calcoliamo quello orizzontale, sia andando verso il senso del moto apparente, sia in senso opposto.

s = γ (1 - β) + γ (1 + β)  = 2γ

Adesso sì che ci siamo!

Cosa abbiamo trovato attraverso questo semplice calcolo?

Mandando la luce in tre direzioni, essa è tornata al punto centrale dopo aver seguito un percorso di pari distanza (e nello stesso tempo). Ovviamente, il punto di invio della luce (A) non si troverà più in A, ma in A’, al momento della ricezione.

Ne segue che il luogo dei punti in cui i raggi luminosi incontrano la circonferenza in movimento devono essere tali che la somma delle loro distanze da due punti fissi rimanga una costante (2 γ).

Abbiamo definito esattamente un’ellisse che ha i fuochi in A e A’ e che ha semiasse maggiore uguale a γ. Il semiasse minore deve essere uguale a 1 e la sua eccentricità è data dalla velocità della sfera β. Infatti, una nota proprietà dell’ellisse dice che la distanza tra centro e fuoco (γ β) divisa per il semiasse maggiore (γ) dà proprio l’eccentricità, ossia β.

E’ allora facilissimo costruirla (potremmo anche disegnarne una a caso e trovare subito a che velocità si riferisce). Nella Fig 41.  usiamo la direzione della luce come abbiamo fatto negli articoli precedenti: A riceve la luce e si muove verso destra, che è poi la stessa situazione di A fermo che vede l’Universo venire verso di lui.

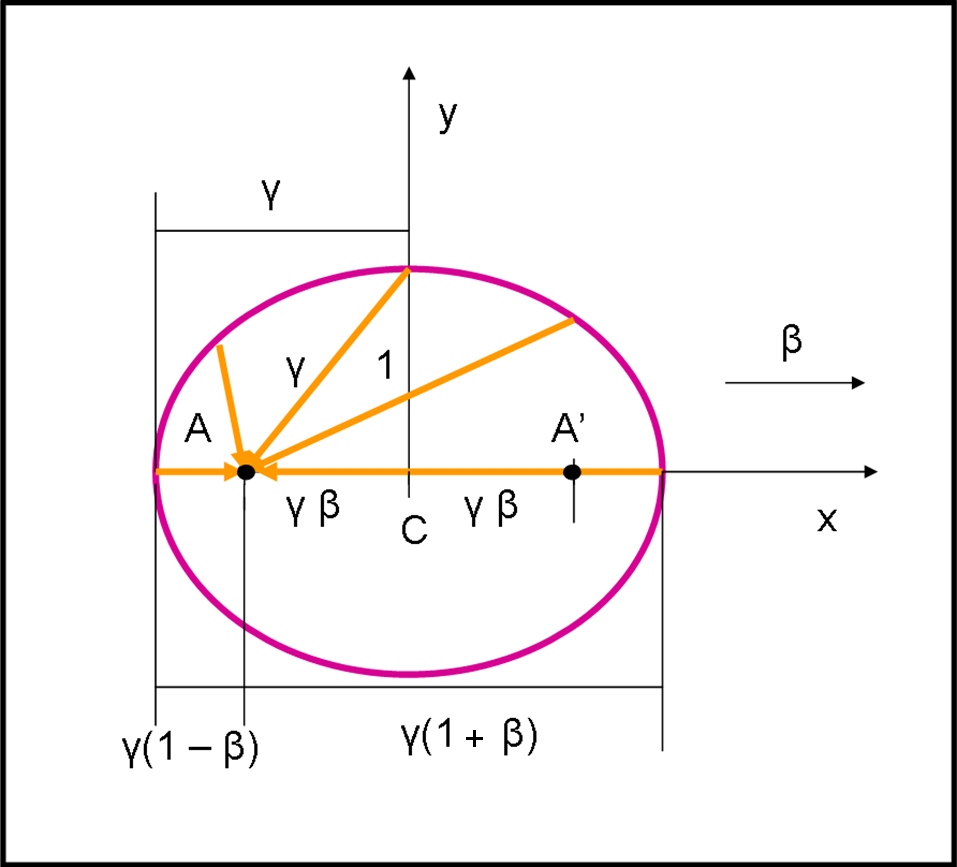
Per ragioni di simultaneità relativa tutti i tratti percorsi dalla luce che arriva dalla sfera all’astronauta devono essere uguali (non lo sono solo perché bisogna tener conto della dilatazione dei tempi relativistica, data proprio dal fattore γ). Notate che abbiamo delle lunghezze e stiamo parlando di tempi… La ragione è semplice: ct = t = spazio percorso.

L’ellisse centrata in C (punto di mezzo tra A e A’) è data da:

x²/a² + y²/b² = 1

nel nostro caso, si ha:

x²/γ² + y² = 1

o, spostando l’origine nel fuoco A:

(x - γβ)²/γ² + y² = 1

Siamo tornati alla nostra rappresentazione della deviazione dei raggi luminosi per effetto dell’aberrazione, ma adesso abbiamo anche la lunghezza dei percorsi compiuti che differiscono a causa del fattore di dilatazione dei tempi γ. Percorsi uguali a tempi dilatati e quindi legati alle frequenze della luce nelle varie direzioni. Potremmo già costruire tutto ciò che vogliamo e, in  particolare, cosa vede un astronauta che viaggi a una certa velocità: luce distorta e colorata in modo diverso. D’altra parte abbiamo tutti i parametri dell’ellisse…

Tuttavia, conosco i miei “polli” e qualcuno storcerà un po’ il naso… Penserà: “Bello, bello... ma non abbiamo tenuto in conto della contrazione delle distanze e, poi, questo fatto che i percorsi sono uguali ai tempi mi convince, ma non poi tanto… sarebbe bello avere una costruzione dell’ellisse più concreta. L’ideale sarebbe vederla nel diagramma di Minkowski!”. E avrebbe proprio ragione…

E’ quello che faremo nella seconda parte, tenendo presente che la descrizione diventerà molto più chiara, dato che seguiremo tutti i passaggi fino a vedere nascere la nostra ellisse come per magia, ma introdurremo il tempo e le figure saranno tridimensionali (per lo più), dato che lo spazio va visto in due dimensioni. Mettete in conto, quindi, una fatica supplementare nel capire le figure (giocoforza più intricate), ma anche una soddisfazione particolare quando tutta l’avventura del nostro astronauta sarà compressa in pieno. Direte sicuramente: “Questo Minkowski era proprio un genio! Col suo diagramma si può ottenere proprio di tutto e di più…”