Questo articolo è stato inserito nella sezione d'archivio dedicata alla Relatività Ristretta, in Relatività, velocità della luce e buchi neri.

 

Questo lungo articolo copre tutti gli aspetti (o quasi) dell'ABERRAZIONE LUMINOSA. Un fenomeno di interesse estremo sia consideratolo attraverso la fisica classica che attraverso la relatività, di cui è una semplice approssimazione. Come si vede gli asterischi sono variabili, da due a quattro, a seconda della trattazione che si utilizza, Sta al lettore decidere se seguire il tutto o saltare gli argomenti più ostici. Per questi ultimi è necessaria una preparazione di base della relatività ristretta e della sua rappresentazione nel diagramma di Minkowski. Per gli altri basta solo un minimo di attenzione e di volontà di capire. In ogni modo, entrambe le strade portano a una conclusione che reputo soddisfacente.

Dico la verità… all’inizio volevo accontentarmi di una descrizione più o meno accurata dell’aberrazione annua (un fenomeno abbastanza controintuitivo e bisognoso di un'accurata e variegata presentazione) e poi estenderla alla visione degli oggetti celesti in movimento (come la stessa spettroscopia e l’effetto doppler) e accennare a ciò che si potrebbe vedere viaggiando a velocità sostenuta.

Ma, come sapete, l’appetito viene mangiando… e mi sono accorto che non solo potevamo introdurre l’ellisse di aberrazione tramite la relatività ristretta, ma che potevamo ricavarne l’equazione abbastanza facilmente.

Non solo, però (sarebbe stato solo un “di più” tecnico)... si poteva sfruttare l’argomento per comprendere meglio l’esperimento dell’orologio di luce e generalizzarlo anche ad altre direzioni dello specchietto. Un lavoro che sarebbe servito per legare ancora una volta fenomeni osservabili, più o meno facilmente, con il diagramma ben più generale di Minkowski, anche se in modo superficiale.

Vi sono vari metodi per arrivare alla conclusione, sia sfruttando la contrazione delle lunghezze sia la dilatazione dei tempi. Ho preferito usare quest’ultima (anche se le cose non cambierebbero) per introdurre facilmente l’effetto doppler e la misura diretta dei parametri fondamentali per disegnare in quattro dimensioni (2 spaziali, una temporale e una energetica). Faremo, così, un bel ripasso e metteremo qualche puntino sulle i.

Ne segue che ciò che poteva essere concluso in un paio di capitoli, è diventato  un articolo decisamente lungo, sia di tipo intuitivo che tecnico e osservativo. D'altra parte, quando analizzeremo gli effetti dovuti all'aberrazione della luce ci renderemo conto che non è stato tempo sprecato...

Inoltre, capiremo ancora meglio che tutti i fenomeni relativistici si riducono sempre e soltanto al problema della simultaneità relativa (non per niente l’ellisse di aberrazione si chiama anche ellisse di simultaneità).

Saremo anche in grado di viaggiare veramente con un'astronave a velocità simili a quelle della luce e a vedere gli effetti a dir poco sconvolgenti. Un'introduzione a un viaggio vero e proprio verso un buco nero.

In generale, però, ricordiamoci fin da subito di una cosa molto importante: l'aberrazione luminosa è un fenomeno prettamente relativistico e la sua trattazione "classica" non è altro che un'approssimazione eseguita con velocità decisamente più basse di quella della luce.

Un giorno di pioggia

Sono le condizioni "meteo" migliori per introdurre l’aberrazione astronomica, la versione più semplice di un effetto ben più generale. Cominciamo a trattarla  in modo super elementare in modo da non lasciare alcun dubbio sull’effetto risultante.

Ci facciamo aiutare dalla Fig. 1.

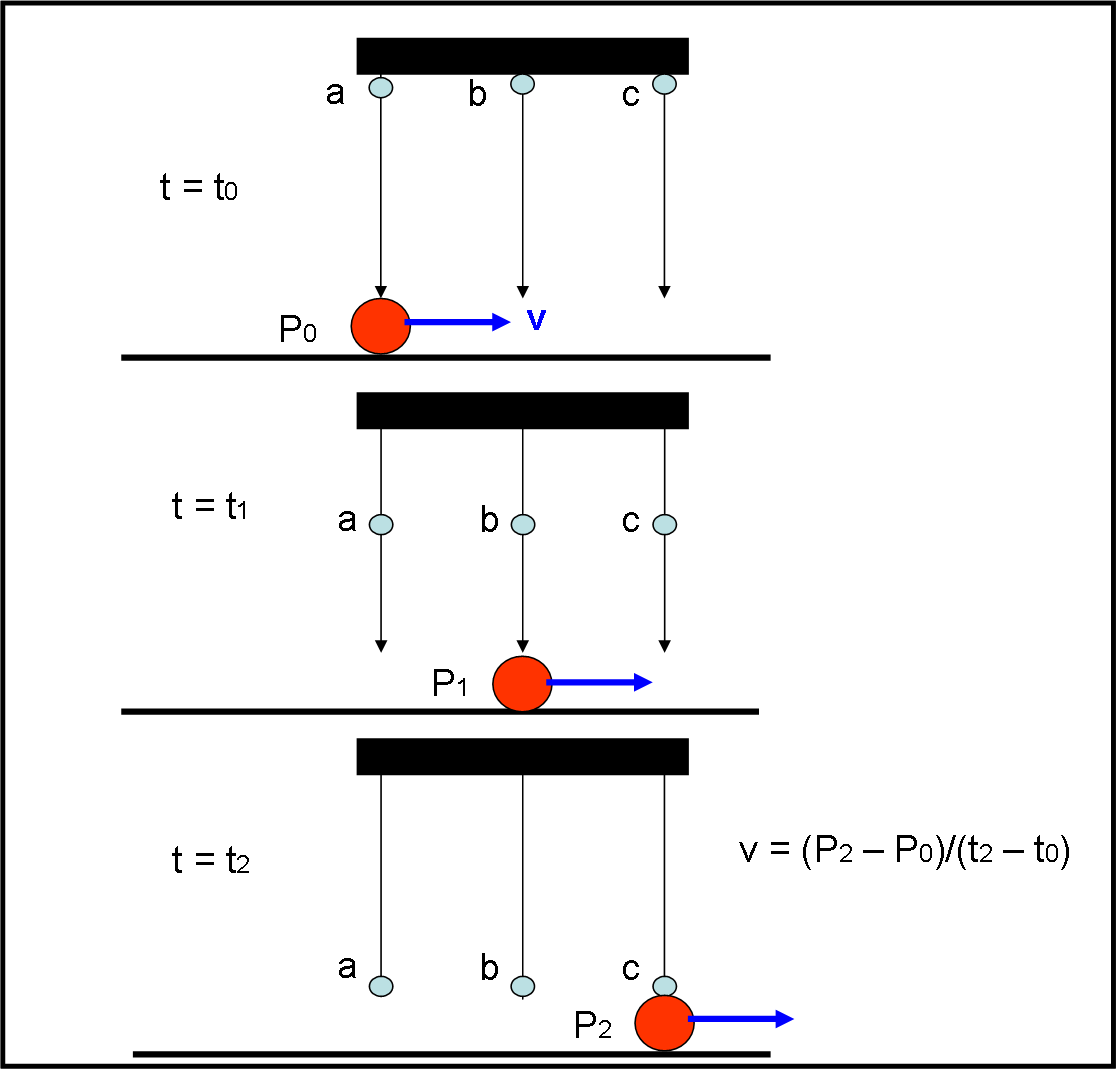
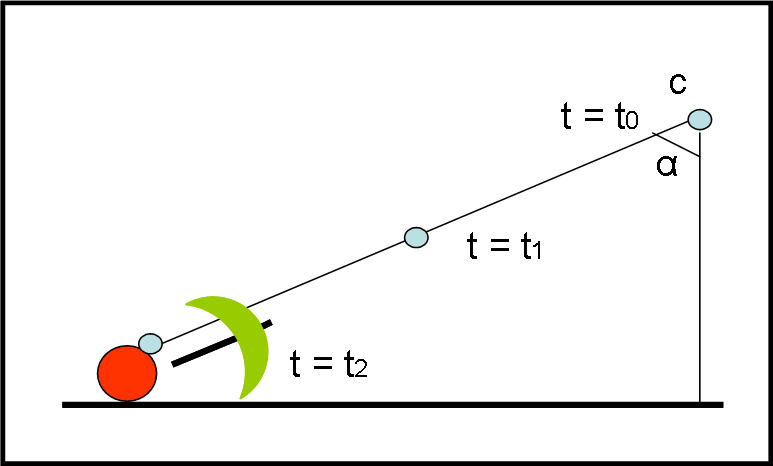
In alto c’è una nube minacciosa, da cui cadono tre gocce di pioggia (a, b e c) allo stesso istante (t = t₀). Esse si dirigono verso il basso con la stessa velocità e quindi toccano il suolo allo stesso istante t = t₂ (figura in basso). All’istante t₁ si trovano, perciò, a una certa altezza (figura mediana). Immaginiamo che ci sia una persona P (forse un papallicolo, vista la sua forma…) sulla strada. Purtroppo, non può fare molto e deve bagnarsi. Tuttavia, cerca di muoversi in fretta per cercare un riparo. La sua velocità (costante) è data da v che è, ovviamente, uguale allo spazio percorso in un certo periodo di tempo. Essa è quindi data dalla differenza delle posizioni P2 e P0 divisa la differenza tra il tempo t2 e il tempo t0. Comunque, per adesso, non ci interessa molto se non per il fatto che P si muove in modo costante.

Un osservatore, al caldo e all’asciutto, vede tutta la scena dalla finestra. Cosa può raccontare? In alto la persona P sta esattamente in P0 sotto la goccia a, ma, dato che si muove, quando essa arriva al suolo, lui non è più in quella posizione. La stessa cosa succede per la goccia b. Quando P si trova n P1 ce l’ha sopra la testa, ma ancora troppo distante. La goccia pericolosa è la c. Essa aspetta al varco la nostra persona. Quando arriva in P2, la goccia c lo colpisce sulla nuca e lo bagna.

L’osservatore esterno conclude, con grande sicurezza, che la pioggia cade esattamente in verticale e che, dato che la persona si muove verso destra, viene colpita dalla terza goccia. Tutto perfetto…

La faccenda, però, cambia notevolmente se cambiamo sistema di riferimento. Il fenomeno fisico deve essere lo stesso (P deve essere colpito in P2 dalla goccia c). Tuttavia, la descrizione del fenomeno visto da P, che si considera fermo, è un po’ diversa.

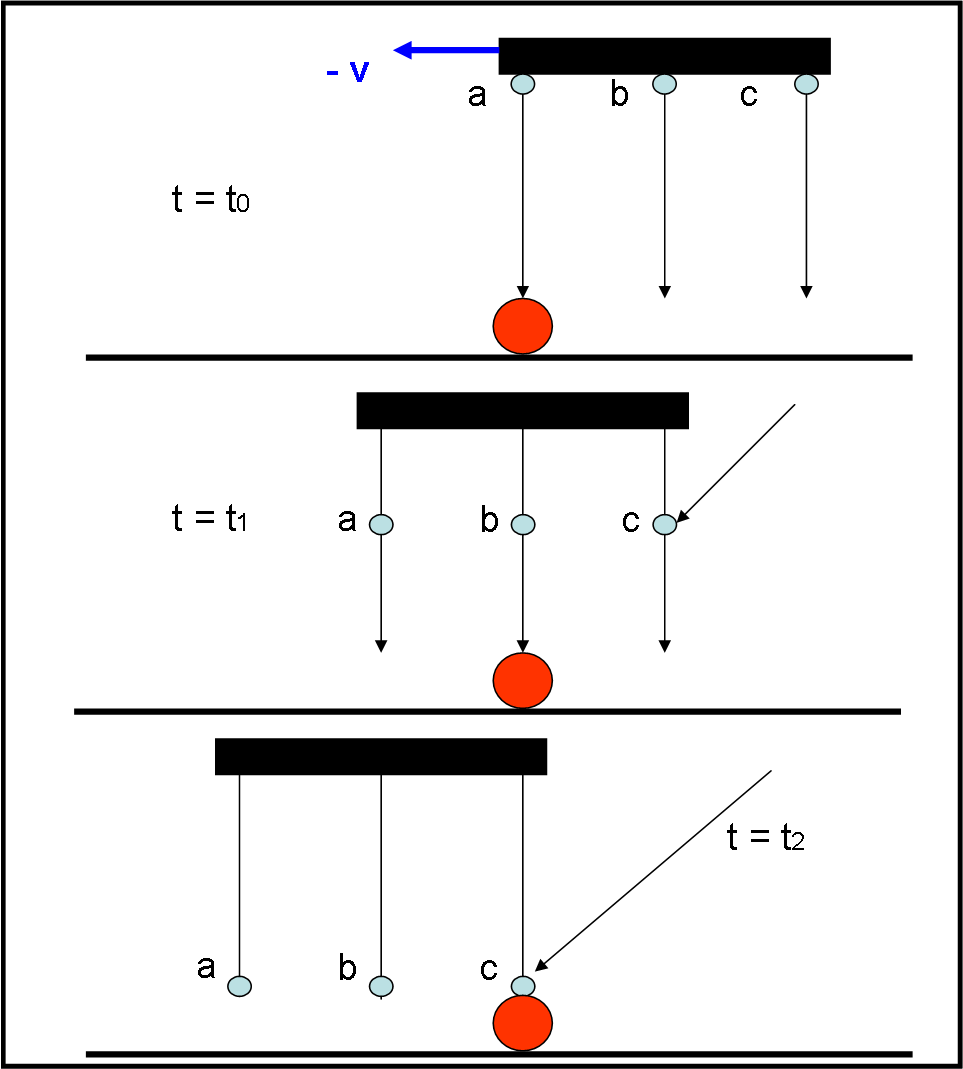
Lui vede, al tempo t = t₀, la goccia a sopra di lui, ma non si preoccupa più di tanto, in quanto tutta la nube nera si sta spostando verso sinistra con velocità -v. Ricordiamo che lui si considera fermo e quindi sono la nuvola e le gocce che si muovono verso sinistra. Non si preoccupa nemmeno della goccia b, in quanto quando arriva sopra la sua testa è ancora troppo in alto. Fin dall’inizio, il nostro P ha puntato la goccia c. Essa sembra proprio spostarsi verso sinistra in modo da colpirlo. E così capita. Il fenomeno si è verificato anche nel sistema di riferimento di P. Ma lui cos’ha visto esattamente? Presto detto: la goccia c si è mossa in diagonale e l’ha colpito in pieno.

La Fig. 2 sintetizza la visione di P.

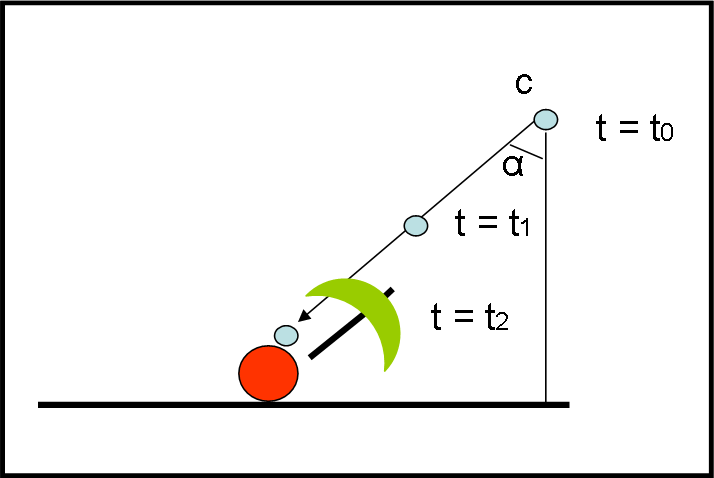
La goccia c si è diretta verso P seguendo una traiettoria rettilinea che forma un angolo α rispetto alla verticale. Se P avesse un ombrello, come dovrebbe sistemarlo per proteggersi dalla goccia c (l’unica che può colpirlo)? Nel modo rappresentato in Fig. 3, ossia diretto verso la traiettoria diagonale!

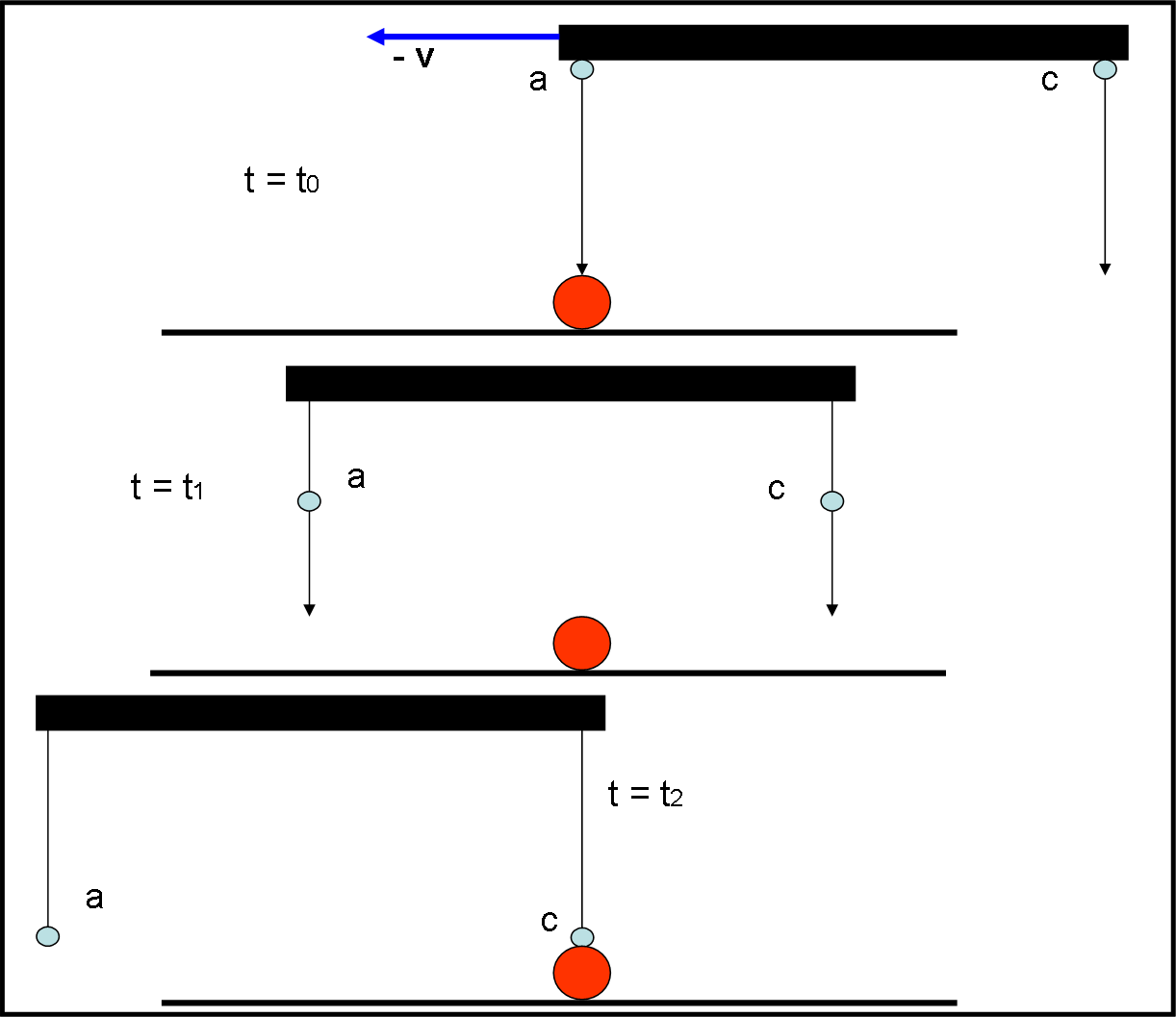
Ecco perché chi si muove mentre piove punta l’ombrello inclinandolo nel verso del moto. E più va veloce e più l’ombrello deve inclinarsi (a pari velocità di caduta della pioggia), come mostrato in Fig. 4 e 5 (abbiamo indicato solo le gocce a e c). Non c’entra niente, quindi, il vento… ma è solo una questione di composizione vettoriale di direzioni di velocità (quella di caduta e quella di fuga della persona P – le nozioni sui vettori le trovate all’inizio di questo articolo)

 

Non è difficile passare a qualcosa di più astronomico. Immaginiamo che, adesso, le gocce di pioggia siano dei fotoni inviati da una stella S (Fig. 6). Il fatto che P si muova a passo svelto conta ben poco. Ma è invece importante il fatto che la Terra si sposti lungo la sua orbita con una velocità v ben maggiore (circa 30 km/s).

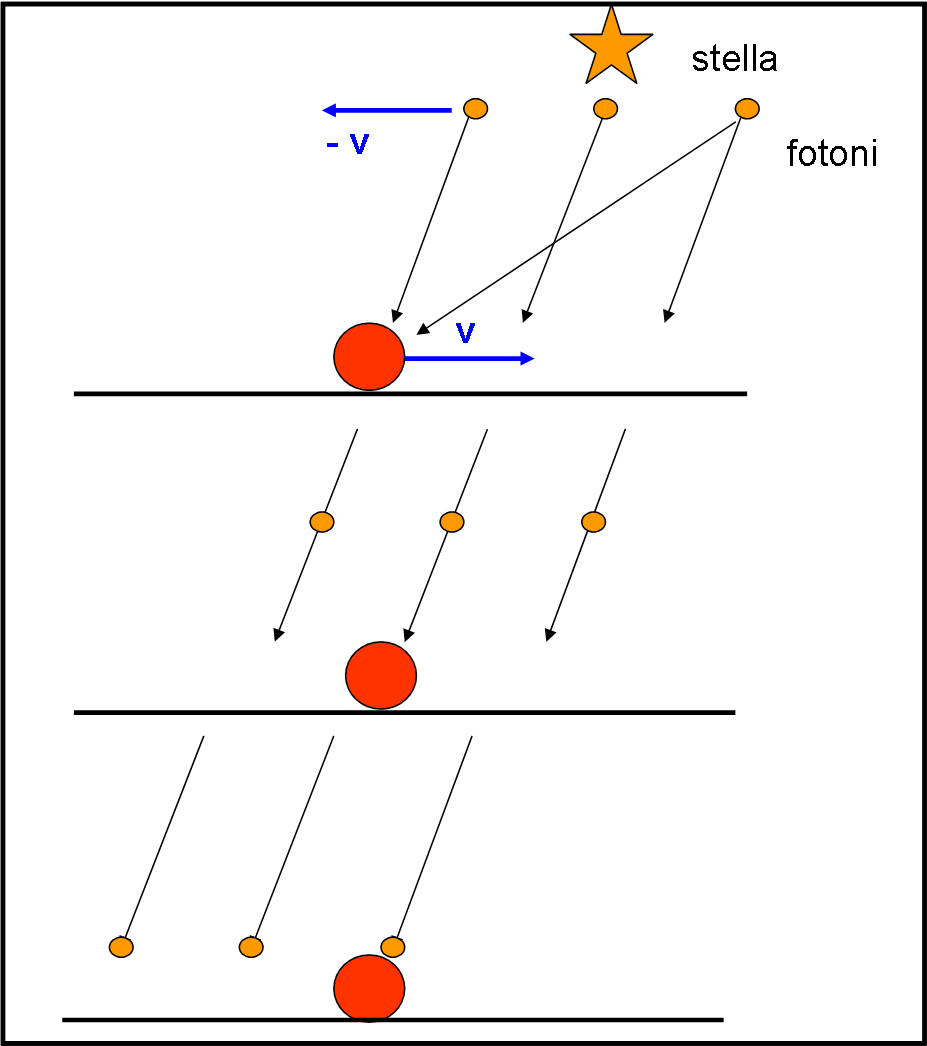
Ne deriva che per essere colpito da un fotone inviato dalla stella bisogna puntare la posizione del terzo fotone. Ne consegue, come prima, che il telescopio va inclinato di un certo angolo rispetto alla direzione vera della stella (quella che determinerebbe un osservatore centrato nel Sole, considerato fisso), come mostrato in Fig. 7. La stella sembra trovarsi in una posizione sempre diversa, che dipende dalla sua posizione nel cielo rispetto al moto orbitale della Terra.

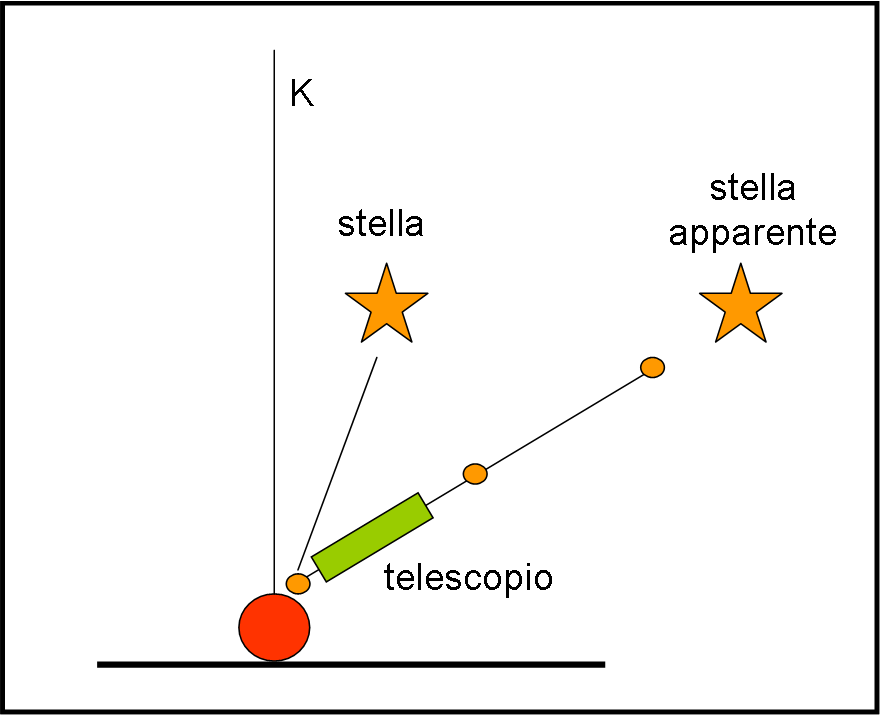
Ovviamente, noi non riusciamo a vedere il singolo fotone quando sta per arrivare, così come non riusciamo a vedere la goccia di pioggia prima che ci colpisca. Comunque, esisterà sempre una goccia o un fotone che si trovano nella posizione giusta al momento giusto. Troveremmo, così, che la posizione della stella rispetto, ad esempio, alla direzione del polo dell’eclittica K (cos’è l’eclittica lo abbiamo spiegato QUI), sarà diversa da quella che ha in un sistema eliocentrico. In realtà, il moto della Terra avviene lungo un’ellisse e quindi la posizione apparente della stella descrive anch’essa un’ellisse seguendo il moto della Terra. Questa ellisse è più grande di quella parallattica e dipende solo dalla posizione delle stelle e non dalla loro distanza.

Scegliamo un fotone fin dall’inizio

Alle stesse conclusioni arriviamo se decidiamo di catturare proprio un fotone, uno solo e non un altro! Partiamo quindi dal momento in cui il fotone tocca il centro dell’obiettivo O del nostro telescopio (a lente, per ipotesi, oppure questo oppure uno dei quali abbiamo parlato QUI). Per semplicità immaginiamo che il fotone arrivi proprio dallo zenit (la vera posizione della stella), ossia viaggi perpendicolarmente rispetto al suolo (Fig. 8).

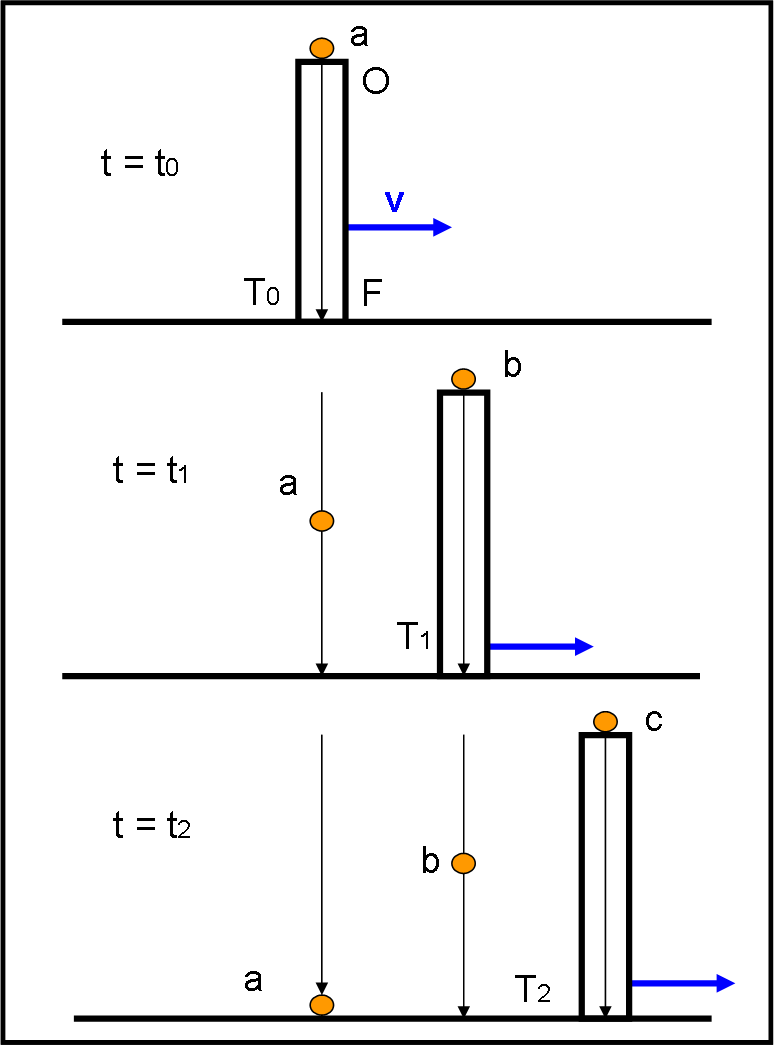
Sembrerebbe ovvio mantenere il telescopio nella stessa direzione perpendicolare… Niente di più sbagliato! Se lo facessimo il fotone finirebbe contro il tubo del telescopio e/o uscirebbe quasi subito da lui se non ci fosse il tubo (come capita per i grandi telescopi a specchio). Perché? Per il semplice fatto che il telescopio si muove insieme alla Terra. Giunto nella posizione mediana catturerebbe un altro fotone, ma non sarebbe quello di prima e inoltre uscirebbe subito anche lui dal tubo e non arriverebbe mai nel fuoco F.

Vediamo la situazione nella Fig. 9, dove ci mettiamo nel sistema di riferimento del telescopio.

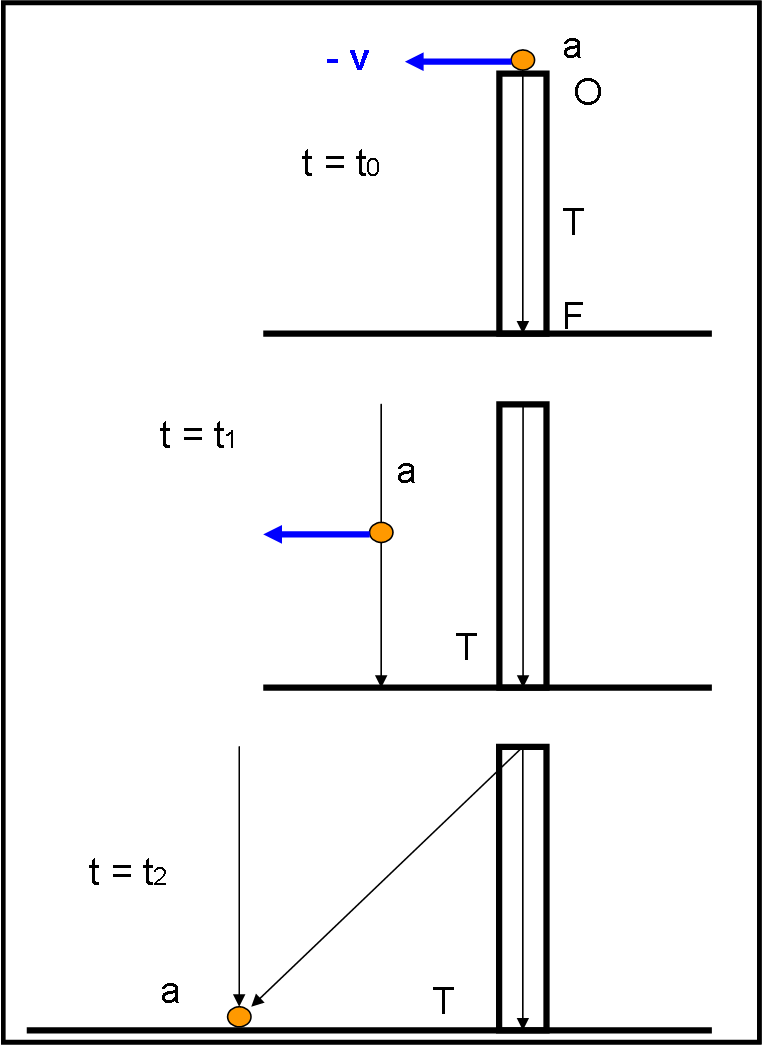
Il fotone “sembra” viaggiare in diagonale verso sinistra. La direzione del fotone è proprio quella che ci serve per puntare esattamente la stella. Dobbiamo piegare il telescopio come illustrato in Fig. 10 . Il fotone continua a cadere perpendicolarmente, ma il telescopio che si muove lo accoglie fino a portarlo al fuoco F.

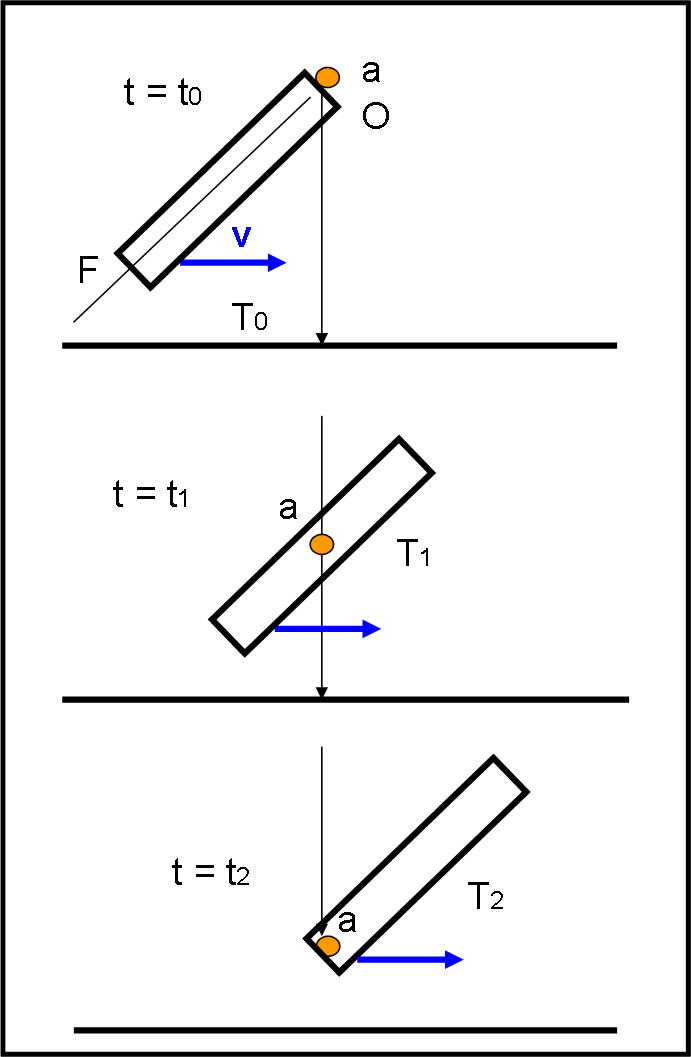
La Fig. 11 mostra cosa capita nel sistema di riferimento del telescopio, del tutto simile a quanto avevamo trovato nella Fig. 7.

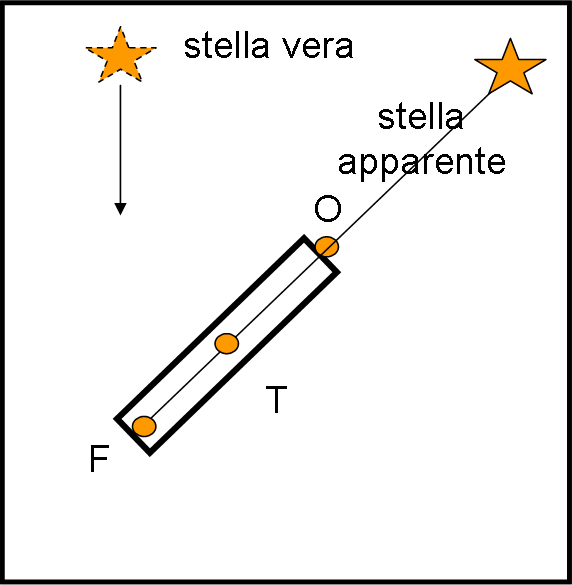
L’argomento esplode letteralmente. Innanzitutto ha permesso di calcolare la velocità della luce. Inoltre si intuisce facilmente che la combinazione vettoriale di velocità della luce e di movimento di P può dare solo una differente direzione, ma non certo una differente velocità (Einstein si arrabbierebbe non poco, visto che la velocità della luce non si può superare!). Ne consegue un legame strettissimo con la relatività ristretta (la nostra astronave sta riscaldando i motori). In altre parole, l’aberrazione è un fenomeno relativistico che può essere risolto anche in modo classico (basta solo evitare di sommare esplicitamente la velocità della luce con la velocità della Terra o di chi per lei.

Insomma, ne avremo per tutti i gusti, non ultimo l’effetto di questo fenomeno sulle coordinate geocentriche delle stelle. La prossima volta inseriremo qualche formuletta veramente banale...per poi arrivare alla formula data dallo stesso Einstein nel 1905. Dovremo stare molto attenti ai segni (sul web si fa un po' confusione), dato che nel caso dell'aberrazione annua  è la Terra che si muove, mentre, in  altre applicazioni relativistiche, si muove la sorgente luminosa. Ancora una volta, occhio ai sistemi di riferimento.

Prima di cominciare a scendere nei dettagli, però, digeriamo bene il concetto di base, altrimenti i dubbi diventeranno ostacoli invalicabili nei prossimi articoli.

Aberrazione annua: una scoperta quasi casuale

Abbiamo appena visto che il moto della Terra attorno al Sole implica un fenomeno di aberrazione che ci fa vedere una stella in una posizione diversa da quella reale. In poche parole è un fenomeno che è strettamente legato a quello della parallasse annua, fondamentale per la determinazione delle distanze stellari.

Sappiamo già che la parallasse annua delle stelle era stata prevista da quel genio assoluto che era Aristarco,  che aveva anche cercato inutilmente di misurarla. Sarebbe stata la prova diretta della teoria eliocentrica. Purtroppo per avere questa “prova” si dovette aspettare il 1727 d.C. per merito dell’inglese James Bradley, ma attraverso un fenomeno del tutto inatteso. Permettiamoci di "colorire" un po’ la “storia”.

Era ormai più di un secolo che  Galileo aveva usato il telescopio per cambiare volto al Cosmo. Tuttavia, la prova diretta della teoria copernicana non era ancora stata ottenuta. Per ottenerla bisognava rifarsi ad Aristarco e “vedere” la rivoluzione della Terra impressa nella variazione apparente della posizione di una stella nel cielo. In altre parole, misurare la sua parallasse.

Nel 1727 Bradley si convinse che la strumentazione era giunta al livello necessario e si dedicò a studiare la variazione della posizione apparente di una stella scelta in modo che gli altri fenomeni, come la rifrazione, non dessero troppo fastidio. La candidata fu γ Draconis. La osservò durante un anno intero e sembra ancora di vederlo gridare: “Eureka!”. Ce l’aveva fatta, la stella si spostava nel cielo seguendo un’ellisse, proprio quella prevista da Aristarco. La prova decisiva che la Terra rivolveva attorno al Sole. Finalmente…

I guai, però, cominciarono presto: la stella scelta doveva essere veramente vicina, molto di più di quanto si pensasse. Lo spostamento era di 20 secondi d’arco che corrisponderebbero (con le nostre unità di misura) a circa 0.16 anni luce (più o meno). Molto, comunque, ma non poi così tanto. La strumentazione era ormai più che capace di misurare senza errori significativi un angolo di questo tipo. Questa sembrava, perciò, la realtà…

Bradley, però, iniziò a misurare altre stelle in posizioni diverse rispetto all’eclittica e ciò che trovò gli fece rizzare i capelli in testa (sempre che fossero realmente suoi e non solo una parrucca). Tutte le stelle mostravano uno spostamento massimo uguale a 20 secondi d’arco. Le ellissi apparenti si schiacciavano ma il semiasse maggiore restava uguale. Per una stella proprio sull’eclittica l’ellisse diventava un piccolo tratto “rettilineo”, il cui spostamento rispetto al centro, però, era sempre di 20 secondi circa.

La conclusione sembrava ovvia e sconvolgente: le stelle erano proprio fisse e tutte poste alla stessa distanza da noi. Era stata dimostrata la teoria copernicana, ma si doveva accettare una specie di telone sferico (sfera di cristallo) su cui erano incastrate le stelle. Accidenti… qualcosa doveva essere sbagliato.

Bradley, tutto era meno che uno sprovveduto e, inoltre, aveva un’intelligenza fuori dal comune. Iniziò, quindi, a pensare e a … controllare. Sì. qualcosa di strano accadeva veramente. Si formava l’ellisse parallattica è vero (o qualcosa che le assomigliava molto), ma lo spostamento della stella era “sfasata” di 90° rispetto a quella prevista a causa della parallasse. Cerchiamo di comprendere bene questo punto, richiamando cosa si dovrebbe vedere nel caso si misurasse veramente la parallasse stellare.

Mettiamoci nelle condizioni più semplici, ossia consideriamo una stella posta perfettamente nella direzione del polo dell’eclittica, ossia perpendicolare all’orbita terrestre.

Consideriamo, perciò, la Fig. 12

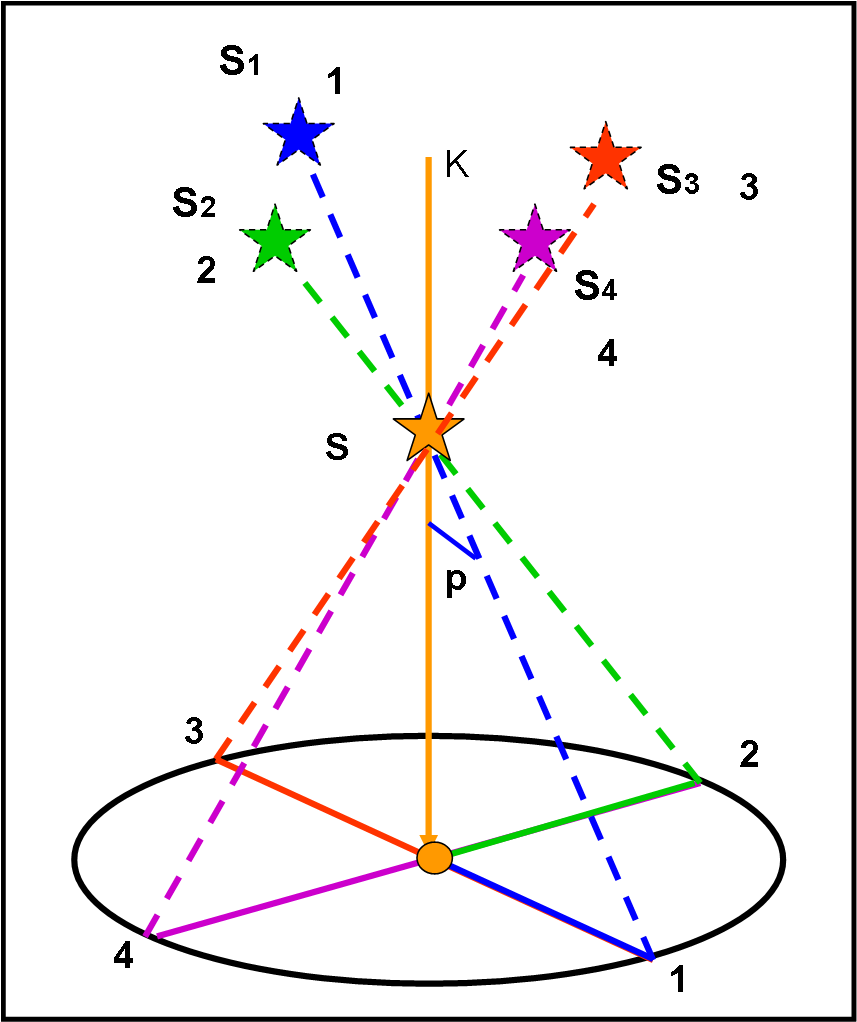
Segniamo 4 posizioni lungo l’orbita terrestre considerata circolare (1, 2, 3 e 4). La posizione vera della stella sia S.

Si tracciano facilmente le direzioni della stella viste dai quattro punti, che differscono tra li loro di circa tre mesi. Nel sistema di riferimento dell’osservatore (che, come al solito si considera fermo), le quattro direzioni danno luogo al cono di Fig. 13.

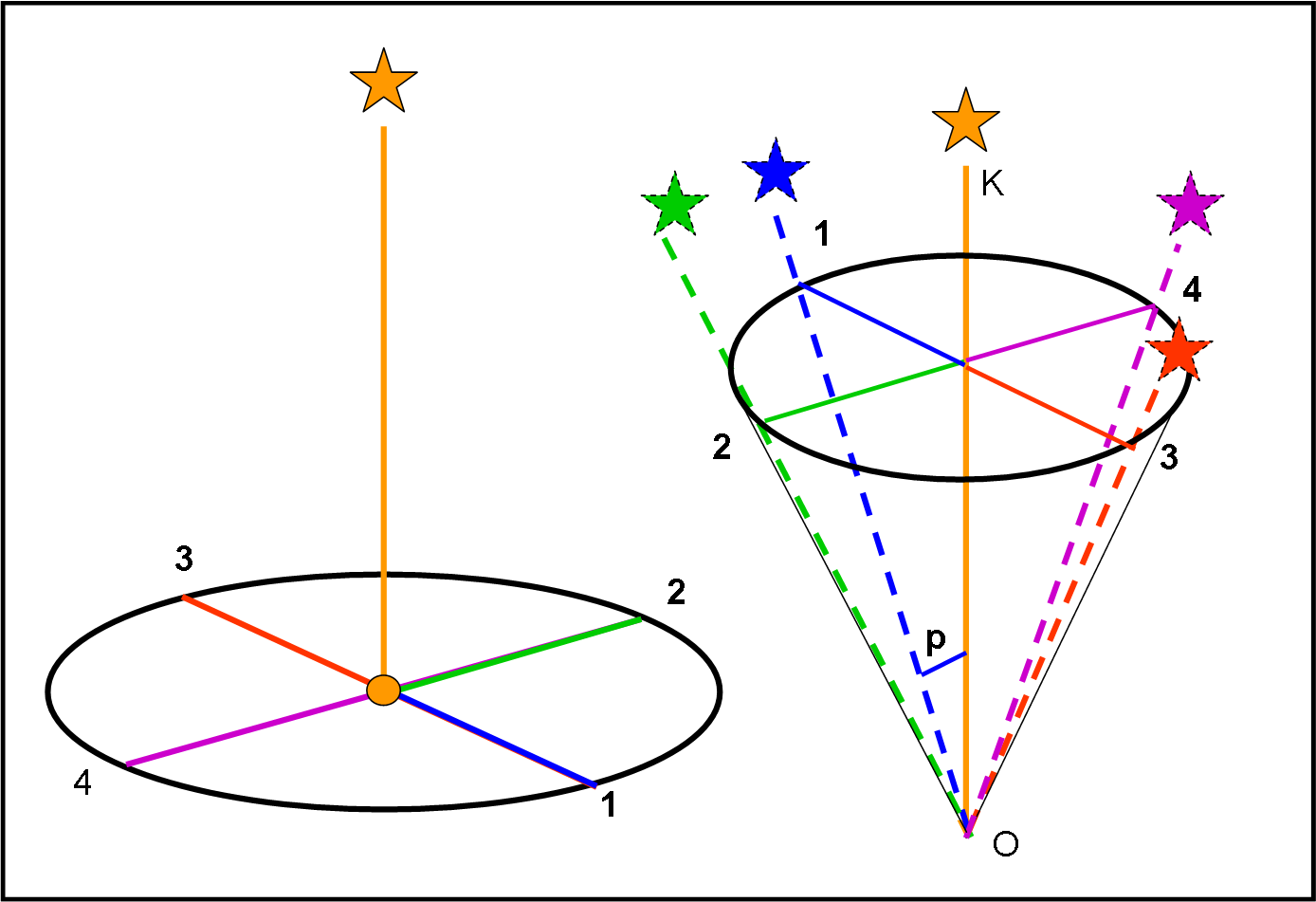
Si vede molto bene come la posizione 1 dia luogo alla direzione di S₁, la posizione 2 alla direzione S₂ e via dicendo. In poche parole, se mi sono spostato verso destra rispetto al Sole seguendo l’orbita terrestre, la direzione apparente della stella si è spostata verso sinistra rispetto al Sole.

L’apertura del cono p è proprio l’angolo di parallasse e dipende fortemente dalla distanza della stella dal Sole. Ovviamente, in questa configurazione (stella perpendicolare al piano dell’eclittica), l’ellisse di parallasse diventa proprio una circonferenza. Per ottenere un’ellisse basterebbe inclinare la direzione della stella S (ad esempio verso la posizione 1). L’asse maggiore rimarrebbe quello che corrisponde alle direzioni 2 e 4, ossia non cambierebbe mai al variare della direzione e a parità di distanza,  mentre l’asse minore sarebbe lungo la direzione da 1 a 3 e quindi si accorcerebbe sempre più. Al limite, per una stella posta proprio sull’eclittica, l’ellisse si ridurrebbe al “segmento” nella direzione da 2 verso 4. In ogni modo, a parità di distanza, il valore del semiasse maggiore, diventato segmento, sarebbe sempre p.

Possiamo vedere l’intera faccenda nella Fig. 14, dove l’orbita terrestre è vista di taglio (direzione da 1 a 3).

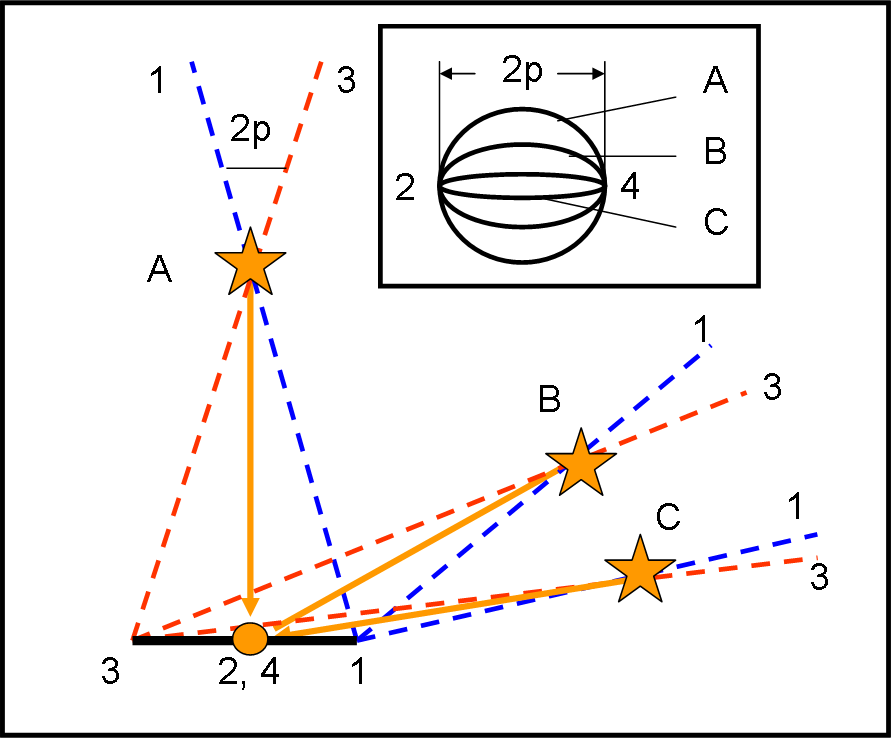
La stella S assume tre posizioni (A, B e C). Nel caso A siamo nel caso precedente e l’ellisse risulta una circonferenza di diametro 2p. Nel caso B, direzione inclinata verso 1, l’ellisse mantiene l’asse maggiore uguale a 2p (due volte l’angolo di parallasse), ma l’asse minore si restringe, per diventare quasi nullo per la posizione C. Il valore del semiasse minore è facilmente ricavabile, ma lo faremo con maggiore precisione riferendoci al quarto sistema di coordinate celesti.

Le cose cambiano di molto se ci occupiamo dell’aberrazione. In questo caso non è necessario fissare una distanza per la stella S. La distanza non conta assolutamente niente e porterebbe a una inutile confusione. Possiamo, perciò, considerare una stella all’infinito in modo che i suoi raggi siano paralleli e tutti perpendicolari al piano dell’eclittica (Fig. 15).

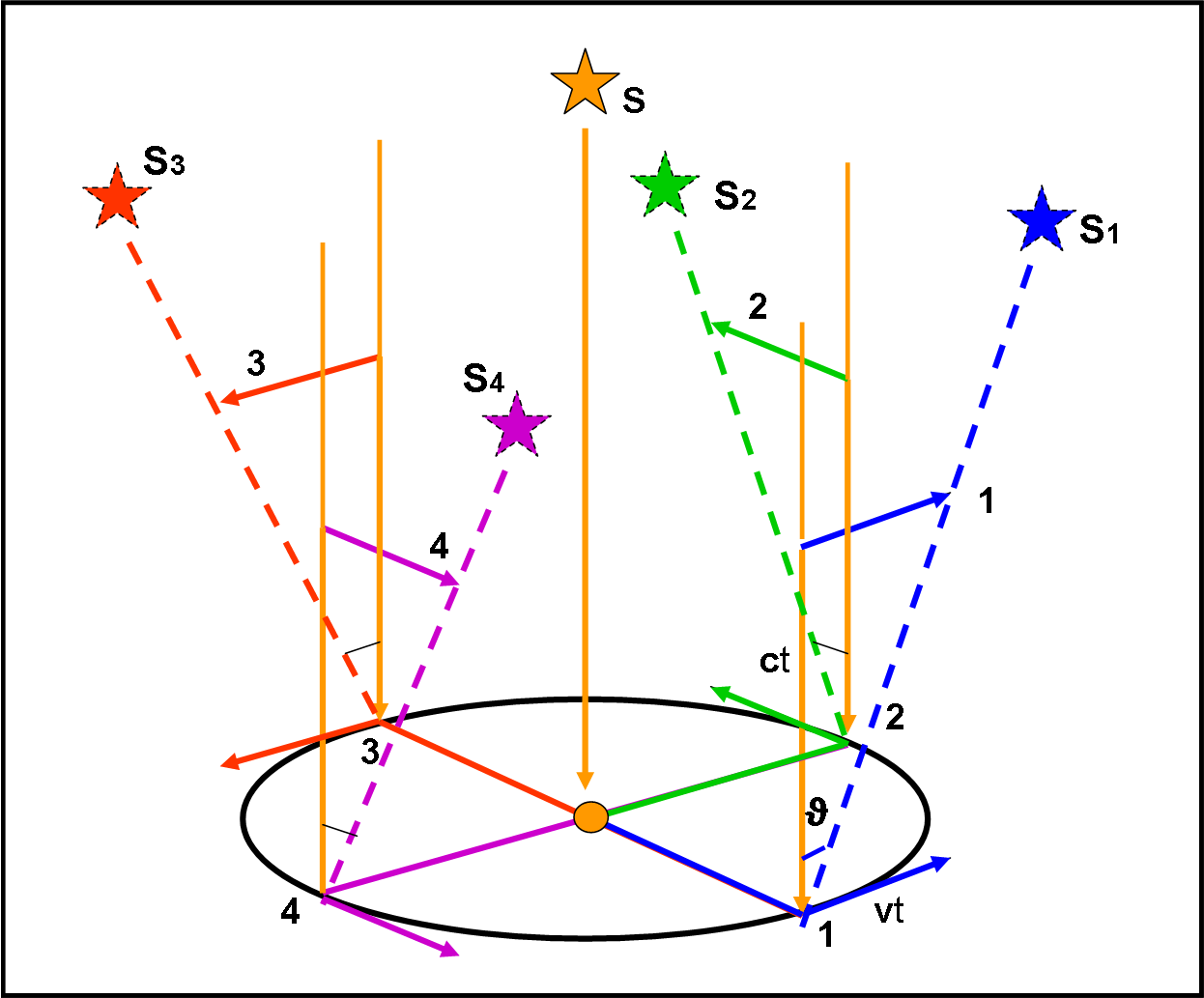
Consideriamo nuovamente le quattro posizioni di prima (1, 2 , 3 e 4). Cosa succede in 1? La stella viene vista più in basso rispetto alla direzione vera, secondo quanto spiegato nel capitolo precedente. Per  trovare l'angolo di "inclinazione" del telescopio, possiamo considerare il tragitto della luce dal momento in cui tocca l'obiettivo del telescopio fino ad arrivare al fuoco. Esso è dato da ct. Nello stesso tempo t il telescopio si è spostato di vt (dove v è la velocità della Terra).  E’ facile disegnare la linea tratteggiata azzurra che forma un angolo ϑ rispetto alla verticale, proprio l'angolo di cui dobbiamo inclinare il telescopio per vedere la stella. Trovato l'angolo possiamo mandare la linea fino alla sfera celeste, dove si possono leggere solo angoli tra i vari astri.

Stiamo molto attenti a ciò che stiamo per dire: alla posizione 1 corrisponde lo spostamento 1. La stessa cosa capita per le altre tre posizioni. Dopo un anno l’osservatore disegna ciò che ha osservato nel suo sistema di riferimento, come mostra la Fig. 16. Tutte le linee dirette verso la stella apparente, nei vari punti dell'orbita, vengono, ovviamente, disegnate a partire da un unico punto-osservatore O. L'ellisse a sinistra indica il percorso effettuato dall'osservatore lungo l'orbita. L'ellisse a destra è quella che identifica il cono formato dalle corrispondenti direzioni apparenti della stella. Per una posizione 1 a sinistra, corrisponde la direzione 1 a destra. Si vede chiaramente che la posizione del punto sull'orbita è dato dal segmento che unisce il Sole al punto 1 (sinistra) nel piano stella-Sole-punto, mentre la direzione della stella vista da punto 1 (linea azzurra) giace nel piano perpendicolare a quello precedente.

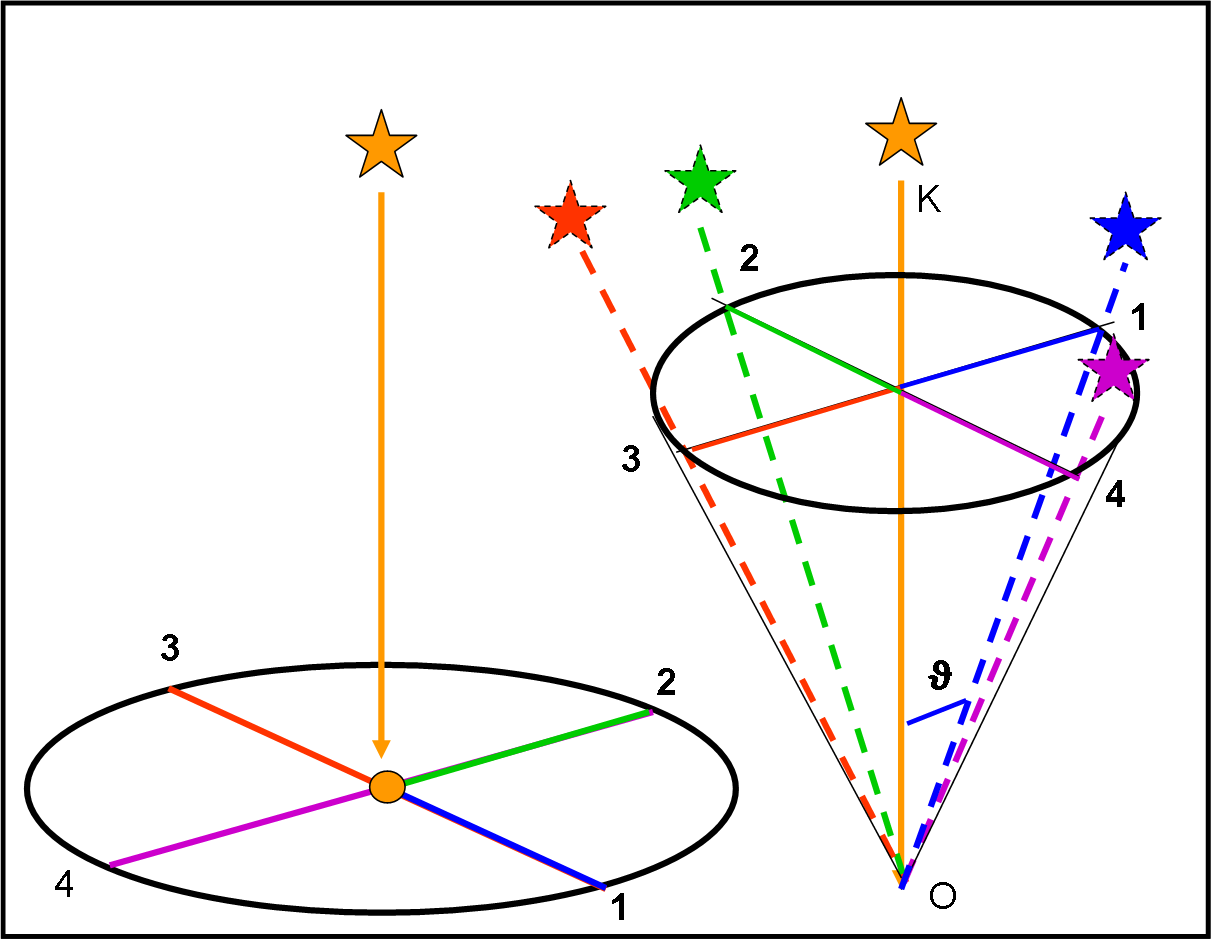
Le cose sembrano identiche alla parallasse (Fig. 13), ma sono, invece completamente cambiate. Quando l’osservatore è nella posizione 1 vede lo spostamento relativo alla direzione della stella S₁. Nella posizione 2 vede lo spostamento relativo alla direzione di S₂ e via dicendo. Tutto uguale a prima? Nemmeno per sogno: lo spostamento nel cielo avviene in una direzione che è ruotata di 90° rispetto alla posizione dell’osservatore. Infatti la Fig. 16 (che rappresenta gli effetti dell’aberrazione) non è altro che la Fig. 13 (che rappresenta gli effetti della parallasse) ruotata verso destra di 90°. Ovviamente, l'ampiezza dell'angolo del cono è decisamente diversa.

Diciamo ancora meglio: la direzione dello spostamento avviene a 90° rispetto alla direzione Sole- osservatore. Ed ecco la grande intuizione di Bradley.

La direzione Sole-osservatore è corrispondente al vettore posizione dell’osservatore 1, 2, ecc., rispetto al Sole. La direzione dello spostamento avviene, invece, secondo una direzione indicata da un vettore perpendicolare a quello della posizione. Ricordiamo che la derivata di un versore (vettore unitario, per semplicità) ha proprio una direzione a lui perpendicolare (chi vuole la dimostrazione la può trovare nell’Appendice in calce a questo capitolo).

Una direzione perpendicolare a quella di un versore posizione non può allora che essere la direzione derivata del versore posizione, che altro non è che il versore velocità.

Bradley conclude perciò che lo spostamento osservato della sua stella non è dovuto alla variazione lungo l’orbita della direzione della posizione dell’osservatore (come nella parallasse), ma è dovuto alla variazione della direzione della velocità dell’osservatore.

Ribadiamo ancora il concetto: quando l’osservatore è in 1 non vede la stella spostata in direzione opposta al Sole (parallasse), ma spostata in una direzione che è a 90° rispetto a quest’ultima, ossia c’è uno sfasamento di tre mesi.

Geniale, veramente geniale. La distanza della stella non c’entra niente: ciò che conta è solo la direzione della luce proveniente dalla stella rispetto alla direzione della velocità orbitale.

Analogamente a quanto trovato per la parallasse, il cerchio diventa un'ellisse sempre più schiacciata a mano a mano che la direzione della stella si abbassa verso l’eclittica. Cosa succede lo illustra la Fig. 17, da studiare con attenzione.

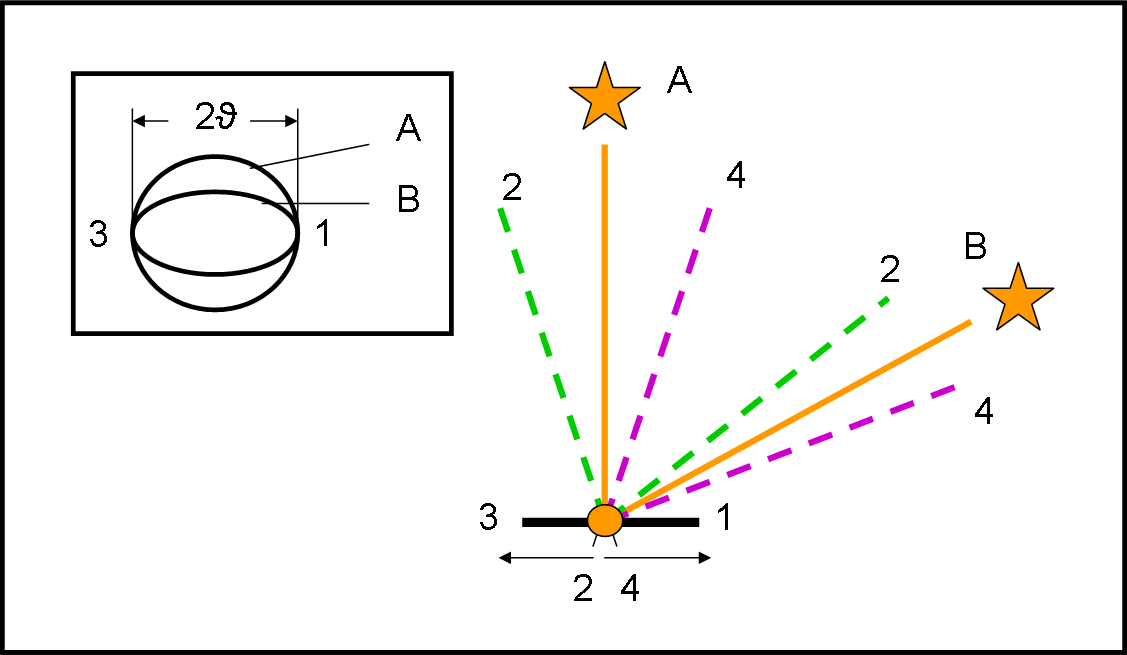
Immaginiamo di vedere di taglio l’orbita terrestre. Trovarsi nei  punti 4 e 2 dell’orbita corrisponde ad avere spostamenti della stella nelle direzioni orbitali 1 e 3 (ossia 4 e 2 sulla sfera celeste). Ciò comporta che un abbassamento verso la posizione 1 (terrestre) della stella causa una variazione degli spostamenti sulla sfera celeste nella direzione da 4 a 2. Sono proprio questi spostamenti quelli che definiscono l’asse minore dell’ellisse. Gli spostamenti lungo la congiungente 1 e 3 sulla sfera celeste rimangono quindi sempre costanti, infatti il vettore luce è sempre perpendicolare al vettore velocità in 1 e in 3 dell’orbita.

Per una stella sull’eclittica ricadiamo nel segmento che rappresenta, comunque, il semiasse che è sempre uguale all’angolo ϑ, angolo di aberrazione. Un percorso fittizio che è uguale per tutte le stelle del cielo.

Ridendo e scherzando, il grande Bradley è riuscito a ottenere un paio di informazioni preziosissime. Innanzitutto, la soluzione del triangolo dell’aberrazione può darci facilmente il valore della velocità della luce e migliorare quello ottenuto da Romer attraverso le eclissi dei satelliti di Giove (prima o poi ne parleremo in dettaglio). Inoltre, e non è cosa da meno, James ha finalmente ottenuto la prova osservativa, tanto cercata da Galileo e non solo, della teoria eliocentrica.

Facciamo fatica a pensare ad Aristarco? Sono decisamente convinto che se avesse avuto la strumentazione adatta avrebbe sicuramente capito anche lui che non si trattava della tanto cercata parallasse, ma di qualcosa relativo alla velocità  di rivoluzione della Terra. E questo malgrado a quei tempi fosse molto più facile credere alle stelle fisse incastrate in una sfera ai confini del Cosmo.

Scommettiamo?

Appendice: derivata di un versore

Conosciamo i versori (QUI) e li usiamo spesso, dato che non si portano dietro nessun modulo (sono unitari).

Eseguiamo il prodotto scalare di due versori:

v x v = |v|² = 1

v x v = 1

Deriviamola…

dv/dt x v + v x dv/dt = 0

2 v x dv/dt = 0

v x dv/dt = 0

Sappiamo che il prodotto scalare di due vettori è uguale a zero solo se i due vettori sono perpendicolari, il che vuole anche dire che la derivata del versore è perpendicolare al versore stesso.

Una ulteriore semplificazione

Per partire con il piede giusto è meglio dare un ulteriore contributo per la spiegazione della differenza tra parallasse e aberrazione.  Purtroppo, ciò che a volte sembra ovvio per chi ne ha avuto a che fare per tanti anni, può sollevare dubbi e confusioni non previsti nei non addetti ai lavori… E’ meglio, quindi, agire subito.

Costruiamo una figura (Fig. 18) di massima semplicità, in cui sono state inserite due stelle: la prima, M_V, è una stella vicina per la quale ha senso misurare la parallasse annua. La seconda, M_L, è una stella lontana che quindi non forma nessun angolo parallattico. Entrambe le stelle sono nella direzione perpendicolare al piano orbitale terrestre.

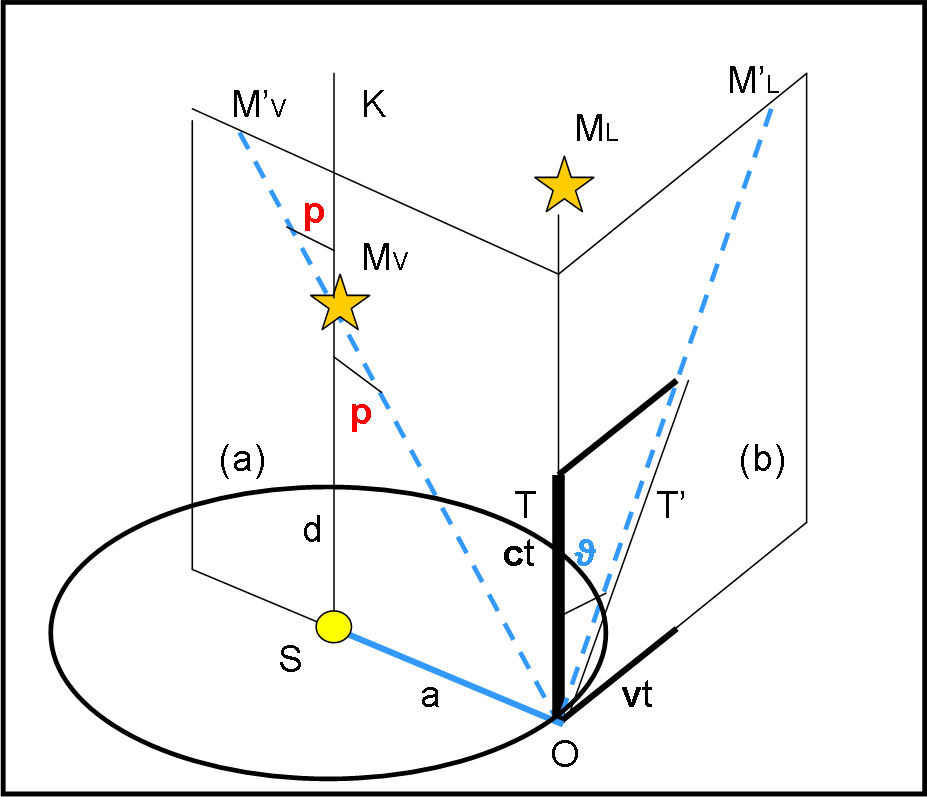
Individuiamo due piani perpendicolari tra loro. Il primo è quello che contiene la posizione O dell’osservatore, il Sole S e la stella vicina M_V (piano (a)). Il secondo piano è quello che contiene la stella lontana M_L e la direzione del moto della Terra (piano (b)). Nel piano (a) si misura la parallasse annua, data dall’angolo p. Nel piano (b) abbiamo il telescopio T che vorrebbe puntare la stella M_L. Tuttavia, a causa del moto dell’osservatore eseguito con velocità v, il telescopio va inclinato dell’angolo ϑ, angolo di aberrazione annua. Come si vede bene i due piani sono perpendicolari e tali sono anche gli spostamenti delle stelle apparenti M’_L e M’_V. Il tutto è comandato dal fatto che v è perpendicolare alla direzione del Sole.

Penso che questa figura sia più che sufficiente per vedere come agiscono parallasse e aberrazione. Tuttavia, abbiamo usato due stelle separate. Possiamo però fare un passetto in più… Se è vero che per una stella lontana non si può misurare la parallasse, ma solo l’aberrazione, non è vero il viceversa. In altre parole, per una stella vicina M_V si può misurare sia aberrazione che parallasse.

La Fig. 19 mostra questa situazione.

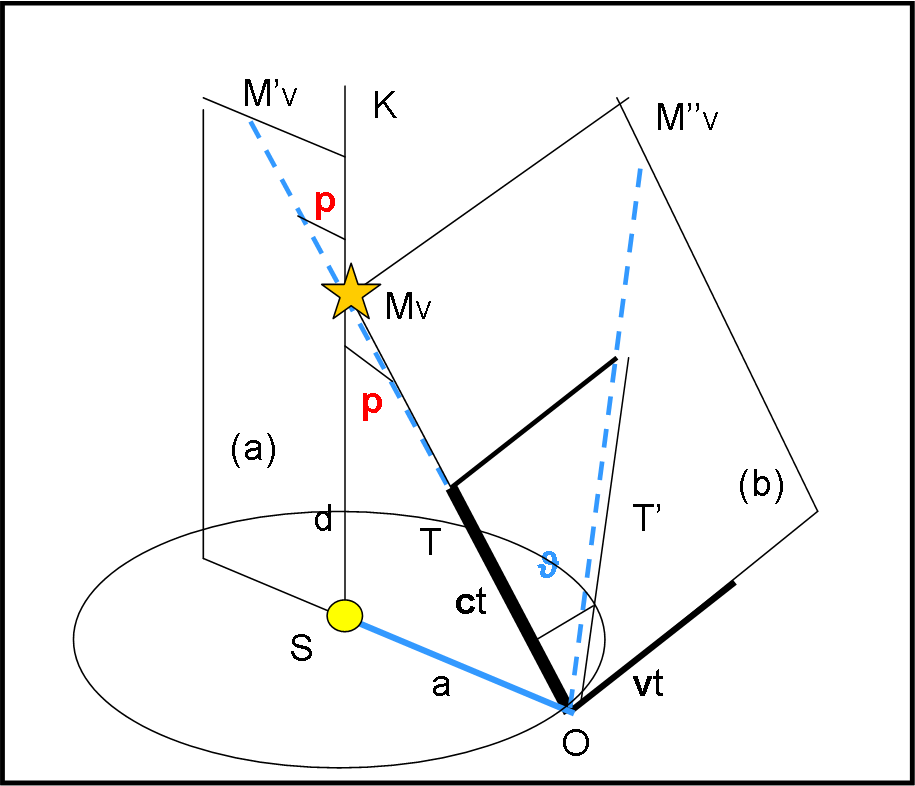
La stella è ora una sola, M_V. Il piano (a) è sempre lo stesso così come la definizione di angolo di parallasse. Il piano (b) deve cambiare, dato che deve contenere sia la direzione del moto della Terra (sempre perpendicolare alla direzione del Sole S), ma anche la stella M_V (che non si trova, perciò, per l’osservatore O, nella direzione perpendicolare al piano orbitale, come capitava prima per la stella M_L). La direzione teorica del telescopio T dovrebbe essere quella diretta verso M_V, ma, a causa del moto della Terra, essa deve piegarsi di un certo angolo ϑ, nel piano individuato dalla direzione O-M_V e da quella del moto terrestre. Notiamo, comunque, che i due piani rimangono perpendicolari tra loro, così come gli spostamenti.

Usiamo le coordinate sferiche e qualche formula

Prima di proseguire con lo studio dell’aberrazione annua e, più in generale, con i suoi effetti relativistici applicati a un astronave in volo a velocità simili a quelle della luce, cerchiamo di comprendere meglio come le ellissi apparenti si disegnino sulla sfera celeste e come si possano esprimere in termini di coordinate del quarto sistema di riferimento (QUI). Non consideratelo un discorso “noioso”… tuttavia, saltare del tutto questo capitolo non è fonte di incomprensione per le argomentazioni future. Si può anche fare, magari seguendo solo la determinazione analitica degli angolo di parallasse e di aberrazione.

Seguiamo il procedimento nel caso della parallasse annua e poi ci accorgeremo che basta ben poco per ottenere il risultato relativo all’aberrazione annua . Penso che questa trattazione dia anche un ulteriore aiuto per coglierne le differenze fondamentali.

Parallasse annua

Consideriamo due punti qualsiasi dell’orbita terrestre considerata circolare, T e T’. M sia una stella relativamente vicina. Disegniamo la Fig. 20 e analizziamo il triangolo MST, dove S è il Sole.

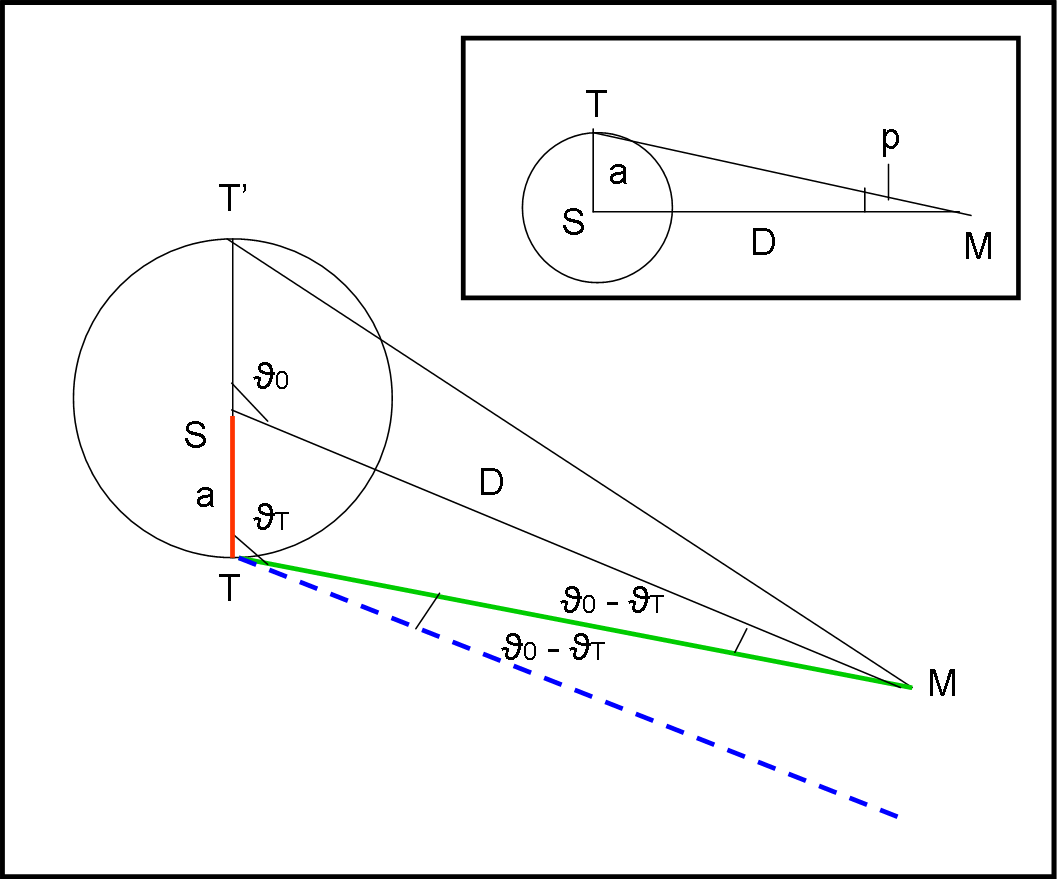
Applicando il  teorema dei seni (il rapporto tra i seni di due angoli è uguale al rapporto tra i lati opposti) si ottiene:

D/sen ϑ_T = a/sen (ϑ₀ - ϑ_T)

sen (ϑ₀ - ϑ_T) = (a/D) sen ϑ_T    ….   (1)

Definiamo parallasse annua della stella M l’angolo p tale che:

tan p = a/D        (vedi riquadro nella Fig. 20)

Essendo p sempre molto piccolo (inferiore al secondo d’arco) si può assumere:

tan p = p = a/D

Questa è la classica definizione di parallasse annua di una stella M.

Torniamo alla (1) ed eseguiamo qualche altra approssimazione più che ammissibile vista la piccola differenza tra ϑ₀ e ϑ_T.

sen (ϑ₀ - ϑ_T) = p sen ϑ_T

ϑ₀ - ϑ_T = p sen ϑ₀             …. (2)

Questa è la formula fondamentale che ci permette di calcolare la parallasse nel quarto sistema di coordinate celesti. Un esercizio che potrebbe sembrare inutile, ma che è della massima importanza per una trattazione “concreta”.

Disegniamo, in Fig. 21, la sfera celeste tracciando sia i cerchi massimi dell’equatore che dell’eclittica.

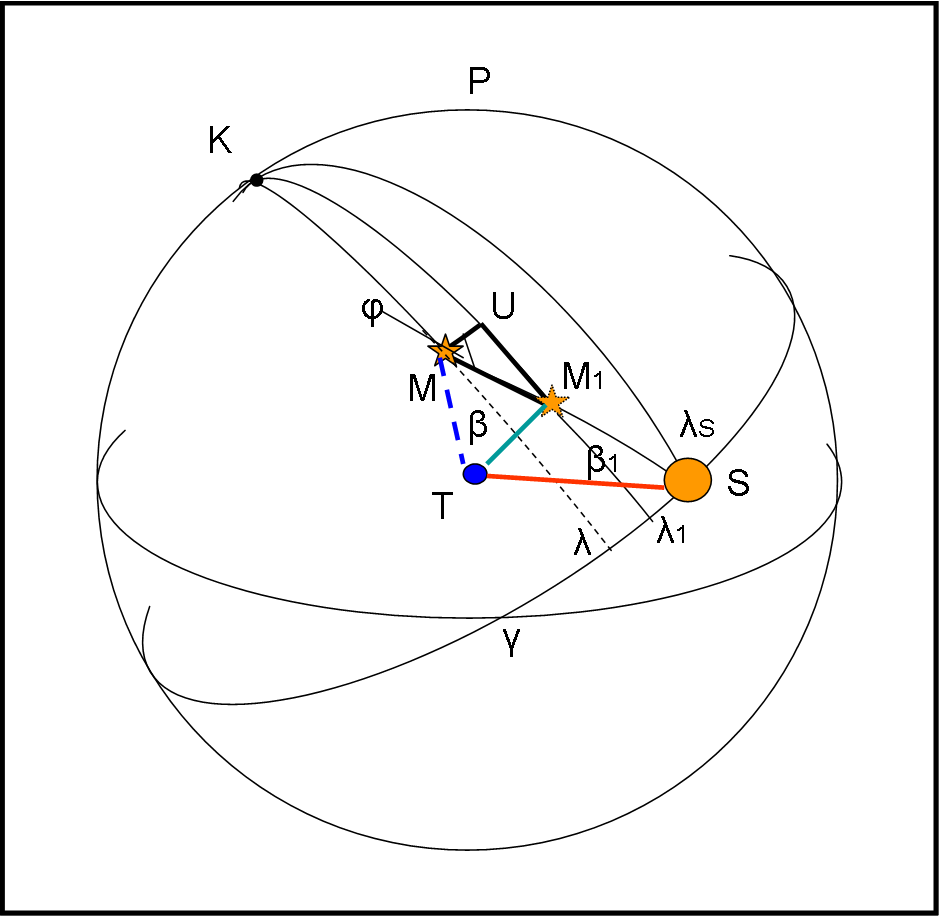
T sia al centro della sfera (condizioni geocentriche) e S sia la posizione del Sole lungo l’eclittica. M sia la posizione eliocentrica della stella (angolo ϑ₀₎. M₁ è invece la posizione della stella vista dalla Terra (angolo ϑ_T ). Per quanto detto precedentemente (basta guardare la Fig. 20 e pensare di prendere quel piano e portarlo nella Fig. 21). M₁ deve stare sullo stesso piano di S, di T e di M, dato che è la posizione di M vista dalla terra. Ne segue che M₁  deve stare sul cerchio massimo che passa da S e M.

Diciamo le stesse cose con maggiore semplicità. Prendiamo il piano di Fig. 20 e segniamo le direzioni che ci interessano a partire da T. Abbiamo la direzione TS, la direzione TM che dà luogo alla posizione M1, la direzione tratteggiata parallela a SM che da luogo a TM. Queste tre direzioni devono stare su un piano e quindi su un cerchio massimo che passa per S, pr M1 e M. In altre parole ancora: il triangolo curvilineo di vertice T e che ha come lato opposto curvilineo  il cerchio massimo SM1M non è altro che il piano di Fig. 20.

Da M tracciamo un arco di cerchio minore parallelo all’eclittica fino al cerchio massimo che passa per M₁. Chiamiamo U il punto intersezione.

Attraverso la trigonometria sferica e i sistemi di coordinate celesti siamo in grado di risolvere il problema cominciando dal triangolo MM₁U (attenzione che non è un triangolo sferico, dato che UM non è un cerchio massimo e, quindi, intrinsecamente UM è una curva e non un lato “sferico rettilineo” come UM₁ e MM₁). I suoi lati, però, sono molto piccoli e possiamo anche trattarlo come un triangolo piano.

Chiamiamo le cose con il loro nome. Le coordinate della stella M siano λ e β, mentre quelle di M₁ siano λ₁ e β₁ (longitudine e latitudine, rispettivamente). L’angolo UMM₁ lo indichiamo con φ.

Possiamo scrivere (QUI, Fig. 15) che:

UM = (λ₁ – λ) cos β

Ma anche che:

UM = MM₁ cos φ

Ponendo

λ₁ – λ = Δλ   e   β₁ - β = Δβ

Abbiamo:

UM = Δλ cos β = MM₁ cos φ          …. (3)

UM₁ è dato da:

UM₁ = - Δβ = MM₁ sen φ      …. (4)

Tuttavia, sappiamo anche che (ricordandoci il piano di Fig. 20, che si trasferisce nell'arco di cerchio massimo MM1S)

MM₁ = ϑ₀ - ϑ_T

MS = ϑ₀

Da cui, la (3) e la (4) diventano:

Δλ cos β = (ϑ₀ - ϑ_T) cos φ

- Δβ = (ϑ₀ - ϑ_T) sen φ                   

E, ancora, ricordando la (2):

Δλ cos β = p sen ϑ₀ cos φ             …. (5)

Δβ = - p sen ϑ₀ sen φ                    …. (6)

Passiamo a un triangolo sferico “vero”: KMS

MKS = λ_S – λ

KS = 90°

KM = 90° - β

KMS = 90° + φ

MS = ϑ₀

Applicando la seconda formula fondamentale (QUI insieme alla terza) si ha:

sen ϑ₀ /sen (λ_S – λ) = sen (90)/sen (90° + φ)

sen ϑ₀ sen (90° + φ) = sen (λ_S – λ)

sen ϑ₀ cos φ = sen (λ_S – λ)                  …. (7)

Applicando la terza formula fondamentale, si ha:

sen ϑ₀ cos (90° + φ) = cos (90°) sen (90° – β)  -  cos (90° – β) sin (90°) cos (λ_S – λ)

- sen ϑ₀ sen φ = - sen β cos (λ_S – λ)

sen ϑ₀ sen φ = sen β cos (λ_S – λ)          …. (8)

Sostituendo la (7) e la (8) nella (5)  e nella (6)

Si ottiene:

Δλ cos β = p sen (λ_S – λ)               …. (9)

 Δβ = - p sen β cos (λ_S – λ)             …. (10)

Possiamo permetterci di indicare UM con x e dalla (3) e dalla (9), si ha:

x = p sen (λ_S – λ)         spostamento parallelo all’eclittica             …. (11)

e indicare UM₁ con y e dalla (4) e (10), si ha

y = p sen β cos (λ_S – λ)    spostamento perpendicolare all’eclittica       …. (12)

Possiamo scriverle:

x/p = sen (λ_S – λ)

y/p sen β = cos (λ_S – λ)

Quadrando e sommando, si ottiene:

x²/p² + y²/(p sen β)² = sen²(λ_S – λ) + cos²(λ_S – λ)

x²/p² + y²/(p sen β)² = 1    equazione dell'ellisse parallattica

Che non è altro che l’equazione di un’ellisse che ha il semiasse maggiore sempre uguale alla parallasse della stella, mentre quello minore varia con la latitudine. Se essa è 90° (stella nel polo dell’eclittica) il semiasse minore diventa p e quindi l’ellisse diventa un cerchio. Se è 0°, stella sull’eclittica, l’ellisse degenera in un trattino lungo la stessa eclittica.

Potrebbe sembrare un qualcosa di “noiosamente” matematico, ma il risultato è estremamente interessante e dimostra elegantemente e compiutamente le caratteristiche dell’ellisse parallattica.

Ciò che abbiamo fatto per la parallasse può essere ripetuto per l’aberrazione annua.

Aberrazione annua

Ripetiamo ciò che capita in realtà, utilizzando il nostro telescopio di obiettivo O e di fuoco F (non fa mai male ribadire certi concetti facili a ritornare confusi).

I raggi luminosi paralleli giungono a noi dalla stella M (Fig. 22).

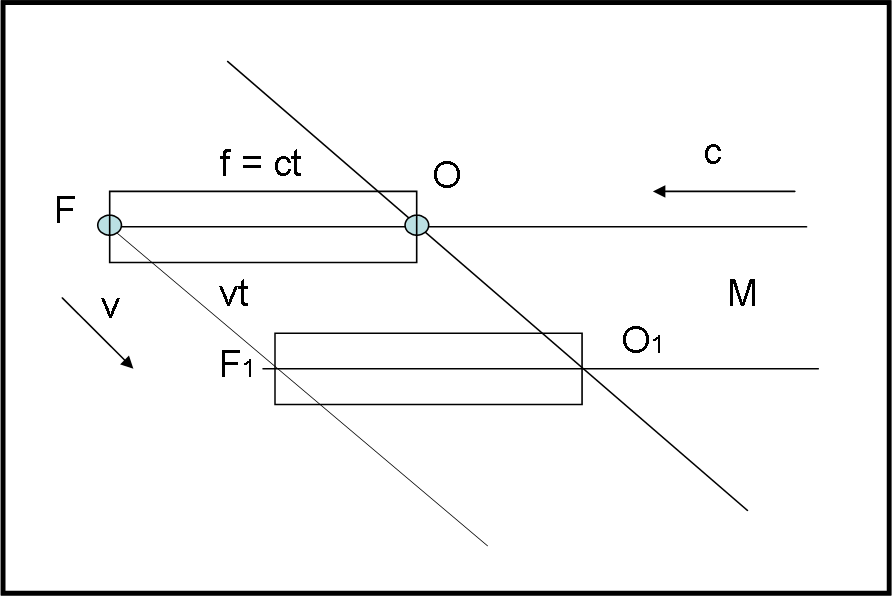
Il fotone azzurro tocca l’obiettivo O. Tuttavia se il telescopio è diretto verso la stella, nel tempo t (v è la velocità orbitale terrestre) esso si è spostato parallelamente a se stesso nella posizione O₁F₁ Nello stesso tempo t, il fotone azzurro ha proseguito la sua corsa e percorre la lunghezza del telescopio f = ct, giungendo nella posizione del vecchio fuoco F, dove non c’è più niente e nessuno ad aspettarlo. L’osservazione è fallita!

Nessun problema. Basta puntare il telecopio nella direzione FO₁ (Fig. 23) e la luce del fotone arancione viene catturata! Infatti nel tempo t che il telescopio impiega per spostarsi da FO₁ in F₁O₂ , il fotone arancione passa da O₁ a F₁ (lui viaggia in linea retta). L’osservazione è riuscita!

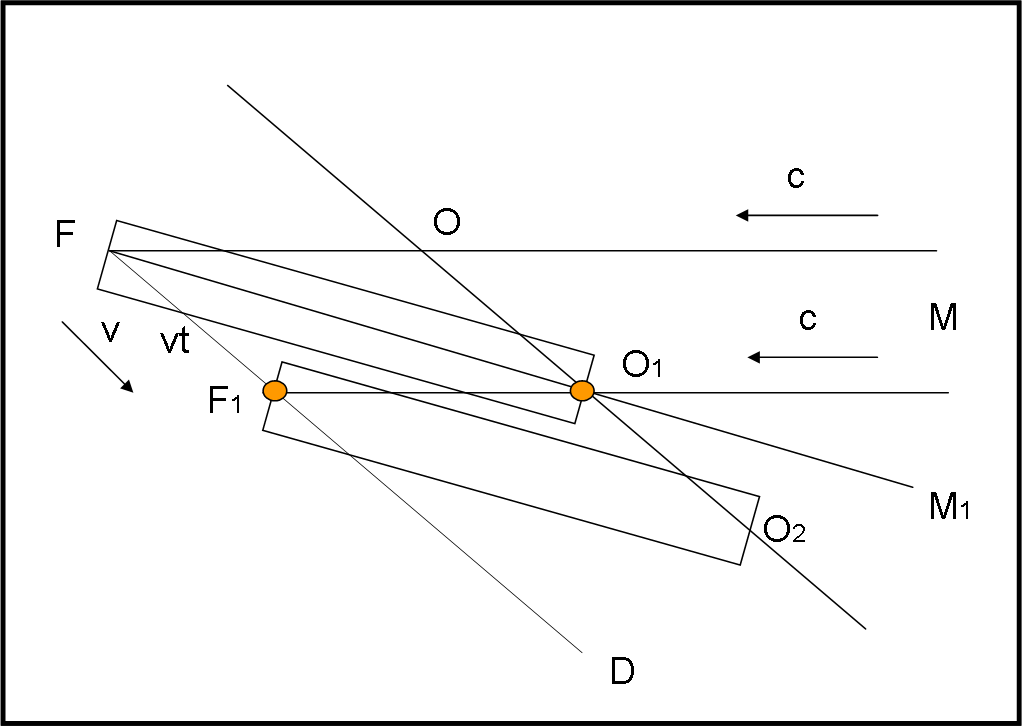
Ma vediamo, grazie a questa animazione papallicola (grazie al nostro "magico" Paolo), cosa accade al fotone sia nel caso descritto nella Fig. 22 che in quello della Fig. 23.

In base al piccolo riassunto possiamo passare tranquillamente a una descrizione puramente geometrica della situazione, dando un nome ai vari angoli che partecipano al fenomeno (Fig. 24).

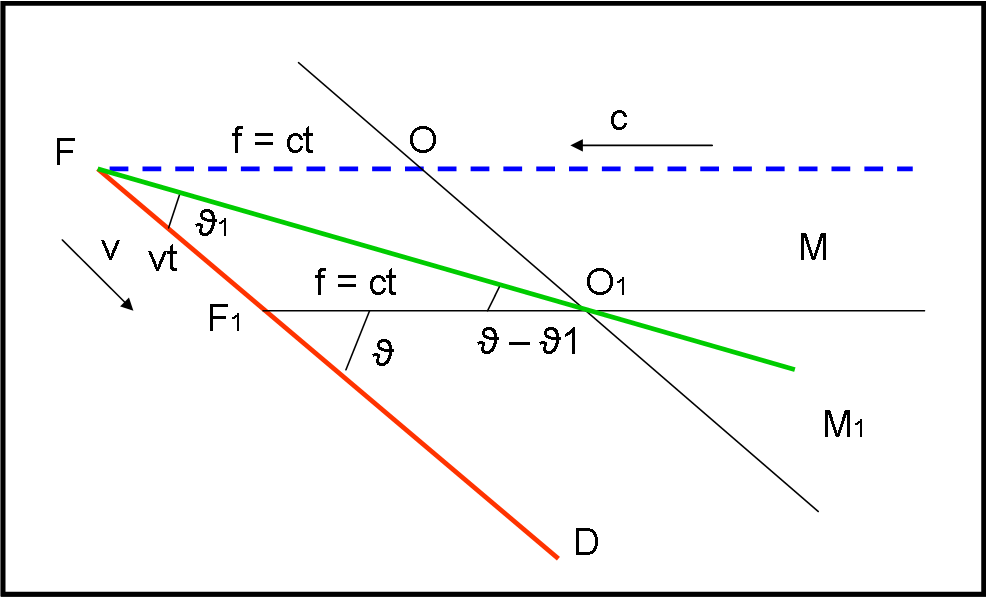
Consideriamo il triangolo FF₁O₁. L’angolo ϑ è l’angolo effettivo tra direzione della stella e lo spostamento lungo l’orbita terrestre, mentre ϑ₁ è l’angolo che l’asse del telescopio deve fare con la direzione del moto terrestre. La loro differenza ci dice di quanto il telescopio vada inclinato e coincide con l’angolo sotto cui l’obiettivo O₁ vede il fuoco F e il fuoco F₁, ossia la distanza vt (angoli alterni interni di rette parallele tagliate da una trasversale).

Possiamo applicare il teorema dei seni e scrivere:

vt/sen(ϑ – ϑ₁) = ct/sen ϑ₁

ossia:

sen(ϑ – ϑ₁) = (v/c) sen ϑ₁

Questa formula ci dice già un paio di cose molto importanti, che incontreremo in seguito: compare il rapporto v/c, il che fa cadere automaticamente il fenomeno nella relatività ristretta; non abbiamo usato composizioni di vettori velocità, ma solo distanze percorse in un certo tempo t e quindi la costanza della velocità della luce non è messa in dubbio. Risulta chiaro che il fenomeno deve essere trattato nella RR qualora v sia comparabile con c (e quindi la eventuale somma di velocità dovrà cambiare), ma può trattarsi in modo classico quando v << c. Non preoccupiamoci più di tanto, quindi, e andiamo avanti in modo classico dato che v è decisamente minore di c e non stiamo commettendo nessun errore significativo. Ricordiamo solo che la formula dovrà cambiare nella RR...

Data la piccolezza di v/c (dell’ordine di 10^-4), si possono fare le solite approssimazioni. Sostituiamo il seno di ϑ – ϑ₁ con l’angolo e al posto del seno di ϑ₁ possiamo scrivere ϑ:

ϑ – ϑ₁ = (v/c) sen ϑ

Trasformando tutto in secondi d’arco, v/c assume il valore fisso di 20”.5 e viene chiamata costante di aberrazione K, ossia:

ϑ – ϑ₁ = K sen ϑ        …. (13)

Non ci resta, adesso, che vedere cosa capita nella sfera celeste e, in particolare, nel quarto sistema di coordinate.

Prima, però, vediamo in Fig. 25, uno schema dell’orbita terrestre, supposta circolare.

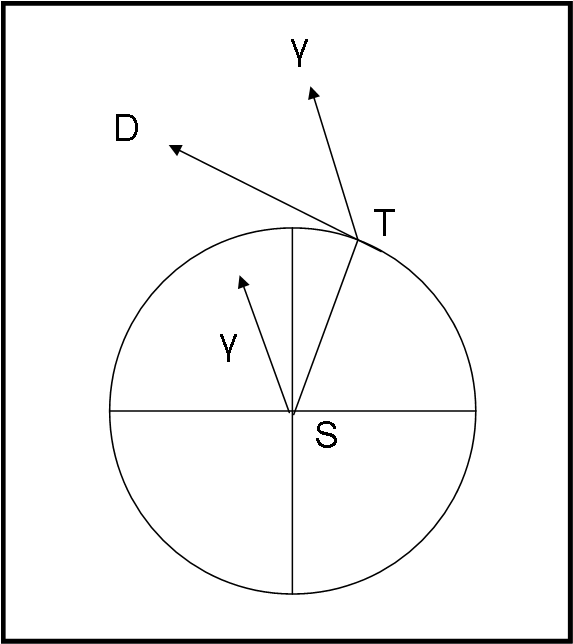
La terra T (dove sistemeremo il centro della sfera celeste) si muove in direzione di D. Questa direzione è perpendicolare alla direzione del Sole S. Sia Tγ la direzione del punto gamma o d’Ariete, da cui si misurano le longitudini. Ne segue che la longitudine geocentrica del Sole è data dall’angolo γTS, mentre quella della direzione D (γTD) è 90° più piccola, ossia vale la relazione

λ_D = λ_S – 90°

Questa semplice relazione non dice altro che la direzione importante non è più quella del Sole ma quella della direzione del moto della Terra che formano, tra loro, un angolo di 90° (posizione e velocità…).

Passiamo alla sfera celeste e utilizziamo, in Fig. 26,  esattamente la stessa figura (Fig. 21) usata per la parallasse.

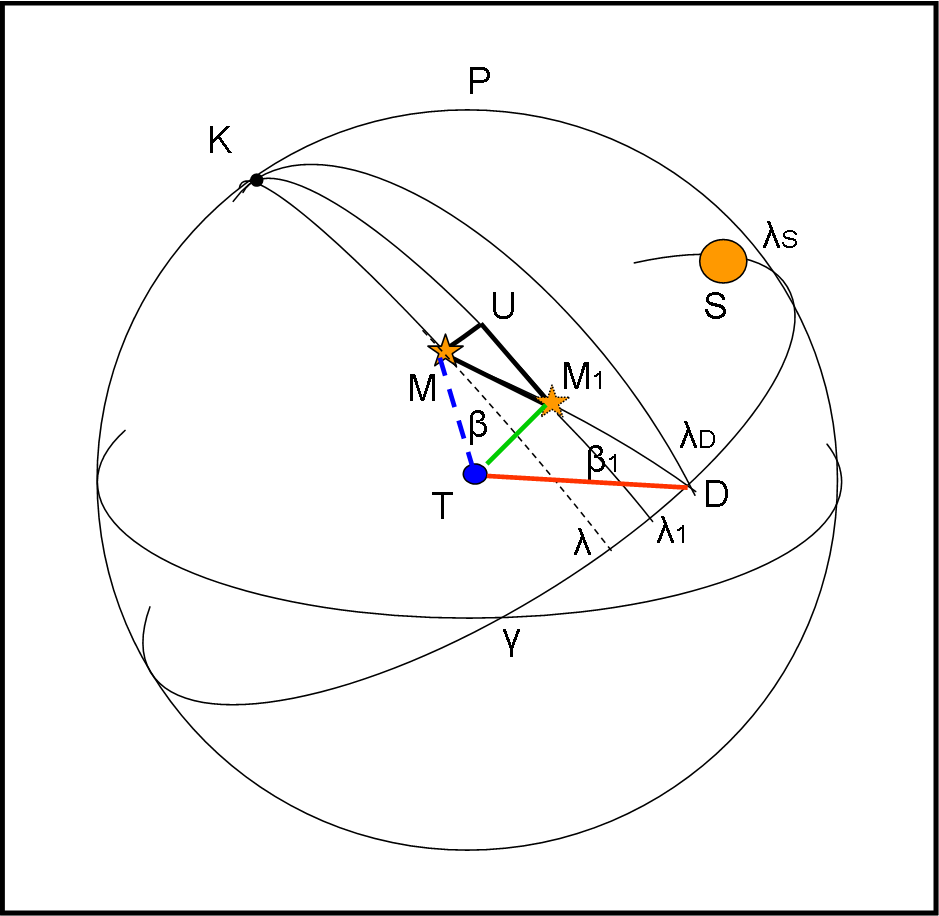
M è la stella come vista dal Sole e M₁ come è vista dalla Terra: il piano di riferimento è, adesso, MTD, il che comporta che il cerchio MM₁D sia un cerchio massimo, quello in cui avviene lo spostamento della stella. Gli unici cambiamenti sono:

(1) Consideriamo λ_D al posto di λ_S

(2) L’angolo ϑ – ϑ₁ prende il posto di ϑ₀ - ϑ_T, il che vuol dire che al posto di p inseriamo K

A questo punto, ripetendo quanto fatto precedentemente per la parallasse (un esercizio veramente banale). Si ottiene:

x = Δλ cos β = K sen ϑ cos φ = - K cos (λ_S – λ)

y = Δβ = - K sen ϑ sen φ = - K sen β sen(λ_S – λ)

x/K = - cos (λ_S – λ)

y/K sen β = sen(λ_S – λ)

Quadrando e sommando:

x²/K² + y²/K²sen²β = 1    equazione dell'ellisse di aberrazione

Che è nuovamente l’equazione di un'ellisse che ha come semiasse maggiore K e come semiasse minore Ksen β. Per una stella sull’eclittica l’ellisse si riduce a una linea che la stella percorre avanti e indietro, mentre per una stella nel polo dell’eclittica l’ellisse diventa una circonferenza di raggio K. Questo vale per tutte le stelle del firmamento e quindi il semiasse maggiore, essendo una costante, è uguale per tutte le stelle.

Bene, la parte più noiosa è terminata (ma tutti gli astrofili, almeno, dovrebbero impararla per sapere cosa vedono realmente sulla sfera celeste). Nel prossimo capitolo entriamo prepotentemente nei  sistemi di riferimento per generalizzare il problema dell’aberrazione e vederla veramente come effetto relativistico. Ci facciamo aiutare da una storia mitologica…

Gli dei greci insegnano l'aberrazione (divertendoci un po')

Approfittiamo di un racconto mitologico greco per dare un’altra versione facilitata dell’aberrazione della luce, capace, però, di introdurci nei due  sistemi di riferimento necessari  e calcolarla sia in modo classico (prima) che relativistico (dopo).

Sappiamo tutti benissimo quanto siano state importanti le due città-stato greche, Atene e Sparta. Purtroppo, le due città ebbero sempre una grande rivalità che le portò a guerre cruenti. Pochi, però, sanno che una delle guerre più violente si ebbe per colpa…. dell’aberrazione annua o di qualcosa di molto simile.

I greci sapevano tante cose sui corpi celesti, ma questo fenomeno gli era sconosciuto per molteplici motivi. E così accadde il gravissimo fatto di Belmina. La storia si mischia alla mitologia, ma non è ancora chiaro se ci sia stato un vero inganno o se entrambi i personaggi chiave fossero in buona fede. Cosa, questa, difficile da credere, ma con gli dei burloni di quei tempi tutto era possibile. Giove, da buon capo della brigata, se ne lavò le mani e mai rivelò la verità.

Era da poco finita la guerra che Sparta aveva vinto contro Argo, ma Atene non era stata da meno e aveva sedato con prontezza una ribellione della regione settentrionale fomentata dai persiani. Entrambe le città erano quindi convinte di meritarsi un premio divino. Giove accolse la richiesta e decise di regalare, a una delle due città, un diamante di grandezza e splendore mai visti. Sì, ma a quale città? Come detto, nessuno lo saprà mai…

Casualmente (ma sarà vero?), due importantissimi uomini di stato, uno ateniese e uno spartano, si trovarono contemporaneamente nei pressi della piccola città di Belmina, ai confini dei due stati, in un momento di pace molto precaria. Poche decine di metri dividevano i due dignitari.

Improvvisamente, sopra una nuvola, apparve Giove in persona e la sua voce tonante rimbombò per chilometri e chilometri: “Il vostro gesto impavido merita un regalo. Eccovi il più gran diamante che mortale abbia mai visto. Sia costruito un tempio in mio nome per conservarlo a memoria futura”. Al breve discorso seguì il lancio del diamante. Così come era apparso, Giove scomparve alla vista dei mortali. Aveva molto da fare con una bella popolana e non sapeva ancora in che animale trasformarsi…

Il diamante iniziò il suo viaggio verso terra ed entrambi i dignitari si convinsero che il regalo era per loro. Sì, ma per uno solo di loro. A insaputa uno dell’altro tirarono fuori una coppa capiente e attesero il dono divino con orgoglio e devozione.

Lo spartano aveva una coppa nera e l’ateniese una coppa rossa. Alla fine, fu l’ateniese a ricevere il regalo, ma entrambi si scagliarono contro l’avversario accusandolo di furto e di tentato furto.

In particolare, l’ateniese disse che mentre lui stava tranquillamente aspettando l’arrivo del diamante, lo spartano corse verso di lui e cercò di mettere la coppa davanti alla sua. Con prontezza lui riuscì a ricevere il dono come era stato stabilito dal Giove, ma proprio per un pelo…

La versione dello spartano fu invece completamente diversa. Mentre lui aspettava il dono con le lacrime agli occhi per la gioia, l’ateniese gli corse incontro e riuscì a inserire la coppa sopra la sua e rubare il regalo di Giove.

Una situazione ambigua e praticamente irrisolvibile. Chi aveva ragione? (Non vi ricorda un poco il celebre e bellissimo film di Akira Kurosawa, “Rashomon”, o la revisione western, “L’oltraggio”, con Paul Newman?)

La Fig. 27 descrive le due versioni.

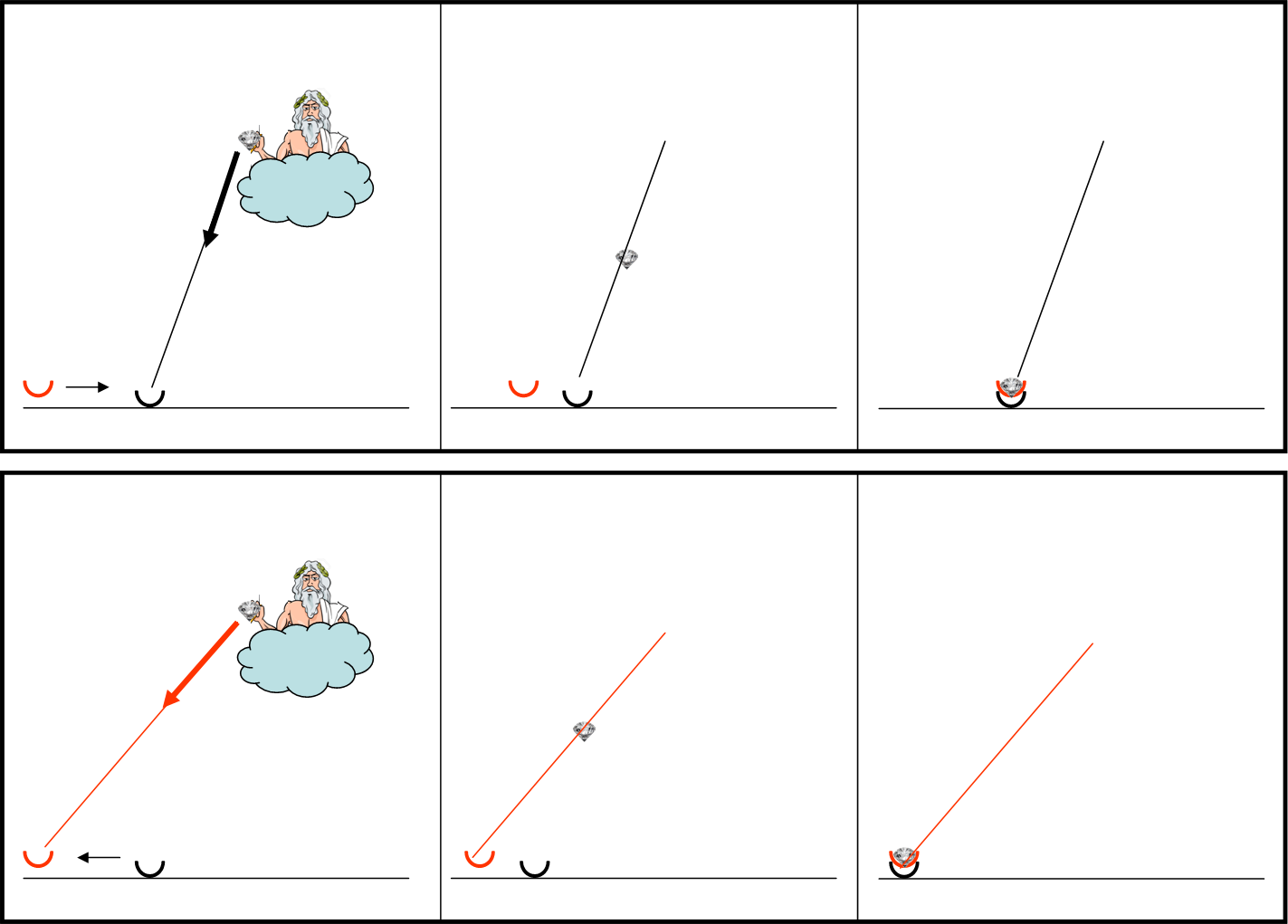
In alto, quella dello spartano. Giove lancia il diamante verso di lui (coppa nera), ma l’ateniese corre velocemente incontro allo spartano e al momento dell’arrivo del diamante riesce a inserire la sua coppa davanti a quella dello spartano. Un vero furto!

In basso, nella stessa figura, vi è la versione ateniese.  Lui è fermo in attesa del dono ed ecco che lo spartano arrivando di corsa cerca di portarglielo via, senza riuscirci. Un tentativo di furto, evitato quasi per miracolo.

La conclusione fu una guerra terribile e mai si seppe  la versione veritiera.

Ovviamente, la storia raccontata vede sicuramente un personaggio bugiardo, dato che si svolge sulla Terra, ossia su un sistema riferimento uguale per entrambi i dignitari. Potrebbe, però, essere facilmente trasportata in campo astronomico e dare il via a una descrizione più accurata dell’aberrazione annua. Basterebbe dire che uno dei due dignitari si trovava nel sistema solidale col Sole e uno nel sistema solidale con la Terra. Non sapendo chi era quello “solare”, entrambe le versioni possono essere ugualmente veritiere ed è impossibile stabilire quale versione è quella vera, dato che lo possono essere entrambe. Con gli dei di quei tempi... tutto era possibile.

Si potrebbe anche dire, in altre parole: entrambi potrebbero essere convinti di non essersi mossi e quindi ognuno avrebbe visto le cose pensando di essere fermo.

Le due versioni sono riassumibili facilmente con la Fig. 28.

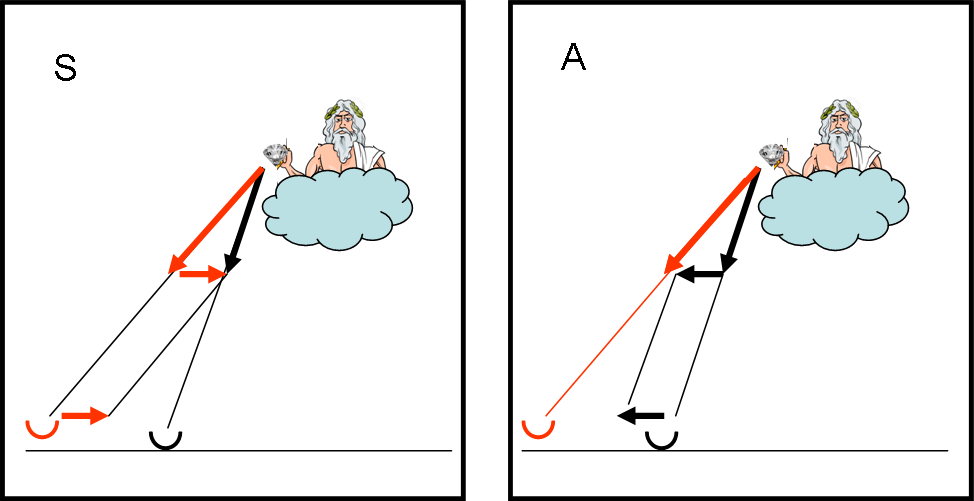
A sinistra vi è la versione spartana; a destra quella ateniese. Basta imporre una velocità di spostamento uguale e contraria per dare ragione a uno o all’altro. Tutto si capisce con un semplice triangolo composto dai vettori velocità (quelle del diamante e quella del dignitario). Ma andiamo avanti con calma.

Rivediamo l’intera scena, secondo le due versioni, applicando pari pari i concetti usati per l’aberrazione annua. Per comprendere al meglio la similitudine, invece di una coppa, i due dignitari usano due lunghi tubi, che tanto assomigliano ai telescopi usati precedentemente.

Iniziamo dalla Fig. 29a (in alto), con la versione dello spartano.

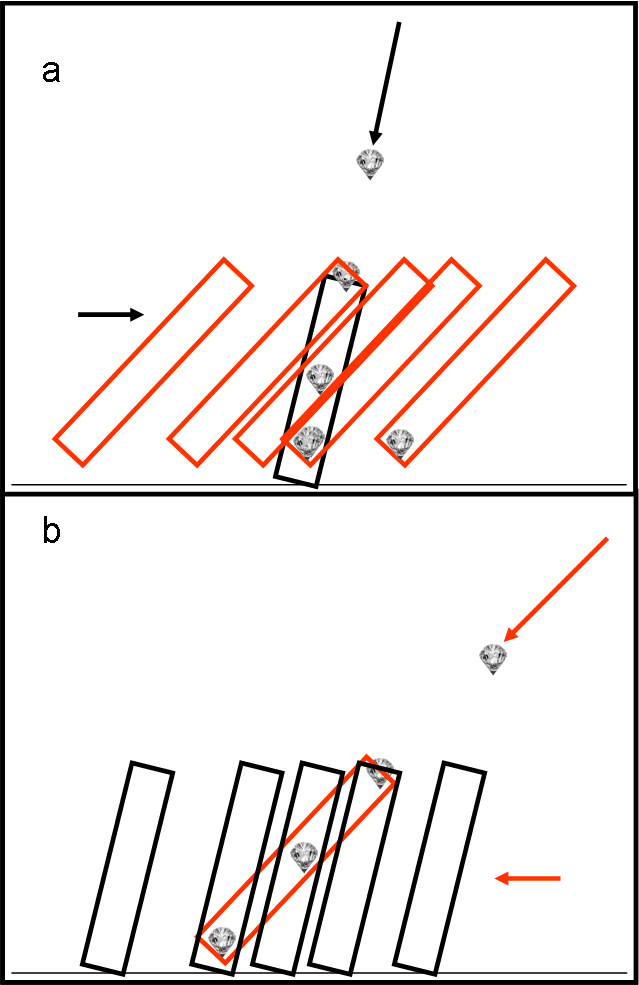
Egli è nel sistema del Sole ed è convinto (giustamente) di non muoversi e vede il diamante venire verso di lui. L’ateniese con il suo tubo rosso arriva nel momento giusto per fare il furto solo perché  sta muovendosi con la Terra, mentre lo spartano no. Il tubo nero è sempre lo stesso, dato che è fermo. Quello rosso invece si muove con la Terra. I vari tubi rossi si riferiscono a istanti successivi e vanno visti da sinistra verso destra. Quando il diamante arriva all’entrata del tubo nero, vi giunge anche il tubo rosso. La sua inclinazione permette al diamante di cadere completamente all’interno del tubo rosso che può trascinarselo via con sé. Un vero furto per lo spartano.

Attenzione! L’inclinazione deve essere proprio quella giusta, ossia quella che risulta dalla combinazione delle velocità. Se l’inclinazione fosse diversa il diamante non arriverebbe fino in fondo al tubo rosso, ma, dato il suo peso, lo bucherebbe e cadrebbe in quello nero (Fig. 30)

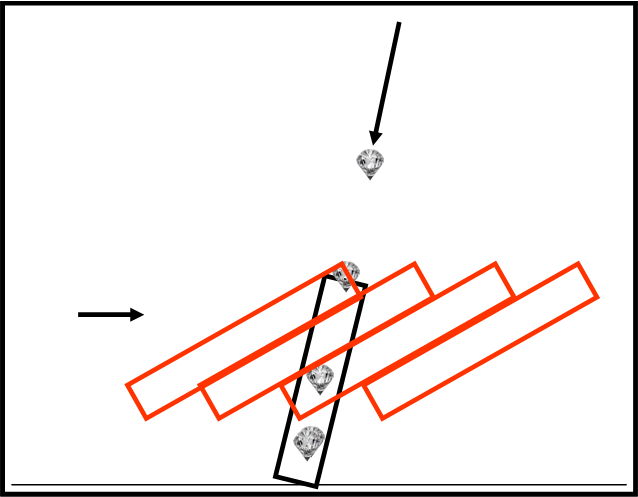
In Fig. 29b (in basso) abbiamo la versione dell’ateniese. Lui si sente fermo (e ci crede veramente). Il suo tubo è inclinato e attende l’arrivo del diamante che appare proprio andare verso di lui. Questa volta è lo spartano che appare muoversi verso sinistra. Quando il suo tubo arriva esattamente a toccare il diamante potrebbe benissimo essere lui a rubarlo all’ateniese e se non ci riesce è solo per l’abilità di quest’ultimo di anticiparlo di una frazione di secondo. Tuttavia, la direzione del tubo nero sarebbe perfetta per rubare il diamante.

Descritta in questo modo, si vede benissimo che l’avventura mitologica rispecchia perfettamente la spiegazione data con il telescopio e la posizione diversa della stella tra un osservatore eliocentrico e uno terrestre.

Possiamo, allora, permetterci di semplificare geometricamente la situazione e utilizzare due sistemi di riferimento in moto relativo e descrivere la composizione delle velocità che ne deriva. Prima lo faremo in modo classico e poi non avremo alcun problema a metterci nella RR.

Disegniamo la Fig. 31 che riassume la configurazione quando entrambi i telescopi abbiano lo stesso punto O al centro del loro obiettivo (il momento del furto…).

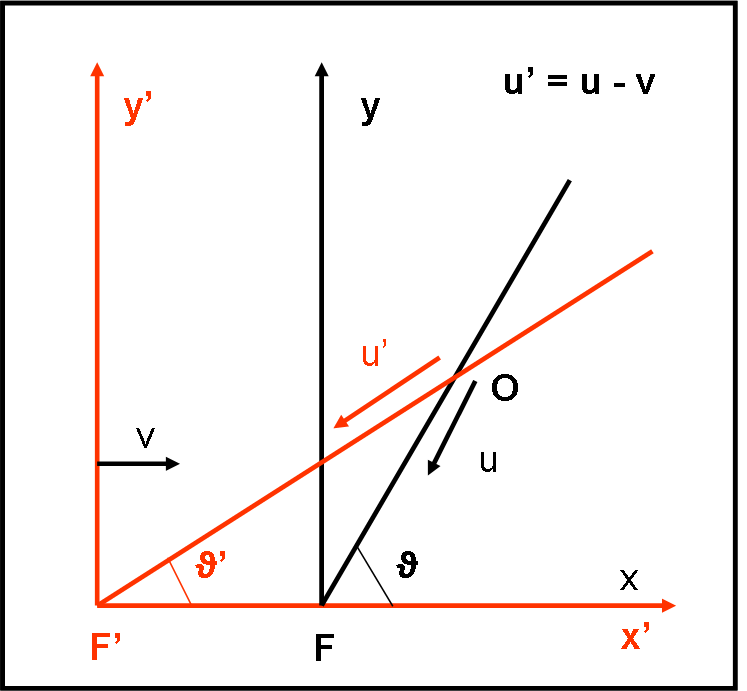
Essendo nel caso classico, possiamo scrivere la relazione:

u’ = u – v

Dove v è la velocità con cui il sistema dell’ateniese (Terra) si muove verso destra. La velocità del diamante vista nel sistema dello spartano (Sole, ossia fermo) è u, mentre u’ è la risultante come appare nel sistema della Terra. Le due direzioni delle velocità (ossia il moto del diamante) sono viste dai due fuochi dei telescopi con angoli ϑ e ϑ’.

Notiamo che continuiamo a usare una velocità u, che nel caso della luce dovrà essere rimpiazzata da c. Tuttavia, dato che dobbiamo sommare vettori è meglio, per adesso, non fare entrare c, dato che sembrerebbe darci valori maggiori di quelli della luce… Continuiamo, perciò, con una qualsiasi velocità u, quella alla portata di … Giove.

Lasciamo passare un po’ di tempo fino a che F’ coincida con F e disegniamo di nuovo la configurazione in Fig. 32, inserendo, questa volta, le velocità con la loro reale intensità. Otteniamo un bel triangolo da studiare con attenzione. Gli angoli sono sempre gli stessi, ovviamente.

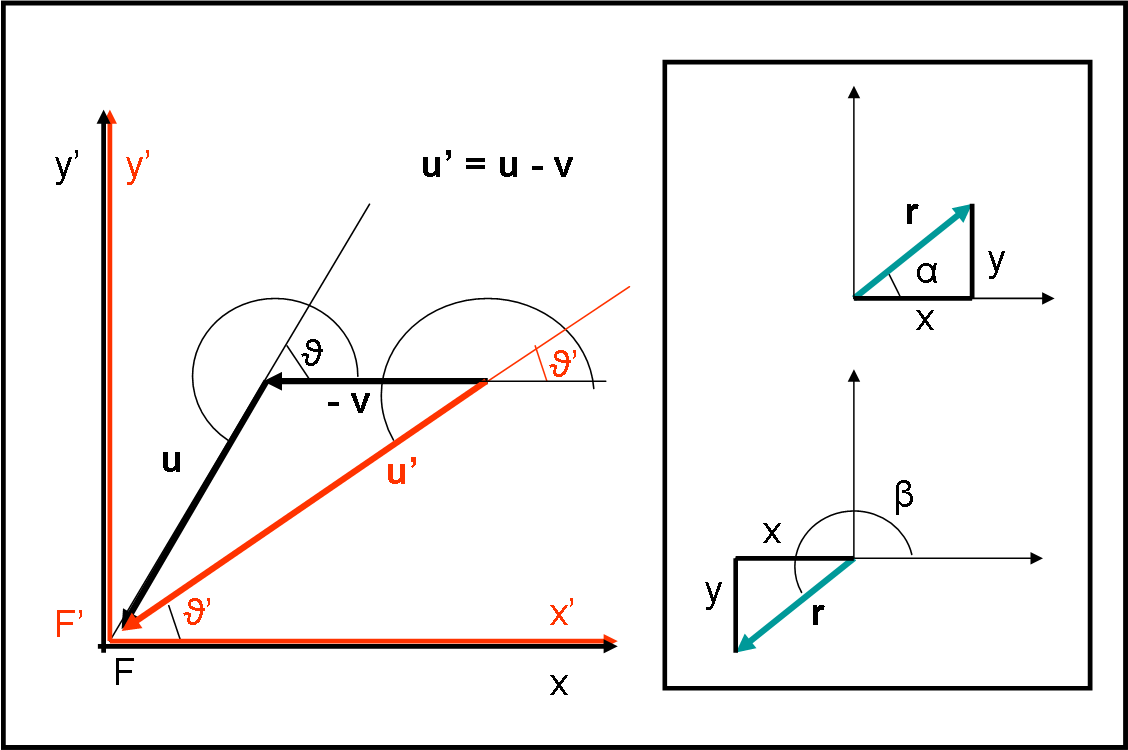
Soffermiamoci sul riquadro di destra. Sono cose che dovremmo sapere, ma è meglio richiamarle…

Come si fanno a trovare le componenti di un vettore lungo due assi cartesiani? Beh… basta usare le coordinate polari (ad esempio, QUI, Fig. 1):

se r è il vettore blu della parte alta, le sue coordinate sono

x = r cos α

y = r sen α

Ma, se portiamo il vettore r dalla parte opposta, ruotandolo di 180° (parte bassa), possiamo ancora scrivere le stesse relazioni? Sicuramente sì, dato che esse devono valere per qualsiasi angolo. Possiamo scrivere tranquillamente:

x = r cos β = r cos (α + 180) = - r cos α

y = r sen β = r cos (β + 180) = - r cos β

Abbiamo fatto un paio di passaggi estremamente banali, ma è meglio richiamarli dato che ci serviranno molto presto.

Torniamo al nostro triangolo, composizione di vettori velocità.

La relazione

u’ = u – v

può essere scritta attraverso le sue componenti secondo gli assi x e y.  Facendo ciò, tratteremo con vettori che hanno la stessa direzione e quindi possiamo utilizzare solo il loro modulo.

Iniziamo con le componenti secondo l’asse x’ che coincide con x:

u’ cos(180 + ϑ’) = u cos(180 + ϑ) – v cos(0)

- u’ cos ϑ’ = - u cos(ϑ) – v

 u’ cos ϑ’ =  u cos(ϑ)  + v             …. (14)

Abbiamo subito capito perché sono state richiamate le componenti con angoli maggiori di 180° …

Passiamo alle componenti secondo y’ coincidente (o, più in generale, parallelo a y):

u’ sin (180 + ϑ’) = u sin (180 + ϑ)

- u’ sin (ϑ’) = - u sin (ϑ)

 u’ sin (ϑ’) = u sin (ϑ)                 …. (15)

Facendo il rapporto tra la (14) e la (15) si ottiene:

u’sin ϑ’/ u’cos ϑ’ = u sin ϑ/(u cos ϑ  + v)

Semplificando e dividendo numeratore e denominatore del secondo membro per u, si ha:

sin ϑ’/cos ϑ’  = sin ϑ/(cos ϑ + v/u)      …. (16)

tan ϑ’  = sin (ϑ)/(cos(ϑ)  + v/u)        …. (17)

Questa è la relazione accurata che lega l’angolo sotto cui viene vista una stella dal Sole con quello visto dalla terra, inclinato a causa dell’aberrazione. Si nota bene che compare solo u che può benissimo essere sostituita con la velocità della luce c. Inoltre, questa formula permette di ricavare immediatamente di quanto va inclinato l’angolo visto da chi si muove (ϑ’) rispetto a quello visto da chi è in quiete. E questa possibilità è importantissima per affrontare il viaggio in astronave.

Si può anche ricavare, facilmente, la formula che abbiamo trovato precedentemente (coordinate sferiche), introducendo la costante di aberrazione  K = v/c.

Dalla (16) si ha:

sin ϑ’ (cos ϑ + v/c)= sin ϑ cos ϑ’

sin ϑ’ cos ϑ + v/c sin ϑ’ = sin ϑ cos ϑ’

sin ϑ’ cos ϑ - sin ϑ cos ϑ’ = - v/c sin ϑ’

Sappiamo però che vale la relazione trigonometrica (QUI, appendice)

sen (ϑ’ - ϑ) = sin ϑ’cos ϑ -  cos ϑ’ sen ϑ

Da cui, sostituendo:

sen (ϑ’ - ϑ) = - v/c sin ϑ’

sappiamo anche che sen (-α) = - sen α, e quindi:

- sen (ϑ – ϑ’) = - v/c sin ϑ’

sen (ϑ – ϑ’) =  v/c sin ϑ’ = K sin ϑ’

E con le approssimazioni fatte, lavorando con le coordinate celesti:

ϑ – ϑ’ = K sin ϑ

Soluzione relativistica

Immaginiamo adesso che la velocità v sia paragonabile a quella della luce (gli dei forse ci riuscivano e potevano anche farlo fare agli umani). In questo caso la composizione di velocità u' = u - v non vale più e dobbiamo affidarci alla Relatività Ristretta. In altre parole, tutto sta nell'utilizzare la composizione delle velocità  e delle loro componenti) in modo relativistico e non galileiano. Il resto sono semplici calcoli poco più che elementari. Abbiamo già ricavato le formule di composizione delle componenti di una velocità se vista da un sistema  che si muove con velocità v rispetto al primo (QUI e QUI ).

Scriviamo perciò le formule relative alle componenti nel sistema S’ (dignitario che si muove) in funzione delle componenti del sistema S (dignitario che sta fermo). La velocità relativa v è diretta lungo l’asse x, mentre la velocità u ha componenti sia in x che in y. Continuiamo a usare una generica velocità u.

u’_x = (u_x - v)/(1 - vu_x/c²)

u’_y = u_y (1 – v²/c²)^1/2/(1- v u_x /c²)

Ricordando il fattore di Lorentz:

γ = 1/(1 – v²/c²)^1/2

Possiamo scriverle:

u’_x = (u_x - v)/(1 - vu_x/c²)         …. (18)

u’_y = (1/γ)( u_y/(1- v u_x /c²))         …. (19)

Sostituiamo i valori delle componenti attraverso le coordinate polari già usate precedentemente

u_x = u cos (180 + ϑ) = - u cos ϑ

u’_x = u’ cos (180 + ϑ’) = - u’ cos ϑ’

u_y = u sen (180 + ϑ) = - u sen ϑ

u’_y = u’ sen (180 + ϑ’) = - u’ sen ϑ’

le (18) e (19) diventano:

- u’ cos ϑ’ = (- u cos ϑ - v)/(1 + u v cos ϑ /c²)

- u’ sen ϑ’= (1/γ)( - u sen ϑ /(1 + u v cos ϑ /c²))

E, ancora:

u’ cos ϑ’ = (u cos ϑ + v)/(1 + u v cos ϑ /c²)

u’ sen ϑ’= (1/γ)( u sen ϑ /(1 + u v cos ϑ /c²))

Dividendo membro a membro si ottiene:

u’ sen ϑ’/u’ cos ϑ’= (1/γ)( u sen ϑ /(1 + u v cos ϑ /c²)) (1 + u v cos ϑ /c²) /(u cos ϑ + v)

tan ϑ’ = (1/γ) (u sen ϑ/(u cos ϑ + v))

tan ϑ’ = (1/γ) (sen ϑ/(cos ϑ + v/u))

tan ϑ’ = sen ϑ/γ(cos ϑ + v/u)        …. (20)

Che diventa quella relativa alla velocità della luce (aberrazione luminosa) per v = c.

Si nota subito che questa relazione è uguale a quella ricavata nella relatività galileiana a parte il fattore γ . Il che vuole anche dire che la formula relativistica diventa quella classica trascurando i termini di secondo ordine in v/c (la parte contenuta nel fattore γ).

La formula (20) ci permette di calcolare la deviazione del raggio luminoso come appare all’osservatore in moto più o meno rapido, qualsiasi sia la direzione della sorgente. Il tutto si risolve applicando la moltiplicazione per 1/γ in caso di velocità di movimento relativistico. A parità di angolo ϑ, l’angolo ϑ’ diventa sempre più piccolo quando si va più veloci, per sorgenti poste davanti a noi (ϑ < 90°). Questo perché 1/γ decresce al crescere di v.

La moltiplicazione degli dei (e delle stelle)

Vediamo, adesso, di generalizzare il risultato e non osservare solo una stella, ma tutto il firmamento attorno a noi. Torniamo, quindi, per un poco nell’antica Grecia, dato che sembra che l’avventura dell’ateniese e dello spartano (con la conseguente guerra) abbia divertito parecchio gli abitanti dell’Olimpo. In molti domandarono a Giove di ripetere il gioco, anzi di farlo ancora più complicato.

Questa volta Giove chiese aiuto sia a Venere che a Ercole e apparvero tutti e tre insieme ai due poveri dignitari (non si sa se fossero realmente gli stessi), ognuno con un diamante in mano. Li gettarono contemporaneamente e poi scomparvero aspettandosi chissà quale zuffa (Fig. 33).

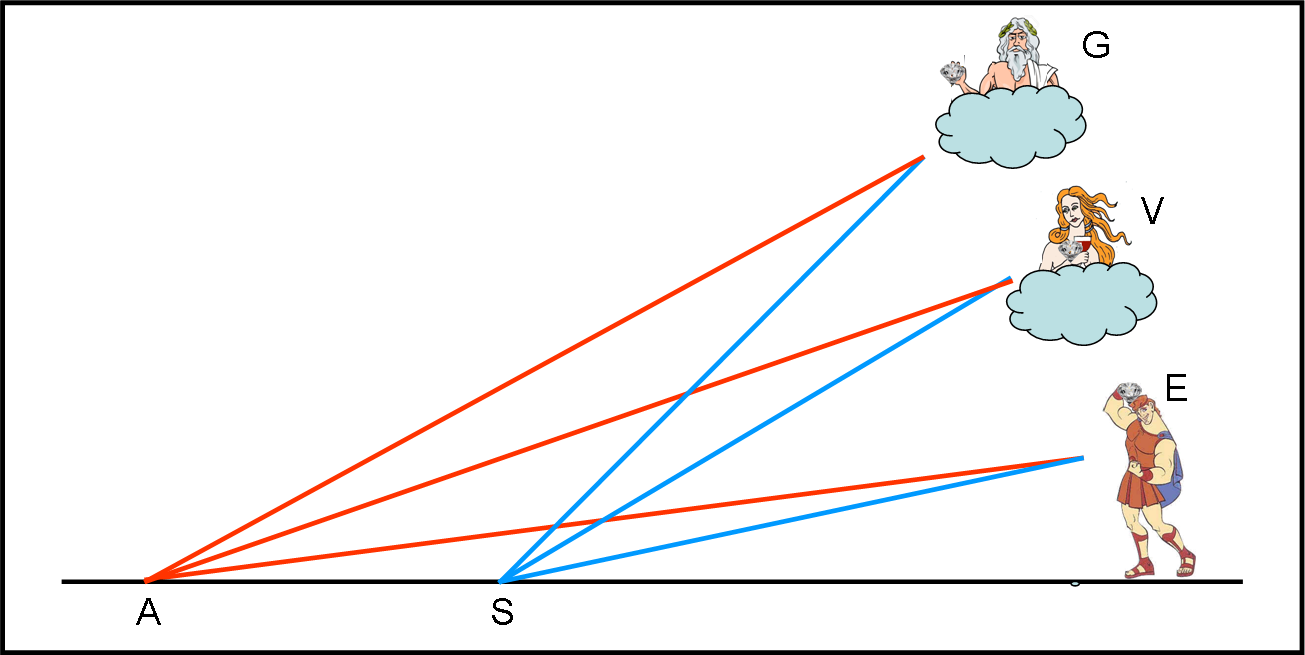
In realtà, le cose non andarono così… Ricordando, forse, il fatto precedente, l’ateniese e lo spartano decisero di dividersi il bottino. In particolare, lo spartano si tenne due diamanti e l’ateniese uno solo, in modo da compensare quello ricevuto precedentemente dall’ateniese che aveva causato una guerra veramente “aberrante”! La parte riflessiva dei due dignitari (ma forse erano scienziati) ebbe la meglio ed essi si scambiarono le impressioni avute durante il fatto.

L’ateniese convenne che aveva dovuto correre verso lo spartano e il discorso cadde sulla posizione assunte dagli dei. Lo spartano disse che erano decisamente separati tra di loro, a partire da Ercole, a livello del terreno, fino a Giove, molto alto sopra di lui. L’ateniese, invece, disse che le cose gli sembravano molto più ristrette: Giove non era poi così in alto.

Ovviamente nessuno poteva sapere la vera distanza in leghe o in chilometri o in passi di cammello, ma poteva stabilire l’angolo che le varie direzioni facevano rispetto a una linea fissa. In altre parole, potevano disegnare le posizioni degli dei su una specie di sfera, di raggio incognito. In poche parole, sulla sfera celeste.

L’ateniese e lo spartano fecero questo esercizio quasi-astronomico, come si vede nella Fig. 34. Si convinsero facilmente che avevano entrambi ragione e che la visione delle posizioni dei tre dei era nettamente diversa per uno e per l’altro.

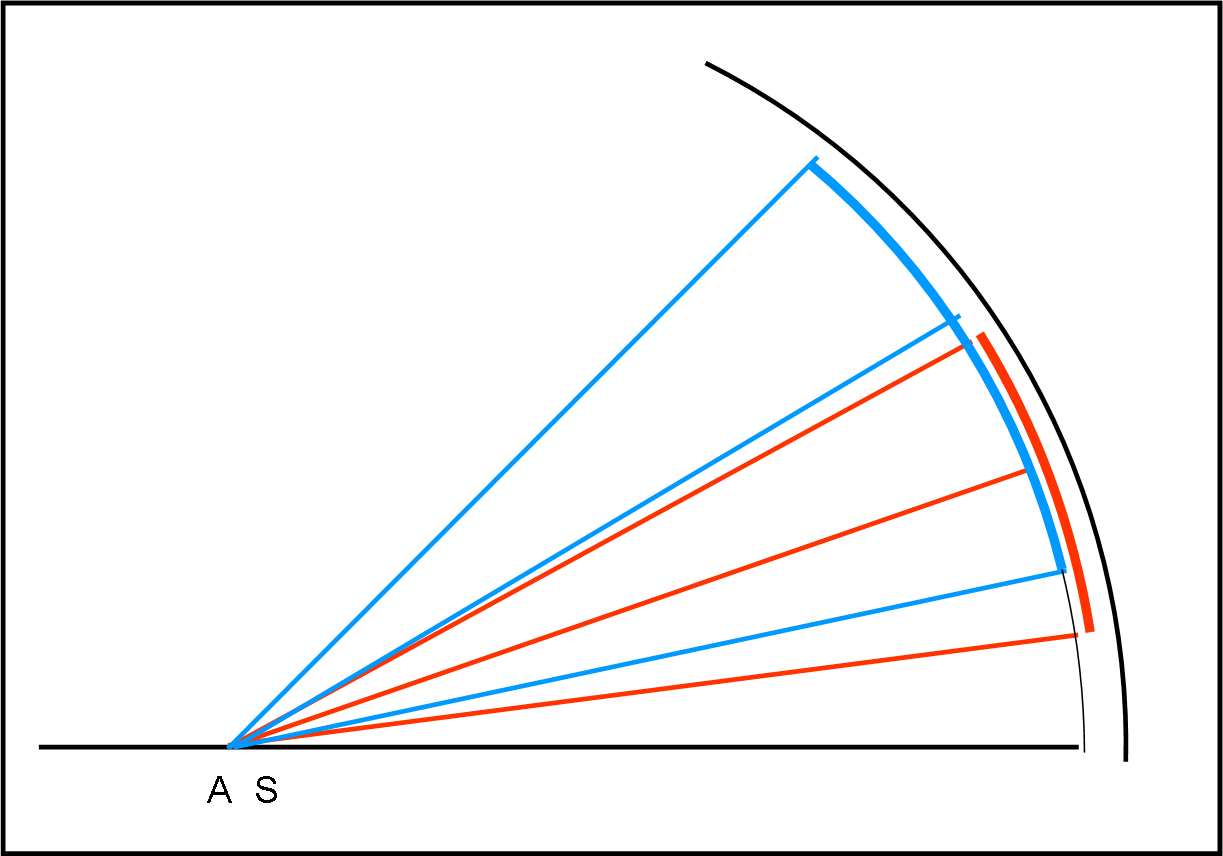
Non essendo frastornati dai media (solo da dei burloni e spesso anche  un po’ maligni) riuscirono a capire che questa conclusione era strettamente legata alle direzioni verso cui entrambi vedevano cadere i diamanti. Chi non si muoveva aveva una visione più ampia rispetto a chi era costretto a correre. Tutto dipendeva dalla combinazione della velocità dei diamanti e della velocità dell’ateniese. In poche parole, avevano scoperto l’aberrazione e avevano anche capito come veniva visto ciò che li circondava, sia se si restava fermi sia se ci si metteva a correre molto velocemente.

Gli dei, che potevano anche essere parecchio permalosi e cattivelli, erano però molto onesti e, malgrado non scoppiasse nessuna guerra, lasciarono ai dignitari-scienziati i diamanti: in fondo, il loro cervello se li era meritati!

L'Universo si stringe

Ringraziamo i due uomini di stato e torniamo alle nostre linee schematizzate. Finora abbiamo solo visto come la luce proveniente da una stella appaia deflessa da chi gli corre incontro. Adesso, possiamo generalizzare l’intera faccenda e dire che se le stelle sono più di una, esse si vedono più vicine sulla sfera celeste (l’angolo tra di loro diminuisce) nella direzione della persona che è in movimento. E più la persona corre veloce e più l’angolo diminuisce. Non esageriamo, però, dato che vogliamo restare nella fisica classica (anche se ormai conosciamo il passaggio successivo, molto più corretto ed essenziale per velocità molto alte). Tuttavia, possiamo sempre considerare “piè veloce” Achille e rendere più macroscopica la differenza tra chi si muove e chi sta fermo.

Immaginiamo di rappresentare i tre dei di prima con tre stelle molto conosciute. Non manteniamo le reali proporzioni, ma esageriamo le variazioni degli angoli in modo da rendere tutto ben visibile (in altre parole, saremmo in ambito relativistico, ma continuiamo a trattarlo in modo classico).

Ecco cosa vedrebbe, in Fig. 35, lo spartano, a sinistra, e l’ateniese (magari Achille), a destra. La costellazione scelta è quella di Orione ed essa si vedrebbe contratta e rimpicciolita da parte di chi si muove.

Un’applicazione semplicissima dell’aberrazione della luce. Siamo passati da un singolo oggetto stellare a tanti oggetti stellari che hanno direzioni diverse e che causano l’effetto dell’aberrazione in modo diverso a seconda della direzione da cui proviene la luce. In qualche modo abbiamo già iniziato il nostro viaggio con l’astronave… Inoltre, se la stella fosse proprio vicina e si potesse vedere il suo disco, quest’ultimo subirebbe una contrazione e la quantità di luce sarebbe la stessa concentrata in una superficie più piccola (e quindi apparirebbe più luminosa). Ovviamente, avvicinandosi, il disco si ingrandirebbe, successivamente, per effetto della distanza decrescente. Questo tipo di risultato lo vedremo più in là sia per la scoperta di sistemi binari sia per effettuare un viaggetto verso il Sole e, perché no?, anche verso un buco nero.

Attenzione che, a volte, nel web si utilizza questa trattazione per mostrare cosa si vede da un’astronave lanciata a grande velocità. La trattazione non è corretta, ma è solo un compromesso tra aberrazione classica e aberrazione relativistica. Se si viaggia piano non si vedrebbe praticamente niente di speciale. Se si vuole vedere le deformazioni bisogna tener conto della RR, come abbiamo già mostrato (gli angoli di aberrazione cambiano). Ci torneremo con molti più dettagli…

Disegniamo, allora, un bello schema che ci mostri un confronto completo tra ciò che vede chi è fermo e chi, invece, si muove in una certa direzione, condendolo con le solite riflessioni sui sistemi di riferimento. Usiamo la Fig. 36.

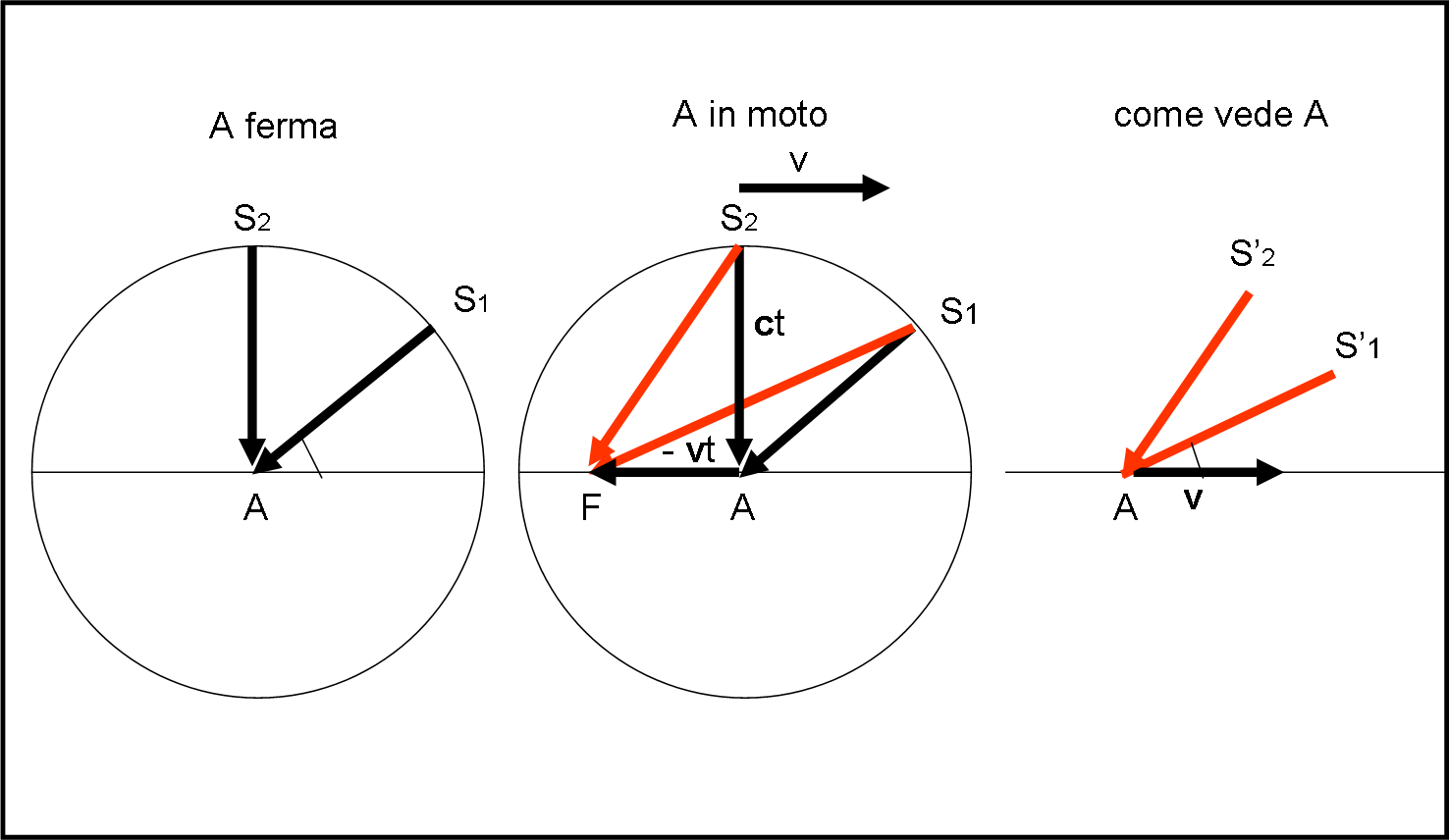
Abbiamo un circonferenza, in cui ogni suo punto dista la stessa distanza dal centro (che scoperta!) dove sta un personaggio, anche… odierno. Immaginiamo che vi sia un numero a piacere di stelle che mandino la loro luce dalle varie direzioni, verso il centro. Potremmo anche coprire tutta la circonferenza di sorgenti di luce. Attenzione, però, lungo la circonferenza non abbiamo le sorgenti, ma la loro luce al momento in cui arriva a una certa distanza dal centro. Agendo in questo modo, si lavora soprattutto sugli spazi percorsi e sugli angoli, senza rischiare di sommare velocità a quella della luce. Qualcosa che abbiamo già usato per descrivere l’aberrazione annua.

Vediamo cosa succede al raggio, che proviene da una certa sorgente, quando arriva a toccare la circonferenza in S_1. Esso è diretto verso il centro della circonferenza A, ma se il centro si sta muovendo versa destra con una certa velocità v, ossia percorre un certo spazio nell’unità di tempo che è quello che serve alla luce di S₁ per raggiungerlo. Siamo esattamente nel caso dell’aberrazione che conosciamo ormai molto bene.

Per essere vista dal viaggiatore la luce deve percorrere il tragitto S₁F. In altre parole, l’osservatore deve guardare secondo la linea rossa S₁F se vuole essere raggiunto dalla luce della stella, in A. La stessa cosa capita, ovviamente, per qualsiasi raggio, come quello molto particolare, S₂. I raggi devono, comunque, arrivare simultaneamente in uno stesso punto. D’altra parte il fenomeno fisico deve essere lo stesso in ogni sistema di riferimento.

In generale, otteniamo una serie di linee rosse che si concentrano in un punto F che, spostato in A ci mostra cosa vede l’astronave A.

Attenzione … non cerchiamo di vedere in F un qualche punto speciale, almeno per adesso. Esso è il punto di raccolta della luce, tenendo conto che A si muove nel tempo in cui la luce compie il percorso dai punti della circonferenza verso il punto di raccolta. E’ un punto che serve per la costruzione di ciò che vede il viaggiatore. In realtà, le distanze da F alla circonferenza hanno ben poco significato a questo livello. Le cose cambieranno passando alla RR. Inoltre, il punto F appare molto distante da A, ma rimanendo nel caso classico, essi dovrebbero praticamente coincidere. Questo è un errore che si fa spesso: quello di mostrare una configurazione relativistica assumendola come classica. Se volessimo essere più corretti, potremmo considerare i raggi non come raggi luminosi, ma come diamanti lanciati dagli dei a velocità nettamente minori di quelli della luce.

Parliamo un attimo di sistemi di riferimento, trattando sempre con grandi deviazioni, pur sapendo a cosa possiamo riferirci.

Consideriamo come sistema di riferimento quello del viaggiatore A. Bene, possiamo dire che esso vedrebbe la stessa identica cosa sia che sia lui a muoversi verso destra, sia che sia la sorgente di luce (o di quello che è) a muoversi verso sinistra. La situazione è esattamente la stessa.

Esprimiamoci meglio. Chi si muove vede giungere a lui luci o diamanti che appartengono a un altro sistema di riferimento (che possiamo considerare fisso). Lui, perciò, vede sicuramente l’effetto di aberrazione. Chi viaggia è proprio colui che vede tutto deformato nel senso del moto. La stessa cosa succederebbe, però,  se lui fosse fermo e le sorgenti luminose (o i lanciatori di diamanti) si muovessero verso di lui.  Al vettore collegato alla direzione della luce andrebbe comunque aggiunto un vettore collegato alla velocità – v.

Si aprono così due scenari, entrambi perfettamente uguali, se osservati dall’osservatore dentro l’astronave. Nel primo abbiamo l’astronave che si muove verso sinistra, ma l’astronauta si sente fermo e vede la luce venire verso di lui. Nel secondo l’osservatore è proprio fermo, ma è la stella che si muove verso di lui. Due scenari, entrambi più che plausibili. Il primo porta alla classica aberrazione annua, il secondo all’osservazione di una stella che si muove verso di noi (come nel caso dei sistemi doppi) e il cui fascio di luce in arrivo si stringe sempre più all’aumentare della velocità (ma non fa solo quello e qui cadiamo subito nell’effetto doppler che è strettamente collegato all’aberrazione della luce).

Una situazione analoga si ha guardando, nel nostro sistema di riferimento fermo, la luce che esce dalla stella in movimento. I raggi luminosi e il movimento dell’astro vanno nella stessa direzione. Ciò comporta che il fascio di luce che esce dall’astro è visto restringersi sempre di più all’aumentare della velocità stellare.

Anche questo caso comporta un risvolto pratico importantissimo. Stiamo parlando dell’effetto sincrotrone sui cui torneremo molto presto. Basta, infatti, non prendere una stella, ma un altro piccolo creatore di luce: l’elettrone accelerato.

In generale, sia la luce che arriva, sia quella che parte da un oggetto in movimento comporta uno stringimento del fascio luminoso (basta usare il sistema di riferimento giusto).

Mamma mia quante cose sono collegate all’aberrazione (le tratteremo tutte in maggior dettaglio, non temete) e ancora non abbiamo provato a viaggiare realmente in astronave a velocità relativistica!

Verso l'ellisse di aberrazione

Ci siamo divertiti un po’ con gli dei greci e siamo arrivati a vedere cosa succede alla luce che proviene dall’esterno mentre un cosmonauta viaggia nella sua astronave. Come già dovevamo immaginare, per effetto dell’aberrazione luminosa, il fascio luminoso si stringe verso la direzione del moto. Stiamo per entrare in un campo decisamente più generale, che comporta, nella seconda parte almeno, una conoscenza più che discreta della RR e del diagramma di Minkowski. Cercheremo, perciò di andare avanti con piedi di piombo e fare tante figure esplicative.

Sappiamo già che l’aberrazione è un fenomeno relativistico che può essere risolto compiutamente solo entrando nella RR. In poche parole, se l’astronave viaggia molto velocemente l’inclinazione dei raggi è data dalla formula relativistica. Si ricade nel caso classico solo se la velocità è decisamente bassa (come quella dell’astronave Terra).

Ci tengo a precisare un punto fondamentale che è sicuramente ovvio per tutti, ma che preferisco mettere in evidenza. Finora abbiamo sempre lavorato su uno spazio a due dimensioni. I raggi che entrano o escono dal viaggiatore, in moto o fermo, sono descritti in un piano. Il tempo scorre sicuramente, ma non è ancora stato preso in considerazione nel suo giusto valore. Ricordiamo sempre che passando da un sistema di riferimento fermo a uno in moto valgono le formule di Lorentz e il tempo e lo spazio sono strettamente collegati.

Con l’articolo precedente potremmo anche accontentarci e dire di aver finito. Potremmo, infatti, già immaginarci scenari fantastici come quello visto andando verso Orione. Ormai sappiamo calcolare le deviazioni dei raggi e valutare quanto un  fascio di luce si stringa o si allarghi. Tuttavia, facendo così, perderemmo molta informazione portata dai nostri amici fotoni.

Innanzitutto non sapremmo che energia trasferiscono all’astronauta. Energia trasferita vuole dire frequenza del fotone che lo colpisce. Siamo, inoltre, nelle condizioni in cui vi è un movimento rispetto alla sorgente di luce, ossia un effetto doppler. Ne segue che a seconda della direzione del moto e della direzione della luce, si ha un cambiamento di frequenza e quindi del colore visto dall’astronauta. Basterebbe calcolare l’effetto doppler relativistico e si potrebbe costruire ciò che vede l’astronauta in tutte le direzioni. Insomma ce la caveremmo con le formule dell’aberrazione e dell’effetto doppler relativistico, legati strettamente tra di loro.

Tuttavia, l’effetto doppler è legato al tempo e il tempo scorre in modo diverso per chi sta fermo e per chi si muove. Se non vogliamo prendere per buone le formule del caso e desideriamo capire bene come i vari parametri escono allo scoperto, non possiamo rinunziare al solito vecchio orologio di luce (per darne una visione semplicistica) e infilarci nello spazio di Minkowski (per entrare nei dettagli). Pensate che la costruzione di quanto andremo a fare viene usata anche per spiegare “in toto” la cinematica della RR e il diagramma di Minkowski. Un metodo alternativo…

Concentriamoci, perciò, e cerchiamo di seguire molto attentamente i vari passaggi. Alla fine otterremo la cosiddetta elisse di aberrazione o di simultaneità (si capirà molto bene il secondo nome).

Ci costruiremo un grafico a… quattro dimensioni. In cui si potranno leggere la deviazione della luce (due dimensioni), la frequenza dei fotoni in arrivo e la dilatazione del tempo lungo ogni direzione. Un’ellisse straricca di informazioni, che sintetizza una bellissima avventura effettuata nello spaziotempo di Minkowski.

Generalizziamo l'orologio di luce

Immaginiamo il nostro viaggiatore, munito del vecchio e sempre utile orologio di luce. Vediamo subito cosa c’entri con l’aberrazione. Beh… la risposta è molto semplice e immediata (Fig. 37). Riprendiamo una figura che conosciamo molto bene, dove vi è una lampadina e uno specchietto posto esattamente sopra di lei (il piano della figura è il piano dello spazio x e y).  Accendiamo la lampadina e vediamo la luce colpire lo specchio a 90° e tornare indietro.  Il sistema è fermo è la luce colpisce lo specchietto dopo un certo tempo t e poi torna indietro nello stesso tempo t.

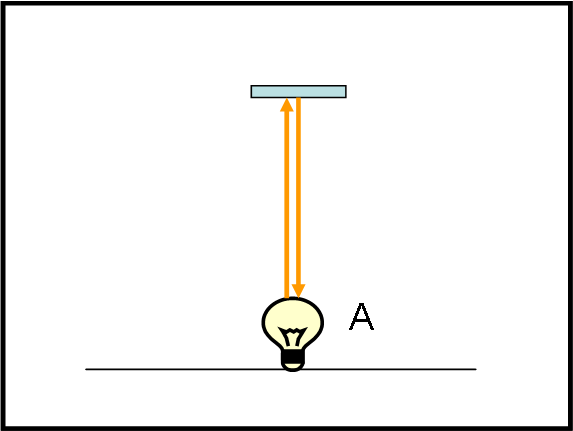
Immaginiamo, adesso, di muoverci verso sinistra con velocità - v e di osservare cosa capita all’orologio di luce (potremmo anche far muovere il viaggiatore e noi rimanere fermi, il succo non cambierebbe). Per il viaggiatore tutto funziona esattamente come prima, ma non certo per noi che ci consideriamo fermi (Fig.  38).

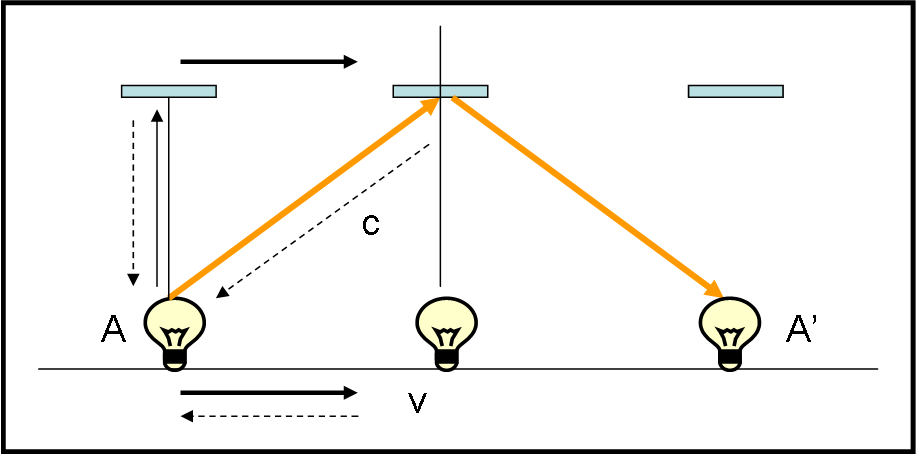
La luce che invia l’astronauta non va certamente lungo la direzione perpendicolare, dato che quando colpisce lo specchietto, lo strumento si è spostato verso destra. La traiettoria della luce è inclinata rispetto a quando l’orologio era fermo. Tuttavia, la luce si riflette comunque (anche se con un angolo diverso da 90°) e si muove in avanti fino a incontrare di nuovo la lampadina. A noi, per adesso, interessa solo la prima parte. Cosa possiamo concludere? Che la luce della lampadina è costretta a piegarsi rispetto alla verticale di un certo angolo per riuscire a raggiungere lo specchio. I vettori coinvolti sono sempre gli stessi e l’inclinazione non è altro che quella che abbiamo imparato a conoscere attraverso l’aberrazione annua.

In questo caso abbiamo inviato della luce, ma la faccenda è del tutto simile: basta invertire il verso della luce e della velocità per ottenere il caso relativo all’osservatore che si muove verso destra e che deve inclinare il suo telescopio per catturare la luce. Per lui è la stella che si muove verso di lui e tutto resta perfettamente uguale, come mostrano le frecce tratteggiate. In poche parole, la prima parte dell’esperienza dell’orologio di luce ci permette di calcolare l’aberrazione della luce da parte di chi si muove verso di lei.

Ricordiamo anche che l’orologio di luce ci aveva permesso di ricavare il tempo t’, relativo a chi si muove, rispetto al tempo t proprio di chi si considera fermo. I due tempi erano legati dal celeberrimo fattore di Lorentz γ, capace di misurare di quanto rallenta un orologio che si muove se visto da chi sta fermo (la famosa dilatazione dei tempi).

Andiamo avanti per gradi e vediamo se è stato solo un caso, oppure se l’orologio di luce può veramente descrivere l’aberrazione per ogni direzione della stella. Basta considerare uno specchietto posto in una posizione avanzata rispetto alla lampadina (ma che sia sempre alla stessa distanza) e mettere “in moto” il viaggiatore (ossia ci muoviamo verso sinistra), come in Fig. 39.

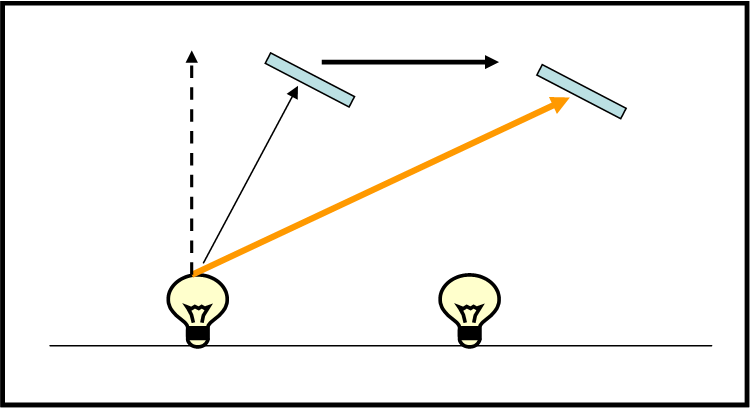
Ancora una volta la luce è costretta a puntare verso destra per poter raggiungere lo specchio e la traiettoria finale è più inclinata di quella vista a vagone fermo. Lo specchio sarà comunque colpito e la luce tornerà sulla lampada ancora più avanti (questa conclusione è obbligatoria, dato che quello che capita nel sistema in moto deve capitare anche se viene visto da fuori; il fenomeno: luce che esce, si riflette e torna da dove è partita, deve SEMPRE capitare).

In modo molto qualitativo abbiamo ritrovato quanto avevamo descritto con i tre dei greci.

Chi si muove appare inviare luce più concentrata in avanti o -se preferite- ricevere luce più concentrata (basta cambiare sistema di riferimento)

E’ giunta l’ora di generalizzare l’intera faccenda. Invece di un semplice orologio a luce consideriamo una circonferenza riflettente con la lampadina al centro.

La nostra circonferenza-astronave è ferma, con il centro-astronauta in A. Lui accende la sua lampada e vede che tutto torna perfettamente: la luce parte, tocca le pareti nello stesso istante (percorrendo uno stesso spazio uguale al raggio della sfera) e torna indietro nello stesso identico tempo. In altre parole, la differenza tra tempo iniziale e tempo finale è proprio quella necessario alla luce per percorrere due volte il raggio della circonferenza.

Il tutto è rappresentato in Fig. 40. Stabiliamo i tre eventi: (a) partenza della luce da A; (b) arrivo della luce sulla superficie sferica; (c) ritorno della luce in A. (a) , (b) e (c) di ogni raggio luminoso sono simultanei, ossi (a) è uguale per tutti; (b) è simultaneo per tutti, così come (c).

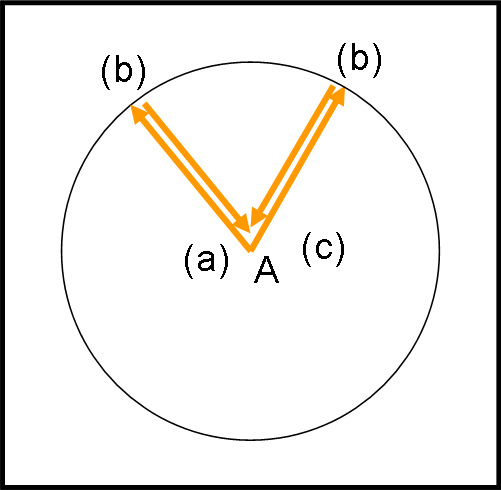
Cominciamo, commettendo un errore madornale ...

Mettiamo in moto la circonferenza verso destra, con un po’ di leggerezza (e spero che tutti voi gridiate allo scandalo), muovendoci verso sinistra con una velocità v =  βc. L’astronauta continua a usare la sua “torcia” e tutto continua a funzionare perfettamente per lui. L’osservatore esterno, invece, vede un orologio di luce esteso a tutta la circonferenza-astronave. E’ inutile complicarci troppo la vita e consideriamo solo due direzioni luminose: quella verticale (la solita che usiamo sempre) e una orizzontale, ad esempio verso sinistra. Vediamo cosa viene fuori, utilizzando la Fig. 41. Per semplificare, consideriamo uguale a 1 il raggio della circonferenza, che vuole anche dire porre t = 1 e c = 1. La velocità orizzontale dell’astronave è, perciò, β = v/c = v.

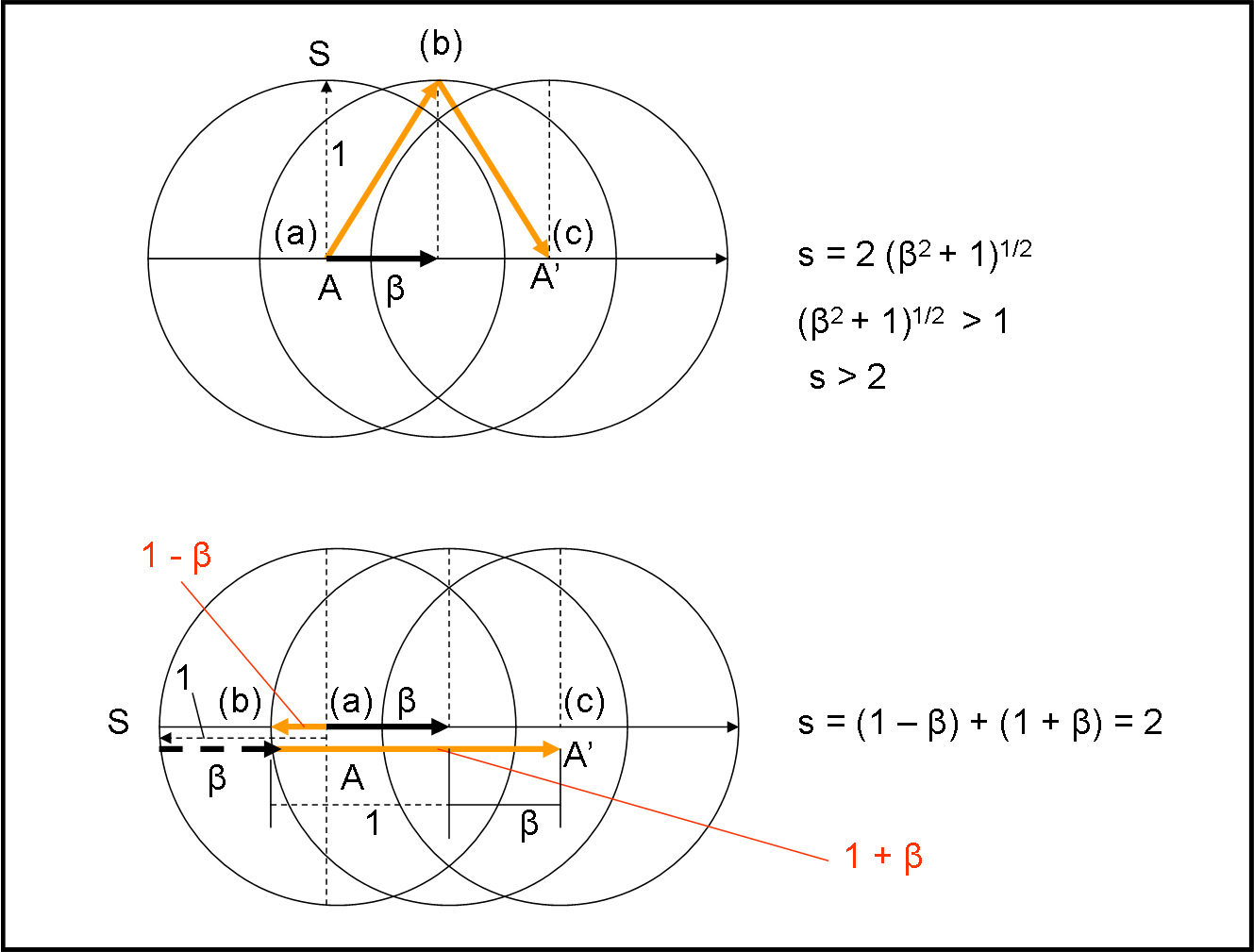
Cominciamo con la parte alta della figura che conosciamo molto bene e calcoliamo il percorso s arancione della luce. Possiamo scrivere, senza porci grandi problemi:

s = 2 (β² + 1)^1/2

Adesso, facciamo lo stesso, nella parte bassa, considerando però un raggio orizzontale. La luce parte da A e va verso sinistra. Nel frattempo, però, la circonferenza si muove verso di lei e la raggiunge in (b), dove avviene la riflessione. A questo punto, per concludere l’esperimento, basta arrivare di nuovo nel centro A’ , in accordo con quanto successo nel caso precedente. Abbiamo già detto che per qualsiasi raggio il tempo trascorso tra inizio e fine deve essere lo stesso. Se il tempo è lo stesso deve essere lo stesso anche il percorso totale s.

Calcoliamolo…

Da (a) a (b) si ha un percorso s₁ uguale a (1 – β) e un percorso s₂ da (b) a (c) uguale a (1 + β). Beh… sicuramente sono percorsi diversi, ma possiamo anche accettarlo, dato che la sfera si muove, ma sulla somma dei percorsi non ci si può sbagliare: s₁ + s₂ deve essere uguale a s del caso precedente!

Proviamo a fare la somma tra s₁ e s₂

s₁ + s₂ = 1 - β  + 1 +  β = 2

esattamente il diametro della circonferenza. Controlliamo s trovato prima:

s = 2(β² + 1)^1/2

Accidenti… (β² + 1) è una quantità sempre maggiore di 1 e tale deve essere anche la sua radice quadrata. Il che comporta che s deve essere  sempre maggiore di 2. Per essere uguale a 2 dovrebbe essere β = 0, ossia astronave ferma!

Insomma, niente da fare… abbiamo sicuramente commesso un errore, e anche piuttosto grave. Ormai lo conosciamo bene: abbiamo considerato uguali i tempi t e t’. Il tempo t funziona solo per chi è solidale con l’astronave, ma è t’ che va considerato per chi guarda da fuori. E’ sempre e soltanto un problema di simultaneità relativa.

Eseguiamo le giuste correzione, tenendo conto della relatività dei tempi, e applichiamole alla nostra astronave in movimento, in Fig. 42.

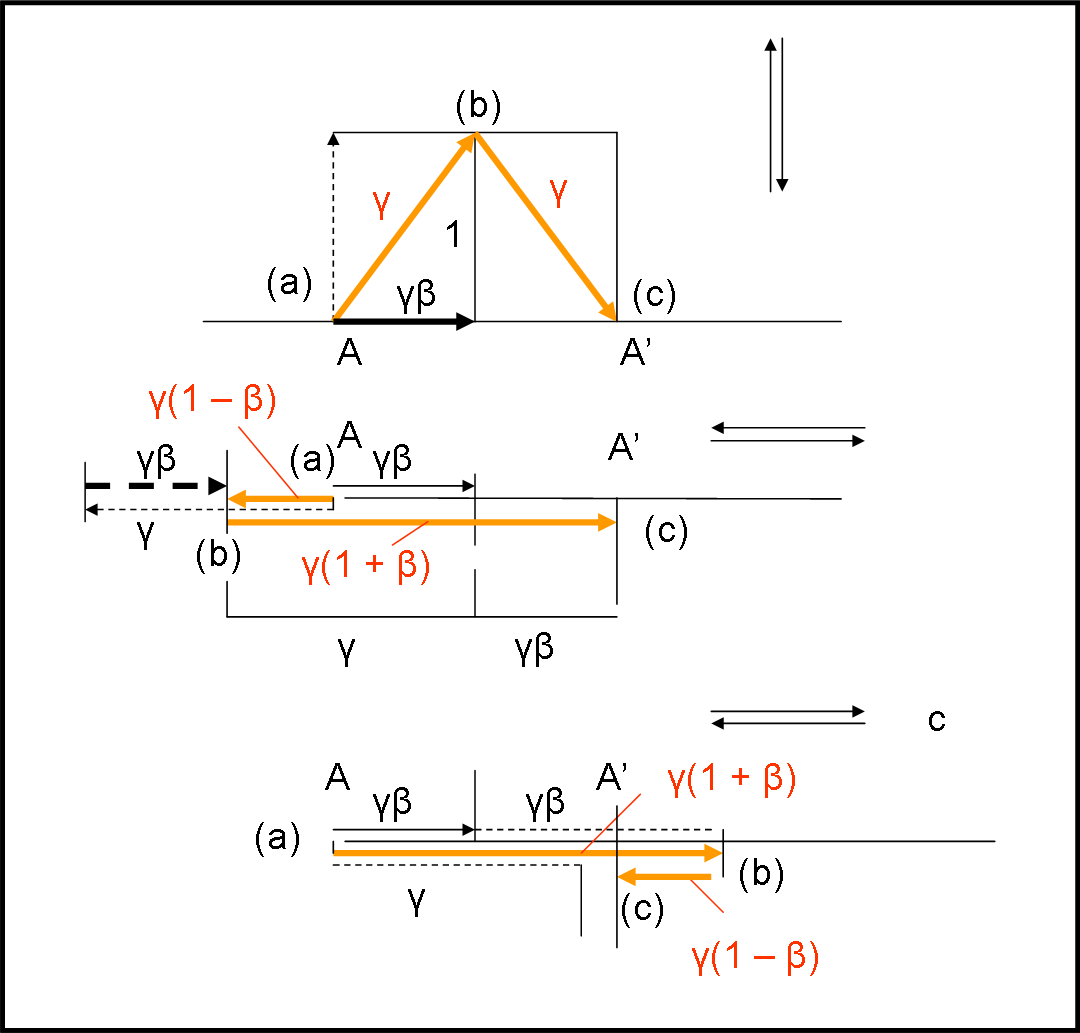
Come si vede chiaramente tutto ciò che è visto da chi sta fuori deve usare un tempo t’ che è legato a t da γ, ossia t’ = γ t. La figura precedente cambia completamente. In particolare, tutte le grandezze lungo l’asse orizzontale, quelle del moto, devono essere moltiplicate per γ.

Rifacciamo, adesso, i nostri calcoli di prima…

Cominciamo con  la luce mandata verticalmente, che ripropone perfettamente il caso classico dell’orologio di luce.

Il percorso della luce dall’inizio alla fine è adesso data da:

s = 2γ

Calcoliamo quello orizzontale, sia andando verso il senso del moto apparente, sia in senso opposto.

s = γ (1 - β) + γ (1 + β)  = 2γ

Adesso sì che ci siamo!

Cosa abbiamo trovato attraverso questo semplice calcolo?

Mandando la luce in tre direzioni, essa è tornata al punto centrale dopo aver seguito un percorso di pari distanza (e nello stesso tempo). Ovviamente, il punto di invio della luce (A) non si troverà più in A, ma in A’, al momento della ricezione.

Ne segue che il luogo dei punti in cui i raggi luminosi incontrano la circonferenza in movimento devono essere tali che la somma delle loro distanze da due punti fissi rimanga una costante (2 γ).

Abbiamo definito esattamente un’ellisse che ha i fuochi in A e A’ e che ha semiasse maggiore uguale a γ. Il semiasse minore deve essere uguale a 1 e la sua eccentricità è data dalla velocità della sfera β. Infatti, una nota proprietà dell’ellisse dice che la distanza tra centro e fuoco (γ β) divisa per il semiasse maggiore (γ) dà proprio l’eccentricità, ossia β.

E’ allora facilissimo costruirla (potremmo anche disegnarne una a caso e trovare subito a che velocità si riferisce). Nella Fig 43.  usiamo la direzione della luce come abbiamo fatto negli articoli precedenti: A riceve la luce e si muove verso destra, che è poi la stessa situazione di A fermo che vede l’Universo venire verso di lui.

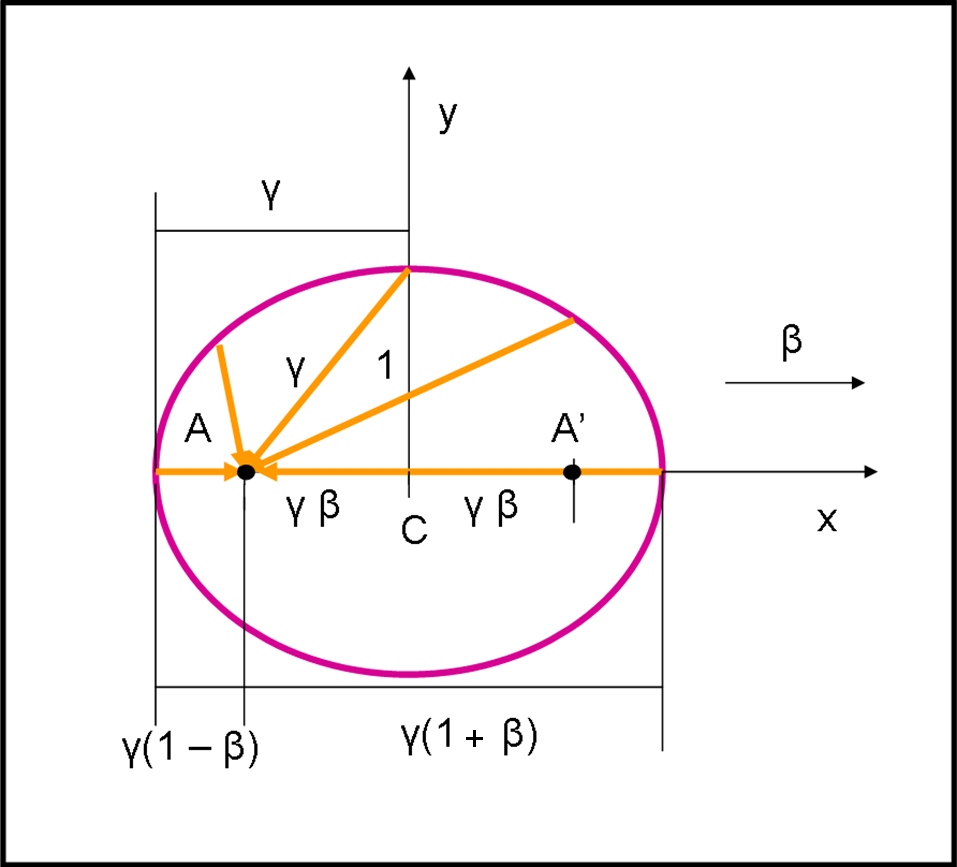
Per ragioni di simultaneità relativa tutti i tratti percorsi dalla luce che arriva dalla sfera all’astronauta devono essere uguali (non lo sono solo perché bisogna tener conto della dilatazione dei tempi relativistica, data proprio dal fattore γ). Notate che abbiamo delle lunghezze e stiamo parlando di tempi… La ragione è semplice: ct = t = spazio percorso.

L’ellisse centrata in C (punto di mezzo tra A e A’) è data da:

x²/a² + y²/b² = 1

nel nostro caso, si ha:

x²/γ² + y² = 1

o, spostando l’origine nel fuoco A:

(x - γβ)²/γ² + y² = 1

Siamo tornati alla nostra rappresentazione della deviazione dei raggi luminosi per effetto dell’aberrazione, ma adesso abbiamo anche la lunghezza dei percorsi compiuti che differiscono a causa del fattore di dilatazione dei tempi γ. Percorsi uguali a tempi dilatati e quindi legati alle frequenze della luce nelle varie direzioni. Potremmo già costruire tutto ciò che vogliamo e, in  particolare, cosa vede un astronauta che viaggi a una certa velocità: luce distorta e colorata in modo diverso. D’altra parte abbiamo tutti i parametri dell’ellisse…

Tuttavia, conosco i miei “polli” e qualcuno storcerà un po’ il naso… Penserà: “Bello, bello... ma non abbiamo tenuto in conto della contrazione delle distanze e, poi, questo fatto che i percorsi sono uguali ai tempi mi convince, ma non poi tanto… sarebbe bello avere una costruzione dell’ellisse più concreta. L’ideale sarebbe vederla nel diagramma di Minkowski!”. E avrebbe proprio ragione…

E’ quello che faremo nella seconda parte, tenendo presente che la descrizione diventerà molto più chiara, dato che seguiremo tutti i passaggi fino a vedere nascere la nostra ellisse come per magia, ma introdurremo il tempo e le figure saranno tridimensionali (per lo più), dato che lo spazio va visto in due dimensioni. Mettete in conto, quindi, una fatica supplementare nel capire le figure (giocoforza più intricate), ma anche una soddisfazione particolare quando tutta l’avventura del nostro astronauta sarà compressa in pieno. Direte sicuramente: “Questo Minkowski era proprio un genio! Col suo diagramma si può ottenere proprio di tutto e di più…”

Entriamo nel diagramma di Minkowski

Cominciamo, nuovamente, l’avventura con una trattazione sul piano (x,y), ma poi passeremo immediatamente nello spaziotempo. Alla fine, troveremo nuovamente l’ellisse, lavorando con la geometria di Minkowski. Ovviamente, per seguire questo approccio è necessario avere già una buona base relativistica (QUI e QUI)

Questa volta non ci facciamo mancare niente e riprendiamo la nostra circonferenza riflettente, introducendo il cono di luce relativo al momento della partenza da un certa origine O. Il cono di luce non è altro che l’espansione dell’onda luminosa della lampadina fino a incontrare i bordi della circonferenza. A quel punto la luce inverte il percorso e torna nell’origine che, intanto, si è spostata lungo l’asse del tempo. Guardiamo l’esperimento dall’alto (ossia nel piano (x,y)), con il tempo che punta verso di noi, in Fig. 44.

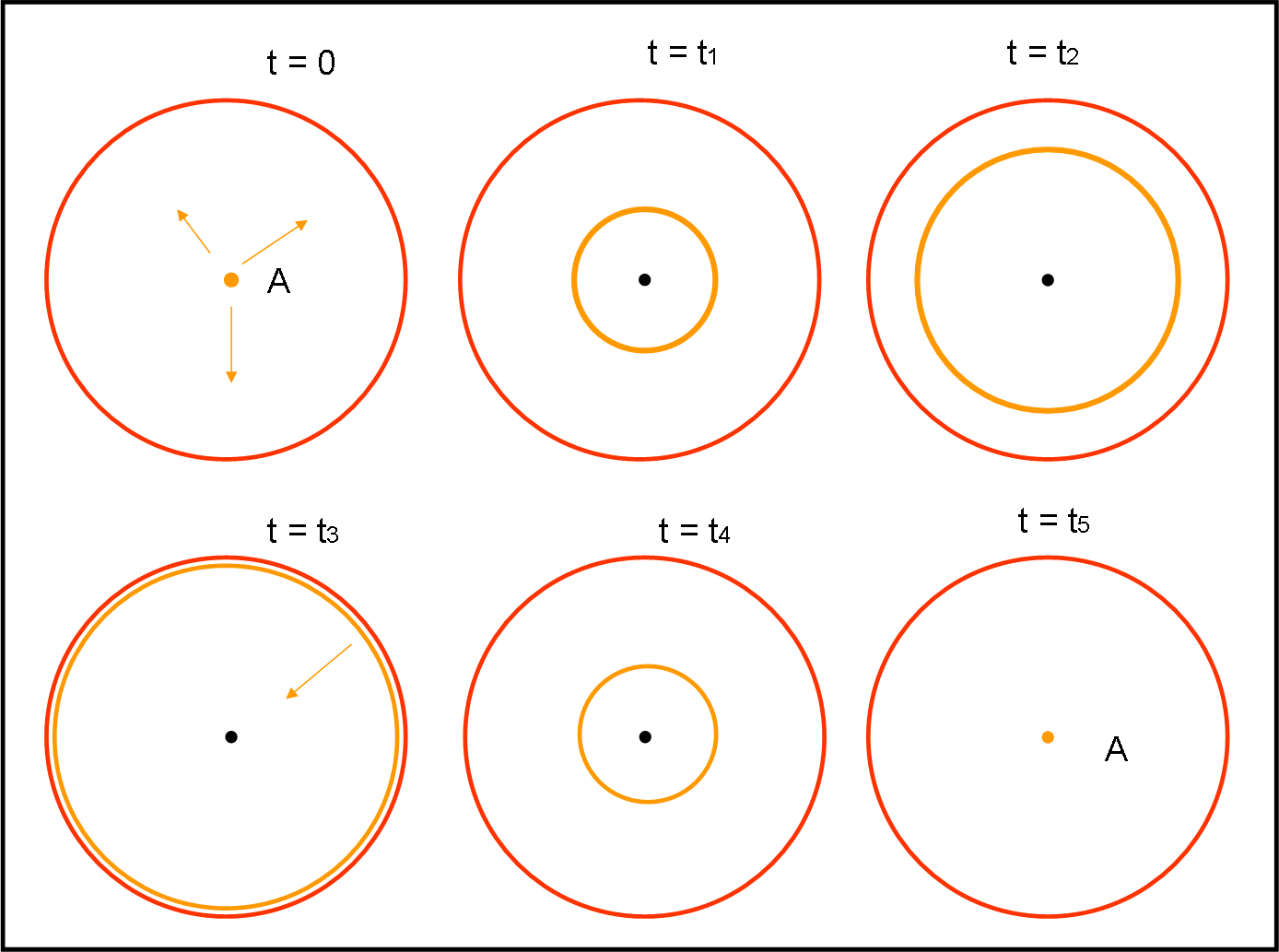
Cosa succede? (scusate se sono quasi infantile, ma è meglio partire non lasciando niente al caso).

La circonferenza rossa rimane sempre al suo posto, dato che si muove solo nel tempo. Dal centro A parte la luce che viene rappresentata dalla circonferenza arancione che si allarga fino a incontrare la circonferenza in t₃. In quel momento, viene riflessa e torna indietro fino a tornare nel punto A in t₅. Banale, ma non sentitevi presi in giro…

Vediamo la stessa situazione nella Fig. 45. A sinistra abbiamo lo stesso esperimento visto nel piano (t,x) con l’asse y che punta verso di noi. A destra vi è una visione tridimensionale che dovrebbe essere chiara a tutti.

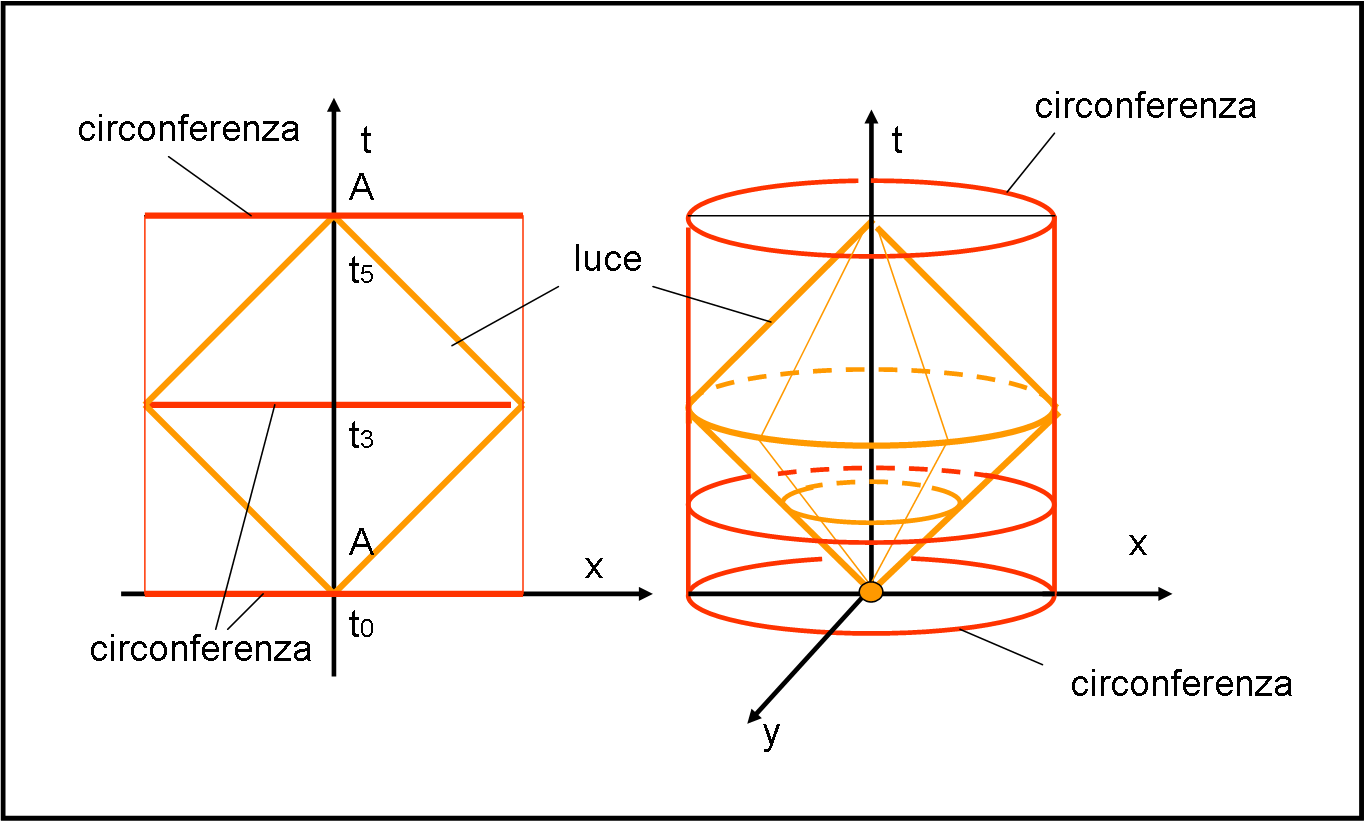
Abbiamo descritto il caso in cui A non si muove. Avete anche notato che la luce si muove a 45°, secondo quanto utilizzato nel diagramma di Minkowski. Anche se non sembra, siano già entrati al suo interno.

Ora complichiamo le cose… e facciamo muovere la sorgente di luce A verso destra. Nel diagramma di Minkowski (Fig. 46) si individuano subito i nuovi assi x’ e t’. L’asse y’ resta, invece, quello che è (y), essendo normale al movimento. Guardiamo il tutto con l’asse delle y diretto verso di noi, ossia il piano del foglio è quello che contiene sia (x,t) che (x’,t’).

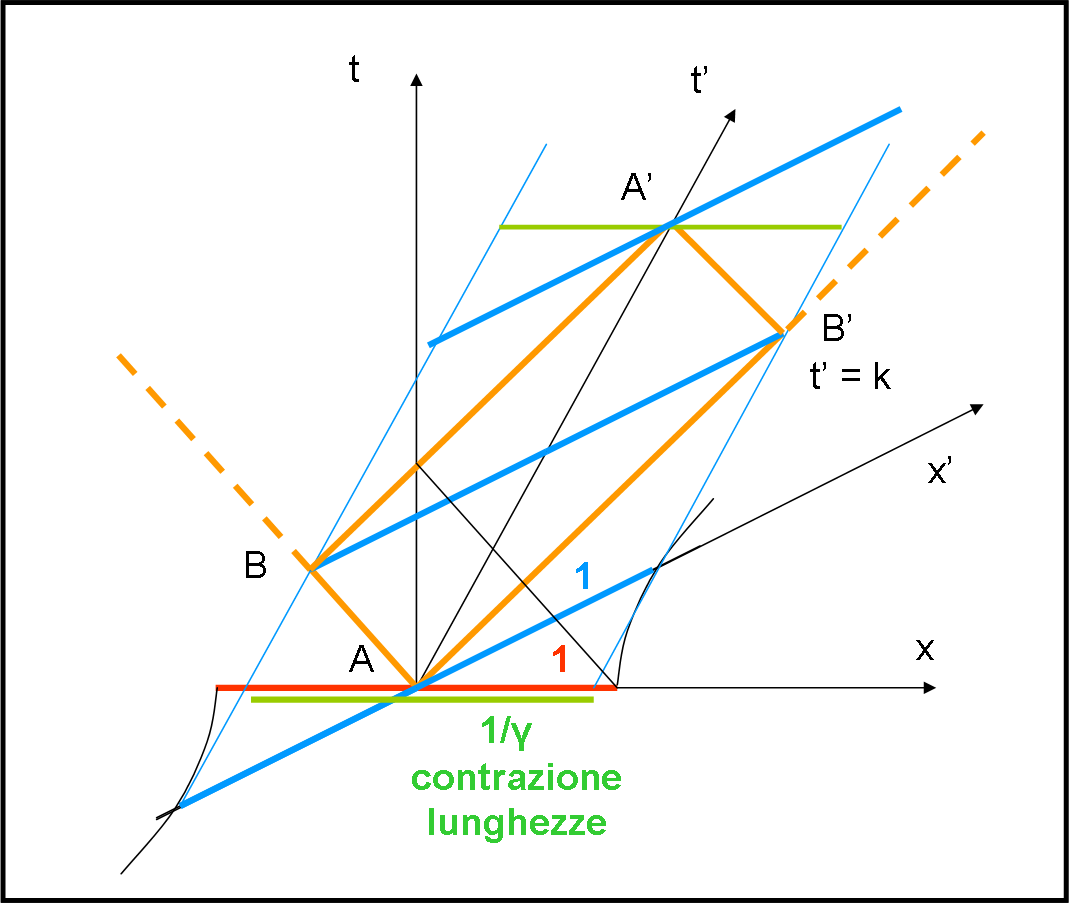
La nostra circonferenza riflettente di partenza (rossa) si trasforma nel segmento inclinato azzurro. Esso individua l’asse di simultaneità per il sistema (x’, t’) ossia t’ = cost. Notiamo che per costruire il segmento azzurro dobbiamo utilizzare l’iperbole di calibrazione in modo da trovare ciò che corrisponde in x’ a un valore di x (nella figura li abbiamo indicati entrambi con 1 per vedere bene come avviene la trasformazione). E poi immediato trovare la distanza contratta sull’asse x (segmento verde). Guardando dall’alto (ossia lungo l’asse t) il segmento verde si trasforma in un’ellisse che ha per semiasse maggiore la lunghezza lungo y (che non è cambiata) e per semi asse minore 1/γ .

Per ripetere quanto fatto con l’orologio di luce, non ci resta altro che vedere il movimento di questa ellisse verde (circonferenza contratta) e seguire i raggi di luce che corrispondono sempre al cono di luce di prima, dato che esso non cambia, cambiando sistema di riferimento. Notiamo anche che il segmento azzurro, se visto dall’asse t, dà luogo anch’esso a un’ellisse, ma con semiasse maggiore allungato verso la direzione del moto, mentre il semiasse minore è sempre uguale a y. Questa ellisse ci interessa per trovare quali sono i punti in cui si ha la riflessione della luce.

Ovviamente, essi devono avvenire nello stesso istante relativamente al viaggiatore A, ossia lungo l’intersezione tra il piano t’ = k e il cono di luce. A quel punto la luce torna indietro e converge nuovamente in A’, che intanto si è mosso lungo t’. La forma “quadrata” della Fig. 45 (viaggiatore fermo) si trasforma in una strana figura (un rettangolo,) che abbiamo spesso usato nella RR per spiegare la relatività della simultaneità nel diagramma di Minkowski.

In poche parole ciò che è simultaneo nel sistema in moto (x’, y, t’) non lo è più nel sistema (x, y, t) proprio quello in cui vogliamo eseguire le osservazioni del nostro esperimento.

La Fig. 46 può sembrare complicata, ma ci torneremo ancora sopra. Per adesso consideriamo l’ellisse verde che tiene già conto della contrazione delle lunghezze e vediamo cosa succede mentre si muove lungo x. guardando tutto dalla direzione t, come fatto nell’orologio di luce. Torniamo, quindi a lavorare nel piano (x,y) con una circonferenza  riflettente contratta, che si muove verso destra (Fig. 47)

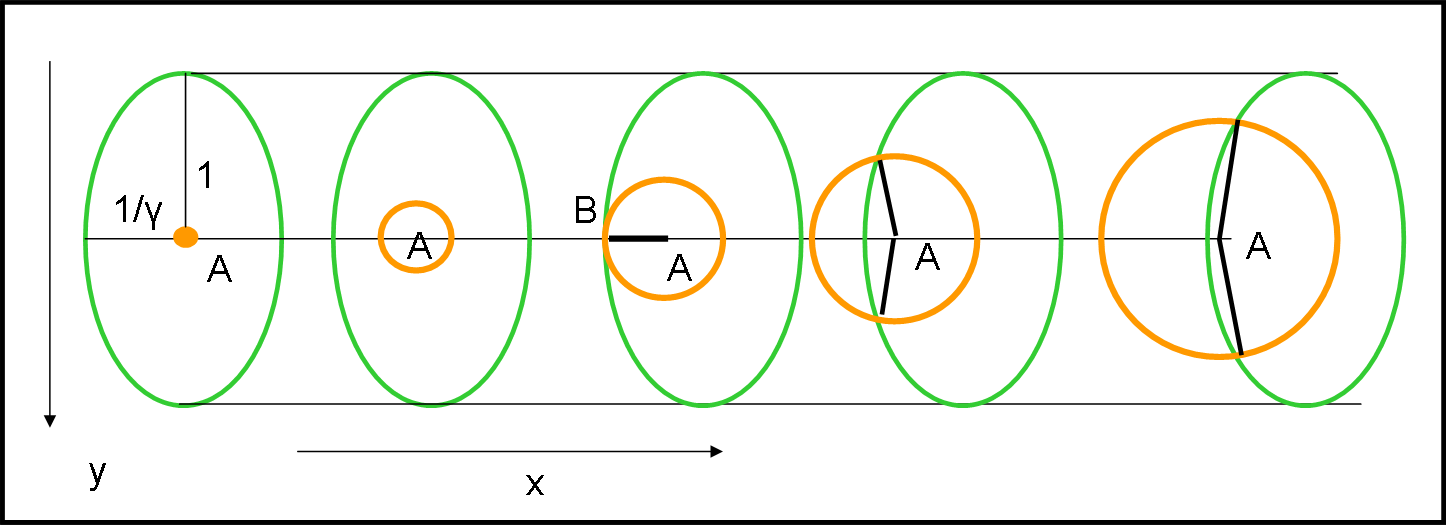
Al tempo t = 0 la lampadina viene accesa e la circonferenza si muove ormai contratta dal fattore di Lorentz, diventando un’ellisse, come detto precedentemente. Nell’istante successivo, l’onda luminosa (il cono di luce) si è già allargata, ma ancora non tocca la parete riflettente. Siamo nel tratto in cui la luce passa da A a B (vedi Fig. 46). La luce ovviamente non riesce a raggiungere tutto il bordo nello stesso tempo (lo fa solo nel sistema x’,t’). Il primo punto della circonferenza-ellisse verde che viene toccata dalla luce è proprio B.

Il cono di luce continua ad allargarsi e poco interessa che esca fuori dalla parte sinistra. A noi interessa quali sono i punti dell’ellisse verde che vengono toccati dalla luce prima di riflettersi.  Altre due posizioni sono disegnate in tempi successivi. Stiamo sperimentando una cosa interessantissima che è in pratica il succo stesso della Relatività Ristretta: la luce continua a toccare punti diversi dell’ellisse verde in tempi diversi, mentre nel sistema di riferimento della circonferenza originaria (rossa) in movimento (ellisse azzurra) questi contatti avvengono simultaneamente (t’ = cost.).

L’intero discorso si riduce al concetto di  relatività della simultaneità: ciò che è simultaneo in un sistema (x’,t’) NON è simultaneo in un altro (t,x). La y continua a disinteressarsi e rimane sempre la stessa dato che non è influenzata dal movimento e dal cambiamento di sistema.

Torniamo alla Fig. 46. Tutto il tragitto tra B e B’  comporta contatti continui con l’ellisse contratta verde, mentre per il sistema in movimento tutti questi contatti avvengono nello stesso istante (mi ripeto per cercare di non far perdere qualche concetto per strada). L’ultimo contatto avviene in B’.

Notiamo bene che stiamo guardando l’ellisse verde mentre si muove lungo il suo asse x, ragione per cui si riescono a evidenziare abbastanza bene solo i punti di contatto iniziale e finale nel sistema (x,t). Quelli relativi a y diverse si intuiscono soltanto. E’ fondamentale riuscire a capire che mentre la luce raggiunge contemporaneamente il segmento (ellisse) rosso, essa tocca l’ellisse verde in tempi diversi che obbligano la luce a fare percorsi sempre diversi, descritti perfettamente dal legame che esiste tra t’ e t, che si ripercuote pari pari su x. Comunque, più di tante parole, vale un’attenta lettura della figura…

Diciamo le cose in altro modo: l’orologio del sistema in movimento non gira tra B e B’ (i due punti sono raggiunti simultaneamente) mentre si muove tranquillamente nel sistema di partenza, fisso..

Quando arriviamo in B’ le cose cambiano drasticamente. Tutti punti dell’ellisse verde sono stati colpiti dalla luce, malgrado i contatti siano avvenuti in tempi diversi. I raggi che ormai hanno colpito l’ellisse verde in tempi t diversi devono convergere simultaneamente in A’. Infatti, il fenomeno fisico deve essere lo stesso in entrambi i sistemi di riferimento.

Ovviamente, il punto A’ ha dovuto spostarsi rispetto ad A, in accordo con la velocità β.

L’esperimento sarebbe finito, ma noi lo analizziamo ancora, non dubitate… Innanzitutto fatemi inserire di nuovo la figura precedente, in cui ho aggiunto un segmento viola (Fig. 48), che corrisponde ai due estremi, in x, in cui abbiamo visto la luce arrivare per toccare l’ellisse verde. E’ un segmento interessante dato che si individuano molto bene i due estremi C e D (la luce tocca per la prima volta l’ellisse e la tocca per l’ultima volta) e la proiezione dei due puti A e A’ di partenza e di arrivo della lampadina.

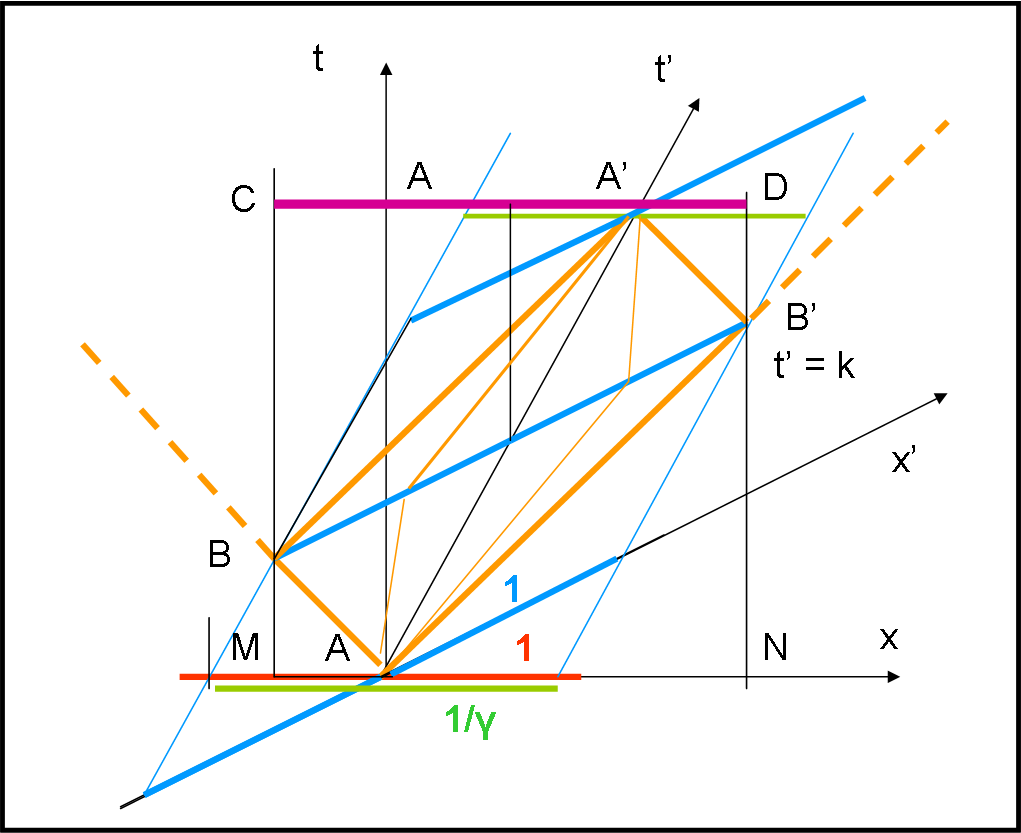
Notiamo anche che, per costruzione, il poligono CMND deve essere un quadrato (la luce va a 45°). Ciò comporta che ciò che capita nei tempi (dilatazione) si rispecchia perfettamente nelle x che misuriamo alla fine. D’altra parte i segmenti sono dati da ct e c è uguale 1. Ma questo è una banalità che abbiamo già affrontato nel diagramma di Minkowski e anche nell’orologio di luce.

Cerchiamo di disegnare in tre dimensioni (due di spazio e una di tempo) quanto descritto finora, usando la Fig. 49 Divertitevi pure, ma dato che siamo in ballo,continuiamo a ballare. Intanto facciamo una scommessa: “Volete vedere che quel segmento viola, se visto dall’asse delle t, diventa proprio l’ellisse di aberrazione?”. I più bravi diranno: “Certo, è ovvio…”, ma forse per qualcuno non è ancora del tutto banale.

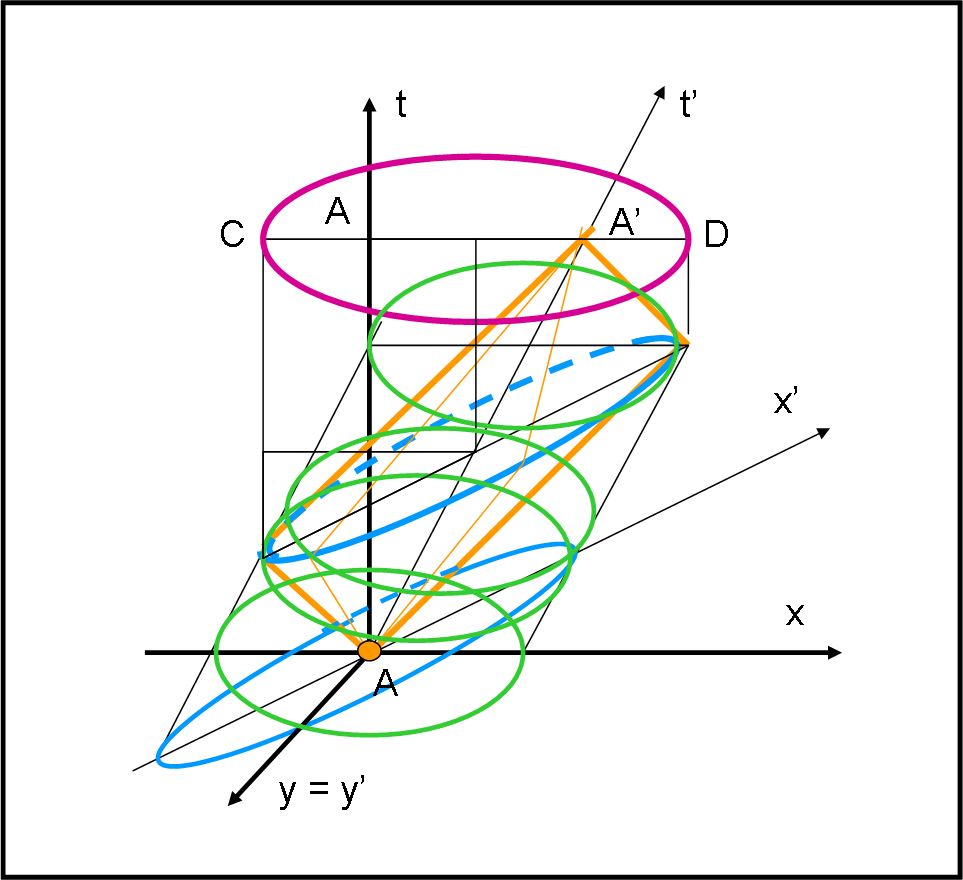
Per cui riprendiamo la Fig. 47 e costruiamola in modo regolare e preciso nella Fig. 50.

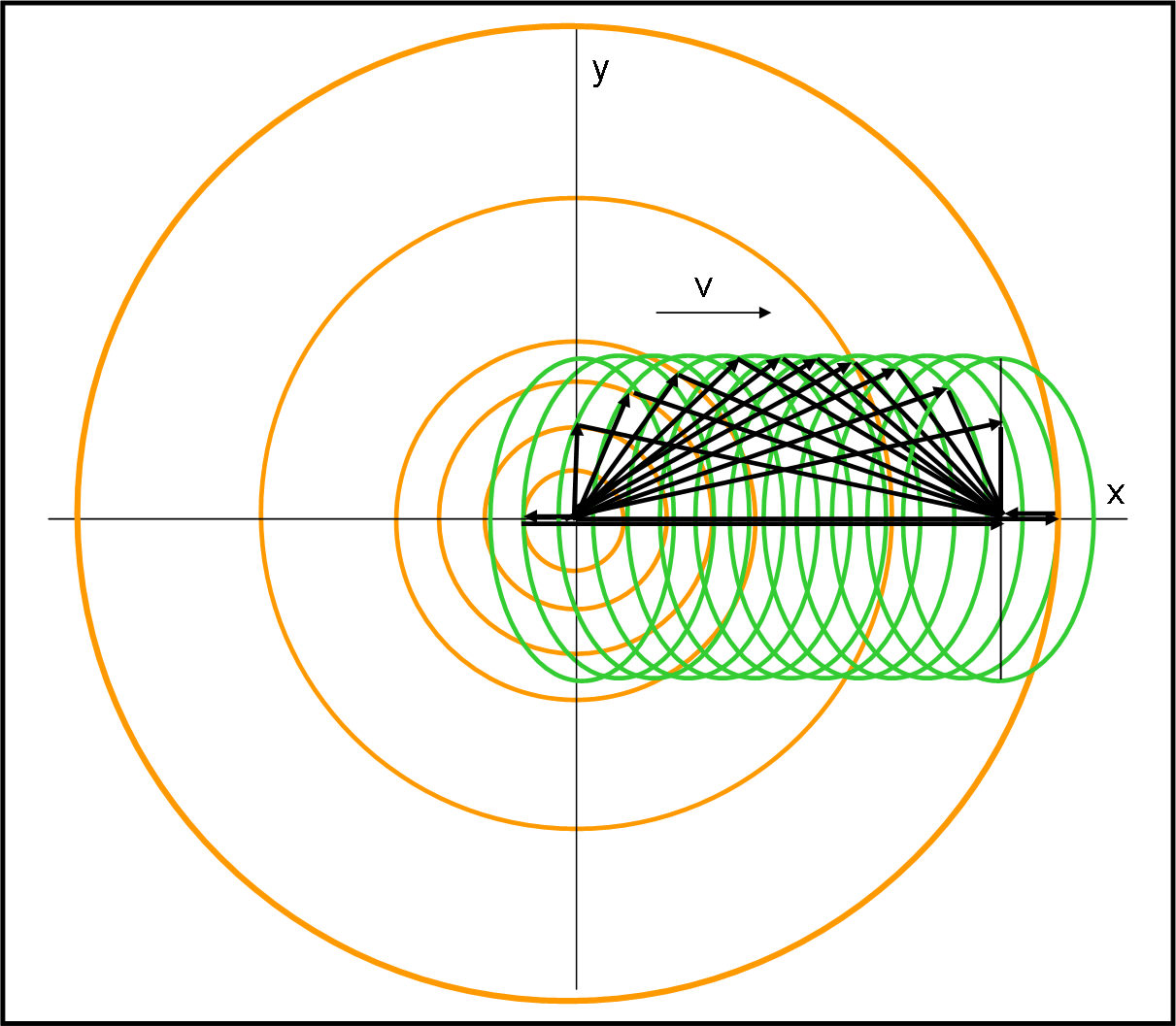
Ci portiamo decisamente nel piano (x,y), lo stesso che avevamo usato per l’orologio di luce (ma in fondo anche la nostra circonferenza è un orologio di luce generalizzato). Lungo l’asse x disegniamo le varie posizioni assunte dall’ellisse verde a intervalli di tempo costanti. La prima ellisse è quella centrata in A e l’ultima è quella centrata in A’. Ho anche inserito alcune visioni del cono di luce tanto per ricordare che i punti di contatto sono sempre quelli tra ellisse verde e cerchi di luce (il cono visto dall’alto).  In questa figura, solo apparentemente intricata, siamo nel piano x, y e il segmento viola della Fig. 49 è esattamente quello che unisce il primo e l’ultimo contatto, ossia i punti di contatto che stanno sull’asse delle x.

Per non esasperare la figura abbiamo solo disegnato la parte superiore, ma la stessa identica cosa capita anche in basso.

Per ogni posizione dell’ellisse verde si determina il relativo punto di contatto con il cono di luce (e l’analogo nella parte sotto). Le righe nere sono il percorso della luce partita da A che si riflette sull’ellisse verde e poi continua per raggiungere A’. Tutte le linee devono, perciò, partire da uno stesso punto (A) fisso (la luce è inviata solo in quel punto e all’istante t = 0), riflettersi e raggiungere tutti lo stesso punto A’ nello spesso istante t = t_F. Come abbiamo già detto parlare di tempi è come parlare di x, per cui le varie righe possono essere considerati legate nello stesso modo sia ai tempi che ai percorsi.

A noi cosa interessa disegnare? Beh… abbastanza semplice: tutti punti di contatto (da un estremo all’altro) che nel sistema in movimento devono essere simultanei, oltre che i due punti A e A’ . La y non  può ovviamente superare il semiasse maggiore dell’ellisse verde, dato che non è influenzata dal movimento. Non ci resta che unire tutti questi punti, come fatto in Fug. 51.

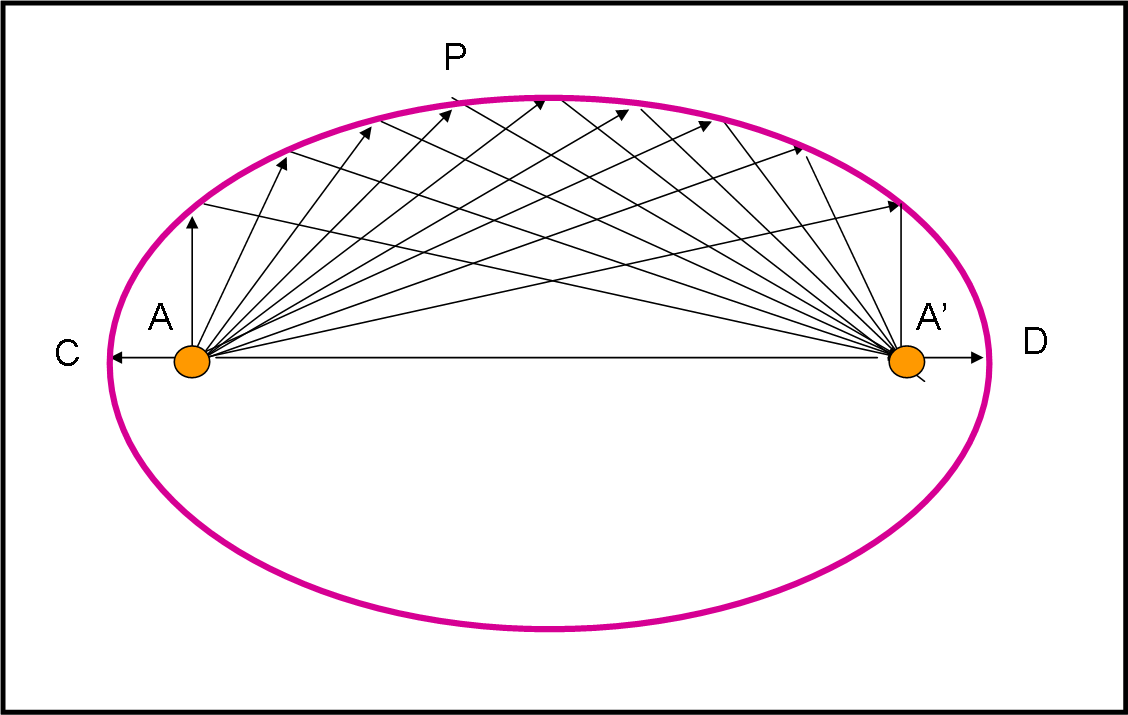
Essi, però, sono quei punti P tali che il percorso da A fino a loro e da loro fino ad A’ deve essere sempre uguale (il fenomeno deve essere lo stesso in ogni sistema). Ovviamente, i percorsi parziali da A al punto di contatto e da questo ad A’ devono essere diversi nel sistema x,y (non lo sarebbero nel sistema x’,y), ma la loro somma deve essere uguale.

Dalle nozioni più spicciole di geometria analitica, sappiamo benissimo che la curva luogo dei punti la cui distanza da due punti fissi è costante non è altro che un’ellisse di cui A e A’ sono i fuochi. Il semiasse minore dell’ellisse finale è sempre uguale all’unità, se tale abbiamo posto il raggio della circonferenza iniziale. Quanto vale il semiasse maggiore dell’ellisse e la distanza focale?

Non sarebbe un problema arrivarci attraverso la RR e le sue trasformazioni. Noi però ci vogliamo divertire a calcolare l’equazione dell’ellisse attraverso le condizioni con cui è stata creata: proiezione sul piano (x,y) dell’intersezione tra il piano di simultaneità t’ = cost, e il cono di luce. 

Questa volta vorremmo calcolare la sua equazione in modo analitico. In realtà, l'ellisse viola non è altro che la proiezione nel piano x, y della ellisse azzurra, la quale a sua volta è l'intersezione tra cono di luce e un piano (x', y'=y).

In poche parole, basta trovare la soluzione del sistema:

x² + y² = t²

t' = γ(t – βx)

La prima è l’equazione del cono di luce (una circonferenza che assume raggi crescenti e/o decrescenti descrive proprio un cono), la seconda è la relazione che lega  t’ con t e x (trasformata di Lorentz) e quindi descrive proprio il piano di simultaneità del sistema x’,y’,t’ nelle coordinate x,y, t.

Basta allora invertire la seconda e ricavare t:

t = t’/γ + βx

Tuttavia, t’ è una costante (simultaneità) e per semplicità possiamo prenderlo uguale a 1.

Sostituiamo t ricavato dalla seconda nella prima equazione e otteniamo la relazione:

(1/γ + βx)² = x² + y²

Che è proprio la curva desiderata che già sappiamo essere un’ellisse. Dobbiamo, però, cercare di scriverla nella forma canonica…

Elevando a quadrato il primo membro si ha:

1/γ² + β²x² + 2 βx/γ = x² + y²

Portiamo tutto al secondo membro e otteniamo:

x² + y² - β²x² - 2 βx/γ - 1/γ²  = 0

Raccogliamo x²

x²(1 - β²) + y² - 1/γ² - 2 βx/γ = 0

Ma…

(1 - β²) = 1/γ²

Da cui:

x²/γ² - 1/γ² - 2 βx/γ + y² = 0

Moltiplichiamo e dividiamo per γ il terzo fattore e raccogliamo 1/γ²:

(x² - 1 - 2 βγx)/γ² + y² = 0

Accidenti… vorremmo un bel quadrato a, numeratore, ma non sembra proprio possibile… a meno di scrivere l’unità in modo un po’ strano…

Ricordiamo che:

1/γ² = 1 – β²

1 = γ² – β² γ²

Andiamo a sostituire questa espressione al posto di -1 al numeratore dell’equazione:

(x² - γ² + β² γ² - 2 βxγ)/γ² + y² = 0

Magnifico, possiamo estrarre dalla parentesi - γ² che diviso per γ² è uguale a -1. L’equazione diventa:

(x² + β² γ² - 2 βxγ)/γ² + y² = 1

Finalmente, abbiamo costruito il quadrato che volevamo e possiamo scrivere:

(x - βγ)²/γ² + y² = 1

Abbiamo ritrovato l’ellisse della volta scorsa (ci mancava altro…) con semiassi  γ e 1 (Fig. 43).

Ovviamente, ho usato un metodo del tutto personale e probabilmente si può fare meglio e più rapidamente.

Notiamo che l’ellisse costruita è veramente fondamentale. Innanzitutto le direzioni dei raggi che partono da A sono proprio quelle che risultano combinando la velocità della luce e la velocità del viaggiatore, ossia sono le direzioni che hanno subito l’aberrazione luminosa. Inoltre, la lunghezza dei percorsi è sempre diversa e, data l’uguaglianza tra x e t, ci dice direttamente di quanto il tempo si è dilatato passando da un sistema fermo a un sistema in moto. Una variazione dei tempi indica anche una variazione di frequenza nella luce (un moto di allontanamento o di avvicinamento) e quindi comporta un effetto doppler che ci permette di colorare ogni direzione, ammettendo che la luce originaria sia bianca o quello che volete. Ne risulta che una lettura diretta delle grandezze dell’ellisse ci permette di ottenere ben quattro dimensioni: x, y, tempo, frequenza, con un righello e un goniometro.

Andiamo con calma e torniamo alla nostra ellisse di aberrazione (o di simultaneità - ormai abbiamo capito bene il significato del suo nome) e alla sua equazione e dedichiamoci all'effetto doppler.

Coloriamo la luce con l'effetto doppler

A questo punto possiamo dimostrare e calcolare la frequenza luminosa che arriva all’osservatore sull’astronave. Come già detto, e per costruzione, la dilatazione del tempo, dovuto al moto, corrisponde perfettamente alla lunghezza delle congiungenti i punti dell’ellisse con uno dei due fuochi.

Conosciamo già l’effetto doppler relativistico (QUI, sottocapitolo "qualche formula e il gioco è fatto") per un moto lungo l’asse x. Tuttavia, vale la pena, adesso, ricavarlo a partire dall’effetto doppler classico.

Definiamo, innanzitutto, la frequenza. Immaginiamo una lampadina che si accenda e si spenga a intervalli di tempo costanti (proprio come appare un faro su un promontorio sul mare): tanti segnali a ritmo regolare. Quanti segnali manderà in certo tempo t? Poniamo che siano n. La frequenza del segnale luminoso è allora data da:

f = n/t

A parità di tempo, maggiore o minore è il numero di segnali, maggiore o minore è la frequenza del segnale.

Immaginiamo (Fig. 52, righe nere) che la sorgente e un  ricevitore siano fermi l’uno rispetto all’altro a una certa distanza d (si muovono solo nel tempo, asse verticale).

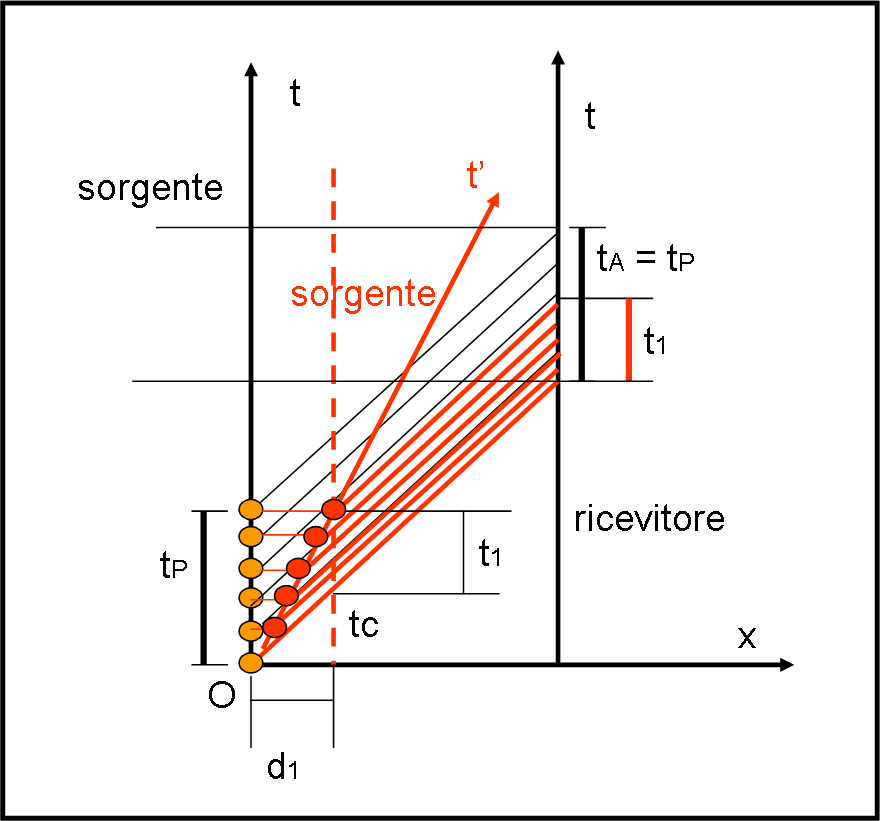
La frequenza dei segnali mandati e dei segnali ricevuti sarà uguale. Il ritardo tra invio e ricezione è ovviamente uguale a t = d/c, da cui d = ct. Nella figura abbiamo usato unità di misura tali che il raggio luminoso (o il fotone) percorra una linea inclinata di 45° nel piano (t,x), come nel diagramma di Minkowski. In altre parole, possiamo porre d = t e c =1 e, come al solito, β = v/c

La frequenza di partenza è data da

f_P = n/t_P

esattamente come quella di arrivo:

f_A = f_P = n/t_P

Adesso, facciamo muovere la lampadina con una velocità v = β, in direzione del ricevitore.

Il primo segnale parte allo stesso tempo di prima. Il secondo, però, dà già un risultato diverso, dato che parte dopo che la lampadina  (rossa) ha già percorso un certo spazio, avvicinandosi al ricevitore. Il che vuol dire che il secondo segnale arriva prima del previsto, dovendo percorrere uno spazio minore. E così via fino all’ultimo segnale. I segnali (rossi), in parole semplici, partono mentre si avvicinano e quindi anticipano il loro arrivo, ossia il ricevitore li vede arrivare con una frequenza maggiore.

Calcoliamo il tutto con la figura, utilizzano un metodo un po’ lungo ma tale da chiarire perfettamente quello che succede.

La linea rossa continua indica lo spostamento della lampadina in funzione del tempo (ossia la sua velocità). Ciò che ne deriva è del tutto equivalente al fatto che i segnali siano mandati a intervalli di tempo minori a partire dalla linea rossa tratteggiata che dista d₁ dall’origine O. A questo punto calcoliamo il tempo totale di invio dei segnali a partire da questa linea. In altre parole dobbiamo calcolare l’intervallo di tempo t₁ che è l’intervallo in cui vengono mandati gli n segnali e che è anche uguale all’intervallo di tempo in cui i segnali sono ricevuti.

Possiamo scrivere d₁ in due modi, sia in funzione della velocità c che della velocità v. Ossia:

d₁ = ct_c = v t_P

Ma, per le ipotesi fatte (c = 1, v/c = β)

t_c = β t_P

E’ immediato ricavare l’intervallo di tempo t₁:

t₁ = t_P – t_c = t_P – t_P β= t_P (1 – β)

Non ci resta che confrontare la nuova frequenza con quella originaria (ossia quella di partenza). Ricordiamo, infatti, che la lampadina continua a mandare i segnali con la frequenza originaria. E’ solo il ricevitore che li riceve in modo diverso, a causa del continuo avvicinamento della sorgente di luce.

La frequenza di partenza, è sempre:

f_P = n/t_P

Quella di ricezione, vale adesso:

f_A = n/t₁ = n/t_P (1 – β)

Ricavando n da entrambe e uguagliando si ha:

n = f_P t_P = f_A t_P (1 – β)

da cui:

f_A = f_P /(1 – β)       …. (1)

Questo è il classico effetto doppler di avvicinamento. Ovviamente cambia il segno se la sorgente si allontana e la frequenza diminuisce.

Aumento o diminuzione della frequenza vuol dire, in poche parole, spostamento verso il blu (o meglio il violetto) o verso il rosso, verso alte o basse energie.

Siamo sicuri di aver fatto tutto bene? In particolare, siamo sicuri che f_P rimanga sempre la stessa? Se la velocità v è relativamente modesta potremmo dire di sì, ma per valori alti di β, la faccenda non torna più.

Siamo stati troppo frettolosi…

La sorgente di frequenza f_P si è messa in movimento e sappiamo benissimo che la Relatività Ristretta ci dice che per chi si muove il tempo subisce un rallentamento rispetto al sistema “fermo”. La f_P originaria diventa una f_P’ che è legata a quella originaria, f_P, dal nostro fattore di Lorentz. Ossia, i tempi sono legati da:

t’_P = γ t_P

e quindi

f’_P = 1/γ t_P

La formula (1) deve perciò contenere la f’_P  e non la f_P. Essa andrebbe, perciò scritta:

f_A = f’_P /(1 – β) =  f_P /γ (1 – β)) o, se preferiamo:

f_A = f_P (1 – β²)^1/2/(1 – β)

Ci piace questa formula? Personalmente non la amo tanto… dato che al numeratore c’è un fattore che diminuisce la frequenza (sempre minore di 1), mentre al denominatore c’è un fattore sempre minore di 1 che, quindi, aumenta la frequenza. Insomma, una relazione che appare poco immediata.

Tuttavia, quando c’è di mezzo il fattore di Lorentz, i piccoli trucchi sono sempre a portata di mano

Proviamo a pasticciarla un po’:

(1 – β²)^1/2/(1 – β) = ((1 – β)^1/2 (1 + β)^1/2)/((1 – β )^1/2 (1 – β)^1/2) = (1 + β )^1/2/(1 – β )^1/2 =

= ((1 + β)^1/2(1 + β)^1/2)/((1 + β)^1/2 (1 – β)^1/2) = (1 + β)/(1 – β²)^1/2

Da cui:

f_A = f_P (1 + β)/(1 – β²)^1/2 = f_P γ (1 + β)

Adesso è molto più chiaro che f_A > f_P

In caso di allontanamento si ha, ovviamente:

f_A = f_P (1 - β)/(1 – β²)^1/2 = f_P γ (1 - β)

Possiamo anche scriverli in altro modo… (β e γ insieme ne fanno di tutti i colori…):

f_A = f_P (1 + β)/(1 – β²)^1/2 = f_P γ(1 + β) = f_P ((1 + β)^1/2 (1 + β)^1/2)/(( 1 + β)^1/2( 1 - β)^1/2)

f_A/f_P  = ((1 + β)/(1 – β))^1/2     > 1             avvicinamento

f_A1 /f_P = ((1 - β)/(1 + β))^1/2       < 1             allontanamento

Torniamo, adesso, alla nostra ellisse e vediamo come possa essere utilissima per il calcolo immediato delle frequenze relative alle varie direzioni, per valori qualsiasi dei raggi provenienti dalla stelle. In pratica dobbiamo riuscire a scrivere i tempi ad essi relativi.

Ricordiamo l’equazione dell’ellisse (QUI, formula (3)):

r = a(1 – e²)/(1 + e cos ϑ)

Nel nostro caso (Fig. 43)

a = γ

e = β

Per cui il raggio vettore, ossia la distanza tra fuoco e punti della curva (che è anche il tempo), è dato da:

t = γ (1 – β²)/(1 + β cos ϑ)

Questa è l'equazione per un'ellisse con ϑ che vale 0 a partire dalla direzione del perielio . In poche parole è ribaltata rispetto all'ellisse di Fig. 43. Poco male, dato che tutto dipende dalla direzione della velocità con cui si muove l'astronave (a destra o a sinistra). Poniamo allora l'asse x diretto verso sinistra e l'angolo ϑ che parte dal punto più vicino al fuoco A (Fig. 53).

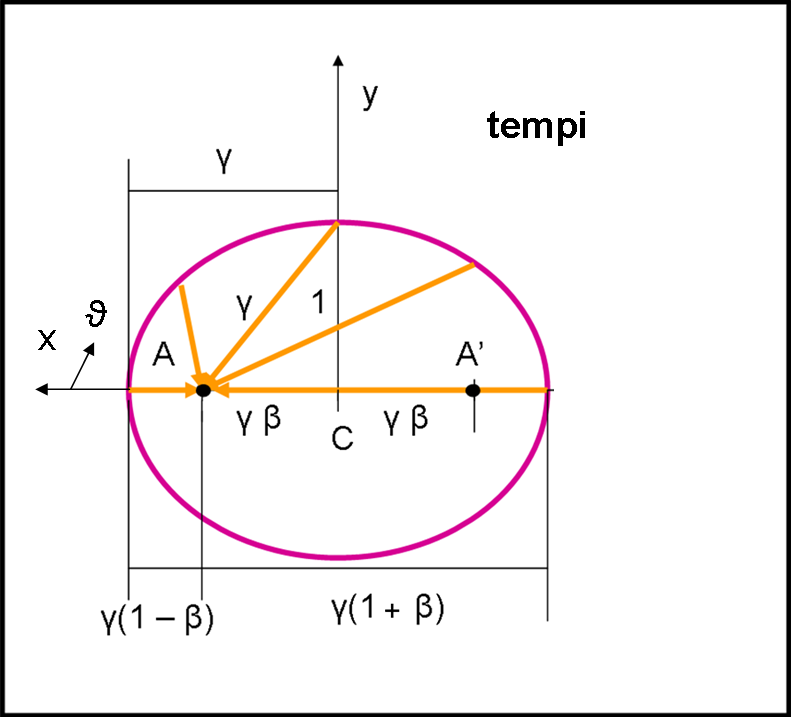
In pratica, per ogni angolo ϑ noi siamo in grado di calcolare il tempo attraverso l'ellisse e, di conseguenza, la frequenza.

Per esempio, per un angolo ϑ = 0, abbiamo

t = γ (1 – β²)/(1 + β ) = γ (1 - β)

Per un angolo ϑ = 180°

t = γ (1 + β)

da cui (come già visto precedentemente):

f_A/f_P = 1/(γ (1 - β)) = (1 – β²)^1/2/(1 - β) =  γ (1 + β)

f_A/f_P  = γ (1 - β)

Particolarmente interessante è l'angolo per cui t =1, ossia la frequenza non cambia rispetto a quella di partenza.

Per esso vale:

t = γ (1 – β²)/(1 + β cos ϑ) = 1

ossia:

t = γ /γ² (1 + β cos ϑ) = 1/γ(1 + β cos ϑ) = 1

γ(1 + β cos ϑ) = 1

γ + γβ cos ϑ = 1

cos ϑ = (1 - γ)/γβ

Il numeratore è sempre minore di 1, per cui ϑ > 90°

Questo è ovviamente anche l'angolo in cui le frequenze di partenza e di arrivo sono uguali.

N.B.: Paolo, nei commenti, ha confermato questo risultato e calcolati due valori particolari.

La situazione si può facilmente riportare al caso che ci interessava fin dall'inizio, ossia quello di un astronave A che viaggia a una certa velocità  β verso destra (così sfruttiamo una bella animazione trovata nel web...), dove inseriamo direttamente le frequenze al posto dei tempi. E' solo una questione di ribaltamento o di cambiamento di fuoco o di verso dell'angolo ϑ (Fig. 54).

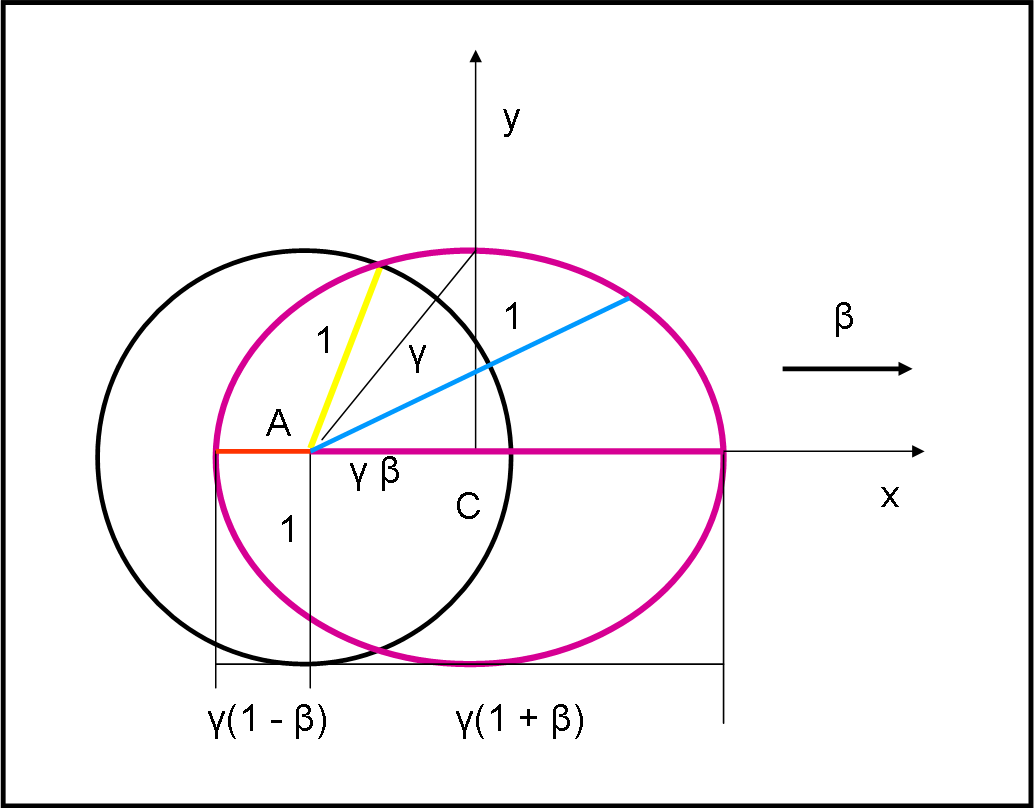
Le  congiungenti più lunghe sono quelle che hanno frequenza maggiore è quindi colore più violetto. Quelle più corte fanno frequenza minore e quindi colore più rosso. Il colore originario (giallo) si ha in una direzione inclinata verso il moto (e si trova facilmente come intersezione tra circonferenza di partenza ed ellisse di abeerrazione)

Il filmato che segue mostra perfettamente come cambiano i colori al crescere della velocità dell’astronave. Vale più di tante parole...

Bene, la nostra ellisse sta svolgendo perfettamente il suo compito e vale sia per oggetti che ricevono o che emettono la luce. Faremo, perciò, alcuni esempi estremamente interessanti.

Un viaggio (semplice) in astronave

Riassumiamo,  in modo semplificato, la nostra ellisse di aberrazione e la sua ricaduta sul panorama che si vede viaggiando in astronave a velocità relativistiche. Chi ha saltatole parti relativistiche più complicate, può anche limitarsi a questa descrizione. Buon viaggio!

Consideriamo, in Fig. 55, la nostra astronave A immobile in un certo punto dell’Universo.

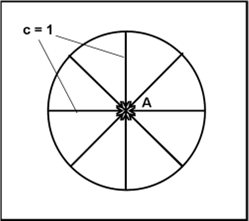
Verso di lei piovono i fotoni provenienti da ogni parte della sfera celeste. Fatemene considerare solo otto, ma più che sufficienti per comprendere la situazione. La circonferenza attorno all’astronave A è relativa a un attimo prima che i fotoni la colpiscano e consideriamo il suo raggio proprio uguale alla velocità c della luce, o meglio allo spazio relativo a un secondo prima dell’arrivo. In tali condizioni, lo spazio diviso il tempo, che è uguale a uno, è proprio la velocità. I vettori che hanno lunghezza uguale al raggio della circonferenza hanno quindi come modulo (ossia valore assoluto) proprio c.

Fin qui direi che non ci sono problemi. E’ quello che capita a un osservatore che guardi il cielo attorno a lui. Ogni momento arrivano i fotoni delle stelle ed essi giungono da ogni direzione con velocità uguale a c. In ogni istante siamo soggetti a una pioggia continua di fotoni che arrivano da ogni direzione e che ci colpiscono tutti assieme, proprio come se stesse piovendo luce. Piovendo… ho detto piovendo. Proprio la pioggia che ci era servita  per spiegare l’aberrazione annua… Tenetelo ben presente, può aiutare molto.

E’ il momento di mettere in moto la nostra astronave. Immaginiamo di raggiungere immediatamente una velocità di crociera v abbastanza elevata, pari a 0.6 volte quella della luce.

Non è male, anche se si può fare di meglio. Non abbiamo considerato una velocità proprio uguale a c, dato che il disegno diverrebbe meno intuitivo e più difficile da rappresentare. Tuttavia, una volta compreso il meccanismo, lo potete fare da soli o almeno comprendere come si deformerebbe.

L’astronave viaggia verso destra. Il che vuol dite che i fotoni che giungono verso di lei sono anche soggetti a una velocità uguale e contraria (ossia a una – v, diretta verso sinistra) disegnata come segmento azzurro. E’ esattamente ciò che capitava con l’aberrazione “normale”, quando combinavamo la caduta della pioggia con la nostra corsa per metterci al riparo.  Costruiamo allora, in Fig. 56, la somma vettoriale delle velocità per ognuno degli otto fotoni che stanno raggiungendo l’astronave.

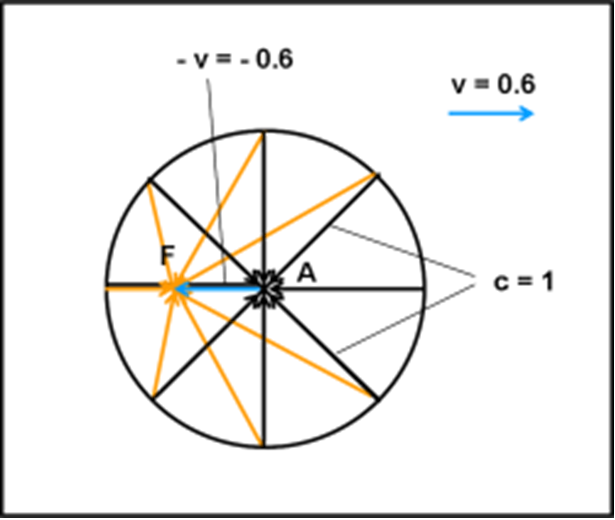
Ovviamente, essi cambiano direzione apparente e i vettori risultanti sono rappresentati dai segmenti arancioni. Quello che è veramente interessante è, però, che i fotoni si dirigono tutti verso uno stesso punto, che ovviamente non coincide più con l’astronave (anche nell’aberrazione annua il telescopio doveva essere puntato verso una direzione diversa da quella teorica). Non era comunque difficile prevederlo da come si costruisce la somma di vettori…

Prima di proseguire, fatemi richiamare un punto essenziale. Tutto ciò che stiamo per fare è relativo al sistema di riferimento dell’astronave in movimento (non per niente la teoria si chiama della relatività). Se cambiassi astronave cambierebbe il risultato. In altre parole, non è l’Universo che cambia, ma solo ciò che vede l’astronave. O, ancora, le lunghezze e i tempi cambiano perché ci riferiamo a un oggetto in movimento. Un oggetto fermo vedrebbe le cose in modo ben diverso.

Il punto F è il punto di raccolta degli otto fotoni. Ciò che vede realmente l’astronave è la situazione relativa proprio a questo punto F. In realtà, potremmo tracciare dal punto A le parallele alle linee che convergono in F e ci accorgeremmo dell’effetto dell’aberrazione. Avremmo una rappresentazione corretta della situazione apparente, ma la limiteremmo solo all’effetto di aberrazione. Molto meglio deformare la Fig. 56 in modo da visualizzare tutto insieme lo spaziotempo e gli effetti dovuti alla velocità dell’astronave.

A questo punto, entra in scena il fattore di Lorentz che già conosciamo. Esso, se ricordate bene, permette di calcolare la dilatazione del tempo e la contrazione delle lunghezze per un sistema di riferimento in moto con una velocità comparabile a quella della luce. L’esatta motivazione della deformazione che stiamo per fare può essere spiegata analiticamente attraverso i capitoli precedenti, quelli che ci hanno portato alla fondamentale ellisse di aberrazione.

In questo capitolo riassuntivo e prettamente divulgativo, ci limitiamo solo a vedere quali sono i risultati pratici della trasformazione introdotta dal fattore di Lorentz.

Cosa dobbiamo fare praticamente? Non molto. Innanzitutto considerare il punto F come il fuoco di un ellisse che abbia il semiasse minore uguale al raggio della circonferenza iniziale. Questo vincolo si può capire abbastanza bene, pensando che la direzione perpendicolare alla direzione del moto dell’astronave deve essere in qualche modo non soggetta a particolari deformazioni. Ma capiremo meglio la situazione, applicando la trasformazione fondamentale.

Dobbiamo, adesso, “stirare” il cerchio originario fino a farlo diventare un’ellisse di cui F è il fuoco. Il fattore di “stiramento” è proprio il fattore di Lorentz γ. In parole più tecniche, il semiasse maggiore dell’ellisse deve essere proprio il fattore di Lorentz, considerando uguale a 1 il raggio della circonferenza (ossia la velocità della luce è posta uguale a 1 e γ viene espresso in funzione di questa scelta semplificativa).

Quanto vale questa dilatazione? Basta ricordare la formula che descrive il fattore di Lorentz  e inserire al posto di v e c i valori attuali, ossia c = 1 e v = 0.6. Per la proprietà dell’ellisse la distanza del fuoco F dal centro dell’ellisse C è dato da vγ. Ai più preparati non è sfuggito il fatto che la distanza tra fuoco e centro di un’ellisse è il prodotto tra il semiasse maggiore e l’eccentricità. Dato che γ è proprio il semiasse maggiore della nostra ellisse, ne segue che la velocità v dell’astronave è l’eccentricità.

D’altra parte se essa tende a zero, C coincide con F e torniamo alla circonferenza iniziale. Se, invece v aumenta può arrivare al massimo a 1, ossia a c (che abbiamo posto uguale a 1). L’ellisse diventa una parabola che definisce le condizioni estreme della deformazione dello spazio tempo. Non complichiamoci le cose (chi se la sente può proseguire tranquillamente) e torniamo alla nostra velocità di 0.6. Il fattore di Lorentz è facilmente calcolabile, ricordando la formula che lo definisce:

γ = 1/(1- v²/c²)^1/2 = 1/(1 – 0.62/1)^1/2 = 1.25

La Fig. 57 ci mostra l’ellisse finale, che ci permette di leggere tutti i più importanti parametri che definiscono lo spaziotempo relativo all’astronave in movimento.

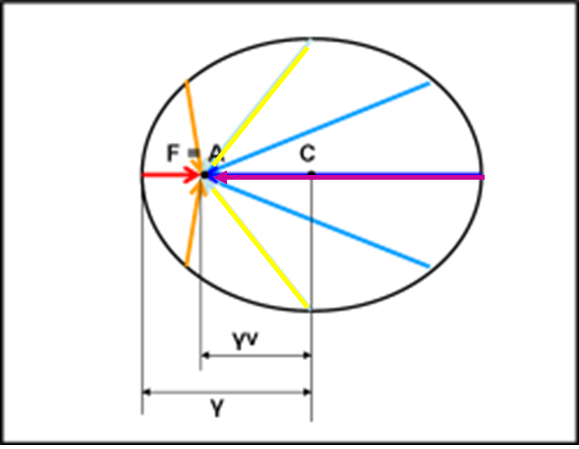
Vediamoli uno per uno e cerchiamo di capire quanto sono stati geniali i signori Einstein e Lorentz.

Il tutto diventa semplicissimo e ovvio, anche se per arrivarci, passo dopo passo, bisognerebbe entrare in una matematica non certo banale (vedi capitoli precedenti). Noi possiamo gustarci il risultato finale e la sua geniale semplicità o -se preferire- semplice genialità.

Innanzitutto, notiamo benissimo che la situazione che appare all’astronave A è aberrata relativisticamente, ossia lo spazio si concentra davanti a lei e si allarga dietro. Nell’ellisse possiamo proprio calcolare i valori corretti delle deformazioni. Inoltre, le lunghezze delle linee dei fotoni, che raggiungono l’astronave a partire dall’ellisse, rappresentano esattamente l’energia che posseggono, o -meglio ancora- la frequenza (e quindi la lunghezza d’onda).

E’ immediato disegnare le linee con il colore corrispondente: davanti all’astronave i segmenti sono più lunghi e quindi è maggiore la frequenza e minore la lunghezza d’onda. In parole povere, siamo nel blu (e oltre) e assistiamo al fenomeno del blueshift relativistico, dovuto al fatto che gli oggetti di fronte all’astronave si avvicinano a lei a grande velocità.

Dietro all’astronave i segmenti s’accorciano e quindi aumentano le lunghezze d’onda e si va verso il rosso e oltre. E’ il redshift relativistico dovuto alla grande velocità di allontanamento degli oggetti posti alle “spalle” dell’astronave.

Notate che lungo l’ellisse vi saranno due punti in cui la lunghezza del segmento che unisce ellisse e fuoco è uguale al raggio della circonferenza di Fig. 55. E’ l’unica direzione in cui la luce non subisce spostamento di lunghezza d’onda e mantiene le condizioni iniziali. E’ lì che bisogna guardare se non si vuole essere travolti dagli effetti spaziotemporali!

Ho detto “temporali”? Sì, esattamente. Le lunghezze dei segmenti indicano anche quanto il tempo si dilati o si accorci nelle varie direzioni. D’altra parte il fattore di Lorentz è come il “prezzemolo” e (ricordate?) ci permette proprio di stabilire la dilatazione del tempo per un viaggiatore spaziale.

Insomma, muniti di un righello e di un goniometro da poco prezzo (e niente di più, nemmeno Celestia...), siamo in grado di misurare direttamente l’energia dei fotoni, la loro frequenza, la dilatazione del tempo e delle lunghezze legata all’angolo di deformazione sotto cui l’astronave vede lo spazio attorno a lei. Siamo anche in grado, perciò, di disegnare la deformazione di una qualsiasi figura sia posta in un certo punto dello spazio.

Potremmo fare un bel disegno e metterlo dietro all’astronave (è il posto migliore per vedere effetti veramente speciali…) e, infine, disegnarlo deformato secondo quanto descritto prima.

Basta seguire le lunghezze dei segmenti fuoco-ellisse a partire dalle condizioni iniziale in cui il disegno era posizionato sulla circonferenza ad astronave ferma, come mostrato in Fig. 58, dove il disegno è d.

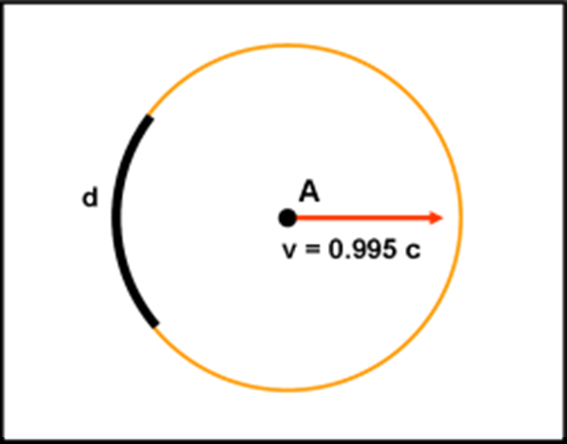
Dato che stiamo parlando di risultati di geni della fisica, voglio proporvi un esempio basato su un capolavoro di un altro genio: Leonardo da Vinci. Anch’egli amava e capiva la Natura come forse nessuno è mai riuscito a fare. Mi sembra quindi ovvio usare un suo celebre dipinto per darci un aiuto.

Sono riuscito a scovare la deformazione subita dall’Adorazione dei Magi (il disegno fantastico di preparazione al quadro, Fig. 59) sia vista proprio nella direzione del movimento dell’astronave sia nel piano dell’ellisse di Fig. 57.

Le Fig. 60 e 61 ci regalano le due rappresentazioni. Come vedete il disegno è posto DIETRO l’astronave, ma, per il fenomeno dell’aberrazione, si vede benissimo anche davanti e, magicamente, si colora da solo. La deformazione è relativa a una velocità veramente prossima a quella della luce, ossia v = 0.995.

 

Questo articolo può essere un punto di partenza per viaggi sempre più avventurosi. Ad esempio, non stupitevi se avessimo davanti il Sole e partissimo verso di lui accelerando fino a raggiungere la velocità della luce: all’inizio sembrerebbe allontanarsi, dato che tutti i raggi luminosi si concentrerebbero verso la direzione del moto e vedremmo la nostra stella rimpicciolire e sempre più oggetti davanti a noi (un po’ come abbiamo visto succedere per Orione ).

Spero di avervi dato materiale per divertirvi pensando e per pensare divertendovi.

Prima di concludere, vorrei ancora ribadire che la Fig. 57 è una perfetta rappresentazione delle quattro dimensioni e siamo riusciti a disegnarla sul piano di un foglio. Si potrebbe facilmente anche portarla nelle tre dimensioni utilizzando un ellissoide a due assi (a > b = c). In ogni modo, essa descrive completamente le variazioni di tutte e quattro le dimensioni dello spaziotempo.

Possiamo quindi consideralo un vero e proprio disegno a quattro dimensioni. Non ci resta che continuare a viaggiare, magari andando  proprio verso il Sole.

Un viaggio verso il Sole

Dopo aver trattato, in modo abbastanza accurato, l’aberrazione, il redshift e il blueshift relativistici, nonché la dilatazione del tempo, utilizzando una figura a quattro dimensioni, vogliamo costruire passo dopo passo un viaggio verso il Sole a velocità più o meno relativistica. Il tutto senza formule e semplificando un poco la trattazione.

Cerchiamo, in pratica, di costruire una specie di filmato relativo a un viaggio verso il Sole (l’astronave non subisce effetti … termici) e confrontare ciò che si vede dagli oblò dell’astronave con quello che vedrebbe un alieno posto molto lontano da lei, in un sistema di riferimento diverso e praticamente immobile (si fa per dire…).

Il nostro “filmato” si compone solo di fotogrammi messi in fila. Per seguire meglio, visivamente, i vari passaggi ci limitiamo alla aberrazione non relativistica e introduciamo, in modo un po’ semplificato e solo alla fine, l’ellisse relativistica per aggiungere indicativamente i colori. Ovviamente, è abbastanza facile, per chi ne abbia voglia, fare i calcoli completi per ottenere una figura (o filmato) perfettamente relativistica (le formule le abbiamo già ottenute tutte).

Spieghiamo, innanzitutto, la Fig. 62. Cerchiamo di capirla bene non solo per la spiegazione del filmato, ma anche per ripassare ciò che normalmente si vede alzando gli occhi al cielo ogni notte. E’ quindi utile a tutti, anche ai meno esperti.

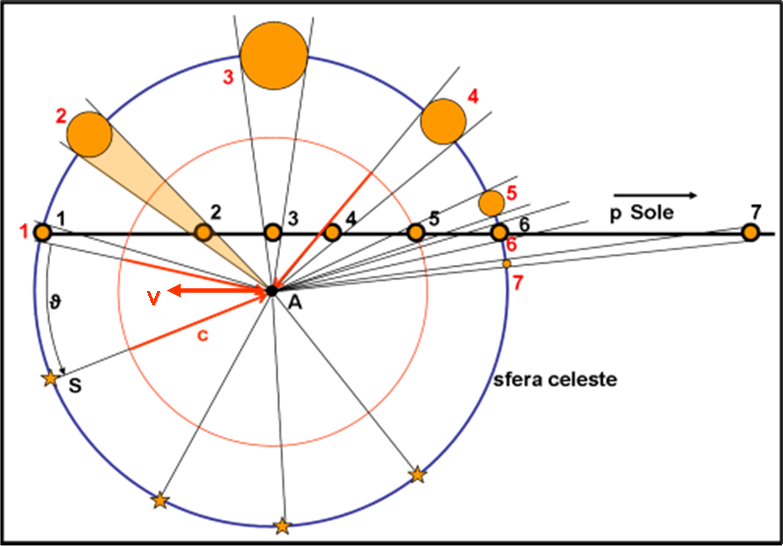
Essa non è altro che la rappresentazione contemporanea di ciò che capita realmente nello spazio e di ciò che noi vediamo in cielo. In altre parole, essa descrive sia ciò che riesce a vedere un alieno posto lontano sia dalla nostra astronave che dal Sole, sia quello che, invece, vediamo noi che siamo sopra l’astronave A.

Iniziamo a considerarla ferma rispetta al Sole (la pallina arancione). L’alieno vede l’astronave  in A e il Sole nella posizione 1. Immaginiamo, adesso di prendere il Sole e di spostarlo nella posizione 2. Non abbiamo ancora parlato di velocità, abbiamo solo preso il Sole con delle pinze speciali e l’abbiamo spostato in un’altra posizione (gli alieni sanno fare di tutto). L’alieno, adesso, vede l’astronave sempre in A e il Sole in 2, mentre chi sta sull’astronave vede il Sole 2 proiettato sulla sua  sfera celeste, di cui A è il centro, nella posizione 2.

Richiamiamo cos’è la sfera celeste. Essa è una sfera ipotetica che ha l’osservatore nel centro e  un raggio qualsiasi. Infatti, non interessa sapere quanto valga il raggio, dato che tutti gli oggetti che sono visti dall’osservatore sono proiettati sulla superficie sferica della sfera celeste. In altre parole, siamo liberi di disegnarla con qualsiasi raggio vogliamo. Quello che conta è l’angolo sotto cui l’osservatore vede l’oggetto celeste rispetto a una direzione fissa nel cielo. Ad esempio, l’angolo θ che il Sole in 1 fa con la stella S, supposta all’infinito, visto da A. Questo angolo rimane sempre lo stesso sia accorciando che aumentando il raggio della sfera celeste. La faccenda risulta ancora più evidente se consideriamo il diametro di un oggetto relativamente vicino, come il Sole, posto in 2. L’alieno vede il Sole sempre grande uguale (ha certe dimensioni angolari che non cambiano mai, data la grande distanza a cui si trova), ma l’osservatore in A lo vede più grande di quanto non l’abbia visto in 1 (dato che adesso il Sole è molto più vicino).

Le dimensioni angolari del Sole sono cambiate, ossia l’angolo colorato in arancione (relativo al Sole 2) è più grande di quello relativo al Sole 1, ma è più piccolo di quello del Sole 3. A questo punto, è del tutto analogo se proiettiamo il Sole su una  sfera celeste qualsiasi, dato che il diametro apparente del Sole visto da A rimane sempre lo stesso. Non per niente, quando parliamo di dimensioni del Sole visto dalla Terra lo facciamo in termini di angolo e diciamo che vale circa trenta primi d’arco. Tutto questo discorso (forse ovvio per la maggior parte dei lettori) è stato fatto solo per poter scegliere la sfera celeste a una certa distanza da A, favorevole per il disegno.

La immaginiamo passare per il Sole in 1, ma abbiamo capito benissimo che potevamo prenderla con un raggio enormemente più grande come anche con uno più piccolo. Ovviamente, per una stella S, a distanza enorme, non si parla normalmente di diametro angolare, ma solo di posizione sulla sfera celeste. Per lei, qualsiasi raggio si voglia dare alla sfera celeste, il risultato è lo stesso: un punto è e un punto rimane.

Ricapitoliamo la Fig. 62 per meglio comprendere ciò che abbiamo voluto puntualizzare. Mettiamoci nelle condizioni di un alieno che vede il tutto da lontano. A lui non interessa la sfera celeste di A, ma la sua, che è proprio il piano del foglio. Lui non ha bisogno di rappresentare la circonferenza nera né le dimensioni angolari del Sole viste dall’astronave. Lui vede solo l’astronave A e il Sole posto sempre in uno stesso punto del suo piano. Immaginiamo che l’astronave viaggi a una certa velocità v verso sinistra, piccola o grande che sia. Immaginiamo, anche che l’alieno abbia puntato il suo telescopio su A e che quindi lo mantenga fisso in quella direzione. In un certo intervallo di tempo gli sembrerà che sia il Sole a muoversi da 1 a 2 a 3, fino a 7. In conclusione, vede il Sole muoversi lungo la linea retta p con una velocità uguale a -v.

Le dimensioni della nostra stella sono sempre uguali e ciò che vede cambiare è solo la posizione relativa del Sole rispetto all’astronave. Può dire tranquillamente che in 3 la nave ha raggiunto il punto più vicino e in 7 quello più lontano. Il moto apparente del Sole rispetto all’astronave avviene nel piano del foglio perpendicolare al suo telecopio. Sarebbe facilissimo fare un filmato che rappresenti questa visione aliena: basterebbe far muovere una pallina gialla verso destra, lungo una retta con un puntino nero fermo al centro (l’astronave A), oppure lasciare ferma la pallina gialla e far muovere l’astronave A verso sinistra. La faccenda è del tutto equivalente, ma a noi fa più comodo per il disegno immaginare ferma l’astronave e far muovere il Sole.

Consideriamo, adesso, la stessa Fig. 62, entrando dentro l’astronave A. La circonferenza rossa ha per raggio il vettore velocità della luce c, proprio quella che hanno i fotoni che partono dal Sole o dalle stelle e che giungono fino ad A sfera celeste (basta assumere che il tempo per arrivare dal cerchio all’astronave sia uguale a un secondo e il raggio diventa proprio uguale a c moltiplicato 1).

L’astronave è  ancora ferma e quindi i fotoni arrivano tutti assieme per oggetti che hanno la stessa distanza da A. All’istante iniziale giungono su A i fotoni delle stelle S e del Sole in 1, ovviamente partiti in tempi diversi (molto prima per le stelle e poco prima per il Sole). Cosa vede l’osservatore in A in quell’istante? Vede tutto proiettato sulla sua sfera celeste (che può avere un raggio qualsiasi). Le stelle S sono in una certa direzione e il Sole nella direzione 1 con un diametro angolare che è dato dall’angolo sotto cui l’osservatore vede il diametro vero del Sole alla distanza in cui esso si trova in quell’istante (ossia alla distanza tra 1 e A).

Come vedremo tra poco, Il fatto che 1 e 1 coincidano si deve solo (lo ripetiamo ancora una volta) al fatto che abbiamo scelto di rappresentare la sfera celeste proprio con un raggio uguale a questa distanza. Una questione di spazio utile per disegnare e di necessità di non tracciare troppe linee che disturbino la visione complessiva del disegno. Tutto lì.

Sarebbe bello far muovere subito l’astronave e vedere cosa succede, ma dobbiamo pazientare un attimo. Sappiamo già dagli articoli precedenti che questa situazione porterebbe a un caos terrificante: colori che cambiano, direzioni che si spostano, tempi che si dilatano e altro ancora. Dobbiamo quindi andare per gradi se vogliamo fare un filmato abbastanza realistico.

Nota bene: ricordiamo ancora che per vedere il vero moto dell’astronave dovremmo mettere il Sole al centro e far viaggiare l’astronave. Tuttavia, per comodità di disegno ci conviene entrare nel sistema di riferimento dell’astronave per la quale è il Sole che viaggia a velocità uguale e contraria alla sua. L’astronauta è convinto di essere fermo. In parole povere, possiamo illustrare il tutto considerando l’astronave ferma e il Sole che si muove lungo p.

Mettiamo pure in moto l’astronave verso sinistra, ma fermiamola ogni volta che il Sole raggiunge (rispetto all’astronave considerata sempre in A) i punti da 1 a 7. In altre parole, trascuriamo ciò che vede A durante il suo moto e apriamo gli occhi solo quando l’astronave si ferma. In quei momenti tutte le varie deformazioni spariscono. Facciamo quindi un filmato composto di 7 fotogrammi, separati temporalmente tra loro. Dato che sono presi quando l’astronave è ferma, non sono minimamente toccati dalla teoria di quel signore che conosciamo ormai molto bene, ossia il dott. Einstein.

Cosa vede l’osservatore in A? In 1 vede il Sole di dimensioni angolari piuttosto piccole che dipendono solo dalla distanza a cui si trova la stella in quel momento. In 2 vede il Sole, che si trova realmente in 2, proiettato sulla sfera celeste in 2, con dimensioni angolari che sono date dall’angolo sotto cui A vede il Sole 2 (angolo arancione).

Attenzione! Le dimensioni di 2 sembrano enormi rispetto a quelle di 2, ma quest’apparenza dipende solo da dove abbiamo messo la sfera celeste. Se la ponessimo ancora più lontana, le dimensioni sembrerebbero ancora più grandi. Ma, in realtà, non è assolutamente vero! Le dimensioni che contano sono quelle angolari e l’angolo non cambia cambiando il raggio della sfera celeste. Ciò che noi vediamo nel cielo sono proprio le dimensioni angolari che dipendono solo dalle dimensioni reali del Sole e dalla sua distanza in quel determinato istante.

Altro spostamento di A ed eccoci (fermi) in 3. Il diametro angolare del Sole è ancora cresciuto. D’altra parte è ovvio, dato che siamo alla distanza minima tra astronave e stella. Anche l’alieno sarebbe perfettamente d’accordo con noi, dato che anche lui vedrebbe il Sole e A alla minima distanza. Il Sole, poi, si allontana diventando sempre più piccolo (angolarmente) fino ad apparire come un dischetto appena percettibile in 7.

Attenzione! In questo caso la sfera celeste scelta ha addirittura un raggio minore della distanza reale astronave-Sole, ma ormai sappiamo  che conta ben poco. L’apparenza nel cielo non dipende assolutamente dal raggio scelto per la sfera di riferimento.

A questo punto, possiamo preparare il filmato che mostra cosa si vede dall’astronave durante il suo viaggio verso il Sole fino al sorpasso e all’allontanamento. Un filmato che va a scatti, però, eliminando in tal modo gli effetti dell’aberrazione e, a maggior ragione, quelli relativistici. Esso mostra un disco solare che da piccolo diventa grande e poi torna a diminuire. Insomma niente di speciale e di veramente strano.

A costo di essere pedanti,  mostriamo questo “filmato” nella Fig. 63.

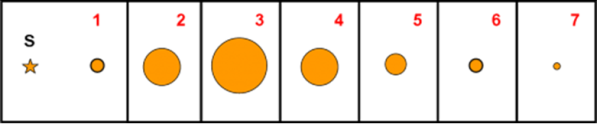
Nel fotogramma 1 abbiamo anche inserito la stella S. Negli altri fotogrammi la stella è sempre nella stessa posizione e, quindi, non si vede più vicino al Sole che è si è spostato, mentre lei è rimasta al suo posto, dato che il movimento dell’astronave è ridicolo rispetto alla sua distanza. Notate anche che, per guardare i panorami raffigurati nei fotogrammi, l’osservatore in A ha dovuto spostarsi dal finestrone di prua a quello di poppa. Infatti 1 si vede praticamente nella direzione del moto, mentre 7 si vede in direzione quasi opposta. Ripetiamo ancora che i sette fotogrammi sono immagini riprese su una piccola parte della sfera celeste, dove il Sole sembra muoversi. I tempi tra i fotogrammi variano a seconda del tempo che l’astronave ha impiegato tra le varie fermate. A noi, per adesso, non interessano. Tuttavia, dato che i tempi si misurano a nave ferma, l’orologio di bordo e quello dell’alieno danno gli stessi risultati (a parte la differenza costante dovuta al tempo che la luce del sistema Sole-astronave impiega a giungere fino al simpatico osservatore extraterrestre).

Sì, lo ammetto, non è un gran bel filmato e tutti potevamo immaginarcelo. Non differisce molto da quello che vedremmo andando in macchina verso un enorme pallone e poi lasciandocelo alle spalle.

Le cose cambiano completamente se decidiamo di costruire un filmato continuo durante tutto il viaggio, senza mai fermare la nave e facendola andare a velocità molto alta, fino a essere comparabile a quella della luce. Più o meno sappiamo già cosa succede, dato che abbiamo letto gli articoli precedenti. Ci aspettiamo che quando il Sole è davanti all’astronave il suo colore appaia azzurro o violetto e molto luminoso anche se ancora lontano. Situazione opposta dopo averlo sorpassato: il suo colore tende al rosso sempre più scuro e anche i tempi relativi ai vari fotogrammi subiscono deformazioni.

Tuttavia, per ricostruire i colori e i tempi, dovremmo considerare l’ellisse che abbiamo costruita utilizzando il fattore di Lorentz. Si può sicuramente fare, ma  complicheremmo di molto le cose fino a fare un po’ di confusione (si dovrebbero calcolare gli angoli di spostamento seguendo la formula relativa). Limitiamoci, perciò, a vedere come le immagini prese dalla nave in movimento deformino la posizione e la grandezza del Sole, attraverso una semplice costruzione grafica. Alla fine, potremo tranquillamente anche aggiungere i relativi colori. La parte più importante del filmato sarà, comunque, compresa appieno. Già così la trattazione non è banalissima. Andate quindi con calma e seguiamo passo passo le varie costruzioni.

Non spaventiamoci della Fig. 64 che andiamo a spiegare senza fretta e in modo particolareggiato.

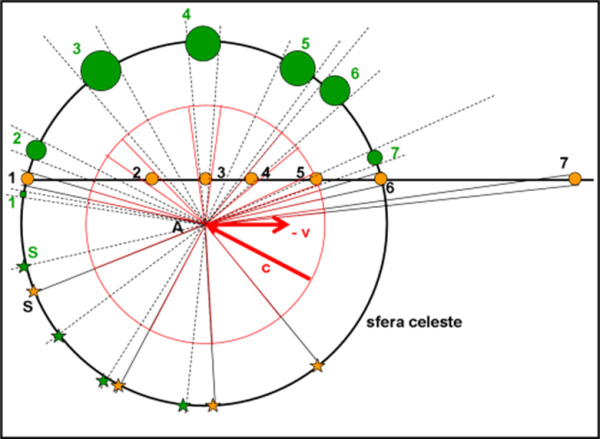
In  fondo, eseguiamo soltanto ciò che è stato fatto negli articoli iniziali per l’aberrazione annua, sommando il vettore velocità della luce c a quello - v, uguale e contrario alla velocità v dell’astronave. Il procedimento lo ripetiamo nella Fig. 65 e poi lasciamo ai lettori l’applicazione a tutte le configurazioni.

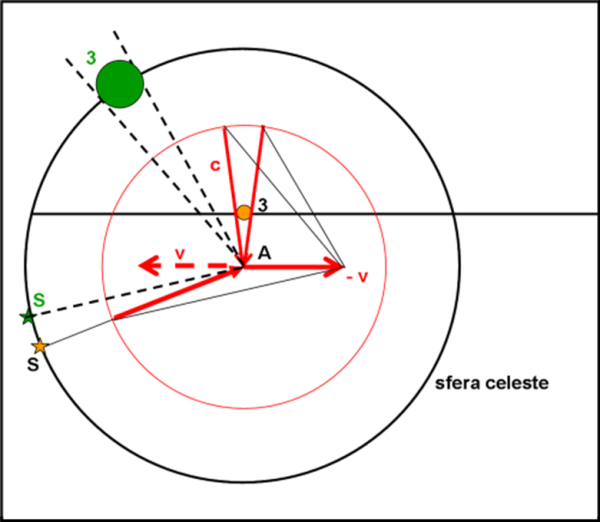
Ricordiamo solo, ancora una volta, che la somma dei vettori la eseguiamo SOLO per trovare la direzione apparente da cui proviene il fotone e NON per determinare il valore del vettore risultante, che deve sempre essere uguale a c (la velocità della luce è la stessa in tutti i sistemi di riferimento, siano fermi o in movimento). In altre parole, ci serve solo per determinare la direzione apparente del Sole mentre l’astronave sta viaggiando. Tuttavia, dato che il Sole ha dimensioni reali non trascurabili, se viste dall’astronave, i fotoni che arrivano dal bordo più lontano vengono deviati in modo diverso da quelli che provengono dal bordo più vicino. Ne consegue che anche le dimensioni apparenti (angolari) del Sole vengono cambiate durante il viaggio dell’astronave e in modo sempre diverso a seconda della direzione.

Le stelle S, invece, vengono spostate in S una volta per tutte, dato che la loro direzione non varia durante tutto il viaggio (rimangono sempre molto lontane anche se ci si muove in direzione del Sole a velocità vicina a quella della luce). Lo sfondo della sfera celeste su cui si muove il Sole apparente non cambia durante il viaggio, ma solo nel breve periodo di tempo necessario per raggiungere la velocità di crociera v (noi lo immaginiamo quasi istantaneo). In quel brevissimo tempo le stelle si spostano da S a S. Poi stanno ferme.

La Fig. 65 ci mostra come abbiamo calcolato il Sole 3 a partire da quello 3. Esso è rappresentato dal disco verde. Abbiamo eseguito la somma dei vettori relativi ai fotoni che partono dai bordi di 3 e la velocità – v (velocità apparente del Sole). Poi abbiamo traslato la direzione del vettore risultante fino a farla passare per A. Il punto in cui essa tocca la sfera celeste è il bordo del Sole. Ne derivano, quindi, sia la direzione apparente che le dimensioni del Sole come appaiono all’astronave. Lo stesso procedimento è stato seguito per trovare la posizione aberrata S della stella S. Come si nota facilmente, il Sole sembra trovarsi decisamente più vicino alla direzione dell’astronave, così come la stella. Anche le dimensioni del Sole appaiono più piccole di quelle che si avevano da fermi nella posizione 3.

Non è difficile completare la Fig. 64. Come si vede bene, appena partiti, il Sole si restringe e si avvicina alla traiettoria. Lo stesso fa la stella. L’apparenza è, quindi, quella di allontanamento del Sole, dato che diventa più piccolo e diminuisce la distanza tra la stella e lui. Tuttavia, in breve, il Sole inizia a ingrandirsi, anche se è sempre più avanti della posizione che avevamo trovato nella Fig. 62. A mano a mano che il Sole si avvicina, le sue dimensioni restano pressoché costanti, come anche dopo che lo abbiamo effettivamente sorpassato e guardiamo dal finestrone laterale. Poi si allontana e diminuisce il diametro angolare, ma molto meno di quanto non farebbe se visto ad astronave ferma. Malgrado sia quasi perfettamente dietro l’astronave, l’osservatore lo vede spostato in avanti nel finestrone posteriore.

La Fig. 66 rappresenta ciò che vede l’osservatore spostandosi da un finestrone all’altro mentre l’astronave viaggia alla velocità v. Confrontatelo con la Fig. 63 che è quella del filmato preparato con singoli fotogrammi. In posizioni, che per l’alieno sono esattamente le stesse (da 1 a 7), l’osservatore in moto vede il Sole ben diversamente da quando faceva le continue interruzioni.

Ragioniamo un poco. La costruzione delle direzioni apparenti del Sole durante il viaggio sono date solo e soltanto dalla somma vettoriale di vettori che rimangono costanti (c e  -v). Cambiano solo le direzioni reciproche e quindi la direzione del vettore risultante. In questo modo si ottengono esattamente le direzioni “piegate” a causa dell’aberrazione classica. Non abbiamo introdotto la relatività ristretta. I veri dischetti li potremmo disegnare solo introducendo l’ellisse di aberrazione relativistica, seguendo le formule ricavate nei capitoli precedenti. Niente di speciale, ma direi che il nostro viaggio è già stato abbastanza articolato.  Limitiamoci a utilizzare ciò che ci ha descritto l’aberrazione classica e aggiungiamo solo i colori che vengono regalati dall’effetto doppler relativistico. Non è comunque difficile passare a una versione più completa e accurata, che invito i più bravi a eseguire, utilizzando l’ellisse di aberrazione.

Possiamo anche introdurla, in prima approssimazione, allungando la circonferenza di partenza (in cui tutti fotoni arrivavano con la stessa lunghezza d’onda) attraverso il fattore di Lorentz. Fatto questo, prolunghiamo le direzioni già ottenute precedentemente (non sono quelle esatte, in realtà, ma noi ci accontentiamo) fino a incontrare questa ellisse. A volte le linee sono più lunghe e a volte più corte del raggio della circonferenza di partenza, ossia a volte la frequenza aumenta e a volte diminuisce,come già discusso negli articoli precedenti. La lunghezza di queste linee ci permette di capire il colore che assume il dischetto del Sole.

Possiamo, perciò, inserire anche i colori nel filmato e determinare quando il Sole viene visto con il suo vero colore, ossia quando la frequenza della sua luce è quella non “deformata”. Ciò capita quando la direzione del dischetto apparente raggiunge l’intersezione tra ellisse e cerchio originario. Infatti, in quel punto la frequenza della luce è uguale a quella con l’astronave ferma. La direzione 3 è quella che meglio approssima questo punto.

La Fig. 67 riassume quanto abbiamo detto, fermo restando che è stata fatta un’approssimazione sempre più importante al crescere della velocità.

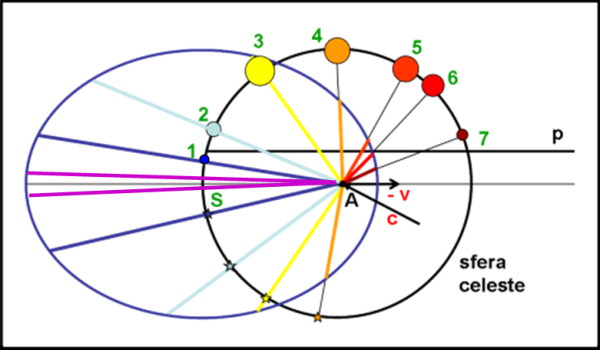
Chi non vuole accontentarsi, può, come già detto, fare qualche calcolo in più (anche usare il solo "righello" nella famosa ellisse) e ottenere una rappresentazione esatta. Si noterà, anche, che una sfera in movimento resta praticamente una sfera, dato che giocano insieme sia contrazione delle lunghezze che dilatazione del tempo. Ricordiamoci, a riguardo, quanto si era visto QUI e QUI, che diventa ancora più peculiare nel caso della sfera.

Mostriamo anche un vero "filmato" che, però, considera anche l'accelerazione e non mette molto in evidenza i colori.

https://jila.colorado.edu/~ajsh/insidebh/hyperlight_640x480_ms.avi

Un dubbio per concludere: chissà se Celestia è capace di darci il risultato in quattro e quattr'otto? Speriamo  di non aspettare troppo la risposta del suo grande esperto.

Concludiamo l'argomento dell'aberrazione della luce con due applicazioni pratiche. In questo articolo parliamo di uno straordinario metodo utilizzato sfruttando i dati di Kepler. Keplero e Einstein: che bella coppia!

 

Il pianeta Einstein

Kepler riesce a misurare la luminosità di una sorgente con una precisione di poche parti su un milione. La variazione di luminosità rivelabile osservata può, perciò, spingersi fino a valori eccezionali che rendono applicabile un metodo mai usato fino a poco tempo fa. L’applicazione è recente, ma l’idea è molto più antica e risale alla fine del secolo diciannovesimo. Chi l’ha avuta era un ragazzo di sedici anni.

C’è bisogno di dirvi chi è? Penso di no. E’ lui, sempre lui, il grande Albert Einstein! Le riflessioni sulla luce inviata da una sorgente in movimento sembra che abbiano dato il via, al suo cervello prodigioso, alla teoria della relatività. Ci limiteremo a velocità basse rispetto a quella della luce e quindi la parte “relativistica” è trascurata, ma il succo del discorso non cambia ed è sempre collegato all’aberrazione luminosa.

Anzi, per semplificare il discorso ci rifacciamo addirittura alla semplice aberrazione annua, ricordando che essa è sostanzialmente causata dalla combinazione di due velocità: quella della luce e quella di rivoluzione della Terra attorno al Sole. Ciò che Einstein aveva ipotizzato (e come sempre è poi stato confermato) era il fatto che la luce inviata da una sorgente in movimento doveva mostrare un simile effetto di  aberrazione, dato che si doveva tener conto sia della velocità della luce che di quella della stella. Il risultato finale, però, andava ben oltre alla determinazione della direzione finale, ma stabiliva che la luminosità di una stella doveva apparire più intensa se essa si muoveva verso di noi, rispetto a quella che avrebbe avuto allontanandosi, e molte altre cose ancora. Il fenomeno, nella sua generalità portata fino a valori di v comparabili a c, prende il nome di aberrazione relativistica, che ormai conosciamo molto bene.

Per permettere una lettura più ampia possibile, descriviamo nuovamente il tutto, in modo estremamente elementare e senza alcuna formula. I più bravi si accorgeranno che stiamo ripetendo cose dette e ridette nell’analisi dell’aberrazione della luce sia classica che relativistica.

Consideriamo subito la Fig. 1.

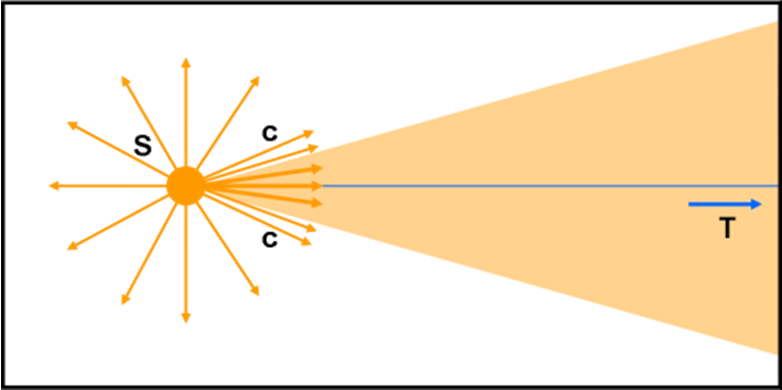
La stella S manda in giro per l’Universo i suoi fotoni che viaggiano alla velocità c, indicata dai vettori arancioni. Solo una parte di essi ha la direzione giusta per giungere sulla Terra T. Essi sono compresi dentro al cono arancione. Immaginiamo che i fotoni siano solo quelli rappresentati in figura. Solo tre sono interni al cono e, quindi, sono gli unici che il nostro pianeta riceve.

Facciamo adesso muovere la stella in Fig. 2 e, per semplicità, proprio lungo la direzione della Terra. Analoga conclusione avremmo, comunque, anche considerando una direzione diversa.

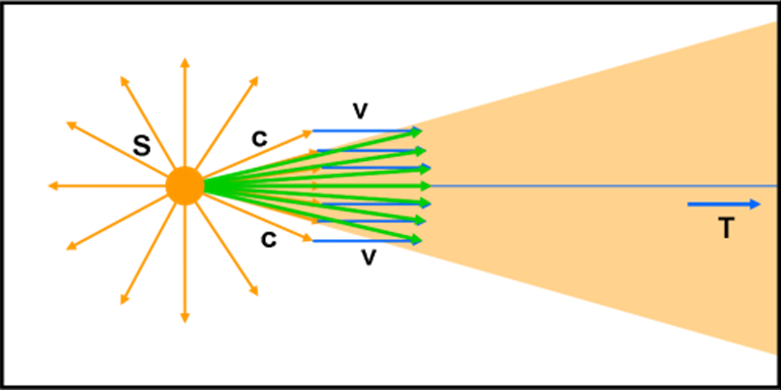
La velocità v della stella è indicata dai vettori azzurri diretti verso di noi. I fotoni sono soggetti a due velocità: quella loro e quella della stella. La velocità risultante si ottiene allora sommando i vettori velocità c e v. Si ottengono i vettori verdi che indicano la direzione dei fotoni. Quanti sono, adesso, quelli che sono contenuti all’interno del cono arancione? Sono saliti addirittura a sette. Cosa significa questa conclusione? Semplice: la luce che riceve la Terra è maggiore di quella ricevuta se la stella fosse ferma. Non ditemi: “Ma come? Sappiamo benissimo che la velocità della luce non si può sommare ad altre velocità!”. Avreste perfettamente ragione. Ma, noi siamo interessati alla direzione apparente dei fotoni e non all’effettiva velocità che, ovviamente, rimane sempre la stessa, ossia c.

Disegniamo, ora, la Fig. 3.

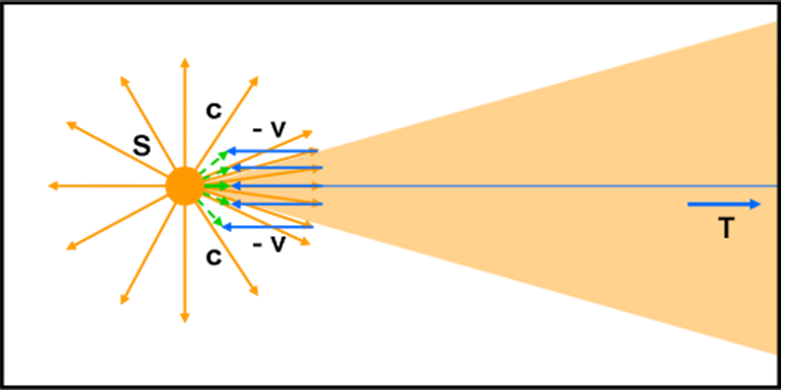
In essa facciamo muovere la stella in direzione opposta con velocità uguale a prima, ossia con velocità –v. I fotoni cambiano, ovviamente, direzione, dato che adesso si muovono lungo la direzione indicata dai vettori verdi che sono la differenza tra c e v o -se preferite- la somma di c e –v. Contiamo quanti vettori verdi sono compresi all’interno del cono arancione. Uno e uno solo. Ciò vuol dire che la luce ricevuta da Terra è inferiore a quella inviata dalla stella ferma e, a maggior ragione, dalla stella in movimento verso T.

Non ci vuole molto a concludere che se una stella si muove avanti e indietro, rispetto alla direzione della Terra, la sua luce aumenta e diminuisce periodicamente. Che cosa può fare oscillare in questo modo una stella? Ovviamente, un pianeta che orbita insieme a lei attorno al comune baricentro.

Capito il concetto di fondo e togliendoci ancora una volta il cappello davanti a un genio come Einstein (a sedici anni pensare in questo modo non è certo normale) arriviamo alla notizia relativa al nuovo pianeta, scoperto utilizzando l’ipotesi del grande fisico. Non per niente è già stato soprannominato “pianeta Einstein”.

Oltre all’effetto spiegato precedentemente ne sono stati usati altri due. Il primo si rifà alla marea. La stella è deformata come una palla da rugby nella direzione del compagno planetario (che lo è ancora di più, ovviamente). Durante la rivoluzione attorno al baricentro, l’area mostrata all’osservatore varia e quindi anche la luminosità. Essa è minima quando la direzione stella-pianeta è verso la Terra; massima, 90° prima o dopo, in modo simile a quanto capita per la curva di luce di un asteroide.

Il terzo effetto è quello dovuto alla luce della stella riflessa dal pianeta. Essa è massima  quando il pianeta è dietro la stella. Notiamo che le tre condizioni non hanno alcun bisogno che vi sia un transito come normalmente richiesto da Kepler. Bisogna, inoltre, tener presente che tutto ciò è indipendente dalla distanza della stella e, in parte, anche dall’inclinazione del piano orbitale

Una volta che il pianeta è stato identificato con questo metodo così sofisticato, esso è stato confermato attraverso misure di velocità radiale.  Un’ulteriore, attenta occhiata ai dati di Kepler ha mostrato, inoltre, che in realtà il pianeta transita, in modo molto marginale, davanti alla stella (ma, come detto, non è una condizione necessaria per il nuovo metodo), come mostrato in Fig. 4.

Il pianeta Einstein, ufficialmente Kepler-76b, è un Giove caldo che rivolve attorno alla stella in un giorno e mezzo. Il suo diametro è di circa il 25% più grande di quello del nostro pianeta gigante e ha una massa doppia. La stella è di tipo F e si trova a circa 2000 anni luce, nella costellazione del Cigno.

Sebbene il nuovo metodo non possa scoprire, con la presente tecnologia, oggetti di dimensioni terrestri, esso offre risvolti unici in quanto non ha bisogno di spettri ad alta definizione e nemmeno di un transito.

Non è facile applicarlo, ma è una conferma meravigliosa del pensiero di un genio e una altrettanto meravigliosa applicazione pratica dell’aberrazione della luce.

A proposito di metodi per la ricerca di eso-pianeti, QUI la storia di Peter Van De Kamp, che negli anni ’60 aveva ipotizzato l’esistenza di molti “pianetoni”. Purtroppo la tecnologia del tempo non era ancora pronta a dargli la soddisfazione che meritava...

 

Elettroni in fuga: la radiazione di sincrotrone

Concludiamo l'aberrazione della luce con un effetto molto particolare, di elevatissima energia, che contraddistingue i getti relativistici degli attori più potenti del Cosmo: la radiazione di sincrotrone, un altro bellissimo gioco messo in piedi da elettroni e fotoni, in grandissima forma, aiutati da un campo magnetico.

Per la nostra chiacchierata non occorre molto. Un bel campo magnetico e un elettrone (meglio se tanti) che sia libero di muoversi al di fuori della sua abitazione “normale” (l’atomo). Non ci vuole altro. Beh… le stelle, in particolari momenti della loro vita, hanno tutto l’occorrente per eseguire l’esperimento. Potremmo già iniziare. Tuttavia, è meglio conoscere un po’ meglio le caratteristiche dell’elettrone quando si trova da “solo” e quando può muoversi a piacimento e -soprattutto- accelerare.  Accelerare, questa è proprio la parola chiave.

Facciamo un piccolo passo indietro. Ciò che riusciamo a vedere nell’Universo dipende da ciò che chiamiamo “luce”. Essa è  l’informazione più importante che gli astri ci inviano, anzi praticamente la sola. Esisterebbe anche la gravità ma non è la stessa cosa. Immaginate di ricostruire la struttura dell’Universo basandoci solo sulla gravità che agisce su di noi da parte di tutti gli oggetti del Cosmo. Non capiremmo niente e -oltretutto- potremmo leggere solo gli effetti relativi a uno spazio molto vicino. Per il momento è così, in attesa -magari- che le orecchie enormi e sensibilissime per le onde gravitazionali comincino a lavorare a  pieno ritmo.

Tuttavia, parlare di luce è inesatto. Più giustamente dobbiamo parlare di radiazione elettromagnetica. Essa si muove come le onde su un mare. L’acqua sale e scende soltanto (oscillazione), mentre l’onda (che fa oscillare l’acqua) si muove in direzione perpendicolare all’oscillazione. Non è certo un discorso nuovo, dato che ormai abbiamo imparato molto sulla natura ondulatoria dei fotoni e di come siano capaci di trasformarsi in particelle. Ma lasciamoli stare, in questo contesto. La radiazione elettromagnetica è un’oscillazione regolata da un campo magnetico e da uno elettrico.

Quando si origina un’onda elettromagnetica? Qui sta il succo dell’intera faccenda. E’ necessario che una particella carica (protone o elettrone) subisca un’accelerazione, a seguito di una qualche forza che la obblighi a cambiare la sua traiettoria. Sappiamo bene che i protoni sono molto più pesanti degli elettroni e quindi decisamente più “pigri” o -meglio- più difficili a spostarsi. Ben più “reattivi” sono gli elettroni, sempre in perfetta forma, agili e leggeri. Addirittura mille volte più leggeri dei fratelli protoni. Ne segue che sono proprio loro le particelle più disponibili a muoversi, ad accelerare e a produrre onde elettromagnetiche.

Se l’elettrone (che ha una carica negativa) si muovesse a velocità costante, si porterebbe dietro il proprio campo elettrico come noi facciamo con un secchio pieno d’acqua. Camminando in modo regolare e facendo molta attenzione l’acqua rimarrebbe immobile. Tuttavia, se qualcuno ci desse uno scossone o una spinta, noi ci fermeremmo improvvisamente o saremmo lanciati in avanti. Cosa capiterebbe all’acqua del secchiello? Si agiterebbe e creerebbe un’onda. Proprio quello che capita al campo di un elettrone se esso subisce una variazione di velocità, ossia un’accelerazione o una decelerazione.

Questo concetto è molto importante: per potere “vedere” qualcosa è necessario che una particella (soprattutto un elettrone) sia libera di muoversi e subisca uno “scossone”. Ricordate l’epoca buia dell’Universo, quando vi erano solo atomi neutri? Nebbia, solo nebbia e nessuna informazione luminosa.

Vediamo, allora, quali sono alcuni tra gli scossoni più importanti che un elettrone può subire. Torniamo all’epoca buia. Quando è cominciata a crearsi la luce? Quando la temperatura all’interno di quegli enormi ammassi di idrogeno, che sarebbero diventate le stelle, ha iniziato a “rompere” gli atomi. Questo è il primo punto necessario: liberare l’elettrone dal legame con il nucleo atomico, dominato da protoni e neutroni.

Il gas si è trasformato in plasma, ossia in un miscuglio di nuclei atomici e di elettroni, liberi di muoversi a piacere. Come si muovono gli elettroni finalmente liberi? Non certo in modo regolare e costante.  Essi eseguono una complicata gincana che riesce a mantenerli liberi grazie alla temperatura che li agita violentemente. In questo continuo cambiamento di direzione è ovvio che essi subiscono violente accelerazioni o decelerazioni.  Ecco che il secchiello pieno d’acqua subisce uno scossone e sull’acqua si formano delle onde. Analogamente i campi degli elettroni producono le loro onde, ossia le radiazioni elettromagnetiche.

Notate che ho  parlato spesso di “campo”. Niente di speciale: è solo una specie di carta geografica che contraddistingue una forza e come essa agisce all’intorno della sorgente che la causa. La forza di gravità crea un campo gravitazionale, definito da certi parametri. La forza elettromagnetica definisce un campo elettromagnetico.

La radiazione che si genera da questo andamento a dir poco caotico degli elettroni, viene chiamata “termica” e non ci vuole molto a capire perché. Essa è causata solo e soltanto dal movimento che gli elettroni subiscono a causa dell’agitazione che è legata direttamente alla temperatura (o -se preferite- anche il viceversa... se vi è grande movimento, l'energia cinetica diventa energia termica). Un caso classico di questo tipo di radiazione è quella che si vede nelle nebulose che circondano le stelle. Il gas della nube è riscaldato dalla luce stellare, gli elettroni  si staccano dal nucleo e vagano con movimento caotico emettendo onde elettromagnetiche.

Guardiamo ciò che capita in prossimità di una stella, dove essa è circondata da un campo magnetico molto intenso. Immaginiamolo proprio come una rete di linee che escono da un polo ed entrano nell’altro. Una calamita, insomma. Cosa fa un elettrone che si trova invischiato in questa ragnatela? Si inserisce in orbita attorno a una linea magnetica. La sua velocità è costante e quindi non dovrebbe emettere radiazione. E qui casca l’asino!

Apro una piccola parentesi. A volte la fisica classica, anche la più elementare, sembra ormai “fuori moda” di fronte alle meraviglie che ci mostrano le strumentazioni più moderne che cercano di studiare le interazioni tra le particelle elementari. Eppure, senza le basi fondamentali, diventa difficile capire la fisica più avanzata. Un moto circolare a velocità costante non vuol dire un moto non accelerato. L’accelerazione esiste e come! Anzi, la particella è costantemente accelerata. Questa accelerazione non è altro che quella causata dalla forza centripeta. Più intuitivamente, essa è quella che permette alla particella di cambiare direzione ad ogni istante e descrivere l’orbita circolare. La corda che tiene unita una sfera di ferro alla mano di un lanciatore di martello. In parole più tecniche, la velocità è costante come intensità, ma varia continuamente in direzione, dato che deve mantenere il moto circolare.

Torniamo al nostro elettrone che durante la rotazione accelera e invia radiazione.  Se la velocità è relativamente bassa la luce si diffonde tutt’attorno e si ha una specie di ciambella attorno all’elettrone, come mostrato schematicamente in Fig.1.

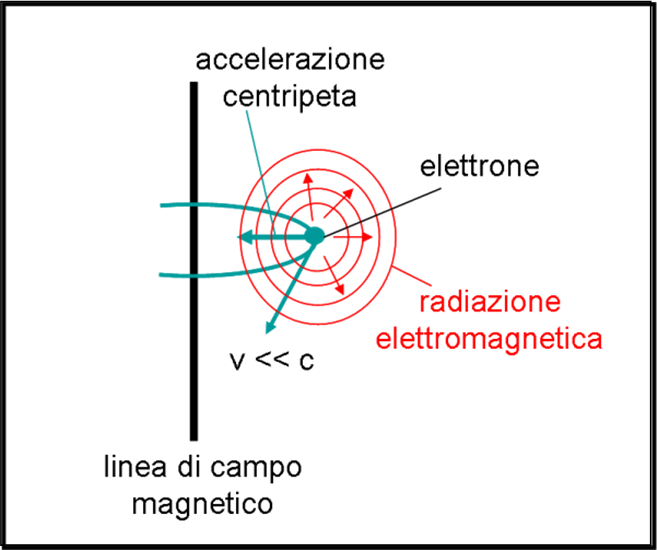
Tuttavia, se la velocità aumenta in modo sensibile, l’emissione non avviene più in tutte le direzioni, ma secondo un cono che punta verso la direzione del moto (Fig. 2). Qualcosa che conosciamo molto bene essendo del tutto simile all’aberrazione della luce. Una sorgente in movimento rapidissimo non può che restringere il fascio emesso.

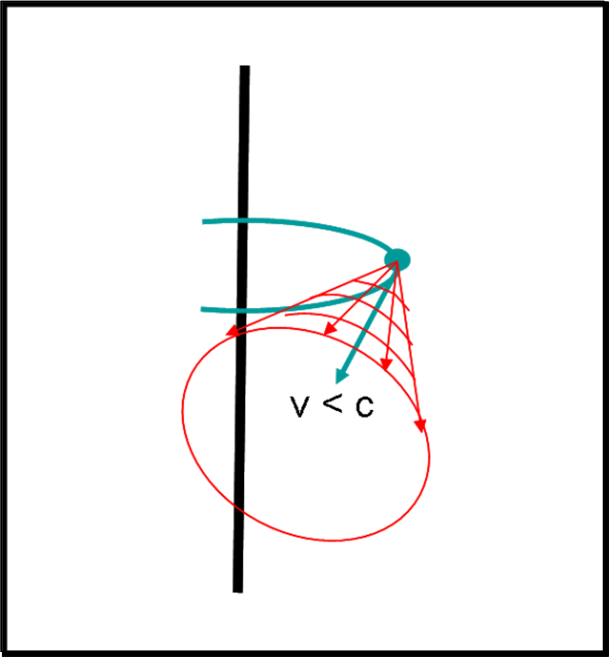
L’asse del cono coincide con la tangente all’orbita, istante per istante. L’elettrone diventa una specie di “faro”, che emette luce solo davanti a sé e che ruota insieme a lui.

Più la velocità orbitale aumenta e più il cono si stringe. Se ci si avvicina alla velocità della luce il cono diventa strettissimo e sembra proprio un “getto” di luce. Ovviamente, tutto ciò capita quando l’energia del campo magnetico è superiore all’energia termica che farebbe muovere gli elettroni in modo del tutto incontrollato. Questo tipo di radiazione, estremamente collimata (ossia circoscritta entro un cono molto stretto) è proprio la radiazione di sincrotrone (Fig. 3).

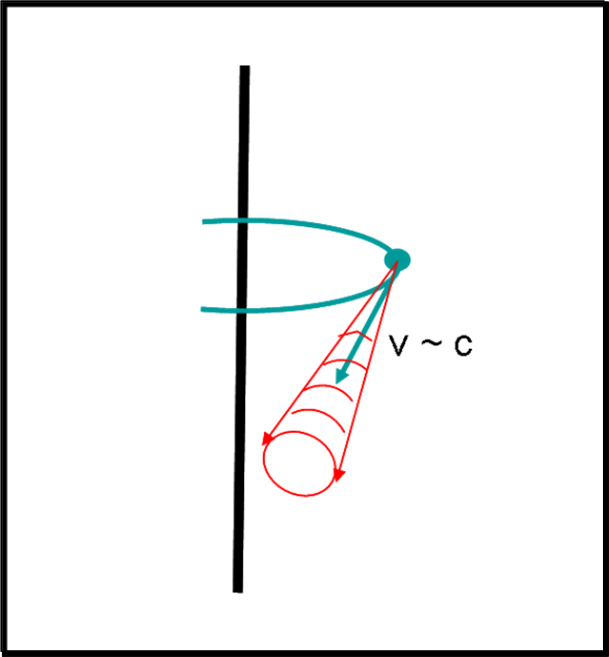
Essa si nota benissimo negli acceleratori di particelle che seguono le loro traiettorie proprio per effetto di campi magnetici. Tuttavia, molto più interessanti sono gli strumenti “naturali”. Campi magnetici capaci di dar luogo a radiazioni di sincrotrone si originano nei resti di supernove, nelle pulsar, nei buchi neri galattici, ecc.

Tuttavia, parlando di fenomeni celesti, dobbiamo tener conto che gli elettroni non sono vincolati a seguire un’orbita fissa nello spazio. Sappiamo bene che le linee di forza del campo magnetico escono da un polo e finiscono nell’altro. L’elettrone, perciò, esegue una danza più complicata, muovendosi a elica attorno alla linea di campo. E mentre si “avvita” aumenta anche la velocità, raggiungendo i valori necessari a creare un getto di radiazione di sincrotrone.

Capita ciò che è illustrato nella Fig. 4.

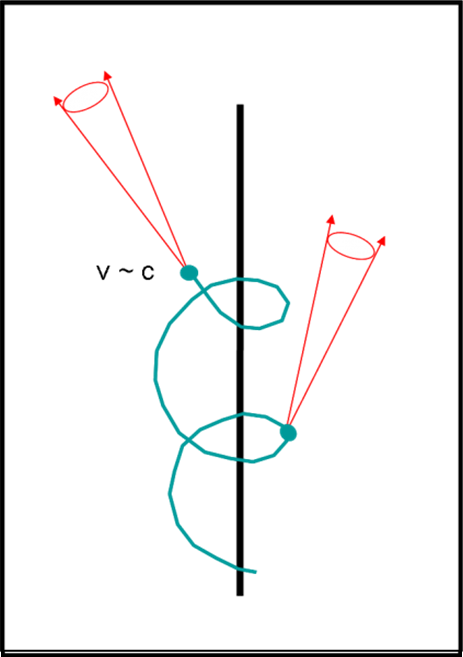
Come si vede chiaramente il getto di radiazione tende a lanciarsi verso le zone polari… Oltretutto, nella zona equatoriale, la trasmissione della luce è anche bloccata dalla materia che si sistema secondo un disco di accrescimento anche piuttosto spesso. Non è difficile, quindi, immaginare questi getti relativistici (radiazioni molto collimate causate da elettroni che girano a velocità prossime a quelle della luce). Accomunare questi fari luminosi con i getti dei buchi neri o delle stelle di neutroni che ingoiano materia dalle compagne non è certo sbagliato! Le radiazioni trascinano con loro anche particelle ed ecco quelle fantastiche fontane che sembrano uscire dai poli magnetici.

Vi è, però, uno scopo particolare che mi ha stimolato a parlare così diffusamente della radiazione di sincrotrone. Anche il nostro Sole, un giorno, potrebbe essere capace di produrla. In un momento molto particolare, di brevissima durata (e quindi difficilmente osservabile), molte sue sorelle devono avere vissuto quella fase così critica. Sto parlando dell’inizio dell’espulsione della nebulosa planetaria. Un momento mai osservato direttamente... tranne un'unica fortunatissima volta, questa QUI. Di solito si vede la supergigante che sta perdendo i primi pezzi oppure la nana bianca con la sua corona bellissima di gas che la circonda. C'è però un momento critico, il vero e proprio inizio del getto che si trasformerà velocemente in nebulosa planetaria. Un getto paragonabile a quello della radiazione di sincrotrone. E ciò dà una spiegazione meno difficile alla formazione di nebulose a “farfalla” che si scoprono sempre più spesso, come descritto QUI.

Voglio fare presente che la trattazione di questo fenomeno, così importante sia per lo studio degli astri sia per ciò che capita negli acceleratori di particelle, è stata estremamente semplificata. Tuttavia, viene proprio a fagiolo parlando del fenomeno dell’aberrazione relativistica.

 

Ritengo che il discorso sia stato abbastanza lungo e articolato. La difficoltà è  variabile e ce n'è per tutti gusti. In ogni modo, direi che il fenomeno dell'aberrazione luminosa a partire da quella annua e per finire ai getti relativistici, possa soddisfare tutti i tipi di lettori. Se necessario, si possono anche saltare certi "ostacoli" e arrivare comunque alla fine della corsa. Resta ancora da dire (e lo vedremo analizzando la storia del calcolo della distanza del Sole) che l'aberrazione è servita per cose decisamente più pratiche: il calcolo della velocità della luce e la determinazione della parallasse solare. Di tutto e di più...