Questo articolo è stato inserito nella pagina d'archivio dedicata all'Astronomia Classica

 

E’ ora di introdurre la sfera celeste e i vari sistemi di coordinate che servono a individuare ogni suo punto. Abbiamo imparato a risolvere i triangoli sferici proprio per potere passare da un sistema all’altro, ricordando che tutto ciò che si può determinare su una superficie sferica con un raggio indefinito,vista dal suo centro, sono solo e soltanto angoli. Nessuno può, infatti, passeggiare sulla sfera celeste e misurare le distanze relative in chilometri o in qualche altra unità di lunghezza.

Abbiamo imparato tante belle cose (che trovate QUI) sulla superficie sferica e, in qualche modo, l’abbiamo confrontata con una superficie piana, dove è molto più semplice lavorare. Tuttavia, ormai sappiamo cosa sono i cerchi massimi e i cerchi minori, così come sappiano riconoscere e risolvere un triangolo sferico. In poche parole, siamo in grado di trovare un sistema di riferimento tale che ci permetta di definire qualsiasi punto della sfera attraverso un paio di coordinate. Ovviamente, non può più essere un sistema di assi cartesiani, ma qualcosa che tenga conto delle caratteristiche essenziali della superficie sferica, dove si opera con angoli, che abbiamo descritto e collegato tra loro sia in modo intrinseco che estrinseco.

Abbiamo tutto e ci manca solo una sfera concreta su cui provare cosa abbiamo imparato. La prima che ci capita a tiro la conosciamo molto bene ed è la nostra Terra. No, non gridate allo scandalo: sappiamo molto bene che la Terra non è una sfera perfetta, ma per lo scopo che dobbiamo raggiungere in questa trattazione, è più che sufficiente. Analogamente, considereremo certe caratteristiche della sfera-Terra come immutabili nel tempo. Se avremo voglia, potremo, in seguito, cercare di andare più nel sottile, tenendo conto di molte variazioni che i manifestano su tempi abbastanza lunghi per noi umani o che comportano errori trascurabili, in prima approssimazione.

Prima di proseguire con l’introduzione di un sistema di coordinate sferiche terrestri, è bene richiamare un concetto sicuramente elementare e ovvio, ma che può essere di un qualche interesse per i meno preparati.

Sfera terrestre e sfera celeste

Facciamoci una domanda: “Qual è la differenza fondamentale tra una sfera come la Terra e una sfera come quella celeste?” Tra le tante, la più importante è che sulla superficie della Terra possiamo camminare e compiere misurazioni dirette, mentre su quella celeste è impossibile arrivare e la si può vedere solo dal suo centro e misurare gli angoli che separano i suoi punti. Questa banale, ma fondamentale differenza, la vediamo nella Fig. 1

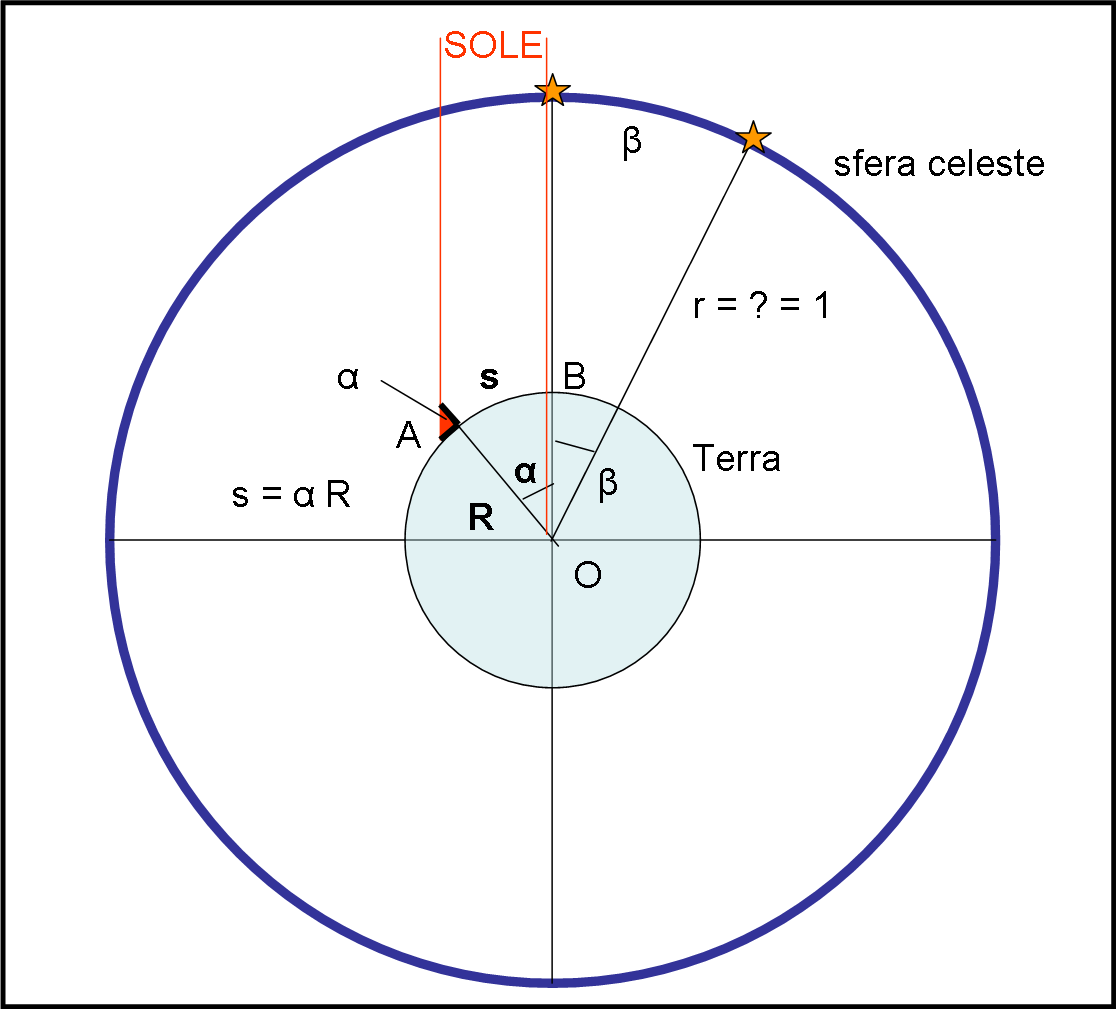
Traducendo il tutto in qualche formuletta, possiamo dire che potendo calpestare la Terra è possibile misurare la distanza, in chilometri, dell’arco di cerchio s e riuscire a determinare la misura della circonferenza, da cui il raggio R e l’angolo α, corrispondente all’arco s. Infatti:

α : s =  360 : 2πR

da cui:

α = 360 s /2πR

Lavorando in radianti:

α = s/R

Quel genio di Eratostene

Ovviamente, vale anche il viceversa. Riuscendo a calcolare l’angolo α e misurando direttamente s si ricava nientemeno che il raggio della Terra che abbiamo sotto i piedi.

Sì, ma come misurare l’angolo α ? Possiamo mica andare e tornare fino al centro della Terra? Beh… non ce n’è bisogno. Basta pensare che la Terra è rotonda, che il Sole può considerarsi a una distanza praticamente infinita (raggi paralleli) e avere una mente di prima classe.

Notiamo quel triangolino rettangolo rosso relativo al punto A che compare in Fig.1. La parte verticale rispetto al suolo è un’asta rigida e quella tangente al suolo è l’ombra dell’asta. Due cose che si misurano facilmente. Se si riesce a misurare anche la distanza s, magari a dorso di un dromedario dal passo molto regolare, e sapendo che in B il Sole è esattamente sulla verticale del luogo, il gioco è fatto.

Il triangolino rosso ci regala l’angolo α (angoli alterni interni di rette parallele tagliate da una trasversale) che, insieme al percorso del dromedario s, ci permette di calcolare la circonferenza della Terra (e/o il suo raggio) con un errore inferiore al 5%!

Quando? pochi secoli fa! No, cari amici, nel terzo secolo avanti Cristo, per merito di un tale Eratostene di Cirene, che non avrà avuto cellulari o telescopi, ma che aveva sicuramente una testa di prima categoria che nel mondo di oggi sarebbe veramente preziosa e rara!

Torniamo a noi… La sfera celeste, invece, la vediamo dal di dentro e da molto lontano. Anzi, la sua distanza è indeterminata. Tutto ciò che possiamo fare è porre questa distanza (il raggio della sfera) uguale a uno e accettare di misurare le distanze tra le stelle come archi di cerchio (massimo!) a cui assegnare il valore dell’angolo β espresso in radianti.

Coordinate geografiche

Fatte queste dovute premesse, rivolgiamoci alla Terra e creiamo su di lei un “comodo” reticolato che ci permetta di identificare ogni suo punto attraverso una coppia di coordinate sferiche. Il vantaggio è enorme…

La Fig. 2 ci mostra una sfera perfetta. La prima cosa da fare è definire un suo cerchio massimo. Niente di più facile. Ve ne sono infiniti: l’importante è che essi siano generati dall’intersezione tra la superficie sferica e un piano qualsiasi che passi per il suo centro C.

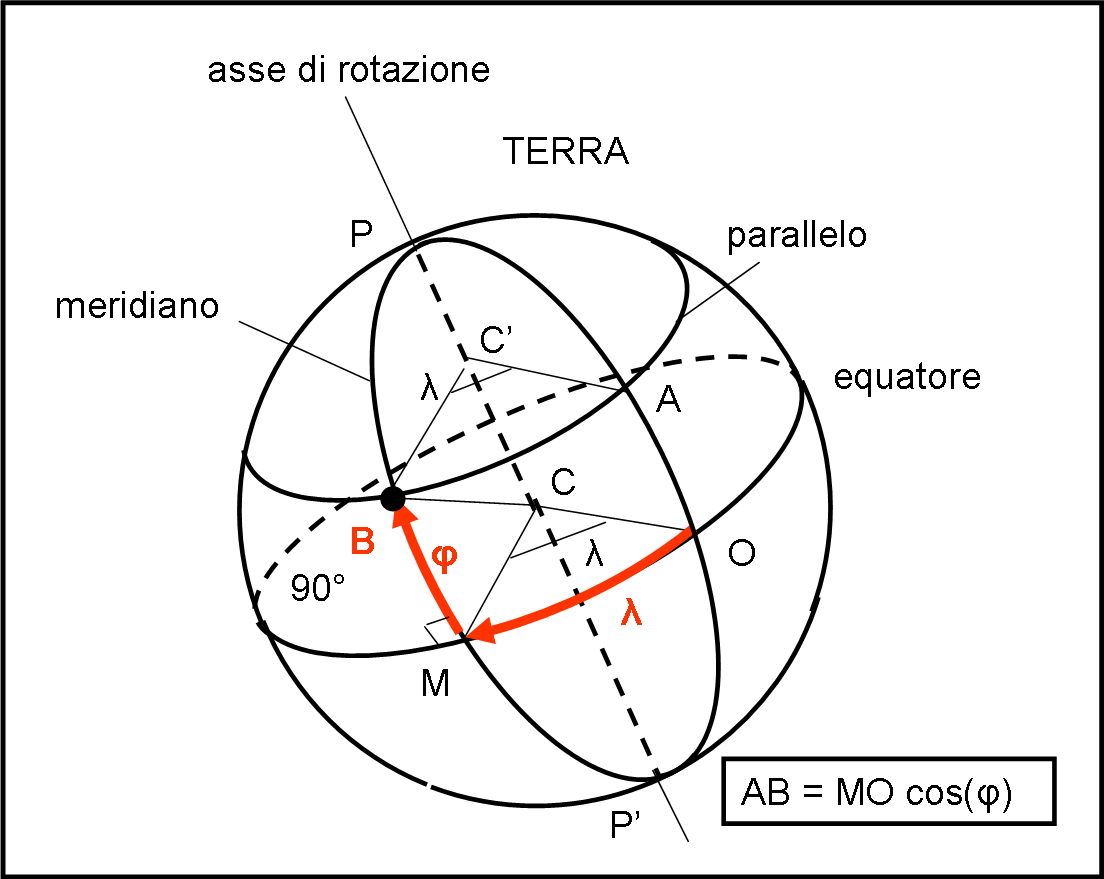
Scegliamone uno a caso, quello che passa per i punti M e O. Definito il cerchio massimo è anche facile definire una retta (estrinseca, ossia tracciata nello spazio a tre dimensioni) che sia perpendicolare al piano che lo ha generato.

Questa retta incontra la sfera in due punti P e P’. Questi punti sono estremamente particolari, dato che tutte le  rette (intrinseche, ossia che siano “rette” per un abitante della superficie sferica) perpendicolari al cerchio massimo devono passare per P e P’. In altre parole, questo fatto ci dice che tutte le rette intrinseche della superficie (cerchi massimi) si incontrano sempre in due punti antipodali (ossia che distino tra di loro di un arco uguale a π).

Possiamo divertirci a tracciare tutte le rette di questo tipo e sceglierne una in particolare, ad esempio quella che passa per O. Ribadiamo, ancora, che questa retta intrinseca non è altro che un cerchio massimo per una visione estrinseca. Tutti i piani che hanno generato i cerchi massimi estrinsechi che passano da P e P’ devono avere in comune la retta estrinseca PP’: siamo di fronte a un fascio di piani aventi come asse la retta PP’, vedi QUI).

A questo punto, siamo tranquilli che, muovendoci lungo il cerchio OM e lungo un qualsiasi cerchio PP’, stiamo percorrendo le traiettorie di minima distanza tra due punti, ossia dei cerchi massimi.

Come abbiamo già detto scegliamo il cerchio massimo POP’ come cerchio di riferimento per le nostre coordinate sferiche, ossia per dare un nome e un cognome a ogni punto della superficie sferica nella nuova geometria.

Consideriamo un certo punto B e tracciamo il cerchio massimo PB che interseca il cerchio massimo OM in M. I due cerchi massimi sono tra loro perpendicolari per costruzione. Definiamo, come prima coordinata λ di B, l’arco di cerchio massimo OM.

Arrivati in M, portiamoci sul cerchio massimo MB fino a giungere in B. L’arco di cerchio massimo MB è la seconda coordinata φ del punto B, che viene perciò identificato come B(λ, φ).

Notiamo subito due punti fondamentali.

La coordinata λ è l’angolo formato dai due piani PCO e PCM. Ne segue che anche l’angolo BC’A è uguale a λ. Tuttavia, non confondiamoci pensando che λ sia anche l’arco AB. Esso non appartiene a un cerchio massimo e lo sarebbe solo se C’ coincidesse con C.

D’altra parte l’arco di cerchio AB non è un cerchio massimo dato che il piano che lo genera, parallelo al piano che genera OM, non passa per il centro della sfera. La lunghezza dell’arco AB è, però, facilmente ottenibile con una della formule che abbiamo ricavato per la trigonometria sferica (QUI) e dipende dall’angolo BCM (in particolare dal suo coseno):

AB =  OM cos(φ)

Si può, però, dire che tutti punti che stanno sul cerchio minore AB hanno lo stesso valore di φ. Risulta, invece, che tutti i punti dei cerchi massimi del tipo PBP’ hanno la stessa λ.

A questo punto, possiamo permetterci di smettere con la generalizzazione e considerare, come piano che contiene il cerchio massimo OM, quello dell’equatore terrestre. Ne segue che P e P’ diventano il Polo Nord e il Polo Sud (l’asse PP’ è l’asse di rotazione della Terra).

I cerchi massimi che passano per P e P’ prendono il nome di meridiani, mentre i cerchi minori che hanno la stessa coordinata φ sono detti paralleli. Per concludere, diciamo ancora che φ si chiama latitudine del luogo B e λ si chiama longitudine.

La prima varia tra 0° e 90° ed è positiva andando verso il Polo Nord e negativa andando verso il Polo Sud. Ricordiamo che il meridiano di riferimento (λ = 0), ossia POP’, è stato scelto come quello che passa per l’osservatorio di Greenwich in Inghilterra. La longitudine varia tra 0° e 180° e le si aggiunge Est od Ovest a seconda del verso. In altre parole, se ponendosi sul Polo Nord si va in verso orario si va verso Ovest, mentre se si va in verso antiorario si va verso Est. Sui punti Est e Ovest ci torneremo tra non molto…

Ridendo e scherzando, abbiamo introdotto le coordinate geografiche di un luogo qualsiasi della Terra.

Alcuni punti hanno coordinate del tutto speciali. Ad esempio, i due poli hanno latitudine +/– 90° e longitudine indeterminata. I punti dell’equatore hanno invece latitudine uguale a zero. Chi sta sul meridiano di Greenwich ha sempre longitudine uguale a zero, qualsiasi sia la sua latitudine.

Il fatto che la Terra ruoti attorno al suo asse ha poca importanza per le coordinate geografiche. Per come sono state definite, rimangono sempre le stesse in qualsiasi ora del giorno.

Tuttavia, il meridiano di riferimento ruota insieme alla Terra e quindi un orologio che sia posto sul meridiano di riferimento impiegherebbe 24 ore a compiere un giro completo e quindi indicherebbe ore diverse in diversi istanti della sua rotazione. Ogni altro meridiano lo seguirebbe o lo precederebbe in modo solidale e quindi il tempo scorrerebbe in modo analogo, anche se con una differenza rispetto a lui.

Questa differenza, espressa in ore, minuti e secondi è la differenza in longitudine tra i meridiani espressa in gradi, primi e secondi. In altre parole, la longitudine può essere benissimo espressa in ore, minuti e secondi tenendo presente la relazione:

24 ore = 360°, ossia:

1 ora = 15°.

Orizzonte e Zenit

Presentiamo concetti estremamente semplici, sicuramente conosciuti da tutti. Tuttavia, dato che diventeranno i punti di riferimento dei vari sistemi usati per individuare gli astri e gli altri oggetti celesti, cerchiamo di definirli in linea con quanto detto finora sulla geometria sferica.

Usciamo all’aperto in un luogo che abbia l’orizzonte il più libero possibile. Poco importa se è notte o giorno: sopra di noi appare in tutta la sua magnificenza la sfera celeste.  In realtà, ne appare solo metà, dato che l’altra semisfera rimane nascosta sotto i nostri piedi. Se siamo di giorno essa è dominata da un bel cielo azzurro oppure coperto da nubi delle più varie sfumature dal bianco  al nero. Un panorama bellissimo, ma che poco ha a che fare con l’astrofisica, ma piuttosto con la nostra atmosfera (in realtà tutto ciò che esiste fa parte dell’astrofisica…)

Al limite appaiono il disco del Sole, quello della Luna e, se siamo vicini alla notte, i pianeti più luminosi. Molto meglio osservarla quando è buio, soprattutto se il cielo è sereno. Tutto ciò solo se vogliamo utilizzare telescopi ottici, dato che gli astri mandano comunque la loro informazione elettromagnetica.

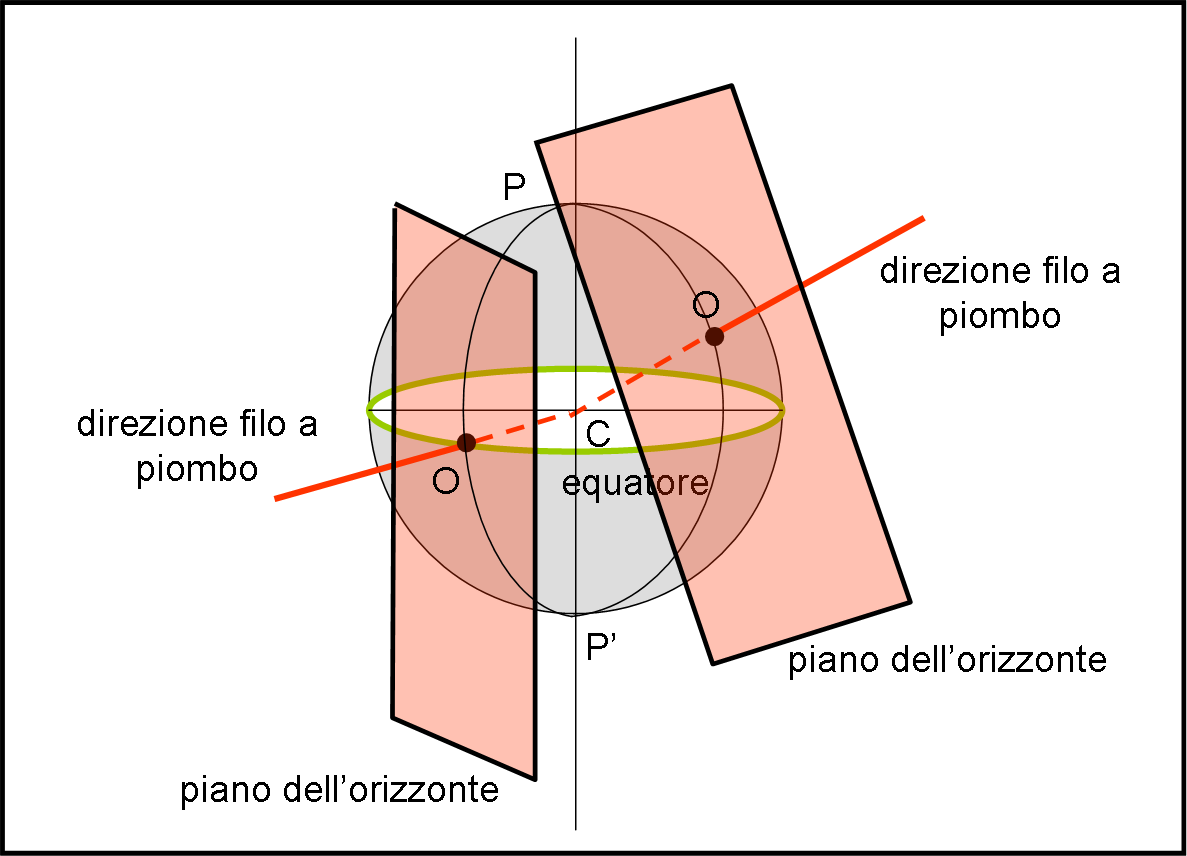
La prima cosa da fare è determinare la direzione del filo a piombo nella posizione O dell’osservatore e poi considerare il piano tangente alla sfera terrestre in quel punto, che è anche perpendicolare alla direzione del filo a piombo, ossia il piano dell'orizzonte (Fig. 3) .Questa retta e questo piano sono quelli fondamentali per il primo sistema di riferimento.

Consideriamo la schematica Fig. 4, dove vediamo diverse sfere celesti per diversi osservatori. Un osservatore qualsiasi O, O₁ , O₂ , O₃ è posizionato in un punto della superficie terrestre e, come già detto, ha a disposizione un filo a piombo che gli permette di individuare la direzione OZ , O₁Z₁, O₂Z₂, O₃Z₃, che indica la verticale del luogo. Ricordiamolo fin d’adesso: per un qualsiasi osservatore, la verticale del luogo è una direzione fissa nel suo sistema di riferimento. Analogamente, per lui la sfera celeste sembra sempre la stessa, anche se prima o poi vede apparire l’alba e, se è attento, vede anche le stelle che compiono strani cerchi nel cielo. Per adesso, però, disinteressiamoci di ciò che si muove o -meglio- che sembra muoversi.

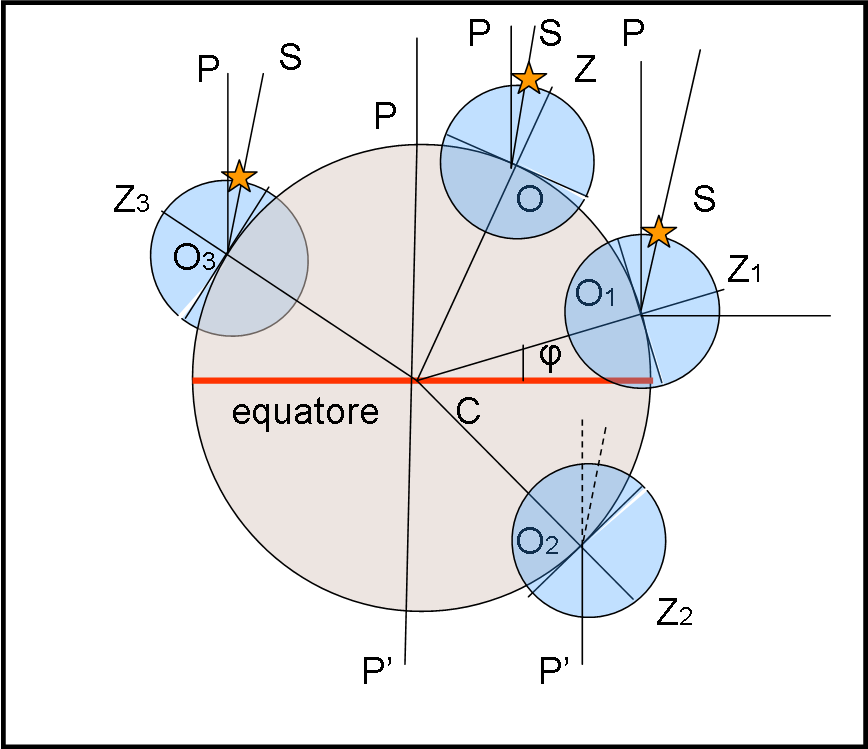
Il punto Z , Z₁, Z₂, Z₃ ,… viene chiamato zenit del luogo (quello opposto, invisibile, si chiama nadir). Assumendo la Terra come una sfera perfetta, la verticale deve passare per il suo centro C.  Come già detto, è facile determinare il piano dell’orizzonte che è, quindi, il piano tangente alla superficie terrestre nel punto O, O₁, O₂, O₃, …

La sfera celeste

Ogni osservatore può facilmente disegnare la sua sfera celeste com'è mostrato in Fig. 5, dove vengono proiettati i vari astri, facendo riferimento al piano dell’orizzonte (e allo zenit).  Il piano dell’orizzonte interseca la sfera celeste e identifica un cerchio massimo di centro O, che si chiama orizzonte celeste del luogo. Dato che misuriamo solo angoli tra gli astri, la sfera celeste di ogni osservatore ha un raggio indeterminato e possiamo, perciò, considerarlo unitario.

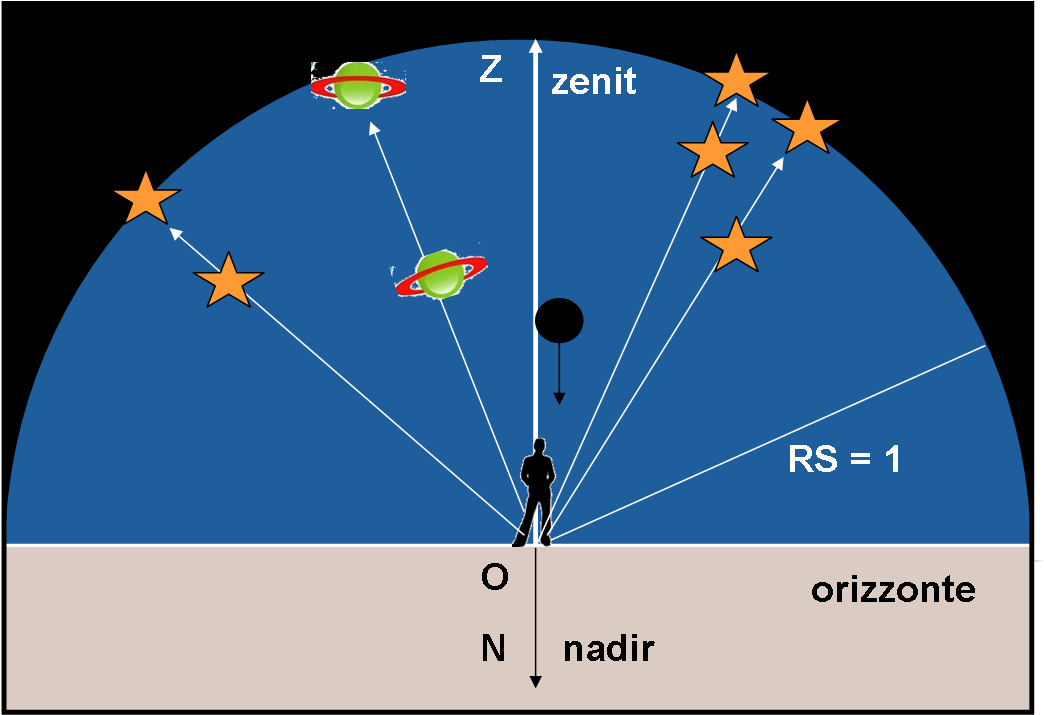
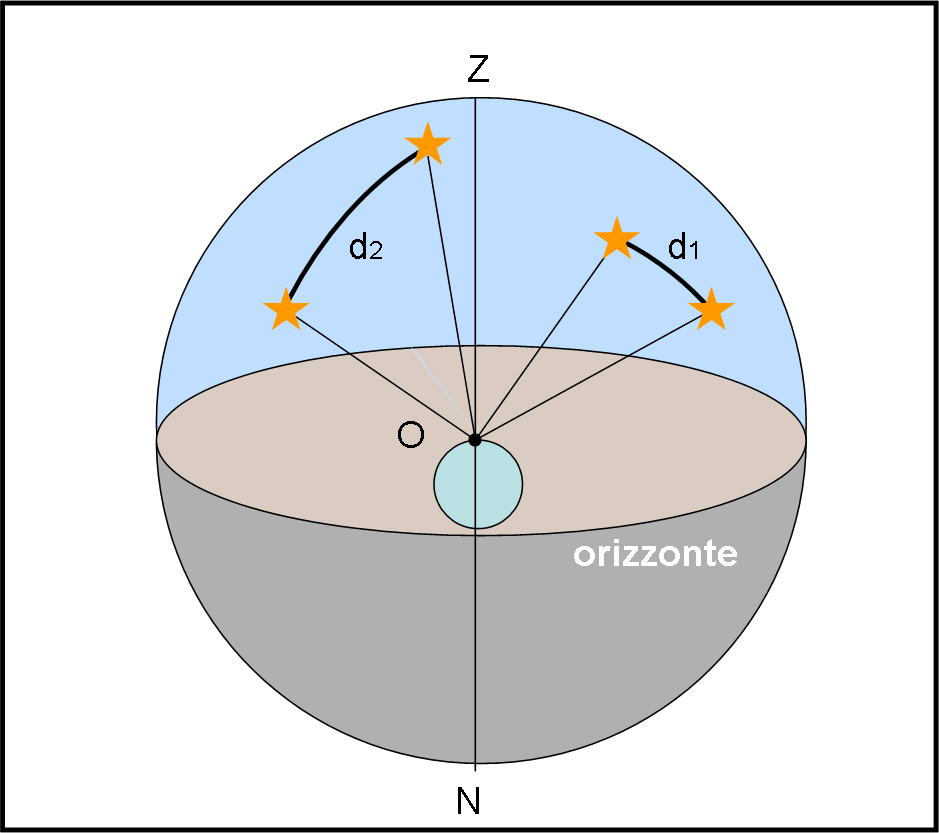
Vale la pena ripetere che la sfera celeste è una sfera fittizia che riproduce ciò che vede l’osservatore, il quale può ricavare solo le direzioni degli astri, ma non la loro effettiva distanza. Ne segue, anche, che la distanza apparente tra due astri è data dall’angolo compreso tra le loro direzioni o, più efficacemente, dall’arco di cerchio massimo (la minima distanza) che li congiunge, come descritto in Fig. 6.

Abbiamo assodato che, nella Fig. 4, quella che vede O₁ non è lo stessa che vede O₂ e via dicendo. Ciò è vero, dato che gli astri possono essere considerati (per lo più) a una distanza infinita e la loro luce giunge a noi secondo rette parallele. La posizione degli astri rispetto allo zenit e all’orizzonte celeste del luogo è quindi diversa da luogo a luogo, come si può notare nella figura. Le distanze angolari tra Z e S è diversa di quella tra Z₁ e S e Z₃ e S. Addirittura l’osservatore O₂ non vede la stella.

Il primo sistema (azimut e altezza)

Immaginiamo che la Terra sia immobile. Siamo già in grado di definire un sistema di coordinate celesti anche se sappiamo che si riferiscono solo al luogo dell’osservatore O. Il cerchio massimo fondamentale è quello dell'orizzonte. Lungo la perpendicolare che passa per O si può subito identificare lo zenit Z.

Nella stessa figura, possiamo anche inserire una “stella” molto particolare. Non sappiamo bene cosa sia, ma è situata nella direzione perpendicolare all’equatore della Terra (questa informazione l’abbiamo già). Per gli osservatori che stanno “sopra” si chiama stella P, per quelli che stanno “sotto” si chiama stella P’. In realtà non è una vera stella, ma essendo determinata in ogni sfera celeste da rette tra loro parallele (e perpendicolari all’equatore), la possiamo tranquillamente indicare come tale. La stella P la vediamo già nella Fig. 4 (O₂ non vede P, ma solo P’). Anche la stella P (e P’) ha una posizione sempre diversa rispetto all’orizzonte del luogo.

Nella Fig. 7 disegniamo, in tre dimensioni, la sfera celeste relativa all’osservatore O .

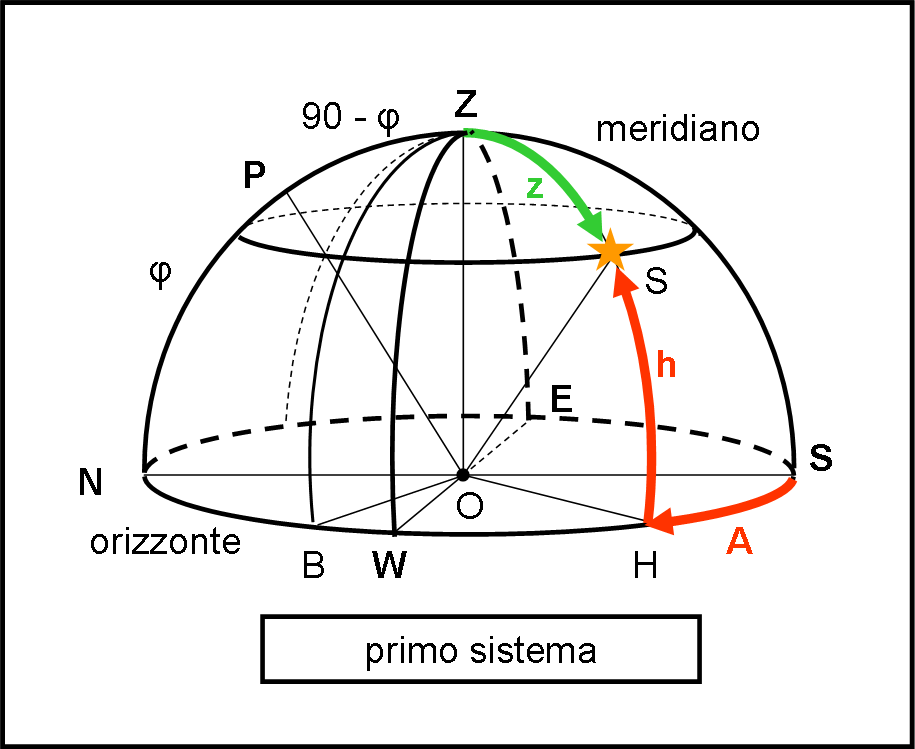
Si nota bene il cerchio massimo che passa per P (e per P’) e per Z. I punti in cui questo cerchio massimo incontra quello dell’orizzonte vengono chiamati N e S. N è quello più vicino a P.  A 90° dal punto N, andando in verso orario segniamo il punto W. In direzione opposta alla sua segniamo il punto E. In parole povere, abbiamo segnato il Polo Nord celeste (P), il Polo Sud celeste (P’), Il Nord (N), il Sud (S), l’Ovest (W) e l’Est (E) e, ovviamente lo zenit Z.

Consideriamo una stella S. Prendiamo un piano parallelo a quello dell’orizzonte, che passi per S. Esso identifica un cerchio minore che ha una ovvia caratteristica: la distanza angolare dal piano dell’orizzonte è costante e viene chiamata altezza h. In figura, ovviamente, h è sia la lunghezza dell’arco SH, sia l’angolo al centro SOH.

Tutte le stelle che stanno su questo cerchio minore hanno la stessa altezza h. h è la prima coordinata di S. I cerchi minori paralleli all’orizzonte vengono chiamati paralleli d’altezza.

Tracciamo adesso il cerchio massimo che passa per lo zenit e la stella S, e tocca l’orizzonte in H. La seconda coordinata si misura lungo il cerchio dell’orizzonte partendo da S e andando in direzione di W fino a incontrare H. L’arco di cerchio SH (che è anche l’angolo al centro SOH) si chiama azimut A della stella S.

A volte, al posto dell’altezza h si usa l’arco complementare, ossia ZS, e viene chiamata distanza zenitale z.

Tutti i cerchi massimi che passano per Z si chiamano cerchi verticali. Quello che passa per N e S prende il nome di meridiano, mentre quello che passa per E e W si chiama primo verticale.

A questo punto non possiamo dimenticare che l’orizzonte varia da luogo a luogo, da cui si deduce che ogni astro S ha un’altezza diversa a seconda del luogo da cui è visto. Inoltre, cosa ancora più importante, la Terra non è immobile, ma ruota attorno al proprio asse (indicato proprio da P-P’) e quindi sia l’altezza che l’azimut di una stella sono costretti a cambiare da istante a istante. Notiamo anche che l’altezza del polo non è altri che la latitudine dl luogo.

Il sistema che abbiamo introdotto è il più immediato e semplice, ma si riferisce solo a un certo istante e a un certo osservatore. Se si volesse osservare una stella qualsiasi con un cannocchiale o un telescopio posizionato secondo questo sistema di riferimento, si sarebbe costretti a spostarlo a ogni istante, altrimenti l’astro scapperebbe velocemente dal campo dello strumento per effetto del moto di rotazione della Terra.

Prima di passare a un altro sistema di riferimento, che sia in grado di tenere in conto il moto di rotazione della Terra, può essere utile ai meno esperti “toccare con mano” cosa capita nel primo sistema, o sistema alto-azimutale, quando si osserva il cielo, introducendo una Terra che ruoti attorno a un asse perpendicolare all’equatore. Notiamo ancora una volta che l’asse polare (e quindi anche l’equatore) forma un angolo diverso rispetto allo zenit del luogo. La Fig 8 mostra immediatamente che questo angolo è il complementare alla latitudine del luogo φ (arco di cerchio massimo tra equatore e zenit), ossia: PZ = 90 – φ. Questa relazione ci sarà molto utile in seguito.

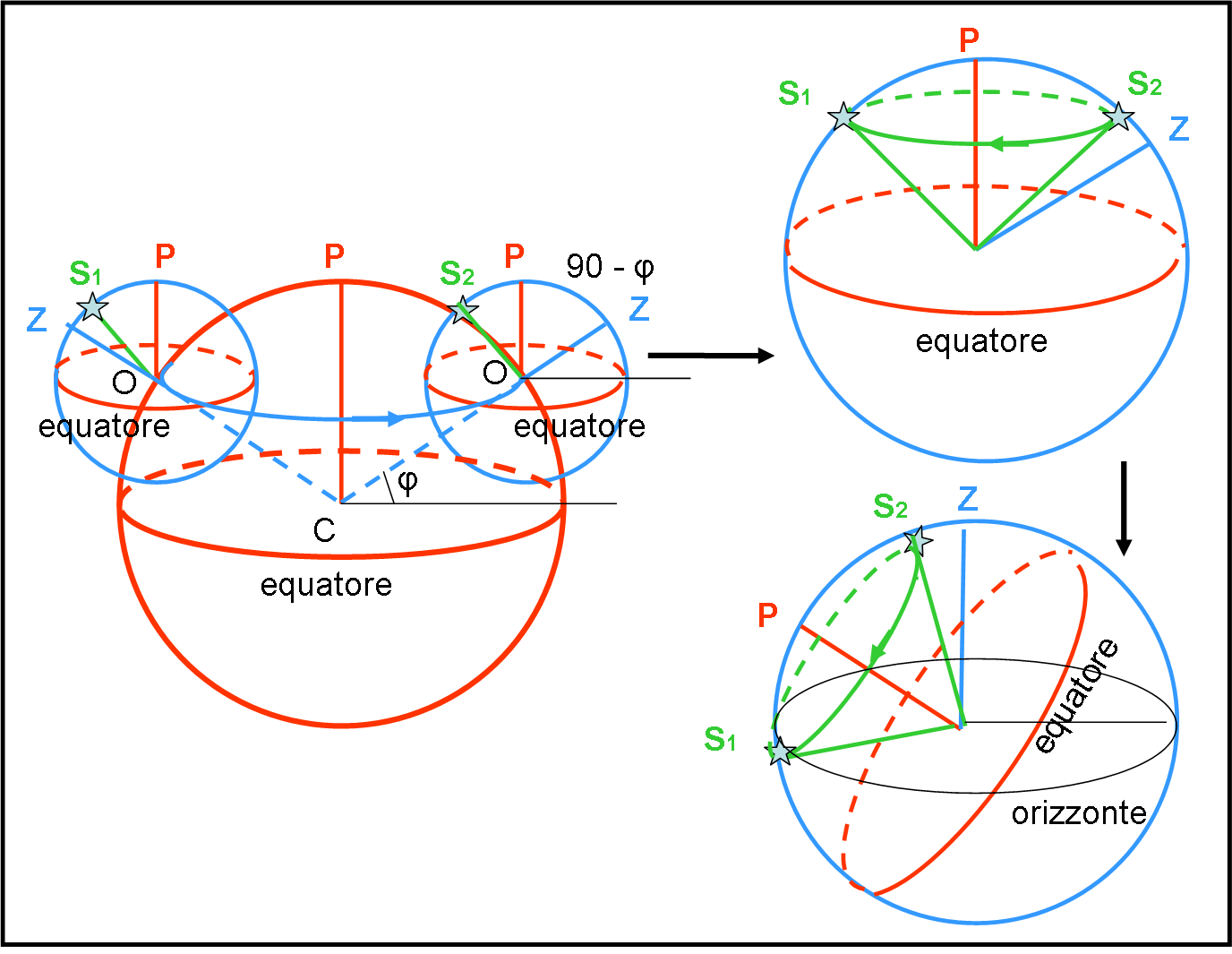
Quello che stiamo per scrivere è di una banalità irrisoria, ma, dato che ci siamo, spieghiamo anche le cose più semplici e ovvie. L’osservatore è posto in O (sul lato sinistro della Terra). In quella posizione il suo zenit è Z (non disegniamo l’orizzonte per non creare troppa confusione), ossia la congiungente centro della Terra e osservatore. La posizione di una certa stella sia S₁. P è la solita direzione dell’asse di rotazione terrestre. Sia S₁ che P non risentono assolutamente del moto di rotazione, dato che la prima è del tutto estranea al nostro pianeta, mentre il secondo è proprio la direzione dell’asse che è per definizione fisso (come già detto è una “stella” molto particolare).

L’osservatore O è costretto a spostarsi a causa della rotazione e descrive un arco di cerchio minore blu parallelo all’equatore (un parallelo, infatti). Lo zenit è obbligato a trovarsi sempre lungo la direzione ZC e questa, vista da un sistema di riferimento esterno alla Terra, descrive un cono di apertura 90 – φ. Chi, invece, vive sulla Terra, proprio in O, continua a vedere la direzione dello zenit sempre secondo la direzione del filo a piombo del luogo. Per lui non ha avuto alcun movimento. Ancora una volta il sistema di riferimento è essenziale!

Dopo 180° di rotazione, fermiamo un attimo la Terra. Per l’osservatore O, Z non si è mosso. Facendo coincidere Z (sfera in alto a destra), P rimane sempre al suo posto, mentre invece cambia completamente la distanza zenitale della stella, che è ora in S₂. S₁ era decisamente più vicina (e quindi più alta nel cielo), mentre, dopo mezza rotazione, si porta nella zona invisibile della sfera celeste, ossia poco sotto l’orizzonte.

Conclusione? L’osservatore O, convinto di essere fermo, vede la stella passare da S₁ a S₂ durante mezza rotazione terrestre, ossia in 12 ore. La situazione apparente nel sistema alto-azimutale, è quella della sfera in basso a destra.

Sintetizzando, ogni stella appare percorrere un cerchio minore (a meno che non si trovi proprio sul piano dell’equatore) parallelo all’equatore, in verso opposto a quello di rotazione della Terra. La "stella" P (o P’, per chi sta dall’altra parte dell’equatore) rimane invece fissa sulla sfera celeste (la rotazione avviene proprio attorno all’asse PP’).

Il Polo Nord ha la fortuna di avere (in questo momento storico, dato che anche l’asse della Terra si muove nel tempo) una stella estremamente vicina che, come già detto, prende il nome di Stella Polare (Alpha Ursae Minoris). Tutte le altre stelle descrivono cerchi minori in 24 ore. Questi cerchi non sono, normalmente, visibili completamente da O, dato che una parte è descritta sotto l'orizzonte. Ma su questa problematica avremo modo di tornare a lungo dopo l’introduzione del prossimo sistema di riferimento.

Il secondo sistema (angolo orario e declinazione)

Quanto detto nel capitolo precedente, esprimiamolo attraverso la Fig. 9.

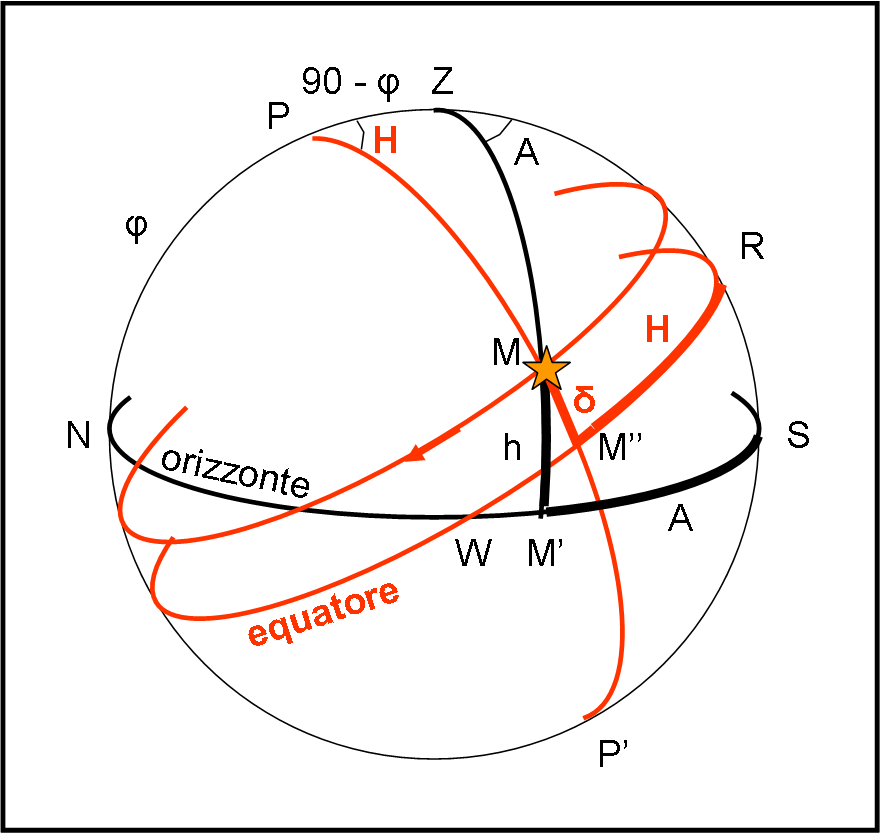
Disegniamo la sfera celeste ponendo sempre l’orizzonte celeste come cerchio massimo orizzontale. Sul cerchio massimo verticale (meridiano), segniamo lo zenit Z e il polo P. Come già sappiamo l’arco PZ è uguale a 90 – φ. E’ immediato tracciare il cerchio massimo che è definito dall’intersezione della sfera celeste con il piano dell’equatore terrestre, ossia l’equatore celeste.

Diamo qualche definizione: tutti i cerchi massimi che passano per il polo P (e P’) sono chiamati cerchio orari. Quello tra essi che passa anche per Z è ovviamente il meridiano.  Le intersezioni di esso con l’orizzonte sono, di conseguenza, i punti N e S (come già visto nel primo sistema).

Dimostriamo subito che i punti intersezione tra orizzonte celeste ed equatore celeste sono i punti W ed E. Infatti, come punto dell’orizzonte il punto W (oppure E) è a 90 ° da Z. Tuttavia, come punto dell’equatore è a 90° da P. Ma se è a 90° da  P e Z deve essere a 90° da tutti i punti del cerchio massimo che passa per P e Z e, quindi, anche da N e S.

Come abbiamo visto nella Fig. 8, le stelle appaiono muoversi da Est verso Ovest lungo cerchi minori paralleli all’equatore celeste (in modo simile ai paralleli terrestri). Nel loro moto apparente devono prima o poi attraversare il meridiano del luogo (il cerchio massimo PZ). Anzi, lo devono fare due volte, una ogni 12 ore. Quando la stella effettua questo passaggio alla massima altezza  il punto rappresenta la culminazione superiore. Dalla parte opposta, si ha la culminazione inferiore, che può  anche avere altezza negativa, ossia avvenire sotto l’orizzonte e quindi non essere visibile.

E’ immediato definire la prima coordinata in questo sistema: l’arco compreso tra il cerchio descritto dalla stella M e l’equatore (con segno più se è nell’emisfero nord e con segno meno se è nell’emisfero sud). Essa prende il nome di declinazione δ ed è una coordinata che non dipende assolutamente dal luogo dell’osservatore e dall’istante dell’osservazione. Ovviamente, essa può variare se la stella non è una stella, ma un corpo planetario o un satellite artificiale.

L’altra coordinata è invece più “ballerina”. Essa è l’angolo sferico ZPM o, se preferite, l’arco di equatore RM'', contato in ore minuti e secondi a partire dal meridiano, in senso positivo verso W e negativo verso E. Prende il nome di angolo orario H e vale 0^h quando la stella si trova alla culminazione superiore e 12^h quando è alla culminazione inferiore. Dato che la stella si muove continuamente, l’angolo orario è una coordinata che cambia da istante a istante, ma lo fa in modo costante (per quanto è costante la rotazione della Terra).

Si può notare, come già accennato, il grande vantaggio di questo sistema rispetto al primo. Una delle due coordinate, che identificano una stella, è uguale per tutti gli osservatori, dato che la distanza angolare tra equatore e cerchio minore a lui parallelo, che passa per la stella, deve rimanere sempre la stessa. Il cerchio minore descritto dalla stella prende anche il nome di parallelo di declinazione. E’ la stessa cosa che capita per i paralleli terrestri: due luoghi hanno sempre la stessa latitudine φ, indipendentemente da come orientate la Terra nello spazio. L’altra coordinata varia, ma in modo costante e basta un motorino per permetterci di seguire il moto di una stella nel cielo. Questo sistema è quello su cui si basano i telescopi a montatura equatoriale.

Finita la semplice descrizione, ci si pone un problema di grande importanza astronomica: conoscendo le coordinate di una stella nel primo sistema come si fa passare alle sue coordinate nel secondo sistema (e viceversa)?

Qual è il problema da risolvere? Conosciamo le coordinate h (altezza sull’orizzonte), oppure z (distanza zenitale) e l’azimut A di una certa stella S, definiti nel prima sistema. Entrambe sono coordinate variabili sia nel tempo che da luogo a luogo. Vogliamo determinare le coordinate δ (declinazione) e H (angolo orario),definite dal secondo sistema, dove la prima è una costante sia rispetto al tempo che al luogo, mentre la seconda varia col tempo in modo costante. In altre parole più sintetiche:

Dal primo al secondo sistema

La figura da utilizzare è nuovamente la Fig. 9, che riportiamo per comodità.

Il triangolo da cui dobbiamo partire è PZM. Innanzitutto… è un triangolo sferico? Sicuramente sì, dato che tutti i suoi lati sono archi di cerchio massimo (non dimentichiamoci mai questa verifica!), lo abbiamo spiegato QUI figura 6.  Se è un triangolo sferico, gli si possono applicare le formule fondamentali.

Definiamo bene ciò che conosciamo. Innanzitutto l’arco PZ, che 90° - φ, dove φ è la latitudine del luogo (coordinata terrestre che deve essere conosciuta da ogni cittadino, astrofilo oppure no). Conosciamo, poi, l’arco ZM che non è altro che la distanza zenitale z (o, se preferite, 90° - h). Conosciamo anche l’arco di cerchio massimo NM' descritto sull’orizzonte. Esso vale 180° - A. Ma esso è anche uguale all’angolo PZM. Ovviamente, vogliamo determinare:

δ = 90° - PM

e

H = ZPM = arco sull’equatore M”R

In parole povere, conosciamo due lati e l’angolo tra essi compresi: PZ, ZM e PZM.

Non ci resta che applicare la prima formula fondamentale della trigonometria sferica (andate a cercarla QUI, dove l’abbiamo ricavata). Essa dice proprio che il coseno di un lato è uguale al prodotto dei coseni degli altri due lati più il prodotto dei loro seni moltiplicati per il coseno dell’angolo opposto al lato da determinare. In parole matematiche:

cos PM = cos PZ cos ZM + sen PZ sen ZM cos PZM

Tutto ciò che compare al secondo membro è, però, conosciuto! Il coseno del primo membro è, invece, proprio il coseno di PM che è legata strettamente con una delle incognite, ossia la declinazione δ.

Sostituiamo i valori è otteniamo:

cos (90 – δ) = cos (90 – φ) cos z + sen (90 - φ) sen z cos (180 – A)

Ossia:

sen  δ = sen φ cos z – cos φ sen z cos A    …. (1)

ricordando che cos (180 – A) = - cos A  (al limite, andate a ripassarvi le basi della trigonometria QUI, capitolo 22)

La (1) è più che sufficiente per determinare δ, dato che il suo seno è positivo per δ positivo e negativo per δ negativo. In poche parole, la (1) ci basta per sapere se la declinazione è positiva o negativa.

Passiamo, adesso, alla determinazione di H.

Usiamo lo stesso triangolo di prima, ma utilizziamo la seconda formula fondamentale, quella dei seni, che ci dice che il rapporto tra i seni degli angoli e dei lati opposti è costante.

Nel nostro caso:

sen PZM/sen PM = sen ZPM/sen ZM

Sostituendo, abbiamo:

sen (180 – A)/sen (90 – δ) = sen H/sen z

sen A/cos δ = sen H/sen z

sen H = sen A sen z/cos δ        …. (2)

Dato che la declinazione δ è già stata ricavata, essa è adesso un valore conosciuto e quindi sembrerebbe che la (2) ci regali l’angolo orario H.

In realtà non è così, dato che il seno di un angolo che può andare da 0° a 180° (o da 0^h a 12^h, cosa del tutto analoga). Vediamo cosa dice allora la conoscenza di un angolo di questo tipo, attraverso il solito cerchio goniometrico di Fig.10.

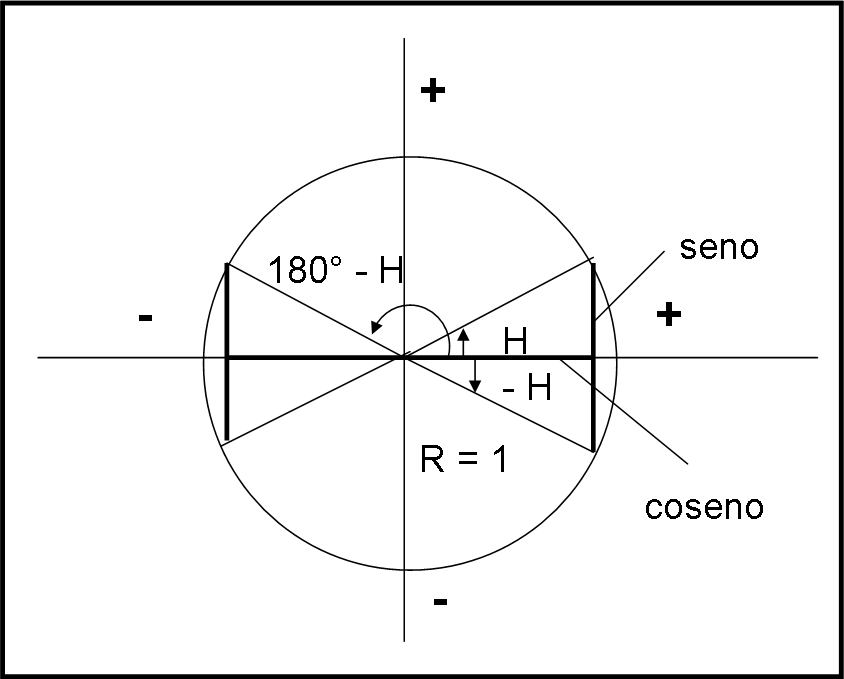
Come si vede molto bene, conoscere il sen H non riesce a dirci se H è proprio H o è 180 – H, dato che i loro seni sono uguali anche nel segno. In altre parole la (2) permette due soluzioni.

Potremmo, allora utilizzare nuovamente la prima formula fondamentale scrivendo:

cos ZM = cos PZ cos PM + sen PZ sen PM cos ZPM

cos z = cos (90 – φ) cos (90 – δ) + sen (90 – φ) sen (90 – δ) cos H

cos z = sen φ sen δ + cos φ cos δ cos H

da cui:

cos H = (cos z - sen φ sen δ)/ cos φ cos δ      …. (3)

Il secondo membro è conosciuto e quindi si ricava H. Ma siamo proprio sicuri? Il coseno di H e di 180 – H cambia di segno e quindi permette di determinare l’angolo giusto attraverso il suo segno. Tuttavia, il coseno di H e –H rimane lo stesso e noi sappiamo che H può assumere valori negativi. Accidenti nemmeno la (3) ci dona il risultato definitivo!

Attenzione, però… noi abbiamo determinato sia il seno che il coseno dell’angolo e quindi confrontando i loro due segni è immediato sapere in che quadrante cadono nel cerchio goniometrico. L’angolo H, quindi, è completamente risolto, utilizzando la (2) e la (3).

In realtà, in giro per il web si potrebbero trovare dei passaggi che portano a determinare la tangente degli angoli, ma per noi è più che sufficiente questa trattazione: più immediata e senza troppi passaggi.

Tanto per fare esercizio, dimostriamo che il coseno di H può essere anche ricavato con la terza formula fondamentale.

Essa dice, applicata al solito triangolo:

sen PM cos ZPM = cos ZM sen PZ – sen ZM cos PZ cos PZM

sostituendo:

sen (90 – δ) cos H = cos z sen (90 – φ) - sen z cos (90 – φ) cos (180 – A)

cos δ cos H = cos z cos φ + sen z sen φ cos A

cos H = (cos z cos φ + sen z sen φ cos A)/ cos δ        …. (4)

Anche nella (4) l’unica incognita è H e quindi può essere usata al posto della (3). Decidete voi quale preferite…

Dal secondo al primo

Ciò vuol dire, conoscere δ e H (e φ, ovviamente) e ricavare z (o h) e A.

Utilizziamo sempre la  Fig. 9.

Consideriamo sempre il triangolo sferico PZM. Questo volta, però, conosciamo δ e H, oltre che al solito φ. Dobbiamo ricavare l’altezza h (o la distanza zenitale z) e l’azimut A.

Ragioniamo un attimo… Del solito triangolo conosciamo due lati e l’angolo compreso. E’ quindi facile utilizzare la prima formula fondamentale per determinare il lato opposto all’angolo:

cos ZM = cos PM cos PZ + sen PM sen PZ cos ZPM

Sostituiamo:

cos z = sen δ sen φ + cos δ cos φ cos H          …. (5)

La coordinata z può variare tra 0 e 90° e tra 0 e – 90°. Ma, in entrambi i casi, il coseno risulta positivo. Abbiamo quindi bisogno di conoscere anche il seno di z. La faccenda si complica un po’, dato che qualsiasi altra relazione si possa applicare fa comparire entrambe le incognite (A e z).

Con grande pazienza, proseguiamo comunque…

La seconda formula fondamentale ci dice:

sin z/sen H = sin (90 – δ)/sin (180 – A) = cos δ/sin A

sen z sen A = sen H cos δ             …. (6)

La terza formula fondamentale dice invece:

sen z cos (180 – A) = cos (90 – δ) sen (90 – φ) – sen (90 – δ) cos (90 – φ) cos H

- sen z cos A = sen δ cos φ – cos δ sen φ cos H

Cambiando di segno:

sen z cos A = - sen δ cos φ + cos δ sen φ cos H       … (7)

Basta, adesso, dividere la (6) per la (7) e ci accorgiamo che il sen z si semplifica. Senza fare troppo calcoli è facile capire che ci troveremo di fronte alla tan A che per la stessa definizione di tangente ci permette di sapere in che quadrante cade l’angolo (A può variare tra 0 e 180 e  0 e -180).

Ricavato A, basta usare la (6) per determinare la z.

Tuttavia, nei casi pratici è ben difficile aver bisogno delle coordinate nel primo sistema a partire da quelle del secondo…

Possiamo tranquillamente passare al terzo sistema, forse il più conosciuto e usato. La vera e propria carta d’identità di una stella. Esso è quello che definisce in modo univoco il nome e il cognome delle stelle, uguale per tutti i luoghi e in ogni istante. Le sue coordinate sono quelle che si usano normalmente nei cataloghi stellari.

Il terzo sistema

Per introdurre il terzo sistema di riferimento (probabilmente il più conosciuto) possiamo sbarazzarci dell’orizzonte (teniamo buono solo il punto S per sapere da dove parte l’angolo orario) e dedicarci completamente all’equatore celeste. Abbiamo visto che le stelle si muovono apparentemente lungo i paralleli di declinazione, mantenendo, perciò, costante la loro declinazione δ.

Decidiamo, perciò, di conservare questa coordinata che non varia assolutamente in funzione del luogo e del tempo. Non ci soddisfa, invece, l’angolo orario H, che varia linearmente col tempo, seguendo il moto apparente delle stelle dovuto alla rotazione della Terra.

Per migliorare la situazione è sufficiente considerare come origine una stella molto particolare che stia proprio sull’equatore. In tal modo, la differenza, tra l’angolo orario di ogni stella e quello della stella scelta come origine, rimarrà costante.

La scelta della stella di riferimento risulta molto facile e fa uso dell’eclittica, ossia dell’intersezione del piano che contiene l’orbita terrestre con la sfera celeste. Essa risulta, quindi, un cerchio massimo che interseca l’equatore in due punti chiamati punto d’Ariete γ e punto della Bilancia Ω.

Il primo di questi punti viene preso proprio come punto di riferimento per la seconda coordinata del terzo sistema. Essa non è altro che l’ascensione retta α e viene misurata positivamente lungo l’equatore in direzione Est (in verso opposto a quanto veniva fatto per l’angolo orario positivo). Come l’angolo orario anche l’ascensione retta si misura in ore, minuti e secondi. Vediamo il tutto nella Fig. 11.

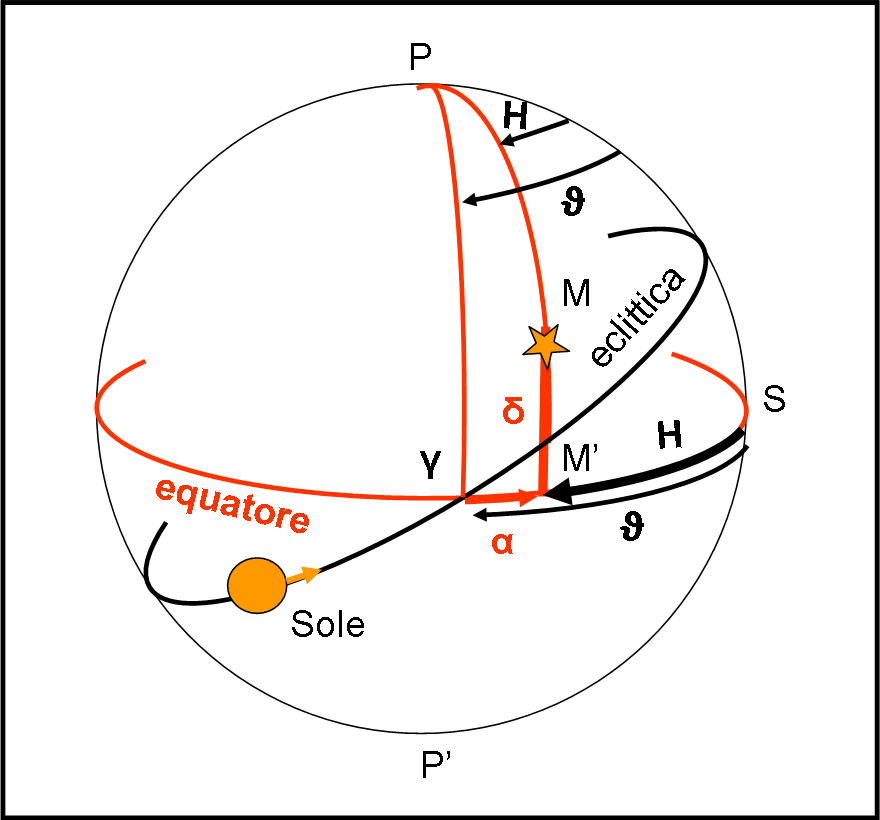
E’ ovvio che il punto γ si comporti come una stella e descriva un giro completo lungo l’equatore come una qualsiasi stella reale. Ne segue che l’ascensione retta è una costante che insieme alla declinazione fornisce il nome e il cognome per qualsiasi oggetto celeste.

Un nome e cognome che non cambiano assolutamente se non in tempi molto lunghi (in modo particolare a causa della precessione) ed è per questo che si usano solitamente riferirle a un’epoca prefissata che corrisponde  un certo istante del moto di precessione. Moto a cui è soggetto lo stesso punto d’Ariete.

Notiamo che il suddetto punto è quello in cui la posizione apparente del Sole (declinazione), nel suo moto annuale lungo l’eclittica, vale ZERO (come per il punto opposto della Bilancia), ma passa da declinazioni negative a declinazioni positive.

Particolare importanza ha anche l’angolo orario del punto γ. Esso si chiama tempo siderale ϑ.

Esistevano (ma esistono ancora) orologi a tempo siderale che, riferendosi a una stella fissa, compiono un giro completo in 23 ore e 56 minuti rispetto a quelli solari che lo compiono in 24 ore.

Questa differenza dovrebbe essere nota a tutti, ma vale la pena dimostrarla con la Fig. 12.

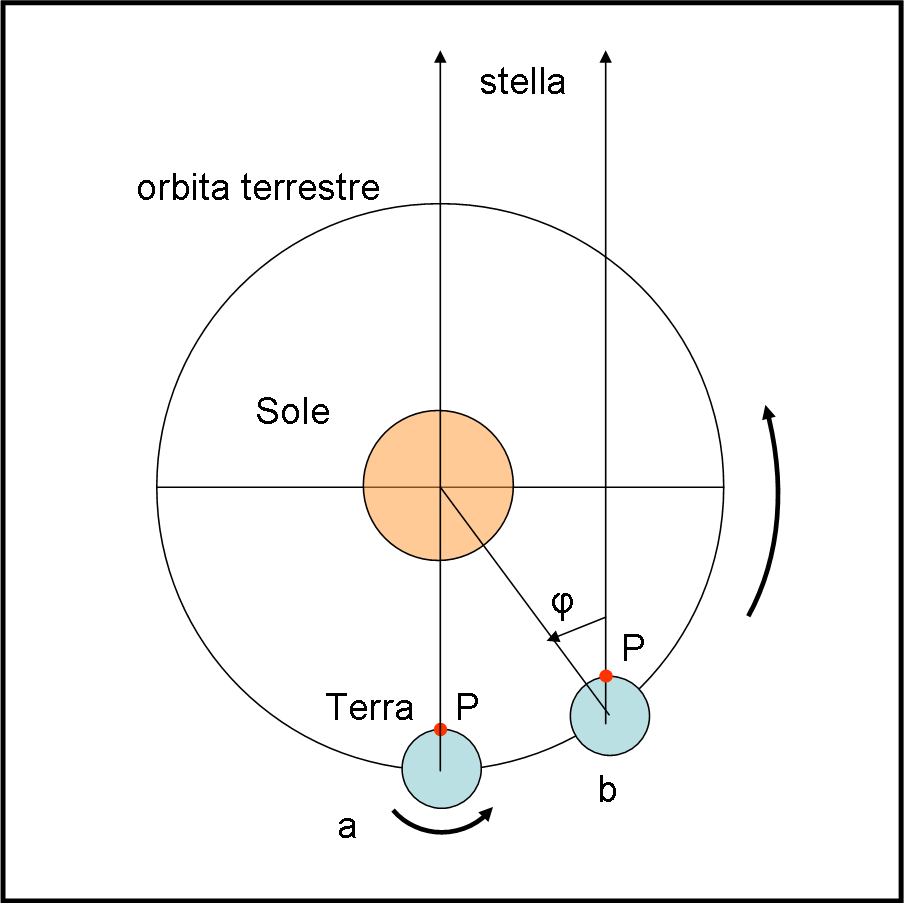
All’istante (a), il punto P della Terra si trova il Sole e la stella lontana nella stessa direzione. Dopo 23 ore e 56 minuti, il punto P si allinea di nuovo con la stella (immobile), mentre deve ancora percorrere un angolo φ (pari a 4 minuti di tempo) per allinearsi di nuovo con il Sole, a causa del moto di rivoluzione terrestre.

Oggi con i PC e altre semplici diavolerie si impostano direttamente le coordinate α e δ e il telescopio si muove fino a raggiungere la stella desiderata; poi, il motore, che segue il movimento apparente degli astri, non la lascia più.

Una volta, però, ai miei tempi arcaici, si doveva inserire direttamente l’angolo orario, la coordinata che permette di trovare la stella all’istante desiderato, dato che le stelle continuano inesorabilmente a muoversi per colpa della rotazione terrestre attorno al proprio asse. Per far ciò era necessario avere in cupola un orologio a tempo siderale (di solito bellissimi e con tante volute in legno…), attraverso il quale, conoscendo l’ascensione retta della stella, data nei cataloghi stellari, si determinava l’angolo orario, la vera coordinata necessaria per trovare la stella desiderata. Oggi, questo lavoro lo fa automaticamente il PC…

Possiamo perciò dire che il secondo sistema è quello realmente usato per i telescopi a montatura equatoriale, mentre le coordinate delle stelle “ufficiali”, date nei cataloghi, utilizzano il terzo sistema che è uguale per tutti. I PC svolgono il monotono lavoro di passaggio da ascensione retta ad angolo orario senza che l’operatore lo percepisca.

E’, quindi, estremamente importante saper passare dal secondo al terzo sistema (e viceversa) se non altro per capire cosa sta facendo il PC che rende tutto banalissimo…

Dal secondo al terzo sistema e viceversa

Questa volta i calcoli da eseguire sono estremamente semplici, dato che una coordinata (la declinazione) rimane quella che è, mentre l’altra (angolo orario o ascensione retta) si misura sullo stesso cerchio massimo della “compagna”. Ricapitolando: l’angolo orario si misura a partire dal punto intersezione tra meridiano ed equatore celeste (S), positivamente verso Ovest; l’ascensione retta si misura a partire dal punto γ positivamente verso Est. Dalla Fig. 10, risulta subito che:

ϑ = H + α   (ricordando che α si misura in senso opposto e quindi va veramente aggiunta per ottenere ϑ)

La semplicissima relazione permette di passare facilmente dal secondo al terzo sistema e viceversa, conoscendo il tempo siderale.

Capisco benissimo che le coordinate sferiche siano una cosa abbastanza “noiosa” e appaiano poco importanti per comprendere i misteri del Cosmo. Tuttavia, esse sono di fondamentale importanza per eseguire calcoli e trasformazioni tra le posizioni apparenti degli astri. E’ un po’ come se volessimo scrivere un grande romanzo, ma considerassimo inutile o quasi imparare l’alfabeto…

Il quarto sistema

Per cui vado avanti, comunque, e lascio un compito per tutti coloro che amano la trigonometria e vogliano capire sempre meglio come si possa lavorare su una superficie sferica. Ricordiamoci che la superficie sferica -e le sue regole- sono la base della Relatività Generale… Concludiamo la nostra trattazione con il quarto sistema di coordinate celesti, particolarmente usato per le posizioni dei corpi celesti “vagabondi”.

Abbiamo già introdotto il piano dell’eclittica e la sua intersezione con la sfera celeste. Questo cerchio massimo è di estrema importanza perché rappresenta il percorso apparente del Sole durante l’anno. Altrettanto importante è il nodo ascendente tra l’eclittica e l’equatore, il celeberrimo punto d’Ariete (γ), da cui si misura l’ascensione retta del terzo sistema.

Le coordinate del terzo sistema sono perfette per dare nome e cognome alle stelle “fisse” (o quasi). Sono coordinate “teoricamente” sempre uguali (a parte le variazioni dovute alle perturbazioni agenti su tempi scala molto lunghi, su tutte la precessione degli equinozi) che permettono di stabilire molto bene i movimenti propri delle stelle (anche loro si muovono sulla sfera celeste, anche se di poco) e la parallasse annua.

La seconda permette di determinare la distanza di stelle relativamente vicine; il moto proprio ci dice quali sono i movimenti reali tra stella e stella, che risentono della rotazione differenziale della galassia, ma anche della loro vicinanza: più una stella è vicina e più il suo movimento rispetto a  noi diventa importante e macroscopico.

Coordinate, quindi, molto utili per la carta d’identità, ma anche per valutare qualsiasi piccolo spostamento non sistematico tra noi e le stelle teoricamente fisse.

Questo sistema di coordinate può andare ancora bene per i pianeti e gli oggetti del Sistema Solare, ma i loro movimenti rispetto a noi sono decisamente più macroscopici, dato che  anch’essi orbitano attorno al Sole.

Risulta ovvio che se i pianeti orbitassero tutti sul piano orbitale della Terra, i loro moti si proietterebbero solo e soltanto sull’eclittica. In realtà non è proprio così, dato che le orbite sono inclinate rispetto alla nostra, a volte di poco (pianeti maggiori), a volte anche di molto (asteroidi, comete, oggetti Kuiper Belt, ecc.).

In ogni modo, è indubbio che l’eclittica risulti un piano di riferimento migliore dell’equatore. Poco importa, in fondo, che i pianeti descrivano traiettorie circolari come le stelle a causa della rotazione del nostro pianeta sul suo asse. Molto più importante, per loro, è sapere di quanto si muovano sulla sfera celeste da un giorno all’altro. Proprio questi movimenti hanno, per secoli e secoli, costretto gli astronomi a inventarsi traiettorie strane, come gli epicicli, per finire, finalmente, con la visione eliocentrica.

Per non farla troppo lunga, è importante, perciò, introdurre un sistema di coordinate che faccia riferimento all’eclittica, che, come sappiamo molto bene, forma un angolo ε “abbastanza” costante rispetto all’equatore terrestre, pari a circa 23.5°.

Ricordiamo anche che proprio l’eclittica definisce le costellazioni dello Zodiaco, ossia quei gruppi di stelle che si trovano attorno a lei, indipendentemente se siano realmente vicine oppure no. Dato che i pianeti si muovo lungo l’eclittica, spostandosi di poco verso l’alto o verso il basso, ecco che nasce una parte fondamentale dell’astrologia,  quella interessata alla posizione dei pianeti rispetto a queste costellazioni, variabile durante l’anno. A noi, però, questa parte interessa ben poco…

Bando alle ciance e veniamo al nostro sistema (Fig. 13).

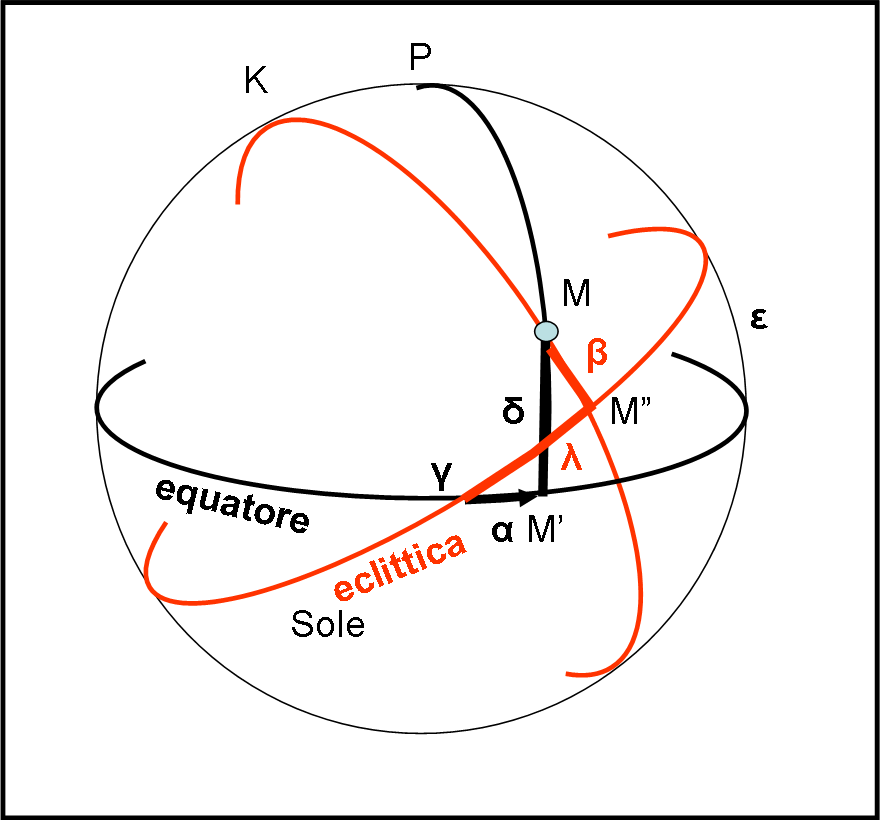
Il punto di riferimento lungo cui misurare gli archi di cerchio massimo dei pianeti lungo l’eclittica resta il punto γ, che può essere considerato fisso come fosse una vera stella. L’altro punto fondamentale, da cui far passare i cerchi massimi perpendicolari all’eclittica, è il polo dell’eclittica K. Ovviamente, l’angolo tra Polo Nord P e polo dell’eclittica K è ancora uguale a ε.

Tracciamo il cerchio massimo che passa per K e per l’oggetto M, fino a incontrare l’eclittica nel punto M”. La distanza in gradi, primi e secondi tra M” e M viene chiamata latitudine celeste e si indica con β. Essa è positiva sopra l’eclittica e negativa sotto. L’arco di eclittica tra il punto γ e il punto M”, anch’esso misurato in gradi, primi e secondi si chiama longitudine celeste e si indica con λ.

A questo punto, per permettervi di esercitarvi con la trigonometria sferica, lascio a voi le formule che permettono il passaggio tra il terzo e il quarto sistema e viceversa. Basta trovare il triangolo  da risolvere e poi tutto risulta un semplice lavoro di routine… Se proprio non ci riuscite e/o volete avere le formule, ditemelo e le inserirò qui di seguito...