Questo articolo è stato inserito nella pagina d'archivio dedicata a Matematica e Geometria e in Astronomia Classica

 

Iniziamo il nostro racconto con un gioco (se volete… chiamatelo pure un quiz ) che serve come porta d’ingresso  per  il nuovo teatro astronomico che andremo a scoprire tra poco.

Parto dal punto A. Cammino lungo una retta fino a B. Poi svolto di un angolo retto e proseguo ancora dritto fino a C. Infine giro di altri 90 gradi e proseguo ritrovandomi al punto di partenza A.

No, non sto dando i numeri… ci riesco facilmente, anche se la Fig. 1 sembra dire di no. Eppure il viaggio è svolto proprio nel nostro mondo, sulla Terra! Chiunque potrebbe farlo…

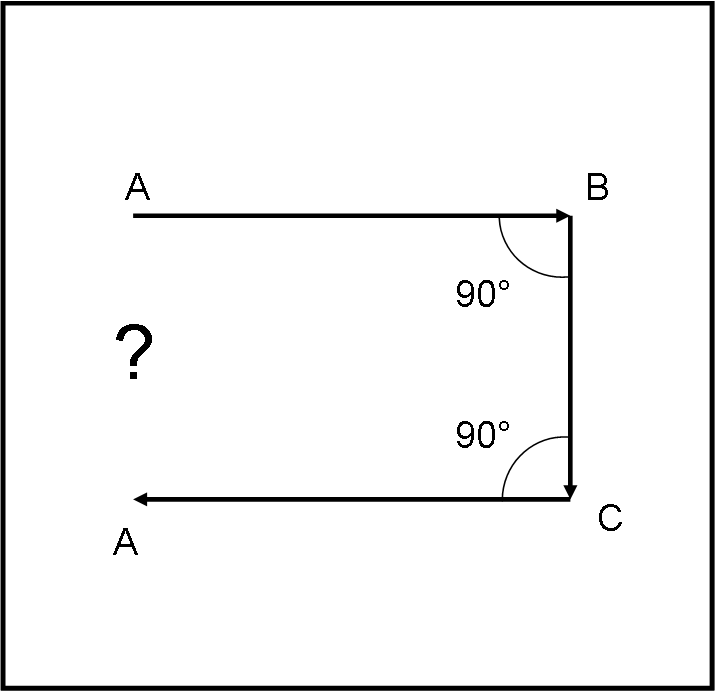
Vi sembra troppo corto? Dovrei camminare ancora un po'? Nemmeno per sogno, basta scegliere il giusto itinerario!

Ricordiamoci che una linea retta è una linea che non cambia mai direzione. Immaginate di usare una bici. Se vi sentite spostato un po’ a destra o un po’ a sinistra vuol dire che state curvando. Dovete sentirvi perfettamente verticale per essere sicuri di essere su una linea retta!

Sospendiamo lo strano viaggio e vedremo che piano piano si risolverà da solo...

Questo lungo articolo vuole essere l’introduzione necessaria per permetterci di descrivere il cielo stellato, le coordinate celesti e per passare da uno all'altro senza problemi (e senza bisogno di programmini pappa-pronta).. Tuttavia, è anche il primo passo verso uno spazio e addirittura uno spaziotempo curvo, base fondamentale per affrontare la Relatività Generale. Non perdetelo, perciò, anche se, a volte, apparirà un po' "pesante".

 

In realtà avevamo già iniziato in qualche modo con il doppio quiz sul programma "stellarium" che ci ha permesso di capire cosa significhi sfera celeste locale e come essa permetta di rappresentare il cielo stellato attraverso angoli e/o archi di cerchio (QUI,  QUI e QUI). Parlare di sfera celeste, però, introduce un “qualcosa” su cui non valgono più certe regole geometriche che siamo soliti usare sui nostri fogli di carta “piani”.

Possiamo riassumere il tutto con una frase alquanto curiosa: “Euclide ha creato la sua geometria proprio in un luogo dove la sua geometria non è applicabile!”.

La superficie della Terra non è un piano, ma una superficie sferica, dove NON VALE la geometria euclidea. Altrettanto possiamo dire della sfera celeste. E’ ora quindi che si prenda coscienza e dimestichezza con una geometria diversa, in grado di disegnare ed eseguire calcoli fondamentali sia per viaggiare sul nostro pianeta sia per utilizzare al meglio la volta celeste. Alcune cose rimarranno identiche, come i punti, ma altre, come le rette e i triangoli, non più.

Iniziamo quindi proprio con l’ABC e piano piano arriveremo a definire le figure geometriche su una superficie curva (e a capire lo strano viaggio iniziale), a introdurre i sistemi di coordinate celesti e a passare da uno all’altro attraverso una trigonometria leggermente diversa, ma non molto più complicata di quella piana.

Tutto ciò sembrerebbe non necessario, a prima vista. Dobbiamo, però, ricordare che l’uomo ha per molti secoli viaggiato solo su territori piccoli rispetto all’intero globo e poteva benissimo ridurre tutte le sue misure su un piano euclideo. E’ un po’ come se avesse potuto confondere un segmento con un arco di cerchio.  Non vogliamo ripassare tutti i principi euclidei, anche perché ci sarebbe da scrivere per pagine e pagine. Basta ricordarne uno: “due rette parallele non si incontrano mai” (a parte i punti all’infinito, ma questa è tutta un’altra storia e ne abbiamo parlato nelle prime lezioni sulla Matematica).Bene, sulla superficie terrestre questo non è più vero, dato che le “sue” rette sono obbligate a incontrarsi.

Queste considerazioni sono vere e già abbastanza sconvolgenti lavorando su superfici curve (spazi a due dimensioni). Si capisce molto bene che se non facciamo nostri i concetti legati a una superficie, sarà impossibile affrontare, con le giuste basi, la Relatività Generale, dove le masse curvano proprio uno spaziotempo a quattro dimensioni. Per capire esattamente come si comporti uno spaziotempo curvo è fondamentale abbandonare Euclide e i suoi principi e immergerci in un mondo che, un po’ alla volta, ci apparirà addirittura più elegante di quello in cui abbiamo sempre pensato di vivere.

Trasferiamoci quindi su una sfera. In particolare su una superficie sferica. Attenzione, però. Come gli abitanti di Flatlandia, noi saremmo obbligati a vivere e a descrivere ciò che accade senza sapere cosa sia veramente una figura a tre dimensioni come la sfera. Tuttavia, per comprendere meglio cosa pensino e come agiscano gli abitanti delle due dimensioni, manterremo la possibilità di guardare il tutto dal di fuori, ossia attraverso una terza dimensione (i soliti raccomandati…).

In altre parole, confronteremo spesso la visione intrinseca di chi vive all’interno con quella estrinseca, osservata da chi ha il vantaggio di potersi spostare in una dimensione aggiuntiva.

Per la sfera celeste e per l’astronomia di base tutto corre abbastanza bene, dovendo passare da due a tre dimensioni (e questo lo sappiamo fare  con facilità). Ben più arduo sarà, a suo tempo, descrivere le cose in uno spaziotempo a quattro dimensioni (definito dalla relatività ristretta), quando non avremo più la possibilità di aggiungere una nuova dimensione; dovremo cavarcela solo attraverso una visione intrinseca con l’aggiunta di ragionamenti generali acquisiti attraverso l’esperienza fatta  passando dalle due alle tre dimensioni.

Bando alle ciance e cominciamo dalla prima elementare di un abitante di una superficie sferica…

Vivendo su una sfera

Normalmente, per definire la geometria che regola una superficie sferica, si usa mischiare visione intrinseca ed estrinseca. Noi, invece, proviamo a usare le due visioni in modo separato, cercando così di entrare più a fondo nei concetti fondamentali e prepararci a quando non sarà più possibile “salire” di una dimensione. Le uniche cose che prendiamo in prestito dalle tre dimensioni sono le figure della superficie sferica. Esse, però, sono descritte da un abitante di questo strano mondo a due dimensioni. In altre parole, non sappiamo assolutamente quello che vi è all’interno della superficie sferica e tanto meno quello che vi è al di fuori.

Immaginiamo, allora, di vivere su una superficie sferica (spazio curvo a due dimensioni) e di cercare di comprenderne i segreti. Questo modo di procedere lo chiamiamo intrinseco, dato che possiamo vederlo e descriverlo solo dall’interno. Ovviamente, anche noi dovremmo avere solo due dimensioni, ma ogni tanto ci permetteremo qualche piccola licenza, per spiegare meglio la situazione. Ammettiamo, anche, che i nostri geometri bidimensionali conoscano abbastanza bene la geometria del piano euclideo.

Per prima cosa vogliamo muoverci in linea retta, Come possiamo essere sicuri di farlo?

Riprendiamo una delle tante definizione di retta del mondo piano a due dimensioni: “una linea che non cambia mai direzione”.

Per vederlo in modo immediato e pratico consideriamo la Fig. 1, dove utilizziamo un carrello a due ruote.

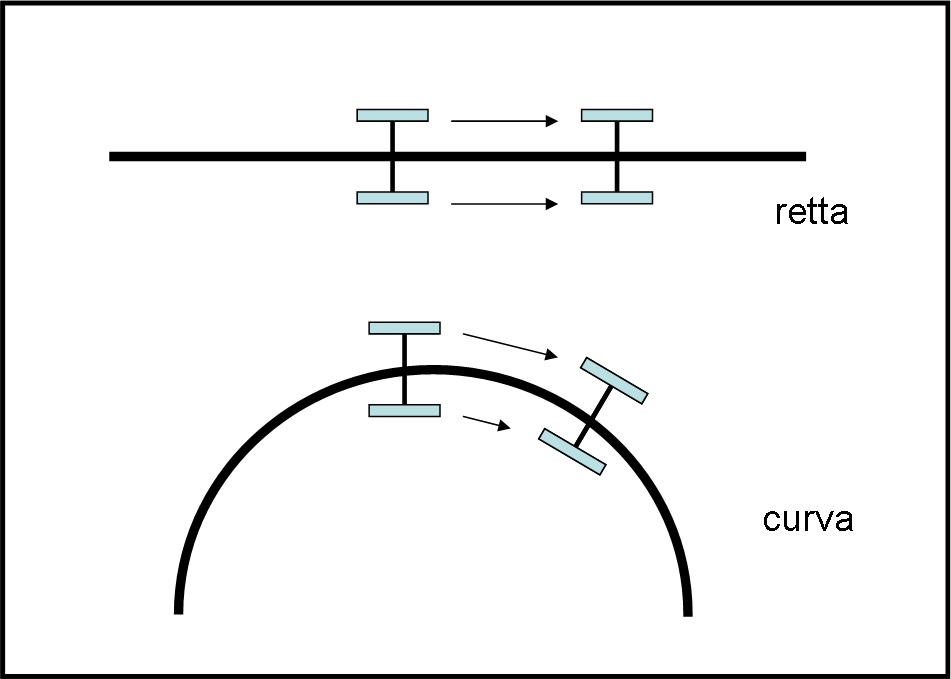
Cominciamo con il provarlo su un piano (spazio a due dimensioni euclideo). Le ruote, per la loro forma, dovrebbero già introdurre una dimensione in più, ma noi immaginiamo che siano piccolissime, praticamente piatte o microscopiche…

Come facciamo a riconoscere se il carrello va dritto o curva? Basta vedere lo spazio percorso dalle due ruote. Se la traiettoria è rettilinea le due ruote descrivono lo stesso percorso. Se, invece, la linea è curva (ossia cambia direzione in modo più o meno costante) una delle due ruote è costretta a compiere un tragitto maggiore dell’altra.

Prendiamo adesso due punti A e B su una retta. La distanza minima è il segmento rettilineo AB. Qualsiasi altra linea che congiunga A e B è sicuramente più lunga. Insomma, per seguire il percorso minimo dobbiamo muoverci su una retta. Una linea di questo tipo viene chiamata geodetica, ossia la traiettoria più corta che unisce due punti.

Possiamo stabilire una facile regola per dimostrarlo, disegnando la Fig. 2, dove come linee curve abbiamo solo utilizzato circonferenze (ma le cose non cambierebbero usando qualsiasi altra curva).

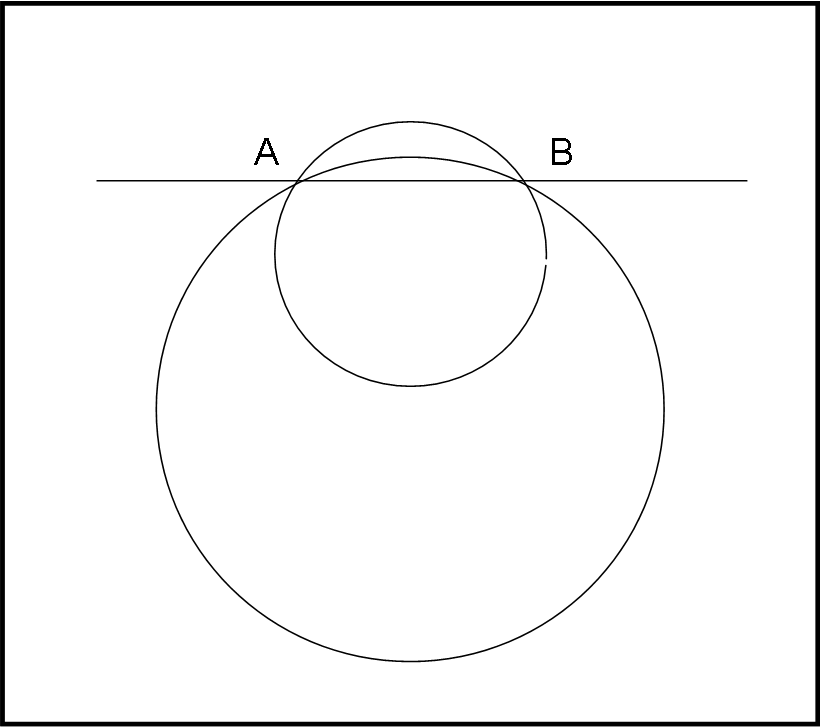
Notiamo che più la circonferenza che passa per A e B rimpicciolisce (raggio minore), maggiore diventa la distanza da percorrere per andare da A e B. In altre parole, una distanza maggiore è legata a un raggio minore. Definiamo curvatura di una circonferenza l’inverso del suo raggio, ossia 1/r. Bene, risulta ovvio che la distanza minima corrisponde alla circonferenza che ha il raggio più grande. Sul piano il raggio può essere anche INFINITO. In tal caso la curvatura 1/r è uguale a zero e cadiamo nel caso della retta. Posiamo, perciò concludere che la distanza minima si misura lungo la circonferenza che ha la curvatura minore, ossia lungo una retta.

Portiamoci adesso su una superficie sferica, senza possibilità di vederla dal di fuori. Esistono delle rette su di lei? Beh… se definiamo una retta un qualcosa che non cambia mai direzione potremmo tranquillamente utilizzare il solito carrello a due ruote, stando attenti a come girano. Mostriamo ciò che otteniamo in Fig. 3.

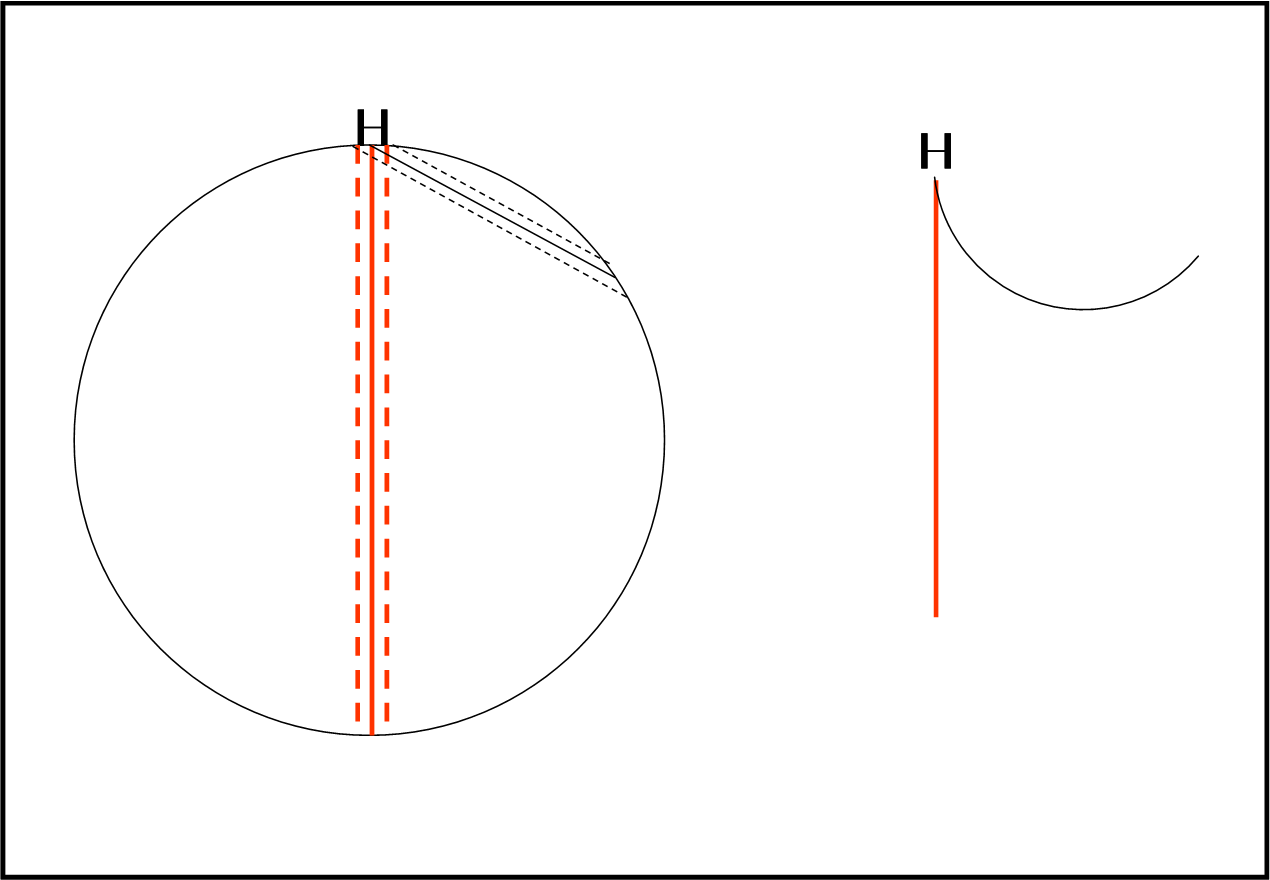
A sinistra vediamo la situazione dal di fuori. Risulta chiaro che se il carrello percorre la linea verticale esso si muove in linea retta, mentre se descrive la linea verso destra le ruote compiono percorsi diversi, quindi, il carrello descrive una curva. La visione intrinseca è quella della parte destra della figura. In altre parole, questa parte è quella che riusciamo a descrivere vivendo sulla superficie sferica. Possiamo concludere che esiste una retta e che esiste una curva. Queste due linee sono intrinseche, ossia dedotte da chi abita nelle due dimensioni. Chiamiamole retta e circonferenza intrinseche.

La faccenda funziona perfettamente, tranne un piccolo problema: pur non piegando mai, percorrendo la retta, ci ritroviamo al punto di partenza! Potremmo anche non accorgercene, ma se abbiamo usato una bandierina o qualche altro segnale, possiamo effettivamente rendercene conto. In fondo, però, ci interessa poco se nel nostro spazio a due dimensioni le rette sono traiettorie chiuse. Come nel piano, possiamo partire da qualsiasi punto della superficie e vi è sempre un retta che passa per quel punto. Anzi, ce ne sono infinite. Analogamente, se prendiamo due punti qualsiasi (che non siano agli antipodi), per loro passa una e una sola retta.

Non è difficile verificare che queste strane “circonferenze”, che chiamiamo, comunque, rette intrinseche (e lo sono a tutti gli effetti per noi), sono quelle più lunghe tracciabili sulla superficie e sono tutte della stessa lunghezza.

Per farlo, basta munirsi di una lunga fune e di fissarla in un qualsiasi punto della superficie, ad esempio P, come mostrato in Fig. 4 (a sinistra la visione da fuori).

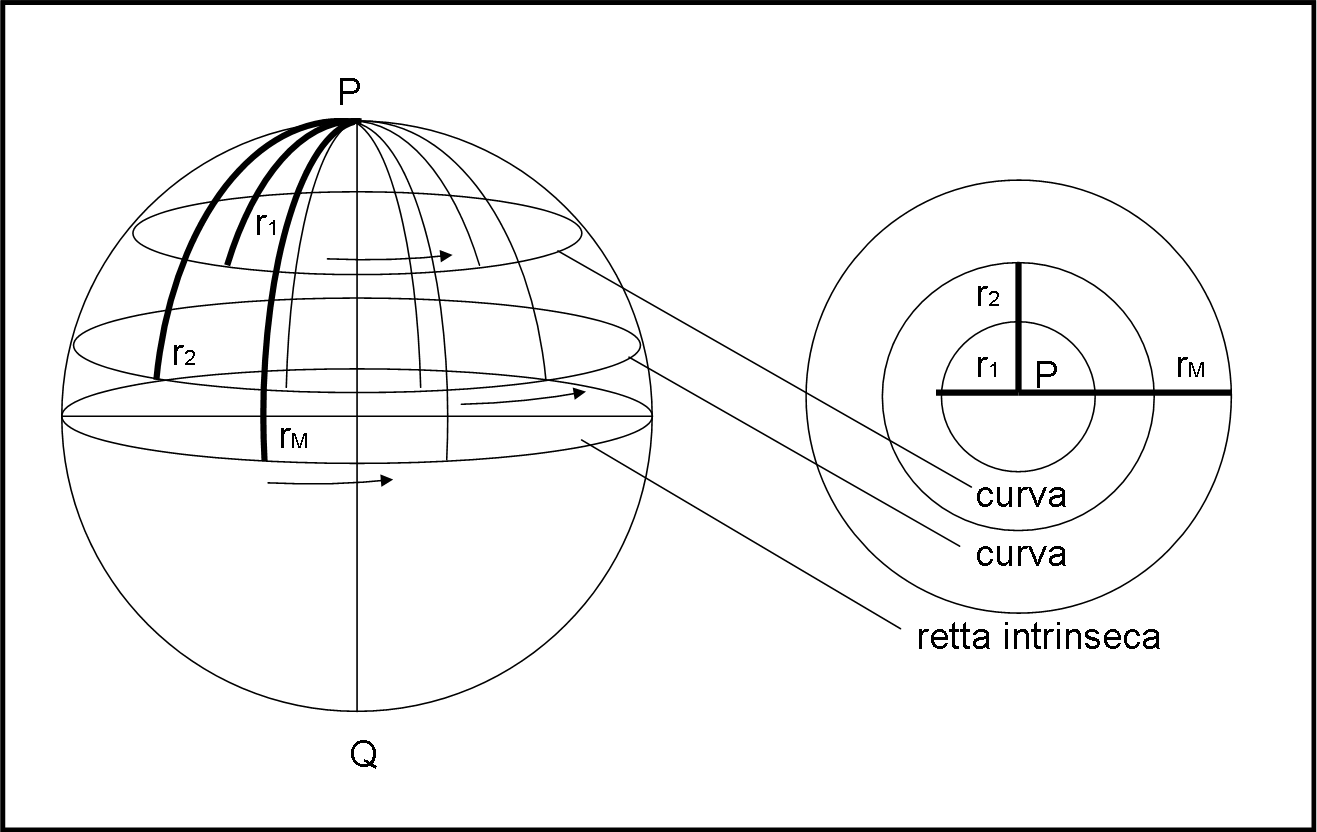
Teniamola ben tesa con una lunghezza uguale a r₁ e cominciamo a camminare (magari anche con il carrello per ulteriore conferma). Descriviamo una certa circonferenza che ha come raggio intrinseco (distanza tra circonferenza e punto P) proprio r₁. Il carrello ci conferma che è proprio una circonferenza intrinseca. Aumentiamo la lunghezza della corda fino a farla diventare r₂ e rifacciamo lo stesso esercizio, costruendo la circonferenza intrinseca di raggio intrinseco r₂. La circonferenza è più lunga di quella precedente. Proseguiamo fino a una certa lunghezza della corda r_M. Questa volta le cose cambiano e il carrello ci dimostra che stiamo percorrendo una retta intrinseca (anche se l’abbiamo disegnata come una circonferenza, dato che sappiamo che è una retta ma che è anche una curva chiusa).

Studiando meglio la situazione vediamo che la distanza tra P e la circonferenza, ossia r_M, è esattamente uguale alla distanza tra essa e il punto opposto di P, ossia Q (punto opposto di un punto è quel punto che sta proprio alla metà della retta intrinseca che passa da P e da Q, ossia la circonferenza sul piano del nostro foglio, a sinistra).

A questo punto, per puro scrupolo, ci possiamo portare su Q e rifare lo stesso lavoro fatto partendo da P. Il risultato è, ovviamente, identico a prima: la circonferenza che ha una lunghezza massima è quella con raggio intrinseco r_M, ossia la retta intrinseca (chiedete al carrello).

Notiamo anche che cambiando il punto P (e Q) possiamo descrivere tutte le rette e le circonferenze intrinseche della superficie.

L’esercizio appena svolto ci ha dimostrato che la lunghezza della retta intrinseca è la massima possibile e che, ovviamente,  il raggio intrinseco della retta (che è anche la circonferenza massima) è il più grande.

Il che vuol dire che qualsiasi circonferenza intrinseca tracciata sulla superficie ha lunghezza e raggio r minore di r_M.

Siamo di fronte a una situazione da un lato abbastanza imbarazzante, ma dall’altro molto elegante!

La retta è per noi un caso particolare di circonferenza, che mostra tutte le caratteristiche di non “piegare” mai. In fondo, non è una curva intrinseca (avrebbe tutte le caratteristiche della retta se non la percorressimo tutta o non mettessimo un segnale per riconoscere da dove siamo partiti). Tuttavia, per un abitante molto attento la sua vera struttura potrebbe anche essere riconosciuta.

Andiamo ancora oltre, rimanendo sempre sulla superficie (che fatica per noi che siamo tridimensionali…). Mettiamoci lungo una retta intrinseca dello spazio curvo a due dimensioni e disegniamo due punti A e B su di lei in Fig. 5 (a sinistra).

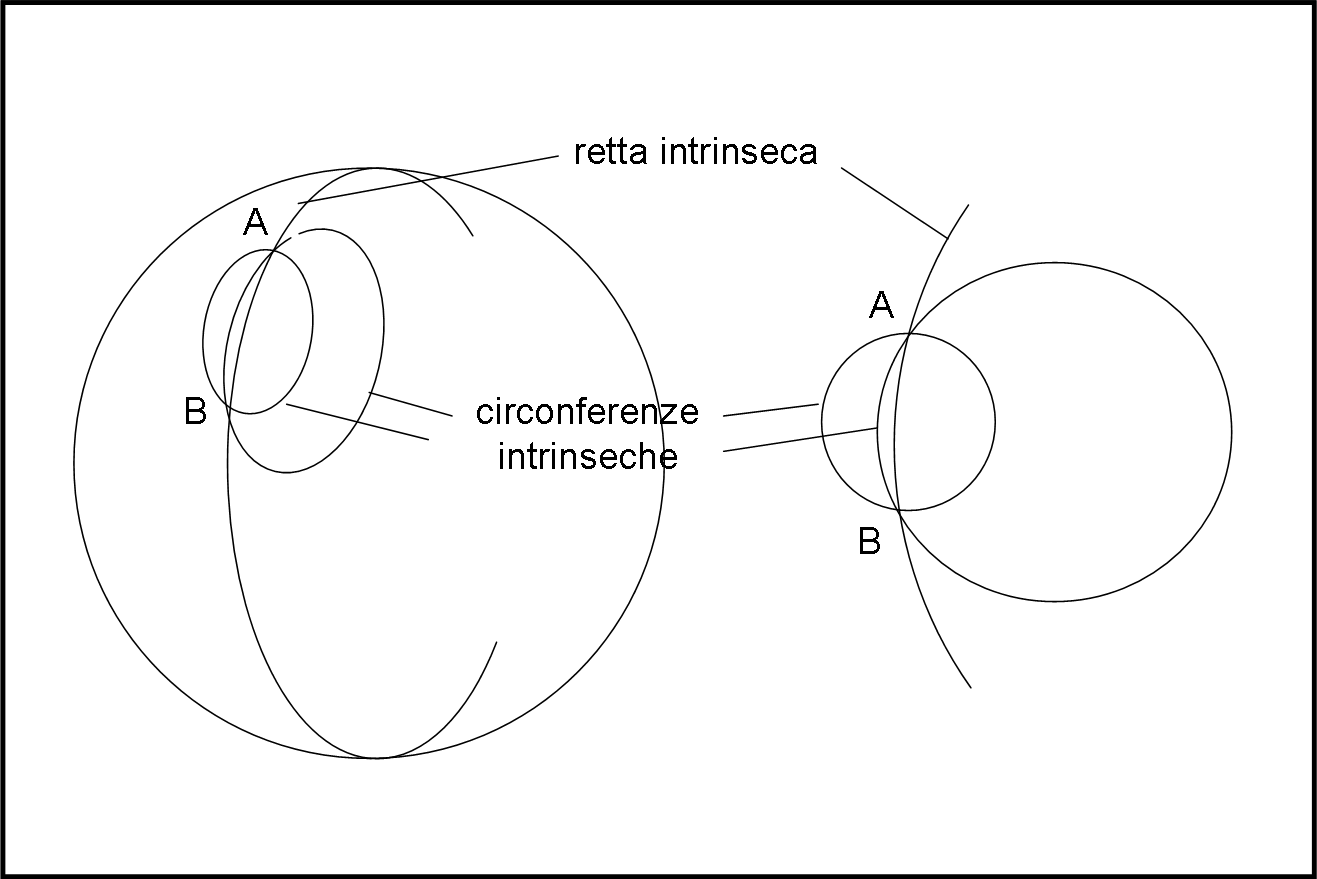
Adesso, possiamo provare ad andare da A a B in tutti i modi possibili, ossia seguendo altre linee, magari proprio archi di circonferenza come avevamo fatto nel piano. Possiamo sbizzarrirci quanto vogliamo, ma il risultato dovremmo già saperlo. La retta intrinseca è quella che ha il perimetro più lungo e quindi anche il raggio più grande. L’unica differenza, rispetto alla superficie piana, è che il raggio può diventare al massimo r_M e non infinito.

Tuttavia, essa rimane comunque la traiettoria con la curvatura minore tra tutte quelle possibili. Per analogia con quanto succede nel piano essa deve perciò fornire la traiettoria minima per andare da A a B. la retta intrinseca è una geodetica della superficie sferica. Una visione più intrinseca la vediamo nella parte destra della figura.

Abbiamo faticato un po’ e abbiamo forzato alcuni concetti per riuscire a dimostrare alcune caratteristiche essenziali della geometria sferica senza sfruttare la nostra capacità di avere una dimensione in più. Al limite, ci siamo fidati dell’intelligenza degli abitanti di “sferilandia” e della loro conoscenza delle regole euclidee.

Tutto diventa più semplice utilizzando una visione estrinseca. Tuttavia, aver lavorato solo su uno spazio a due dimensioni non euclideo (a parte le figure) ci ha sicuramente fatto entrare meglio nella problematica.

Alziamoci in volo e guardiamo dentro

Per vedere i risultati ottenuti precedentemente, basta utilizzare una visione dall’esterno, immergendo la superficie sferica in uno spazio a tre dimensioni. Non solo la vediamo, però, ma possiamo manovrare a nostro piacimento altre superfici, come ad esempio i piani. In particolare, siamo in grado di descrivere perfettamente cosa avviene all’interno della superficie sferica, cosa del tutto vietata agli abitanti di sferilandia.

Tagliamo, subito, la sfera con un piano che non passa per il suo centro (lo possiamo fare dato che VEDIAMO il centro della sfera) e otteniamo una circonferenza in cui le due ruote del carrello girano in modo diverso. Bene. Le circonferenze così costruite sono curve sia intrinseche che estrinseche. Ossia esse sono curve sia per chi abita sulla sfera sia per chi vede la sfera da fuori. Chiamiamole cerchi minori.

Prendiamo meglio la mira e utilizziamo un piano che contenga il centro della sfera. E’ immediato comprendere che l’intersezione è ancora una circonferenza, ma questa volta è proprio la linea che abbiamo chiamato geodetica e che non ha curvatura per il carrello che la percorre. Essa è proprio un cerchio massimo. Per chi abita sulla sfera essa non è una circonferenza ma una retta intrinseca (a meno che non sia molto intelligente e si dedichi a un suo studio accurato come abbiamo fatto noi la volta scorsa). L’abitante “medio” della superficie sferica, definisce rette i cerchi massimi, mentre definisce cerchi tutte le intersezioni con piani non passanti per il centro. Per noi che vediamo il tutto da fuori sia i cerchi massimi che quelli minori sono entrambi delle curve. Ne segue che entrambi sono curve estrinseche.

Volendo si può nuovamente dimostrare, ancora più facilmente della volta scorsa, che il cerchio massimo è quello che descrive la minima distanza tra due punti della superficie sferica. Prendiamo due punti qualsiasi e tracciamo la retta (estrinseca) che li congiunge.

A questo punto consideriamo un piano che contiene questa retta. La sua intersezione con la superficie sferica è una circonferenza che deve passare sia per A che per B (per costruzione). Facciamo ruotare il piano attorno alla retta AB e abbiamo infinite circonferenze di raggio sempre diverso. Basta rappresentare tutte queste circonferenze su un piano e si vede immediatamente che la circonferenza di minima curvatura è proprio quella che ha il raggio uguale a quello della sfera, ossia che passa per il suo centro. Questa circonferenza è anche unica.

Ne segue che la distanza minima tra A e B viene misurata lungo un cerchio massimo e che esiste solo un cerchio massimo che passa per due punti, proprio come capita per una retta nella geometria euclidea. Si potrebbe anche fare una figura attraverso un programma raffinato e a questo punto avrebbe senso (come mostrato da Arturo Lorenzo nei commenti al quiz (QUI))

Ribadiamo ancora l’eleganza dello spazio sferico. Nello spazio euclideo rette e circonferenze sono due entità geometriche diverse (a parte il considerare un raggio infinito), mentre in quello sferico le rette sono particolari circonferenze, descrivibili con parametri finiti

A costo di essere pedante, fatemi ancora ripetere un concetto importante da non dimenticare mai nella trattazione della geometria sferica: le sue rette sono i cerchi massimi, ossia le intersezioni con qualsiasi piano passante per il centro e la superficie sferica. Sopra di loro si misurano le distanze minime tra due punti.  Le rette della superficie sferica non sono illimitate, dato che sono circonferenze, ma, a parte questo, i cerchi massimi possono essere considerati a tutti gli effetti l’equivalente della retta. Ricordiamolo molto bene!

Vediamo, in Fig. 6, una conseguenza IMPORTANTISSIMA di quanto appena detto. A destra abbiamo un triangolo APB che giace sul piano della figura. I suoi lati sono ovviamente segmenti di retta. Se considerassimo la figura PCD, con CD curvilineo, NON avremmo un triangolo, ma, ad esempio, un settore di cerchio o anche qualcosa di più complicato. Una conclusione analoga succede sulla superficie sferica, a sinistra. Un triangolo sferico deve avere dei lati intrinsecamente rettilinei, ossia archi di cerchi massimi. Ne segue che la figura PAB è un vero triangolo sferico (i suoi lati sono segmenti rettilinei intrinseci), mentre la figura PCD non è un triangolo, dato che CD è un tratto di circonferenza intrinseca, appartenendo a un cerchio minore.

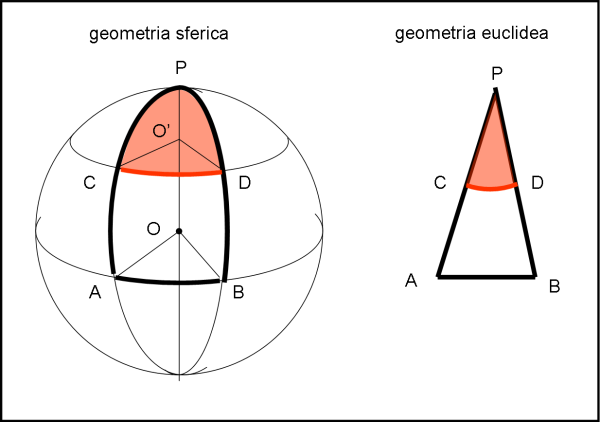
Quanto appena detto risponde in parte al quiz iniziale: qualsiasi percorso lungo un cerchio minore non può appartenere a un triangolo sferico. Per completare la soluzione ci serve, però, qualche altra considerazione che vedremo più in là.

Possiamo notare attraverso la Fig. 7, un’altra conseguenza da non dimenticare mai: la distanza minima tra due punti della superficie sferica viene descritta dal cerchio massimo che unisce i due punti, dato che rappresenta una geodetica, ossia il segmento intrinsecamente rettilineo. Qualsiasi altro cerchio minore che li congiunga è sicuramente più lungo, avendo una curvatura maggiore.

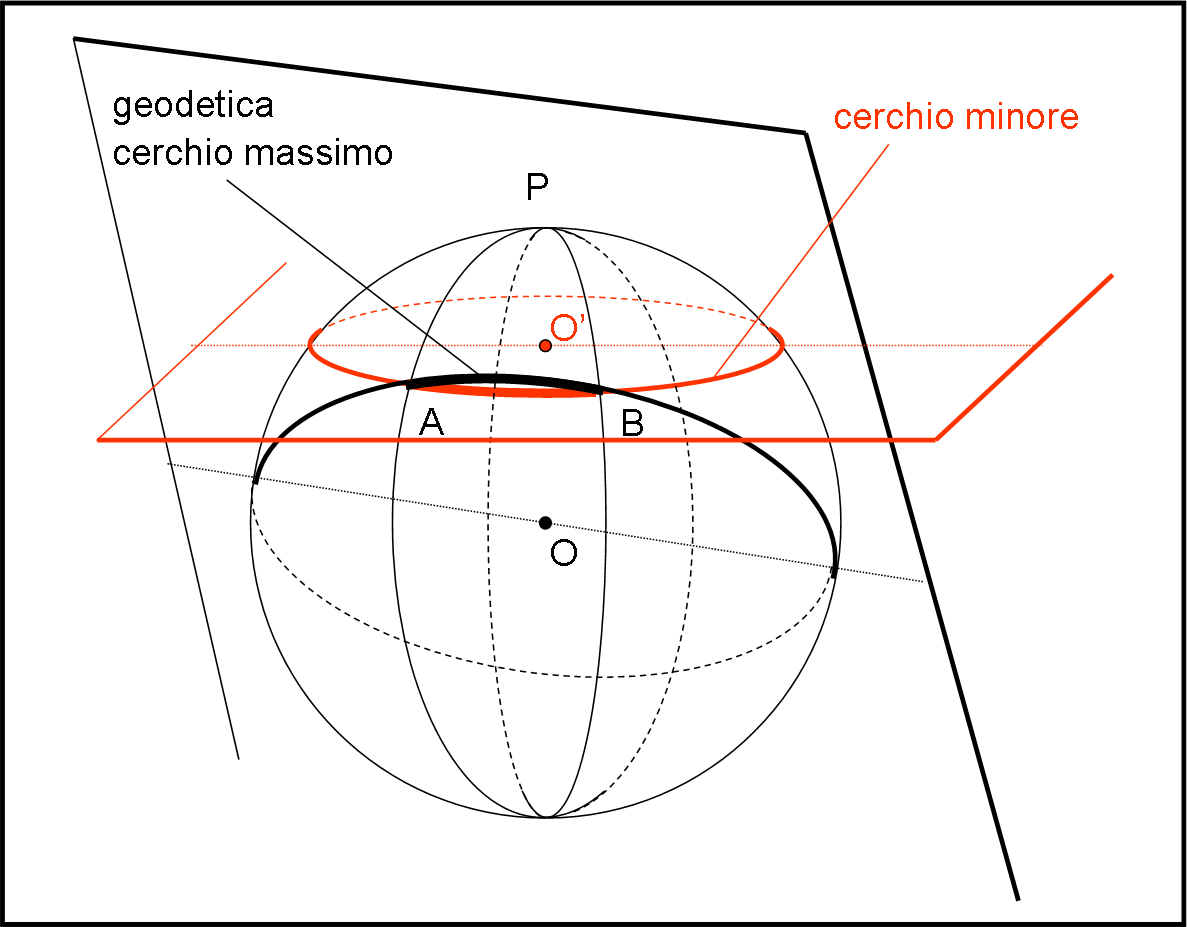
Abbiamo deciso di utilizzare la nostra capacità di vedere una superficie sferica in tre dimensioni e allora diamoci dentro, scoprendo un mucchio di cose veramente interessanti.

Tanto per cominciare partiamo dalla definizione di lato di un triangolo sferico. Poi passeremo ai suoi angoli.

Mettiamo, innanzitutto, in rilievo la differenza tra raggio di una circonferenza misurato sulla superficie sferica (intrinseco) e quello della stessa circonferenza misurato nello spazio con una dimensione in più (estrinseco). Vediamolo subito nella Fig. 8.

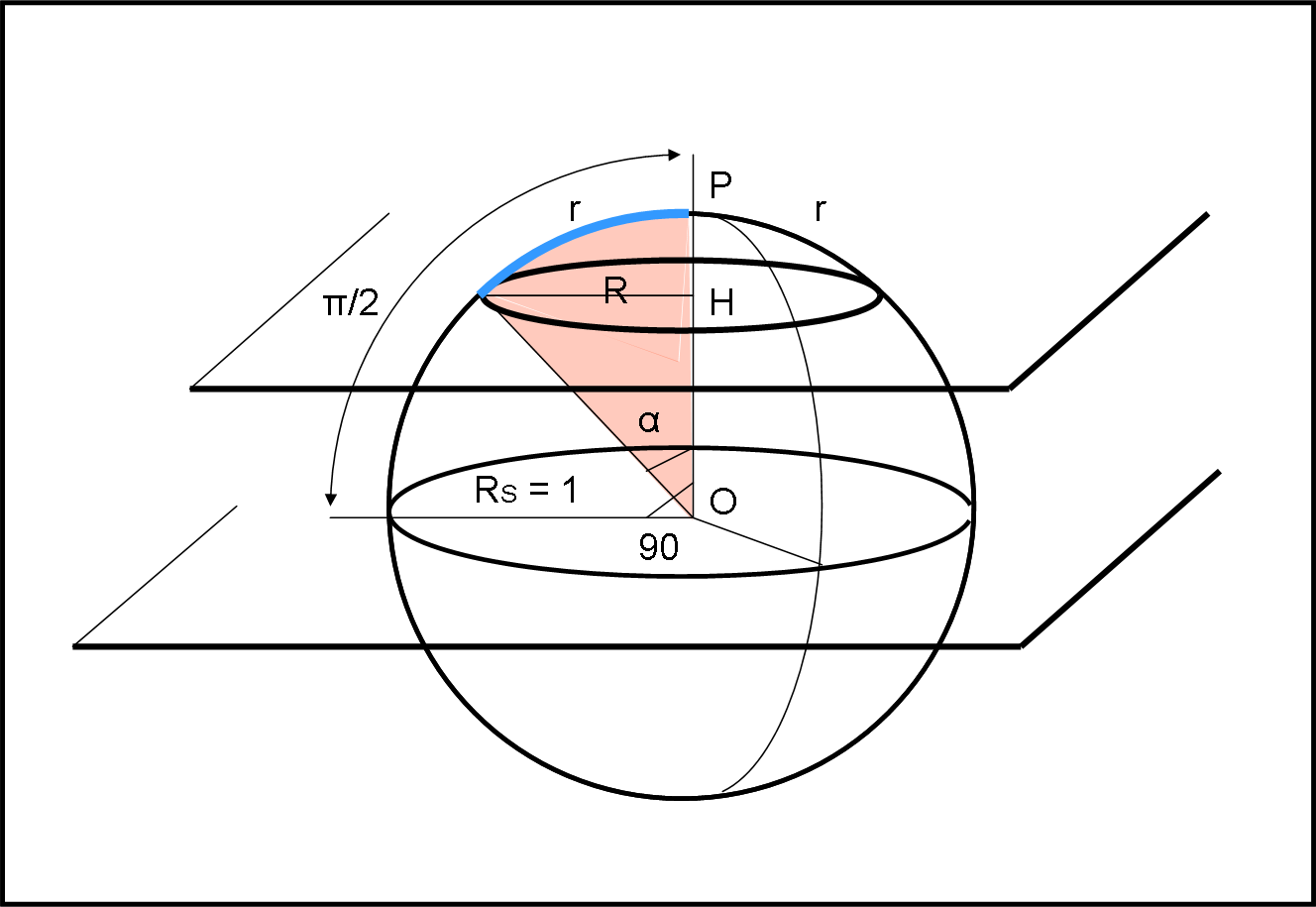
Per chi vive nel mondo sferico (sulla superficie) il raggio del cerchio, in alto, è r. Ma per chi può vedere la superficie dal di fuori, la stessa circonferenza ha un raggio nettamente minore, uguale a R. Ovviamente R esiste solo nel mondo a tre dimensioni e non può essere misurato direttamente da che vive sulla superficie sferica.

La relazione tra i due raggi è banale, considerando, oltretutto, il raggio della sfera R_S uguale all’unità (come faremo sempre con la sfera celeste).

Abbiamo:

R = sin α

Vale, però, la proporzione:

r : 2π R_S= α : 360

r : 2π = α : 360

esprimendo α in radianti, abbiamo:

r : 2π = α : 2π

r = α                                        …. (1)

Da cui si può scrivere che

R = sin r

La banale relazione (1) è fondamentale nella sfera celeste in quanto definisce la misura di un arco di cerchio massimo, proprio ciò che diventa un lato di un triangolo sferico.

Anche il cerchio massimo può essere espresso in questi termini: il suo raggio intrinseco è uguale a π/2, mentre quello estrinseco è uguale a R_S = 1

Infatti, come dice la (1), abbiamo proprio

R_S = sin(π/2) = 1

Le “rette” intrinseche della superficie sferica sono le circonferenze di raggio intrinseco uguale a π/2, che corrispondono a un raggio estrinseco uguale all’unità. In altre parole, l’arco di cerchio massimo corrispondente a un angolo al centro di 90° è proprio uguale a π/2

Torniamo ai nostri triangoli sferici, ribadendo ancora il concetto base, ricordandoci che:

un triangolo piano è formato da tre lati che sono dei segmenti rettilinei. Nel caso del triangolo sferico abbiamo, perciò, bisogno di tre segmenti di retta, ma le rette sono i cerchi massimi, e allora possiamo concludere che un triangolo sferico ha per lati tre segmenti di cerchio massimo (ovviamente minori di π).

Come si calcolino i segmenti di cerchio massimo l’abbiamo appena visto: essi non sono altro che gli archi di cerchio massimo, espressi in radianti, corrispondenti a un certo angolo al centro.

Possiamo perciò dire, per definizione di cerchio massimo, che:

 i triangoli sferici sono i triangoli generati sulla sfera dall’intersezione di 3 piani passanti per il centro della sfera stessa

ATTENZIONE: Chiediamoci sempre, prima di applicare le formule di trigonometria sferica che descriveremo di volta in volta, se i lati del triangolo che stiamo considerando sono realmente archi di cerchio massimo e non archi di cerchio minore. Se anche un solo lato non fosse arco di cerchio massimo, le formule non varrebbero più ed è come se volessimo applicare le formule euclidee relative a un triangolo piano, a una figura che ha un lato curvilineo.

Prima di concludere questa prima parte, pensate alle traiettorie degli aerei che sembrano percorre archi di cerchio lunghissimi per unire due città che sembrano molto più vicine se raggiunte attraverso una retta. Ebbene, l’apparenza inganna, dato che sulla cartina di volo si rappresenta la superficie sferica come un piano (i paralleli che non sono cerchi massimi sono spesso disegnati rettilinei) e quindi le vere distanza sono trasformate. La linea apparentemente curva è proprio la più breve.

Una cosa simile capita in uno spazio a tre o quattro dimensioni curvo, dove il percorso minimo non corrisponde alla nostra retta piana. Ed ecco servita su un piatto d’argento la relatività generale…

Scusate se sono stato ripetitivo e assillante, ma per poter utilizzare al meglio la trigonometria sferica è essenziale non confondere i veri triangoli sferici con i triangoli solo “apparenti”.

Bene. Abbiamo definito i lati di un triangolo sferico. Non ci resta che definirne anche gli angoli e poi, con calma, potremo divertirci con la trigonometria sferica…

Misurare gli angoli su sferilandia

Definiti i lati di un triangolo sferico, non ci resta che definire quali siano i suoi angoli. Nel fare questo, risolviamo il vecchio quiz e stabiliamo anche un’altra proprietà molto interessante dei triangoli sferici. Concludiamo con due nuovi quiz, che saranno risolti successivamente.

Per un abitante della superficie sferica, il problema di definire un angolo sulla sua superficie non è certo irrisolvibile. Lui può girare su stesso fino a ritrovarsi nella stessa direzione di partenza. Questa azione gli dice di avere descritto un angolo di 360°. Può, perciò, valutare a quale rotazione corrisponde un grado. Tracciando due rette intrinseche, è allora facile per lui calcolare quanti gradi sono contenuti in uno dei quattro angoli che le due rette definiscono, come rappresentato in Fig. 9, a sinistra.

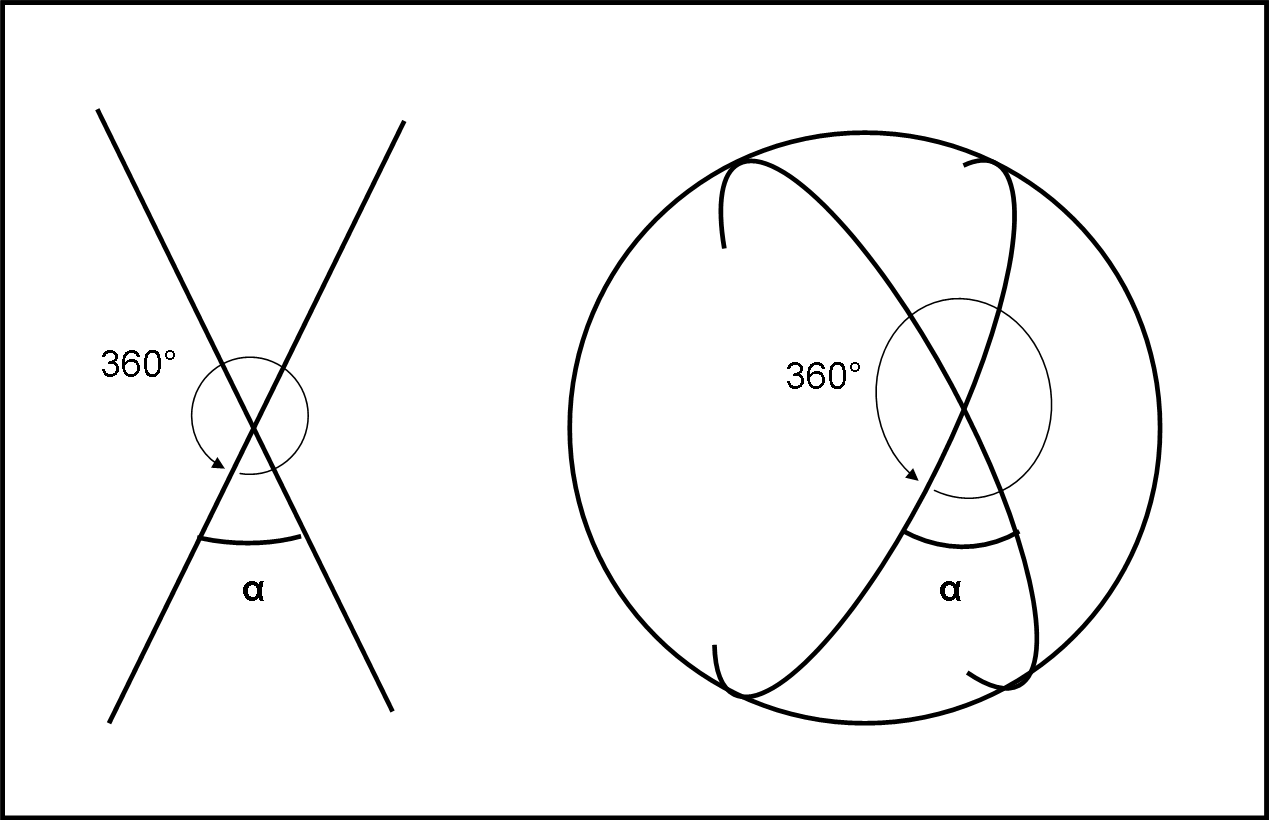
A destra della stessa figura, vediamo come questa descrizione intrinseca venga vista dal “di fuori” (visione estrinseca). Notiamo, ovviamente, che le rette non sono altro che cerchi massimi.

Per noi abitanti delle tre dimensioni, però, questo sistema per misurare gli angoli sulla superficie sferica diventa un po’ troppo macchinosa e, approfittando della nostra capacità di osservare dall’alto e di potere usare enti geometrici che gli abitanti di sferilandia non possono nemmeno intuire, possiamo definire gli angoli sferici in modo molto più immediato e utile per i futuri calcoli, così come abbiamo fatto per gli archi di cerchio massimo (ossia i lati intrinsechi).

Sappiamo perfettamente che un angolo sferico deve essere compreso tra due cerchi massimi, che si ottengono tagliando la sfera con due piani. Basta allora definire come angolo sferico l’angolo formato dalle tangenti ai due cerchi massimi nel vertice considerato. Sostituiamo, all’angolo misurato sulla superficie, un angolo compreso tra dure rette vere e proprie dello spazio tridimensionale. Vediamo la semplice costruzione nella Fig. 10.

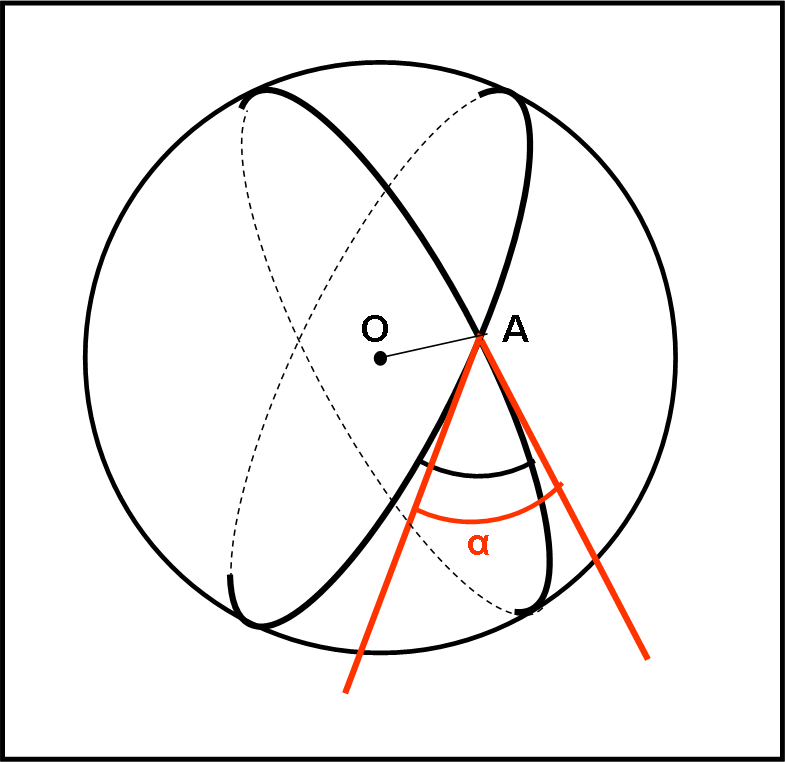
Utilizziamo anche un’altra definizione. Anche se non abbiamo ancora trattato la geometria tridimensionale e i suoi abitanti, come piani, sfere, rette, ecc. (lo sta facendo Arturo, QUI), possiamo facilmente definire un angolo tra due piani, chiamato angolo diedro. Esso esiste sempre quando i piani non sono paralleli e, quindi si incontrano lungo una retta. Bene, l’angolo diedro è quello formato da due rette perpendicolari alla retta comune e appartenenti ai due piani, come mostra la Fig. 11.

O, se preferite, possiamo considerare un terzo piano perpendicolare alla retta comune e definire come angolo diedro l’angolo formato dalle due rette intersezione di questo piano con quelli originali. L’angolo sferico è proprio l’angolo diedro tra i due piani contenenti i due cerchi massimi. Se ci riflettiamo un attimo ci accorgiamo di aver detto la stessa cosa con parole diverse.

Scegliendo la definizione che preferiamo (io penso sia meglio parlare di tangenti ai cerchi massimi, che, come tali devono appartenere ai piani dei cerchi massimi), si è facilmente risolta anche la questione degli angoli. Siamo ora in grado di lavorare con i triangoli sferici, conoscendo perfettamente i parametri che li caratterizzano. Parametri che, in qualche modo, si rifanno sempre al centro della sfera. In altre parole, dopo aver conosciuto e compreso la visione intrinseca, lavoriamo, d’ora in poi, solo con la visione estrinseca, decisamente più facile.

Ah… come sarebbe bello fare lo stesso con uno spazio a tre dimensioni o con uno spaziotempo a quattro dimensioni!

Accontentiamoci e prepariamoci psicologicamente a "divertirci" con le funzioni trigonometriche.

Qualcuno potrebbe dire: “Accidenti, andava tanto bene così… senza formule…”. Purtroppo, per introdurre le coordinate sferiche e i passaggi da un sistema all’altro abbiamo bisogno di legare tra loro i vari parametri e questo si può fare solo con le funzioni trigonometriche. Forza e coraggio… non ce ne pentiremo!

Prima di andare avanti, però, è giusto dare la risposta al quiz  iniziale che aspetta una risposta da tanto tempo. E’ ormai chiaro che per potere tornare al punto di partenza, con due sole deviazioni di 90°, non possiamo che essere su una superficie sferica. Tuttavia, abbiamo anche capito che dobbiamo muoverci lungo i lati di un triangolo sferico, trascurando qualsiasi curva intrinseca che sembrerebbe utilizzabile. Se è curva intrinseca non avremmo più un percorso lungo segmenti rettilinei!

Disegniamo la Fig. 12, che spiega tutto e che ci fa conoscere un’altra caratteristica fondamentale dei triangoli sferici.

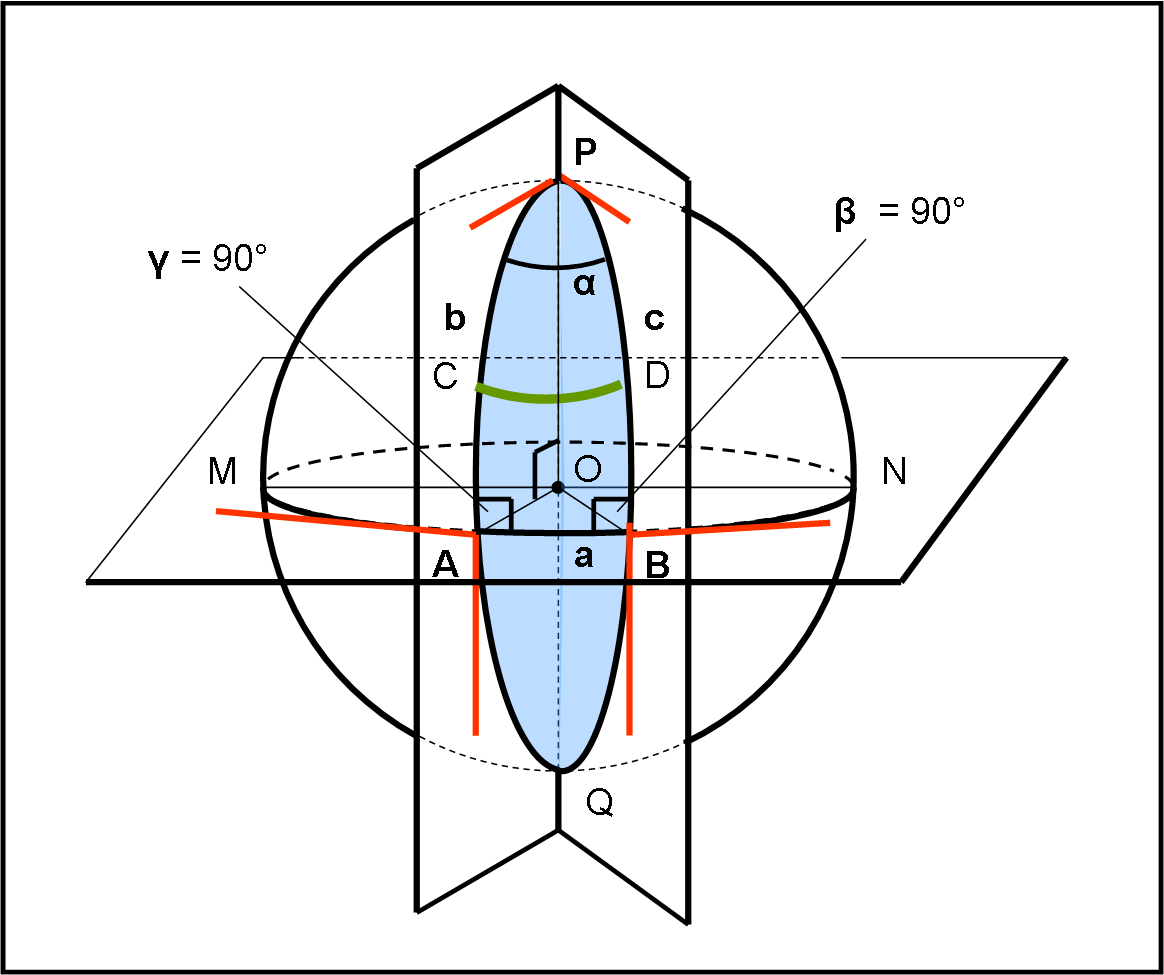
Consideriamo un piano qualsiasi passante per il centro O della sfera e il cerchio massimo da lui determinato. Questo cerchio massimo lo mettiamo “in orizzontale” (chiamiamolo, per adesso,  piano orizzontale) ed è individuato dai punti MABN. Tracciamo dal centro O la retta perpendicolare al piano: questa interseca la superficie sferica in punto P, che possiamo chiamare polo (dall’altra parte della sfera determina un punto diametralmente opposto Q, detto antipodale). Consideriamo due piani qualsiasi che passino per il centro e che siano perpendicolari al piano, ossia che passino per l’asse QOP. La loro intersezione con la superficie sferica dà luogo ad altri due cerchi massimi, PCAQ e PDBQ (abbiamo tracciato solo la parte che sta “davanti” per evitare troppe linee, ossia abbiamo tracciato solo dei semicerchi massimi).

Tanto per gradire, possiamo anche dire che la parte di superficie sferica (azzurra) compresa tra questi due semicerchi massimi prende il nome di fuso sferico, ma a noi interessa relativamente…

Consideriamo, invece, solo la figura sferica PAB. Che cos’è? Beh… dovremmo ormai saperlo molto bene. Essa è composta da tre segmenti di cerchio massimo e quindi è un triangolo sferico a tutti gli effetti. Possiamo subito chiamare a, b, c i suoi lati, sapendo esattamente che coincidono, misurati in radianti, con gli angoli corrispondenti al centro della sfera.

Facendo questo gioco, scopriamo subito che il lato rettilineo (intrinseco) PA non è altro che:

PA = b = π/2

Così come

PB = c = π/2

La stessa cosa varrebbe per qualsiasi cerchio massimo passante per P (e Q). Ad esempio:

PM = PN = π/2

Infine si ha che:

AB = a

Non è difficile immaginare che a varia al variare dei due piani verticali e che quindi potrebbe benissimo essere uguale a π/2. In poche parole, il triangolo sferico PAB potrebbe tranquillamente avere i sui tre lati uguali a π/2.

Ancora più interessante è il calcolo degli angoli α, β e γ. Ormai sappiamo che si determinano guardando l’angolo tra le tangenti ai cerchi massimi nel punto di vertice. Ne segue che β e γ risultano essere proprio uguali a 90° (le tangenti sono perpendicolari per costruzione), mentre α dipende dall’angolo diedro formato dai due piani perpendicolari al piano orizzontale o, se preferite, dalle due tangenti rosse in P.

Prima di proseguire con il quiz, deduciamo subito una caratteristica veramente peculiare della geometria sferica (ma che già avevamo intuito). Le rette parallele si incontrano tutte in un punto.

Tutti i cerchi massimi perpendicolari al cerchio orizzontale sono intrinsecamente paralleli tra loro (ognuno forma un angolo di 90° con lui). Sappiamo, però, che i cerchi massimi sono le rette intrinseche, così come lo è il cerchio orizzontale, per cui abbiamo un fascio di rette che formano lo stesso angolo con un’altra retta. Nella geometria euclidea ciò vuol dire che sono rette parallele. Tuttavia, nel caso sferico, tutte queste rette intrinseche parallele devono  passare per il polo P, ma anche dal punto antipodale Q. Possiamo quindi dire che per due punti qualsiasi di una sfera passa un solo cerchio massimo, ma se i punti sono antipodali  passano infinite rette parallele tra loro. Il che vuole anche dire che due rette qualsiasi (cerchi massimi) devono sempre avere due punti in comune (polo e punto antipodale).

Fatemi fare anche una riflessione, che sarà molto utile se un giorno decideremo di rappresentare i buchi neri nel diagramma di Penrose: “I poli di un cerchio massimo possono rappresentare i punti all’infinito di un fascio di rette parallele”.

Torniamo a noi e alla soluzione del quiz, che ormai dovreste intuire perfettamente. Partiamo da P e andiamo in linea retta verso A. Attenzione! Guai a cercare di abbreviare il percorso e piegare di 90° nel punto C. Ci troveremmo su un cerchio intrinseco (arco verde) che non è rettilineo e quindi non corrisponde ai requisiti del quiz. Dobbiamo proseguire fino ad A dove incontriamo il cerchio massimo “rettilineo” AB che si segue proprio dopo aver piegato di 90° (angolo γ). Continuiamo ad andare dritti fino al punto B e poi giriamo di 90° (angolo β) prendendo il cerchio massimo BP che ci riporta fino al punto di partenza.

Notiamo che possiamo scendere e risalire secondo qualsiasi cerchio massimo il cui piano sia perpendicolare a quello orizzontale. In altra parole, l’angolo α può essere qualsiasi. Magari proprio uguale a 90°. In questo caso otteniamo un triangolo sferico i cui tre lati sono uguali tra loro e a π/2 (ossia 90° espressi in radianti) e i cui tre angoli sono anch’essi uguali tra loro e a 90°. Mamma mia… che strano mondo sferilandia! Ci sarebbero da osservare molte cose, ma almeno una deve essere detta subito, attraverso una semplice somma:

α + β + γ = 90° + 90° + 90° = 270°

Accidenti… questa è proprio una scoperta eccezionale: la somma degli angoli di un triangolo sferico può superare abbondantemente i 180°. Non solo, però: la somma varia al variare del triangolo. Si dimostra subito, facendo variare l’angolo α: il triangolo sferico ABP mantiene due angoli uguali a 90°, mentre il terzo può cambiare sia in più che in meno…

Bene, prima di passare a operazioni più pratiche, una facile domanda: Fino a quale valore può arrivare la somma degli angoli di un triangolo sferico? Teniamo presente che se un angolo raggiunge 180° il vertice sparisce e cadremmo in un caso degenere (tre vertici su uno stesso cerchio massimo non possono esistere)

Tanto che ci siamo, eccovi anche un problemino un po’ più complicato…

Consideriamo la Fig. 13, dove abbiamo un cerchio massimo orizzontale su cui è evidenziato un arco AB.

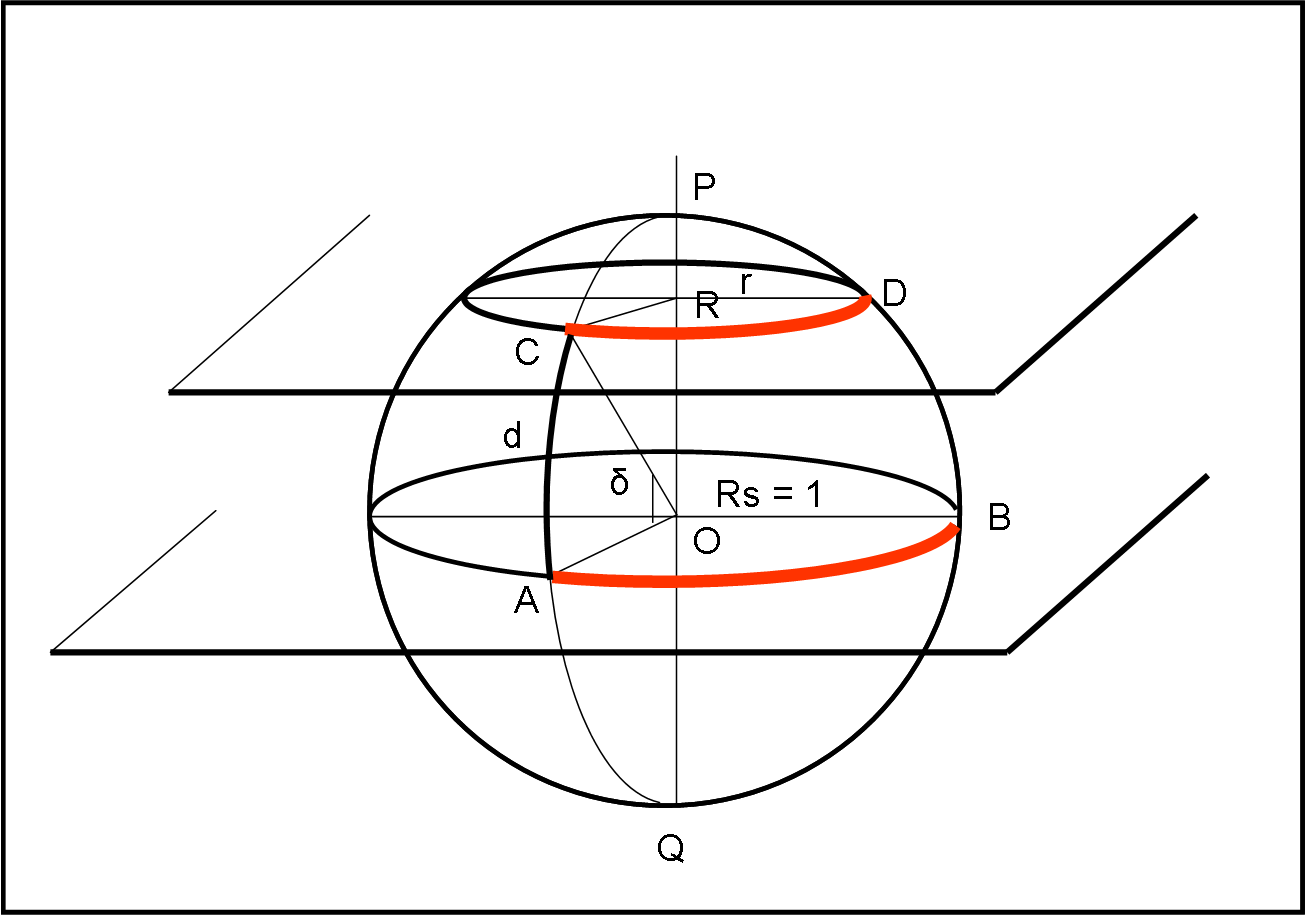
Tagliamo la sfera con un piano non passante per il centro ma parallelo a quello orizzontale. Otteniamo un cerchio minore di centro R e raggio r. Immaginiamo di conoscere l’arco di cerchio massimo AC = d, ossia l’angolo al centro COA= δ (sono la stessa cosa, a parte che l’arco si esprime in radianti). Conoscendo la misura di AC, quanto vale l’arco di cerchio minimo CD, in funzione di AB?

Diamo la soluzione dei due quesiti e poi torniamo (per poco) alla trigonometria piana per conoscerla un po’ meglio…

Il primo quesito è veramente semplice: basta pensare che se uno dei tre angoli raggiungesse 180°, automaticamente i tre vertici apparterrebbero alla stessa circonferenza e cadrebbe la definizione di triangolo. Ne segue che il valore limite, per la degenerazione del triangolo, è dato da 3∙180° = 540°. Un triangolo sferico vicino al limite massimo della somma dei tre angoli è riportato nella Fig. 14.

I tre lati sono relativi ai tre piani di colore diverso (rosso, blu e verde). Il cerchio verde è quello che giace sul piano del foglio. Poco importa se i lati curvano e se gli angoli si allargano, l’importante è che si utilizzino tre piani passanti per il centro della sfera.

Una formula fondamentale

Più interessante e utile è la soluzione del secondo quiz. Dato un cerchio massimo cerchiamo di stabilire la relazione che vi è fra un suo arco, compreso tra due cerchi massimi a lui perpendicolari, e i cerchi minori ottenuti, compresi sempre tra i due cerchi massimi, a differente distanza da lui. Il tutto è rappresentato molto meglio nella Fig, 15 che non è altro che la precedente Fig. 13.

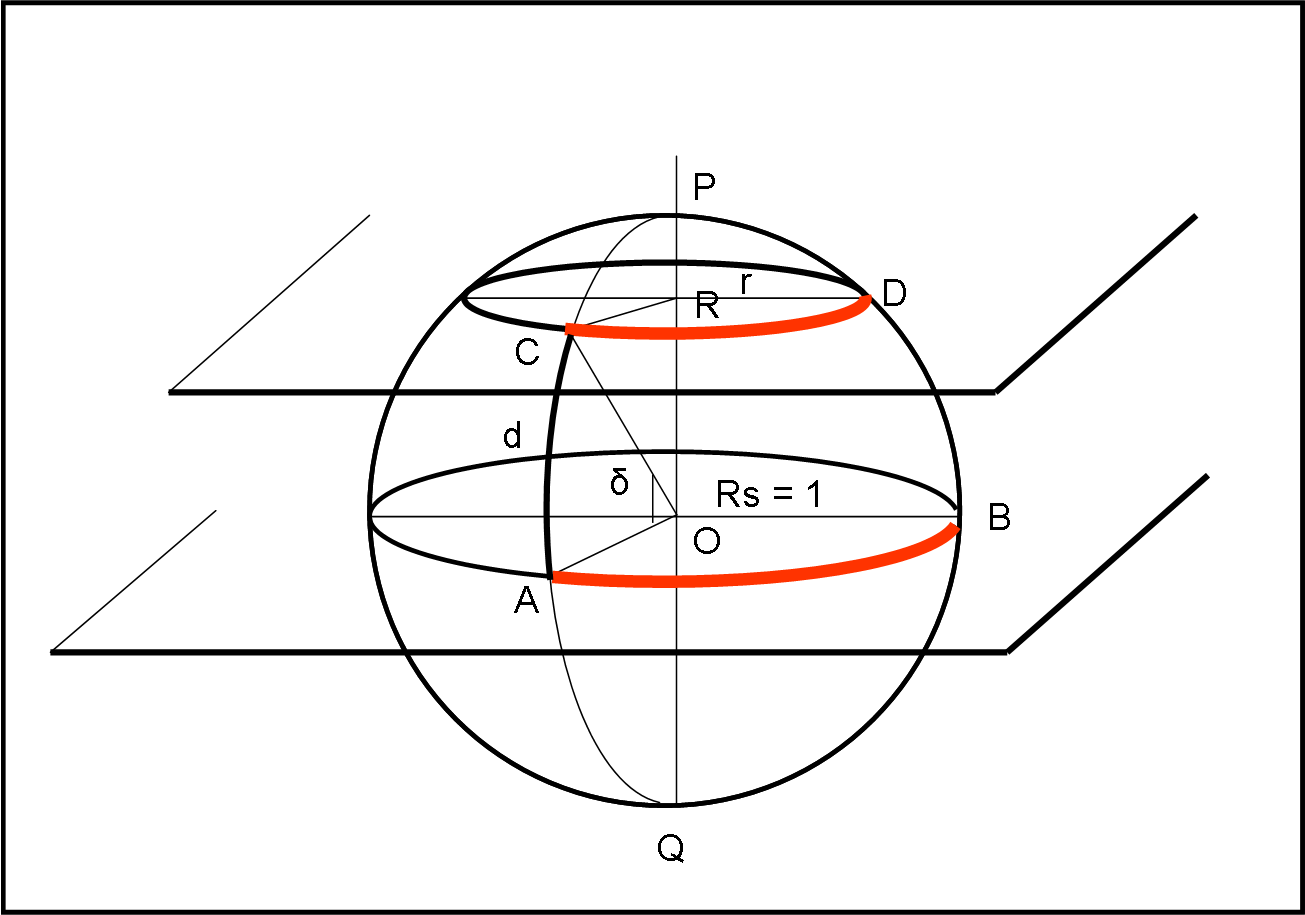
Conosciamo AB e vogliamo trovare CD per varie posizioni lungo la sfera celeste. Si capisce subito l’importanza di questa relazione pensando alle misure lungo i paralleli terrestri…

Chiamiamo δ l’angolo al centro che determina la posizione del piano non passante per il centro. Per δ = 0 il cerchio minore coincide con il cerchio massimo, per δ = 90°, il cerchio degenera nel punto P. Cosa analoga (cambiando di segno) capita nell’emisfero in basso.

La definizione dell’angolo δ identifica immediatamente l’arco di cerchio AC, dato che essi sono esattamente uguali assumendo Rs = 1. Chiamiamo d questo arco, ricordando bene che:

d = δ (rad.)

Consideriamo il triangolo rettangolo CRO. CR non è altri che il raggio r (estrinseco) del cerchio minore. L’angolo COR vale, ovviamente, 90° – δ = π/2 – d. CO è il raggio della sfera e vale 1.

Ne segue che:

r = Rs sen (π/2 – d) = cos (d)

L’arco di cerchio CD vale, però:

CD = r ∙ angolo (CRD)

L’arco di cerchio AB vale anche:

AB = Rs ∙ angolo (AOB) = angolo (AOB)

Ma l’angolo AOB è uguale all’angolo CRD, dato che entrambi sono formati dagli stessi due piani e sono misurati su piani a loro perpendicolari o (se preferite) sono formati da coppie di rette parallele.

Ne segue che:

CD = r ∙ angolo (CRD)  = r ∙ angolo (AOB) = r ∙ AB

Ma abbiamo appena trovato che:

r = cos (d)

Si ha infine:

CD = AB cos (d)

In poche parole, l’arco di cerchio minore è uguale all’arco di cerchio maggiore corrispondente (relativi a due piani paralleli), moltiplicato per il coseno dell’arco di cerchio massimo che li separa.

Questa è una formula estremamente importante per le coordinate sferiche.

Torniamo al piano (ma solo per poco)

Facciamo adesso un passo indietro e torniamo alla trigonometria piana. L’abbiamo trattata parzialmente QUI, ma è adesso necessario aggiungere qualche nozione e almeno un paio di formule. Alcune le avevamo già ricavate e/o usate affrontando il QUIZ su stellarium (QUI, QUI e QUI).

Teorema dei seni

Consideriamo un triangolo (piano) ABC qualsiasi, come mostrato in Fig. 16

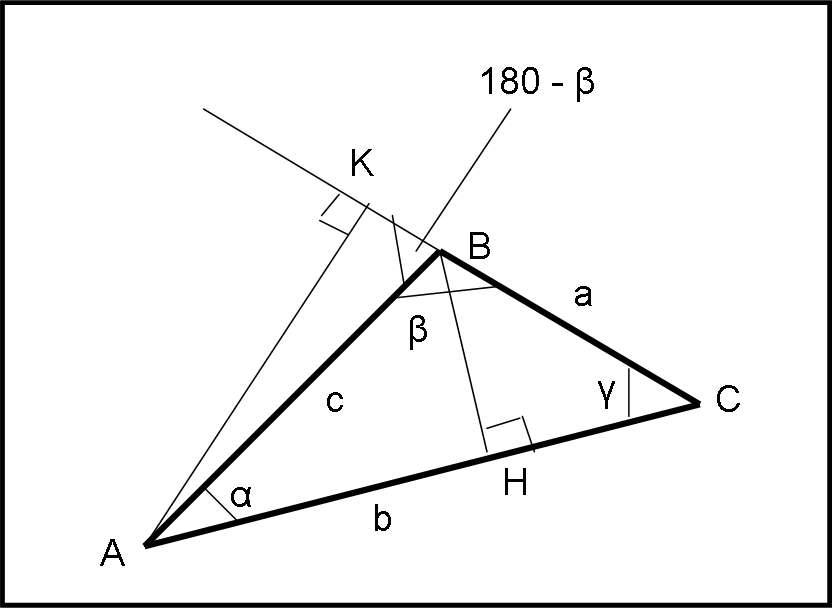
Tracciamo da B la perpendicolare al lato opposto e sia H il punto di intersezione. Otteniamo due triangoli rettangoli, AHB e CHB.

Dal primo abbiamo:

BH = c sen (α)

Dal secondo:

BH = a sen (γ)

Uguagliando:

c sen (α) = a sen (γ)

O, ancora:

c/sen (γ) = a/sen (α)       …. (2)

Tradotto in parole: il rapporto tra un lato e il seno dell’angolo opposto rimane costante.

Proviamo con un altro vertice:

Tracciamo da A la perpendicolare al lato BC e chiamiamo K il punto d’intersezione (prolungando il lato, ovviamente).

I due triangoli AKB e AKC sono rettangoli. Possiamo quindi scrivere:

AK = c sen (180 – β) = c sen (β)

AK = b sen (γ)

Uguagliando:

c sen (β) = b sen (γ)

E, ancora:

c/sen (γ) = b/sen (β)

Ricordando la (2)

Si ha la formula generale dei seni:

c/sen (γ) = a/sen (α) = b/sen (β)      …. (3)

Il teorema di Carnot

Questo teorema, detto anche del coseno, permette di ricavare un lato di un triangolo qualsiasi, conoscendo gli altri due e l’angolo tra essi compreso. Utilizziamo la Fig. 17.

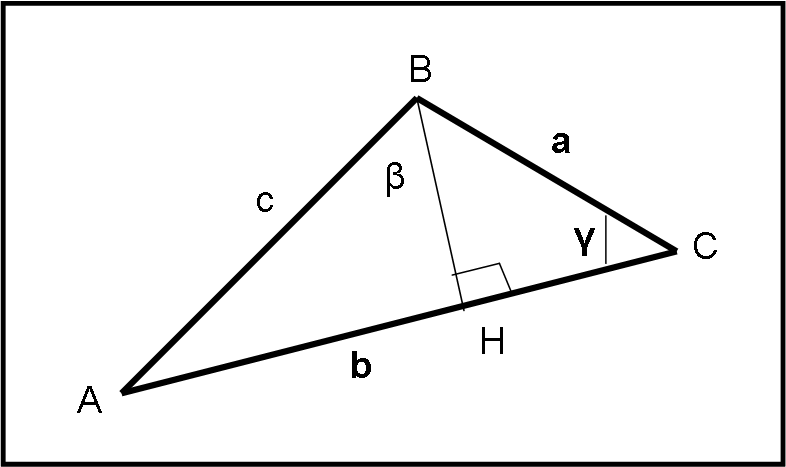
Conosciamo a, b e l’angolo γ e vogliamo ricavare il lato c.

Tracciamo da B la perpendicolare BH al lato b = AC.

Dal triangolo rettangolo BHA si ha:

c² = AH² + BH²         …. (4)

dal triangolo rettangolo BHC, si ha:

BH = a sen (γ)

Ma vale anche:

AH = b – HC = b – a cos (γ)

Sostituendo le ultime due relazioni nella (4) si ha:

c² = AH² + BH² = (b – a cos (γ))² + a² sen²(γ) = b² + a² cos²(γ) – 2ab cos (γ) + a² sen²(γ)

Abbiamo, raccogliendo a²:

c² = b² + a² (cos²(γ) + sen²(γ)) – 2ab cos (γ)

Ricordando che

sen²(γ) + cos²(γ) = 1

si ha, infine:

c² = a² + b² - 2ab cos (γ)       …. (5)

La (5) rappresenta la formula di Carnot

Essa si riduce al teorema di Pitagora quando l’angolo  γ vale 90°, dato che il coseno va a 0. La formula, ovviamente può applicarsi a qualsiasi lato, facendo “girare” le lettere.

Secante, cosecante e cotangente

Da un punto di vista puramente matematico è immediato definire la secante (sec), la cosecante (cosec) e la cotangente (cot o cotan):

sec (ϑ) = 1/cos (ϑ)

cosec (ϑ) = 1/sen (ϑ)

cotan (ϑ) = 1/tan (ϑ)

Da un punto di vista grafico, basta richiamare il cerchio goniometrico (di raggio unitario), come si vede in Fig. 18

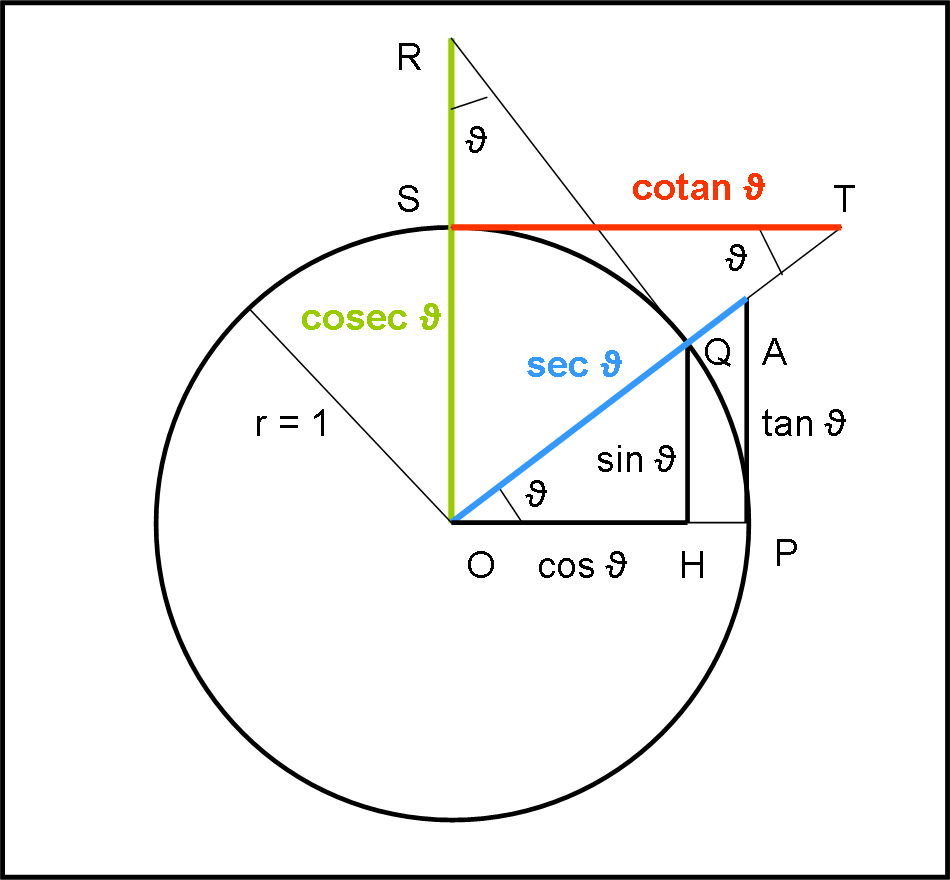
I triangoli rettangoli OHQ e OPA sono simili e quindi vale la proporzione:

OH : OP = OQ : OA

OA e la secante di ϑ

Infatti:

sec (ϑ) = OA = OP ∙ OQ/OH = 1∙1/cos (ϑ) = 1/cos (ϑ)

Nel triangolo rettangolo OPA, il teorema di Pitagora ci dice anche che:

sec²(ϑ)  = OP² + PA² = 1 + tan²(ϑ)       …. (6)

Ricaviamo geometricamente anche la cosec (ϑ), tracciando la tangente alla circonferenza goniometrica nel punto Q e considerando il triangolo rettangolo OQR. Quest’ultimo è simile al triangolo OQH (due angoli uguali). Ne segue che OR = cosec (ϑ). Infatti:

OR : OQ = OQ : QH

Ossia:

cosec (ϑ) = OR = OQ ∙ OQ/QH = 1/sen (ϑ)

Possiamo anche definire la funzione

cotan (ϑ) = 1/tan (ϑ) = cos (ϑ)/sen (ϑ)

Geometricamente essa è rappresentata dal segmento ST. Infatti, dai triangoli simili OST e OHQ si ha:

ST : SO = OH : QH

e, quindi:

cotan (ϑ) = ST = SO ∙ OH/QH = 1∙ cos (ϑ)/sen (ϑ) = cos (ϑ)/sen (ϑ)

Non preoccupatevi… useremo soltanto la definizione di secante, ma è più che giusto conoscere queste funzioni così semplici, sia matematicamente che geometricamente. Chi vuole divertirsi (ma non è importante per il proseguo della trattazione) può anche fare il grafico delle tre funzioni sec, cosec e cotan. Un bell’esercizio per ricordare lo studio di funzioni (vedi QUI)

Torniamo alla superficie sferica e affrontiamo la trigonometria sferica

Definito il triangolo sferico, sia intrinsecamente che estrinsecamente, non ci resta che determinare alcune formule fondamentali che leghino tra loro  i lati e gli angoli. Esse vengono proprio chiamate le tre formule fondamentali della trigonometria sferica.

Non è solo un gioco matematico, ma è la base per definire i sistemi di coordinate astronomiche e per passare da uno all’altro. Chi ha un telescopio sa benissimo che esso può essere sia altoazimutale che equatoriale. Bene, noi vogliamo svelare tutti i segreti delle varie montature, evidenziare i loro pregi e i loro difetti. Un qualcosa, quindi, che dovrebbe essere l’ABC degli astrofili anche più tecnologici e assidui adoratori di stellarium & co.

Per tutti gli altri, una trattazione elegante ed essenziale per saper affrontare e descrivere ciò che avviene su una superficie sferica. La matematica la fa da padrona, ma non dimentichiamo la sua applicazione alla fisica più moderna, tipo la RG.

La prima formula fondamentale della trigonometria sferica

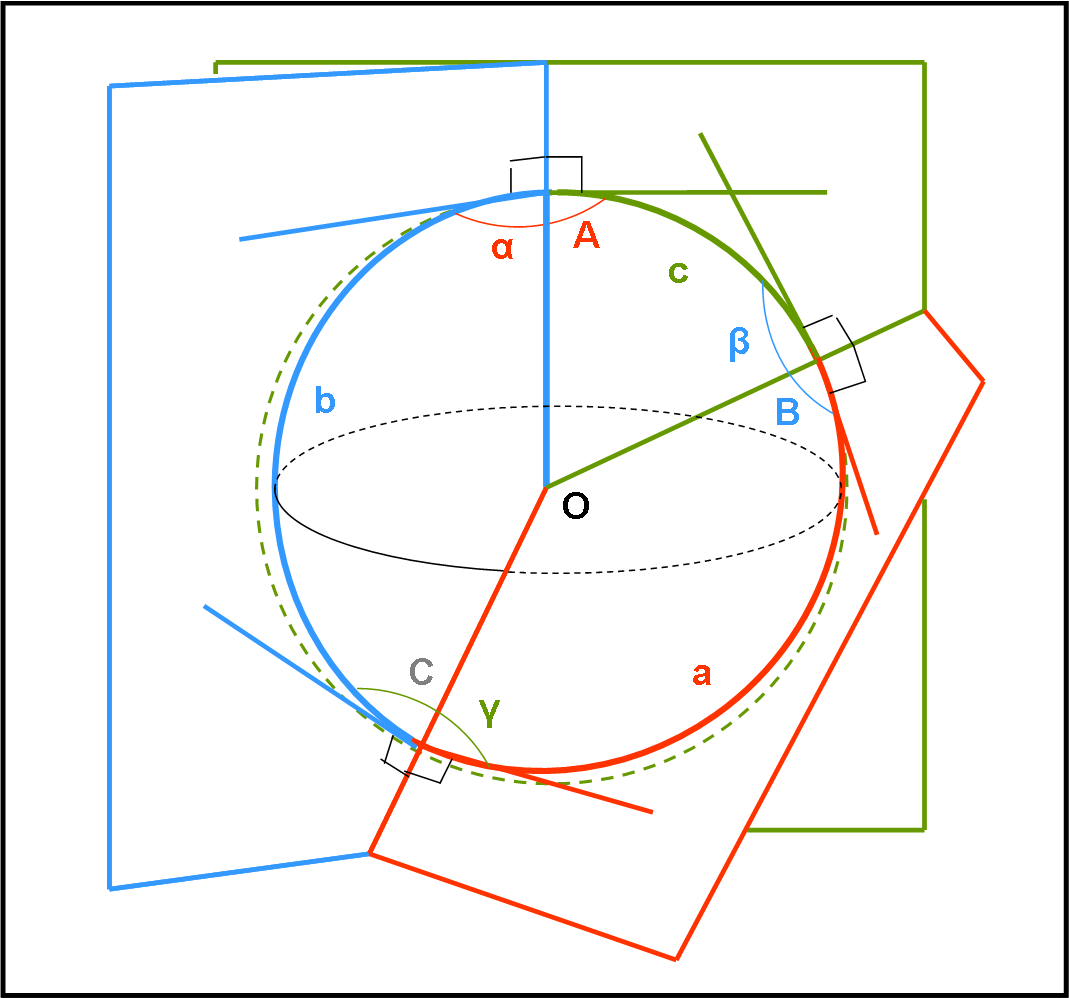
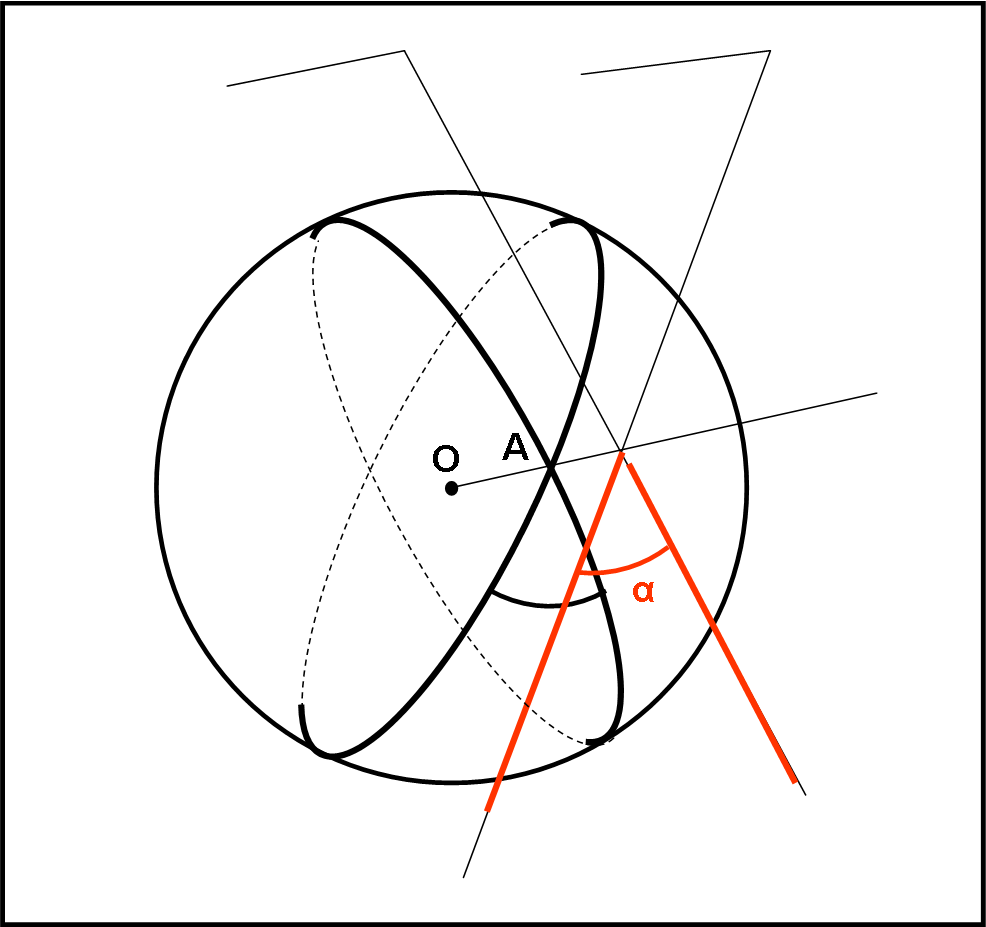
Introduciamo e spieghiamo molto attentamente la Fig. 19.

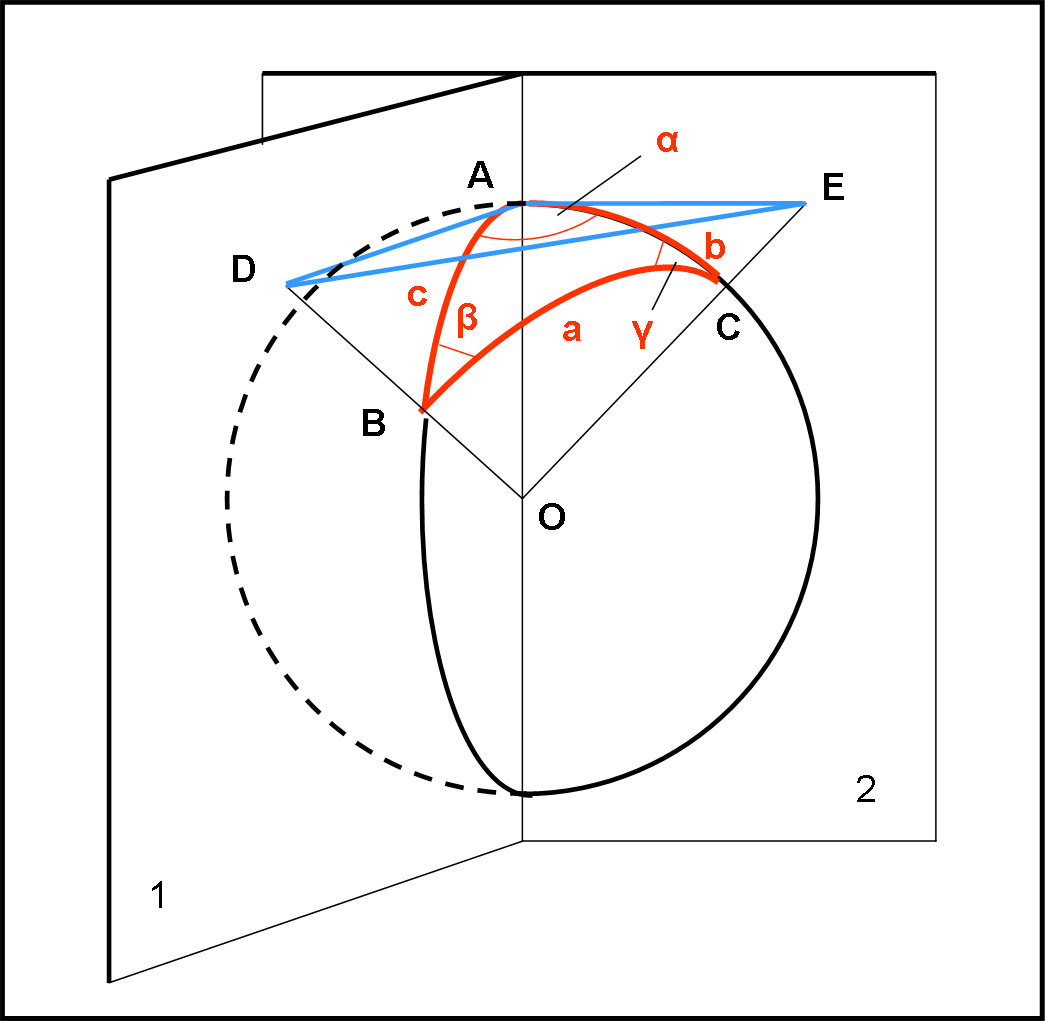
In essa è stato disegnato in rosso un triangolo sferico. Come tale esso deve avere per lati tre archi di cerchio massimo, che abbiamo chiamato a, b e c. Sappiamo benissimo che il raggio della sfera è unitario e quindi la misura dei tre lati non è altro che l’angolo che sottendono al centro della circonferenza, espresso in radianti. Non spaventiamoci dei radianti: è solo un modo diverso di rappresentare un angolo o un arco (che in questo caso coincidono). Esiste, perciò sia il seno di 90° sia il seno di π/2. Niente di strano, quindi, che d’ora in poi avremo a che fare con funzioni trigonometriche dei tre lati a, b e c. Essi sono angoli a tutti gli effetti e come tali li trattiamo.

Nella figura si sono evidenziati anche i due piani che individuano l’angolo sferico in A: li abbiamo chiamati 1 e 2. Essi contengono quindi i lati b e c e anche le rette tangenti ai cerchi massimi che i due piani determinano sulla sfera. Le rette tangenti sono AE e AD. L’angolo tra loro formato è proprio l’angolo α che viene considerato come l’angolo tra i lati b e c. Ne segue che il segmento OBD sta sul piano 1 e il segmento OCE sta sul piano 2. Dato che AE e AD sono tangenti ai relativi cerchi massimi in A, gli angoli DAO e EAO sono retti. Per chiarire ancora meglio la figura, ricordiamo che l’angolo α è l’angolo diedro formato dai piani 1 e 2. Inoltre, risulta ovvio (contiene due rette entrambi perpendicolari nello stesso punto all’asse OA) che il triangolo ADE giace su un piano perpendicolare all’asse OA.

Bene, dopo aver compreso perfettamente la figura, è ora di applicare ad alcuni suoi triangoli le funzioni trigonometriche, che conoscevamo già e che abbiamo imparato a conoscere la volta scorsa (in particolare la secante).

Iniziamo con il triangolo rettangolo OAD. Ricordiamo ancora una volta che l’angolo in O non è altro che l’arco c. Per facilitare la trattazione, riportiamo il piano del triangolo OAD sul piano del foglio nella Fig. 20.

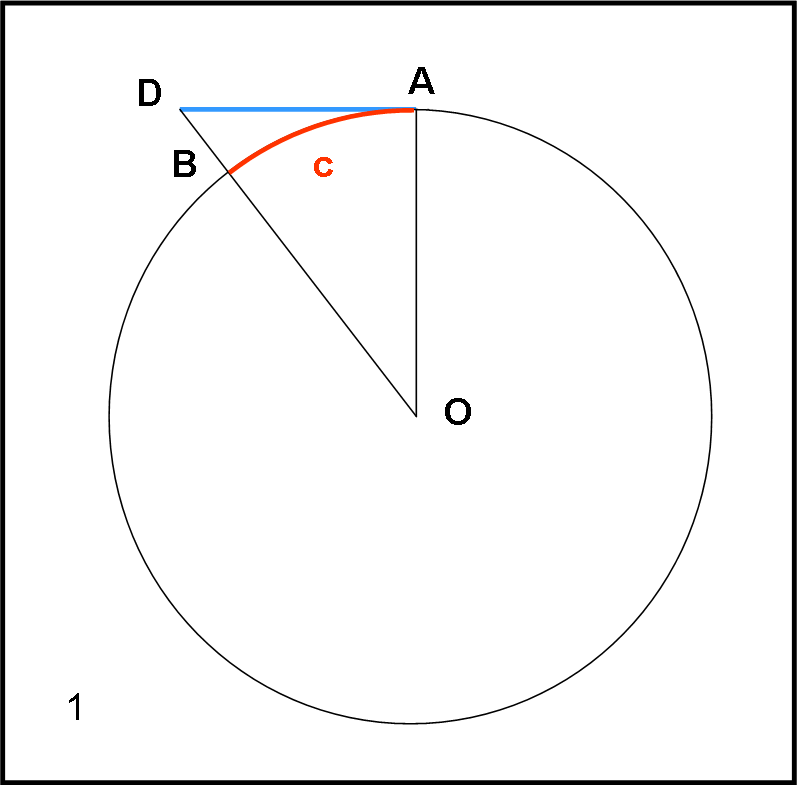
A questo punto, andando a rivedere quanto detto sulle secanti nel capitolo precedente (5), e ricordando, in generale, che la tangente è il rapporto tra il seno e il coseno, possiamo scrivere alcune relazioni e applicare qualche teorema.

Essendo OA = 1, si ha:

AD = tan (c)

OD = sec (c)

Analogamente dal triangolo piano AEO si ottiene:

AE = tan (b)

OE = sec (b)

Portiamoci adesso sul triangolo piano ADE. Esso è un triangolo qualsiasi di cui, però, conosciamo un angolo (DAE = α) e due lati (AD e AE). Per trovare il terzo lato, ossia DE, non ci resta che applicare il teorema di Carnot , descritto la volta scorsa.

DE² = AD² + AE² – 2AD∙AE cos (DAE)

Sostituendo quanto trovato, abbiamo:

DE² = tan²(c) + tan²(b) – 2 tan(c) tan(b) cos(α)      …. (7)

Consideriamo adesso il triangolo piano EDO (esso sta sul piano che definisce l’arco di cerchio massimo a).

Di lui conosciamo due lati (OD e OE) e l’angolo in O che è proprio uguale all’arco a. Mi raccomando! Non confondiamo l’angolo che uguaglia l’arco a con l’angolo α, che è tutt’altra cosa, come abbiamo appena visto.

Possiamo trovare nuovamente il lato DE attraverso questo triangolo, applicando anche a lui il teorema di Carnot:

DE² = OD² + OE² – 2 OD∙OE cos(DOE)

Sostituendo ciò che abbiamo ricavato precedentemente e ricordando che DOE = a, si ha:

DE² = sec²(c) + sec²(b) – 2 sec (c) sec (b) cos (a)        …. (8)

Uguagliano la (7) e la (8), otteniamo:

tan²(c) + tan²(b) – 2 tan(c) tan(b) cos (α) = sec²(c) + sec²(b) – 2 sec (c) sec (b) cos (a)   …. (9)

Tuttavia, ricordiamo, dalla volta scorsa, che:

sec²(c) = 1 + tan²(c)

e

sec²(b) = 1 + tan²(b)

Sostituendo nella (9) si ha:

tan²(c) + tan²(b) – 2 tan(c) tan(b) cos(α) = 1 + tan²(c) + 1 + tan²(b) – 2 sec (c) sec (b) cos (a)

e, ancora:

- 2 tan(c) tan(b) cos(α) = 2 – 2 sec(c) sec(b) cos(a)

- sen(c) sen(b) cos(α)/(cos(c) cos(b)) = 1 –  cos(a)/(cos(c) cos(b))

- sen(c) sen(b) cos(α)/(cos(c) cos(b)) = (cos(c) cos(b) –  cos(a))/(cos(c) cos(b))

- sen(c) sen(b) cos(α) = cos(c) cos(b) –  cos(a)

sen(c) sen(b) cos(α) = - cos(c) cos(b) + cos(a)

cos(a) = cos(b) cos(c) + sen(b) sen(c) cos(α)           …. (10a)

La (10a) è chiamata prima formula fondamentale della trigonometria sferica.

Essa permette di ricavare la lunghezza di un arco conoscendo gli altri due e l’angolo tra essi compreso.

Ovviamente, cosa analoga può essere fatta per ogni lato del triangolo (chi vuole provare può divertirsi) e si ottengono le altre due formule del tutto simili (basta ruotare le lettere):

cos(b) = cos(c) cos(a) + sen(c) sen(a) cos(β)        …. (10b)

 cos(c) = cos(a) cos(b) + sen(a) sen(b) cos(γ)          …. (10c)

Dove gli angoli β e γ sono indicati nella Fig. 19.

Può sembrare qualcosa di complicato, ma vi posso assicurare che è veramente utile per legare tra loro i vari sistemi di coordinate.

La seconda formula fondamentale della trigonometria sferica

La seconda formula fondamentale è sicuramente la più “difficile” da ottenere. Non spaventatevi, però… sono solo passaggi matematici alla portata di tutti. Inoltre, si può notare come piccoli “trucchi” possano rendere la matematica estremamente intrigante e utilissima per mettere alla prova la nostra capacità di seguire ragionamenti logici di importanza ben più generale.

Lo scopo è quello di enunciare la seconda formula fondamentale della trigonometria sferica, una delle più “semplici”, ma che abbisogna di una dimostrazione oltremodo “noiosa”, almeno per molti. Tuttavia, dato che cerchiamo di non dare mai la “pappa pronta”, vogliamo presentare due vie, esteticamente e concettualmente diverse, che riescano a dimostrarla. Un esercizio di pura matematica, che sicuramente fa piacere a coloro che amano questo linguaggio così rigoroso, ma anche così fantasioso e stimolante.

La formula che vogliamo presentare è del tutto analoga a quella del teorema dei seni della geometria piana. Tuttavia, la dimostrazione è abbastanza ingarbugliata ed è destinata ai “solutori più che abili”. Non perché sia realmente difficile, ma perché necessita di svariati passaggi di trigonometria di base. Vi sono diversi metodi usati per la dimostrazione: ne abbiamo scelto due puramente matematici.

Possiamo dire che questa formula deriva direttamente dalla prima formula fondamentale e si ottiene manovrando abilmente quest’ultima. Per non obbligare tutti a seguire la parte più difficoltosa, scriviamo subito il risultato che può essere più che sufficiente per il suo utilizzo nei problemi legati alle coordinate astronomiche.

Dato un triangolo sferico di lati a, b e c, e di angoli α, β, γ, come riportato in Fig. 19, si può scrivere:

sin (a)/sin (α) = sin (b)/sin (β) = sin (c)/sin (γ)       …. (11)

Una formula che sarà oltremodo utile. Essa permette di calcolare un lato conoscendo l’angolo opposto, un angolo adiacente e un altro lato. Oppure, di calcolare un angolo, conoscendo il lato opposto, un lato adiacente e l’angolo opposto a quest’ultimo.

Un metodo puramente matematico

Qui di seguito riportiamo la prima dimostrazione, che si affida a piccoli giochi di prestigio applicati a vari gruppi di funzioni trigonometriche.

Dalla derivazione della prima formula,  recuperiamo le  (10b) e (10c), ossia:

cos(b) = cos(c) cos(a) + sen(c) sen(a) cos(β)         

cos(c) = cos(a) cos(b) + sen(a) sen(b) cos(γ)

Le riscriviamo portando qualcosa da una parte e qualcosa dall’altra del segno di uguale:

sin(c) sin(a) cos(β) = cos(b) - cos(c) cos(a)

sin(a) sin(b) cos(γ) = cos(c) - cos(a) cos(b)

Eleviamo al quadrato entrambi i membri delle due equazioni e sottraiamo membro a membro:

sin²(c) sin²(a) cos²(β) - sin²(a) sin²(b) cos²(γ) = cos²(b) + cos²(c) cos²(a) - 2 cos(b) cos(c) cos(a) -cos²(c) - cos²(a) cos²(b) + 2 cos(c) cos(a) cos(b)

Semplificando e raccogliendo:

sin²(a) (sin²(c) cos²(β) – sin²(b) cos²(γ)) = (cos²(b) – cos²(c)) – cos²(a) (cos²(b) – cos²(c))

sin²(a) (sin²(c) cos²(β) – sin²(b) cos²(γ)) = (1 – cos²(a)) (cos²(b) – cos²(c))     …. (12)

Ricordando che, in generale, per qualsiasi angolo ϑ, vale la fondamentale relazione sin²(ϑ) + cos²(ϑ)  = 1, ossia sin²(ϑ)  = 1 - cos²(ϑ)  e/o cos²(ϑ)  = 1 - sin²(ϑ), si ha:

sin²(a) (sin²(c) cos²(β) - sin²(b) cos²(γ)) =  sen²(a) (cos²(b) - cos²(c))

e dividendo entrambi i membri per sin²(a), si ottiene:

sin²(c) cos²(β) - sin²(b) cos²(γ) =  1 - sen²(b) -1 + sen²(c)

sin²(c) cos²(β) - sin²(b) cos²(γ) =  - sen²(b) + sen²(c)

sen²(b) - sin²(b) cos²(γ) = sen²(c) - sin²(c) cos²(β)

sen²(b) (1 - cos²(γ)) = sen²(c) (1 - cos²(β))

sen²(b) sen²(γ) = sen²(c) sen²(β)

Poiché gli archi e i lati non possono superare π o 180°, i seni non sono mai negativi e possiamo scrivere:

sen(b) sen(γ)= sen(c) sen(β)

E, infine:

sen (b)/sen (β) = sen(c)/sen (γ)

Che è quanto volevasi dimostrare. Ovviamente, prendendo altre due relazioni della (10) (o anche solo ruotando le lettere) si ottiene la formula completa:

sin (a)/sin (α) = sin (b)/sin (β) = sin (c)/sin (γ)

Un metodo alternativo

L’appetito vien mangiando e, probabilmente, qualcuno potrebbe essere interessato a una dimostrazione alternativa che, pur facendo uso di sola matematica, usa spunti di logica molto eleganti. Un “racconto” per chi ama divertirsi con il linguaggio della fisica e che ne cerca tutti i risvolti più razionali e raffinati… Come già detto, queste due dimostrazioni, che portano allo stesso risultato, possono essere tranquillamente tralasciate.

L’inizio è simile e utilizza nuovamente la prima formula fondamentale. Riscriviamo la (10a)

cos (a) = cos (b) cos (c) + sen (b) sen (c) cos (α)    

Riscriviamola come segue:

sen (b) sen (c) cos (α) = cos (a) - cos (b) cos (c)

Eleviamola a quadrato

sen²(b) sen²(c) cos²(α) = cos²(a) + cos²(b) cos²(c) - 2 cos(a) cos(b) cos(c)     …. (13)

Ricordando che:

cos²(α) = 1 - sin²(α)     (e formule analoghe)

il primo membro può essere scritto:

sen²(b) sen²(c) cos²(α) = sen²(b) sen²(c) - sen²(b) sen²(c) sen²(α)

sen²(b) sen²(c) cos²(α) = (1 - cos²(b)) (1 - cos²(c)) - sen²(b) sen²(c) sen²(α)

sen²(b) sen²(c) cos²(α) = 1 - cos²(c) - cos²(b) + cos²(b) cos²(c) - sen²(b) sen²(c) sen²(α)

Andiamo a inserirlo nella (13)

1 - cos²(c) - cos²(b) + cos²(b) cos²(c) - sen²(b) sen²(c) sen²(α) = cos²(a) + cos²(b) cos²(c) - 2 cos(a) cos(b) cos(c)

1 - cos²(c) - cos²(b) - sen²(b) sen²(c) sen²(α) = cos²(a) - 2 cos(a) cos(b) cos(c)

sen²(b) sen²(c) sen²(α) = 1 - cos²(a) - cos²(c) - cos²(b) + 2 cos(a) cos(b) cos(c)

cos²(a) + cos²(c) + cos²(b) - 2 cos(a) cos(b) cos(c) = 1 - sen²(b) sen²(c) sen²(α)

Attenzione, adesso, al ragionamento di pura logica matematica!

Il primo membro contiene la somma dei quadrati dei tre coseni dei lati. Il che vuol dire che ruotando le lettere questa parte non cambia. Ma non cambia nemmeno la seconda parte del primo membro dato che vi è il prodotto dei  dei tre coseni. Ne consegue che il primo membro non cambia facendo girare le lettere: esso è quindi una costante per un certo triangolo sferico.

Se è costante il primo membro deve esserlo anche il secondo (è un’uguaglianza!).

Scriviamo il secondo membro ponendo:

sen²α = K² sen²a

Esso diventa:

1 – K² sen²(b) sen²(c) sen²(a)

Sappiamo che non deve cambiare ruotando le lettere. Tuttavia, il prodotto dei quadrati dei tre seni non può cambiare ruotando le lettere e altrettanto fa il numero 1. Ne segue che ruotando le lettere anche K² non può cambiare.

K² = costante nella rotazione delle lettere.

Ma questo vuol dire che:

sen²(α)/sen²(a) = sen²(β)/sen²(b) = sen²(γ)/sen²(c) = K² = costante

Estraiamo la radice quadrata e prendiamo il segno positivo, dato che i lati e gli angoli sono minori di π e/o 180° e quindi i seni sono sempre positivi.

sen (α)/sen (a) = sen (β)/sen (b) = sen (γ)/sen (c)

Come volevasi dimostrare!

La terza formula fondamentale

Anche la terza formula fondamentale si ottiene partendo dalla prima e giocando un po’ con la matematica (roba da poco).

Riprendiamo ancora una volta la (10b), scrivendola in modo un po’ diverso:

sen (c) sen (a) cos (β) = cos (b) - cos (c) cos (a)

E poi anche la (10a)

cos (a) = cos (b) cos (c) + sen (b) sen (c) cos (α)

Sostituiamo cos (a), dato dalla seconda equazione, nella prima:

sen (c) sen (a) cos (β) = cos (b) - cos (c)(cos (b) cos (c) + sen (b) sen (c) cos (α))

sen (c) sen (a) cos (β) = cos (b) - cos²(c) cos (b) - cos (c) sen (b) sen (c) cos (α))

sen (c) sen (a) cos (β) = cos (b) (1 - cos²(c)) - sen (b) sen (c) cos (c) cos (α)

ma:

1 - cos²(c) = sen²(c)

quindi:

sen (c) sen (a) cos (β) = cos (b) sin²(c) - sen (b) sen (c) cos (c) cos (α)

Semplificando, si ottiene:

sen (a) cos (β) = cos (b) sin (c) - sen (b) cos (c) cos (α)            …. (14)

Che è la terza formula fondamentale. Ovviamente, anche lei dà luogo a due formule simili facendo girare angoli e lati.

Sembra piuttosto complicata, ma può essere di grande utilità per risolvere i triangoli sferici, soprattutto quando qualche angolo diventa 90°.

Verso la sfera celeste

Conclusa questa parte puramente didattica, necessaria per sapere con chi abbiamo a che fare e cosa si deve usare per muoversi da un triangolo a un altro, passeremo decisamente alla sfera celeste, il regno dei corpi celesti, dove è necessario saper identificare ogni oggetto utilizzando un solo sistema di coordinate. Vedremo che i triangolo sferici sono il cibo principale, il più delle volte semplificati, ossia con qualche angolo o arco uguale a 90 (o π/2).

Bene, possiamo alzare gli occhi al cielo e scegliere le coordinate celesti che preferiamo e/o che sono più utili allo scopo. Ormai la sfera celeste non ha più segreti.

Nel frattempo, se volete vedere come questo tipo di problematica possa influenzare facilmente addirittura la descrizione dei buchi neri, eccovi accontentai QUI  e anche QUI e QUI dove, alla fine, si ha già un primo approccio con lo spazio tempo curvo.

 

Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.

QUI trovate l'approfondimento dedicato alla Relatività Generale