Categorie: Astronomia Elementare Matematica
Tags: astronomia sferica distanze angolari quiz risoluzione sfera celeste Sole stellarium
Scritto da: Vincenzo Zappalà
Commenti:5
Soluzione del doppio quiz su stellarium **
Ecco le soluzioni ai due quiz sulla costruzione del cielo visto da un’altra stella. La prima è ovvia, la seconda ha diverse possibilità. Io ho descritto quella che mi sembra più semplice, senza introdurre (ancora) teoremi trigonometrici non affrontati. Ma è solo questione di tempo… non illudetevi!
Il primo quiz è veramente banale e la soluzione è stata usata per molti altri esercizi, prima fra tutte la parallasse annua che permette di misurare la distanza delle stelle relativamente vicine.
Sappiamo benissimo qual è il raggio del Sole in km. Quello che vogliamo trovare è il suo diametro angolare, se visto da una stella qualsiasi. Siamo costretti a parlare di angoli, dato che essi sono le uniche quantità leggibili sulla sfera celeste, una sfera che ha come centro l’osservatore e raggio indeterminato, per definizione. Poco importa, però, questo fatto, dato che qualsiasi sia il raggio della sfera celeste l’angolo rimane sempre lo stesso.
Ricordiamo che due stelle che stanno a distanze anche molto diverse dall’osservatore, possono essere viste molto vicine nella sfera celeste, dato che l’angolo tra le congiungenti osservatore-stella può essere molto piccolo. Per maggiori chiarimenti potete guardare QUI.
Teoricamente, la misura di un diametro angolare stellare potrebbe dirci la distanza della stella. Basterebbe che un fotone che arrivasse da lei ci comunicasse, in gran segreto, il diametro reale. Noi misureremmo quello angolare e un semplice triangolo ci darebbe la distanza tra noi e la stella, come mostrato in Fig. 1.
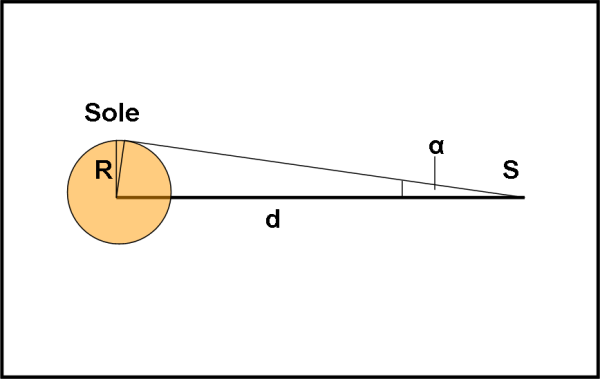
Non ci sarebbe nemmeno bisogno di usare il seno o la tangente dell’angolo, dato che i diametri stellari sono ridicoli rispetto alla distanza delle stelle e gli angoli sono piccolissimi. In altre parole la tangente coincide con il seno e anche con l'angolo stesso espresso in radianti. In parole matematiche, possiamo scrivere:
tan α = R/d
sin α = R/d
α = R/d (con α espresso in radianti)
Ogni scrittura è praticamente la stessa identica cosa. Ne segue che possiamo scrivere:
d = R/α
Si capisce benissimo che questo metodo è praticamente impossibile da utilizzare, dato che la misura del raggio R in km non ci viene detto da nessun fotone… e anche quello angolare non è cosa facile da determinare.
Per il nostro quiz, invece, conosciamo il raggio del Sole e conosciamo le distanze delle stelle da cui vogliamo vedere il Sole. La formula di prima viene scritta:
α = R/d
Essa ci fornisce immediatamente il raggio angolare del Sole, ossia quello che la stella scelta vede proiettato sulla sua sfera celeste.
Se, poi, non ci piacciono i radianti, basta moltiplicare il risultato per 57.30 e abbiamo il valore espresso in gradi.
Più che il calcolo del diametro apparente (basta moltiplicare il raggio angolare per due) per ogni singola stella, conviene disegnare una figura che riporti in ascissa la distanza delle stelle e in ordinata il diametro espresso in gradi. In tal modo si capisce subito se vale la pena disegnare il Sole come un dischetto o come un punto!
La funzione da rappresentare è:
y = R/x (dove y è il raggio angolare del Sole e x è la distanza dal centro del Sole).
La funzione la conosciamo molto bene ed è un’iperbole con asintoti gli assi x e y.
Attenzione, però… per valori della distanza comparabili con quelli del raggio solare, la formula non può essere approssimata e va usata, ad esempio, quella con sen α. A noi però non interessa più di tanto, dato che lavoriamo con distanze sicuramente maggiori di 4 anni luce… Possiamo perciò far partire la curva da quel punto (se volessimo il diametro solare visto dai suoi pianeti useremmo la formula più esatta).
Ma, vale la pena disegnare la curva? Alla distanza di 4 anni luce, il Sole avrebbe un raggio pari a circa 4 millesimi di secondo d’arco. Tanto vale disegnarlo sempre come un punto… In realtà, non sono molte le stelle di cui si riesce a misurare il diametro con metodi interferometrici.
Ammetto di averla fatta lunga, quando bastavano poche righe. Tuttavia, abbiamo cominciato a parlare di distanze angolari, la base della trigonometria sferica.
Passiamo, perciò al secondo quiz, decisamente più interessante.
Ripeto ancora una volta quanto richiesto. In qualsiasi notte limpida vediamo il cielo trapuntato di stelle. Alcune di loro appaiono molto vicine. Ma lo sono realmente? Spesso e volentieri no e tra di loro vi sono, magari, molti anni luce di differenza. Ne segue che tutto ciò che vediamo in cielo è solo e soltanto “apparenza”, del tutto relativo alla posizione dell’osservatore (ossia del Sole), così come le figure che, con grande fantasia, gli antichi hanno chiamato costellazioni.
Niente di fisico, quindi, ma un qualcosa che può, comunque, essere utile per identificare di quale stella stiamo parlando. Di ogni stella, infatti, siamo in grado di dare nome e cognome, ossia un paio di coordinate che la identificano tra tutte le altre. Di questi tipi di coordinate parleremo durante la trattazione dell’astronomia sferica. Al momento ci basti dire che le stelle sono separate tra loro da angoli (o archi) che si misurano in gradi, primi e secondi (o anche in ore, minuti e secondi).
Se vediamo una certa stella in cielo, ad esempio Vega, vedremmo intorno a lei molte stelle più o meno luminose, a volte realmente vicine a lei, ma a volte molto più lontane o -magari- anche più vicine. La sfera celeste del Sole è quella che vediamo (la distanza tra Terra e Sole è irrilevante per lo scopo del nostro esercizio) e le distanze angolari possono essere misurate con grande accuratezza, ma ben poco si può fare di più.
Ad esempio, se volessimo disegnare il cielo stellato visto da Vega (ossia la SUA sfera celeste) non potremmo farlo assolutamente, dato che non abbiamo la più pallida idea di come siano veramente distanti tra loro le stelle che vedrebbe la stella. Ovviamente, se una stella fosse realmente vicina al Sole, è molto facile che Vega la vedrebbe vicina alla nostra stella, ma… anche Vega non è molto lontana e gli angoli fanno in fretta a cambiare.
Lasciamo, quindi, da parte per un attimo la sfera celeste dell’osservatore e parliamo soltanto di angoli. A partire da questi, sarà poi facile disegnare la sfera celeste corrispondente, rappresentabile da distanze angolari di varia lunghezza, dipendenti, ovviamente dal punto di vista.
Consideriamo la Fig. 2, dove S è il Sole e S1 la stella di cui vorremmo rappresentare la sfera celeste e, in particolare, quella parte che sta vicino al Sole. A questo punto è fondamentale conoscere la distanza di S1 da S, così come è obbligatorio conoscere la distanza delle altre stelle dal Sole. C’è bisogno di sapere anche la distanza di S1 dalle stelle? No, non ce n’è bisogno, dato che basta un semplice triangolo per ricavarla. Possiamo, quindi, trascurarla del tutto (almeno per adesso).
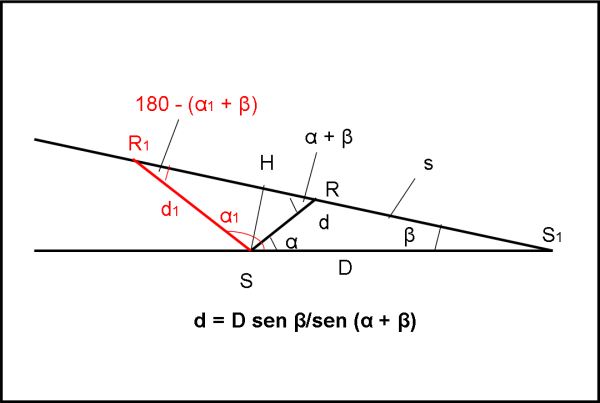
Possiamo partire con la nostra strategia operativa, che è facilmente trasferibile a un semplice programmino da computer, anche antidiluviano.
Cominciamo, ad esempio, a scegliere le stelle che sono viste da S1 in un intorno che sottende un certo angolo β rispetto alla posizione del Sole. β è l’angolo formato da S1S e S1R, dove R identifica tutte le stelle che sono viste (sempre che siano abbastanza luminose) da S1 a una distanza uguale a β gradi rispetto al Sole.
La Fig. 2 è una figura piana, ma è facile intuire che essa rappresenta la sezione di un cono di apertura β, con S1S come asse. Possiamo, perciò, dire che tutte le stelle che sono contenute entro un angolo β dal Sole sono quelle che la stella S1 vede in un cerchietto di β gradi rispetto alla posizione centrale del Sole, sulla sua sfera celeste. Solo loro hanno una distanza angolare dal Sole, se viste da S1, minore o uguale a β.
Simpatica conclusione, ma come scegliere queste stelle fra tutte quelle catalogate? Non è difficile. Basta trovare una relazione che leghi l’angolo α, sotto cui è vista, dal Sole, una certa stella R rispetto alla stella S1 (ossia la distanza angolare tra S1 e R nella sfera celeste del Sole) e la sua distanza d, tale che finisca dentro al cono definito precedentemente.
Ripassando al piano, ciò vuol dire risolvere il triangolo SRS1. Notate che R può stare sia dalla parte di S1 sia dalla parte opposta rispetto a S. L’importante è che sia posizionata all’interno del cono.
Cosa conosciamo del triangolo S1RS? Molte cose… L’angolo α, la distanza d = SR, la distanza SS1 = D e l’angolo β, scelto come primo passo per costruire il disegno della sfera celeste di S1 nella direzione del Sole.
La relazione cercata si trova subito attraverso il teorema dei seni che noi ancora non conosciamo. Possiamo, comunque ottenere lo stesso risultato in modo leggermente diverso (e non è l’unico modo).
Consideriamo il triangolo SRH (H è il piede della perpendicolare da S alla retta S1R). Da lui si ottiene:
SH = d sen (α + β)
Infatti, l' angolo SRS1 è uguale a 180 - (α + β) e, quindi, l'angolo HRS è proprio α + β
Dal triangolo S1SH si ha:
SH = D sen β
E, quindi:
d sen (α + β) = D sen β
d = D sen β/sen (α + β) …. (1)
D e β sono costanti e quindi la (1) è la relazione cercata tra α e d. In altre parole, al variare di α si trova il corrispondente valore di d che pone la stella a una distanza angolare uguale a β.
Notiamo che la relazione vale ovviamente anche per una stella R1 posta dalla parte sinistra del Sole a una distanza d1, dato che:
sen (180 - (α1 + β)) = sen (α1 + β) (disegnato in rosso nella Fig. 2)
Se siamo interessati solo alle stelle comprese entro l’angolo β, basta inserire il segno minore nella (1). Se, invece vogliamo conoscere la posizione delle stelle che distano dal Sole esattamente l’angolo β si tiene l’uguale. Ovviamente, abbiamo fatto vedere il tutto su un solo piano, ma la stessa situazione vale per tutto il cono.
Facendo variare β tra 0 e la distanza angolare massima richiesta, si descrive la parte di sfera celeste vista da S1 nei dintorni del Sole.
Per completare il disegno alla “stellarium”, basta calcolare le magnitudini apparenti rispetto a S1 delle varie stelle comprese nel campo attorno al Sole. Di esse si deve conoscere la magnitudine assoluta e la distanza da S1. La seconda non è altro che s = RS1, ricavabile facilmente dal triangolo SRS1 con il teorema di Carnot:
s2 = D2 + d2 – 2Dd cosα …. (2)
Lo so, lo so, non lo conoscete ancora, ma lo affronteremo prima di iniziare la trigonometria sferica. Chi vuole, però, può ricavare la formula (2) da solo, trafficando un po’ con triangoli rettangoli. Esso è detto anche il teorema di Pitagora dei triangoli non rettangoli. D’altra parte, per α = 90, la (2) diventa proprio il ben più celebre teorema.
Conosciuta anche s, la magnitudine apparente m vista da S1 di una stella R è data da:
m = M – 5 + 5 log s
dove M è la magnitudine assoluta e s è la distanza espressa in parsec. Formula questa usata spesso, ma che quanto prima ricaveremo direttamente (non l’ho trovata nell’archivio…).
Considerate tutto ciò l’antipasto per l’astronomia sferica. D’altra parte, conoscere la geometria sferica è un passo importante anche per relatività generale…
QUI potete trovare il quiz.






5 commenti
Nelle vostre risposte c'è stata inizialmente un po' di incomprensione del significato del quiz. Pensavo di essere stato chiaro, ma mai essere sicuro di qualcosa ;-) . Qualcuno ha scelto la strada giusta, ma in generale mi sono accorto di non avere mai approfondito i temi dell'astronomia sferica. Cosa non giusta, anche perché trattare con una geometria non euclidea può essere molto utile come preambolo alla relatività generale. Tuttavia, prima, finiremo il problema della derivazione delle leggi di Keplero dalla legge di Newton.
Ancora matematica e geometria... ma ci penseranno i nostri ricci a farci sorridere e riflettere... e magari anche Giorgia che è da un po' che latita con le sue splendide fotografie
e magari anche Giorgia che è da un po' che latita con le sue splendide fotografie 
Caro Enzo, come al solito quando c’è qualcosa che non conosco (Teorema di Carnot) mi piace ricavarlo…
La figura mostra un triangolo simile a quello che nel quiz è indicato come S0-R-S1
http://postimg.org/image/f1982iqy3/
Dapprima ho suddiviso il triangolo in due triangoli rettangoli: (S0-R-B) e (B-R-S1).
Applicando il teorema di Pitagora al Triangolo rettangolo (B-R-S1), il quadrato della sua ipotenusa S è uguale alla somma dei quadrati dei due cateti (B-R) e (B- S1):
S² = (B-R)² + (B-S1)²
Guardando, invece, l'altro triangolo rettangolo (S0-R-B), la cui ipotenusa non è altro che d, il cateto (B-R) è uguale a d sin (α).
Ne segue che (B-R)² = d²sin²(α).
L'altro cateto di questo triangolo, ossia il segmento (S0-B) è uguale a d cos (α).
Per trovare il valore di S, non resta che ricavare il valore del secondo cateto (B-S1), partendo dalla relazione (B-S1) = D – (S0-B), ricordando che (S0-B) = d cos (α).
(B-S1) = D – d cos (α), quindi:
(B-S1)² = (D - d cos(α))² = D²+ d²cos²(α) - 2Dd cos(α)
Non resta che applicare il teorema di Pitagora al triangolo rettangolo (B-R-S1):
S² = (B-R)² + (B-S1)²
S² = d²sin²(α) + D²+ d²cos²(α) - 2Dd cos(α)
S² = D²+ d²(sin²(α) + cos²(α)) - 2Dd cos(α)
Dal cerchio trigonometrico di raggio unitario 1, si ottiene la relazione generale:
(sin²(α) + cos²(α)) = 1
Ne segue che:
S² = D²+ d²(1) - 2Dd cos(α)
S² = D²+ d² - 2Dd cos(α)
che è proprio la formula indicata come (2) nel quiz.
Paolo
Ottimo!!!!
(anche se io mi ero fatto scappare uno 0 al posto di 9o... devo fare le cose con più calma... scusate!)
Caro Enzo sono andato a ripescare questo vecchio quiz.
Ho provato a realizzare una figura sulla base di quanto descritto nella soluzione, usando più stelle.
L'angolo β rappresenta il campo visivo entro cui devono stare le stelle che vengono viste nei dintorni del Sole , viste dalla stella di riferimento.
Per esempio ponendo β = 20°, si possono mostrare tutte le stelle che appaiono entro il limite di 20° di distanza angolare rispetto al Sole in ogni direzione spaziale (visto in 3 dimensioni si tratta di un cono).
Nella figura (piana) viene mostrato anche la parte di sotto, in cui la visuale è speculare (stesso angolo β).
Ovviamente tutte le stelle che soddisfano la relazione d < D sen β/sen (α + β) si trovano all'interno del campo visivo fissato (angolo β) rispetto alla posizione del Sole.
Non contento ho provato a rappresentare la curva che descrive d in funzione della variazione dell'angolo α (posizione stella rispetto al sole).
In pratica ho fissato una distanza D tra stella e Sole pari a 4 anni luce, ho fissato un angolo β= 20°, dopodiché facendo variare l'angolo α, ho indicato come varia la distanza d (ovviamente le stelle visibili sono quelle che in relazione all'angolo α hanno una distanza uguale o inferiore a d ≤ D sen β/sen (α + β))).
Non contento, usando la relazione s² = D² + d² – 2Dd cos α, ho mostrato anche la curva della distanza s delle stelle dalla stella di riferimento (utile per calcolare la magnitudine apparente).
Mi sembra inutile commentare queste due curve (sempre che la rappresentazione sia corretta)....
Paolo
Sei fantastico Paolino... rappresenti proprio la voglia di conoscere e di provare!!