Categorie: Astronomia Elementare Matematica
Tags: diametro apparente distanza angolare geometria sfera celeste Sole e stelle vicine trigonometria
Scritto da: Vincenzo Zappalà
Commenti:29
Doppio QUIZ per ridimensionare stellarium & co.(e i loro ammiratori incondizionati) */***
Non stiamo, infatti, parlando delle equazioni della RG di Einstein, ma di piccole prove che possono servire per comprendere meglio la struttura dell’Universo a noi vicino. Niente pappa-pronta alla stellarium (che è utilissimo solo per orientarsi nel cielo), ma esercizi che stimolino la mente. Grazie quindi a questi “grandi” astronomi e alle loro “scoperte” per darci il via…
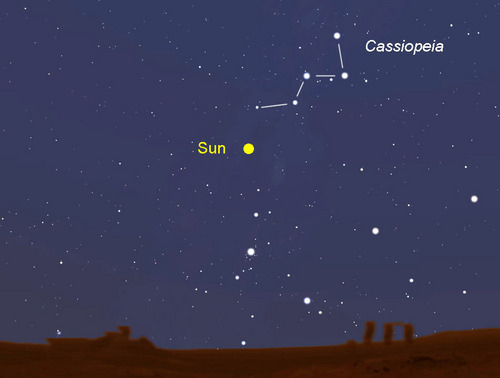
La frase che riporto la dice lunga sull’umiltà intellettuale di chi scrive: “ … e vogliamo parlare delle loro foto, in cui si vede come appare il nostro Sole se visto da un pianeta ruotante intorno alle stelle più vicine? Innovative anche quelle foto: in internet si trovavano finora solo rare rappresentazioni del Sole visto da alcune pochissime stelle vicine (Alpha Centauri ad esempio con la ben nota estensione della costellazione di Cassiopea...). Probabilmente nessuno aveva mai pensato di parlare di come si vedrebbe il Sole ad esempio dalla stella 41 Arae: io l'ho fatto!!”.
Mamma mia, siamo di fronte a un genio? No, cari amici, basta un calcoletto quasi infantile (triangolo rettangolo) per la parte essenziale e un minimo di costruzione geometrica per la parte di rifinitura. E poi saremo in grado di competere con stellarium e con chi lo usa per farsi credere un innovatore astronomico.
PRIMO QUIZ *
Come fare a disegnare il diametro apparente del Sole visto da una stella qualsiasi posta a una certa distanza d?
Vi chiedo, ovviamente il procedimento geometrico e -se volete- potete fare anche una semplice tabellina dove a ogni distanza in anni luce si può affiancare il relativo diametro solare espresso in secondi d’arco, ricordandoci che sulla sfera celeste i diametri e le distanze, in genere, si misurano in gradi, primi e secondi d’arco. In altre parole, le distanze sulla sfera celeste sono distanze angolari.
Mi vergogno quasi di aver proposto questo quiz, di una banalità estrema, ma potrete rendervi conto di quanto sia semplice rappresentare il Sole visto da una QUALSIASI stella della nostra galassia. Ovviamente, bisogna conoscere la distanza della stella…
Non è molto che questo tipo di approccio è stato usato per illustrare qualcosa di molto più vicino…
SECONDO QUIZ ***
Leggermente più difficile, ma piuttosto interessante.
Come trovare, graficamente, le stelle che sarebbero viste, da un data stella, a una certa distanza angolare dal Sole ?
Mi spiego meglio..
Immaginiamo di trasportarci su una certa sella, come Sirio o Vega o quella che volete. Da questa stella il Sole si vede con un certo diametro angolare (come si ricava dal PRIMO quiz). Tuttavia, si vedrebbero moltissime stelle di sfondo, più o meno vicine angolarmente al Sole. Non sono certo le stesse che noi vediamo vicino a Vega o Sirio o quello che volete. Il QUIZ ci chiede di sviluppare il procedimento che ci permetta di disegnare le stelle (solo come un punto, per facilitare la faccenda) nella posizione relativa al Sole, se viste da Sirio o Vega o quello che volete. Direi che più chiaro di così... Insomma, vogliamo disegnare il Cielo stellato visto da una stella qualsiasi nei dintorni del nostro Sole.
Nuovamente, abbiamo bisogno, di conoscere le distanze dal Sole. Non è probabilmente difficile trovare anche la formula ricorrente. In altre parole, data la distanza angolare rispetto al Sole (vista da una certa stella), a che distanza e in che posizione nella sfera celeste devono essere cercate le stelle che soddisfino quanto richiesto. Penso che potremo sfruttare questo secondo esercizio per imparare qualcosa di più sulla trigonometria. In fondo, basta trovare la relazione tra posizione nella sfera celeste e distanza della stelle richieste. Può anche darsi (e lo spero) che qualcuno trovi un sistema più rapido e semplice del mio. Ben venga, ne sarei pienamente soddisfatto.
In questo modo sapremmo quali stelle mettere come sfondo al nostro Sole… partendo da zone vicinissime e spostandosi verso l’esterno (ossia, cambiando la distanza angolare tra Sole e stelle prospetticamente vicine)
Ovviamente, le figure sono essenziali!
Ripeto ancora il succo di questo articolo e di altri come lui. Si vedono spesso risultati visivamente interessanti forniti come “atti di fede”. A volte, ciò può anche essere dovuto a un’effettiva difficoltà dei calcoli necessari (vedi il caso dell’equazione differenziale che troveremo per arrivare alla prima legge di Keplero); altre volte (e sono i casi più frequenti), non si vuole assolutamente che i lettori riescano a capire il procedimento per rendere più essenziale il ruolo di chi dovrebbe, invece, spiegare e divulgare. Quest’ultimo caso rappresenta un esempio di pessima divulgazione.
Dopo aver capito il come e il perché, ben vengano le figure “barocche” dei vari programmini pappa-pronta, dato che il procedimento che usano è ormai stato recepito perfettamente. Considerare, per partito preso, i lettori "troppo ignoranti per capire", è un segno di arroganza intellettuale se non, addirittura, di puro desiderio di mettersi in mostra o -addirittura- di scarsa conoscenza intrinseca.
QUI trovate qualche suggerimento e QUI la soluzione del quiz






29 commenti
beh? nessuno risponde? capisco che il primo quiz è veramente banale (e già toccato altre volte), ma il secondo è divertente e può dar luogo a varie metodologie d'approccio.
Avanti miei prodi!!!!!!!!!!!!!!
mi limito al primo quiz
considero un osservatore posto sulla superficie di una stella a distanza d dal Sole. Se ho compreso bene la richiesta del quiz, devo determinare il diametro apparente del Sole misurato in secondi di arco, così come visto dal suddetto osservatore.
con riferimento ai simboli indicati in figura, il diametro apparente del Sole sarà pari a
Considerando uno dei due triangoli rettangoli visibili in figura, sarà:
da cui
essendo R = metà del diametro , posso scrivere :
quindi:
Se l'osservatore, anziché trovarsi su una stella , si trovasse sulla Terra , sapendo che D = 1.391.400 km e d = 149.600.000 km, otterremmo un diametro apparente del Sole pari a 0,533 gradi, pari a 31,97 primi, pari a circa 1918 secondi d'arco.
In merito al secondo quiz, non sono sicuro di avere capito bene la richiesta.
aiuto, non si vede la figura ! Questo è il link :
http://propagazioneionosferica.altervista.org/diametroapparentedelsole.jpg
aiuto(2) : non si vedono neanche le formule
Ho fatto due prove, tutto sembra funzionare ;-)
Non so il motivo, ma io continuo a non vedere né le formule né l'immagine. Le formule le avevo scritte con il Latex equation editor disponibile nella finestra di scrittura delle risposte (fx).
Ad ogni modo, allego qui la risposta in formato immagine (scritta con word e poi salvata come immagine):
Se non si vede , questo è il link:
http://propagazioneionosferica.altervista.org/rispostaquizdiametroapparanete.JPG
Cerco di rispondere alla seconda domanda: "Come trovare, graficamente, le stelle che sarebbero viste, da un data stella, a una certa distanza angolare dal Sole ?"
Per brevità chiamo la stella dalla quale vediamo il sole e le altre stelle S1.
Gli oggetti che visti da S1 sono ad una certa distanza angolare (beta) dal Sole si trovano sulla superficie di un cono che ha al vertice S1 e il Sole sull'asse.
Prova ad allegare una figura che si trova a questo indirizzo: http://i.imgur.com/S7qYOmk.jpg
Quindi gli oggetti che S1 vede ad una certa distanza angolare (beta) dal Sole possono essere ovunque intorno al Sole ad esclusione di un'area opposta ad S1 di raggio angolare beta.
Quello che cambia è la distanza di questi oggetti dal Sole che dipende in modo complesso dalla distanza angolare (alpha) che li separa da S1.
Nella prossima figura provo a ricavare questa relazione con un po' di trigonometria applicata al triangolo Sole-S1-Oggetto.
La figura si trova qui: http://i.imgur.com/vJPeYt0.jpg
Nella prossima figura ho messo in un grafico questa relazione tra la distanza angolare di O da S1 (alpha) e la distanza di O dal Sole per due valori di beta.
La figura è qui: http://i.imgur.com/ZSSgm6q.jpg
Il grafico conferma che gli oggetti che S1 vede ad una certa distanza angolare (beta) dal Sole possono essere ovunque intorno al Sole ad esclusione di un'area opposta ad S1 di raggio angolare beta dove il grafico si impenna.
Fabrizio
Neanche io riesco a vedere le figure che ho provato a caricare.
Inserisco una formula per vedere se si vede:
Fabrizio
non riesco a capire... Marko ci sta studiando... speriamo che riesca a risolvere...
Caro Enzo, innanzitutto provo a rispondere alla prima parte del quiz.
La prima figura si limita a mostrare come l'immagine del Sole con l'aumentare della distanza d si rimpicciolisce sempre più, secondo la relazione Diametro apparente = Diametro Reale /distanza.
http://postimg.org/image/qljy6poor/
La figura, però indica solo come cambia la scala dell'immagine all'aumentare della distanza... qualcosa di simile all'esempio dei binari delle prime lezioni di matematica
http://www.infinitoteatrodelcosmo.it/2013/10/10/1-zero-e-infinito/
http://www.infinitoteatrodelcosmo.it/2013/10/29/2-zero-e-infinito-si-incontrano-e-si-sommano/
In questo caso però abbiamo a che fare con la proiezione del diametro del Sole su una circonferenza (disegnando in due dimensioni), ossia con un tratto di circonferenza pari al diametro del Sole.
Un radiante è proprio la proiezione del raggio sulla circonferenza (un arco di circonferenza lungo quanto il raggio).
http://postimg.org/image/hl2zwwrsr/
Per ottenere le misure in gradi, basta vedere a cosa corrisponde un radiante, ricordando che la circonferenza = 2 π radianti e che una circonferenza = 360°:
1 radiante = 360°/2 π = 57,29578°, moltiplicando i gradi per 3600 si ottiene l'equivalente in secondi d'arco:
1 radiante = 206264,81 secondi d'arco.
Per trasformare il Raggio del Sole in secondi d'arco, basta moltiplicare il raggio per 1 radiante espresso in secondi d'arco.
Qui, però, sulla circonferenza si proietta il Diametro, ossia 2 volte il raggio per cui basta moltiplicare il Diametro del sole per 1 radiante espresso in secondi d'arco, ossia: 206264,81.
Il Diametro Reale del Sole espresso in chilometri è uguale a 1391400 Km, ma man mano che ci si allontana il Suo Diametro apparente diventa sempre più piccolo secondo la proporzione
Diametro apparente = D/d
Quindi basta moltiplicare il Diametro apparente per 206264,81 per ottenere la dimensione apparente del Sole espressa in secondi d'arco:
Diametro apparente (in secondi d'arco) = D/d 206264,81.
http://postimg.org/image/cini7me9n/
Applicando la formuletta appena ricavata, risulta facile trovare la dimensione apparente del Sole al variare della distanza d:
Distanza minima dalla Terra : 147 098 074 Km
Diametro apparente = 1 391 400/147 098 074 (206264,81) = 1951”
Distanza massima dalla Terra : 147 098 074 Km
Diametro apparente = 1 391 400/152097701 (206264,81) = 1887”
Distanza 1 anno luce (in km) = 299792 x 3600 x 24 x 365,256 = 9460895365148 Km
Diametro apparente = 1 391 400/9460895365148 (206264,81) = 0,030335”
A 4,5 anni luce Diametro apparente = 0,00674”
A 30 anni luce Diametro apparente = 0,0010”
A 100 anni luce Diametro apparente = 0,0003”
Per ora mi fermo qui...
Paolo
Alcune informazione per Marko.
Le figure e le formule si vedono correttamente durante la composizione del messaggio. Spariscono dopo il send. Il mio browser è Firefox.
Vedo anche che il mio commento è mercato come "Your comment is awaiting moderation."
Fabrizio succede lo stesso anche a me.... inoltre se carichi più di 3 immagini il commento viene messo automaticamente in attesa di moderazione...
Speriamo che Marko riesca a risolvere il primo problema... a me sembra un problema di filtri antispam...
Paolo
il problema dei commenti in attesa è dovuto a troppi link (è cosa normale). Non è normale invece il resto... mando anche il tuo secondo commento a Marko, intrecciando i diti....
Paolo,
se tu calcoli l'angolo che sottende il raggio del Sole hai già il raggio angolare. Con i numeri a disposizione va più che bene...
Per la seconda parte poter disegnare è fondamentale....
AIUTO MARKO!!!!!!!!!!!!!!!!!!!!!!!!!
a me funziona per le formule...
Forse non servirà a niente... però potreste provare a ripulire la cache premendo contemporaneamente ctrl+maiusc+canc, dare ok alla finestra di dialogo, poi chiudere e riaprire il browser. Male che vada, sarà inutile, ma non farà danni!
ora tutto sembra a posto (parola di Marko!).
A parte Fabrizio, nessuno ha provato a risolvere la seconda parte, di cui vorrei però un'azione pratica atta a selezionare le stelle necessarie allo sfondo dell'immagine di stellarium...
Forza con le figure!!!
Temo di non aver capito ancora bene il problema, ovvero se devo considerare inizialmente il sole come sistema di riferimento.Comunque provo a fare un disegno.Per costruirlo, avendo a disposizione le distanze d1,d2,d3 dal sole e gli angoli fra S1 S2 prima disegno la parte blu (l'angolo e la distanza determinano le posizioni reali S1,S2,S3) ; se devo vedere la situazione da S3 traccio semplicemente le congiungenti che andranno ad intersecare la sfera celeste nei punti rossi dalla parte opposta.
caro Umberto,
il suco è proprio quello. COME FARE A DISEGNARE I DINTORNI DEL SOLE SULLA SFERA CELESTE SE FOSSIMO SU UNA STELLA QUALSIASI.
Dunque, se ora ho capito bene, con riferimento alla figura di Umberto, sono note le distanze angolari tra S1, S2 ed S3 viste dal Sole (cioè sulla sfera celeste centrata sul Sole) nonché le distanze vere di S1, S2 ed S3 dal Sole, e dobbiamo calcolare , per esempio, le distanze angolari tra Sole, S2 ed S1 come viste da S3. Se questa è la "consegna" del secondo quiz, restando nel caso, più semplice, illustrato dalla figura di Umberto, cioè nel caso che Sole, S1, S2 ed S3 giacciono tutte su uno stesso piano, allora mi verrebbe da applicare il teorema dei seni al triangolo (indico il Sole con "S") S3-S-S2 e poi al triangolo S3-S-S1. Chiamo con :
"alfa" l'angolo S3-S-S2
"beta" l'angolo S2-S-S1
"gamma" l'angolo S-S3-S2
"delta" l'angolo S2-S3-S1
Considero il triangolo S3-S-S2. Per il teorema dei seni:
S2S/sen(gamma) = S3S/sen[180-(alfa+gamma)]
cioè:
S2S/sen(gamma) = S3S/sen(alfa+gamma)
da cui, sviluppando ed esplicitando rispetto a gamma, ottengo:
gamma=arctan[sen(alfa)/(S3S/S2S-cos(alfa))]
una volta noto gamma, fissato il raggio della sfere terrestre (che in verità in questo caso sarebbe una circonferenza..) centrata su S3, posso disegnare su essa la posizione di S2 rispetto al Sole, come visti appunto da S3.
Analogamente, per S1, considero il triangolo S3-S-S1 e applico il teorema dei seni. Ma aspetto per sapere se ho capito bene la "consegna" . In fondo, credo che la difficoltà di fondo del secondo quiz sia proprio dovuta alla non sicura comprensione di ciò che si sa e di ciò che si vuole determinare.
. In fondo, credo che la difficoltà di fondo del secondo quiz sia proprio dovuta alla non sicura comprensione di ciò che si sa e di ciò che si vuole determinare.
Provo a rispondere alla seconda domanda con il fuoco sulla questione "COME FARE A DISEGNARE I DINTORNI DEL SOLE SULLA SFERA CELESTE SE FOSSIMO SU UNA STELLA QUALSIASI".
Se centro una sfera celeste su questa stella (S1) vedrei tutte le stelle proiettate su questa sfera. Centrando la nostra immagine sul Sole (S) avrei una situazione come quella in questa figura.
http://i.imgur.com/oX70oqR.jpg
Per comodità di immagine ho preso la sfera di raggio pari alla distanza tra Sole e S1, ma questa può essere riproporzionata arbitrariamente. Le immagine degli oggetti O1 ed O2 su questa sfera sono rispettivamente I1 ed I2, ottenuta dalla intersezione della sfera celeste e con le rette che congiungono S1 con gli oggetti.
Quello che ci interessa per determinare la distanza dal Sole di una delle immagini, per esempio I1, è l'angolo beta o la sua tangente, che per beta piccolo sostanzialmente coincidono. Comunque devo considerare la tangente di beta se voglio ottenere una immagine piatta.
tan(beta) dipende dalla distanza angolare vista dal Sole tra S1 e O1 (alpha) e dalle distanze dal Sole di S1 (ds) e O1 (do).
Nella prossima figura c'è come credo si possa trovare la relazioni tra queste variabili lavorando sul triangolo Sole-S1-O1. In particolare sfrutto il fatto che l'altezza n mette in relazione le grandezze dette sopra.
http://i.imgur.com/W1z2dsU.jpg
Questo ci permette di trovare a che distanza posizionare l'immagine I1 dall'immagine del Sole. Per completare la figura occorrerebbe aggiungere l'angolo, ma non ho ancora trovato come.
Fabrizio
devo conoscere le coordinate polari delle stelle a noi vicine (rispetto al sole o alla terra mi sembra indifferente date le grandi distanze delle altre stelle rispetto alla distanza terra-sole)
penso possa essere utile usare le coordinate equatoriali di Stellarium per gli angoli e la distanza delle stelle
scelta la stella questa sarà individuata dalle coordinate polari relative al piano equatoriale
infine eseguo un cambio di sistema di riferimento
il cambio di sistema di riferimento mi sembra eccessivo, dovrebbero bastare le nuove coordinate angolari
caro Gianni,
non capisco bene cosa intendi con: le coordinate equatoriali di Stellarium per gli angoli e la distanza delle stelle.
Cosa c'entrano le coordinate con la distanza?
E poi cosa intendi con coordinate polari?
Infine, usare stellarium è proprio quello che NON vogliamo fare.
Noi vogliamo proprio trovare un metodo che ci permetta di disegnare il cielo stellato visto da un'altra stella che non sia il Sole. Non mi sembra di avere descritto la richiesta in modo confuso...
Se poi non ho capito cosa intendi dire, ti pregherei di fare una figura chiarificatrice...
Per TUTTI:
temo che le idee sulla sfera celeste e sull'apparenza delle stelle nel cielo sia un argomento un po' confuso. Direi che, dopo la soluzione, sarebbe meglio buttarsi a pesce sulla trigonometria e astronomia sferica. Vedete com'è facile, a volte, parlare di RR e poi non sapersi districare sull'astronomia più antica e primitiva...
Bene, meno male che ho buttato lì questo quiz che pensavo molto più immediato... C'è sempre qualcosa a cui non pensi e che invece è molto importante
ci provo con le coordinate galattiche l e b
conosco la posizione della stella S1 di coordinate l1 e b1 e distante r1 da cui voglio vedere i dintorni della terra (o del Sole) e della stella S2 di coordinate l2 e b2 e distante r2
le coordinate da cui si vede la stella S2 dal punto di vista di S1 sono
l21= atan (r2 sen l2 - r1 sen l2)/(r2 cos l2 - r1 cos l1)
b21= atan (r2 sen b2 - r1 sen b2)/(r2 cos b2 - r1 cos b1)
credo di avere commesso un errore grave (ed alcuni di trascritta dalla brutta)
perché devo usare le proiezioni dei vettori r su due piani ortogonali: quello galattico e quello ortogonale ad esso che contiene l'asse polare (si chiama così?), per cui
l21= atan (r2*cos b2*sen l2 - r1*cos b1*sen l1)/(r2*cos b2*cos l2 - r1*cos b1*cos l1)
b21= atan (r2*cos l2*sen b2 - r1*cos l1*sen b1)/(r2*cos l2*cos b2 - r1*cos l1*cos b1)
caro Gianni... è molto più semplice... dai oggi scrivo la risposta (ma ci sono vari modi per ottenere lo stesso risultato)...
lo sapevo, comunque devo avere di nuovo commesso errori