Categorie: Relatività
Tags: contrazione delle distanze fattore di Lorentz Lampa Penrose quiz rotazione apparente Terrell
Scritto da: Vincenzo Zappalà
Commenti:19
La rotazione di Lampa-Terrell-Penrose, ovvero un cubo dispettoso **
Il quiz proposto non è un’idea scherzosa o poco più, ma ha un nome ben definito: effetto Terrell-Penrose ed è stato descritto solo nel 1959, anche se l’idea di base era già stata esposta nel 1924 da Lampa (più correttamente, alcuni lo chiamano effetto Lampa-Terrell-Penrose).
Esso spiega un’apparente discrepanza tra quanto aspettato dalla semplice contrazione delle lunghezze, descritta nella relatività speciale, e la realtà della situazione che simula perfettamente una rotazione dell’oggetto. L’aggettivo “apparente” nasce dalla visione delle cose che noi abbiamo nel mondo normale, dove le velocità sono nettamente inferiori a quella della luce. Un oggetto visto in movimento rapidissimo assomiglia perfettamente a ciò che noi associamo a una semplice rotazione.
La causa di questa “confusione” visiva è dovuta alla somma di due effetti relativistici, di cui uno è proprio la contrazione di Lorentz.
Andiamo con ordine e permettetemi di essere esageratamente minuzioso ed elementare nell’esposizione. Vi riempirò di figure (anche se ne basterebbero meno della metà…) per cercare di far comprendere a tutti un effetto veramente divertente oltre che geometricamente e fisicamente importante.
Se il quiz si meritava cinque asterischi, la spiegazione della soluzione non supera i due asterischi. Ha solo bisogno della formula della contrazione di Lorentz, di una semplicissima trigonometria e di un po’ di geometria elementare. Oltre che di molta attenzione…
Iniziamo partendo dalla figura tridimensionale che compariva nell’articolo che proponeva il quiz (Fig. 1): un cubo che si muove rapidissimo lungo l’asse x e viene visto (e fotografato) da un osservatore molto lontano dal cubo nella direzione dell’asse y. La lontananza dell’osservatore elimina ulteriori deformazioni di comprensione ben più ardua.
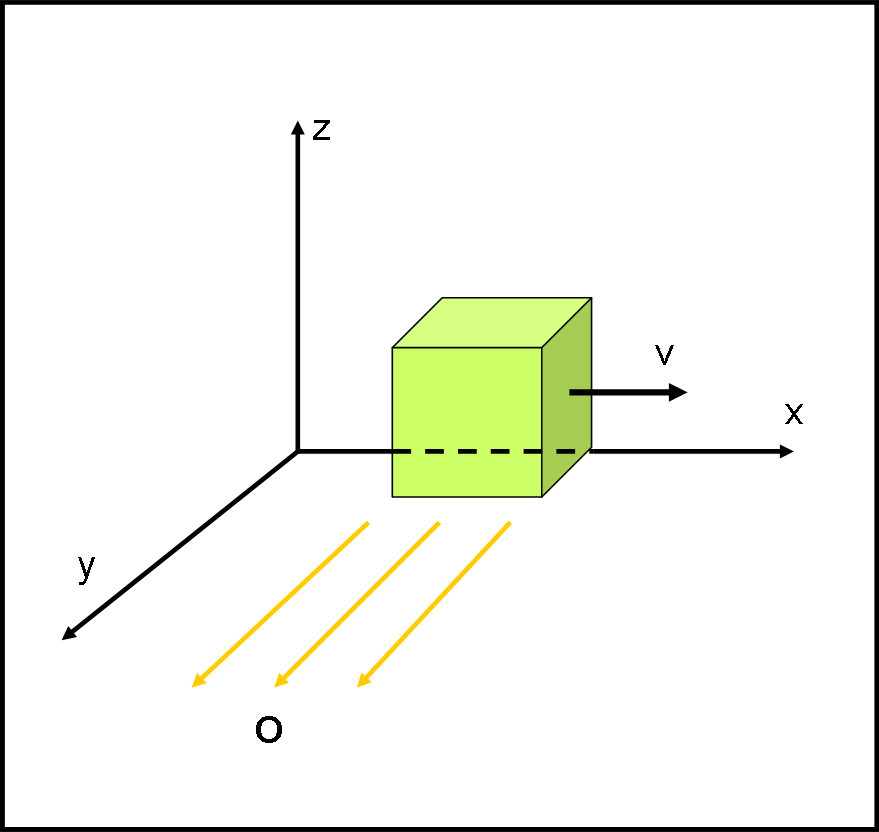
Iniziamo dalla Fig. 2 che ritrae il cubo fermo visto nel piano (x,z) dall’osservatore posto lungo y. Ciò che vede O è solo e soltanto un quadrato perfetto di lato L.

Se il cubo è, però, in movimento lungo x con velocità v, in questa direzione agisce la contrazione di Lorentz. L’altezza lungo z rimane, invece, inalterata. Da quanto sappiamo sulla relatività ristretta la lunghezza del lato L deve contrarsi in funzione del rapporto v/c. In particolare:
AB’ = L’ = l /γ = L (1 – (v/c)2)1/2
Questo risultato DEVE essere valido se no dovremmo buttare al macero la relatività ristretta…
Ciò che dovrebbe vedere l’osservatore è quindi un rettangolo di altezza uguale a L (non può avere contrazione) e di lunghezza AB’ = L’, minore della lunghezza propria L = AB, come mostrato in Fig. 3.
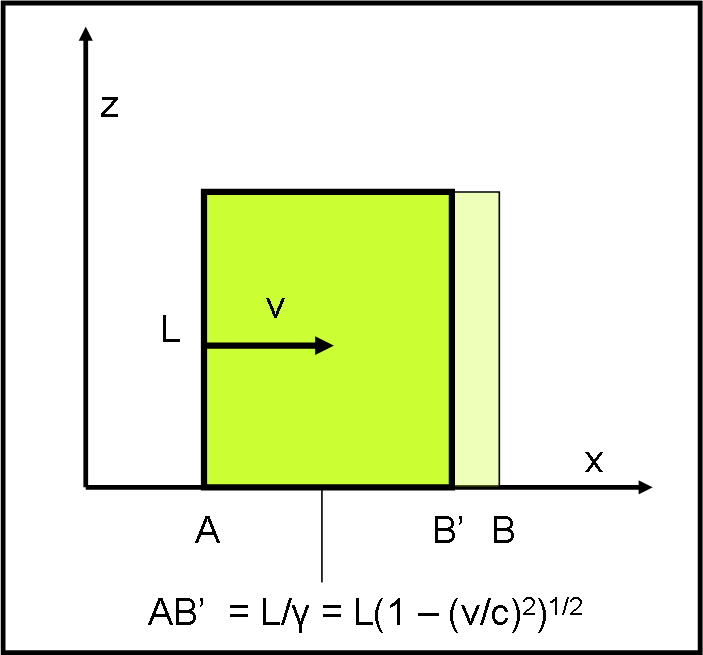
Vede davvero questo? Nemmeno per sogno… Dobbiamo, infatti, tenere conto di un altro effetto relativistico.
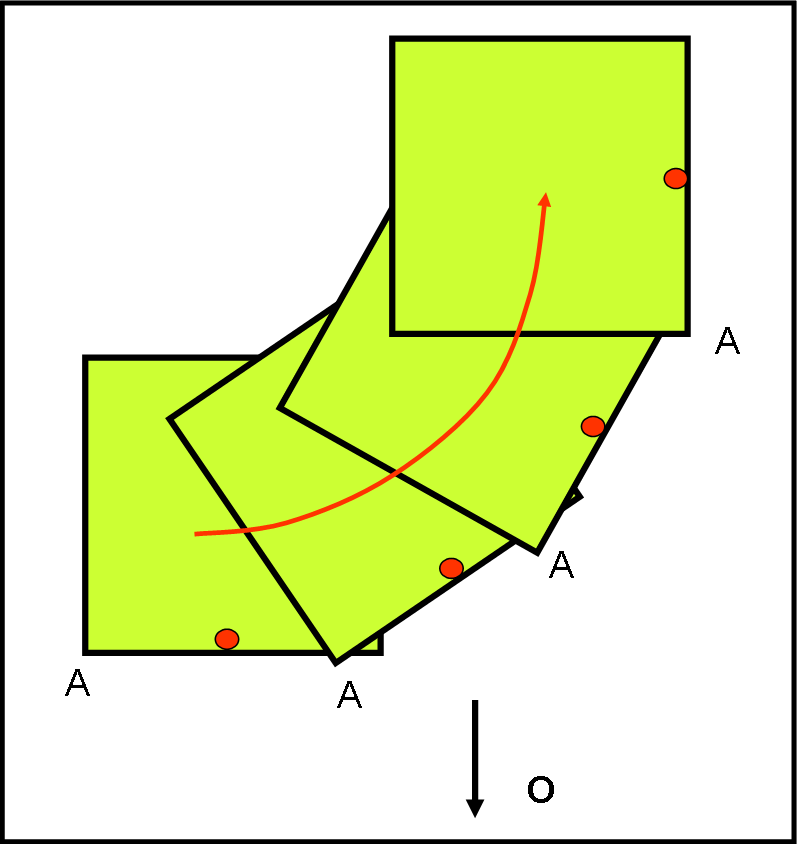
Consideriamolo a se stante…e utilizziamo la Fig. 4, in cui il cubo è visto dall’alto, ossia nel piano x,y. In un certo istante iniziale il cubo è quello verde scuro.
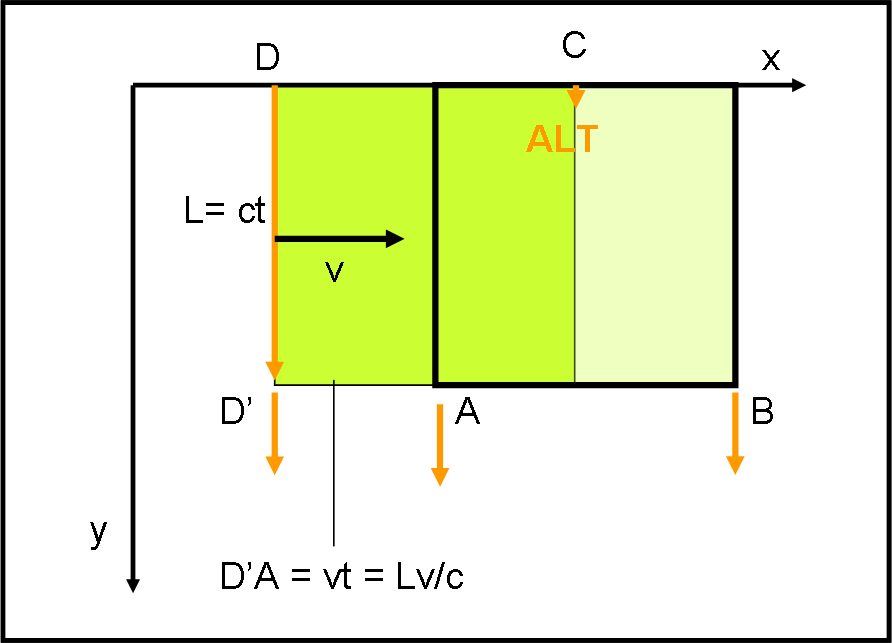
L’osservatore potrebbe ricevere, teoricamente, la luce che proviene da ogni parte del cubo (in fondo la QED non lo esclude…). Una buona parte di questa, però, non riesce ad arrivare, in quanto il cubo stesso la blocca (la probabilità ci aiuta in questo). Tuttavia, la luce che parte dalla faccia laterale sinistra (il moto è verso destra), di vertice D, può in realtà arrivare tranquillamente fino all’osservatore, dato che il cubo si sposta continuamente verso destra e le lascia via libera.
La luce di D, ad esempio, deve percorrere un certo tragitto (il lato L) prima di arrivare in D’ e assumere la stessa y del vertice A. Da quel punto in poi, viaggia di conserva con quella che parte da A. In modo molto brutale, potremmo dire che la luce di A (che deve arrivare fino all’osservatore O), aspetta che la luce di D l'affianchi prima di partire verso l’osservatore. In realtà nessuno aspetta nessuno, ma l’osservatore, in un certo istante, vede tutta la luce che arriva fino a lui, senza curarsi se è partita prima o dopo: l’importante è che giunga a lui nello stesso istante. Pensateci bene… è come il cielo notturno che vediamo in un certo istante, che contiene sia stelle vicine che stelle lontanissime, sia i pianeti che la Luna e magari anche qualche albero in primo piano. La luce è partita in tempi molto diversi, ma noi la vediamo tutta assieme nello stesso istante in cui facciamo una fotografia. Chiedete a Giorgia se non ci credete…
Tutto ciò capita, nel cubo, se la velocità del cubo è relativistica. Nel tempo t, in cui la luce percorre il tragitto L, da D a D’, il cubo si è spostato di una certa quantità non trascurabile verso destra, raggiungendo la posizione relativa al punto A dello spigolo in basso a sinistra. Ricordiamo ancora che lo spostamento del cubo ha fatto sì che la luce proveniente dal lato posteriore e da quello di destra si fermi subito, bloccata dal cubo, e quindi non possa arrivare fino all’osservatore. Solo la luce di D, del lato DA di sinistra, può giungere in D’ indisturbata.
Non solo quella però. A mano a mano che il cubo si muove, anche tutti gli altri punti del lato DA riescono a fare arrivare la loro luce fino all’osservatore, nello stesso istante in cui arrivano sia quelli di D che quelli di A e B (Fig. 4a).
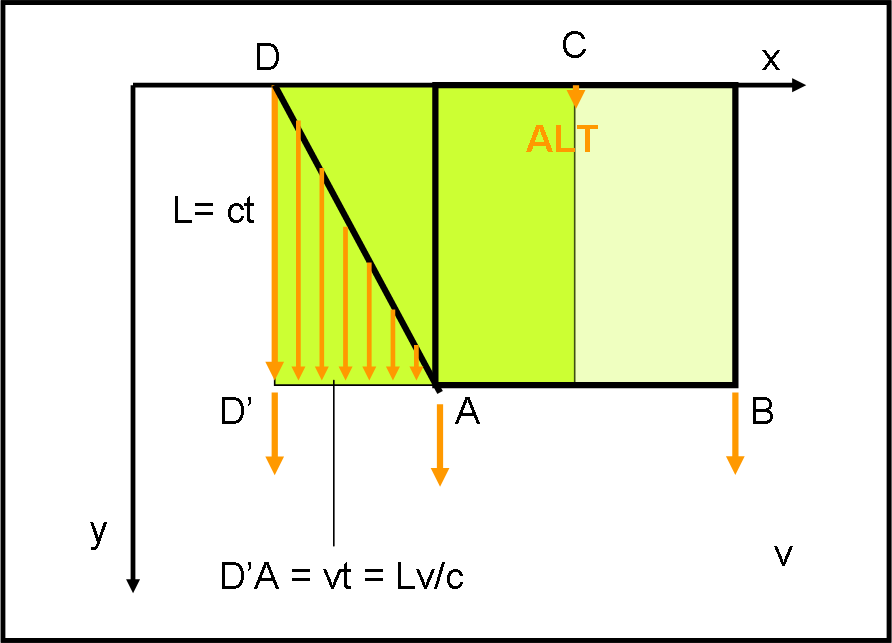
Ognuno la fa partire un po’ dopo, ma quello che conta è il momento in cui arrivano tutte insieme alla stessa distanza da O (considerato all’infinito). In altre parole, è necessario (per ottenere un arrivo contemporaneo in O) che tutta la luce proveniente dal cubo) giunga nello stesso istante sulla linea che va da D’ ad A, fino a B. Da quel momento in poi, la luce di tutti i punti viaggia parallela, coprendo lo stesso percorso, fino a giungere in O.
Ho sprecato un mucchio di parole, ma il concetto, come si vede chiaramente dalle Fig. 4 e 4a, è molto semplice.
Da quanto detto, possiamo ora scrivere due formule veramente elementari.
Quanto tempo impiega la luce a viaggiare da D a D’? Basta ricordare che la velocità della luce è pari allo spazio percorso diviso il tempo impiegato a percorrerlo, ossia:
c = L/t
da cui
t = L/c
Nello stesso intervallo di tempo t, però, il cubo si è spostato verso destra a causa della sua velocità v. Vale quindi anche:
D’A = v t
Ma t è lo stesso e, quindi, sostituendo, si ottiene:
D’A = v t = L v/c.
In conclusione, sulla base di quest'unica considerazione relativistica, ciò che l’osservatore vedrebbe nel piano (x,z) sarebbe quello che è mostrato in Fig. 5: la faccia laterale “contratta” di base D’A e la faccia frontale del cubo di base AB = L.

Accidenti, vedrebbe una figura dilatata, composta dalla faccia frontale senza deformazione e da quella laterale “ristretta” per un effetto di tipo “prospettico-relativistico”
Beh… fermi tutti! Non abbiamo tenuto conto della contrazione di Lorentz, che abbiamo già studiato precedentemente. Basta, allora, aggiungerla alla Fig. 5 e ottenere la Fig. 6. Notate che abbiamo solo contratto il lato AB e non certo quello D’A, dato che quest’ultimo si riferisce al lato lungo l’asse y e quindi non può subire contrazione.
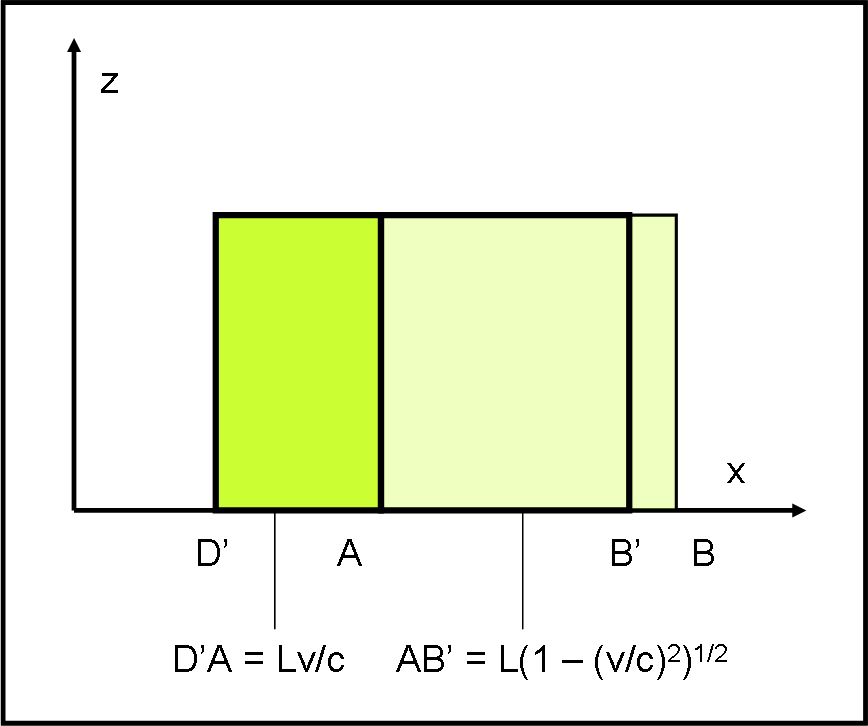
In conclusione, l’osservatore vede quello che è mostrato in Fig. 7: una faccia laterale contratta e una parte frontale, anch’essa contratta per effetto di Lorentz.
La lunghezza totale D è comunque maggiore del lato L che vedrebbe se il cubo fosse fermo. Altro che contrazione di Lorentz… lui vede una dilatazione!
D = Lv/c + L(1 – (v/c)2)1/2 ≥ L
Soffermiamoci, però, sui valori delle due lunghezze “visibili” D’A e AB’. In particolare, ricordiamoci di una celebre relazione tra seno e coseno di un angolo qualsiasi:
sin2α + cos2α = 1
da cui:
cos α = (1 – sin2α)1/2
Che ne direste, allora, se considerassimo un angolo α tale che
sin α = v/c ?
Andiamo a sostituire al posto di v/c il seno di questo angolo e i due segmenti diventano:
D’A = L v/c = L sin α
e
AB’ = L (1 – (v/c)2)1/2 = L (1 – sin2α)1/2 = L cos α
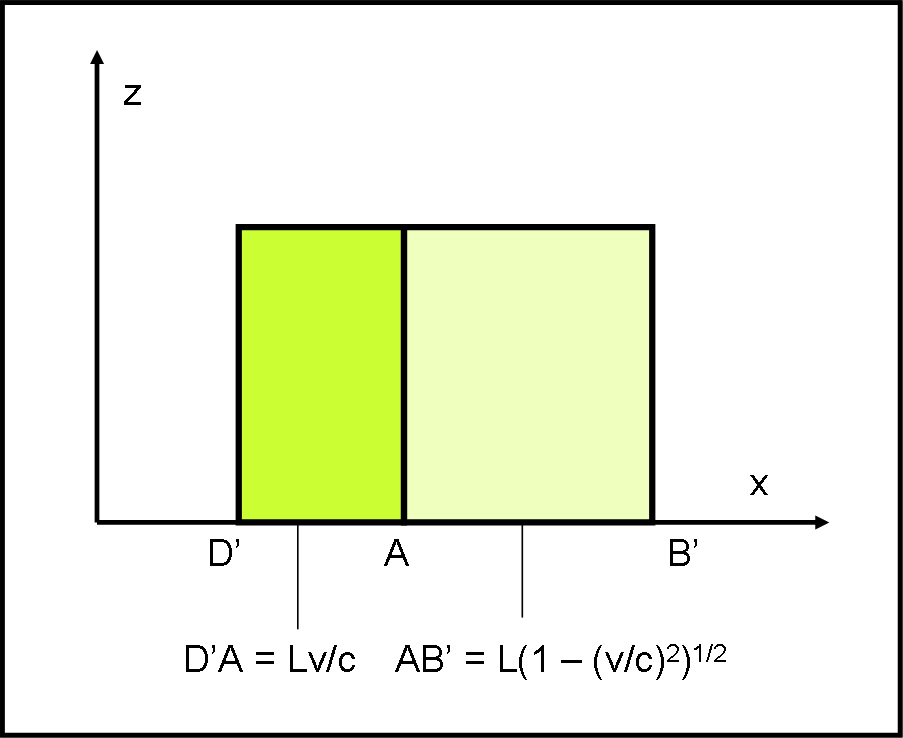
Queste due relazioni sono esattamente quelle che si aspetta di vedere l’osservatore, abituato a vivere sul nostro mondo in cui tutto viaggia lentamente, se il cubo fosse ruotato, verso destra rispetto all’asse x, di un angolo uguale ad α, come mostrato in Fig. 8.
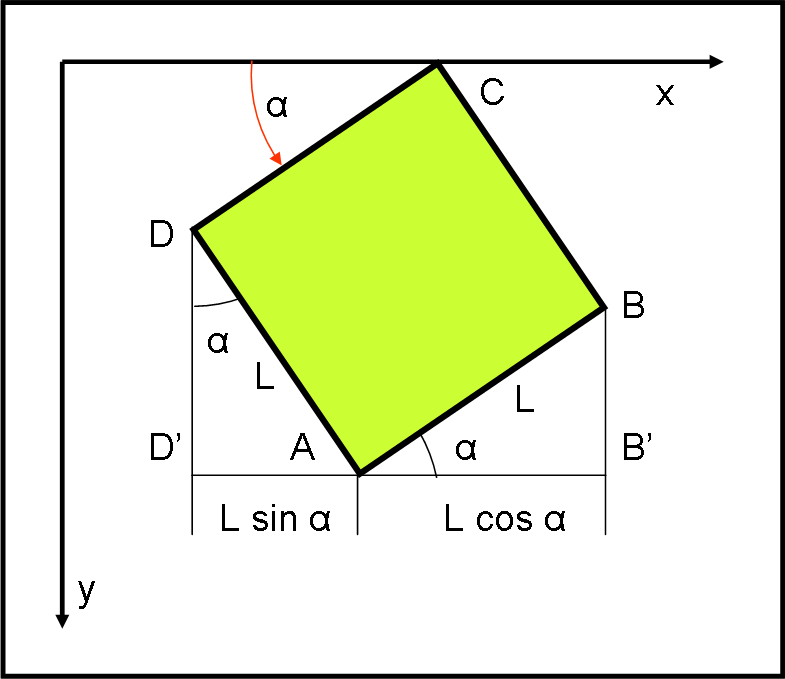
Come già detto, quest’ultima situazione è decisamente più comune nella vita di tutti i giorni e l’osservatore concluderebbe allora che in ciò che vede non ha agito nessun effetto relativistico, ma solo e soltanto una rotazione del cubo di un angolo α tale che sin α = v/c, come riassunto nella Fig. 9.
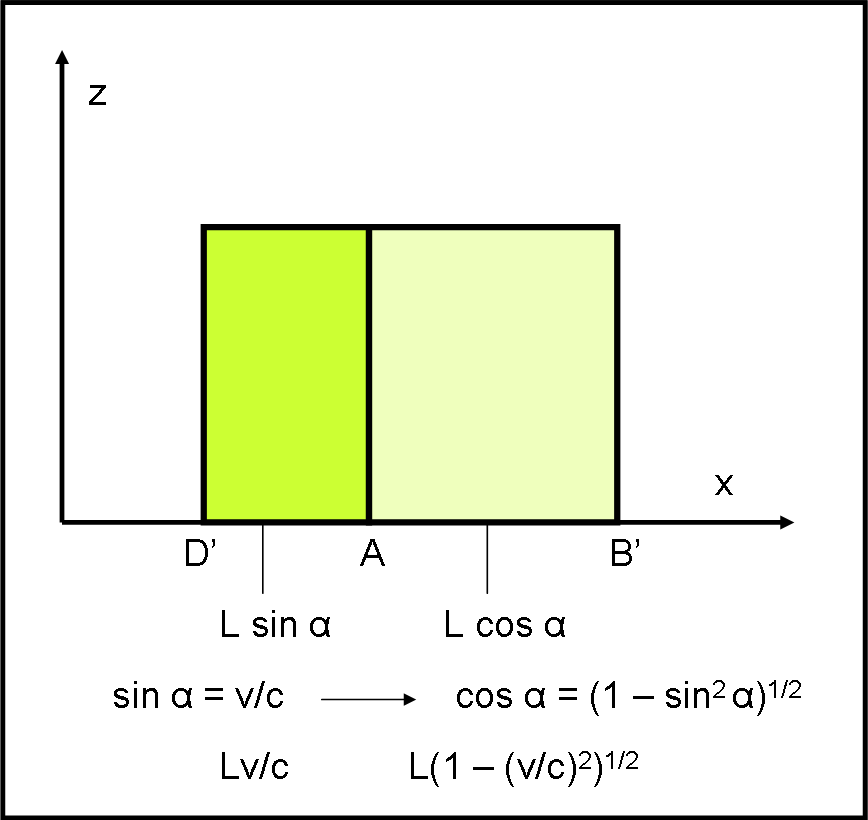
In conclusione, alla nostra domanda, risponderebbe di getto che no, non vede nessuna contrazione di Lorentz (se mai una dilatazione). Inoltre, la sua esperienza direbbe che ha assistito solo e soltanto a una rotazione istantanea del cubo.
Potrebbe perfino pensare che il cubo stia per andare in una direzione opposta alla sua… Se all’inizio il cubo fosse fermo lo vedrebbe come un quadrato perfetto. Poi, se il cubo si muovesse con una velocità v crescente (a scatti) penserebbe -magari- di vederlo ruotare continuamente di un certo angolo e… allontanarsi da lui, come mostra in modo molto poco realistico, ma apparentemente reale, la Fig. 10! D'altra parte, O è a distanza infinita e non potrebbe accorgersi se il cubo si è allontanato in senso radiale (lungo y) di una minima quantità pari al suo lato L... Potrebbe tranquillamente pensarlo, visto che il cubo ruota sempre di più. Più la velocità aumenta, infatti, più lungo appare il lato D'A e più corto (per colpa di Lorentz) appare quello AB'. Teoricamente, per velocità v = c, si vedrebbe solo il lato DA = L, mentre scomparirebbe alla vista quello frontale AB.
In modo molto più realistico, si può, invece, calcolare la lunghezza totale apparente D del cubo, vista dall’osservatore, in funzione della velocità v. Un bell’esercizio di studio di funzione (vale almeno quattro asterischi!).
Ricordiamola ancora:
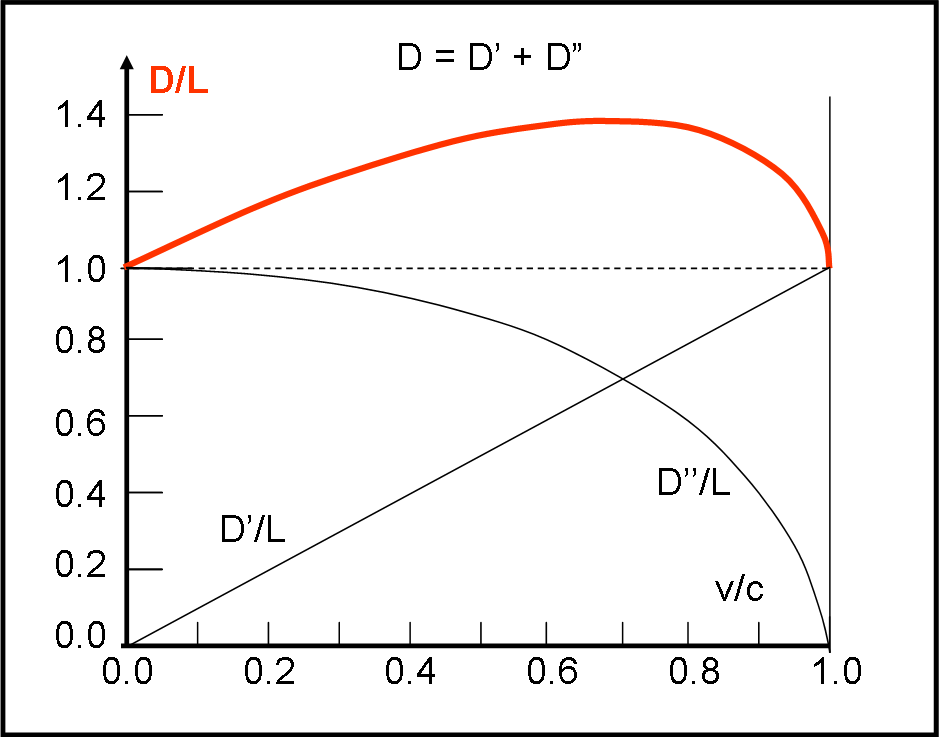
D = L v/c + L (1 – (v/c)2)1/2
In realtà, si può evitare l’analisi di questa funzione dividendola in due parti molto più semplici. Tuttavia, i lettori del nostro circolo non scappano davanti alle difficoltà…
Nella Fig. 11 riporto la rappresentazione del segmento D in funzione di v/c e i due “spezzoni” che semplificano la funzione. Mi raccomando: guardatela solo dopo averci provato!
Buon divertimento e tanto ragionamento…
QUI trovate tutti gli altri quiz del blog






19 commenti
Cavolo, non ho sudato tanto nemmeno per l'esame di meccanica razionale!
che dici? dai... in fondo è semplicissimo... ma di grande effetto!!! Spero tanto di ritrovare Penrose se e quando descriveremo attentamente il suo diagramma. Ma la strada è ancora lunga...
Allora, a velocità c vediamo un quadrato , a velocità inferiori vediamo un rettangolo , poniamo al posto del cubo una sfera , per lo stesso effetto vediamo un cerchio , a velocità inferiori cosa vediamo ? mi viene da dire che è sempre un cerchio . Giusto ?
direi proprio di sì, Claudio anche se non è facilissimo da dimostrare...
anche se non è facilissimo da dimostrare... 
La funzione è:
y = L*x + L*√(1-x^2)
Calcolo la derivata prima:
y’ = L + L*[0,5*(1-x^2)^-0,5]*(-2*x)
Sviluppando e semplificando:
y’ = L – x*L/√(1-x^2)
Provo a vedere se l’equazione di y’ ha radici, ponendo y’=0:
L = x*L/√(1-x^2)
Sviluppando i calcoli ottengo:
x = √(1-x^2)
Elevo al quadrato e risolvo l’equazione: 2*x^2 = 1
X = 1/√2
La funzione ammette due minimi o massimi relativi in:
x1 = -1/√2 (***).
X2 = +1/√2.
Per x < -1/√2 la derivata prima è negativa (curva decrescente).
Per -1/√2 < x +1/√2 la derivata prima è negativa (curva decrescente).
Deduco che:
x1 = -1/√2 (y = 0) è un minimo relativo.
X2 = +1/√2 (y = L*√2) è un massimo relativo.
Inoltre, per:
x = 0; y = L
x = 1; y = L
La funzione è asimmetrica rispetto al massimo, visto che assume lo stesso valore (y = L) per x = +1/√2 anziché nel punto di mezzo (x = 0,5)
(***) Dal punto di vista fisico, x negativo vuol dire (v/c) <0, quindi cubo in fuga verso sinistra.
Mi tocca lavorare pure il primo maggio ....
va beh... può andare, può andare... ma solo perché è il primo maggio...
COM'E' BUONO LEI .....
Non so perchè ma sono saltate alcune righe ... e poi c'è un passaggio errato che avevo eliminato ed è stato ... magicamente mantenuto ... BOH?!?!
Sovrapposizione di stati?!?! Scherzi della MQ?
Beh, però quando scrivo si dovrebbe verificare la riduzione del pacchetto d'onda probabilistica ... oppure la riduzione si ha in uno stadio successivo?
Ah si, certo! Quando rileggo!
In effetti stavolta non ho riletto; capirete, stavo per andare a pranzo!
Ha ragione Enzo, la MQ è tutta intorno a noi...
Devo dire che non ci sarei mai arrivato, anche perchè non avevo capito che valesse solo la sagoma esterna e che lo spigolo non si vedesse.
C'era il trucco
Non funziona se le facce sono di colore diverso?
caro Gaetano,
perché dici che lo spigolo non si vede? proprio perché si vede, l'osservatore crede di vedere una rotazione. O, forse, non ho capito cosa intendi dire....
Sto parlando dello spigolo in A, se si vedesse vedremmo anche la contrazione.
Mentre l'ipotesi era che non si potesse fotografare la contrazione
beh...la contrazione della faccia parallela al moto si vede, ma la lunghezza totale si dilata comunque. e poi quello che conta è l'apparente rotazione. Questa sarebbe la vera conclusione di O. Comunque, hai ragione. Se l'osservatore fosse furbo ci arriverebbe e noterebbe la parte dovuta alla contrazione di Lorentz. Per lui sarebbe meglio non cambiare colore...

Caro Enzo, ammetto che ci si poteva arrivare .... il fatto è che DOPO LA SPIEGAZIONE è tutto facilissimo.
Ti chiedo se affronterai la faccenda dell'aberrazione della luce che, a prima vista, sembrerebbe abbastanza semplice ma, in realtà, immagino che nasconda qualche complicazione logica.
Pensavo di conoscerla ma alcune tue frasi mi hanno fatto riflettere.
Per il momento ti saluto perchè sono in partenza. Ci risentiamo alla fine della prossima settimana.
caro Alvy,
di aberrazione della luce ne avevo già parlato (non so più dove e quando...)... comunque ci si potrà tornare.
Buon viaggio! Prima o poi riusciremo a partire anche noi...
Caro Enzo, vedendo la soluzione mi rendo conto che pur avendo intuito l'apparente rotazione del cubo, nel tentativo di mostrare anche il fenomeno di contrazione delle lunghezze, ho commesso diversi errori di impostazione.
In particolare ho mantenuto costante lo spazio percorso dalla luce, invece di soffermarmi sul fatto che non ve ne era alcun bisogno, poiché la luce che parte da più lontano impiega più tempo, ma può arrivare contemporaneamente a quella che parte dopo, da una fonte più vicina.
Alla luce di questo articolo, vediamo se riesco almeno a descrivere e ragionare sulla funzione che lega la lunghezza apparente del cubo (D) al rapporto v/c, considerando i due fenomeni relativistici che modificano la visione della sua lunghezza “reale”, ossia:
D = D'A + AB'
D = L v/c + L (1 – (v/c)^2)^1/2
Per descrivere la funzione corrispondente, è necessario decidere cosa rappresentare nell'ordinata y e cosa nell'ascissa x.
Da una parte ho il rapporto v/c, che d'ora in poi sostituisco con β (che posso indicare sull'asse x), per cui:
D = L β + L (1 – β^2)^1/2
Dall'altra ho il valore di D, ossia della lunghezza apparente del cubo vista dalla macchina fotografica, ma dato che L è la lunghezza “reale” del cubo, vista dal suo sistema di riferimento in movimento, per vedere come la sua “visione” varia, posso usare il rapporto tra questi due differenti modi di misurare la lunghezza, ossia D/L.
Ne segue che:
D/L = β + (1 – β^2)^1/2
Quindi sull'asse y indico il valore del rapporto D/L.
La funzione corrispondente è del tipo:
y = x + (1 – x^2)^1/2
Quindi, il valore di y (D/L) dipende dalla somma di due funzioni.
La prima funzione, deve rappresenta il rapporto tra D'A/L e β:
D'A = L v/c
D'A/L = β
Ossia la funzione è rappresentabile con una retta passante per l'origine degli assi: y= x
Il rapporto D'A/L è sempre uguale al rapporto v/c, per cui se β tende a zero (cubo fermo, ossia v=0) il segmento D'A scompare (la luce della faccia sinistra è bloccata dal cubo stesso), mentre se β tende a 1, D'A diventa uguale a L (D'A/L=1), ossia se il cubo si muove alla velocità della luce, si vede l'intera lunghezza L della faccia sinistra del cubo.
La seconda funzione, invece è un po' più complessa, infatti:
AB'/L= (1 – β^2)^1/2 , per cui:
y = (1– X^2)^1/2
Si tratta di una funzione inversa a quella esponenziale (dato che è sotto una radice quadrata), rappresentabile con una curva.
Per rappresentare la curva mi limito a considerare alcuni punti significativi, inserendo alcuni valori di β, compresi tra 0 ed 1 (ossia i suoi valori limite).
La curva taglia l'asse x quando y=0, quindi:
0 = (1 – x^2)^1/2
Solo se x (β)= +/-1 tale condizione può essere soddisfatta, ma i valori di β negativi non sono considerati, per cui la curva taglia l'asse x nel punto (1;0).
La curva taglia l'asse y nel punto (0;1), infatti se x=0:
y(AB'/L) = (1 – 0^2)^1/2 = 1
E' evidente che se il cubo è fermo (β = 0) non vi è alcuna contrazione delle lunghezze, dato che AB' = L, mentre se il cubo viaggia alla velocità della luce (v=c) il segmento AB' non è più visibile dalla macchina fotografica poiché la sua lunghezza appare uguale a zero.
Per disegnare la curva della funzione y = (1 – x 2)1/2 posso usare alcuni valori di x (β) e trovare il relativo valore di y (AB'/L)
con β = 0,2: y = (1 – 0,2^2)^1/2 = 0,979
con β = 0,4: y = (1 – 0,4^2)^1/2 = 0,916
con β = 0,5: y = (1 – 0,5^2)^1/2 = 0,86
con β = 0,6: y = (1 – 0,6^2)^1/2 = 0,8
con β = 0,7: y = (1 – 0,7^2)^1/2 = 0,714
con β = 0,8 y = (1 – 0,8^2)^1/2 = 0,6
con β = 0,9: y = (1 – 0,9 2)1/2 = 0,43
con β = 0,95: y = (1 – 0,95 2)1/2 = 0,31
con β = 0,98: y = (1 – 0,98 2)1/2 = 0,19
Tutti questi punti consentono di disegnare immediatamente anche la funzione iniziale cercata, che può essere descritta come:
D/L = β + (1- β^2)^1/2
y = x + (1- x^2)^1/2
Quindi, ai valori di y(AB') trovati prima basta sommare sempre il corrispettivo valore di x (β), per ottenere il rapporto D/L:
con β = 0: y = 0 + (1 – 0^2)^1/2 = 1
con β = 0,2: y = 0,2 + (1 – 0,2^2)^1/2 = 1,179
con β = 0,4: y = 0,4+ (1 – 0,4^2)^1/2 = 1,316
con β = 0,5: y = 0,5 + (1 – 0,5^2)^1/2 = 1,36
con β = 0,6: y = 0,6 + (1 – 0,6^2)^1/2 = 1,4
con β = 0,7: y = 0,7 + (1 – 0,7^2)^1/2 = 1,414
con β = 0,8 y = 0,8 + (1 – 0,8^2)^1/2 = 1,4
con β = 0,9: y = 0,9 + (1 – 0,9 2)1/2 = 1,33
con β = 0,95: y = 0,95 + (1 – 0,95 2)1/2 = 1,26
con β = 0,98: y = 0,98 + (1 – 0,98 2)1/2 = 1,17
con β = 1: y = 1 + (1 – 1^2)^1/2 = 1
La curva non taglia l'asse x, infatti nessun valore di x soddisfa l'equazione y= 0:
0= x + (1- x^2)^1/2
La curva, invece, taglia l'asse y nel punto (0;1), da che se x= 0:
y= 0 + (1- 0^2)^1/2 = 1
Prima di proseguire cercando minimi, massimi e flessi, una piccola considerazione: sommare un valore al rapporto incrementale, per una retta significava y= mx + n, qui però n è variabile e si tratta di una curva il cui andamento è opposto a quello della retta (la retta al crescere di x (β) parte da y = 0 ed arriva ad y= 1, la curva riferita alla contrazione delle lunghezze parte da y= 1 ed arriva ad y= 0).
Per cercare altri punti particolari della curva, calcolo la derivata prima delle funzione:
y = x + (1- x^2)^1/2
Si tratta di una somma di funzioni di cui una è una funzione di funzione.
f(x) y= x
f'(x) y' = 1
g(x) = (1- x^2)^1/2 si tratta di una funzione di una funzione
derivata di (1- x^2)^1/2 = ½ (1- x^2)^-1/2
derivata di -x^2 = -2x
y' = ½ (1- x^2)^-1/2 -2x
y' = -x/(1- x^2)^1/2
La derivata della somma di due funzioni è uguali alla somma delle derivate delle funzioni, per cui:
y' = 1 - x/(1- x^2)^1/2
La derivata prima si annulla, se:
0 = 1 - x/(1- x^2)^1/2
1 = x/(1- x^2)^1/2
(1- x^2)^1/2 = x
1- x^2 = x^2
1 = 2 x^2
x = (½) ^1/2 = 1/2^1/2 = 0,707
A questo valore di x corrisponde un valore di y:
y = x + (1- x^2)^1/2
y = 0,707 + (1- 0,707^2)^1/2 = 0,707 + (1- 0,5)^1/2 = 0,707 + 0,707 = 1,414
Perciò il Punto (0,707;1,414) rappresenta il massimo della curva, infatti variando il valore di x rispetto a quello che annulla la derivata prima (x=0,707), il valore di y aumenta man mano che ci si avvicina a x=0,707, dopodiché diminuisce:
y = 0,5 + (1 – 0,5^2)^1/2 = 1,36 (è inferiore rispetto a 1,414)
y = 0,8 + (1- 0,8^2)^1/2 = 1,4; (1,414 è più elevato di 1,4)
Anche il comportamento della derivata prima indica che si tratta di una massimo, dato che questa al crescere di x passa da valori positivi, a zero e poi a valori negativi:
y' = 1 - x/(1- x^2)^1/2
y' = 1 – 0,5/(1- 0,5^2)^1/2 = 1 – 0577 = + 0,423
y' = 1 – 0,8/(1- 0,8^2)^1/2 = 1 – 1,333 = - 0,333
A questo punto non resta che calcolare la derivata seconda:
y' = 1 - x/(1- x^2)^1/2
f(x) = - x
f'(x) = -1
g(x) = (1- x^2)^1/2
g'(x) = ½ (1- x^2)^-1/2 -2x = -x/(1- x^2)^1/2
Dato che la derivata del rapporto di due funzioni y = f(x)/g (x) è uguale a:
y’ = f'(x) g(x) - f(x) g'(x)/g(x)2
y'' = (-1 (1- x^2)^1/2 - (-x) -x/(1- x^2)^1/2 )/(1- x^2)
y'' = (-1 (1- x^2)^1/2 (1- x^2)^1/2 - x^2/(1- x^2)^1/2 )/(1- x^2)
y'' = -1 (1- x^2) - x^2/(1- x^2)^1/2 (1- x^2)
y'' = -1+ x^2 - x^2/(1- x^2)^3/2
y'' = -1/(1- x^2)^3/2
Se x = 0,707 (valore che annulla la derivata prima)
y''= -1/(1- 0,707^2)^3/2 = -2,828
La derivata seconda ha sempre segno negativo , grazie al suo segno meno iniziale(ciò conferma ulteriormente che il punto (0,707;1,414) rappresenta un massimo)....
Anche assumendo come valore di x=0, si ottiene al massimo:
y'' = -1/(1- 0^2)^3/2 = -1
per x=1
y'' = -1/(1- 1^2)^3/2 = -1/0 = - ∞
Non vi sono valori di x che annullano la derivata, per cui non vi sono né flessi obliqui né flessi orizzontali.
Volevo, però far notare, ammesso che il ragionamento fatto fin qui sia corretto, un altro punto particolare, quello in cui la derivata prima assume il valore di -∞, poiché rappresenta una retta tangente la curva parallela all'asse y.
Se x = 1 (anche y = 1)
y' = 1 - 1/(1- 1^2)^1/2 = 1 -1/0 = - ∞
Ossia la retta tangente la curva nel punto (1;1) è parallela all'asse y (m= - ∞).. a me sembra un asintoto che contiene la curva (d'altronde x non può assumere valori maggiori di 1, ossia la velocità della luce è invalicabile).
La figura mostra il risultato grafico di tale ragionamento:
http://www.astrobin.com/full/34215/F/
Paolo
caro Paolo,

non ho controllato tutti i calcoli, ma il procedimento è giusto! L'unica cosa che voglio farti notare è che non esiste un asintoto che contiene la curva, dato che un asintoto è un qualcosa che la funzione non può mai raggiungere se non all'infinito. Diciamo, quindi, molto meglio, che la curva nel punto v/c = 1 ha una tangente verticale...
Caro Enzo, ho deciso di fare un piccolo esperimento, ossia ho provato a ricavare la funzione in un altro modo (giusto per sperimentare come trattare una funzione trigonometrica... spero sia corretto).
Questa volta sono partito dalla relazione:
D = L sin α + L cos α
D/L = sin α + cos α
Sull'asse delle ordinate metto il rapporto D/L e sull'ascissa il valore dell'angolo α
Tale angolo dipende dal rapporto v/c, dato che sin α= v/c, per cui:
se v/c =0 l'angolo α vale 0° (sin 0° = 0),
se v=c v/c=1 l'angolo α vale 90° (sin 90° = 1),
Per cui la funzione D/L = sin α + cos α, può essere descritta come:
y= sin (x) + cos (x)
Per rappresentare la curva della funzione, trovo una serie di punti:
con x = 0°: y = sin 0° + cos 0° = 0 + 1 = 1
con x = 10°: y = sin 10° + cos 10° = 0,17 + 0,98 = 1,16
con x = 20°: y = sin 20° + cos 20° = 0,34 + 0,94 = 1,28
con x = 30°: y = sin 30° + cos 30° = 0,5 + 0,86 = 1,36
con x = 40°: y = sin 40° + cos 40° = 0,64 + 0,76 = 1,4
con x = 45°: y = sin 45° + cos 45° = 0,707 + 0,707 = 1,414
con x = 50°: y = sin 50° + cos 50° = 0,76 + 0,64 = 1,4
con x = 60°: y = sin 60° + cos 60° = 0,86 + 0,5 = 1,36
con x = 70°: y = sin 70° + cos 70° = 0,94 + 0,34 = 1,28
con x = 80°: y = sin 80° + cos 80° = 0,98 + 0,17 = 1,15
con x = 90°: y = sin 90° + cos 90° = 1+ 0 = 1
La figura mostra la curva così ottenuta.
http://www.astrobin.com/full/34215/G/
In ultimo, provo a calcolare la derivata prima:
y= sin (x) + cos (x)
y'= cos (x) - sin (x)
la derivata prima si annulla quando il coseno dell'angolo α è uguale al suo seno, ossia quando l'angolo è di 45°
0 = cos (x) - sin (x)
0 = cos 45° - sin 45° = 0,707 – 0,707
Il punto Massimo della curva ha coordinate x = 45° e y= 1,414.
Per passare da questa curva a quella precedente basta porre sull'ascissa invece di α, sin α, ossia il rapporto v/c (il dato sul valore corrispondente a sin α è già presente dei punti ricavati prima).
http://www.astrobin.com/full/34215/H/
Disegnando i punti trovati la curva sembra proprio identica, volevo però una conferma su questo piccolo esperimento.
Paolo
Che dirti Paolo... PERFETTO! Non l'avevo proposta per non complicare le cose, ma sei stato brillantissimo e logicissimo (come sempre)... BRAVO!!!!
