Dopo aver fatto il lavoro dei “salumai”, affettando un salame conico, vediamo di analizzare un po’ meglio le “fette” che abbiamo ottenuto. Introduciamo anche la matematica e troviamo nuovamente le nostre care funzioni. Cominciamo con l’ellisse e la sua figlia prediletta, la circonferenza.

Abbiamo descritto abbastanza esaurientemente le coniche da un punto di vista puramente geometrico, ossia come intersezioni tra un cono circolare e un piano-coltello vagabondo. Si potrebbero, però, fare un mucchio di giochini guardando il cono da varie angolazioni… la geometria è imprevedibile! Tuttavia, il nostro vero scopo è quello di cercare di descrivere le curve trovate, come funzioni nel piano cartesiano.  Per far ciò, è utile introdurle anche attraverso altre caratteristiche geometriche, che, oltretutto, dimostrano ancora meglio il loro interesse astronomico. In questo modo faranno il loro ingresso parametri che ben conoscete e che si usano normalmente nella fisica del Cosmo, come l’eccentricità e il fuoco (se non ci credete chiedete al signor Keplero e alle sue leggi…). Ovviamente, tutto ciò che descriveremo adesso è una conseguenza dei “tagli” fatti precedentemente, ma per rendersene veramente conto bisognerebbe immergersi completamente nella geometria proiettiva. Magari lo faremo in seguito, ma adesso è meglio non perdere di vista lo scopo finale.

Due chiodi, uno spago e una matita

Come possiamo disegnare un’ellisse qualsiasi su un foglio di carta? Facilissimo anche per un bambino (anzi, fateglielo fare, aiutandolo a preparare la strumentazione necessaria). Prima di cominciare, voglio farvi notare che abbiamo abbandonato le figure a tre dimensioni e  siamo tornati, finalmente, nel nostro caro e semplice piano del foglio. Questo foglio cosa rappresenta rispetto al discorso della lezione precedente? Facile: proprio il piano-coltello dove si forma la curva tagliando il cono.

Siete pronti? Bene. Mettetevi su un tavolo di legno che non sia prezioso e in cui si possano piantare dei chiudi o al limite inserire della puntine da disegno. Inserite i due chiodi nel legno a una certa distanza tra di loro (quella che volete). Prima di piantarli a fondo, prendete un pezzo di corda, uno spago o un filo resistente che sia più lungo della distanza tra i due chiodi e legatelo ai suoi estremi strettamente ai chiodi. Fatto? Bene. Adesso potete piantare completamente i chiodi in modo che il filo o lo spago non  si slacci da loro. Non resta ora che prendere una bella matita e infilarla all’interno dello spago e tenderlo al massimo (se non è ben “tirato”, addio curva...). Iniziate a spostare la matita tutt’attorno ai due chiodi. Il filo non vi permette di andare dove volete, ma vi obbliga a percorrere una curva ben definita (sempre che il filo sia sempre ben teso, mi raccomando!). Tornando al punto di partenza vi accorgete di avere ottenuto una curva chiusa, che altro non è che un’ellisse. La Fig. 42 illustra l’intero procedimento.

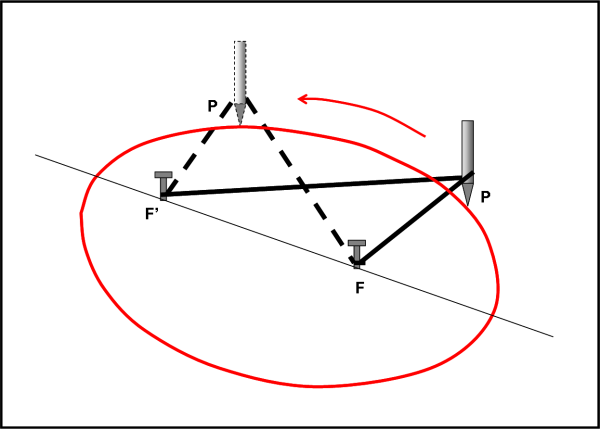
Ora, potete anche tagliare il filo e ragionare su quello strano disegno che ha al suo interno ancora i due chiodi. Potete anche usare un righello per unire alcuni punti che di volta in volta vado a indicarvi. Lavoriamo sulla più seria Fig. 43.

Innanzitutto i chiodi. Essi si chiamano fuochi dell’ellisse. Che caratteristiche hanno? Per come è stata costruita l’ellisse, potete prendere un punto qualsiasi di essa e misurare la sua distanza dai due fuochi. Al variare del punto, sommando queste due distanze troverete sempre lo stesso valore. Vi stupite? No, di certo. Ogni punto dell’ellisse è stato proprio costruito con un  filo di lunghezza fissa che la matita faceva spostare mentre girava. Questa situazione vuole proprio dire che il pezzo di filo che andava fino al primo fuoco più il pezzo di filo che andava al secondo fuoco deve  rimanere costante e uguale alla lunghezza del filo. In termini matematici: l’ellisse è il luogo dei punti che mantengono costante la somma delle loro distanze da due punti fissi chiamati fuochi. Siano essi F e F’ e P un punto qualsiasi dell’ellisse, si deve avere:

PF + PF’ = costante (lunghezza del filo)  …. (1)

Se disegnassimo due assi cartesiano x e y che abbiano la loro origine nel punto di mezzo tra i due fuochi e siano diretti uno verso i fuochi e l’altro perpendicolarmente ad esso, basterebbe scrivere le coordinate del punto P e troveremmo l’equazione che ci regala il legame tra la x e la y dei punti appartenenti all’ellisse. L’ellisse è una curva chiusa e forse non è molto importante nello studio delle funzioni, ma è fondamentale per le orbite dei corpi celesti. Keplero insegna… Vale, perciò la pena di eseguire un po’ di passaggi matematici abbastanza “noiosi” per ottenere la funzione matematica che lega y con x. Se non altro servirà per pendere dimestichezza con semplificazioni, spostamenti, prodotti notevoli, ecc.  Lo faremo tra poco e troveremo un’equazione di questo tipo:

x²/a² + y²/b² = 1    ….. (2)

Dove a e b sono le distanza tra l’origine e i punti dell’ellisse sull’asse delle x e delle y (A e B). La distanza più grande (quella che si ottiene sull’asse delle x) si chiama semiasse maggiore dell’ellisse, mentre b prende il nome di semiasse minore.

La famosa costante, uguale alla lunghezza del filo, non è altro che 2a. Posso anche dimostrarvelo rapidamente dalla (1). Prendiamo il punto dell’ellisse che si trova in A, proprio sull’asse delle x. Il filo, ossia la costante da trovare, non è altro che FA + F’A (per definizione di ellisse). Tuttavia, posso anche scrivere:

F’A + FA  = FF’ + F'A + F'A.

Basta guardare la figura e ragionarci un attimo sopra per concludere che F'A = FC. Sostituiamo uno dei due F'A che abbiamo nella relazione con FC (tanto sono uguali). Otteniamo:

F’A + FA  =  FF’ + FC + F'A

Ma la somma dei tre segmenti del secondo membro (che è proprio la costante cercata) dà proprio la distanza tra C e A, ossia due volte il semiasse maggiore, ossia 2a.

Dato che la costante deve essere una costante, essa vale per qualsiasi punto P si scelga sull’ellisse e quindi la (1) diventa:

PF + PF’ = 2a     …. (3)

Un rapporto un po’ … eccentrico

Qualche altro segmento interessante? Sicuramente sì. Almeno uno. Anzi, più che un segmento è il rapporto tra due segmenti:

FF’/2a = e

e sta per eccentricità dell’ellisse e ci dice quanto l’ellisse e più o meno “allungata”, ossia di quanto differiscono tra loro il semiasse maggiore e quello minore (anche se quest’ultimo non compare direttamente, ma è facile introdurlo e lo faremo tra poco). Si definisce eccentricità di una ellisse il rapporto tra la distanza tra i due fuochi e il doppio del semiasse maggiore. Oppure, se preferite, il rapporto tra la distanza di uno qualsiasi dei fuochi dall’origine e il semiasse maggiore. Infatti:

e = FF’/2a = 2FO/2a = FO/a     …. (4)

Possiamo esprimere la (4) come:

FO =  F’O = ae

Sì, non sbagliate. E’ proprio l’eccentricità che caratterizza le orbite dei pianeti e di moltissimi corpi celesti, il numero senza dimensioni (è dato, infatti, dal rapporto di due lunghezze) che indica quanto è “allungata” l’ellisse. Non si misura in metri o centimetri o quello che volete, ma è un numero puro. Inoltre, essa non può assumere qualsiasi valore, come vedremo tra poco.

Ho detto poco fa che a e b sono legati tra loro attraverso l’eccentricità. Non è difficile ricavare questa relazione. Consideriamo la nostra solita ellisse di Fig. 43, col centro nell’origine degli assi O e disegniamo qualche segmento particolarmente interessante. Il punto P è stato preso proprio sull’asse y (non c’è niente di male, dato che anche lui appartiene all’ellisse) e lo chiamiamo B. In queste condizioni è facile ricavare la relazione tra i semiassi e l’eccentricità. La distanza tra l’origine e i fuochi è proprio FO (o F’O) che abbiamo già trovato essere proprio uguale ad ae. Il segmento BF è uguale a BF’, ma la loro somma deve essere, per definizione di ellisse, uguale a 2a. Ne segue  che BF + BF’ = 2a, ma anche 2BF = 2a, ossia BF = BF’ = a. Infine il segmento BO non è altro che il semiasse b. Basta richiamare il solito “vecchio” teorema di Pitagora e abbiamo:

BF² = BO² + F’O²

sostituendo:

a² = b² + a²e²

Spostando i termini un po’ a destra e un po’ a sinistra (basta cambiargli di  segno e li possiamo portare dall’altra parte dell’uguale):

b² = a² – a²e²

mettendo in evidenza a²:

b² = a² (1 – e²)

e, infine, estraendo la radice quadrata:

b = a(1 - e²)^1/2

Beh… a questo punto, possiamo fare quel passo in più che ci porterà all’equazione dell’ellisse (2). Cosa si deve fare? Beh, sulla base della definizione di ellisse, bisogna trovare il legame tra la x e la y di un suo punto qualsiasi, ossia trovare la funzione che lega x con y, in cui devono, ovviamente, comparire anche i parametri che la definiscono (ossia i semiassi a e b).

Dalla geometria alla matematica

Consideriamo sempre la Fig. 43. Il punto P è un punto qualsiasi dell’ellisse e ha coordinate P(x,y). L’origine degli assi è il centro dell’ellisse, per cui OB è il semiasse minore b e OA è il semiasse maggiore a. Le coordinate dei fuochi F e F’ sono, rispettivamente, F(c,0) e F’(-c,0).

Sappiamo già che quel c non è altro che ae e che è collegato anche a b. Per adesso, però, lasciamolo scritto così: alla fine metteremo a posto le cose, ricordando che c = FO = F’O e quindi  che c² = a² – b², come già ricavato precedentemente (a²e² = c² = a² – b²)

Cosa devo fare adesso? Scrivere la relazione che definisce l’ellisse

PF + PF’ = 2a

E poi inserire al posto dei due segmenti PF e PF’ qualcosa che sia collegato alle coordinate dei loro punti iniziali e finali, ossia le distanza tra i punti P e F e P e F’.

Beh… questo lo sappiamo fare molto bene (la distanze tra punti l’abbiamo già studiata). In ogni modo, richiamiamola ( basta, in fondo, applicare il “solito” teorema di Pitagora).

Dati due punti R(x₁,y₁) e S(x₂,y₂), la distanza RS è data da:

RS = ((x₁ – x₂)² + (y₁ – y₂)²)^1/2

Quindi, applicandola al nostro caso e ricordando, ancora, che P(x,y), F(c,0), F’(-c,0),

PF = (( x - c)² + (y - 0)²)^1/2 = (( x - c)² + y ²)^1/2

e

PF’ = ((x - (- c))² + (y – 0)²)^1/2 = ((x  + c)² + y²)^1/2

E, quindi:

PF + PF’ = ((x - c)² + y²)^1/2 + ((x + c)² + y²)^1/2 = 2a

Abbiamo due radici quadrate dalla stessa parte dell’uguaglianza. Non conviene mai mantenere questa situazione, dato che in un modo o nell’altro dobbiamo farle sparire. Bisogna isolarne almeno una in modo da poterla elevare al quadrato. Poi toccherà anche all’altra. Avanti, senza fretta e con molta attenzione ai segni.

((x + c)² + y²)^1/2 = 2a - ((x – c)² + y²)^1/2

Ho portato una radice al secondo membro, cambiandole ovviamente di segno. Adesso, devo elevare al quadrato tutta l’uguaglianza per eliminare almeno la radice di sinistra. Attenzione al quadrato del secondo membro. E’ come se facessi il quadrato di una differenza tra due termini di cui uno è A = 2a e l’altro è B = (y² + (x – c)²)^1/2. Ossia (A – B)² = A² + B² - 2AB (ricordate?). Forza e coraggio:

(x + c)² + y² = 4a² + ((x - c)² + y²) – 2 ∙ (2a) ∙ ((x - c)² + y²)^1/2

Se trovate difficoltà, sostituite alle espressioni del secondo membro  A e B, e poi, alla fine, rimettete il loro valore effettivo. Può essere più semplice… Comunque, ho solo eseguito dei quadrati e un doppio prodotto (per facilitarvi ho anche inserito delle parentesi “inutili”…).

Eliminiamo subito i termini che compaiono tali e quali al primo e al secondo membro. D’altra parte è ovvio farlo dato che, se ho  x + m = y + m, posso scrivere x + m – m = y, ossia x = y. m può essere eliminato al primo e al secondo membro. Insomma, cerchiamo di semplificare al massimo una relazione che si sta allungando notevolmente. Nell’espressione precedente abbiamo y² sia da una parte che dall’altra e quindi possiamo eliminarli (meglio dire “semplificarli"). Si ottiene:

(x + c)² = 4a² + (x - c)² – 4a(y² + (x - c)²)^1/2

Eseguiamo i quadrati (x + c)² e (x - c)², che compaiono nel primo e nel secondo membro, sperando di semplificare ancora qualcosa…

x² + c² + 2xc = 4a² + x² + c² - 2xc – 4a(y² + (x - c)²)^1/2

Che bello! Ho parecchia “roba” da semplificare. x² e c² compaiono sia a destra che a sinistra: e possiamo toglierceli dai piedi!

2xc = 4a² - 2xc – 4a(y² + (x - c)²)^1/2

Aspettate, aspettate, posso ancora fare qualcosa. A secondo membro c’è 2xc con il segno meno e posso portarlo al primo membro con il segno più. In questo modo può sommarsi tranquillamente al 2xc che era già lì ad aspettarlo. Otteniamo.

4xc = 4a² - 4a(y² + (x - c)²)^1/2

Beh… l’espressione si è ridotta di molto, ma posso ancora eliminare il numero 4 che compare in tutti i termini. Dividere tutta un'uguaglianza per uno stesso numero non cambia assolutamente niente. Eseguo questa semplificazione e, intanto, porto a² al primo membro tanto per isolare la radice quadrata come avevo già fatto in precedenza.

xc - a² = - a(y² + (x - c)²)^1/2

Bene… adesso posso nuovamente fare il quadrato di entrambi i membri (ricordando che  meno per meno dà più):

x²c² + a⁴ - 2a²xc = a²(y² + (x - c)²)

Finalmente, non ho più radici quadrate tra i piedi e posso eseguire l’ultimo quadrato al secondo membro:

x²c² + a⁴ - 2a²xc = a²(y² + x² + c² - 2xc)

Ci resta solo da eseguire un prodotto tra un monomio e un polinomio, nel secondo membro (basta moltiplicare il monomio per ogni singolo fattore del polinomio):

x²c² + a⁴ - 2a²xc = a²y² + a²x² + a²c² - 2a²xc

Rapidi come dei fulmini semplifichiamo subito il termine -2a²xc che compare in entrambi i membri e poi riflettiamo un attimo:

x²c² + a⁴ = a²y² + a²x² + a²c²

Cosa possiamo fare di “furbo”? Cercare di portare dalla stessa parte i termini che hanno le x e le y e dall’altra i termini costanti (ossia che non abbiano né x né y). Proviamo:

x²c² – x²a² - a²y² =  a²c² - a⁴

Finora abbiamo sempre eseguito moltiplicazioni. Sarebbe ora di raccogliere i termini in comune, ossia mettere in evidenza qualcosa sia a sinistra che a destra. Un qualcosa che ci permetta di avere nuovamente un qualcosa di uguale da entrambe le parti. A primo membro metto in evidenza x² e nel secondo a². Perché? Vi è subito chiaro:

x²(c² – a²) – a²y² = a²(c² – a²)

Perfetto! In entrambi i membri è comparsa la differenza c² – a². Ma essa è una nostra cara e vecchia amica e vale proprio - b². Sostituiamo subito:

- x²b² - a²y² = - a²b²

Accidenti, l’uguaglianza è diventata ben poca cosa e, inoltre, contiene solo a e b oltre a x e y. Ma non è finita… intanto cambiamo tutti i segni meno in segni più (è come moltiplicare tutto per -1):

x²b² + a²y² = a²b²

e, infine, dividiamo a destra e a sinistra per a²b²:

x²b²/ a²b² + a²y²/ a²b² = a²b²/ a²b²

Non ci resta che semplificare tra numeratore e denominatore e si ha finalmente:

x²/ a² + y²/ b² = 1

che è proprio la (2), quella che volevamo ricavare.

Mamma mia che fatica! Ma no, mica tanto… ed è stato molto piacevole applicare alcune regolette imparate con i prodotti notevoli e cose del genere. In ogni modo, abbiamo fatto una cosa molto importante: abbiamo dimostrato che la relazione geometrica: “la somma delle distanze di ogni punto dell’ellisse da due punti detti fuochi è costante” ci ha permesso di scrivere l’equazione matematica che lega tra loro le ordinate e le ascisse attraverso le caratteristiche della curva, ossia i semiassi maggiore e minore. Una sposalizio magnifico tra geometria e matematica che ricade pesantemente sulla fisica dato che l’ellisse è la traiettoria descritta da un pianeta attorno a una stella. Vi sembra poco?

Non allarghiamoci troppo, però. L’equazione dell’ellisse (2) è relativamente semplice, in quanto  riferita agli assi cartesiani con l’origine nel centro dell’ellisse. Purtroppo, però, il Sole (e non solo) non si piazza al centro dell’ellisse, ma preferisce stare in uno dei due fuochi. Per descrivere, quindi, il moto di un pianeta attorno al Sole, si deve spostare l’origine degli assi nel fuoco F (o F’). L’equazione si complica non poco e si preferisce  (per vari motivi fisici) descriverla con la trigonometria. Ecco perché l’equazione che deriva dalla prima legge di Keplero è alquanto diversa dalla (2). Ma questo è un altro problema, che riguarda la cinematica…

L’ellisse limite e le nostre “vecchie” funzioni

Consideriamo un’ellisse molto particolare, quella ottenuta con un  piano-coltello perpendicolare all’asse del cono. Cosa si otteneva? Una circonferenza. E’ questo è proprio il caso in cui l’eccentricità diventa uguale a zero. Cosa succede alla nostra costruzione geometrica con il filo e i due chiodi. Niente di speciale… i due chiodi diventano uno solo e coincidono con l’origine degli assi cartesiani. Se fissate il filo a un solo chiodo, gli mettete in mezzo la matita e poi girate tendendo bene il filo otterrete esattamente una circonferenza. I due semiasse dell’ellisse coincidono tra loro e sono uguali al raggio r della circonferenza. La (4) diventa:

e = FO/r = 0/r = 0

La circonferenza è un caso particolare dell’ellisse quella in cui i due fuochi coincidono e l’eccentricità diventa zero.

Possiamo scrivere velocemente anche l’equazione (2) per la circonferenza. Essa diventa (dato che a = b = r):

x²/r² + y²/r² = 1

e anche:

x² + y² = r²    ….  (5)

Beh… questa formuletta sapremmo ricavarla da soli con quel poco che abbiamo imparato sugli assi cartesiani e sulle distanze di un punto dall’origine.

Ricordate la distanza di un punto P(x,y) dall’origine? Essa era data da:

d² = x² + y²

Ma questa distanza è la stessa se il punto P ruota attorno all’origine mantenendo sempre la stessa distanza. Chiamiamo r la distanza d.  Ossia:

r² = x² + y²

Cosa vuol dire allora la (5)? Essa descrive il luogo dei punti del piano che hanno la stessa distanza r dall’origine, ossia è proprio una circonferenza di raggio r e di centro O.

Vi spaventa un po’ una funzione in cui x e y compaiono al quadrato? No, nessuna paura… si fa presto a ridurre l’espressione alla nostra solita y = f(x)

Scriviamola sotto questa forma:

y² = r² – x²

Non ci resta che estrarre la radice quadrata e otteniamo:

y = +/- (r² - x²)^1/2  ….. (6)

Ed ecco che siamo tornati alla nostra solita “fabbrica”. Cosa si deve fare alla x? Bisogna moltiplicarla per se stessa, cambiarla di segno, sommargli il quadrato del raggio (che è una costante) e infine estrarne la radice quadrata. Una bella fabbrica, non c’è che dire! Ma vedrete che si può fare di più e meglio.

La funzione ottenuta ha delle caratteristiche molto interessanti. Innanzitutto, avete visto che ho aggiunto un + e un - davanti alla radice quadrata. Perché? Ovvio… perché fare il quadrato di +5 o -5 porta allo stesso risultato, ossia a + 25. Ciò vuol dire che per ogni x scelto, avremo la possibilità di avere una coppia di y che soddisfano la funzione. D’altra parte ce lo dovevamo aspettare disegnando una circonferenza di centro O e di raggio r nel piano cartesiano. Data una x (positiva o negativa) abbiamo sempre e comunque due valori di y corrispondenti. Questo capita perché la nostra curva è chiusa. Otteniamo la stessa cosa disegnando l’ellisse (2). Anche quell’espressione porta a una funzione del tipo y = f(x). Vogliamo provare?

y²/b² = 1 – x²/a²

e ancora

y² = b² – (b²/a²) x²

e infine:

y = +/-  (b² – (b²/a²) x²)^1/2   …. (7)

La “fabbrica” f  lavora sodo: prende la x e le fa il quadrato. La moltiplica per il quadrato del rapporto dei semiassi (b/a). Le cambia di segno e le aggiunge il quadrato del semiasse minore. Poi ne fa la radice quadrata. Infine, come prima, si pone l’alternativa del segno. Uffa, che lavoraccio.

Vogliamo vedere, di nuovo, come la circonferenza sia proprio un caso particolare di (7)?  Basta inserire b = a = r e otteniamo:

y = +/-  (r² – x²)^1/2       come volevasi dimostrare (ricordando che b/a = r/r = 1)

Per divertirci un po’ scriviamo la (7) in modo più compatto. Basta giocare un pochino:

y = +/- ((b²a² –b² x²)/a²)^1/2 = +/- (b²(a² – x²)/a²)^1/2 = +/-  (b²/a²( a² - x²))^1/2

e infine:

y = +/-  b/a(a² – x²)^1/2  .... (8)

Ve beh…. Vi spiego passaggio per passaggio, ma prima cercate di farlo da soli…

Moltiplico e divido la prima b² per a². In  questo modo posso mettere in evidenza (dentro alla radice) il termine (b/a)² . Essendo un quadrato lo posso portare fuori estraendogli la radice quadrata e diventa b/a. Tutto lì. Non ho detto e fatto niente di nuovo rispetto a quanto descritto nell’articolo-libro sui monomi, binomi e cose del genere.

Ovviamente anche la (8) si riduce alla (6), ossia alla circonferenza, ponendo a = b = r.

Quale altra caratteristica hanno le curve chiuse, come l’ellisse e la circonferenza?  A loro non interessano assolutamente i limiti, dato che non possono andare a zero né tanto meno a infinito. Sia la x che la y possono solo raggiungere a e – a e b e – b ( o r e – r, nella circonferenza). Un binario molto simpatico, come quello dei trenini di casa, senza punti all’infinito, senza Achille e tartarughe e limiti che ci sono e non si raggiungono mai. Fosse per loro, tutta l’analisi delle funzioni sarebbe inutile… a parte, però, le situazioni “degeneri” che abbiamo descritto affettando il cono.

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica

 

QUI analizziamo una "strana uguaglianza" tra due definizioni di ellisse che sembrano non avere niente in comune