Categorie: Relatività
Tags: aberrazione della luce effetto doppler relativistico ellisse aberrazione relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:8
ABERRAZIONE DELLA LUCE. 8: ELLISSE DI ABERRAZIONE (PARTE TERZA) ***
Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.
A questo punto possiamo dimostrare e calcolare la frequenza luminosa che arriva all’osservatore sull’astronave. Come già detto, e per costruzione, la dilatazione del tempo, dovuto al moto, corrisponde perfettamente alla lunghezza delle congiungenti i punti dell’ellisse con uno dei due fuochi.
Conosciamo già l’effetto doppler relativistico (QUI, sottocapitolo "qualche fomula e il gioco è fatto") per un moto lungo l’asse x. Tuttavia, vale la pena, adesso, ricavarlo a partire dall’effetto doppler classico.
Definiamo, innanzitutto, la frequenza. Immaginiamo una lampadina che si accenda e si spenga a intervalli di tempo costanti (proprio come appare un faro su un promontorio sul mare): tanti segnali a ritmo regolare. Quanti segnali manderà in certo tempo t? Poniamo che siano n. La frequenza del segnale luminoso è allora data da:
f = n/t
A parità di tempo, maggiore o minore è il numero di segnali, maggiore o minore è la frequenza del segnale.
Immaginiamo (Fig. 50, righe nere) che la sorgente e un ricevitore siano fermi l’uno rispetto all’altro a una certa distanza d (si muovono solo nel tempo, asse verticale).
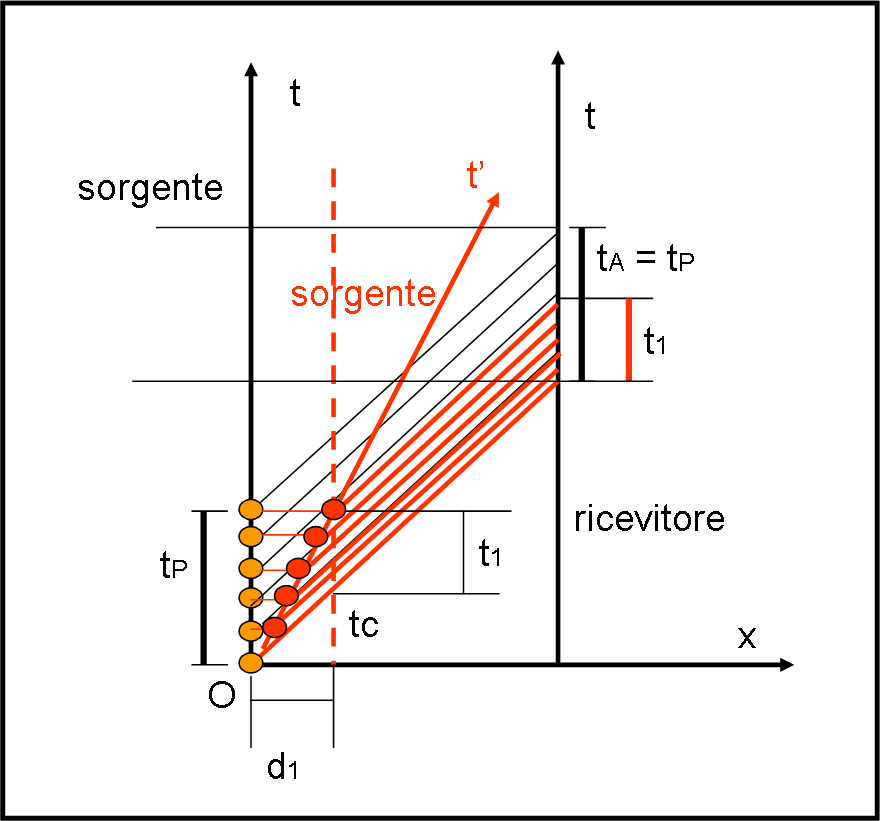
La frequenza dei segnali mandati e dei segnali ricevuti sarà uguale. Il ritardo tra invio e ricezione è ovviamente uguale a t = d/c, da cui d = ct. Nella figura abbiamo usato unità di misura tali che il raggio luminoso (o il fotone) percorra una linea inclinata di 45° nel piano (t,x), come nel diagramma di Minkowski. In altre parole, possiamo porre d = t e c =1 e, come al solito, β = v/c
La frequenza di partenza è data da
fP = n/tP
esattamente come quella di arrivo:
fA = fP = n/tP
Adesso, facciamo muovere la lampadina con una velocità v = β, in direzione del ricevitore.
Il primo segnale parte allo stesso tempo di prima. Il secondo, però, dà già un risultato diverso, dato che parte dopo che la lampadina (rossa) ha già percorso un certo spazio, avvicinandosi al ricevitore. Il che vuol dire che il secondo segnale arriva prima del previsto, dovendo percorrere uno spazio minore. E così via fino all’ultimo segnale. I segnali (rossi), in parole semplici, partono mentre si avvicinano e quindi anticipano il loro arrivo, ossia il ricevitore li vede arrivare con una frequenza maggiore.
Calcoliamo il tutto con la figura, utilizzano un metodo un po’ lungo ma tale da chiarire perfettamente quello che succede.
La linea rossa continua indica lo spostamento della lampadina in funzione del tempo (ossia la sua velocità). Ciò che ne deriva è del tutto equivalente al fatto che i segnali siano mandati a intervalli di tempo minori a partire dalla linea rossa tratteggiata che dista d1 dall’origine O. A questo punto calcoliamo il tempo totale di invio dei segnali a partire da questa linea. In altre parole dobbiamo calcolare l’intervallo di tempo t1 che è l’intervallo in cui vengono mandati gli n segnali e che è anche uguale all’intervallo di tempo in cui i segnali sono ricevuti.
Possiamo scrivere d1 in due modi, sia in funzione della velocità c che della velocità v. Ossia:
d1 = ctc = v tP
Ma, per le ipotesi fatte (c = 1, v/c = β)
tc = β tP
E’ immediato ricavare l’intervallo di tempo t1:
t1 = tP – tc = tP – tP β= tP (1 – β)
Non ci resta che confrontare la nuova frequenza con quella originaria (ossia quella di partenza). Ricordiamo, infatti, che la lampadina continua a mandare i segnali con la frequenza originaria. E’ solo il ricevitore che li riceve in modo diverso, a causa del continuo avvicinamento della sorgente di luce.
La frequenza di partenza, è sempre:
fP = n/tP
Quella di ricezione, vale adesso:
fA = n/t1 = n/tP (1 – β)
Ricavando n da entrambe e uguagliando si ha:
n = fP tP = fA tP (1 – β)
da cui:
fA = fP /(1 – β) …. (1)
Questo è il classico effetto doppler di avvicinamento. Ovviamente cambia il segno se la sorgente si allontana e la frequenza diminuisce.
Aumento o diminuzione della frequenza vuol dire, in poche parole, spostamento verso il blu (o meglio il violetto) o verso il rosso, verso alte o basse energie.
Siamo sicuri di aver fatto tutto bene? In particolare, siamo sicuri che fP rimanga sempre la stessa? Se la velocità v è relativamente modesta potremmo dire di sì, ma per valori alti di β, la faccenda non torna più.
Siamo stati troppo frettolosi…
La sorgente di frequenza fP si è messa in movimento e sappiamo benissimo che la Relatività Ristretta ci dice che per chi si muove il tempo subisce un rallentamento rispetto al sistema “fermo”. La fP originaria diventa una fP’ che è legata a quella originaria, fP, dal nostro fattore di Lorentz. Ossia, i tempi sono legati da:
t’P = γ tP
e quindi
f’P = 1/γ tP
La formula (1) deve perciò contenere la f’P e non la fP. Essa andrebbe, perciò scritta:
fA = f’P /(1 – β) = fP /γ (1 – β)) o, se preferiamo:
fA = fP (1 – β2)1/2/(1 – β)
Ci piace questa formula? Personalmente non la amo tanto… dato che al numeratore c’è un fattore che diminuisce la frequenza (sempre minore di 1), mentre al denominatore c’è un fattore sempre minore di 1 che, quindi, aumenta la frequenza. Insomma, una relazione che appare poco immediata.
Tuttavia, quando c’è di mezzo il fattore di Lorentz, i piccoli trucchi sono sempre a portata di mano
Proviamo a pasticciarla un po’:
(1 – β2)1/2/(1 – β) = ((1 – β)1/2 (1 + β)1/2)/((1 – β )1/2 (1 – β)1/2) = (1 + β )1/2/(1 – β )1/2 =
= ((1 + β)1/2(1 + β)1/2)/((1 + β)1/2 (1 – β)1/2) = (1 + β)/(1 – β2)1/2
Da cui:
fA = fP (1 + β)/(1 – β2)1/2 = fP γ (1 + β)
Adesso è molto più chiaro che fA > fP
In caso di allontanamento si ha, ovviamente:
fA = fP (1 - β)/(1 – β2)1/2 = fP γ (1 - β)
Possiamo anche scriverli in altro modo… (β e γ insieme ne fanno di tutti i colori…):
fA = fP (1 + β)/(1 – β2)1/2 = fP γ(1 + β) = fP ((1 + β)1/2 (1 + β)1/2)/(( 1 + β)1/2( 1 - β)1/2)
fA/fP = ((1 + β)/(1 – β))1/2 > 1 avvicinamento
fA1 /fP = ((1 - β)/(1 + β))1/2 < 1 allontanamento
Torniamo, adesso, alla nostra ellisse e vediamo come possa essere utilissima per il calcolo immediato delle frequenze relative alle varie direzioni, per valori qualsiasi dei raggi provenienti dalla stelle. In pratica dobbiamo riuscire a scrivere i tempi ad essi relativi.
Ricordiamo l’equazione dell’ellisse (QUI, formula (3)):
r = a(1 – e2)/(1 + e cos ϑ)
Nel nostro caso (Fig. 41)
a = γ
e = β
Per cui il raggio vettore, ossia la distanza tra fuoco e punti della curva (che è anche il tempo), è dato da:
t = γ (1 – β2)/(1 + β cos ϑ)
Questa è l'equazione per un'ellisse con ϑ che vale 0 a partire dalla direzione del perielio . In poche parole è ribaltata rispetto all'ellisse di Fig. 41. Poco male, dato che tutto dipende dalla direzione della velocità con cui si muove l'astronave ( a destra o a sinistra). Poniamo allora l'asse x diretto verso sinistra e l'angolo ϑ che parte dal punto più vicino al fuoco A.
In pratica, per ogni angolo ϑ noi siamo in grado di calcolare il tempo attraverso l'ellisse e, di conseguenza, la frequenza.
Per esempio, per un angolo ϑ = 0, abbiamo
t = γ (1 – β2)/(1 + β ) = γ (1 - β)
Per un angolo ϑ = 180°
t = γ (1 + β)
da cui (come già visto precedentemente):
fA/fP = 1/(γ (1 - β)) = (1 – β2)1/2/(1 - β) = γ (1 + β)
fA/fP = γ (1 - β)
Particolarmente interessante è l'angolo per cui t =1, ossia la frequenza non cambia rispetto a quella di partenza.
Per esso vale:
t = γ (1 – β2)/(1 + β cos ϑ) = 1
ossia:
t = γ /γ2 (1 + β cos ϑ) = 1/γ(1 + β cos ϑ) = 1
γ(1 + β cos ϑ) = 1
γ + γβ cos ϑ = 1
cos ϑ = (1 - γ)/γβ
Il numeratore è sempre minore di 1, per cui ϑ > 90°
Questo è ovviamente anche l'angolo in cui le frequenze di partenza e di arrivo sono uguali.
N.B.: Paolo, nei commenti, ha confermato questo risultato e calcolato due valori particolari.
La situazione si può facilmente riportare al caso che ci interessava fin dall'inizio, ossia quello di un astronave A che viaggia a una certa velocità β verso destra (così sfruttiamo una bella animazione trovata nel web...), dove inseriamo direttamente le frequenze al posto dei tempi. E' solo una questione di ribaltamento o di cambiamento di fuoco o di verso dell'angolo ϑ
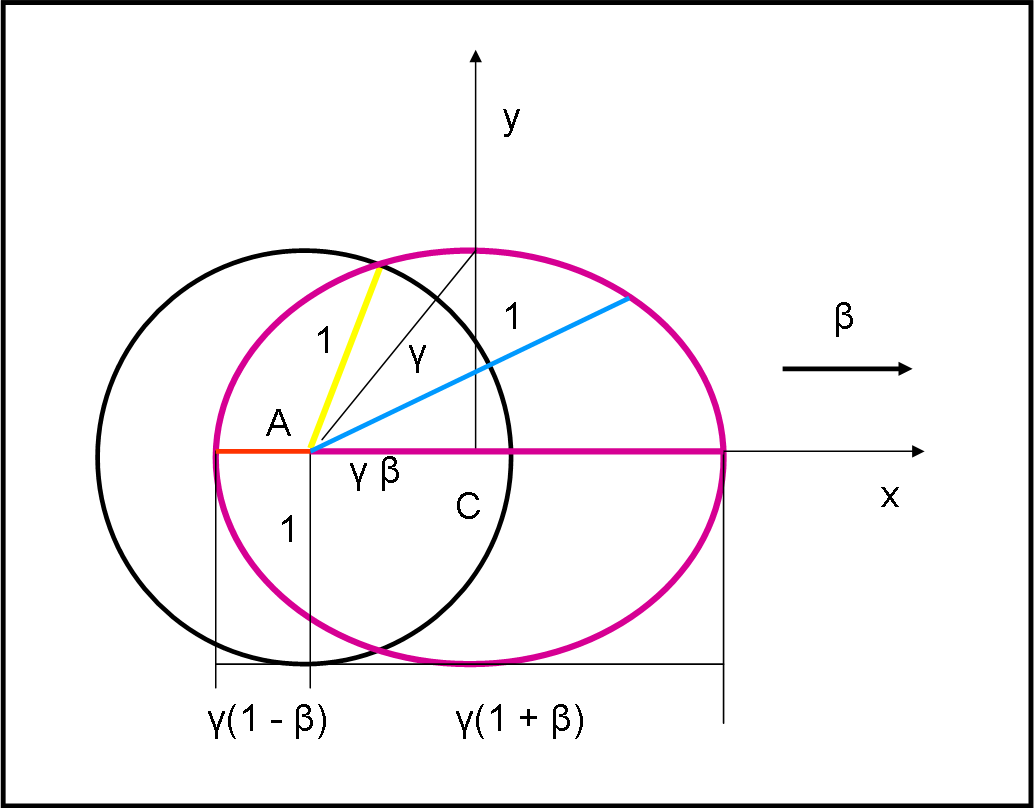
Le congiungenti più lunghe sono quelle che hanno frequenza maggiore è quindi colore più violetto. Quelle più corte fanno frequenza minore e quindi colore più rosso. Il colore originario (giallo) si ha in una direzione inclinata verso il moto (e si trova facilmente come intersezione tra circonferenza di partenza ed ellisse di abeerrazione)
Il filmato che segue mostra perfettamente come cambiano i colori al crescere della velocità dell’astronave. Vale più di tante parole...
Bene, la nostra ellisse sta svolgendo perfettamente il suo compito e vale sia per oggetti che ricevono o che emettono la luce. Potremo fare alcuni esempi estremamente interessanti. Innanzitutto cominceremo a illustrare come si vedrebbe, andando a grande velocità, un oggetto di dimensioni non trascurabili. Poi passeremo all’effetto sincrotrone, a una tecnica particolare per scoprire gli esopianeti e finiremo con uno viaggio verso il Sole (muniti di uno scudo termico adeguato!).







8 commenti
Help! Ci deve essere qualcosa che sbaglio o che interpreto male.
Ho cercato di ricavare la formula che lega la frequenza di arrivo con quella di partenza senza utilizzare l'ellisse ottenuta negli articoli precedente. Pensavo che mi avrebbe aiutato a capire l'utilizzo dell'ellisse che non mi è chiaro. Invece il risultato mi ha confuso ancora di più perchè la relazione che ho ottenuto è la reciproca di quella dell'articolo.
Questo è il percorso che ho fatto partendo dalla figura 50 ed aggiungendo la dimensione y.
Le coordinate della sorgente nel suo riferimento sono) che nel riferimento del ricevitore sono:
che nel riferimento del ricevitore sono:
Per ottenere il tempo di arrivo occorre sommare al tempo di emissione il tempo per raggiungere il ricevitore.
Nelle unità di misura dove c=1 avrei
La relazione tra intervalli di arrivo e intervalli di partenza
e intervalli di partenza 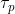 può essere calcolata con la derivata
può essere calcolata con la derivata
quindi mi verrebbe che}) ?
?
caro Fabry,
la frequenza di arrivo deve per forza essere maggiore di quella di partenza. Attenzione a non confondere i tempi con le frequenze che compaiono nell'ellisse...e/o con il moto di avvicinamento o di allontanamento...
La frequenza è l'inverso del tempo...
E' proprio la verifica del rapporto tra la frequenza di arrivo e quella di partenza che mi ha convinto a scrivere.
Prendo come riferimento la fig.50. La sorgente si muove lungo l'asse x nel verso positivo dell'asse. Nella situazione fissata nella figura il ricevitore vede la sorgente a 180°. Poiché la sorgente va incontro al ricevitore credo ci sia da aspettarsi fA/fp>1 (spostamento verso il blu). La verifica della formula mi sembra torni.
Quando la sorgente supera il ricevitore, il ricevitore vede allontanarsi la sorgente a 0°. Credo che qui sia da aspettarsi fA/fp<1 (spostamento verso il rosso). Anche qui la verifica della formula mi sembra torni.
Per ultimo il caso della sorgente che viene vista dal ricevitore a 90°. L'effetto doppler classico è istantaneamente sospeso. Rimane solo la dilatazione del tempo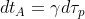 , che in termini di fequenze si inverte
, che in termini di fequenze si inverte 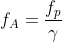 . Verifico la formula ottenendo lo stesso risultato.
. Verifico la formula ottenendo lo stesso risultato.
Forse ho capito.
L'angolo che considero è quello visto in arrivo, mentre nella formula dell'articolo c'è l'angolo di partenza.
Tenendo conto della relazione tra i due angoli arrivo alla formula del'articolo.
Ora devo capire il significato dei colori dell'animazione dove a 90° c'è uno spostamento verso il rosso. Forse li si considerano gli angoli di arrivo.
certo Fabry,
l'aberrazione c'è comunque e quindi la linea a 90° originaria si sposta in avanti...
Angoli di arrivo e di partenza sono equivalenti, basta solo cambiare il sistema di riferimento...
Caro Enzo, ho provato a ricavare il valore dell'angolo ϑ corrispondente ad un'uguale frequenza di arrivo e partenza...

Parto dalla formula ricavata nell'articolo: fA = fP(1 + β cos ϑ)/γ(1 – β²)
a cui però applico un ulteriore semplificazione, dato che 1/(1 – β²) = γ²
fA = fP (1 + β cos ϑ) γ²/γ
fA = fP γ (1 + β cos ϑ)
Ovviamente, si deve avere: fA = fP
fA/fP = 1
fA/fP = γ (1 + β cos ϑ)
γ (1 + β cos ϑ) =1
1 + β cos ϑ = 1/γ
ma 1/γ = √(1 – β²)
1 + β cos ϑ = √(1 – β²)
β cos ϑ = √(1 – β²) -1
cos ϑ = (√(1 – β²) -1)/β
ϑ = arccos (√(1 – β²) - 1)/β
oppure:
1 + β cos ϑ = 1/γ
β cos ϑ = 1/γ -1
β cos ϑ = (1- γ) /γ
cos ϑ = (1- γ) /β γ
ϑ = arccos (1- γ)/β γ
Giusto per fare una prova con β = 0,6
ϑ = arccos (√(1 – 0,6²) – 1)/0,6 = 109,47 °
γ = 1/√(1 – 0,6²) = 1,25
ϑ = Arccos (1- 1,25)/(0,6 x 1,25) = 109,47°
con β = 0,9
ϑ = arccos (√(1 – 0,9²) – 1)/0,9 = 128,81°
γ = 1/√(1 – 0,9²) = 2,2941573
ϑ = Arccos (1- 2,29)/(0,9 x 2,29) = 128,81°
Quindi tale angolo, a cui corrisponde fa =fp, se non ho sbagliato qualcosa, cresce oltre i 90° al crescere della velocità ...
Paolo
Paolo
cari TUTTI:
I commenti di Fabrizio e di Paolo, mi hanno fatto capire che ho fatto alcuni passaggi senza averli spiegati molto bene. In particolare, ho sempre usato la stessa ellisse sia per i tempi che per le frequenze senza esplicitare questo fatto. In realtà poco importa data la simmetria della faccenda. Tuttavia, risulta un po' oscuro il fatto che l'angolo che porta alla stessa frequenza di partenza sia maggiore di 90, mentre invece nella Fig. 51 risulta minore di 90. Il fatto, come vedrete nel testo corretto, è che per calcolare gli angoli usavo la figura che ho aggiunto prima della Fig. 51. La Fig. 51 è invece quella con le frequenze relativa a un astronave A che viaggia verso destra (ossia un astronave che si crede ferma e vede il cielo che "cade" verso di lei con velocità - beta ...).
Forse dovrei cambiare tutto il testo per non farvi saltare in questo modo dai tempi alle frequenze, ma spero che anche così, come è stato impostato, sia comprensibile...
Fatemi sapere...
Ringrazio, ovviamente, Paolo e Fabrizio, anche perché ho potuto correggere due refusi nelle formule.