Questo articolo è adatto a tutti, in particolar modo ai bambini che sprizzano fantasia da tutti i pori. Partiamo da una farfalla e ci accorgiamo che la geometria ci porta quasi automaticamente a spiegare alcuni tra gli oggetti più misteriosi e affascinanti del Cosmo. L'articolo era già apparso molto tempo fa, ma ho giudicato interessante riproporlo dato che con oltre 1800 articoli, i nuovi arrivati (e sono tanti) potrebbero trovare difficoltà a trovarlo nell'archivio... Se la cosa piacerà, ogni tanto faremo lo stesso con altri articoli particolarmente stimolanti e sempre attuali.

La Fig. 1 ci mostra una bellissima farfalla colorata. Non è difficile disegnarla, ma è ancora  più facile stilizzare al massimo la sua forma. Molti bambini lo fanno e continuano a vedere sempre, nei due triangoli e nella barretta centrale, lo stesso magnifico insetto. Basta solo un po’ di fantasia e di immaginazione.

A questo punto la farfalla è libera di volare e assumere varie posizioni, come mostra la Fig. 2.

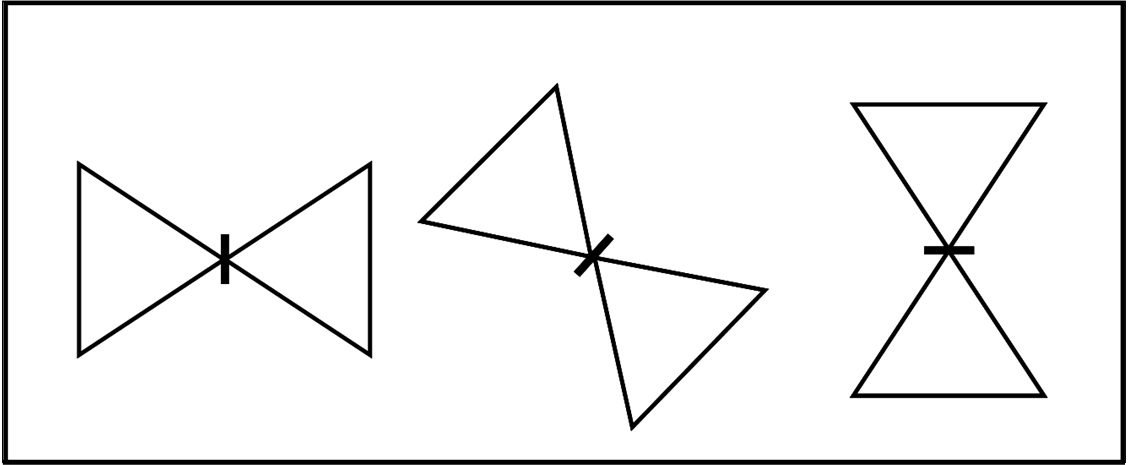
Tuttavia, questo semplice disegno può anche rappresentare una forma geometrica leggermente più complicata. Basta pensare che ciò che stiamo vedendo sia solo la proiezione su di un piano di qualcosa di tridimensionale. Questo qualcosa non è altro che un cono, come quello di Fig. 3, disegnato nelle tre dimensioni.

Tuttavia, ogni volta che guardiamo il cono lungo una direzione perpendicolare al suo asse,  esso si mostra sempre come farfalla. Le cose cambiano, però, se lo guardiamo secondo una direzione che non è più perpendicolare all’asse. La nostra farfalla assume una forma del tutto diversa al variare della direzione di vista.  Se poi l’asse si dirige proprio verso di noi, il cono diventa un semplice cerchio. Anche la barretta centrale la possiamo rappresentare come un cerchietto, che, se vista perpendicolarmente all’asse del cono, si trasforma proprio nel  corpo della farfalla.

Molto meglio trasformare anche le parole in semplici disegni. La Fig. 4 mostra la nostra farfalla vista dall’alto. Immaginiamo, però, di ammirarla secondo le direzioni indicate dalle frecce nella figura.

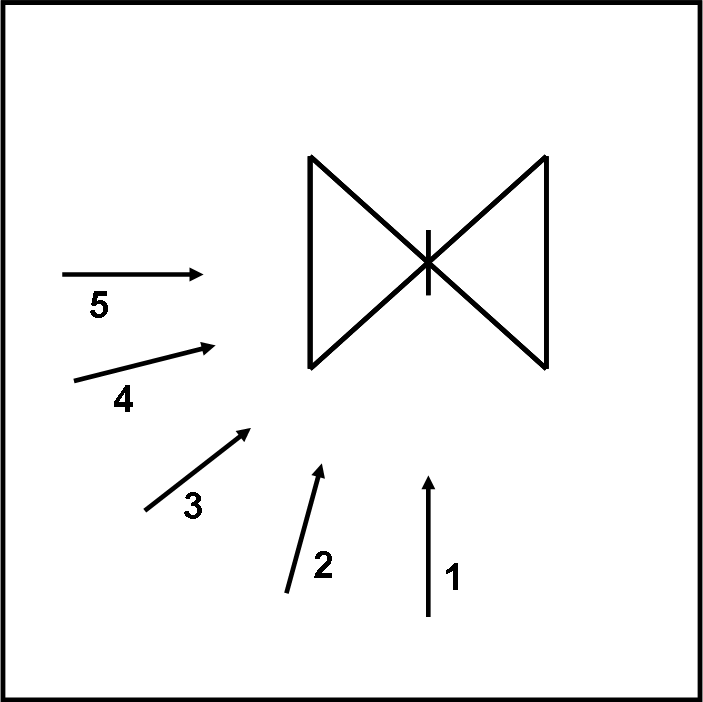
Il cono-farfalla si mostrerà secondo proiezioni continuamente diverse, come indicato nelle Fig. 5 e 6.

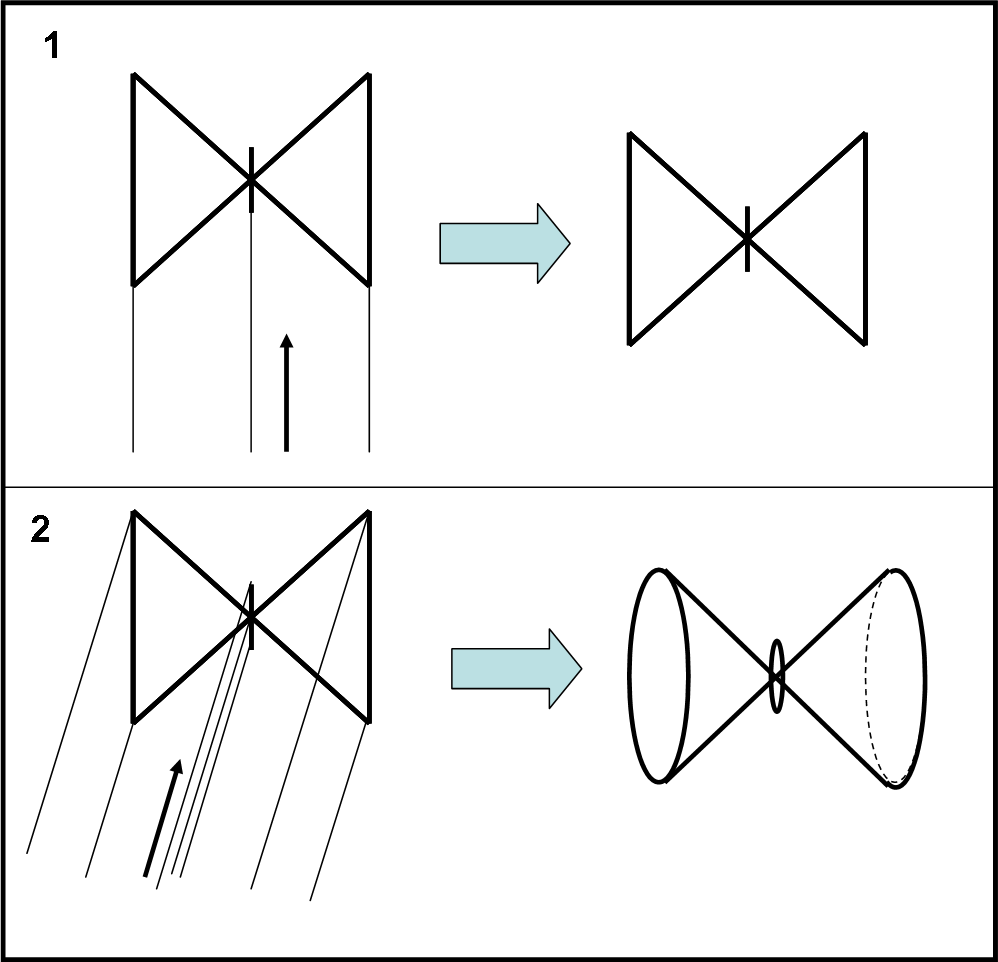
Nella posizione (1) la direzione di vista è perpendicolare all’asse del cono e si riottiene la farfalla stilizzata con il corpo centrale simile a un segmento. A mano a mano che ci sposta verso sinistra, il cono fa notare le sue due sezioni circolari che si manifestano come ellissi (2) . Anche il corpo della farfalla diventa una piccola ellisse. In (3) stiamo guardando il cono proprio lungo una sua generatrice e otteniamo come risultato due circonferenze tangenti tra loro e in mezzo l’ellisse del corpo. In (4) le due ellissi si avvicinano sempre più a due circonferenze e si intersecano tra di loro. Finalmente, in (5) il cono si trasforma in una sola circonferenza con al centro una più piccola che è il corpo della farfalla. I bambini possono divertirsi a girare intorno alla farfalla-cono e trovare altre situazioni divertenti. Anche senza internet, videogiochi e telefonini, ci si può divertire imparando.

Il gioco geometrico è praticamente finito. Delusi? Assolutamente no, dato che questo semplice gioco prospettico diverte moltissimo anche l’Universo che lo esegue continuamente. Tuttavia, quando lo esegue “lui”, l’apparenza cambia e il risultato finale diventa entusiasmante.

La Fig. 7 ci mostra quattro nebulose. Le due in alto sono celebri e a lungo considerate misteriose. I loro nomi sono molto indicativi:  quadrato rosso e  rettangolo rosso, rispettivamente. I gas da loro espulsi hanno preso la forma di un cono quasi perfetto, con la stella (o più esattamente, il sistema doppio) posta proprio nel vertice del cono. Esse sono viste esattamente di lato come nel primo caso della Fig. 5. Attorno a loro un denso e piccolo disco di polvere, che non si riesce a vedere nelle immagini, ma che rappresenta il cerchietto-corpo della farfalla. Stiamo guardando le due nebulose perpendicolarmente all’asse del cono e non ci possiamo, quindi, stupire della loro forma stilizzata a farfalla,  quasi perfetta.

Lo stesso cono, girato di un certo angolo, dà luogo alle due immagini inferiori. Dato che la parte più visibile e densa è quella lungo il bordo del cono, le nebulose sembrano composte solo dalle ellissi che ne definiscono i contorni. Quella di destra è la celebre supernova della Nube di Magellano vista esplodere nel 1987 e che oggi ci meraviglia con il suo cono visto “di taglio” e il cerchio centrale relativo al disco più luminoso.

Altri due casi di nebulose viste di lato sono riportate in Fig. 8. L’ultima è proprio chiamata “farfalla”. In tutti i casi le nebulose sono di tipo planetario o proto planetario (espulsione di gas e polvere di poco precedente alla trasformazione finale), tranne quella relativa alla supernova, come già detto prima. Le ultime due hanno forme un po’ più fantasiose rispetto a quelle del quadrato e del rettangolo, che invece hanno una geometria quasi perfetta. Le stelle quando si trasformano per andare in pensione lo fanno inventando mille e uno giochi di prestigio! D’altra parte, anche certe farfalle esotiche mostrano forme molto elaborate…

La geometria è semplicissima, ma il risultato è davvero affascinante. l’Universo è come i bambini di una volta: sa proprio divertirsi con niente! Provate a far giocare i bambini vicino a voi con le farfalle cosmiche. Basta cercare nel web “nebulosa planetaria” e vi divertirete a trovare molti altri casi nati tutti da una semplice … farfalla-cono. Ormai il gioco lo conoscete…

Qualche parola “scientifica”. Molte idee sono cambiate rispetto all’espulsione “classica” di materia da una stella di tipo solare (ma anche nelle supernove) rispetto a quanto si credeva una volta. Non abbiamo soltanto il palloncino semplice di gas che si espande e che dà luogo a un cerchio nel telescopio, più denso al bordo per ovvi motivi geometrici (è lo stesso fenomeno che ci fa vedere l’atmosfera più densa verso l’orizzonte), ma getti di materia che, per varie ragioni legate al campo magnetico, alla  presenza di un sistema binario (come questo, per esempio), alla rotazione, alla presenza di un disco di gas centrale, e cento altre situazioni particolari, assumono la forma di due getti conici lanciati in direzione opposta. Insomma, le farfalle sono sempre più comuni…

Anche le nebulose planetarie meglio conosciute e pubblicizzate nascondono spesso la loro forma reale a causa di una prospettiva un po’ “malandrina”. Il caso più celebre è forse quello della nebulosa della Lira, la più classica delle nebulose planetarie, a lungo pensata come una sfera di gas omogenea attorno alla nana bianca centrale. E, invece anche lei è una farfalla piuttosto particolare.

La nebulosa di cui parlo è ovviamente M57, meglio conosciuta come ring nebula (nebulosa anello) o, appunto, nebulosa della Lira. Un anello quasi perfetto!

Hubble e il telescopio binoculare dell’Arizona (LBT) hanno mostrato, con osservazioni infrarosse molto accurate, una situazione ben più complessa. La nuova immagine di Fig. 9 mostra una corona tenue e rossastra che si estende tutt’attorno all’anello centrale. Con i giusti occhiali, può addirittura sembrare una rosa appena sbocciata!

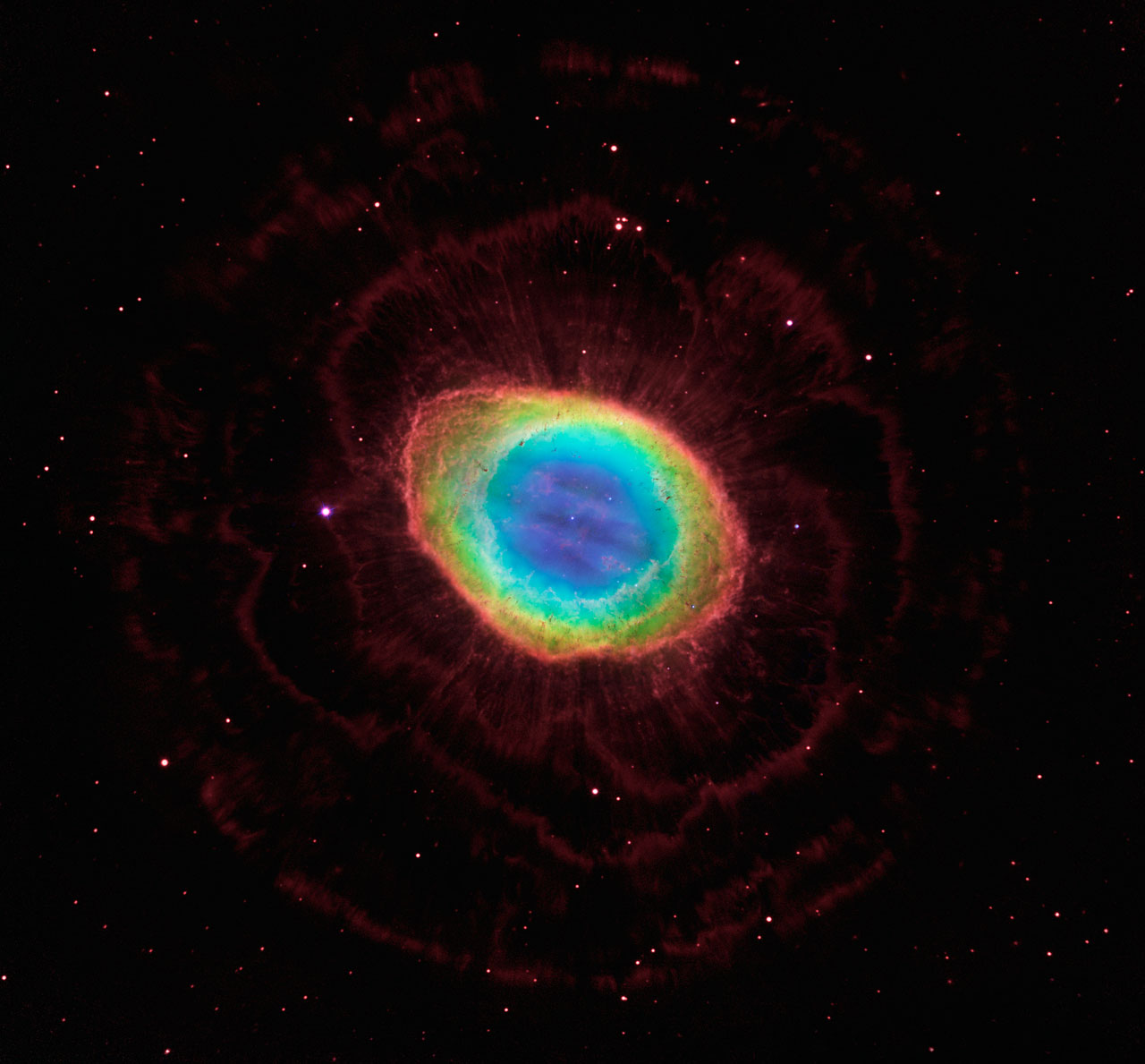
La prima fase di espulsione di materia dovrebbe essere iniziata circa 4000 anni fa e la nebulosa continua ad allargarsi alla velocità di oltre 60000 km/h. La parte centrale è quella più visibile e conosciuta, ma essa si divide in due parti che la visione quasi frontale, che abbiamo da terra, rende di difficile comprensione. La parte giallo-arancio è il disco di materia che circonda la nana bianca (il corpo della farfalla), il cui colore deriva dalla temperatura più bassa. La parte azzurra che sembra colorare l’interno dell’anello non è altro che uno dei due lobi (le ali della farfalla) che si espandono verso l’esterno con temperatura più alta. Il gas è soprattutto elio. Questa parte si espande a velocità maggiore rispetto alla corona tenue e sfrangiata  più esterna che ha una forma sferica.

La Fig. 10 ci mostra la geometria della parte centrale. A sinistra notiamo che il corpo è molto grosso (un po’ come quello delle farfalle notturne), mentre le ali azzurre sono relativamente piccole e assomigliano a due mezze ellissi.

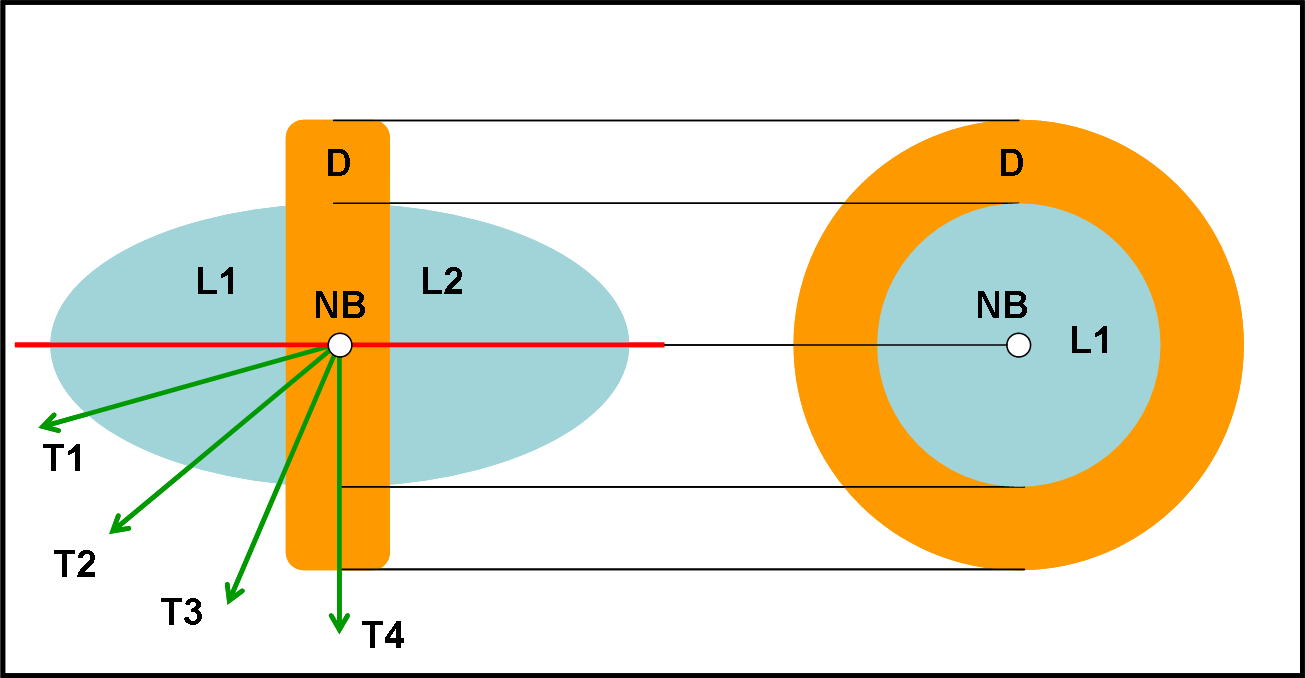
A destra la vista della farfalla-Lira vista di fronte, dove il corpo più grande crea la corona esterna che contiene al suo interno le ali azzurre.  L’angolo che la direzione della Terra forma con l’asse della nebulosa è abbastanza piccolo (T1), per cui siamo praticamente nella configurazione di destra. Il disco arancione assomiglia, quindi, a un’ellisse poco schiacciata, mentre le ali sembrano solo un colore di sfondo di questo anello.

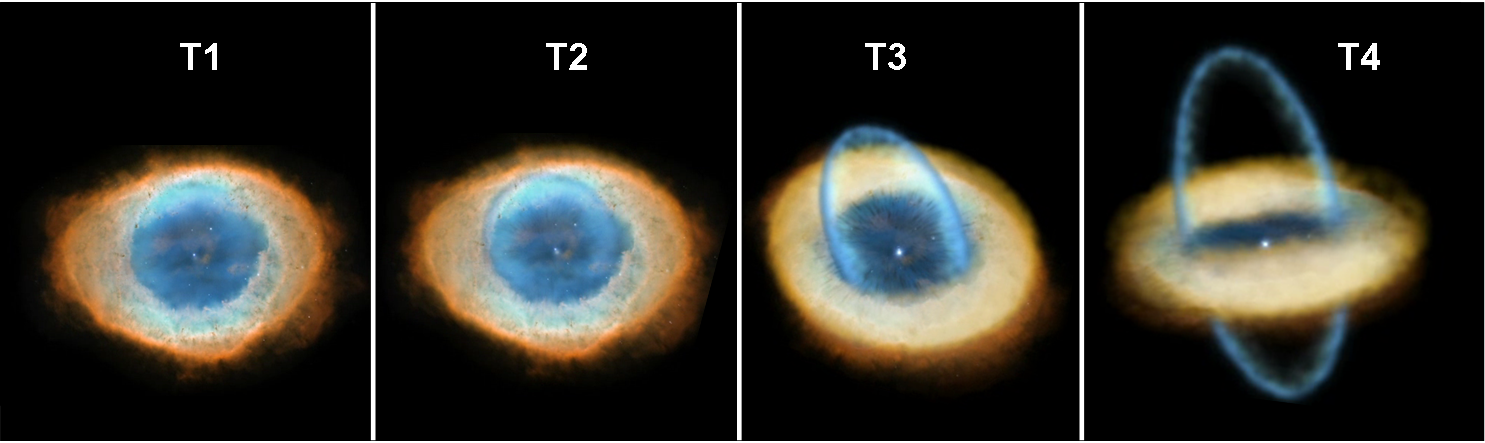
Ormai, sappiamo, però, come cambierebbe la farfalla se la potessimo vederla da posizioni più angolate, come T2, T3 e T4 della Fig. 10. L’ultima sarebbe proprio una visione “di taglio” con i due lobi perfettamente distinti, ossia con le ali spiegate. La Fig. 11 ci fa vedere questa variazione. In T2 si comincia ad avvertire che la parte azzurra supera il disco ed è davanti a lui. In T3 il lobo superiore è ormai nettissimo. In T4 la farfalla si mostra in tutta la sua bellezza.

Lo spettacolo sparirà lentamente entro i prossimi 10 000 anni, quando il gas si disperderà nello spazio. Il nostro Sole, decisamente più piccolo della stella che ha originato M57, non riuscirà a dar luogo a uno spettacolo così affascinante, ma farà sicuramente del suo meglio.

Quando punterete il vostro telescopio verso M57, pensate a quante cose sono nascoste dalla particolare visione prospettica. Anche gli oggetti del cosmo si divertono e fanno i misteriosi. Se la farete vedere ai vostri bambini, loro sapranno subito riconoscere una bellissima farfalla che sta volando ad angolo retto rispetto a noi…