Questo articolo è stato inserito nella sezione d'archivio dedicata alla Relatività Ristretta, in Relatività, velocità della luce e buchi neri.

Quando si parla di Teoria della relatività, di spaziotempo, di deformazione spaziotemporale e via dicendo si entra in un mondo descritto da formule di grande complessità e si perde spesso il filo del discorso. Purtroppo, per visualizzare ciò che capita realmente, la matematica è l’unica salvezza. Le parole tendono sempre più a confondere o a risolvere solo un lato del problema. Ad esempio, lo stesso concetto di spazio può essere descritto in vari modi, a seconda dello scopo che abbiamo in testa: ciò che contiene la materia; il luogo dove i corpi possono muoversi; l’insieme delle relazioni che legano la materia; ecc., ecc.

Sono tutte definizioni giuste, anche se estremamente particolari e legate al tipo di discorso che si sta facendo. Analogamente lo spaziotempo è spesso un concetto che sembra apparire ovvio e poi improvvisamente si complica e ci fa perdere del tutto il filo del discorso. Tutto sembra andare bene, ad esempio, se consideriamo il cono di luce. Molto meno quando scopriamo che esso non è altro che una delle tante rappresentazioni matematiche che può descriverlo. La verità è che io l’ho sempre introdotto in modo quantomeno imperfetto o parziale, non occupandomi di ciò che realmente capita allo spazio e al tempo. Esso nasce, in realtà, all’interno del diagramma di Minkowski, una soluzione geometrica che permette di descrivere lo spazio-tempo introducendo la relatività speciale di Einstein. Per potere fare ciò deve basarsi sulle trasformazioni di Lorentz e le cose diventano, apparentemente, sempre più intricate.

Il fatto di averlo sempre usato in modo “parziale” ha spesso causato problemi interpretativi. Primo fra tutti perché mai assume forme che tutto sono meno che quelle di un vero cono? A parole si fa presto a mettere le cose a posto: lo spazio si espande. Punto e a capo. Se vogliamo vedere dei coni dobbiamo cambiare coordinate e cose del genere. Tuttavia, non è solo l'espansione a creare problemi. Teniamo, infatti, ben presente che quanto stiamo per raccontare non si occupa minimamente dell'espansione dell'Universo. Eppure, già così, la visione di ciò che capita cambia completamente forma e struttura. Ricordiamoci anche, però, che NON distrugge la fisica classica. Essa continua a essere valida se si studiano fenomeni che sono relativi a velocità decisamente minori di quelle della luce. Lo stesso diagramma di Minkowski si trasforma in un qualsiasi diagramma della geometria euclidea.

Questo "circolo" e i suoi lettori sono ormai maturi per capire finalmente (se già non lo sanno, ovviamente) cosa rappresenta il diagramma di Minkowski, il “suo” cono di luce e -soprattutto- come serva per leggere geometricamente intervalli di tempo e di distanza in uno spaziotempo che segua la relatività ristretta. Per essere sinceri fino in fondo, dovrei dire che il diagramma si inserisce in un quadro più ampio che prende proprio il nome di spaziotempo di Minkowski. La sua definizione può spaventare nella sua semplicità: è un oggetto matematico  utile a descrivere lo spaziotempo della relatività speciale. Una frase banale e terribile nello stesso istante (attenzione a parlare di istante…. però…), soprattutto per quel “matematico” che incombe. Noi non andremo a fondo di questa rappresentazione (almeno per adesso) e ci limiteremo al diagramma che ne è una visione puramente geometrica, per la quale non ci sarebbe nemmeno bisogno di utilizzare formule.

Vale però la pena di ricordare come lo stesso Minkowski definiva il suo “oggetto” matematico:

“Un punto dello spazio a un punto del tempo, cioè, un sistema di valori x, y, z, t lo chiamerò un punto dell’Universo. La molteplicità di tutti i pensabili sistemi di valori x, y, z, t, la battezzeremo universo ”. In altre parole, uno spaziotempo così definito è uno spazio matematico a quattro dimensioni senza proprietà fisiche, i cui punti sono definiti punti-evento. Il moto degli oggetti è rappresentato da linee di universo, che uniscono i punti-evento corrispondenti alle coordinate istantanee degli oggetti stessi.

Fermiamoci qui, altrimenti farei scappare la voglia di proseguire anche a un santo. Vedremo che, una volta che saremo ben allenati, tutto apparirà di un’armonia perfetta e di una semplicità meravigliosa, a patto di aver fatto girare le rotelle del nostro cervello.

Per le stesse motivazioni dello spaziotempo costruito da Minkowski è, ovviamente, necessario conoscere la relatività speciale e le sue implicazioni sulle coordinate spazio e tempo. Il diagramma è stato costruito proprio per lei! Inoltre, dato che Einstein ha avuto bisogno di usare delle trasformazioni di coordinate un po’ speciali, quelle già introdotte da Lorentz, saremo anche obbligati a fare la loro conoscenza. Niente di veramente complicato, dato che, con un po’ di fatica, si possono descrivere utilizzando solo e soltanto il teorema di Pitagora.

Immergiamoci, quindi nel mondo creato da questi tre personaggi non certo banali: Einstein-Lorentz- Minkowski e vediamo di riuscire a disegnare nello spazio relativistico con la stessa facilità con la quale sappiamo farlo nello spazio euclideo (quello che ci hanno insegnato a scuola). Nel frattempo, avremo anche capito la relatività speciale di Einstein… niente male, no?

La velocità è la chiave di tutto

Prima di cominciare, vi offro una relazione semplicissima che potrebbe farvi avvicinare un po’ alla volta alla problematica nel suo insieme. Una relazione che tutti conoscete e che usate quotidianamente. Vi sembrerà una cosa ovvia e banale, ma, pensandoci bene, il segreto di tutto è proprio lei.

Nella fisica classica esiste una relazione fondamentale, alla portata di tutti e che tutti conoscete sicuramente: la definizione di velocità. Essa è data dal rapporto tra lo spazio percorso e il tempo impiegato a percorrerlo. La velocità, quindi, è la più semplice relazione possibile che lega lo spazio con il tempo. Ed è anche la grandezza fisica di partenza di tutta la meccanica. Essa, però, non pone nessun vincolo effettivo tra spazio e tempo. Posso farli variare a piacere e ottenere tutti i valori che voglio. In questo contesto, posso, quindi, considerare spazio e tempo come due grandezze del tutto indipendenti tra loro. Li posso manipolare uno alla volta e ottenere alla fine il valore corrispondente della velocità. Questa è la visione di Newton che va benissimo per un mondo alla portata dell’uomo e delle sue azioni quotidiane.

Se invece impongo un valore fisso alla massima velocità raggiungibile, creo immediatamente un legame indissolubile tra spazio e tempo. In altre parole, non posso cambiare lo spazio quanto voglio e fare lo stesso con il tempo. Potrei, infatti, trovare un valore superiore alla velocità della luce. La costanza della velocità della luce impone quindi che, fissato uno spazio (o un tempo), il tempo (o lo spazio) debba variare in modo da non superare quel valore. Questo fatto cosa ci dice? Che per certi valori della velocità, molto prossimi a quelli della luce, una variazione dello spazio obbliga a far variare il tempo entro certi confini e viceversa. Ed ecco nascere le relazioni della dilatazione dei tempi e dell’accorciamento dello spazio e tutte le deformazioni susseguenti.

In fondo, la teoria della relatività è tutta qui… o quasi…

Ancora una cosa, prima di iniziare. Dobbiamo essere sinceri: se il diagramma di Minkowski può essere descritto e utilizzato anche senza l'uso di formule (o quasi), lo stesso non è possibile per la relatività speciale. Sì, potremmo descrivere a parole certi concetti (dilatazione del tempo, contrazione delle lunghezze, composizione della velocità, ecc.), ma alla fine faremmo solo una grande confusione se non potessimo rappresentare certe quantità (che sono poi sempre le stesse) con valori ben determinati e calcolabili.  Niente di trascendentale (sono, in fondo le trasformazioni di Lorentz), ma più che necessarie. Cercheremo, perciò, di far capire molto bene prima il concetto qualitativo e solo dopo inseriremo la rappresentazione quantitativa. In tal modo, quando si introdurrà un certo parametro sapremo subito che significato "pratico" si porta dietro.

Andremo avanti con molta calma e ripeteremo i concetti varie volte, magari guardandoli da angolazioni leggermente diverse.

Il tempo non è niente di speciale

Passiamo a qualcosa che è poco più che uno scherzo e prende spunto da quello splendido romanzo che è Flatland (Flatlandia), scritto nel 1884 da Edwin Abbott Abbott (chi non lo ha letto vada subito a comprarlo!). Un romanzo essenzialmente satirico, che si definisce come “romanzo a più dimensioni”, e che, quindi, la dice lunga sulla sua importanza in un discorso che vuole fare abbracciare strettamente lo spazio con il tempo, ossia riuscire a passare dalle tre alle quattro dimensioni.

A molti di noi sembra ovvio aver capito la rappresentazione grafica dello spaziotempo, dopo aver accettato di sacrificare una o due dimensioni dello spazio. Tuttavia, il concetto più profondo di questo passaggio è molto più sottile di quanto sembri. Solo comprendendolo bene si può capire la vera differenza tra relatività galileiana e relatività einsteniana. Il tempo, anche se non ce ne accorgiamo, continua a essere considerato come una coordinata “diversa” rispetto a quelle spaziali. La usiamo anche nei grafici della meccanica classica, quando si descrive, ad esempio, la velocità. Però, però, è sempre qualcosa che vive in modo indipendente, capace di modificare lo spazio, ma in qualche modo “intoccabile”. Lui è quello che è e nulla sembra mutarlo.

Invece, per introdurre lo spaziotempo è necessario fare un passo in più e considerarlo, sotto tutti i punti di vista, una coordinata perfettamente simile alla lunghezza, all’altezza e alla larghezza.  Un’ulteriore informazione che serve per caratterizzare un certo evento. Addirittura può essere espressa nella stessa unità di misura delle altre. Può servire a questo scopo una frase di Einstein che descrive molto bene il problema di fondo che analizzeremo attentamente: “Siccome nella struttura a quattro dimensioni dello spaziotempo non è più possibile rappresentare obiettivamente l’adesso, sembra naturale pensare alla realtà come a una esistenza quadridimensionale, piuttosto che all’evoluzione nel tempo di una esistenza tridimensionale”.

Pensiamoci sopra e, un po’ alla volta, il mondo di tutti i giorni ci appare come una errata visione della realtà.  Pur rischiando una trattazione che sembra sconfinare nella “filosofia”, dobbiamo ammettere che il “nostro” tempo è veramente una “strana” grandezza. Diciamo, normalmente, che esso si può dividere in passato, presente e futuro. Tuttavia, il presente, l’unica situazione che fa parte della realtà quotidiana, è quanto di più sfuggente possa esistere. Quanto dura? Un minuto, un secondo, un millisecondo? E’ un po’ come il discorso del limite… dato un certo numero piccolo a piacere possiamo sempre considerare un intervallo di tempo che sia più piccolo di quel numero. In parole povere, il presente, l’unica cosa che ci sembra concreta, è quando di meno reale possa esistere.

Molto più facile è definire il passato e il futuro. Nel primo caso si tratta di tutti gli eventi che non esistono più, ma che sono sicuramente accaduti, nel secondo caso di tutti gli eventi che devono ancora accadere, ma che possono essere legati a quelli passati attraverso le leggi fisiche. La dipendenza di ogni singolo istante con il passato e il  futuro fa sparire qualsiasi concretezza del presente.

E’ molto più logico pensare che la nostra realtà si svolga all’interno di un continuo spaziotemporale quadridimensionale che contiene tutti gli infiniti universi tridimensionali. Ognuno di essi è relativo a un certo istante, ma lo spaziotempo deve contenerli tutti.

Riflettete bene su questa frase perché già contiene il succo di tutto il discorso.

Matematicamente, anche se appare assurdo per i nostri sensi, ogni avvenimento che a noi sembra svilupparsi nel tempo è già scritto nel continuo spaziotemporale. Non mi picchiate, ma si deve concludere che passato, presente e futuro esistono contemporaneamente. Un diagramma che descrive lo spaziotempo deve, quindi, essere in grado di riprodurre questa situazione. Solo così si inserisce correttamente la quarta coordinata.

Questa visione va sicuramente contro il concetto di “divenire” che domina ancora il nostro pensiero e quindi è necessario uno sforzo particolare per cambiare la strategia descrittiva. Non per niente, la matematica è perfettamente in grado di descrivere uno spaziotempo realmente quadrimensionale, mentre la filosofia, ossia la scienza del pensiero, non è ancora riuscita a far suo questo cambiamento rivoluzionario.

Non confondiamo, però, la relatività con la meccanica quantistica. La prima non va contro la logica, ma la descrive più correttamente. Essa è quanto di più reale ci sia ed è dominata proprio dalla causalità. La meccanica quantistica, invece, va contro la logica del pensiero e annulla il legame causa-effetto.

Basta, non vogliamo fare filosofia, ma solo mettere i puntini sulle “i”. In poche parole, prima di studiare i passaggi matematici e concettualmente logici introdotti dalla relatività di Einstein e dal metodo grafico di rappresentarla, è bene iniziare a capire esattamente con quale “sistema” abbiamo a che fare. In ogni modo, non preoccupatevi. A mano a mano che andremo avanti, questi concetti saranno ripresi costantemente…

Torniamo al nostro scherzo, che vuole solo mostrarci come sia poco comprensibile (in prima battuta) un passaggio da un mondo  basato su n dimensioni a uno definito da n+1 dimensioni.  Per semplicità descrittiva, seguiamo allora lo schema proposto da Abbott ed eseguiamo il nostro scherzo dimensionale su un abitante del mondo a due dimensioni. Il vantaggio di questa scelta  è indubbio: noi siamo in grado di vederlo dal di fuori, ossia da uno spazio a tre dimensioni, di cui quello a due è solo un caso particolare. Anche questa frase è molto importante: noi cerchiamo sempre di vedere lo spazio dal di fuori, ma in realtà lo vediamo dal di dentro.

Facciamo impazzire un povero cerchio

Noi viviamo in uno spazio a tre dimensioni e lo indichiamo con S3. In questo “mondo” abbiamo un serie infinita di amici che possono aiutarci nello scherzo. Ne abbiamo convinti tre che dopo un po’ di resistenza (sono sempre figure geometriche…) hanno accettato. Non li presento ancora per creare un po’ di “suspence”, ma penso che li riconosciate velocemente.

Chi subisce lo scherzo è un cerchio, di nome CE,  di grande intelligenza (anche se un po’ superbo), che vive nello spazio S2, a due dimensioni. In quello strano spazio, non è facile intuire facilmente con chi si ha a che fare. Un rettangolo e un segmento si vedono nello stesso modo, ma anche una circonferenza, e molte altre figure (pensateci bene). Tutte appaiono come dei segmenti! Bisogna toccare, valutare attentamente lo spessore delle linee e applicare tanti altri piccoli accorgimenti per identificare i vari abitanti. Inoltre, nello spazio di CE, la differenza tra bambini e adulti sta solo nelle loro dimensioni (questa è una mia aggiunta…).

Il nostro amico  CE sa di essere particolarmente dotato e… se la tira un po’. E’ il personaggio giusto per subire uno scherzo un po’ “cattivo”, ma anche per imparare  qualcosa che per lui è veramente incredibile. Per noi, invece, tutto è più semplice, dato che possiamo spostarci nella terza dimensione (che lui non può vedere) e assistere alla sua disperazione crescente. Immaginiamo di posizionarci a una certa altezza (parola sconosciuta a  CE) e disegnare cosa succede nello spazio piano S2.

In Fig. 1 ci sono diversi momenti dello scherzo “visti dall’alto”. Ciò che si vede è, quindi, lo spazio di CE a due dimensioni.

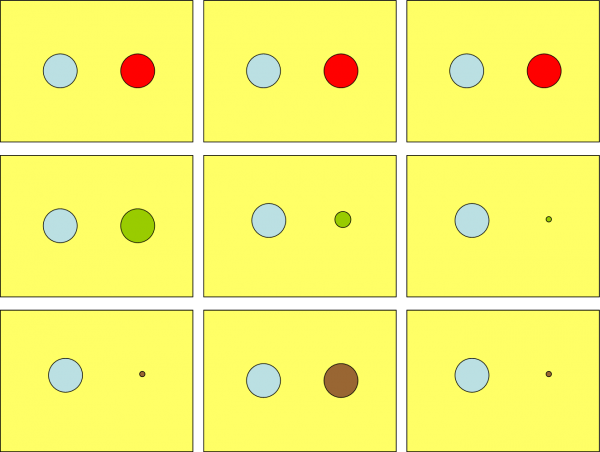
Cominciamo con la prima riga. A sinistra CE vede improvvisamente comparirgli davanti CI. Un attimo di sorpresa, ma subito dopo inizia il colloquio. CI chiede a CE: “Chi sono?” CE non ha problemi a dirlo: “Sei un cerchio come me, di colore rosso; ti riconosco da tante piccole sfumature e so che non puoi essere altro che un cerchio”. CI si mette a ridere e poi dice a CE che adesso si muoverà rispetto a prima ma resterà sempre lì davanti a lui.

Un attimo dopo ecco la seconda scena. CE non ha problemi a dire: “Sei rimasto tale e quale a prima. E’ ovvio…”. CI risponde: “Nemmeno per sogno. Ti posso assicurare che mi sono mosso e anche di molto! Ti voglio aiutare e mi muovo di nuovo, ma cerca di guardare meglio…”. La situazione è quella della terza scena della prima riga. Ancora una volta niente sembra cambiato, ma CI scoppia in una risata sguaiata: “Niente da fare, non riesci a vedere nessuna differenza. Sei proprio un incapace. E tutti dicono che sei intelligente…”.

CE rimane solo e non sa che pensare: “Quello strano cerchio è sicuramente fuori di testa. Restava fermo e mi voleva convincere che si muoveva.  La voce era la sua e anche l’aspetto. Mah… ce ne sono di tipi strani…”.

Poco dopo si passa alla situazione descritta nella seconda riga. Accidenti… eccolo di nuovo! Ma no, non è lui, dato che è di colore verde. CE prende l’iniziativa: “Non dirmi chi sei. Ti vedo benissimo sei un cerchio come me.” Il nuovo personaggio risponde subito: “Ciao, mi chiamo CO e sono amico di CI…  Voglio una conferma della tua incapacità nel riconoscere le persone. Stai attento, perché adesso mi muoverò”. Nella seconda immagine CE "vede" un cerchietto verde un po’ più piccolo di prima. Ma la voce è la stessa e anche la sfumatura del colore. “E allora” dice “chi sono?”. CE è un po’ interdetto. Non può dire che CO è rimasto uguale a prima. E’ sempre un cerchio, ma di dimensioni minori, proprio come se fosse diventato più giovane. D’altra parte, colore e voce non possono ingannarlo: è sempre la stessa persona… solo che è ringiovanita! Impossibile…

CE è ancora lì con la bocca aperta ed ecco che CO cambia ancora. Adesso non è altro che un cerchietto talmente piccolo che sembra un punto, un vero neonato. Eppure è sempre lui e sa parlare già molto bene, quando gli chiede: “Sai dirmi, finalmente, chi sono?”. CE non sa che dire e non riesce a spiaccicare una parola che sia una. E’ del tutto allibito: mai aveva visto un cerchio ringiovanire!

Non si è ancora ripreso dallo stordimento ed ecco che davanti a lui si presenta un nuovo cerchio dal nome di SFE. “Basta, caro CE, questo è l’ultimo tentativo. Sono una cara amica di CI e di CO. Se non sai dirmi chi sono vuol dire che non vali niente!”. Nel mondo di CE nessuno può cambiare il colore e la voce: è costretto ad ammettere che chi è davanti a lui è un personaggio ancora diverso. L’aspetto, però, è lo stesso con cui l’aveva lasciato CO. Davanti a CE c’è un piccolo cerchietto, molto giovane, che sa parlare molto bene ed è di colore marrone.

Un attimo dopo, SFE diventa improvvisamente come gli erano apparsi sia CI (per tutto il tempo dell’incontro) sia CO (al momento iniziale). CE suda abbondantemente (sudano anche nello spazio S2…) e si mette quasi a urlare: “Tu sei un cerchio, solo e soltanto un cerchio come me, ma come accidenti hai fatto a invecchiare così velocemente!? Un attimo fa eri un neonato e adesso sei un adulto tale e quale a me. Che stregoneria è mai questa?”. SFE sembra divertirsi moltissimo e gli risponde: “Questo è niente. Io posso variare la mia età come voglio, anche muovendomi sempre in avanti”.

Accidenti… CE si sente svenire e teme di diventare una parabola, l’aspetto di tutti i cerchi poco prima di morire. Davanti a lui SFE è tornata a essere una neonata, un punto, o poco più, di color marrone. Questo è veramente troppo anche per lui e sicuramente, se ne uscirà vivo, non se la tirerà più. Ci sono persone sicuramente più intelligenti di lui!

CO, CI e SFE decidono che lo scherzo è finito e ricompaiono tutti e tre assieme nelle forme del cerchio simile a CE. Poi iniziano a spiegare…

Non voglio certo scrivere un altro romanzo, scopiazzando da Flatlandia, e quindi posso svelare il semplice trucco. CO, CI e SFE non sono altro che un cono, un cilindro e una sfera, abitanti dello spazio S3 (Figura 2). Loro non hanno fatto altro che muoversi dall'alto verso il basso nella “loro” dimensione z (del tutto invisibile a CE) e fermarsi di tanto in tanto. La sezione con il piano-spazio S2 ha fatto vedere a CE  figure sempre uguali, ma di dimensioni diverse. Qualcosa che CE credeva di conoscere, ma che invece non conosceva affatto: a volte -ha imparato- l’apparenza inganna.

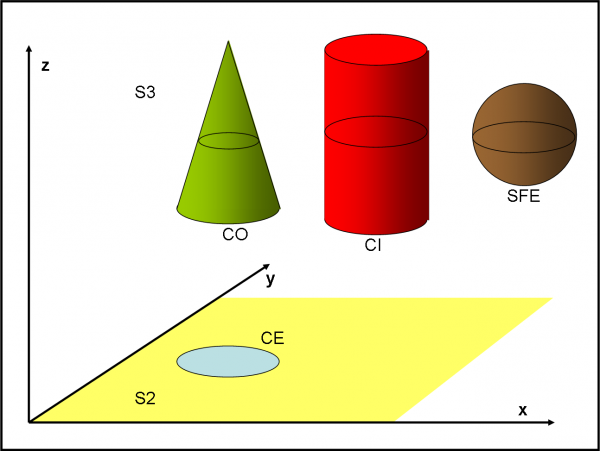
Giura che non sarà più superbo o arrogante e chiede ai nuovi tre “strani” amici di spiegare esattamente cosa o chi sono. Loro lo fanno e CE, che intelligente lo è per davvero, capisce tutto, anche se sa che non potrà mai disegnare esattamente il mondo S3. Sa, però, come fare a rappresentare una sfera, un cono  e un cilindro nel suo spazio S2: qualcosa uguale a un cerchio che può ingrandire o restringersi o anche rimanere sempre uguale a se stesso. Impara anche il modo di legare la nuova coordinata che non può disegnare alle due che invece conosce. Basta usare un po’ di matematica e scrivere delle formule di trasformazione o qualcosa del genere. A questo punto, anche CE potrebbe vivere in S3, anche se solo con le sue due dimensioni. Resterebbe sempre lo stesso, ma potrebbe spostarsi lungo la nuova coordinata z.

Bene, tante parole per dire che cosa? Ben poco di più (però… mi sono divertito a raccontare lo scherzo!). Il concetto è semplice: per aggiungere veramente una nuova dimensione a S2 bisogna trovare un modo rigoroso che la sappia legare alle altre due. In qualche modo mettere la terza coordinata sullo stesso livello delle compagne.

Quello che dobbiamo fare noi, allora, è solo e soltanto cercare di legare il tempo allo spazio, considerandolo, però, come una "normale" coordinata in più.

Il tempo quindi deve essere qualcosa che esiste in tutta la sua totalità nel nuovo spazio (lo spazio-tempo) e che può assumere valori negativi e positivi e anche zero, tale e quale alle ben conosciute x,y,e z. Niente di più e niente di meno.

I punti spaziali diventano eventi spaziotemporali

Faccio un esempio per far comprendere meglio il concetto finale. Nello spazio S2 posso scrivere una grandezza, ad esempio la distanza, utilizzando una combinazione di x e y. Lo stesso posso fare nello spazio a tre dimensioni con una combinazione di x, y e z. Non resta che poter scrivere una distanza (o quello che sarà) anche nello spazio a quattro dimensioni, dove ovviamente le quattro dimensioni sono x, y, z e t. Il punto nello spazio S2 è definito da una x e una y. Nello spazio S3 da una x, una y e una z. Nello spazio S4 (lo spaziotempo) il punto prende il nome di evento ed è caratterizzato da una x, una y, una z e una … t. Niente di così difficile, direi… Avendo due punti si può sempre scrivere la loro distanza. Lo stesso dobbiamo riuscire a fare nello spaziotempo scrivendo la "distanza" di due eventi.

Capito il concetto, non vi è poi nessun problema a eliminare una o anche due delle coordinate per semplificare i disegni. Ovviamente… non il tempo!

Il tempo è una coordinata speciale?

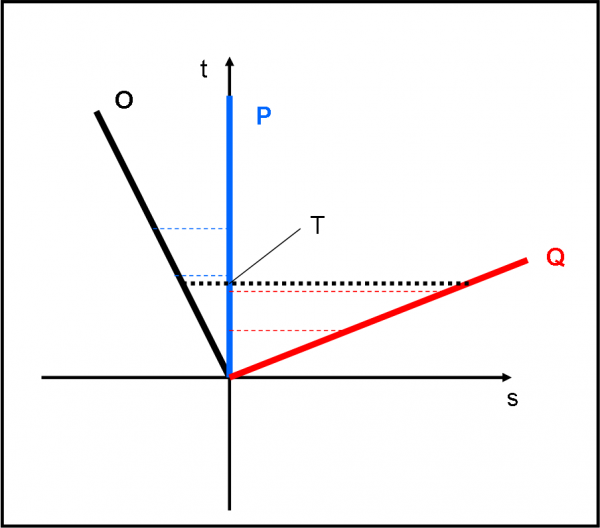
Il concetto che ho cercato di spiegare è tutt’altro che banale. Credetemi. Qualcuno potrebbe pensare: “Sappiamo già come collegare il tempo con le altre coordinate. Lo facciamo tutte le volte che descriviamo il moto di un oggetto.” Dobbiamo, però, fare sempre molta attenzione. Ad esempio, i due diagrammi riportati nella Fig. 3 sembrano uguali ma rappresentano concetti profondamente diversi. La distanza tra P e Q nella parte di sinistra è una distanza spaziale, calcolabile facilmente nello spazio euclideo (x,y). P e Q sono due posizioni dell’oggetto che descrive la traiettoria. Il secondo, a destra, mostra, invece, come varia lo spazio (tre dimensioni compresse in una sola) in funzione del tempo. I due punti P e Q rappresentano, adesso, due eventi dell' oggetto. La "distanza" PQ è un intervallo tra due eventi. La differenza esiste e come!

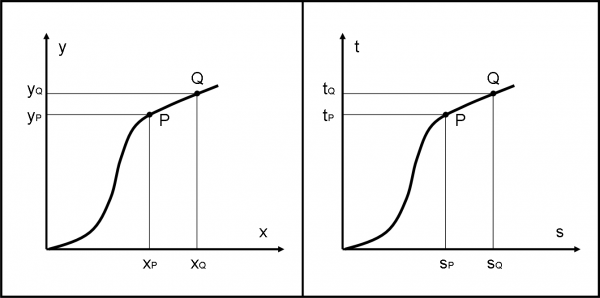
In poche parole, la prima è una traiettoria spaziale, la seconda è la famosa linea di Universo… Nella prima non sappiamo come viene percorsa la traiettoria. Nella seconda sì: conosciamo tutto di lei.

Non fatevi confondere dal fatto che vi è solo una s e non uno spazio a tre dimensioni. Basterebbe disegnare uno spazio a tre dimensioni e aggiungere la quarta (se ne fossimo capaci). Tuttavia, una, due o tre coordinate spaziali fanno poca differenza, concettualmente, e quindi adattiamoci a vedere lo spazio molto "ristretto". L'importante è avere inserito il tempo e disegnare un diagramma spaziotemporale. Ci torneremo a tempo debito, ovviamente. Ricordate, però, che l'ultimo tipo di diagramma l’abbiamo usato molto spesso sia per disegnare il cono di luce che  le figure degli ultimi capitoli della QED. D'ora in poi dovremo sempre usare questa rappresentazione, se vogliamo che il tempo entri  in gioco ad armi pari.

Galileo e Newton cominciano a barcollare

La differenza concettuale è già evidente nello spaziotempo euclideo (quello di Galileo e Newton). Lo sarà molto di più nello spaziotempo della relatività enisteniana. Il concetto va capito adesso, prima di complicare le cose con trasformazioni più intricate e meno intuitive. Anzi, la prossima volta, disegneremo lo spaziotempo galileiano, tanto per capirne l'essenza. Poi lo lasceremo da parte, per confrontarlo, alla fine, con quello relativistico. Vedremo che in esso il tempo rimane qualcosa di scollegato dal resto. Solo la relatività ristretta  riuscirà a fare veramente ciò che è capitato al nostro amico CE.

Il tempo è una "brutta bestia" e solo Einstein poteva trattarlo con tanta disinvoltura, aiutato dal quel genio della geometria che era Minkowski.

Torniamo a trovare Galileo

Vogliamo fare tre cose:

(1) Introdurre  la relatività galileiana e la trasformazione corrispondente.

(2) Capire bene cosa vuol dire ridurre le dimensioni dello spazio

(3) Rappresentare graficamente lo spaziotempo galileiano

Il punto (1) lo avevamo già trattato poco tempo fa. Tuttavia, preferisco riportare le nozioni principali per non costringere i lettori a fare avanti e indietro nel sito del circolo …

Quello che vogliamo fare è ricavare le formule (ma anche solo i concetti) che legano le coordinate spaziotemporali di uno stesso evento visto in due diversi sistemi di riferimento inerziali. Ciò vuol dire che essi si muovono uno rispetto all’altro con velocità costante. Sappiamo già che le leggi della meccanica non cambiano passando da un sistema all’altro.

E’ meglio togliere subito un paio di dubbi. Ho scritto “meccanica” e non “fisica” perché, in realtà, l’elettromagnetismo non segue la stessa regola. Basti pensare che essa tratta di un qualcosa che viaggia alla velocità della luce (la luce, appunto!) e questo era un problema che non poteva interessare Galileo e Newton (per loro la luce si trasmetteva istantaneamente). Inoltre, non pensiate che la relatività speciale parta da una “base” diversa. Essa si riferisce solo e soltanto a trasformazioni tra sistemi inerziali, proprio come quella galileiana. Il vantaggio sarà quello di poter inserire la parola “fisica” al posto di “meccanica”.  Ma torniamo a Galileo…

La trasformazione galileiana e la somma delle velocità.

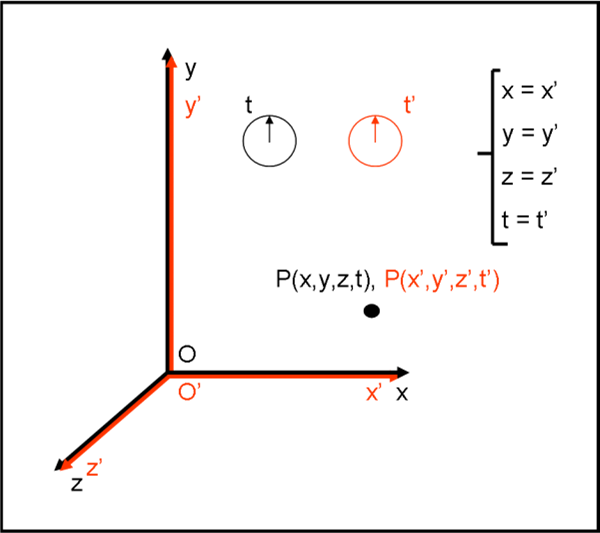
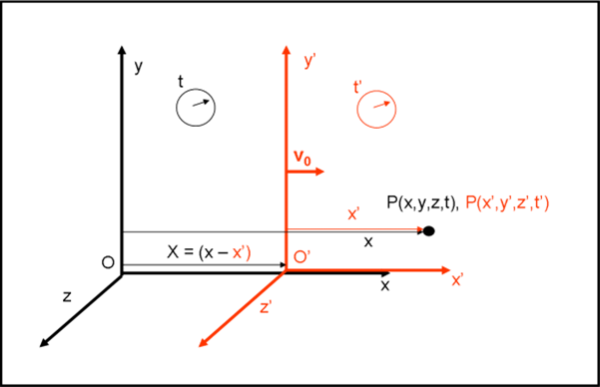
Consideriamo due sistemi cartesiani: O(x,y,z,t) e O’(x’,y’,z’,t’). Entrambi si muovono di moto rettilineo uniforme rispetto a un ipotetico riferimento fisso. Possiamo fare due semplici semplificazioni che derivano dal principio d’inerzia, ossia da quanto abbiamo detto precedentemente. Innanzitutto, consideriamo fisso uno dei due sistemi e riferiamo il moto del secondo al primo. In altre parole, consideriamo fisso O e studiamo il movimento di O’ rispetto a lui. Il movimento, inoltre, può avvenire in qualsiasi direzione, ma è possibile scegliere gli assi cartesiani in modo che il movimento avvenga solo lungo l’asse x, coincidente con x’.

Dobbiamo fare, inoltre, un’altra ipotesi di partenza: il tempo t è identico al tempo t’, ossia scorre nello stesso modo in entrambi i sistemi di riferimento. In altre parole, gli orologi in O e O’ segnano sempre la stessa ora. Questa assunzione sembrerebbe derivare da una mancanza di approfondimento da parte di Galileo. Invece, il grande pisano era del tutto conscio del fatto che per essere sicuri che gli esperimenti fatti nei due sistemi di riferimento fossero veramente istantanei si poneva il problema della velocità della luce. Infatti, per dare il via allo sperimentatore che si sarebbe mosso, Galileo doveva fare segnali con una lanterna. Egli fece molti tentativi a distanze crescenti e ne dedusse, ovviamente, che la luce era sicuramente “rapidissima”, concludendo che, qualsiasi possibile valore essa avesse realmente avuto, sarebbe stata del tutto irrilevante ai fini pratici. L’uguaglianza t = t’ non è quindi assolutamente arbitraria, ma basata anch’essa sulla sperimentazione, in accordo col metodo scientifico.

Assumiamo che all’istante t = 0, O’ coincida con O, come rappresentato in Fig. 4. Entrambi gli orologi segnano t = t' = 0 e le coordinate nei due sistemi sono perfettamente identiche.

Facciamo adesso muovere O’ con velocità v₀ (posso considerare solo i moduli dato che tutto avviene lungo una sola coordinata spaziale) costante rispetto ad O, come mostra la Fig. 5.

Permettetemi, adesso, di inserire qualche formula, dato che il concetto finale è più che “leggibile” attraverso le figure (così accontento le due schiere di lettori…)

Dopo un  tempo t = t’ (gli orologi segnano lo stesso tempo), l’ascissa del punto O’ rispetto a O sia X. Per definizione di velocità:

v₀ = (X - 0)/(t - 0) = X/t

ossia:

X = v₀ t

Un punto P qualsiasi ha coordinate (x,y,z,t) nel sistema O e coordinate (x’,y’,z’,t’) nel sistema O’.

Per come è stato costruito il secondo sistema, valgono sicuramente le uguaglianze:

y = y’

z= z’

t = t’

Calcoliamo, invece, la relazione tra x’ e x

Dalla figura si ha subito:

x = x’ +OO’ = x’ + X = x’ + v₀ t

Otteniamo, allora:

x = x’ + v₀t

y = y’

z = z’

t = t’                        …. (1)

Queste relazioni descrivono la trasformazione galileiana per passare da un sistema di riferimento inerziale a un altro (ottenuto per pura traslazione, ossia attraverso una velocità relativa costante).

Tutto qua. Ripeto, ancora, che mi sono permesso di inserire delle formule, dato che il concetto di sistema di riferimento e di velocità le considero completamente assimilate. Chi avesse dei problemi a questo punto, è inutile che continui. Prima deve assolutamente fare suoi questi concetti. Per semplificare i passaggi successivi, trascuriamo l’asse z (lo potremmo immaginare perfettamente diretto verso di noi). D’altra parte sappiamo che nulla cambia, dato che z’ = z.

Le velocità si sommano

Immaginiamo che il nostro punto P si muova con una certa velocità v’ nel sistema di riferimento di O’. Attenzione: questa velocità può anche non essere COSTANTE. Essa si riferisce a un certo fenomeno  meccanico che capita nel sistema di O’, ma non inficia assolutamente la definizione di sistema inerziale per O’. Perché un sistema non sia più inerziale è necessario che la velocità tra i due sistemi sia variabile. Il fenomeno descritto dal punto P può, quindi, avere a una velocità NON costante, mentre i due sistemi restano, comunque, inerziali.

A questo punto conosciamo la velocità costante v₀ e quella qualsiasi v’. Per semplicità, imponiamo che anche la velocità v’ vada nella stessa direzione di v₀. Come facciamo a determinare la velocità v del punto P rispetto al sistema di riferimento O? Beh… ormai siamo capaci di effettuare le derivate e non ci dobbiamo più spaventare ad applicarle. Sappiamo benissimo che la velocità può essere scritta come ds/dt, ossia come derivata dello spazio rispetto al tempo.

Prendiamo, allora, la prima relazione delle trasformazioni di Galileo (che descrive la relazione tra le ascisse di un punto P qualsiasi):

x = x’ + v₀ t

Per calcolare la velocità del punto P, basta derivare questa espressione rispetto al tempo (la derivata determina, infatti, la variazione istantanea dell’ascissa rispetto al tempo, ossia proprio la velocità):

dx/dt = dx’/dt + d(v₀ t)/dt

il primo termine è proprio la velocità v cercata (la variazione di x nel sistema O). Il secondo termine è la velocità v’ (la variazione di x’ nel sistema O’). Per il terzo termine dobbiamo ricordare la derivata di un prodotto, o -ancora meglio- la derivata del prodotto di una variabile  per una costante.

In un modo o nell’altro, si ricava che la derivata di un prodotto di una costante per una variabile è uguale al  prodotto della costante per la derivata della variabile. In altre parole, la costante esce dall’operazione derivata senza nessun problema (non confondetevi, però: la derivata di una costante è sempre zero). Un’ottima occasione per ripassare la derivata: avete voluto le derivate? Adesso usiamole nella pratica!

In poche parole:

d(v₀ t)/dt = v₀ dt/dt = v₀       (dt/dt è ovviamente uguale a 1).

Alla fine si ottiene la fondamentale relazione:

v = v’ + v₀   …. (2)

Perché è così fondamentale, pur essendo di una semplicità spaventosa oltre che estremamente intuitiva? Perché sarà proprio questa espressione che diventerà insostenibile quando le velocità si avvicineranno a quella della luce. Capire la rivoluzione di Einstein senza aver bene digerito la trasformazione galileiana è un assurdo. Soprattutto perché essa sarà confrontata con la sua trasformazione equivalente valida SEMPRE, quella di Lorentz.

Torniamo a noi…

La relazione precedente esprime il principio galileiano (e poi anche newtoniano) di addizione di velocità. Sembra una sciocchezza, ma solo attraverso di lei è stato possibile sviluppare tutta la meccanica classica… Potevamo anche fare a meno di formule e dedurre il risultato direttamente dalla figura precedente assumendo che il punto P si muovesse nel suo sistema di riferimento con velocità v’. bastava sommare segmenti paralleli…

Cosa abbiamo fatto finora? Riassumiamolo a parole.

Abbiamo calcolato come si trasformano le coordinate di un certo evento (il tempo è una coordinata a tutti gli effetti) cambiando il sistema di riferimento. Ci siamo accorti che ciò che cambia è (nelle condizioni favorevoli scelte) solo e soltanto la coordinata x. La nuova x’ è legata alla x attraverso la velocità relativa dei due sistemi di riferimento inerziali (mi raccomando questo aggettivo, non dimentichiamolo mai!).

Con pochi passaggi matematici, abbiamo anche trovato che se un oggetto si muove in un sistema di riferimento con una certa velocità (qualsiasi e anche variabile) e questo sistema di riferimento fa lo stesso (con velocità costante, però) rispetto a un altro sistema di riferimento, la velocità dell’oggetto rispetto a quest’ultimo è data dalla somma delle due velocità. Un concetto, questo, ovvio e intuitivo nella vita di tutti i giorni.

Pensiamo di essere su un  treno che viaggia velocemente. Lo stiamo, inoltre, attraversando, dalla coda verso la testa, per trovare un posto libero. In poche parole, ci stiamo muovendo con una certa velocità nel sistema di riferimento treno, mentre il sistema treno si muove anch’esso rispetto al sistema di riferimento del capostazione. Come fa il capostazione (fermo sul binario) a sapere la nostra velocità. Deve solo e soltanto sommare la velocità del treno alla nostra che stiamo attraversando il treno. Banale direi… ma solo e soltanto nello spaziotempo di Galilei.

Notiamo anche bene che finora abbiamo descritto tutto nello spazio, tenendo il tempo da parte. D’ora in poi dobbiamo farlo entrare veramente in gioco come nuova coordinata a tutti gli effetti. Per poter fare ciò è necessario ridurre il numero di coordinate relative allo spazio se no non saremmo in grado di disegnare un bel niente… pensiamo al nostro amico CE…

Riduciamo lo spazio

E’ ora di smettere di passare dal mondo di CE al mondo di CO, CI e SFE e viceversa. Alla fine faremmo solo confusione. E’ anche inutile tirarsi dietro la y e la z nella trasformazione galileiana. L’abbiamo già imposte sempre uguali, attraverso un movimento lungo la sola x. Tagliamo la testa al toro e immaginiamo di vivere in uno spazio S1, dove l’unica coordinata sia la x che potremo poi chiamare anche s (dato che è l’unica).

Non dobbiamo avere paura di farlo. Basta chiedere a CE e lui ormai sa benissimo come fare per passare di nuovo a S2 e poi a S3. Facciamoci aiutare dalla semplicissima Fig. 6 per eseguire questa riduzione di spazio (il tempo lo lasciamo da parte perché è fondamentale conservarlo).

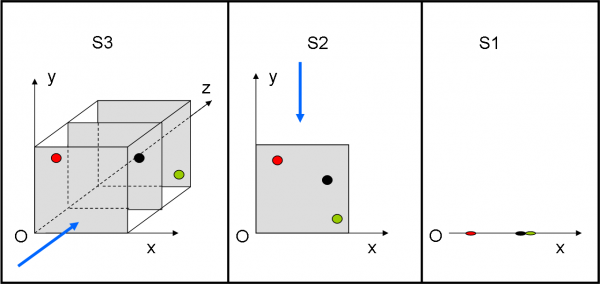
A sinistra, abbiamo il solito spazio tridimensionale (x,y,z). Consideriamo tre diversi piani paralleli al piano (x,y). Il punto rosso ha una certa z (ad esempio, proprio zero), che è diversa da quella nera e da quella verde. Guardiamo la figura secondo la direzione blu. I tre piani contenenti i tre punti si sovrappongono e ciò che vediamo è ora (parte centrale) solo il piano (x,y), con i tre punti ben visibili sistemati con le loro x e y di partenza.

Non ci basta ancora? Bene guardiamo la situazione secondo la linea azzurra parallela all’asse y. Tutto viene proiettato solo e soltanto sull’asse x e la y sparisce, come è riportato nella parte destra. I punti non hanno più dimensioni, se no il nostro amico CE ci riprenderebbe. Lo spazio a tre dimensioni è stato “concentrato” in uno spazio a una sola dimensione. Poco male, l’importante è sapere cosa abbiamo fatto e che cosa possiamo fare per tornare indietro.

Ogni azione svolta dai punti può svolgersi solo e soltanto sulla retta x, che d’ora in poi potremmo anche chiamare s. Ogni punto, ha però, dentro di sé anche i valori di y e z, anche se non li rappresentiamo.

A questo punto possiamo facilmente disegnare un evento, ossia aggiungere la coordinata t. Abbiamo, perciò, un piano (s,t) dove possiamo descrivere tutti possibili eventi che avvengono nello spazio-tempo, tenendo presente la trasformazione galileiana  che lega tra loro eventi rappresentati in diversi sistemi di riferimento. Detto in parole ultra semplici, il piano (s,t) rappresenta tutto ciò che esiste, è esistito ed esisterà. Qualsiasi avvenimento può essere rappresentato e i vari eventi possono essere collegati oppure no attraverso linee di universo (non sono più traiettorie, dato che ogni traiettoria puramente spaziale avviene nell’asse s).

Lo spazio-tempo galileiano

Disegniamo innanzitutto, in Fig. 7, il nostro spazio-tempo (piano) segnando le due coordinate s e t. Immaginiamo che il nostro sistema di riferimento sia quello segnato in nero e che sia fermo (si può sempre fare… come ci dicono Galileo & Co.). Attenzione! A questo punto immaginiamo anche di poter vedere tutto lo spazio-tempo da fuori. Questo è un concetto che troppo spesso si dimentica. E’ una cosa teoricamente impossibile, ma il disegno a due dimensione ce lo permette (ricordiamo il caso di CE ed amici) e sfruttiamo questa possibilità.

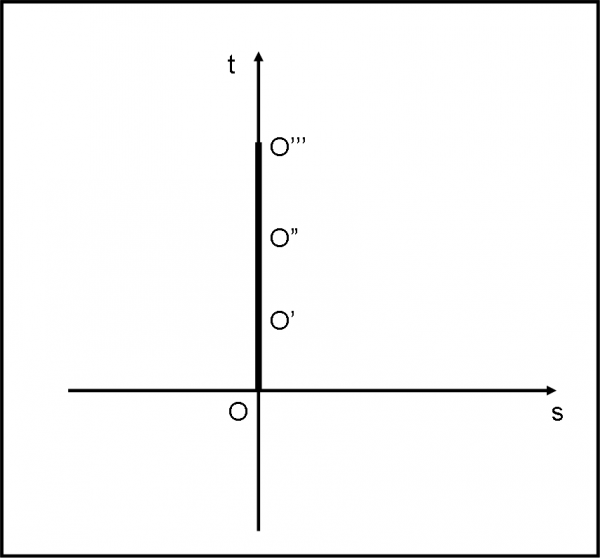
Noi siamo in O. Possiamo stare fermi in questa figura? Assolutamente no. Questa è una caratteristica della coordinata tempo che non possiamo dimenticare. Possiamo anche non muoverci nello spazio s, ma il movimento lungo t non possiamo assolutamente vietarlo o contrastarlo. Il tempo, come già detto, è una brutta “bestia”.

In ogni modo, il punto O rappresenta un evento a cui partecipiamo, anzi è proprio noi. Questo evento è completamente localizzato dalle coordinate s = 0 e t = 0 (potevamo, però, assegnargli valori qualsiasi…). A quali eventi andiamo incontro se continuiamo a non muoverci? Facilissimo, a O’, O”, O’’’, ecc. In altre parole, gli eventi futuri sono proprio localizzati lungo l’asse del tempo. La linea del tempo è la nostra linea di universo.

Attenzione. Stiamo mettendo in pratica quanto detto a parole nel capitolo precedente e che ci ha ricordato anche Einstein con le sue parole. Stiamo, infatti, usando il tempo come una coordinata qualsiasi, dato che possiamo rappresentare contemporaneamente, in una sola figura, sia il passato che il presente che il futuro. Sembra una banalità, ma non lo è, dato che è proprio uno dei requisiti fondamentali per dare al tempo la stessa caratteristica delle altre coordinate (lo spazio, in questo caso semplificato).

Qual è la nostra velocità mentre passiamo da un evento a un altro? E’ esattamente zero (d’altra parte non ci muoviamo). In parole matematiche v = s/t, ma se s = 0, sempre, anche la velocità è uguale a zero, sempre.

Consideriamo, adesso, un nostro amico P (meglio l’evento P) che all’istante t = 0 coincide perfettamente con noi. Lui, però, non ha nessuna voglia di stare fermo e intende muoversi, anche se in modo costante. In altre parole, si muove con velocità costante v_PO (velocità di P rispetto a O), ossia rappresenta un sistema inerziale rispetto a noi. P se ne va quindi per la sua strada e istante dopo istante la sua distanza spaziale rispetto ad O vale v_POt_O, dato che per definizione v_PO = s_PO/t_P = s_PO/t_O. Ricordiamo che Galileo assume che t sia lo stesso sia per chi sta fermo che per chi si muove, ossia t_O = t_P.

E’ immediato tracciare la linea di universo di P: essa è una retta inclinata. Inclinata di quanto indica la velocità v_PO. Ricordiamo, infatti, che v_PO è proprio il coefficiente angolare della retta.

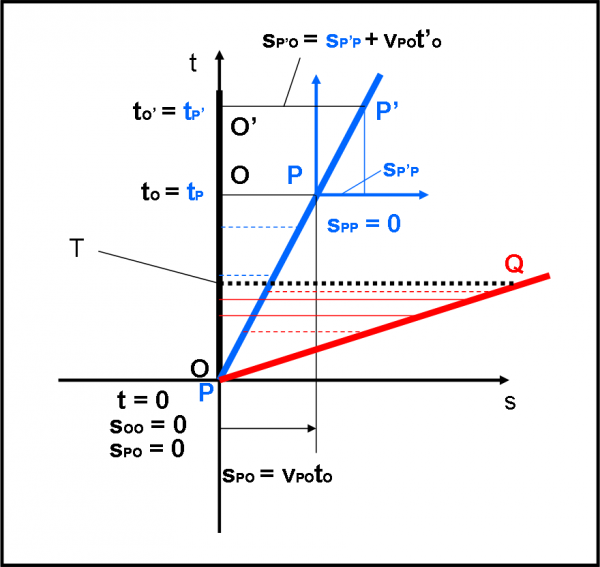
Non facciamoci prendere dall’agitazione. Stiamo solo rappresentando il moto rettilineo uniforme nel diagramma spaziotempo, come già fatto infinite volte per la retta. Nella Fig. 8 la linea di Universo di P non è altri che la retta azzurra.

Ripetiamo il tutto con parole che ci colleghino alla trasformazione galileiana. Riscriviamola con lo spazio concentrato in una retta.

s = s’ + vt

t = t’                  …. (2)

Nel nostro caso particolare, abbiamo un sistema con origine in P che si muove di moto rettilineo uniforme, con velocità v_PO, rispetto a un sistema che ha origine in O. All’istante t_O La coordinata spaziale di P rispetto al suo sistema di riferimento (s_PP) è zero (P è l’origine). La coordinata spaziale di P rispetto a O è invece s_PO.  Se scriviamo la trasformazione di Galileo con le nuove notazioni, abbiamo:

s_PO = s_PP + v_POt_O = 0 + v_POt_O = v_POt_O

t_O = t_P

Ovviamente è la stessa cosa che avevamo descritto prima.

Per capire ancora meglio come vanno le cose, consideriamo un evento P’, che non è altro che la posizione spazio-temporale di P a un certo tempo t_^’P= t’_O. Questo evento P’ (solidale col sistema di P) ha, adesso, una sua coordinata spaziale rispetto a P, s_PP’ che è diversa da zero, misurata nel sistema di O. Tuttavia la velocità di P’ rispetto al sistema di O è sempre la stessa, dato che sta sulla linea di Universo di P (v_P’O = v_PO). La coordinata spaziale di P’ rispetto a O è s _P’O. In queste condizioni possiamo scrivere:

s_P’O = s_P’P + v_PO t’_P

t_^’O = t’_P

E’ di nuovo la trasformazione di Galileo, ovviamente, scritta nella sua forma classica. Queste banali rappresentazioni ci fanno però capire come il tempo abbia ormai assunto una vera e propria fisionomia di coordinata. Lo trattiamo tranquillamente sia nel presente come nel futuro e lo potremmo anche fare nel passato. Anche se rimane ancora qualcosa di assoluto (è sempre lo stesso in ogni sistema di riferimento) ha già cambiato forma e sostanza. Stiamo veramente lavorando in uno spaziotempo per semplificato che sia. Le posizioni sono diventati eventi che rispettano la relatività galileiana. Pensiamoci bene sopra, dato che è un concetto che sarà fondamentale quando le cose si complicheranno.

Bene, adesso possiamo divertirci a disegnare, sempre in Fig. 8, qualcosa di più … complicato. Poniamo ad esempio, che ci sia un altro personaggio Q che, all’istante t = 0, sia insieme a noi (O e P). Anche lui non vuole stare fermo e si muove di moto rettilineo uniforme rispetto ad O. Anzi, va molto veloce, ossia v_QO > v_PO. La sua linea di Universo non può essere altro che quella rossa. Il nostro spazio-tempo funziona molto bene, dato che è facile verificare che se Q si muove lungo una linea retta rispetto a O, esso si muove anche secondo una linea retta rispetto a P. D’altra parte sappiamo che le velocità si sommano, ossia:

v_QO = v_QP + v_PO

Lascio a voi la semplice verifica di quanto ho appena detto, facendo le differenze tra le tre linee di Universo lungo le linee orizzontali rosse che rappresentano eventi che si verificano in tempi uguali.

Devono, ovviamente, valere sia la trasformazione galileiana che la composizione della velocità.

Cambiamo sistema di riferimento

Finora abbiamo considerato il sistema di O come quello di riferimento. Possiamo cambiare sistema di riferimento? Sicuramente, dato che sono inerziali, non deve modificarsi niente: ciò che era inerziale deve continuare a essere inerziale. Cambiamo persona e diventiamo P. Adesso  è P che sta fermo e descrive la retta verticale t = 0. Trasformiamo, perciò, lo spazio-tempo riferito a noi con lo spazio-tempo riferito a P.

Cosa dobbiamo fare? Semplicissimo: ruotiamo la linea azzurra fino a farla coincidere con quella nera. Le altre due devono ruotare di conseguenza, mantenendo le stesse distanze tra di loro. Otteniamo la Fig. 9. Il tempo, ovviamente, deve restare quello che è.

Non ne siete convinti? Il segmenti rossi tratteggiati di Fig. 8 sono esattamente gli stessi che abbiamo riportato in Fig. 9. La stessa cosa capita per i segmenti tratteggiati blu. Si vede bene che la linea rossa rimane una retta anche rispetto a P, preso come sistema di riferimento. Non dobbiamo certo stupirci dato che linee di universo rettilinee indicano sistemi tra loro inerziali. Un moto rettilineo uniforme resta tale passando da un sistema di riferimento a un altro. Proprio ciò che ci dice Galileo!

Non fatemi scrivere ulteriori formule che sarebbero sempre le stesse. Conviene capire il succo solo graficamente. E’ sicuramente più semplice, anche intuitivamente. E non chiedetemi perché ho ruotato la linea blu e non l’asse dello spazio. E’ una condizione ovvia, dato che adesso è P che rimane fermo e quindi deve muoversi solo lungo l’asse del tempo. In poche parole, la trasformazione ha mantenuto i moti relativi tra le tre linee di Universo, proprio come vuole Galileo. Ma, soprattutto, notate che gli eventi neri, blu e rossi, avvengono sempre allo stesso tempo, indipendentemente dal sistema di riferimento utilizzato. Ciò vuol dire, in “soldoni”, proprio che per Galileo il tempo è assoluto e non cambia a causa di trasformazioni.

In parole più generali: se disegno una retta parallela all’asse s (ossia una retta che identifica un tempo t uguale per tutti) come quella nera puntinata di Fig. 8, essa identifica gli stessi eventi anche dopo avere applicato la trasformazione di sistema di riferimento, in Fig. 9. Eventi che avvenivano nelle tre rette a un certo istante T, continuano ad avvenire sempre in quel momento. Pur cambiando sistema di riferimento, il tempo di un certo evento non cambia. Gli orologi dei tre sistemi in moto inerziale segnano sempre la stessa ora quando accadano gli stessi eventi.  Più tecnicamente: la trasformazione di Galileo conserva la simultaneità degli eventi. Che frase importante è questa! Fondamentale per la relatività. Teniamola in dovuto conto perché non ce la toglieremo più dai piedi…

Provate a cambiare ancora il sistema di riferimento e considerare fermo quello rosso. Disegnate da soli la trasformazione e poi controllate, con la Fig. 10, se tutto è andato bene…

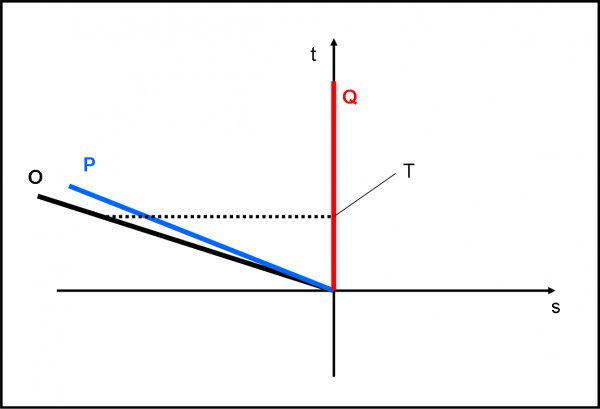
Lo ammetto, i diagrammi spazio-tempo di Galileo sono decisamente semplici. Tuttavia, conviene digerirli molto bene per valutare al meglio la rivoluzione di Einstein.

Lo spazio è già diventato “relativo”

Analizziamo ancora meglio la definizione di “relatività” galileiana. Sembra ormai di averla compresa perfettamente, quando si dice che le leggi della meccanica sono le stesse in tutti i sistemi di riferimento inerziale. Questa frase si lega perfettamente alla trasformazione di coordinate e alla composizione delle velocità. Perché allora chiamarla “relatività”?

La risposta è semplice: “essa impone un tempo assoluto, ma non uno spazio assoluto”. In altre parole, lo spazio è relativo all’osservatore. Due osservatori che si muovono, l’uno rispetto all’altro, di moto rettilineo uniforme, non sono assolutamente in sintonia quando descrivono lo spazio percorso da un terzo oggetto, anch’esso in moto rettilineo uniforme rispetto a loro. Questa conclusione porta proprio a dire che lo spazio è relativo all’osservatore. Il tempo invece rimane lo stesso. Metà teoria della relatività ristretta è quindi giù impostata nei grafici che abbiamo visto finora. Vogliamo averne una conferma ulteriore? Lo so che sto girando attorno a banalità, ma è sempre meglio vedere il problema da tutti i punti di vista.

Immaginiamo, In Fig. 11a, di essere su un’astronave A nello spazio vuoto, ma così vuoto che lo spostamento della nostra astronave non possa essere assolutamente percepito da noi che stiamo all’interno. Non esiste vibrazione alcuna e non vi è niente che possa essere preso come punto di riferimento. Nel solito diagramma noi ci sistemiamo lungo la linea verticale (linea di universo nera). Non c’è nessun problema a considerarci fermi, anzi noi siamo sicuri di essere fermi.

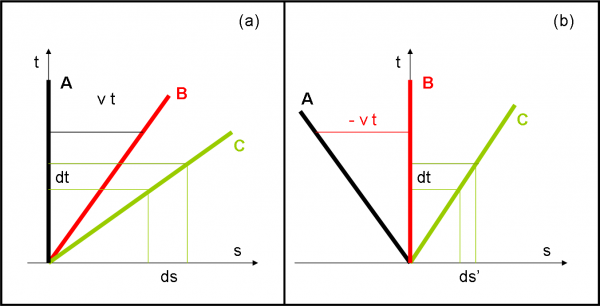
Finalmente, a un certo momento, ecco comparire un’altra astronave B che ci raggiunge da dietro e ci supera con grande facilità. Cosa possiamo concludere? Che essa sta viaggiando a grande velocità. (Attenzione: riducendo lo spazio a una sola dimensione è ovvio che quando l'astronave ci raggiunge coincide proprio con noi. In realtà essa può avere y e z diversi...).

Nel nostro sistema di riferimento possiamo disegnare la linea di universo dell’altra astronave (linea rossa). La sua velocità è costante e nell’unità di tempo descrive un certo spazio costante.

La stessa cosa, però, dice anche l’equipaggio dell’altra astronave (B). Il suo equipaggio è convinto di non muoversi e pensa che siamo noi (A) ad andare a marcia indietro, a grande velocità. Bene, lei può benissimo rappresentare se stessa nel diagramma (Fig. 11b) come linea verticale (rossa) e disegnare la nostra linea di universo come linea nera. Poco male, in fondo, le due velocità hanno solo cambiato di segno, ma hanno lo stesso modulo. Per l’altra astronave siamo noi a percorrere lo stesso spazio nella stessa unità di tempo. Cambia solo il verso del moto.

Immaginiamo adesso che mentre noi (A) e gli altri (B) stiamo facendo questi bei calcoletti (perfettamente in linea con i principi di Galileo), appaia un terza astronave C (probabilmente aliena, dato che la disegniamo verde come i… marziani).

A noi sembrava che l’astronave “amica” andasse veloce. Assolutamente no: questa sembra solo un puntino, ma in brevissimo tempo supera sia noi che l’altra. Nel nostro sistema di riferimento (Fig. 11a) facciamo in fratta a disegnare la sua linea di universo verde e possiamo dire con sicurezza che ha percorso un certo spazio ds nell’unità di tempo dt.  Cosa dicono, invece, i nostri amici dell’astronave B? Anche loro vedono andare veloce l’astronave aliena, ma non certo come la vediamo noi. Se essi tracciano la linea verde nel loro sistema di riferimento (Fig. 11b), dicono che C ha percorso un certo spazio ds’, sempre nella stessa unità di tempo dt, identica alla nostra. Ma ds’ è nettamente inferiore a ds e, quindi, cosa possiamo concludere? Semplice: lo spazio, percorso da un oggetto in movimento rettilineo uniforme, è RELATIVO al sistema di riferimento da cui si osserva. E’ o non è una teoria della relatività molto … ristretta?

Tempo e lunghezze  assolute

Quanto appena detto non deve, pero, confonderci. Anche se lo spazio è relativo al sistema di riferimento, le misure di lunghezza e di intervalli di tempo restano immutati qualsiasi sia il sistema di riferimento inerziale da cui si osservano. Questo fatto non deve essere dimenticato, dato che è proprio quello che ci mostrerà le maggiori differenze rispetto alla visione relativistica di Einstein. Scusate se batto ancora sullo stesso chiodo, ma è fondamentale non avere dubbi.

Sappiamo ormai molto bene, proprio per ciò che dice la trasformazione galileiana, che il tempo scorre nello stesso modo in qualsiasi sistema di riferimento inerziale. In altre parole, un orologio che si trova sopra una nave che viaggia velocemente rispetto a noi, che ci consideriamo fermi, rimane sempre sincronizzato con il nostro. Diciamo ancora meglio questo dato di fatto. Se noi guardiamo il nostro orologio e quello della nave li vediamo andare d'amore e d'accordo. Ne segue che gli intervalli di tempo rimangono uguali.  Stiamo bene attenti a ciò che questo vuol dire: chi  viaggia su una nave vede girare il suo orologio nello stesso modo di come noi, fermi, vediamo girare il nostro orologio. Fin qui nessun problema. Tuttavia, chi viaggia e chi sta fermo non possono  confrontare direttamente come scorre il tempo dell'altro. Non possono certo sdoppiarsi. l'unico modo per farlo è guardare, dal proprio sistema di riferimento, come gira l'orologio dell'altro. E qui le cose si possono complicare...

Notate la differenza essenziale: una cosa è vedere girare il proprio orologio in diversi sistemi di riferimento e un'altra cosa è vedere girare, dal proprio sistema di riferimento, quello che si trova all'interno di un altro sistema di riferimento. Non confondiamo le due situazioni!

Nella relatività galileiana tutti questi tempi sono uguali. In particolare, come già detto, un intervallo di tempo è lo stesso in ogni sistema ed è lo stesso se visto da qualsiasi sistema inerziale. Ciò deriva dal fatto che t' = t. Per un intervallo di tempo tra due eventi (P e Q), si ha:

t_P –t_Q = t’_P –t’_Q

L'intervallo di tempo tra due eventi rimane lo stesso, qualsiasi sia il sistema di riferimento da cui si osserva.

Consideriamo, adesso, una lunghezza spaziale. Ad esempio, un righello che ha per estremi A e B. In questo caso A e B sono posizioni spaziali e non eventi, ovviamente.

Il righello sia situato nello spazio del nostro sistema di riferimento fermo. Come viene visto il righello da colui che viaggia a velocità v rispetto a noi? Beh... semplice lui vede tutto ciò che fa parte del nostro spazio muoversi a velocità uguale e contraria, ossia -v. Con la scelta che abbiamo fatto, possiamo tranquillamente sostituire al vettore il suo modulo.

La trasformazione galileiana dice che:

s’_B = s_B – vt_B

s’_A = s_A – vt_A

da cui:

s’_B- s’_A = s_B – s_A - v(t_B – t_A)

Tuttavia, le posizioni di A e B (che sono punti) vengono misurati nello stesso istante di tempo, ossia:

t_B = t_A

Sostituendo, si ha:

s’_B - s’_A = s_B – s_A

la relazione ci dice che anche la distanza tra due punti, ossia la lunghezza di un righello, rimane la stessa qualsiasi sia il sistema di riferimento da cui si guarda e si misura. Possiamo perciò concludere che: secondo la trasformazione galileiana le misure di intervalli temporali e spaziali sono ASSOLUTE, cioè indipendenti dal sistema riferimento inerziale da cui si effettuano le misure.

Probabilmente ho ripetuto le stesse cose fino alla nausea. Però, vi prego di leggere e rileggere molto bene ogni cosa che ho scritto. Sono costretto a ribadire ancora una volta che se esistono problemi con la trasformazione galileiana, quando il tempo si metterà a variare con lo spazio e lo spazio si muoverà come una fisarmonica, non ne usciremo più vivi… Mi raccomando!

Un'avventura spaziale

E' il momento di  introdurre concettualmente la rivoluzione operata da Einstein attraverso la relatività speciale o ristretta. Utilizzo un approccio che può apparire diverso dal solito e oltremodo semplicistico. Tuttavia, spero che riesca a mettere tutti in grado di capire l’esigenza di un cambiamento drastico nella visione globale della realtà dell’Universo e dello spaziotempo che ne è il suo palcoscenico.

Prima di procedere, riassumiamo brevemente (ancora una volta... scusate!)  la relatività galileiana che abbiamo spiegato a fondo e che ci ha permesso di disegnare i primi diagrammi spaziotemporali. Nessun sistema di riferimento inerziale è favorito rispetto agli altri, poiché le leggi della meccanica sono le stesse in tutti i sistemi inerziali. Quindi non c’è nessun riferimento in quiete assoluta fisicamente definibile.

Chi si sta muovendo con una certa velocità costante su una navicella spaziale e guarda un’altra astronave da un oblò, non può assolutamente dire se è lui che si sta muovendo o è il velivolo alieno. Non ha, quindi, senso parlare di sistema “fermo” in senso assoluto. Tutti i sistemi inerziali possono essere considerati fermi da chi ci vive all’interno. Ciò che si può osservare è solo il moto relativo.

Notiamo, però, un altro fatto fondamentale di questa rappresentazione: il tempo è separato dallo spazio. E’ vero che il loro legame ci permette di calcolare la velocità, ma nessuno dei due influisce sull’esistenza e sul comportamento dell’altro. Possono variare in modo indipendente. Nella relatività galileiana il tempo può essere considerato assoluto, ossia uguale per tutti gli osservatori. Un evento che capita all’astronauta O è osservato simultaneamente anche dall’alieno O’. Ricordiamoci, infatti, che t = t’. Ovviamente, in questa rappresentazione, le velocità si sommano e/o si sottraggono.

Se succedesse la stessa cosa anche per i fenomeni dell’elettromagnetismo potremmo dire che il principio di relatività galileiana è valido per tutta la fisica e non solo per la meccanica newtoniana. Non avremmo avuto bisogno di Einstein… In altre parole, qualsiasi esperimento di fisica facessimo a bordo della nostra astronave non potrebbe dirci se siamo in moto oppure no. O, ancora meglio, non potremmo sapere a che velocità stiamo, realmente, andando.

Fatemi ricapitolare il tutto attraverso un’avventura spaziale…

Immaginiamo, per assurdo, che l’astronave A sia stata inviata nello spazio tanto tempo fa. L’equipaggio è stato messo in ibernazione per decenni e decenni (magari secoli) e ora, finalmente, è giunta l’ora di svegliarsi. I processi di ibernazione hanno fatto dimenticare molte nozioni  e per un po’ i nostri eroi rimangono alquanto storditi. Tuttavia, il capitano è il capitano e, perciò, deve prendere in mano la situazione. Guarda dall’oblò e vede che vi è una’altra astronave sicuramente aliena che chiamiamo B.

Il comandante è convinto di muoversi (tanto tempo passato nello spazio sarà  servito a qualcosa!) e decide che l’astronave B è FERMA. Ne deduce immediatamente che il suo movimento apparente è dovuto solo e soltanto al moto di A. Se B gli appare muoversi con velocità v, calcola rapidamente che la sua astronave viaggia alla velocità assoluta uguale a –v.

Tuttavia, dall’oblò opposto, il capitano in seconda vede l’astronave C. Essa si muove con velocità u rispetto ad A. E’ pur sempre un ufficiale con molta responsabilità ed esegue i calcoli da solo. Anch’egli decide che l’astronave C è realmente FERMA. Ne deduce che la sua astronave sta viaggiando a velocità –u.

Quando il capitano e il suo vice si incontrano nasce una discussione molto accesa: ognuno è convinto di avere ragione e ne porta le prove strumentali. Prima che nasca un ammutinamento o qualcosa del genere, il vice-vice capitano risolve il problema, facendo ragionare i suoi superiori. Basta porgli la domanda: “Che prove avete che l’astronave B o C sia realmente ferma?”

Nessuno è in grado di rispondere e devono ammettere che non vi sono assolutamente prove concrete su cosa stiano veramente facendo B o C. Potrebbero benissimo muoversi anche loro e tutti i calcoli fatti andrebbero a farsi benedire. Sono costretti ad ammettere che le uniche velocità che possono determinare per la loro astronave sono velocità relative. In parole più tecniche: non esiste un sistema di riferimento assoluto.

Beh… abbiamo ripetuto quello che già sapevamo sulla relatività galileiana. Niente di più e niente di meno.

Tuttavia, mentre il capitano e i suoi secondi sembrano essersi ormai riappacificati, ecco che appare un’astronave molto strana che si chiama LUCE. Il capitano di questa astronave è l’ammiraglio Maxwell, ben noto nell’Universo per non dire mai bugie. Egli comunica a tutti gli equipaggi che incontra che sta viaggiando a una velocità costante c. Una velocità enorme, per cui bisogna stare molto attenti al suo passaggio.

L’astronave A deve, perciò, osservare una velocità di LUCE che può essere sia v + c o v – c, a seconda della direzione del movimento. Il capitano e tutto il suo equipaggio si guardano in faccia ed esultano: finalmente sanno esattamente a che velocità stanno muovendosi o, almeno, sanno come fare per poterla calcolare. Basta fare la differenza tra il valore fisso c e quello che osservano per determinare la loro velocità assoluta.

Tutto ciò che sembrava assurdo ottenere con le leggi della meccanica viene risolto brillantemente con l’elettromagnetismo (così si chiama il mezzo di propulsione di LUCE). Finalmente hanno trovato un sistema di riferimento assoluto!

Mentre nell’astronave si festeggia, il vive-vice-vice capitano si mette a fare quattro calcoli e ricava la loro velocità assoluta. Ha quasi paura a dirlo ai superiori: essa risulta essere uguale a zero. Sono fermi. Potrebbe anche essere vero, ma vale la pena provare… Accende per un attimo i motori  e poi li spegne in modo da essere sicuro di essere tornato su  un sistema inerziale, ma con velocità v diversa da zero… Riprova a calcolare la loro velocità assumendo sempre come costante quella dell’astronave LUCE.

Niente da fare continuano a essere fermi. Impossibile! Da qualche parte ci deve essere un baco. Si erano illusi di aver trovato un sistema di riferimento assoluto.  Quel Maxwell li ha presi in giro! Eppure sembra proprio convinto di ciò che dice. Quando riferisce il tutto al capitano, cala un triste silenzio a bordo…

Il vice-vice-vice-vice  capitano si schiarisce la voce e sussurra: “Potrebbe esserci una soluzione a tutto questo… basterebbe ammettere che la meccanica newtoniana non è esatta. Vale per velocità relativamente basse, ma non per valori troppo alti come quelli prossimi a c. In particolare, la velocità di LUCE è costante per tutti i sistemi di riferimento e non si può sommarle o sottrarle altre velocità… come abbiamo fatto con quelle delle altre astronavi. Ne consegue che può veramente esistere una relatività che vale sia per la meccanica che per l’elettromagnetismo, ma la trasformazione galileiana va rivista completamente”.

Potremmo concludere la “favola” dicendo che il nome del vice-vice-vice-vice capitano è Albert Einstein!

Una teoria che crede al capitano Maxwell

Qualcuno mi potrebbe dire: “E se Maxwell fosse veramente un terribile bugiardo?”. Beh… non chiedetemi di descrivere “semplicemente” le equazioni di Maxwell (sarebbe, però, una bella impresa ... chissà…). Tuttavia, la prossima volta utilizzeremo un metodo molto più intuitivo e “osservativo” per dimostrare la costanza della velocità della luce e l’impossibilità di sommarle o toglierle un’altra velocità. Adesso torniamo a noi…

Einstein ha riscritto la trasformazione galileiana attraverso la teoria della relatività. I suoi punti di partenza sono in pratica solo due, più che sufficienti:

1) Le leggi della fisica sono le stesse in tutti i sistemi inerziali. Non esiste un sistema inerziale assoluto. (Principio di relatività)

2) La velocità della luce nel vuoto ha lo stesso valore c in tutti i sistemi inerziali. (Principio della costanza della velocità della luce)

Il principio di relatività di Einstein va ben al di là del principio di relatività Newtoniana, che si riferiva solo alle leggi della meccanica, dato che include tutte le leggi della fisica. Esso afferma che è impossibile, per mezzo di qualsiasi misura fisica, definire un sistema inerziale come intrinsecamente in quiete o in movimento:  possiamo solo parlare del moto relativo dei due sistemi. Quindi, nessun esperimento fisico eseguito interamente all’interno di un solo sistema inerziale può dire all’osservatore qual è il moto del suo sistema rispetto ad un qualunque altro sistema inerziale.

Il secondo principio è, invece, in netta contraddizione con la trasformazione Galileiana delle velocità

Vale la pena riproporre poche frasi scritte da Einstein nella presentazione della sua teoria:

“… per tutti i sistemi di coordinate per i quali valgono le equazioni della meccanica, valgono anche le equivalenti equazioni dell’elettrodinamica e dell’ottica. In quanto segue facciamo questa ipotesi (che chiameremo poi il principio di relatività) e introduciamo l’ulteriore postulato, un postulato che è a prima vista inconciliabile con le ipotesi precedenti, che la luce si propaga nello spazio vuoto con una velocità c che è indipendente dalla natura del moto del corpo che la emette. Queste due ipotesi sono del tutto sufficienti a darci una semplice e consistente teoria dell’elettrodinamica dei corpi in movimento basata sulla teoria di Maxwell per i corpi in riposo…”

L’intera teoria della relatività ristretta si deduce direttamente da due semplici principi o postulati. Il successo di una teoria si misura soltanto dal confronto con gli esperimenti, reali o di laboratorio che siano. Ebbene, la teoria della relatività ristretta (d’ora in poi RR) non solo è riuscita a spiegare tutti i risultati sperimentali esistenti ma ha predetto molti nuovi effetti che sono stati confermati da successivi esperimenti. Finora non si è trovata alcuna obiezione alla RR.

Ricordiamo, però, che la RR si occupa solo di sistemi inerziali e non considera sistemi accelerati e, quindi, non si può occupare di gravità (all'interno di un sistema, però, può avvenire qualsiasi fenomeno fisico).

Le stelle fantasma e la costanza della velocità della luce

La teoria della relatività formulata da Einstein estende, in qualche modo, la relatività galileiana, confermando che non solo le leggi della meccanica sono le stesse in tutti i sistemi inerziali, ma anche quelle dell’elettromagnetismo. Impone, però, un altro postulato che si riferisce alla costanza della velocità della luce.

In tal modo riesce a spiegare l’apparente incongruenza tra elettromagnetismo e fisica classica newtoniana. Sono argomenti che analizzeremo a fondo. Tuttavia, prima di iniziare nella descrizione delle ripercussioni della relatività ristretta è meglio dimostrare la costanza della velocità della luce. In altre parole, confermare che la velocità della luce non segue la relatività galileiana e rimane la stessa in tutti i sistemi inerziali.

Vi ricordate che avevamo proprio dimostrato il contrario parlando di somma delle velocità nella trasformazione galileiana, utilizzando anche alcune linee di Universo nel suo spaziotempo. Lo spostamento, nell’unità di tempo, era relativo al sistema inerziale considerato. Se un certo corpo si muove con una certa velocità in un sistema di riferimento, anch’esso in movimento rispetto a noi, la sua velocità, misurata nel nostro sistema, è la somma di quella rispetto al sistema in movimento e di quella dello stesso sistema rispetto a noi. Insomma, la ben nota regola della somma delle velocità.

Tutto ciò potrebbe andare bene anche per Einstein, a parte il fatto che la velocità della luce non soddisfa a questa regola: essa rimane costante (nel vuoto) in tutti i sistemi di riferimento. Il che vuole anche dire che la somma della velocità della luce c e di qualsiasi altra velocità porta sempre allo stesso risultato, ossia sempre alla stessa velocità c. In altre parole, la velocità della luce non si somma ad altre velocità.

Questo postulato non distrugge la relatività galileiana, che continua a valere per velocità nettamente inferiori a quella della luce, ma, ovviamente, perde di significato per quei fenomeni, come l’elettromagnetismo, in cui “certe” particelle raggiungono velocità simili a quelle della luce.

Non esistono i fantasmi

Cerchiamo di dimostrare la costanza della velocità della luce con osservazioni astronomiche, introducendo il paradosso delle stelle fantasma di De Sitter, enunciato nel 1913, sicuramente la più geniale e semplice intuizione a riguardo.  De Sitter, una grande mente raramente ricordata, si è basato su una dimostrazione per assurdo. Ossia, ha accettato la possibilità di sommare la velocità della luce ad altre velocità e ha verificato che l’ipotesi porta a un assurdo osservativo.

Senza bisogno di strane apparecchiature, né di lavorare con numeri infinitesimi, egli ha dimostrato, come ipotizzato da Einstein, che la velocità della luce non può sommarsi ad altre velocità: è quella che è, in qualsiasi sistema di riferimento ed è il valore massimo raggiungibile. Egli ha guardato direttamente all’Universo e a oggetti che si possono vedere un po’ dappertutto, a qualsiasi distanza e con caratteristiche sempre diverse. Tra tanti esempi reali, con osservazioni astronomiche “mirate”, dovevano esserci sicuramente quelli che servivano a lui.

Stiamo parlando dei sistemi binari stellari. Il “problemino” cinematico è quello illustrato nella Fig. 12.

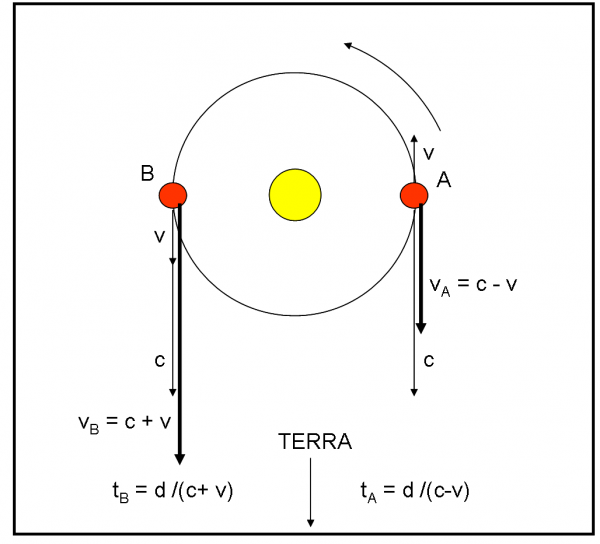
La stellina rossa rivolve attorno alla compagna gialla con un certo periodo di rivoluzione P. Consideriamo la sua posizione in A. Essa sta allontanandosi dalla Terra con velocità v. In meccanica classica, la luce che viene inviata verso di noi è determinata vettorialmente dalla velocità c della luce, a cui deve essere sottratta quella dell’astro che viaggia in senso opposto. Così, almeno, ci dice Galileo.

Quanto tempo impiega per arrivare sulla Terra la luce di A? Indichiamo con t_A questo tempo e con d la distanza della stella binaria da noi. Ricordando che la velocità è uno spazio diviso per un tempo, abbiamo:

t_A = d/(c – v)

Dopo mezzo periodo di rivoluzione (P/2), la stellina rossa si viene a trovare in B. In quelle condizioni, essa si muove verso di noi con velocità v. La velocità della luce e la velocità orbitale si sommano. Quanto tempo impiega ad arrivare sulla Terra la luce di B? Sia esso t_B, dato da:

t_B = d/(c + v)

Si vede subito che la luce partita da A viaggia più piano della luce partita da B.  Ne consegue che impiega più tempo per giungere a noi (t_A > t_B). E’ facile calcolare la differenza tra i tempi di percorrenza della distanza d da parte della luce di A e di quella di B. Essa è data da:

t_A - t_B = d(1/(c - v) - 1/(c + v)) = d((c + v – c + v)/((c –v)(c + v))) = 2 d v/(c² – v²)                    … (1)

Potrebbe capitare che la luce partita da A arrivi all’osservatore nello stesso istante di quella partita da B ?

Quella di A parte per prima, ma viaggia più lentamente e, quindi, potrebbe benissimo accadere. Basta che la differenza di tempo scritta nella (1) sia proprio uguale alla metà del periodo di rivoluzione. Se questo fosse vero, la luce di A arriverebbe con una differenza di tempo rispetto a quella di B proprio uguale al tempo in cui la stellina rossa ha percorso metà della sua orbita. Cosa vorrebbe dire tutto ciò

Facile! L’osservatore sulla Terra dovrebbe vedere nello stesso istante la stellina sia nella posizione A che nella posizione B.

E’ una situazione impossibile da ottenere praticamente? Nemmeno per sogno. Basta che:

2 d v/(c² – v²) = P/2.

Tra le tantissime stelle doppie osservabili ce ne sono molte che soddisfano questa relazione. Ricordiamoci che essa dipende sia dalla velocità di rivoluzione v, sia dalla distanza d da noi, sia dal periodo P.

De Sitter ne ha identificato un certo numero, ma in nessun caso è stato possibile vedere sdoppiarsi la stellina. Essa rimane un vero “fantasma”!

L’unico modo per spiegare la mancanza degli “spettri” (quelli veri, tipo castelli inglesi…) è che:

c + v = c - v = c

Proprio come enuncia la teoria della relatività speciale.

Bello, veramente bello, e geniale!

Un sistema inerziale e una sfida tra geni

Siamo arrivati al punto fondamentale. Abbiamo enunciato i principi di una nuova teoria che estende la relatività galileiana all’intera fisica (e non solo alla meccanica) e stabilisce la costanza della velocità della luce. Adesso non ci resta che valutare ciò che essa comporta nella struttura spaziotemporale della realtà.

Prima di iniziare, però, dobbiamo essere sicuri di predisporre nel migliore dei modi un sistema di riferimento inerziale. Ricordiamo, infatti, che questa teoria non si occupa dei moti accelerati, ma solo dei sistemi in moto inerziale. Già così, però, vedremo che i concetti normali di spazio e tempo subiscono cambiamenti drastici.

Il punto più importante riguarda il tempo, inteso come una coordinata a tutti gli effetti e anch’esso da considerare una grandezza relativa e non assoluta.  Per capire bene cosa implicano queste asserzioni, immaginiamo che due studenti vengano esaminati da una commissione al di fuori delle parti. Ciascuno di loro deve presentare il proprio progetto di sistema inerziale. Fatto questo, dovrà descrivere il moto di un punto all’interno del sistema così costruito. Questa specie di esame richiamerà ancora una volta i limiti della relatività galileiana  e imposterà i capisaldi di quella einsteniana.

Uno strano esame

I due studenti hanno dei nomi molto indicativi: il primo si chiama Newton e il secondo Einstein (che fantasia!).

La commissione d’esame chiede a Newton di quali oggetti abbia bisogno per la sua rappresentazione. Per ragioni di estrema semplicità, immaginiamo che lo spazio sia a una sola dimensione. Newton sembra molto deciso: il suo sistema di riferimento è un segmento di retta nello spazio monodimensionale, abitato da tre punti (a, b e c). Inoltre, lo studente chiede un’asta rigida di lunghezza costante ben determinata, che chiama “metro”. Infine, domanda un ottimo orologio, che scandisca i “secondi”, ben visibile da qualsiasi punto del suo segmento che funge da sistema di riferimento.

A questo punto inizia la costruzione del sistema. a e b sistemano l’asta rigida in modo che il suo bordo sinistro coincida con l’inizio del segmento. Il punto d’inizio viene chiamata spazio s = 0. Il punto finale dell’asta rigida viene chiamato spazio s = 1. c controlla che tutto venga eseguito alla perfezione. a e b sistemano ora l’asta in modo che il suo bordo sinistro coincida con s = 1. Il bordo destro viene chiamato s = 2. Il procedimento continua fino alla fine dello spazio a disposizione sul sistema di riferimento.

L’unico orologio a disposizione viene inserito nel centro del segmento, per controllare meglio l’ora esatta, ma potrebbe essere messo ovunque.

Ovviamente, asta, abitanti dello spazio e orologio non si potrebbero vedere, avendo una sola dimensione, ma noi li abbiamo evidenziati per seguire meglio il procedimento.

E’ ora di descrivere il moto di c che parte dal punto 0 e si muove verso a e b, che controllano posizione e tempo. Per ragioni di semplicità, c si muove di moto costante (ma poteva fare qualsiasi cosa). Quando inizia il suo movimento, l’orologio segna 0 secondi. Come giunge nel punto 1, l’orologio segna 5 secondi, e via dicendo fino a raggiungere il punto 3 quando l’orologio segna 15 secondi. Newton non ha problemi a descrivere il moto di c, come si vede in Fig. 13.

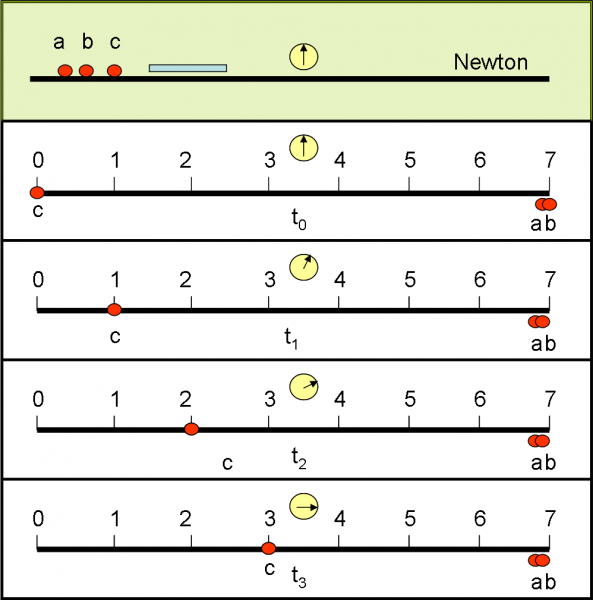
Nel caso scelto si tratta di un moto rettilineo uniforme eseguito con una velocità costante u = 1/5 = 0.2 m/sec. Come già detto, il tipo di movimento di c è del tutto ininfluente e può essere qualsiasi, dato che si svolge all’interno del sistema di riferimento. Quello che sarà veramente importante nel prosieguo dell’esame è che TUTTO il sistema di riferimento si muova di velocità v costante rispetto alla commissione d’esame.

La commissione mormora qualcosa e chiede a Newton quale sia la ragione che l’ha spinto a usare una sola asta e un solo orologio. Newton sorride e risponde : “Il tempo è assoluto e uguale per tutti. Una lunghezza rimane la stessa in qualsiasi sistema di riferimento si sia. Segnata la divisione dello spazio essa non cambia più ”. La commissione invita Newton a ritirarsi. Newton si sente molto tranquillo, dato che è sicuro che anche la commissione ha visto esattamente ciò che hanno visto i punti a e b in movimento insieme al segmento. D’altra parte sa bene che qualsiasi legge della meccanica si descrive nello stesso modo se i sistemi di riferimento sono inerziali.

Descriviamo in modo più rigoroso la legge del moto che si è verificata nel sistema di riferimento in movimento. Essa collega una serie di eventi capitati su di esso. Il primo è stato “la presenza di c nel punto 0, all’istante 0”. Il secondo, “la presenza di c al punto 1, all’istante 5 secondi”, e via dicendo. La legge del moto va quindi considerata non solo come una variazione di spazio, ma come una successione di eventi. In altre parole come una funzione s(t), dove ogni s_i(t_i) rappresenta un evento.

Bene, anche noi siamo pienamente d’accordo con questa visione della realtà e ci ricordiamo lo spaziotempo disegnato da Newton basandosi sulla relatività galileiana.

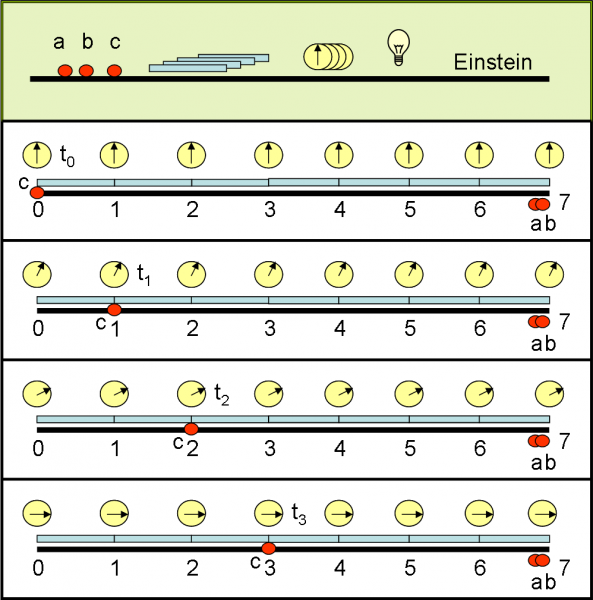
Tocca ora a Einstein. Egli chiede le stesse cose di Newton, ma vuole tutta una serie di orologi e di aste rigide. Inoltre chiede una lampadina che possa accendersi e spegnersi, ovviamente. Fa sistemare da a e b le aste, una davanti all’altra a partire dall’inizio del segmento-spazio. Gli orologi sono posti uno per ogni punto di contatto tra le aste.

Einstein dice anche che, prima di iniziare l’esperimento, a, b e c devono eseguire una procedura che serve per fare in modo che gli orologi segnino tutti veramente la stessa ora, una volta che siano posti nella loro posizione; in poche parole, gli orologi devono essere sincronizzati perfettamente.

Einstein afferma, infatti, che per definire un evento ha bisogno della posizione di chi si sta muovendo, ma anche del tempo corrispondente misurato da un orologio che sia posto esattamente nel punto in cui si trova il corpo che si muove. Descrive, in modo analogo a Newton, la legge del moto con la funzione s(t) dove ogni s_i(t_i) rappresenta un evento in cui, però, l’orologio -ripetiamolo ancora-  deve essere posto nel luogo in cui si trova, istante per istante, il corpo in movimento. Anzi, preferisce dire che un evento è rappresentato dalla coppia di coordinate (s_i,t_i). Il tutto è rappresentato in Fig. 14.

La commissione d’esame sembra approvare con maggiore enfasi, mentre Newton è convinto che Einstein abbia fatto la stessa identica cosa che ha fatto lui. Anzi, l’uso di tanti orologi può aver reso imprecisa la misura degli eventi. Nel suo mondo, trovare due orologi che segnano lo stesso tempo è un bel problema.

La commissione chiede a Einstein: “Perché hai lasciato le aste e gli orologi al loro posto?”. Einstein risponde che ha bisogno di avere sempre a disposizione un sistema sicuramente ben determinato per non mandare in confusione il segmento e i suoi abitanti quando saranno visti da un altro sistema di riferimento. Almeno localmente, bisogna avere delle certezze (e sorride) e il reticolo di lunghezze e orologi, così costruito, assicura che il sistema sia sempre lo stesso, qualsiasi cosa dicano gli altri…

Newton non è certo uno stupido e comincia a intuire che tutto quel lavoro di Einstein non è sicuramente stato un puro divertimento. Da un momento all’altro, si aspetta qualche novità che non aveva previsto.

Sembra che la commissione gli abbia letto nella mente. Infatti gli chiede: “Potresti dirci come faresti a sincronizzare tutti quegli orologi?” Newton non ha problemi a rispondere: “Niente di più semplice. Porto tutti gli orologi nel punto O, inserisco perfettamente la stessa ora e poi li trasporto nei vari punti di lettura degli eventi. Vorrei, però, ribadire che tanto valeva che mettessi un solo orologio bene in evidenza…”.

La stessa domanda viene fatta a Einstein. Egli risponde, molto gentilmente, che quanto proposto da Newton può anche andare bene, ma gli orologi devono essere trasportati molto lentamente, dato che per muoversi e per fermarsi devono subire una accelerazione e una decelerazione. Niente può assicurargli che durante questa manovra l’ora che un orologio segna alla fine del trasporto rimanga la stessa di quella che avrebbe segnato se fosse rimasto fermo in 0. Lui preferisce una procedura più sicura e accurata.

Newton è sempre meno sicuro di sé, mentre la commissione è estremamente interessata.

Sincronizziamo gli orologi 

Einstein fa sistemare gli orologi nella loro posizione, senza curarsi tanto di ciò che segnano. Poi dice una frase molto indicativa: “Se potessimo creare un segnale che viaggiasse a velocità infinita, esso impiegherebbe un tempo uguale a zero per raggiungere tutti gli altri orologi. Porrei a in 0 e b in 1. a metterebbe la lancetta sullo zero e contemporaneamente manderebbe il segnale a b che istantaneamente sistemerebbe anche le lancette del secondo orologio sullo zero. Poi si sposterebbero su 1 e 2 e ripeterebbero la procedura fino a sincronizzare anche il numero 7.

A quel punto sarei sicuro che tutti gli orologi del sistema inerziale segnerebbero la stessa ora e continuerebbero a segnarla. Purtroppo, non abbiamo a disposizione un segnale che viaggia a velocità infinita e ci dobbiamo accontentare del segnale più veloce che possediamo: il segnale luminoso.

Sappiamo che la luce non viaggia a velocità infinita, ma soltanto a 300 000 km/sec (anzi poco meno). La fortuna è, però, che la velocità della luce è una costante per qualsiasi sistema di riferimento. Questa costanza diventa fondamentale”. Newton ha ormai le idee veramente confuse e comincia a capire che la sua visione della realtà è troppo semplicistica. Einstein invita gli abitanti del suo sistema di riferimento a proseguire con l’operazione di sincronizzazione.

a si mette in 0 e b in 1. c, invece si pone esattamente a metà dell’asta che congiunge 0 con 1. Non hanno certo problemi a misurare il punto di mezzo, dato che è una semplice misura spaziale. c, che si trova in s = 0.5 prende in mano la lampadina. Poi, avvisa i compagni e l’accende. A questo punto Einstein tira fuori la sua carta vincente (ampiamente dimostrata) che dice che la velocità della luce è indipendente dal sistema di riferimento usato e che è la stessa in qualsiasi direzione vada (isotropia dello spazio). Può quindi essere sicuro che la luce percorre spazi uguali in tempi uguali ed è sempre uguale a c, comunque si muova il sistema di riferimento. Ne consegue che la luce arriva in 0, dove si trova a, e in 1, dove si trova b, nello stesso istante (gli spazi sono uguali e quindi anche il tempo impiegato).

All’arrivo della luce, a e b fanno partire i loro orologi che DEVONO segnare lo stesso tempo. L’orologio in 0 e quello in 1 sono sincronizzati. La semplice operazione è riassunta in Fig. 15.

Per sincronizzare gli altri orologi è solo questione di pazienza e precisione. Ad esempio, possono fare come riportato di seguito. a si sposta in 1 e b si sposta in 2, così come c si sposta tra 1 e 2, in 1,5. Accende di nuovo la lampadina. A questo punto, a, che vede girare il proprio orologio sincronizzato con quello di 0, prende nota della differenza di tempo tra il tempo segnato dall’orologio e quello di arrivo della luce, che considera come un nuovo tempo zero. Sia esso un certo dt. Questo è un valore sicuramente corretto dato che tutte le misure sono state svolte nello stesso luogo e con lo stesso orologio. b, invece, ha fatto partire l’orologio in 2 (lancetta rossa). Attende che a lo raggiunga (poco importa il tempo che ci mette) e gli comunica il valore dt. b non deve fare altro che aggiungere dt all’ora che segna la lancetta rossa e ottiene la lancetta nera che è per definizione sincronizzata con quella dell’orologio in 1 e, quindi, anche con quello in 0. La Fig. 16 mostra questa procedura.

Basta ripetere l’operazione e tutti gli orologi del sistema di riferimento sono sincronizzati, ossia essi segnano sempre lo stesso tempo, indipendentemente dal moto del sistema. Notiamo, ancora una volta, che tutto ciò è stato possibile perché la velocità della luce è una costante.

Il tempo assoluto di Newton subisce un duro colpo e, dato che  lo studente è decisamente intelligente, capisce già che la sua teoria si sta sgretolando come un castello di carte colpito da una raffica di vento. E’ costretto ad ammettere che Einstein ha ragione, dato che la costanza della velocità della luce è stata dimostrata. Si siede ed è estremamente interessato a vedere cosa impone questa nuova visione della realtà. Gli stessi professori fanno silenzio e invitano Einstein a proseguire. L’esame è terminato e ora tutti desiderano solo imparare!

Da questo momento in poi, perciò, affrontiamo tutti assieme la teoria della relatività ristretta.  Se pensiamo che finora sono state dette delle banalità, stiamo molto attenti! E’ essenziale digerire bene il procedimento eseguito e ricordare sempre le condizioni di partenza della nuova avventura.

Cosa significa simultaneità?

Il punto di arrivo di tutta questa sceneggiata preliminare si riferisce alla simultaneità di due eventi. L’evento “luce che arriva in 0” e quello “luce che arriva in 1”  sono eventi simultanei, dato che gli orologi in 0 e 1 sono stati sincronizzati. Non dimentichiamolo!

Nella relatività galileiana il concetto di simultaneità è assoluto, qualsiasi sia il sistema di riferimento, dato che il tempo è assoluto. In altre parole, se due eventi accadono nello stesso momento in un sistema di riferimento, lo devono fare in qualsiasi altro sistema di riferimento. Nella relatività ristretta ciò non è più vero e il sistema di riferimento appena costruito da Einstein ce lo dimostra molto chiaramente.

Eseguiamo, quindi, un esperimento atto proprio a mostrare la relatività della simultaneità di due eventi. Questo è un fatto normalmente trascurato in molte trattazioni. A prima vista sembrerebbe del tutto inutile, una volta che si sono acquisiti i concetti della dilatazione dei tempi e della contrazione delle distanze (ecco perché Einstein ha voluto che nel sistema di riferimento ci fosse un reticolo spaziotemporale ben determinato). E’, invece, un fatto che va studiato indipendentemente anche se, ovviamente, è collegato strettamente alle ripercussioni più famose che vedremo in seguito.

Non lo possiamo trascurare, dato che sarà estremamente importante quando passeremo alla rappresentazione grafica di Minkowski. Per cui, mi raccomando, cerchiamo di capire bene il profondo significato di ciò che Einstein ci sta per mostrare.

Prima di proseguire, è bene porre attenzione all’utilizzo della parola "osservatore", che viene spesso usata nella relatività. Sembrerebbe impossibile e invece può portare a gravi fraintendimenti. Per questo motivo è bene ribadire, una volta per tutte, cosa si deve intendere con la frase "osservatore in un riferimento S ". Con tale frase non si deve intendere una singola persona ma, in realtà, un riferimento, a ogni punto del quale siano associate tre coordinate x,y,z (noi spesso ne useremo una sola, la s), che ne individuano la posizione spaziale (in altre parole, proprio l’insieme di aste rigide che hanno usato i nostri amici a, b e c) e un insieme di orologi sincronizzati fra di loro, posti nei vari punti dello spazio.

Non trascuriamo questa definizione, anche se a prima vista sembrerebbe ridondante e inutile. Lo stesso Einstein l’ha descritta nei dettagli e nessuno può credere che si divertisse ad aggiungere cose superflue alla sua teoria.

Anche la simultaneità è relativa

Va bene, iniziamo, introducendo finalmente un osservatore esterno al nostro sistema di riferimento abitato da a, b e c. Osservatore esterno, vuol dire sistema di riferimento con tanto di orologi sincronizzati e punti definiti spazialmente da tante aste rigide. Questo nuovo sistema lo possiamo chiamare S’, mentre quello precedente lo chiamiamo S. Dato che entrambi sono stati “preparati” adeguatamente è del tutto analogo considerarne uno fermo e l’altro in moto o viceversa: sappiamo ormai benissimo che il movimento può essere solo relativo e non esiste un sistema di riferimento assoluto. L’unica cosa di assoluto è la costanza della velocità della luce.

Per eseguire l’esperimento sicuri di noi stessi, chiediamo nuovamente al sistema S (ossia ad a, b e c) di mostrarci senza ombra di dubbio che abbiano eseguito perfettamente quanto richiesto da Einstein.

Cambiamo solo leggermente le condizioni di partenza, ma il succo rimane lo stesso. Diamo una lampadina ad a e una a b, posti ai due bordi opposti del sistema. c occupa, come sempre, il punto di mezzo. Alla stessa ora a e b accendono la loro lampadina (ognuno si fida del suo orologio che sa essere perfettamente sincronizzato con quello dell’amico). Come era del tutto prevedibile, c riceve la luce esattamente allo stesso istante (anche il suo orologio è sincronizzato e quindi deve segnare la stessa ora di quello di a e di b). A c non resta che concludere che l’evento “accensione della luce di a” e “accensione della luce di b” sono eventi simultanei.  La Fig. 17  mostra questo esperimento che è del tutto simile a quello che era servito per sincronizzare gli orologi di S. Il risultato è quindi del tutto ovvio, ma è sempre meglio non fidarsi mai… (come vedremo tra poco).

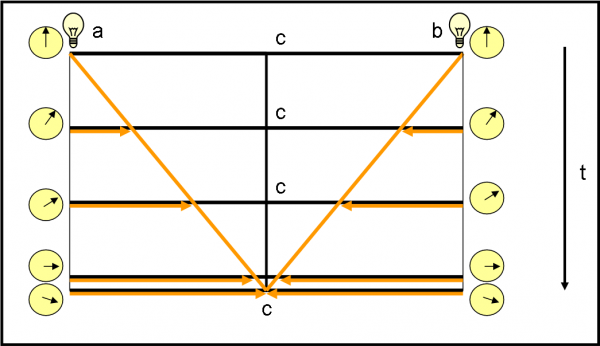
Abbiamo fatto scorrere il tempo verso il basso e di tanto in tanto abbiamo disegnato il punto di arrivo della luce partita da a e b nello stesso istante. Un espediente un po’ infantile che possiamo sintetizzare nella Fig. 18, utilizzando solo le linee diagonali che individuano i punti raggiunti dalla luce istante per istante. Ovviamente le due diagonali si incontrano in c nello stesso istante. Scusate la pedanteria, ma è meglio camminare molto lentamente ed essere ridondanti.

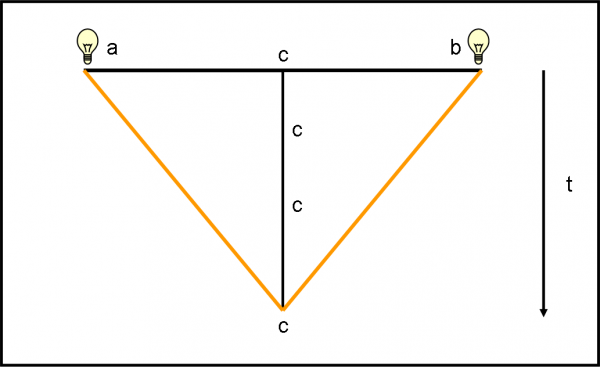
Introduciamo il nuovo sistema S’, in cui ci può essere uno, due, cento osservatori. Poco importa, dato che anche in questo sistema tutto è stato predisposto perfettamente, con le aste rigide e gli orologi sincronizzati. Disegniamo la Fig. 19.

I sistemi S e S’ coincidono al momento dell’ipotetica accensione delle due lampadine in a e b. Siano a’, b’ e c’ gli osservatori di S’ che coincidono in quell’istante con a, b e c.

Tuttavia, il sistema S si muove rispetto a S’. La luce, invece, viaggia sempre nello stesso modo ed è del tutto indipendente dal sistema in cui la lampadina è stata accesa. Essa quindi deve seguire due linee diagonali esattamente come prima (la loro inclinazione deve essere la stessa). Il signor c deve essere raggiunto nello stesso istante sia dalla luce inviata da a sia da quella inviata da b. Tuttavia per ottenere questo risultato, all’osservatore S’ risulta ovvio che a deve aver acceso la lampadina PRIMA di b. Non vi è altro modo perché la luce che viaggia sempre con la stessa velocità sia per S che per S’ giunga nello stesso istante in c . Per S' non è assolutamente vero che a e b abbiano acceso la lampada nello stesso istante: i due eventi, “a accende la lampada” e “b accende la lampada”, non sono simultanei!

D’altra parte, questa conclusione non è difficile da ottenere con il ragionamento. La luce di a deve percorrere uno spazio maggiore per arrivare a c di quello che deve percorrere la luce di b. Dato che la luce viaggia sempre alla stessa velocità, per percorrere uno spazio maggiore bisogna che la lampada si accenda prima. Se su S sono convinti di avere sincronizzato gli orologi si sbagliano di grosso. Infatti, l’orologio in a e quello in b segnavano la stessa identica ora quando le lampade si sono accese.  Ma, per S’ risulta chiaro che i due eventi non sono simultanei e quindi gli orologi non sono sincronizzati.

In breve, gli abitanti di S dicono che le due lampade si sono accese simultaneamente e che i loro orologi sono sincronizzati. Gli abitanti di S’ dicono invece che la  lampadina di a si è accesa prima di quella di b, ossia che l’orologio di a va avanti rispetto a quello di b! Possiamo anticipare (ma ci servirà, e come!,  per la rappresentazione di Minkowski) che la simultaneità nel sistema S,  vista nel sistema S’, è data dalla linea tratteggiata.

Possiamo anche descrivere, in Fig. 20,  il problema in modo leggermente diverso (ognuno scelga quello che preferisce).

Siamo nelle stesse condizioni di prima, con S che dice di essere sicuro di avere sincronizzato i suoi orologi. Lo stesso dice S’. a e b accendono la loro lampadina e la luce comincia a viaggiare come prima. Cosa si aspetta S’? Beh, dato che S gli ha detto che le due lampade si sono accese simultaneamente, la loro luce deve raggiungere il signor c’ nello stesso identico tempo. D’altra parte, la luce è partita in corrispondenza di a’ e b’, quando coincidevano con a e b. E se è partita simultaneamente per a e b, lo stesso deve anche valere per a’ e b’, anch’essi con gli orologi sincronizzati! Ne consegue che la luce deve raggiungere contemporaneamente c’.

a’ e b’ fanno in fretta a capire che S ha detto una falsità (almeno per loro). Infatti, è abbastanza evidente che quando la luce emessa da a arriva in c, insieme a quella di b, essa è già passata da c’, mentre quella partita da b deve ancora arrivarci. Se è già passata da c’ vuol dire che ha già raggiunto il punto di mezzo, dove avrebbe dovuto incontrare quella di b, se le lampadine fossero partite in simultanea (per S’). Invece la luce di b deve ancora raggiungere c’ (ha appena raggiunto c). L’unica conclusione possibile è che la luce di b sia partita dopo quella di a (o -se preferite- quella di a è partita prima di quella di b).

In realtà hanno ragione sia gli osservatori di S che quelli di S’. La verità è che il concetto di simultaneità di eventi separati spazialmente dipende dal sistema di riferimento in cui si osserva.

Notiamo, infatti, che stiamo trattando con eventi che si riferiscono a due punti diversi dello spazio (a e b).

Facciamo ancora un piccolo ragionamento che anticipa quello che troveremo. Se nel sistema S le lampadine si accendono nello stesso istante, vuole anche dire che i due orologi posti in a e b segnano lo stesso tempo (ta = tb). Ma, se nel riferimento S’ gli eventi appaiono non simultanei, gli orologi posti a terra nei punti a’ e b’ segnano tempi ta’ e  tb’ diversi fra loro e, quindi, almeno uno dei due tempi deve differire da quelli misurati dagli orologi in a e b. Il tempo segnato dagli orologi non è, perciò, un tempo assoluto ma è relativo al sistema di riferimento.

E’ importante notare che, secondo questo ragionamento, i due sistemi S e S’ sono del tutto equivalenti. Potevamo agire al contrario, piazzando le lampade su S’  in a’ e b’ e accenderle simultaneamente (ta’ = tb’)). In questo caso, se a e b sono i due punti di S che coincidono con a’ e b’ al momento dell’accensione delle lampadine, i tempi di accensione misurati su S (ta e tb) devono apparire diversi.

Simmetria 

Questa perfetta simmetria deve già farci riflettere. Non abbiamo trovato che solo uno dei due sistemi ha sincronizzato male i suoi orologi, ma che entrambi sembrano aver sbagliato la sincronizzazione se visti dall’altro sistema. Non vi è una variazione in un particolare sistema, ma una variazione che dipende solo e soltanto da quale sistema si osserva. Il lungo procedimento usato da Einstein per fissare con sicurezza lo spaziotempo in qualsiasi sistema di riferimento ci dà una perfetta garanzia che niente può cambiare nel singolo sistema di riferimento, ma cambia solo la sua apparenza se visto da un altro. Viene ribadito ancora una volta che non vi è un sistema di riferimento assoluto.

Scusate la pedanteria, ma facciamo un piccolo passo in avanti. Se il tempo in S variasse veramente e, per esempio, scorresse più lentamente, in S dovremmo vedere quello di S’ scorrere più velocemente. Invece, ciò che si osserva è che anche il tempo di S’ scorre più lentamente se visto da S. Questa perfetta simmetria garantisce che il tempo può anche cambiare ma solo in relazione al sistema scelto per osservare. Il tempo è quindi grandezza relativa. Altrimenti accetteremmo l’esistenza di un tempo assoluto.

Non anticipiamo, però, il futuro. Il vero problema è che la dilatazione del tempo di un orologio in movimento, e l’accorciamento di un’asta, fanno parte della consueta trattazione della relatività ristretta e non necessitano di un grande sforzo mentale per essere compresi. Lo stesso non capita per la relatività della simultaneità. E’ un concetto molto più difficile da “digerire”. Essa dice, in sintesi, che non vi è una  relazione assoluta tra i tempi relativi a due eventi che si riferiscono a luoghi distanti tra loro.

Un esempio terra-terra, anzi terra-luna. Immaginiamo di avere due alberi di Natale, uno a Parigi e uno a Los Angeles. Predisponiamo tutto affinché essi si accendano alla stessa ora nel sistema Terra. Non è difficile ottenere questo risultato. Noi siamo contenti di esserci riusciti, ma, nel frattempo, un osservatore sulla Luna, che si muove rispetto alla Terra, dice che abbiamo fallito!

Simultaneità apparente

Attenzione, però, a non confondere questa relatività della simultaneità con la simultaneità apparente di due eventi che capitano normalmente nella nostra vita quotidiana. Consideriamo la Fig. 21.

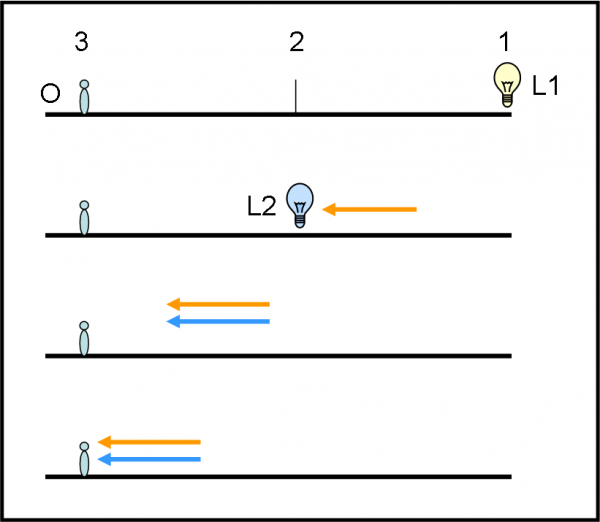
P è un osservatore fisso situato nel punto 3. A un certo istante t1, si accende la lampadina gialla nel punto 1. Quando la sua luce arriva nel punto 2 (al tempo t2), si accende anche la lampadina azzurra. La luce gialla e azzurra adesso viaggiano insieme e raggiungono l’osservatore allo stesso istante t3. P conclude che l’accensione delle due lampadine è stata simultanea, dato che la loro luce arriva nello stesso istante. E’ la stessa cosa che capita quando accendiamo una lampadina a due metri di distanza e abbiamo la fortuna di vedere esplodere nello stesso istante una supernova a 20000 anni luce, oppure quando sentiamo, contemporaneamente, il segnale orario della radio sul tavolo e il segnale inviato dalla sonda Rosetta (sperando che sia reso di dominio pubblico).

Tuttavia, la simultaneità è solo apparente, dato che le due lampadine si sono realmente accese in luoghi diversi nel sistema di riferimento di P. Lui considera come istantaneo solo l’evento che avviene in 3 e giudica simultanei anche gli eventi avvenuti in 1 e in 2. Ciò non è vero! Prima di giudicare la simultaneità dell’evento a cui ha assistito, egli deve controllare gli eventi avvenuti in 1 e in 2. Si accorgerebbe che le lampadine sono poste a distanze diverse da lui e quindi deve tenere in conto della maggiore distanza percorsa dalla luce 1 rispetto a quella di 2. Solo dopo aver eseguito la correzione può veramente parlare di eventi realmente simultanei nel suo sistema di riferimento!

Non per niente nei casi precedenti abbiamo sempre considerato eventi che raggiungono un luogo posto a metà strada tra le loro posizioni. In tal modo abbiamo evitato qualsiasi simultaneità apparente, dato che le distanze da percorrere sono esattamente le stesse. Ancora una volta, lo strano reticolo, costruito da Einstein sul sistema di riferimento, appare come un fatto tutt’altro che infantile!

Quantità relative

Abbiamo scoperto una nuova “quantità” che si aggiunge a quelle relative. Richiamiamole, anche se alcune devono ancora essere introdotte: non possiamo sapere se una nave spaziale si muove di moto rettilineo uniforme rispetto a un’altra oppure sta ferma; non possiamo stabilire se un’asta è lunga un metro come non possiamo concludere se un certo fenomeno dura un minuto: questi valori sono veri solo in un particolare sistema di riferimento. A questa piccola lista possiamo adesso aggiungere che non si può stabilire in modo assoluto se due eventi, lontani tra loro, sono simultanei. O -ma è la stessa cosa- se due orologi posti a una certa distanza sono sincronizzati tra loro. Nuovamente, ciò può essere vero solo per un sistema di riferimento, ma non per un altro.

Il tempo non cambia, cambia la sua apparenza

La relatività della simultaneità ci ha già convinto di parecchie cose. Innanzitutto che la misura del tempo non è un qualcosa di assoluto come ipotizzato da Newton, ma qualcosa che dipende dal sistema di riferimento. Attenzione, però, a non commettere un errore che spesso si intrufola  nella mente e fa poi fatica a essere eliminato (un po’ come quando si considera l’Universo come un palloncino e ci si dimentica che lo spazio è solo la sua superficie).

Quanto detto finora, e sarà ripetuto in seguito, non vuole assolutamente significare che il tempo scorre in modo diverso per chi sta fermo (anche se essere “fermo” non ha senso fisico) e per chi si muove. Chi fa parte di un certo sistema e ha sincronizzato i suoi orologi vede scorrere il tempo in modo del tutto uguale a chi si trova in un altro sistema di riferimento con orologi altrettanto sincronizzati. Non è assolutamente vero che chi viaggia più velocemente ha un orologio che rallenta per chissà quale magia introdotta dalla velocità.

Il tempo che cambia, ossia il moto delle lancette, appare (ed è) diverso, quando viene osservato da un sistema di riferimento diverso. Se l’osservatore O è fermo rispetto ad O’, è l’osservatore O che vede l’orologio di O’ andare più piano, ma non certo O’. Anzi, per lui, è vero il viceversa: è l’orologio di O che va più piano dato che per O’ è O che si muove. La relatività della simultaneità, su cui abbiamo passato parecchio tempo, vuol dire proprio questo, così come la perfetta simmetria tra O e O’.

In altre parole ancora, se O’ viaggia nello spazio, vede trascorrere tranquillamente il suo tempo. Tuttavia, egli può essere osservato da centinaia di alieni O che si muovono in modo diverso tra loro. Ognuno di questi alieni giudica l’orologio di O’ in modo diverso. Ognuno lo vede muoversi in modo diverso. Questa relatività della misura non dipende però da O’, ma solo e soltanto dalla velocità relativa dei vari O. Analogamente, O’ vede orologi che camminano in modo diverso dal suo, a mano a mano che incontra gli alieni O, sparsi per la galassia.

Tuttavia, non dimentichiamo nemmeno che questa diversa apparenza, simmetrica nella relatività speciale, causa una differenza concreta nella relatività generale: chi va più veloce invecchia realmente di meno!  Il riferimento al paradosso dei gemelli NON è affatto casuale! Tutto ciò dipende dal fatto che nella relatività ristretta NON si accelerano i sistemi di riferimento, mentre in quella generale sì e, di conseguenza, s'incurva lo spaziotempo e molte cose possono realmente cambiare in modo non simmetrico. Ma torniamo a noi...

Anche se ancora non l’abbiamo trattata direttamente, la non simultaneità tra sistemi di riferimento, in moto relativo, comporta automaticamente anche una percezione diversa delle lunghezze (misurate con le aste rigide in ogni sistema di riferimento). Anche loro sono quelle che sono in ogni sistema di riferimento, ma variano se osservate da altri sistemi. Misurare un lunghezza, infatti, significa localizzare simultaneamente i suoi due estremi. Tuttavia, sappiamo che la simultaneità è relativa e tale deve essere quindi anche la misura di una lunghezza.

Il succo di tutto ci porta a dire che le equazioni di Galileo devono essere sostituite da nuove equazioni che siano in accordo con l’esperienza e che valgano anche per velocità relative comunque elevate.

Trasformiamo la trasformazione

Questa trasformazione di coordinate esisteva già al tempo della descrizione della relatività speciale ed era stata formulata da Lorentz prendendo atto delle leggi di Maxwell, dove quella di Galileo era incapace di descrivere i risultati sperimentali. Lorentz, però, aveva eseguito un brillante artificio matematico che ben poco aveva a che fare, direttamente, con i postulati di Einstein.

Non pensiamo, quindi, che Lorentz abbia formulato la teoria della relatività ristretta prima di Einstein. In qualche modo, lui aveva già fornito la risposta matematica a un bisogno pratico di un concetto del tutto nuovo introdotto da Einstein.

Proprio per evidenziare questa netta differenza concettuale, cerchiamo di costruire le nuove equazioni (quelle di Lorentz), utilizzando soltanto i postulati della teoria della relatività ristretta. In altre parole, vogliamo dimostrare che partendo dai due postulati si possono tranquillamente ricavare le equazioni di trasformazione.

Il postulato nascosto

In realtà, è fondamentale introdurre un terzo postulato che, però, è già compreso in quello della costanza della velocità della luce: il postulato di omogeneità, ossia l’ipotesi che lo spazio e il tempo siano omogenei. Ciò vuol dire, in pratica, che i risultati relativi a intervalli di lunghezza e/o di tempo di un certo evento non dipendono da dove e quando le misure sono state eseguite in un certo sistema di riferimento.

Se lo spaziotempo è omogeneo ne segue che la velocità della luce nel vuoto deve essere uguale ovunque. O, se preferite, se la velocità della luce nel vuoto è uguale ovunque, vuol dire che lo spaziotempo è omogeneo.

Questa ulteriore precisazione è fondamentale per calcolare i coefficienti della trasformazione di Lorentz. Anzi, può perfino aiutarci a escludere certi calcoli formali e usare solo semplici deduzioni e conclusioni, impostate essenzialmente sul ragionamento e sulla logica.

Omogeneità = semplicità

Facciamo due esempi che ci serviranno tra poco. Innanzitutto, possiamo essere sicuri che le equazioni di trasformazione da una coordinata x a una x’ devono essere lineari! Ammettiamo, infatti, per assurdo, che la relazione tra x e x’ sia di secondo grado, del tipo:

x’ = ax²   

dove a è, ovviamente, una costante.

Se così fosse, troveremmo che la distanza tra due punti del sistema “accentato” dipenderebbe dal luogo in cui si effettua la misura nel sistema non accentato. Infatti, avremmo:

x₂’ – x₁’ = a(x₂² – x₁²)

Se un asta rigida di lunghezza unitaria nel sistema di x ha come coordinate dei suoi estremi x₁ = 1 e x₂ = 2, segue che la stessa asta nel sistema di x’ ha differenza di coordinate (ossia lunghezza):

x₂’ – x₁’ = a(4 - 1) = 3a

Tuttavia, se rifacciamo la misura, quando le coordinate, nel sistema di x, sono x₁ = 4 e x₂ = 5 (la lunghezza rimane, ovviamente, invariata), otteniamo che:

x₂’ – x₁’ = a(25 – 16) = 9a

Troveremmo che la lunghezza dell’asta rigida, osservata dal sistema di x’, dipende dalla posizione occupata nello spazio. La sua lunghezza deve sicuramente dipendere dal sistema di riferimento, ma non può certo variare da luogo a luogo dello spazio. Questo risultato va contro l’ipotesi di omogeneità! Ne segue che la trasformazione può essere solo e soltanto lineare.

Infatti, se:

x’ = ax

si ha:

x₂’ – x₁’ = a(x₂ – x₁)

Sia inserendo x₁ = 1 e x₂ = 2 , sia  x₁ = 4 e x₂ = 5, otteniamo sempre:

x₂’ – x₁’ = a(2 - 1) = a(5 - 4) = a

L’ipotesi di omogeneità è verificata!

Analoga conclusione si ottiene per la coordinata temporale.

Inoltre, se consideriamo la direzione del moto relativo lungo l’asse x, che coincide con x’, risulta abbastanza ovvio che gli assi y e z non possono essere influenzati dal movimento. Se così fosse vorrebbe dire che lo spazio non è  omogeneo. Forse questo punto è meno immediato, ma lo riprenderemo in seguito.

Siamo adesso pronti a cercare le equazioni di trasformazione dal sistema S a quello S’, senza dimenticarci mai delle limitazioni (meno male!) imposte dai postulati di Einstein.

La parte che segue potrebbe sembrare noiosa e addirittura superflua. Vi prego di non sottovalutarla e nemmeno di saltarla come “inutile”. Solo capendo bene i vari passaggi saremo in grado di comprendere appieno la semplice genialità di Einstein, le basi della relatività ristretta e riuscire a fare il passo decisivo verso il diagramma di Minkowski. Non vogliamo, infatti, descrivere solo la relatività ristretta, ma essere in grado di disegnare su un foglio tutte le linee che vogliamo e capire cosa significano da un  punto di vista relativistico. Allora sì che ci divertiremo davvero!

Ho deciso di presentare prima la derivazione della trasformazione di Lorentz rispetto alle sue conseguenze. Sembrerebbe un procedimento ovvio e, invece, spesso si fa il contrario. Si parte dai fenomeni sperimentali che derivano dai postulati e si trovano abbastanza facilmente le “stranezze” della relatività, come la dilatazione dei tempi e la contrazione delle lunghezze. Da questi risultati di descrivono le trasformazioni matematiche necessarie per ottenerle. Niente di male, ovviamente, dato che la trasformazione di Lorentz nasce in modo indipendente prima dei postulati di Einstein…

Tuttavia, da buon matematico, reputo che sia più giusto (e anche istruttivo) andare per gradi.  Il procedimento inverso può essere considerato come una specie di esercizio.

Vi sono vari modi per descrivere la derivazione della trasformazione di Lorentz. Alcune sembrano più rapide e semplici, altre più formali e “corrette”. Preferisco usare le seconde perché non mettono polvere sotto al tappeto e non obbligano ad accettare derivazioni logiche poco intuitive e non sempre realmente precise. Se poi, vogliamo usarle, lo possiamo sempre fare…

Bando alle ciance e partiamo, ricordando che usiamo solo e soltanto i due postulati di Einstein con l’aggiunta di quello (apparentemente separato) dell’omogeneità dello spaziotempo.

Abbiamo visto dalla relatività della simultaneità che la trasformazione di Galileo non può funzionare, ma abbiamo anche visto che le relazioni devono essere lineari. Ne segue che esse devono avere questa forma generale

x’ = a₁x + a₂ y + a₃ z + a₄ t

y’ = b₁x + b₂ y + b₃ z + b₄ t

z’ = c₁x + c₂ y + c₃ z + c₄ t

t’ = d₁x + d₂ y + d₃ z + d₄ t         …. (1)

In poche parole, vogliamo trovare i coefficienti a_i, b_i, c_i e d_i che legano le coordinate di un sistema di riferimento a quelle di un altro sistema in moto rettilineo uniforme rispetto a lui (proprio come aveva fatto Galileo).

Notiamo subito un fatto molto importante: il tempo entra in ballo come una qualsiasi coordinata e non è esclusa assolutamente nessuna sua dipendenza delle coordinate spaziali e viceversa. Ricordiamo ancora che Galileo se l’era “cavata” imponendo subito t = t’ (tempo assoluto). Ammissione che ormai sappiamo essere ASSURDA sulla base dei nuovi postulati e della relatività della simultaneità.

Mamma mia, quanti coefficienti da ricavare! Un sistema di quattro equazioni in sedici incognite: impossibile! No, non spaventiamoci… molti di loro si annullano o si determinano in modo intuitivo con piccoli ragionamenti…

Innanzitutto, sappiamo che questi coefficienti devono dipendere dalla velocità del moto relativo dei due sistemi. Infatti, nel caso che la velocità v fosse uguale a zero (sistemi in quiete relativa), è ovvio che dovremmo trovare a₁ = b₂ = c₃ = d₄ = 1 e tutti gli altri uguali a ZERO. E’ l’unico modo per ottenete una NON trasformazione del tipo x’=x, y’=y, z’=z, t’=t, che descriverebbe la perfetta uguaglianza tra le coordinate di due sistemi coincidenti!

Scegliamo una direzione del moto (come avevamo fatto con Galileo) e questa sia proprio l’asse x (possiamo sempre scegliere l’asse x come vogliamo). L’asse x’ coincide, quindi, con l’asse x (ma questo non vuole dire che la x’ di un punto sia uguale alla x del punto! Questo capiterebbe solo se i due sistemi fossero fermi tra loro).

Cosa impone questa scelta agli alti due assi x e y (e ai loro fratelli in movimento y’ e z’)? Una cosa molto importante e intuitiva: se y = 0 e z = 0, deve anche essere y’ = 0 e z’ = 0. Non ho detto niente di speciale! Ho solo detto che i punti dell’asse x (quelli per i quali y e z sono uguali a zero) devono trasformarsi nei punti dell’asse x’ (quelli per i quali y’ e z’ sono uguali a zero). In altre parole, l’asse x (definito proprio da y = 0 e z = 0) rimane sempre se stesso, e coincide con l’asse x’. Questo fatto vuol dire che le relazioni tra y e z e y’ e z’ non devono dipendere da x e x’ e da t e t’. Infatti, se y’ dipendesse anche dal termine in x (o in t), quando si ponesse y = 0 e z = 0, si otterrebbe y’ = b₁x (o b₄t), che non potrebbe essere vero per definizione, dato che y’ deve essere sicuramente uguale a zero. Qualche coefficiente comincia ad andarsene…

Possiamo scrivere:

y’ = b₂y + b₃z

z’ = c₂y + c₃z      …. (2)

Ossia:  b₁ = b₄ = c₁ = c₄ = 0

Non basta ancora, però…

Il piano xy deve trasformarsi nel piano x’y’, così come il piano xz deve trasformarsi in x’z’. Il piano xy è definito da z = 0, così come quello xz da y = 0. Ne segue che la relazione y = 0 deve portare anche a y’ = 0 e z = 0 a z’ = 0. Il che vuole dire, in soldoni, che b₃ = c₂ = 0, come si deriva immediatamente dalla (2).

La (2) diventa:

y’ = b₂y

z’ = c₃z      …. (3)

Cosa vuol dire la (3)? Che le coordinate y’ e z’  potrebbero variare linearmente con y e z. In poche parole, se il sistema S’ si muove rispetto a S nella direzione x = x’, le coordinate y e z si potrebbero allungare o accorciare. Capiamo benissimo che questo è un risultato del tutto assurdo, ma la matematica ci impone di essere rigorosi… Consideriamo, allora, il postulato di relatività e applichiamolo al caso in oggetto. Prendiamo la nostra asta rigida e mettiamola lungo l’asse y nel sistema di riferimento S. La sua lunghezza risulta essere uguale a 1. Come la vede l’osservatore in S’? Basta usare la formula precedente che ci porta a:

y’ = b₂∙1

Ora prendiamo la stessa asta rigida di lunghezza unitaria e la portiamo in S’ lungo l’asse y’. L’osservatore posto in S’ non può che concludere che questa asta ha lunghezza uno nel suo sistema di riferimento. Tuttavia, che cosa dice l’osservatore posto in S ? Utilizziamo nuovamente la formula precedente:

y = y’/b₂ = 1/b₂

Il primo postulato, però, non può che “arrabbiarsi”! Esso dice chiaramente che le misure devono dare risultati identici (siamo o non siamo in sistemi in moto rettilineo uniforme?). Se così non fosse i sistemi di riferimento non sarebbero fisicamente equivalenti, ossia non permetterebbero di descrivere nello stesso modo qualsiasi fenomeno fisico.

L’unico modo per cui questo possa succedere (senza fare arrabbiare il primo postulato) è che b₂ = 1/b₂ , ossia:

b₂ = 1

Analogamente, deve anche essere:

c₃ = 1

Tante parole per concludere, finalmente, che:

y’ = y

z’ = z     …. (4)

Le stesse relazioni descritte da Galileo.

Fermiamoci un attimo a riflettere. Avremmo facilmente potuto concludere subito che un moto lungo un asse cartesiano non può influire sulle coordinate perpendicolari. Quante volte è stata usata questa banale conclusione per dire che la contrazione della lunghezza avviene nel verso del moto? In realtà, si usa, spesso, uno spazio a una dimensione (cosa che noi abbiamo fatto e faremo in futuro) e quindi ciò comporta un’automatica ammissione delle (4).

Altre volte, si utilizzano ragionamenti semplicistici, tipo lo spazio è omogeneo e quindi y e z non possono variare dato che non subiscono l’influenza della velocità v, che si applica solo ai punti dell’asse x. Insomma, ne potete trovare di tutte e di più. E certi ragionamenti “sembrano” rendere più semplice la determinazione delle equazioni di Lorentz.

Non parliamo poi se le ricaviamo DOPO aver visto le conseguenze sperimentali dei postulati di Einstein. In realtà ce lo potevamo anche permettere, dato che l’importante è l’applicazione di qualcosa. Ancora più semplicemente, potevamo riportare le trasformazioni di Lorentz senza dimostrare come si ricavano. In fondo, la descrizione delle conseguenze sperimentali le avrebbero confermate.

Insomma, è una questione di … principio. Abbiamo cercato di usare la matematica e tutti i suoi risvolti decisamente diversi dalla fisica. Abbiamo anche visto, però, che il seguire la sua quasi paranoica ricerca di rigore formale ci ha fatto comprendere molte applicazioni fondamentali per la fisica (come i limiti e le derivate). Accettiamo, quindi, questo “noioso” utilizzo nella trasformazione di Lorentz come un dovuto contributo al linguaggio… della fisica. Poi, potremo anche dimenticarcelo, ma avremo senz’altro fatto una bella ginnastica  mentale.

Tuttavia, dato che per introdurre la matematica (e la sua ossessionante ricerca della perfezione) avevamo usato una linea ferroviaria (ricordate?), la proponiamo di nuovo per dare una spiegazione qualitativa della impossibilità di una contrazione o dilatazione delle componenti perpendicolari alla direzione del moto. Seguitemi senza preoccupazioni, dato che la logica è estremamente semplice.

Ragioniamo per assurdo. Ossia, ammettiamo che vi sia una contrazione delle dimensioni trasversali, quando il fenomeno è visto da un sistema in moto relativo. Immaginiamo che ci sia una lunga galleria nella nostra linea ferroviaria. Ammettiamo, ancora, che, per questioni di spesa, la galleria sia solo leggermente più larga dei vagoni del treno. Ossia, il treno ci passi giusto giusto.

Imponiamo la nostra “strana” legge: chi sta fermo nella galleria vede che le dimensioni trasversali del treno (ossia la sua larghezza e/o altezza) diminuiscono all’aumentare della velocità. Saremmo molto contenti: abbiamo speso poco e il treno, a causa della sua velocità, ci aiuta a non avere problemi di urti contro le pareti della galleria.

Purtroppo, la situazione è ben diversa per chi sta sul treno. Per lui è la galleria che si muove a velocità elevata e, quindi, deve valere la stessa regola che vale per il sistema di riferimento precedente (principio di relatività). In poche parole, le dimensioni della galleria (in senso trasversale alla direzione del moto) devono diminuire.

Accidenti, che disastro! La galleria si stringe sempre più e il treno non può che finire incastrato tra le sue pareti: una catastrofe dovuta solo e  soltanto all’aver voluto risparmiare  sulla spesa del tunnel!

No, non è possibile! Si ha un'assurdità perché non può capitare assolutamente che uno stesso fenomeno fisico avvenga (il treno si incastra nelle pareti) o non avvenga (i vagoni scorrono perfettamente) per due osservatori posti in sistemi di riferimento in moto rettilineo uniforme tra loro. I fenomeni fisici devono essere descritti nello stesso modo!

Otterremmo lo stesso risultato assurdo se  l’osservatore fermo in galleria vedesse il treno “allargarsi” al crescere della velocità. La catastrofe ci sarebbe solo per lui, dato che l’osservatore sul treno vedrebbe la galleria allargarsi senza alcun timore di “incastro”.

Insomma, scegliete voi la dimostrazione che preferite! Sia attraverso il rigore matematico sia attraverso il solito treno che viaggia verso l’infinito...

Torniamo alle (1), dato che, in fondo, siamo solo all’inizio. Il bello deve ancora venire!

Cominciamo con la relazione che lega t’ alle coordinate del sistema S. Essa vale:

t’ = d₁x + d₂y + d₃z + d₄t

Tuttavia, t’ non può dipendere dalle coordinate y e z. Se così fosse, un orologio posto in y e uno in – y (o in z e in –z’) segnerebbero ore diverse se visti da S’. Ma questo fatto va contro alla simmetria della situazione e, in particolare, contro l’omogeneità dello spazio. L’orologio posto in y e quello in y’ devono comportarsi allo stesso modo. Ne segue che d₂ = d₃ = 0. Ossia:

t’ = d₁x + d₄t

Consideriamo, adesso, la prima equazione:

x’ = a₁x + a₂y + a₃z + a₄t     …. (5)

Siamo proprio nella direzione del moto. Sappiamo che esso avviene con velocità v. Il che vuol dire che per x’ = 0 si deve avere x = vt. Le due relazioni devono essere la stessa cosa: una implica l’altra e viceversa. Vale perciò una relazione del tipo:

x’ = a₁(x – vt)   … (6)

Infatti, per x’ = 0 si ha anche x = vt e viceversa.

Automaticamente si dimostra che y e z non partecipano (come è ormai ovvio) alla trasformazione tra x e t (quindi a₂ = a₃ = 0).

Possiamo scrivere un’uguaglianza banale, ricordando la (5) e la (6):

x’ = a₁(x – vt) = a₁x + a₄t

Risolvendola si ottiene che:

a₄ = - a₁v

Possiamo, adesso, riscrivere le (1), imponendo i valori dei vari coefficienti trovati un po’ alla volta…

x’ = a₁x – a₁vt = a₁(x –vt)

y’ = y

z’ = z

t’ = d₁x + d₄t                       …. (7)

Beh… niente male, da 16 ci siamo portati a 3 coefficienti soltanto! E’ arrivato il momento di mettere in funzione il secondo postulato, quella della costanza della velocità della luce in qualsiasi sistema di riferimento.

Finalmente torniamo alla nostra cara amica “luce” e la trattiamo come un’onda sferica (ma anche come fotoni, tanto è lo stesso...). In realtà, a questo punto, date le relazioni tra y e y’ e tra z e z’, potremmo anche trattarla come un raggio o qualcosa del genere. Ma manteniamo il rigore formale fino in fondo! L’onda parte da O, quando O’ coincide proprio con lui. Una volta partita, l’onda deve essere trattata nello stesso modo nei due sistemi di riferimento, altrimenti il secondo postulato si arrabbierebbe non poco! Qual è il raggio della sfera? Bene è dato dalla distanza di ogni suo punto dall’origine degli assi, ossia:

x² + y² + z² = r²

ma anche da:

x’² + y’² + z’² = r’²

Il raggio non è altro che una distanza e quindi è una velocità moltiplicata per un tempo. Qual è, però, la velocità con cui si propaga l’onda? Beh… proprio c e questo valore DEVE essere lo stesso in entrambi i sistemi! Possiamo allora scrivere l’equazione della sfera come:

x² + y² + z² = c²t²     …. (8)

e anche:

x’² + y’² + z’² = c²t’²     …. (9)

Non ci resta che inserire le equazioni di trasformazione date dalla (7) nell’equazione (9):

a₁²(x –vt)² + y² + z² = c²(d₁x + d₄t)²

Sviluppiamo i calcoli e raccogliamo i termini in x², y², z², t² e xt:

(a₁² – c²d₁²)x² + y² + z² – 2(a₁²v + c²d₁d₄)xt = (c²d₄² – a₁²v²)t²

Questa equazione, però, deve essere uguale alla (8), dato che la sfera è quella che è.

Affinché ciò avvenga deve essere:

a₁² – c²d₁² = 1

a₁²v + c²d₁d₄ = 0

c²d₄² – a₁²v² = c²        …. (10)

Questo è un sistema di tre equazioni in tre incognite che si può risolvere in vari modi e con qualche trucchetto per sveltire i calcoli. Teoricamente, si potrebbe ricavare una variabile da una qualsiasi equazione in funzione delle altre due. Sostituire il risultato in un’altra equazione. Ricavare da questa una variabile in funzione dell’altra e poi, finalmente, sostituire il tutto nella terza equazione. Ormai, comparirebbe solo una variabile e si avrebbe il primo risultato. Poi con questo risultato in mano di andrebbe a ritroso ricavando la seconda e, infine, la prima variabile… Insomma, un grande confusione se detto a parole. Meglio passare ai fatti.

Potete svolgere il procedimento da soli come esercizio di pura matematica elementare. Se poi riuscite a trovare da soli qualche “trucchetto” (tipo moltiplicare una certa equazione per qualcosa e un’altra per qualcos’altro in modo da sommarle ed eliminare le parti uguali e di segno opposto) tanto meglio. Consideratelo un esercizio molto utile per prendere dimestichezza con la matematica. Fidatevi! Non è tempo perso e la passione per l’astrofisica e per la spiegazione del “tutto” si ottiene anche con questi lavori da “manovale”….

Le soluzioni sono:

a₁ = 1/(1 – v²/c²)^1/2

d₁ = - (v/c²) /(1 – v²/c²)^1/2

d₄ = a₁ = 1/(1 – v²/c² )^1/2              …. (11)

Infine, sostituendo questi coefficienti nella (7), si ottiene la trasformazione di Lorentz:

x’ = (x – vt)/(1 – v²/c²)^1/2

y’ = y

z’ = z

t’ = (t – vx/c²)/(1 – v²/c²)^1/2         …. (12)

Il rapporto v/c viene spesso indicato con β. La quantità ricorrente 1/(1 – v²/c²)^1/2  =  1/(1 –β²)^1/2   prende il celeberrimo nome di fattore di Lorentz. 

E’ bene ricordarcelo, dato che lo useremo spesso e volentieri

β = v/c

γ = 1/(1 –β²)^1/2   

Prima di passare alla verifica “pratica” e sperimentale della trasformazione (i tanto celebri effetti di dilatazione del tempo e di contrazione delle lunghezze), dobbiamo controllare che la (12) segua due regole fondamentali per la sua validità: (a) le equazioni devono valere anche invertendo S’ con S, (b) per velocità molto basse, devono ridursi alla trasformazione di Galileo.

(a) Basta ricavare x, y, z e t in funzione di x’, y’, z’ e t’, tenendo conto che la velocità v vale adesso –v, dato che se S’ si muove verso destra rispetto a S con velocità v, si ha che S si muove verso sinistra con velocità –v rispetto a S’. Il risultato sarà identico alle (12)… provare per credere!

(b) Dobbiamo metterci nelle condizioni in cui v << c  ed eseguire le relative approssimazioni. Sicuramente la quantità v²/c² tende a zero, così come v/c² e le (12) diventano:

x’ = (x – vt)/(1)^1/2

y’ = y

z’ = z

t’ = (t – v·0)/(1)^1/2

Ossia:

x’ = x –vt

y’= y

z’= z

t’ = t                     …. (13)

Le (13) rappresentano proprio la trasformazione di Galileo, che quindi può considerarsi più che sufficiente quando i sistemi di riferimento si muovono reciprocamente a velocità decisamente inferiore a quella della luce. In altre parole, basta lei per inviare una sonda in giro per il  Sistema Solare o per descrivere il mondo che riusciamo a toccare e a vedere…

Soffermiamoci a lungo a controllare la diversità effettiva tra il risultato di Galileo e quello di Einstein e cominciamo a notare come il tempo sia diventato una vera e propria coordinata come le altre. Facciamo anche caso che la quantità ct è una lunghezza, uno spazio, e che, quindi, si misura esattamente come la x, la y e la z. Se ponessimo c = 1 (prendessimo la velocità della luce come unità), ct si scriverebbe t e si misurerebbe in metri! Ci torneremo sopra a tempo debito, ma già potete intuire la rappresentazione di uno spaziotempo relativistico, in cui il tempo t scende a stringere la mano allo spazio s… Minkowski sta, infatti, già sogghignando!

Non ho inserito figure, dato che, in fondo, la figura è la stessa che è servita per la relatività galileiana: due sistemi in moto relativo (uniforme) con l’asse x coincidente con x’ (asse del moto) e gli assi x e y coincidenti con y’ e z’ che vengono trascinati solidalmente… La vera differenza è che un fotone che parte da O, quando coincide con O’, si muove con la stessa velocità c nei due sistemi. In ogni istante le distanze del “fotone” dalle origini dei due sistemi di riferimento è sempre data da ct e da ct’… Costruitevela da soli… è veramente immediata.

Questo articolo sembra semplice (e lo è), ma -come già detto- va digerito molto bene prima di passare agli effetti relativistici ed essere sicuri di affrontarli nel migliore dei modi.

Riflessioni

Abbiamo ricavato le equazioni di Lorentz, che Einstein ha usato per rappresentare il legame che esiste tra spazio e tempo in due sistemi in moto relativo. Il tempo è una coordinata non più assoluta, ma si abbraccia costantemente con la x (direzione del moto) e vale, ovviamente, il viceversa. Che questo capiti lo si vede benissimo dalla prima e dall’ultima equazione delle trasformazioni di Lorentz.

Qualcuno potrebbe dirmi: “Ma capitava già per la trasformazione di Galileo… Anche in quel caso la coordinata x’ era legata alla x attraverso la velocità v e il tempo t, infatti x’ = x – v t ”. Non facciamoci ingannare: vt = s e, quindi, la relazione si riduceva a x’ = x – s, del tutto indipendente dal tempo. In altre parole, il tempo era assoluto e non mutava da un sistema di riferimento a un altro. Il tempo viveva una sua vita indipendente, del tutto estranea a cosa stessero facendo i sistemi di riferimento. Dava il suo contributo alla velocità, ma lo faceva sempre  nello stesso identico modo senza guardare in faccia nessuno.

Nelle equazioni di Lorentz le cose sono nettamente diverse: il legame tra x e t è ben più profondo e il tempo è costretto a cambiare se osservato da diversi sistemi di riferimento. Ci torneremo sopra ancora molte volte, ma cerchiamo fin da subito di non farci ingannare dalla solita frase: “Per chi viaggia più velocemente il tempo rallenta!”. Questa frase comporterebbe immediatamente la soluzione “apparente” del paradosso dei gemelli. Infatti: se vado più veloce invecchio di meno…

No, stiamo commettendo una serie di terribili errori! Innanzitutto, per chi viaggia velocemente il tempo NON rallenta assolutamente, il suo orologio gira sempre allo stesso modo. E’, invece, esatto dire che il suo orologio gira più lentamente quando viene visto da un osservatore in quiete rispetto a lui. La differenza dei tempi ha senso solo se si confrontano tempi che scorrono in diversi sistemi di riferimento, ma che sono osservati da un solo sistema di riferimento. L’orologio  di un certo sistema di riferimento  S gira in modo diverso per ogni altro sistema che si muova rispetto a lui. Esistono quindi infiniti movimenti del suo orologio quanto sono infiniti i sistemi di riferimento che si muovono di moto rettilineo uniforme rispetto a lui.

L’unica cosa che possiamo già azzardarci a dire (e ci torneremo presto) è che il tempo che S  misura sul suo orologio è sicuramente il più breve tra tutti quelli che gli vengono attributi dagli altri viaggiatori. Gli altri lo troveranno sempre più lento di quanto non sia il tempo misurato sul loro orologio, che è, però, identico a quello che misura il sistema di riferimento S  sul suo orologio.

Non ha alcun senso confrontare tempi misurati su sistemi di riferimento diversi. Innanzitutto, perché non potrebbe mai essere fatto! Come fare, infatti a essere presente contemporaneamente sia nel sistema esterno che in quello in moto? Dovremmo o fermare quello in moto oppure muoverci e raggiungerlo. I entrambi i casi, tuttavia, alla fine, vedremmo orologi che camminano allo stesso modo, dato che siamo ormai nello stesso sistema di riferimento: la velocità relativa è uguale a ZERO.

Quindi è tutta un’apparenza? Non c’è niente di vero nella differenza dei tempi e delle lunghezze? Beh, se rimaniamo nella relatività ristretta potremmo anche dire di sì, dato che se io viaggio con una certa velocità rispetto a un sistema, anche lui viaggia con una certa velocità rispetto a me e quindi vi è una perfetta simmetria: io posso dire che il suo tempo sembra rallentare, ma lui può dire che è il mio tempo che sembra rallentare. E abbiamo entrambi ragione, come ci dice perfettamente la trasformazione di Lorentz che può essere invertita tra i due sistemi con la sola accortezza di cambiare v in –v.

In realtà, però, le cose vanno in modo ancora diverso: vi è veramente una dilatazione dei tempi per un viaggiatore spaziale (anche se di tipo simmetrico) quando viene osservato da un altro. Lo è a tal punto che se lui tornasse a casa sarebbe decisamente più giovane del fratello gemello. Siamo quindi sicuri che viaggiando più veloci, il tempo scorre più lentamente per un osservatore esterno che guarda il viaggiatore, ma la simmetria della relatività ristretta ci assicura che è impossibile dato che per colui che viaggia siamo noi a muoverci con velocità uguale e contraria e quindi ad avere orologi che girano più lentamente.

Proprio qui nasce il paradosso dei gemelli: il rallentamento visto da fuori è giusto e REALE per entrambi, ma alla fine uno solo è veramente invecchiato di più. Come già abbiamo visto (e ci torneremo ancora sopra) questa assurdità nasce dal fatto che per confrontare gli orologi, REALMENTE nello stesso sistema di riferimento, uno dei due sistemi deve accelerare o decelerare e quindi cadono i principi della relatività ristretta e si deve entrare nella relatività generale.

Per i nostri scopi attuali, quindi, cerchiamo di non confondere le cose. Noi stiamo assistendo a legami tra spazio e tempo e alle loro deformazioni che sono sicuramente reali, ma che esistono solo se osservate da un unico sistema di riferimento. L’osservatore terrestre T può misurare un fenomeno attraverso il suo orologio e attraverso quello dell’astronauta visto da T. Solo in queste condizioni vede una diversità nei due tempi. Non pensiamo assolutamente che l’orologio di chi viaggia cammini intrinsecamente in modo diverso da quello di chi osserva da fuori. Fosse così non avremmo una teoria della relatività, dato che essa dice proprio che ciò che capita è relativo al sistema in cui si osserva.

Questa differenza che sembrerebbe solo apparente e poco importante è invece fondamentale per l’osservazione dell’Universo. Lo abbiamo già visto nella relatività della simultaneità, da cui, in pratica, deriva tutto il resto. In altre parole, senza tener conto della relatività ristretta non saremmo capaci di descrivere ciò che osserviamo realmente nello spazio (anzi spaziotempo), dato che saremmo sconvolti da assurdità verificabili direttamente. E questo vale comunque, anche lontano da masse tali da introdurre accelerazioni, ossia dal regno della relatività generale. La relatività ristretta è di per sé rivoluzionaria anche se trascura le masse e le loro azioni a distanza. Va quindi perfettamente compresa, e … DISEGNATA, per poter effettuare il passo successivo, dove la gravità entrerà in gioco a piedi uniti.

Qualche piccola modifica

Spero di non aver confuso le idee invece di chiarirle… In ogni modo, torniamo alla nostra trasformazione di Lorentz e vediamo di modificarla per meglio capire la sua importanza decisiva. Quanto detto sopra lo ritroveremo e lo capiremo meglio andando avanti.

Cosa vogliamo dimostrare, in particolare? Solo e soltanto che il tempo può tranquillamente diventare una coordinata uguale alle lunghezze x, y e z. Se riusciamo a fare ciò, abbiamo in mano la possibilità di trattare il tempo come la coordinata x, ad esempio, quella che indica il verso del moto.

Spazio e tempo per me pari sono

Le conseguenze sono enormi: come possiamo considerare punti di ascissa negativa e positiva, così possiamo trattare punti con tempo negativo e positivo, ossia eventi del passato e del futuro. Qui sta proprio la grandezza della rappresentazione spaziotemporale di Minkowski. Entriamo veramente nelle quattro dimensioni, dove le coordinate x, y, z, t diventano coordinate misurate con la stessa unità di misura, quella spaziale. I “punti” diventano “eventi”, ma possono essere trattati con le stesse regole geometriche. E vedremo che, con qualche accorgimento, si può benissimo estendere il teorema di Pitagora alle quattro coordinate (tranne tener conto di qualche segno…).

Riscriviamo la trasformazione di Lorentz e usiamo i simboli delle grandezze adimensionate che abbiamo definito come γ e β (le formule diventano più maneggiabili).

x’ = (x – vt)/(1 – v²/c²)^1/2

y’ = y

z’ = z

t’ = (t – vx/c²)/(1 – v²/c²)^1/2    …. (1)

 

β = v/c

γ = 1/(1 – β²)^1/2     …. (2)

Attraverso le (2), le (1) diventano:

x’ = γ(x – vct/c) =  γ(x – βct)

y' = y

z’= z

t’ = γ(t – βx/c)                            …. (3)

Anche se abbiamo ottenuto delle relazioni molto più compatte, ci accorgiamo che la prima e l’ultima hanno ancora dimensioni fisiche diverse. Non è un grave problema e possiamo facilmente superarlo proprio perché ormai abbiamo le relazioni che legano spazio x e tempo t, ossia esse non sono più variabili indipendenti.

Decidiamo, allora, di definire un nuovo tempo

T = ct

esso ha proprio la le dimensioni di una lunghezza che si può misurare in metri (ad esempio).

La nuova unità di tempo T = 1 m, è legata al tempo t espresso in secondi dalla relazione 1 m = c t, da cui si deduce t = 1 m / (300000000 m/s ). La nuova unità “metrica” di tempo corrisponde al tempo che occorre alla luce per percorrere uno spazio di un metro. Un tempo T di 300 000 km corrisponde, quindi, a un secondo.

Attenzione: in tale sistema di unità, la velocità di un corpo è il rapporto fra uno spostamento (in metri) e il tempo (anch’esso espresso in metri), ossia non è altro che il parametro adimensionale β.

Facilissimo da dimostrare:

v = ds/dT =ds/(cdt ) = (1/c) ds/dt = v/c = β.

Ricordiamoci, sempre, che tutto ciò può essere ottenuto perché la velocità della luce è una costante.

In questo sistema, la velocità della luce diventa c =1.

Sostituendo t = T/c e t' = T'/c nelle (3), esse si riducono a espressioni del tutto simmetriche nello scambio di x con t e x' con t':

x’ = γ(x – βct) = γ(x – βT)

y' = y

z’= z

T’ = cγ(T/c – βx/c) = γ(T – βx)      …. (4)

La prima e l’ultima sono esattamente la stessa relazione a patto di sostituire la x con la T . Il tempo è veramente diventato una lunghezza a tutti gli effetti.

Notate che potevamo anche lavorare al contrario, ossia trasformare le unità di misura di lunghezza in unità di tempo. Lasciavamo l’unità di tempo pari a 1 secondo e avremmo ottenuto qualcosa di ben conosciuto a tutti noi: il secondo luce. Infatti, esso non è altro che lo spazio percorso dalla luce in un secondo, ossia 300 000 km.

Chi si sente disorientato dall’uso di un tempo misurato in metri, pensi a quante volte ha già usato la distanza misurata in secondi (o anni o miliardi di anni): quella stella ha una distanza di x anni luce. E’ del tutto analogo al dire che un intervallo di tempo tra due eventi è pari a x metri. La prima non vi spaventa e la seconda sì? Basta rifletterci sopra e vedrete che ha la stessa difficoltà concettuale.

Cosa abbiamo imparato con queste semplici trasformazioni di variabili? Che è possibile disegnarle, con le stesse regole, in uno spaziotempo a quattro dimensioni e misurarle con la stessa unità di misura! Vi sembra poco? Se poi, ci ricordiamo che y e z si trasformano in loro stesse, risulta immediato che l’intero spaziotempo a quattro dimensioni può essere schematizzato facilmente sul piano del foglio, a due dimensioni, dato che non avviene nessuna deformazione nelle due coordinate rimanenti.

Torniamo alla trasformazione “canonica” e vediamo di ricavare, direttamente da lei, quali sono i fenomeni apparentemente assurdi che riesce a produrre. Già sappiamo che un sistema in movimento pone non pochi problemi alla sincronizzazione degli orologi che sembra giusta o sbagliata a seconda di dove si cerchi di verificarla. Non possiamo, perciò, stupirci più di tanto se il tempo e lo spazio diventano qualcosa di … relativo.

Due fattori fondamentali

Prima di partire in quarta, è utile prendere maggiore dimestichezza con i due parametri adimensionali β e γ che abbiamo introdotto la volta scorsa. Essi sono fondamentali per capire al meglio a cosa si va incontro. Il primo ci dice chiaramente quanto sia veloce il nostro sistema di riferimento che si muove di moto rettilineo uniforme rispetto a un altro. Infatti, non è altro che il rapporto tra la velocità relativa e quella della luce. E’, allora, interessante vedere come γ, molto meno intuitivo, varia in funzione di β. Potrebbe essere un semplice esercizio di studio di funzione dato che abbiamo:

γ = 1/(1 – β²)^1/2

dove β fa la parte della x e γ quella della y. E’ una funzione che vede una radice quadrata, in cui compare il quadrato di x, al denominatore. Stiamo parlando di relatività ristretta e sembrerebbe puerile parlare di funzioni elementari, ma noi cerchiamo di non perdere mai di vista una visione globale di ciò di cui discutiamo. Invito, perciò, chi vuole imparare meglio il calcolo delle derivate, di trovare i possibili massimi e/o minimi della funzione.

A noi interessa mostrare il risultato finale per avere un’idea di come il parametro γ vari con β, ossia con la velocità del moto relativo riferita alla costante c (velocità della luce). Per semplicità, possiamo considerare solo valori positivi di v (il risultato non cambia per valori negativi, dato che la velocità compare al quadrato). Il valore minimo di v è quindi ZERO, ossia abbiamo sistemi fermi uno rispetto all’altro. Per v = 0, anche β = 0 e γ = 1. Il valore massimo “plausibile” per v è dato da c, ossia β = 1. Questo valore comporta γ = + ∞. La funzione, perciò, tende a infinito (positivo) per v che tende a c. La curva risultante è riportata in Fig. 22.

Si nota molto bene che per valori anche grandi di v (e quindi di β) il valore di γ si discosta poco da 1. In altre parole, guardando la trasformazione di Lorentz relativa alla x, si ha che x’~ x – vt, ossia si ricade nella trasformazione galileiana.

La fisica di tutti i giorni, quella che ci circonda, si svolge praticamente tutta in questo ambito. Pensiamo a un aereo supersonico che viaggi a 3600 km/h, ossia 1 km/sec. Niente male anche per l’uomo “normale” del 2015. Eppure, in questo caso avremmo β = 1/300 000 = 0.00000333... che porta a un valore di γ = 1.0000000000055. Pochi strumenti potrebbero rendersi conto della differenza tra questo valore e quello “galileiano” perfettamente uguale a 1.

Per valori di v prossimi a quelli della luce, però, γ parte come una “scheggia” e tende rapidamente a infinito. Per v > c (valore  matematicamente plausibile) avremmo una radice quadrata negativa e γ perderebbe di significato. La faccenda non ci disturba affatto, dato che nessun corpo dotato di massa può raggiungere o superare la velocità della luce. La figura precedente ci mostra matematicamente che la velocità della luce è un limite insuperabile.

Tuttavia, l’intero microcosmo, il “nocciolo” concettuale di tutta la fisica macroscopica, vive muovendosi a velocità molto prossime a c. Ne segue che la relatività ristretta è fondamentale per descriverlo correttamente. Oggi che siamo capaci di arrivare vicino a c anche nei laboratori terrestri, la relatività ristretta diventa dominatrice di moltissimi fenomeni, insieme alla sua sorella maggiore (la relatività generale) e alla nuova e scomoda arrivata (la meccanica quantistica). Insomma, per vedere veramente in grande bisogna guardare sempre più verso il piccolo. E dispiace sempre di più che per sentir parlare di questi tre "giganti" della fisica è necessario, spesso, arrivare all'Università...

Applichiamo la trasformazione

Bando alle “ciance” e torniamo alla nostra trasformazione e ai suoi effetti più evidenti. Teniamo ben presente il legame tra v/c e il fattore di Lorentz, dato che β ci dice praticamente la velocità a cui viaggia il sistema in movimento relativo e γ ci quantifica i suoi effetti sul tempo e la lunghezza.

Consideriamo, in Fig. 23, un sistema di riferimento S’ di origine O’. Poniamo un bell’orologio C’ su di esso, a una distanza fissa x₁’ dall’origine.

Facciamolo partire e guardiamolo girare. L’orologio, trovandosi sempre nella stessa posizione rispetto all’origine, segnerà esattamente il tempo misurato in quel punto. Vi sembra che stia dicendo una banalità quasi ridicola? Bene, pazienza… ma teniamola bene a mente: stiamo misurando un tempo sempre dallo stesso punto fisso, quello in cui si trova l’orologio. Segniamo l’ora in un dato momento t₁’.  Lasciamolo girare per qualche minuto e leggiamo di nuovo l’ora: essa è quella relativa al tempo t₂’. Attenzione: sia t₁’ che t₂’ sono stati misurati, con lo stesso orologio, sempre nello stesso punto, quello in cui si trova l’orologio. Non vi è stato bisogno di eseguire nessuna sincronizzazione. In altre parole sia t₁’ che t₂’ sono stati misurati nella posizione fissa  x₁’ del sistema S’. La differenza tra i due tempi misurati in questo modo (ossia lo scorrere del tempo misurato su uno stesso orologio in uno stesso punto) lo indichiamo in un modo speciale, ossia:

Δt_P = t₂’ – t₁’

Scendiamo dal sistema S’ e portiamoci su un altro sistema S di origine O (Fig. 24).

Lungo l’asse x di S si sono posizionati moltissimi orologi, tutti sincronizzati tra loro (ma sappiamo quanto la sincronizzazione sia relativa…). Ci accorgiamo che , in realtà, il sistema S’, in cui avevamo misurato quel tempo così speciale, è in movimento rispetto a S con velocità uguale a v. Da questa posizione “esterna”  vediamo passare l’orologio C’ nel punto di coordinate x₁ (del sistema S). Quando C’ segna t₁’, viene misurato il tempo t₁ attraverso l’orologio C₁ posizionato in x₁. Il tempo passa e il sistema S’ con il suo orologio C’ scorre verso destra rispetto a S. Nel momento in cui l’orologio C’ segna il tempo t₂’, utilizziamo l’orologio C₂ posto nella posizione x₂ per misurare t₂. Attenzione! Ci siamo fidati ciecamente della sincronizzazione dei due orologi C₁ e C₂ posti in due punti x₁ e x₂, diversi, del sistema S.

Tuttavia, sappiamo che questa sincronizzazione non è valida per tutti i sistemi in movimento tra loro… Ne vediamo subito gli effetti, utilizzando la trasformazione tra t e t’ che abbiamo ricavato solo e soltanto attraverso i postulati di Einstein. Ribadiamo ancora la netta differenza tra i tempi t₁’ e t₂’, misurati sullo stesso orologio posto sempre nello stesso punto x₁’ del sistema S’ e i tempi t₁ e t₂, misurati  su due orologi diversi posti in punti diversi del sistema S.

Questo è il punto fondamentale della relatività ristretta, espressa matematicamente dalla trasformazione di Lorentz.

Ricapitoliamo, facendo uscire allo scoperto la relazione che lega t e t’.

t’ = (t – vx/c²)/(1 – v²/c²)^1/2

Riferiamola al momento in cui l’orologio C’ segna t₁’ e  quello C₁, posto in x₁ segna t₁:

t₁’ = (t₁ – vx₁/c²)/(1 – v²/c²)^1/2     …. (1)

Riferiamola, adesso, al momento in cui l’orologio C’ segna t₂’ e quello C₂, posto in x₂ segna t₂.

t₂’ = (t₂ – vx₂/c²)/(1 – v²/c²)^1/2     …. (2)

Per vedere come scorre il tempo non dobbiamo fare altro che fare la differenza tra la (2) e la (1)

t₂’ - t₁’ = (t₂ – vx₂/c² – t₁ + vx₁/c²)/(1 – v²/c²)^1/2  = ((t₂ - t₁) – v(x₂ – x₁)/c²)/(1 – v²/c²)^1/2

Chiamiamo Δx la differenza tra x₂ e x₁ e Δt la differenza tra t₂ e t₁ (misurati con orologi diversi posti in punti diversi). Δt_P sappiamo già cos’è.

Δt_P = (Δt – vΔx/c²)/(1 – v²/c²)^1/2

Ma  Δx = vΔt , per definizione di velocità costante misurata nel sistema S.

E, quindi:

Δt_P = (Δt – Δt v²/c²)/(1 – v²/c²)^1/2  = Δt (1 –v²/c²)/(1 – v²/c²)^1/2 = Δt (1 – v²/c²)^1/2

E, infine:

Δt = Δt_P/(1 – v²/c²)^1/2 = γ Δt_P

Ossia:

Δt = γ Δt_P            …. (3)

Fantastico e semplicissimo risultato: la differenza di tempo misurato attraverso i due orologi posti in punti diversi di S è legata alla differenza di tempo, misurata attraverso un unico orologio posto nel punto fisso x’ di S’, solo attraverso il fattore di Lorentz!

Il tempo proprio non cambia

Sappiamo, però, benissimo che il fattore γ rimane sempre maggiore di 1, a mano a mano che la velocità relativa aumenta. Questo vuol dire che il tempo segnato da un orologio che si muove con velocità v appare andare sempre più lento rispetto a quello misurato dagli orologi posti in un sistema che si considera fermo. Facciamo attenzione che la stessa identica cosa accadrebbe se S’ si considerasse fermo e volesse misurare il tempo che scorre sul sistema S in movimento con velocità –v rispetto a lui. In queste condizioni l’orologio fisso sarebbe quello in S e gli orologi differenti apparterebbero a S’. A S’ sembrerebbe che il tempo di S scorra più lentamente del suo. Esattamente la stessa cosa che dice S. La trasformazione è sempre la stessa, con l’accortezza di cambiare v in –v.

Proprio da questa simmetria, insita nella relatività ristretta, nasce il ben noto paradosso dei gemelli.

Per comprenderne appieno il significato, ripetiamo ancora il risultato ottenuto: l’intervallo di tempo Δt che viene misurato nel sistema di riferimento in cui l’orologio C’ viene visto muoversi con velocità v è sempre maggiore del valore Δt_P misurato dall’orologio C’. Questo risultato è quello che viene comunemente chiamato dilatazione relativistica del tempo.

Come già accennato, c'è una differenza sostanziale fra gli intervalli di tempo Δt_P  e Δt che appaiono nella (3). L'intervallo di tempo Δt_P, infatti, è il tempo misurato da un unico orologio C’ e, quindi, non è in nessun modo influenzato dalle procedure di sincronizzazione. Questo tempo è, quindi,  una grandezza fondamentale  di tutta la teoria e viene chiamato  TEMPO PROPRIO. L'intervallo di tempo Δt, invece, è quello misurato da due orologi diversi (C₁ e C₂), posti in punti diversi di posizione x₁ e x₂, e, quindi, dipende fortemente da come gli orologi del sistema S sono stati sincronizzati fra di loro.

Non dobbiamo, perciò, travisare il concetto di tempo dilatato per chi viaggia a una certa velocità v rispetto a noi. Il suo tempo, misurato all’interno del sistema, è quello proprio. Esso appare scorrere più lentamente solo se “osservato” dal nostro sistema di riferimento che lo vede muoversi con velocità v. Questo effetto appare identico a quello che misura un osservatore del sistema S’ mentre ci vede muovere con velocità uguale e opposta –v.

A questo punto, si capisce molto bene perché è stato più giusto iniziare con il concetto di sincronizzazione degli orologi su un certo sistema di riferimento e della sua relatività rispetto a sistemi in moto tra di loro. Ciò ci ha indotto a pensare che il tempo non potesse essere assoluto ma relativo. Attraverso l’utilizzo dei soli postulati di base abbiamo ricavato la trasformazione di coordinate che lega i due sistemi di riferimento. L’abbiamo infine applicata a un caso reale, verificando matematicamente il concetto che la sincronizzazione relativistica ci aveva suggerito.

Il semplice fatto che v = x/t ci dice subito che se t è relativo al sistema di riferimento e v è una costante, deve essere relativa anche la lunghezza x. Lo vedremo tra breve…

L'asta si contrae

Partendo dalla trasformazione di Lorentz l’effetto di contrazione delle lunghezze diventa un fenomeno estremamente interessante -e semplice- dal punto di vista della logica. Gli orologi sistemati in un sistema di riferimento (e sincronizzati tra loro) permettono di afferrare perfettamente l’effetto della contrazione della lunghezza di un’asta rigida in movimento rispetto al sistema in cui si effettua la misura.

Consideriamo la Fig. 25. In alto abbiamo un sistema S’ di origine O’. Su di esso non abbiamo bisogno di usare orologi sincronizzati, dato che abbiamo già stabilito la lunghezza effettiva di un asta rigida. La sua lunghezza è  L₀ = x₂’ – x₁’. Come detto, può essere misurata tranquillamente attraverso il metro campione che è solidale con il sistema.

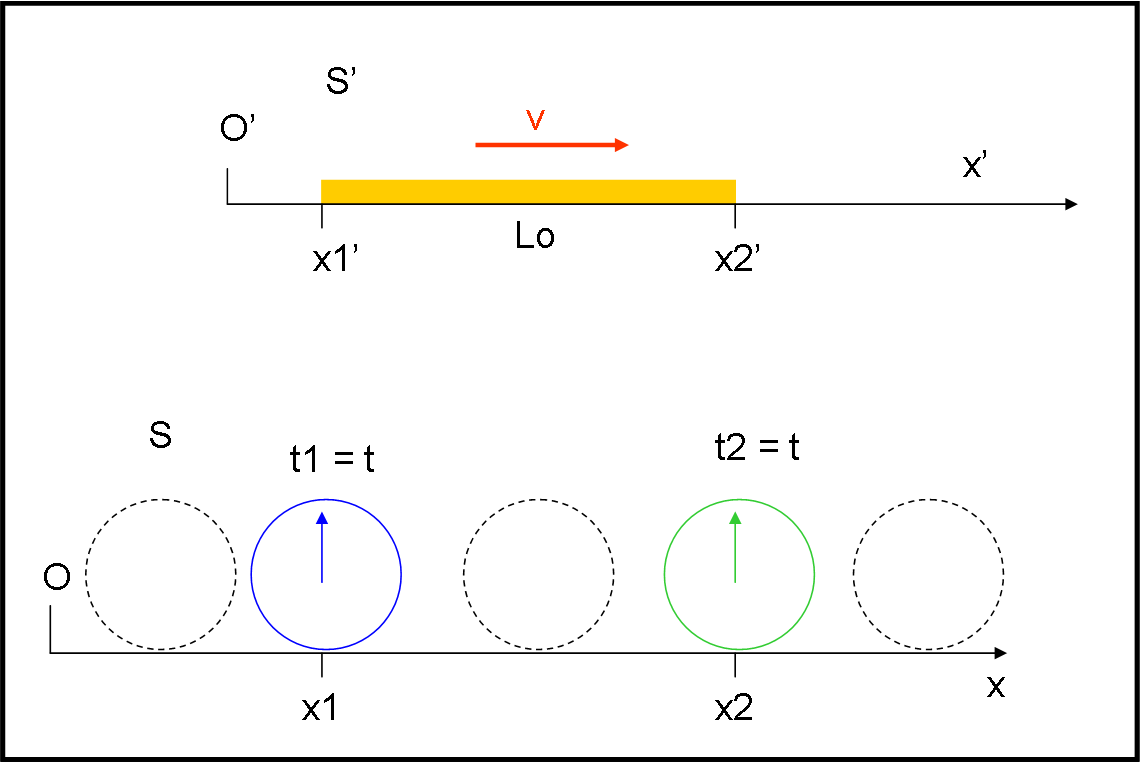
Mettiamo in moto il sistema S’ con velocità v rispetto a un sistema S di origine O. Lungo tutto il sistema S sono posti orologi sincronizzati, che quindi segnano la stessa ora. Per misurare la lunghezza dell’asta basta utilizzare i due orologi che vedono passare i due estremi dell’asta nello stesso istante t. Se gli orologi sono ovunque ciò è sempre possibile, dato che esiste sicuramente un orologio  che è posto esattamente nel punto in cui passa il limite sinistro e uno che è posto esattamente nel punto in cui passa il limite destro dell’asta in movimento con S’. Le posizione di questi due orologi siano x₁ e x₂, nel sistema S. Ovviamente, per come è stato effettuata la misura, t₁ = t₂ = t.

A questo punto, non ci resta che considerare la prima delle equazioni della trasformazione di Lorentz, quella che lega x a x’.

x’ = (x – vt)/(1 – v²/c²)^1/2

Applichiamola alla posizione dei due estremi dell’asta. Nel sistema S’, la posizione dell’estremo sinistro è x₁’, mentre nel sistema S è x₁. L’estremo destro ha ascisse x₂’ e x₂, rispettivamente. Il tempo misurato in x₁ e x₂, come già detto, deve essere lo stesso, per definizione, ossia t₁ = t₂ = t. Nell’equazione non compare assolutamente il tempo t’ misurato su S’ (la misura della lunghezza L₀ non ne ha avuto bisogno). La velocità di S’ rispetto a S sia, come al solito, v.

x₁’ = (x₁ – vt)/(1 – v²/c²)^1/2

x₂’ = (x₂ – vt)/(1 – v²/c²)^1/2

Sottraendo la prima equazione dalla seconda, si ha:

x₂’ – x₁’ = (x₂ – x₁)/(1 – v²/c²)^1/2

Ma x₂’ – x₁’ è proprio la lunghezza L₀ dell’asta, misurata in S’, mentre x₂ – x₁ è la lunghezza L dell’asta, misurata da S:

L₀ = L /(1 – v²/c²)^1/2

Ossia:

L = L₀/γ     …. (1)

Essendo 1/γ  sempre minore di 1, possiamo concludere che la lunghezza di una asta in movimento con velocità v rispetto a un sistema S, viene “contratta” se misurata da S. La contrazione avviene nella direzione del moto.

Dobbiamo notare che anche questa volta c'è una differenza sostanziale fra L₀ e L. Infatti, L₀ rappresenta la lunghezza dell’asta misurata nel riferimento in cui essa è ferma. La sua lunghezza viene misurata confrontandola con il metro campione e non ha bisogno di nessun orologio.

Non confondiamoci, mi raccomando. Se la stessa asta fosse stata messa nel sistema S, la sua lunghezza sarebbe rimasta L₀, dato che sarebbe ferma in questo sistema. L₀, quindi, rappresenta la lunghezza di un asta, in qualsiasi sistema essa venga posta, a patto di misurarla in quel sistema. Questa lunghezza, similmente a quanto fatto per il tempo, viene chiamata LUNGHEZZA PROPRIA (o a riposo). L, invece, è una misura effettuata mentre l’asta si muove, utilizzando due orologi posti in posizioni diverse, anche se sincronizzati. L rimane quindi influenzata dalla sincronizzazione degli orologi effettuata su S, ossia nel sistema in cui è misurata.

Proprio per  il principio di relatività, essendo i due sistemi equivalenti, se la stessa asta viene posta nel sistema S, l’osservatore che si muove con velocità v arriva alla stessa identica conclusione, ossia la lunghezza dell’asta appare contratta come dice la (1).

Ricavata in questo modo, la contrazione delle lunghezze diventa di estrema ovvietà. A patto di aver utilizzato i postulati di Einstein per scrivere la trasformazione di coordinate.

Non vi è ovviamente bisogno di ripetere che la contrazione avviene solo nella direzione del moto, dato che abbiamo già dimostrato che la y e la z non subiscono alterazioni. L’altezza di un asta appare sempre la stessa a qualsiasi velocità vada, rispetto a un altro sistema di riferimento.

Tutto ciò che abbiamo ricavato finora sulla dilatazione dei tempi e sulla contrazione delle lunghezze, può essere dimostrato in modo molto più diretto e intuitivo, attraverso pochi e semplici grafici. Perché, allora, costringervi a trafficare con equazioni e con formule più o meno complicate e monotone? Presto detto. Innanzitutto, perché solo così si capiscono  molto bene le ipotesi di partenza di Einstein; inoltre, si deve comprendere che esiste una trasformazione di coordinate, che coinvolge anche il tempo, in grado di sostituirsi  a quella di Galileo e Newton. Essa rappresenta la realtà globale, di cui quella galileiana è solo una prima approssimazione, validissima per le velocità con cui l’uomo si scontra tutti i giorni. Guardando, però, le stelle e le particelle che vengono scaraventate verso di noi, non si può più fare a meno di una legge che le inglobi nello stessa visione d’assieme. Solo con questa nuova trasformazione sarà “facile” disegnare compiutamente lo spaziotempo.

Orologio a luce

Introduciamo, allora, un orologio molto semplice il cui tic-tac è veramente rapidissimo. Lo chiamiamo orologio a luce.

Per costruirlo abbiamo solo bisogno di due specchi piani e di una lampadina che invii un impulso luminoso in un certo istante. Dopo, possiamo tranquillamente spegnerla. I due specchi sono sistemati uno di fronte all’altro “in verticale”, in modo che il movimento della luce avvenga lungo l' asse y. La lampadina che invia la luce è posta al centro dello specchio A. A noi interessa solo ciò che fa la luce emessa a un certo istante t. Essa si dirige verso lo specchio B e poi torna indietro, riflettendosi, per colpire di nuovo lo specchio A. Nuova riflessione e via dicendo. Un’operazione semplicissima che conosciamo molto bene anche attraverso la QED.  La distanza tra i due specchi sia, ad esempio, L₀ = 1 m. La luce viaggia a circa 300 000 km/sec, il che vuol dire che per andare da A a B e tornare in A il tempo è stato solo di 6.6 10^-9 sec. Questo può essere considerato il tic-tac dell’orologio. Il tic è da A a B e il tac da B ad A. Avevo o non avevo ragione a dirvi che il tic-tac era rapidissimo? La Fig. 26 illustra l’orologio a  luce.

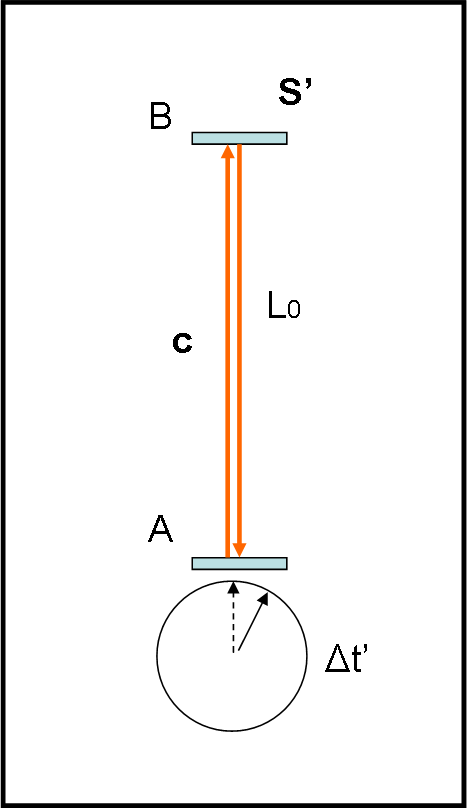
Tutto queste banali operazioni le abbiamo fatte su un sistema di riferimento S’. Il nostro orologio è solidale con questo sistema e i tempi di partenza e di arrivo della luce sono misurati, ovviamente, con lo stesso orologio. I due specchi e l’impulso di luce sono, infatti, veramente un orologio, in quanto basterebbe inserire un contatore in A che segnali ogni arrivo della luce e che, quindi, scandisca il tempo ogni 6.6 10^-9 secondi (o quello che scegliamo, cambiando la distanza L₀). O, se preferite, che ad ogni arrivo della luce in A faccia girare di una certa quantità costante una lancetta.

Il tempo tra l’invio della luce e il suo ritorno in A è quindi un tempo proprio, ossia misurato in un sistema di riferimento con un solo orologio. Possiamo facilmente scrivere una formula che lo rappresenti e che si basi su due grandezze costanti per definizione: la distanza tra i due specchi L₀ e la velocità della luce c. Il tempo necessario per andare da A a B non è altri che la lunghezza L₀ divisa per la velocità c (la velocità costante non è altro che lo spazio diviso per il tempo), ossia:

t’_B – t’_A = L₀/c

t₁’_A – t'_B = L₀/c

Dove t₁’_A è l’istante di ritorno in A, mentre t’_B è sia il momento di arrivo della luce in B che il momento della sua riflessione (è lo stesso identico evento). Indichiamo t’_1A– t'_A come Δt’ (dato che si riferisce al sistema S’ e indica il battito costante dell’orologio). Possiamo quindi scrivere che:

Δt’ = 2L₀/c        …. (1)

Un orologio fantastico, estremamente preciso, almeno per chi vive su S’…

Vediamo, adesso, cosa succede se il sistema S’, e con lui l’orologio, è in moto con una certa velocità v rispetto a un sistema S. Scendiamo da S’ e guardiamo l’orologio dal sistema “fermo” S.

La figura da considerare è, adesso, la Fig. 27. Il movimento di S’ rispetto a S avviene lungo l’asse x, come al solito. La luce parta da A, ma, mentre viaggia verso l’alto, gli specchi si muovono solidalmente con il sistema S’. Quando la luce partita da A raggiunge B, questo si è spostato rispetto alla posizione che aveva al momento della partenza dell’impulso di luce. Esso si trova in B₁ corrispondente al punto A₁. La luce torna indietro, ma il movimento continua e ritorna in A quando questo specchio si è ormai portato in A₂.

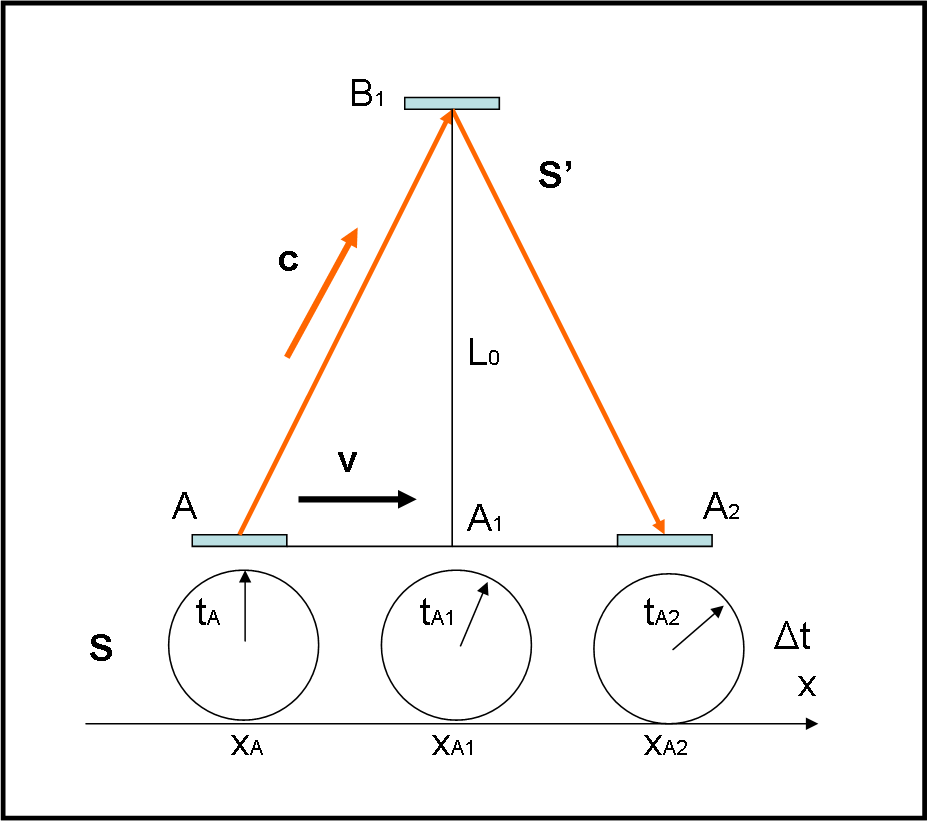
Fermiamoci un attimo per dimostrare esattamente la plausibilità di questa serie di eventi. Qualcuno potrebbe dire: “Perché mai devo considerare un raggio luminoso che viaggia da A a B₁? La luce viaggia in verso verticale e non obliquo…”. Questa è una domanda che molti si fanno, ma che spesso “non si osa”  esporre… E, invece è una domanda molto istruttiva perché ci riporta al postulato che dice che ogni fenomeno fisico deve essere identico se osservato in sistemi in moto uniforme tra loro. Non è molto diverso dall’uomo che versa l’acqua in un bicchiere a terra o su una nave, nella relatività galileiana.

Un “osservatore” nel nuovo riferimento deve sempre  vedere il fascio di luce che parte dallo specchio inferiore, batte su quello superiore e torna di nuovo nello specchio inferiore (la coincidenza del fascio con i vari specchi, nei vari istanti, è un fatto fisico e deve essere uguale per tutti gli osservatori). In poche parole, la luce deve andare da A a B₁ e poi da B₁ ad A₂.

Assodato questo fatto, consideriamo un'altra conseguenza della trasformazione di Lorentz. La distanza L₀ è diretta lungo l’asse y e sappiamo benissimo che non vi è alcuna contrazione o dilatazione lungo le direzioni perpendicolari all’asse del moto x. Si può quindi essere sicuri che L₀ mantiene la stessa lunghezza sia in S che in S’. Anche questa considerazione viene spesso tralasciata, ma è fondamentale per comprendere appieno il significato della relatività einsteniana.

Infine, non dimentichiamo che c deve essere la stessa in ogni sistema di riferimento.

Possiamo, finalmente, descrivere cosa avviene se l’orologio di luce viene visto da S.

Tutto si riassume benissimo nella Fig.27. La luce descrive il percorso A B₁ A₂. S non può che concludere, qualitativamente, che il percorso della luce deve essere più lungo di quello misurato nel sistema S’. Tuttavia, la luce ha sempre la stessa velocità c,  e, quindi, se il percorso è più lungo deve essere più lungo anche il tempo impiegato a percorrerlo, dato che la velocità è pur sempre uno spazio diviso un tempo.

Passiamo, ora, a una descrizione quantitativa. Il percorso dello specchio A, mentre va da A a A₁, è dato da (per semplicità, consideriamo sempre il centro dello specchio):

AA₁ = x_A1 –x_A = v (t_A1 – t_A)

La distanza AB₁ è data dalla differenza di tempo t_A1 – t_A (t_A1 è uguale a t_B1) moltiplicata per la velocità della luce c, ossia

AB₁ = c (t_A1 – t_A)

Non ci resta che applicare il teorema di Pitagora al triangolo AB₁A₁.

AB₁² = AA₁² + A₁B₁²

Ossia:

c² (t_A1 – t_A)² = (x_A1 –x_A)² + L₀²

e anche:

c² (t_A1 – t_A)² = v² (t_A1 – t_A)² + L₀²

Per semplicità chiamiamo Δt₁ la differenza di tempo tra la partenza della luce da A al suo arrivo in B₁ (che corrisponde al punto A₁), ossia t_A1 – t_A. La formula precedente diventa:

c² Δt₁² = v² Δt₁² + L₀²

Ricaviamo Δt₁ …

Δt₁²(c² – v²) = L₀²

Δt₁²= L₀²/(c² – v²) = L₀²/(c² (1– v²/c²)) = (L₀²/c²)(1/(1– v²/c²))

Non abbiamo fatto altro che usare un piccolo trucchetto, mettendo in evidenza c² al denominatore… in modo che venisse fuori la quantità 1/(1– v²/c²) che ormai conosciamo molto bene!

Non ci resta, ora, che eseguire la radice quadrata e si ottiene:

Δt₁ = (L₀/c)(1/(1– v²/c²)^1/2)

Tuttavia, lo stesso procedimento lo possiamo utilizzare per trovare la differenza di tempo Δt₂ necessario per andare da A₁ ad A₂, ossia fino al ritorno del fascio di luce nello specchio di partenza A. Risulta immediato che Δt₁ = Δt₂. Ne segue che il tempo complessivo Δt perché la luce parta da A arrivi in B₁ e torni in A₂ non è altro che:

Δt = Δt₁ + Δt₂ = 2 Δt₁ = (2L₀/c)(1/(1– v²/c²)^1/2)

Tuttavia, dobbiamo ricordare dalla (1) che:

Δt’ = 2L₀/c

Sostituendo, otteniamo, infine:

Δt = Δt’/(1– v²/c²)^1/2   …. (2)

Che non è altro che la trasformazione di Lorentz relativa al tempo.

Non dimentichiamoci mai che abbiamo ottenuto questo risultato, così discordante tra i due sistemi di riferimento, per il solito “vecchio” dato di fatto che abbiamo evidenziato fin dall’inizio, descrivendo la relatività della simultaneità: nel sistema S’ abbiamo utilizzato un solo orologio situato sempre nello stesso punto; nel sistema S abbiamo dovuto misurare il tempo attraverso orologi diversi, uno posto nella posizione A e uno in A₂ (volendo, anche uno intermedio  in A₁). Il primo tempo è per definizione un tempo proprio, mentre il secondo è un tempo improprio.

Ribadiamo ancora che ∆t non ha, perciò, nulla a che vedere con il tempo segnato dall’orologio a luce che è sempre dato dal tempo proprio ∆t’, qualsiasi sia il sistema di riferimento. Non commettiamo l’errore di pensare che un orologio a luce si comporti in modo diverso cambiando il sistema di riferimento! E’ la stessa cosa che si otteneva con l’uomo sulla nave. L’azione di versare acqua in un bicchiere non cambia tra chi sta a terra o sta in nave. Il principio di relatività vale sempre. Nella relatività ristretta (e quindi nella trasformazione di Lorentz) ciò che cambia è la misura effettuata da un sistema in moto relativo rispetto a un altro.

N.B. Questa conclusione continua a essere valida anche se l’orologio a luce viene ruotato di 90° in modo che gli specchi siano allineati lungo l’asse x e, più in generale, per qualunque altro tipo di orologio (a pendolo, a quarzo, atomico, ecc...). Tuttavia, quando si dice “qualsiasi orologio” si intende proprio qualsiasi! Ad esempio, anche un orologio “biologico”, come il battito del cuore o il processo di invecchiamento. Esso non deve cambiare se l’essere vivente in questione si trova a terra o su una nave o su un razzo che viaggia a velocità costante, altrimenti vorrebbe dire che le leggi fisiche che sono alla base del funzionamento del cuore sarebbero diverse nei due riferimenti in aperto contrasto con il Principio di Relatività. Qualsiasi riferimento al paradosso dei gemelli NON è casuale…

Bene… attraverso il semplice teorema di Pitagora abbiamo ricavato nuovamente la trasformazione di Lorentz relativa al tempo, ossia la sua dilatazione. Con un procedimento analogo troviamo anche la contrazione delle lunghezze.

Appendice preveggente

Prima di proseguire in questa direzione, fatemi scrivere una relazione che deriva dal solito triangolo rettangolo che abbiamo usato precedentemente e che ci ha portato a:

c² (t_A1 – t_A)² = (x_A1 –x_A)² + L₀²

Tuttavia, sappiamo che:

Δt’ = 2L₀/c

Ossia:

L₀ = c Δt’/2

Ponendo Δx = x_A2 – x_A = 2(x_A1 –x_A)

c² Δt²/4 = Δx²/4 + c² Δt’²/4

Ossia:

c² Δt’² = c²Δt² - Δx²

Il primo membro è il quadrato del tempo proprio (qualsiasi sia il sistema di riferimento) moltiplicato per la velocità della luce al quadrato, il secondo membro è un qualcosa di “strano” che fa ricordare il teorema di Pitagora, ma con un segno invertito… Notiamo, però, che ogni fattore rappresenta uno spazio (il tempo per una velocità è uguale a uno spazio). Bene, non voglio anticipare molto di più, dato che ci torneremo sopra per affrontare in pieno il diagramma di Minkowski, mi basta dire che c² Δt’² è un invariante dello spaziotempo.

In poche parole, qualsiasi sia il sistema di riferimento S in moto rispetto a S’, la quantità precedente non cambia! Essa è una distanza invariante dello spaziotempo, così come la distanza tra due punti è un’invariante nello spazio euclideo. Senza nemmeno accorgercene abbiamo “toccato” lo spazio di Minkowski, capace di rappresentare la relatività ristretta con quattro coordinate (due se consideriamo lo spazio solo come x). Uno spazio quasi-euclideo, ma non euclideo, dato che vedremo che un’ipotenusa  di un triangolo è più corta di un cateto… Tuttavia, come già detto, affronteremo nuovamente e con maggiore attenzione questo importantissimo argomento.

Un orologio che misura le lunghezze

Per dimostrare graficamente la relazione che lega le lunghezze della trasformazione di Lorentz, continuiamo a usare il nostro orologio a luce. Dobbiamo, però, aver già ricavato la relazione che “dilata” i tempi. Questa volta sistemiamo l’orologio a luce in posizione orizzontale, lungo l’asse dello spazio, ossia dell’ascissa x. Ci sistemiamo in un sistema di riferimento “fermo” S e osserviamo ciò che avviene a un orologio a luce posto nel sistema S’ che si muove rispetto a noi con velocità v.

Lo specchio A coincida con un certo punto dell’asse x che chiamiamo x_A nel momento in cui la luce parte da A (Fig. 28a).

Il tempo relativo, misurato con un orologio posto in x_A sia t₀. La luce viaggia, ma viaggia anche l’orologio a luce. A un certo tempo t₁ la luce colpisce lo specchio B, giunto nella posizione B₁ e viene rimandata indietro (Fig. 28b). Questa posizione la chiamiamo x_B1. Nello stesso istante lo specchio A si trova in A₁ di ascissa  x_A1. La distanza tra A₁ e B₁ è misurata nello stesso istante da due orologi sincronizzati del sistema S ed è pari alla lunghezza L dell’orologio a luce. Qual è la distanza d₁ percorsa dalla luce che è partita da A all’istante t₀ e arriva in B₁ all’istante t₁?

La Fig. 28b ce lo dice subito:

d₁ = (x_A1 – x_A) + L      …. (1)

ma

x_A1 – x_A = v(t₁ – t₀)

Per semplicità scriviamo:

Δt₁ = (t₁ – t₀)

Da cui

d₁ = v Δt₁ + L

Andiamo avanti e stabiliamo il nuovo tempo t₂ in cui la luce, che è tornata indietro, colpisce lo specchio A che si è portato in A₂. Ovviamente, il tempo è misurato dall’orologio posto in A₂. Quanto vale, adesso, la distanza d₂ percorsa dalla luce che è partita da B₁ all’istante t₁ ed è arrivata in A₂ al tempo t₂?

Non è difficile rispondere guardando la Fig. 28c. La luce è partita dal punto di ascissa x_B1 e torna indietro al punto di ascissa x_A2. Notando che x_B1 non è altro che d₁, possiamo allora scrivere:

d₂ = d₁ – (x_A2 – x_A) = (x_A1 – x_A) + L - (x_A2 – x_A) = (x_A1 – x_A) + L – ((x_A2 – x_A1) + (x_A1 - x_A)) = x_A1 – x_A + L - x_A2 + x_A1 - x_A1 + x_A

d₂ = L – (x_A2 - x_A1)

Ma

x_A2 – x_A1 = v(t₂ – t₁)

Ponendo, come prima:

Δt₂ = t₂ – t₁

Si ha

d₂ =  L - v Δt₂

Tuttavia, dobbiamo ricordare che la distanza d₁ è il percorso compiuto dalla luce per andare dallo specchio A allo specchio B e d₂ è il percorso compiuto dalla luce per tornare da B ad A.

Ne segue che

d₁ = c Δt₁

e

d₂ = c Δt₂

Da cui:

d₁ = v Δt₁ + L = c Δt₁

e

d₂ = L - v Δt₂ = c Δt₂

Dalla prima si ottiene:

Δt₁ = L/(c – v)

Dalla seconda:

Δt₂ = L/(c + v)

Sommando:

Δt = Δt₁ + Δt₂ = L/(c – v) + L/(c + v) = (L c + L v + L c – L v)/(c² – v²) = 2L c/(c² – v²)

Mettendo in evidenza c² al denominatore, abbiamo:

Δt = (2L c/c²)(1/(1 – v²/c²)) =  (2L/c)(1/ (1 – v²/c²))   …. (2)

Ma, quando abbiamo ricavato lo stesso valore la volta scorsa (poco prima di giungere alla relazione relativa al tempo della trasformazione di Lorentz), si era ottenuto:

Δt = (2L₀/c)(1/(1– v₂/c₂)^1/2)     …. (3)

Il sistema di riferimento è lo stesso e quindi la  (2 ) e la (3) devono coincidere!

Questo capita se e solo se:

L = L₀ (1– v²/c²)^1/2

Che è proprio la relazione della trasformazione di Lorentz che dimostra la contrazione delle lunghezze.

Se ne conclude che  la dilatazione dei tempi implica la contrazione delle lunghezze e viceversa.

Tutti questi esperimenti "teorici" hanno applicazioni pratiche. Dobbiamo, infatti, ricordare che la RR descrive la realtà in modo più accurato della relatività di Galileo e Newton. Non è assolutamente un gioco matematico! Inseriamo, allora, una bella favola reale (o realtà fantastica) per non dimenticarci il nostro pianeta amico Papalla...

La favola

La gente lo chiama mesone μ, ma il suo nome ufficiale è “muone”. Poca importa, comunque. Lui vive, in media,  molto meno delle farfalle, soltanto due milionesimi di secondo. Qualcuno un po’ di più, qualcuno un po’ di meno. Indovinate qual è il suo sogno nel cassetto? Poter vivere più a lungo, magari dieci volte di più: due centomillesimi di secondo… che meraviglia, quante cose potrebbe fare!

Su Papalla hanno molta simpatia per i muoni e farebbero di tutto per accontentarli. I matematici hanno scritto formule e gli ingegneri hanno costruito strumenti enormi in cui farli viaggiare a piacimento. I fisici hanno legato le due cose e sono molto soddisfatti: ce l’hanno fatta anche se con qualche difficoltà.

Come tutte le grandi conquiste della Scienza il procedimento è veramente semplice. E’ bastato farli viaggiare al 99.5% della velocità della luce. Su schermi giganti, adeguatamente predisposti, è stato reso visibile a tutti i papalli il risultato raggiunto. Sì è vero, è proprio vero, i muoni vivono molto più a lungo di prima. Chissà come sono contenti! Tutti si aspetterebbero di vederli sorridere e, invece, sembrano sempre uguali, anzi addirittura più tristi.

Svolgono le loro azioni quotidiane senza manifestare alcuna soddisfazione. In realtà, ciò che vedono i papalli è che ogni cosa che fanno i muoni è decisamente rallentata. Per spostare un quark da un nucleo a un altro ci mettono dieci volte di più. Il loro cuoricino subatomico batte dieci volte più lentamente. I papalli sono sicuri di questo risultato, dato che lo controllano con il loro orologio. Ogni cosa che fanno viene svolta in un tempo dieci volte superiore.

I papalli iniziano a capire cosa sta realmente succedendo: sono solo loro che vedono la vita dei muoni più lunga. I simpatici amici subatomici non se ne rendono assolutamente conto. Loro continuano a vivere come prima e la loro vita non si è allungata per niente. L’unico vantaggio dell’esperimento lo hanno avuto i papalli che sono riusciti a vedere al rallentatore l’intera vita di un muone, dato che, per gli orologi papalliani, invece di due milionesimi di secondo è durata ben due centomillesimi di secondo.

Se sapessero cosa pensano i muoni sarebbero ancora meno contenti. Altro che soddisfazione! Essi già invidiavano i papalli perché vivevano molto più a lungo di loro: tanti anni invece che minime frazioni di un secondo. Tutte quelle nuove apparecchiature che hanno costruito sono servite solo a farli vivere ancora più a lungo. Non più 80 anni di vita medi, ma addirittura 800 anni. Non possono certo verificarlo, ma hanno potuto facilmente controllare che ciò che i papalli facevano in due milionesimi di secondo, adesso lo compiono in due centomillesimi di secondo. Accidenti, i papalli hanno tutte le fortune.

I muoni vivono troppo poco per capire che anche i papalli non si rendono conto che l’allungamento della loro vita esiste solo per i muoni che li stanno osservando. I papalli continuano a vivere la solita vita di tutti i giorni. Purtroppo, i muoni non conoscono la matematica, l’ingegneria e nemmeno la fisica. Loro non sanno che cos’è la relatività speciale… e non riescono nemmeno a sfruttare adeguatamente l’apparente rallentamento del tempo di chi si muove ad altissima velocità rispetto a loro. I papalliani, invece, sono riusciti, almeno, a studiare meglio la vita dei cari amici muoni. Le stesse cose che facevano in due milionesimi di secondo lo hanno “diluito” in due centomillesimi di secondo. Un “rallenty” importantissimo.

Anche perché, avendo a disposizione un tempo più lungo, è aumentato anche il percorso che i muoni sono riusciti a compiere. E poco importa, in fondo, che i muoni, invece che piccole sfere, gli appaiono come delle ellissi molto schiacciate.

La favola è quanto di più reale ci possa essere e i terrestri sono riusciti a “copiare” i papalliani, anche senza usare apparecchiature ultra sofisticate: gli è bastata la velocità intrinseca dei raggi cosmici e la loro atmosfera.

Possiamo, ora, iniziare a parlare più seriamente.

La realtà

I raggi cosmici sono particelle subatomiche che si originano durante le fasi più violente della vita stellare e che colpiscono continuamente l’atmosfera terrestre. Urtando a grande velocità le molecole dell’aria, le distruggono creando nuove particelle. Queste ultime proseguono verso la Terra con energia cinetica elevatissima e quindi con velocità molto prossime a quella della luce.

Non tutte, però, sono particelle stabili (come i protoni e gli elettroni) e decadono molto in fretta. Tra queste ce n’è una particolarmente interessante che è stata chiamata mesone μ, o, ancor meglio, muone. Essa si disintegra spontaneamente dopo aver vissuto solo due milionesimi di secondo (in media). I muoni si formano, solitamente, a un’altezza atmosferica intorno ai 10 km.

Se noi ragionassimo come Newton o Galileo dovremmo concludere che nel loro viaggio verso il nostro pianeta coprirebbero una distanza decisamente piccola. Pur ammettendo che essi raggiungano la velocità della luce c, la distanza non è altro che la vita media del muone moltiplicata per c (la distanza è uguale alla velocità moltiplicata per il tempo). Ossia:

d = c Δt₀ = 660 m

dove Δt₀ è il tempo che misura la vita media del muone e che vale circa 2 milionesimi di secondo. Se ne dovrebbe concludere che i muoni muoiono subito dopo essersi formati in alta atmosfera e raggiungere la Terra è per loro un sogno irrealizzabile. E, invece, molti di loro ci riescono! Com'è mai possibile? Presto detto.

Il tempo di vita Δt₀ è un tempo proprio misurato nel sistema di riferimento del muone, attraverso un solo orologio “biologico”, come mostrato in Fig.29. Il muone appena nato è disegnato in blu, mentre appena muore è disegnato in rosso.

Il muone, però, viene osservato dalla Terra, in un sistema di riferimento “fisso” che vede viaggiare il muone a grande velocità. Per l’osservatore terrestre è come se il muone vivesse al rallentatore (come nella favola) e il suo tempo di vita si allunga come previsto dalla trasformazione di Lorentz e dalla relatività speciale. Sappiamo ormai benissimo come calcolarlo attraverso due orologi:

Δt = γ Δt₀

Ne segue che il percorso effettuato dal muone osservato da Terra diventa:

L₀ = v γ Δt₀

Dove v è la velocità del muone rispetto al sistema di riferimento terrestre A-T (dove A è lo strato atmosferico a 10 km, dove nasce il muone, e T è la superficie terrestre).

I 660 m ipotetici, newtoniani, sono diventati ben 10 km, come mostrato nella Fig. 30.

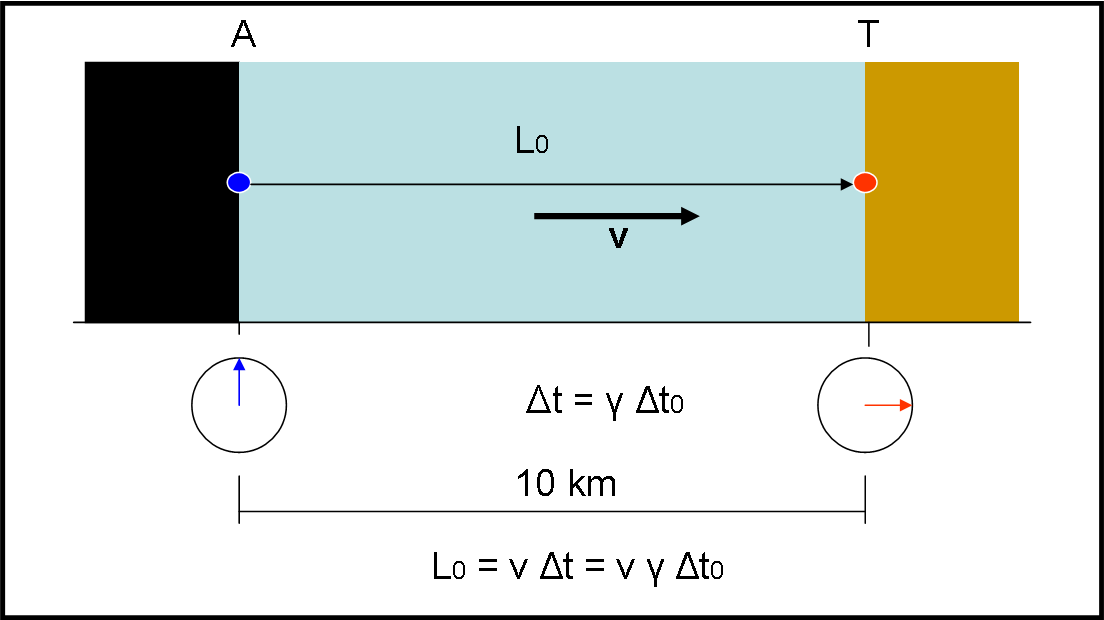
Questo è un dato di fatto, osservato e misurato, e va quindi accettato completamente. Tuttavia è anche vero che il tempo di vita proprio del muone rimane sempre di due milionesimi di secondo.

Portiamoci, allora, sul muone nato in A e vediamo come osserva l’intero fenomeno. Deve accettare il fatto che esso morirà solo dopo che la superficie della terra T lo avrà raggiunto. Questo è un postulato della relatività speciale. Infatti, il fatto che esso nasca in A e che muoia in T è stato verificato nel sistema terrestre e la relatività dice che un certo evento fisico è indipendente dal sistema in cui si osserva: deve essere sempre uguale. La nascita in A e la morte in T è un evento fisico e deve valere anche per il sistema di riferimento del muone!

La relatività speciale è molto bella, ma a questo punto sembra veramente assurdo che il muone possa percorrere una distanza così lunga. Lui sa benissimo che può vivere solo due milionesimi di secondo e lo può dimostrare con un solo orologio, come visto in Fig. 29, ossia la sua vita è un tempo proprio. Il muone sembra sconvolto, ma la relatività speciale ha pronta la risposta anche per lui.

Nel sistema di riferimento del muone, considerato fermo, è la Terra che si muove verso di lui con velocità –v. A e T sono punti solidali con la Terra e si muovono all’unisono. La distanza A-T è misurabile con un asta rigida sulla Terra ed è una lunghezza propria L₀. Questa lunghezza, però, non rimane certo la stessa se misurata nel sistema del muone. Essa è un’asta rigida, solidale con la Terra, che viaggia a una velocità – v e quindi deve contrarsi nel senso del moto, come mostrato in Fig. 31.

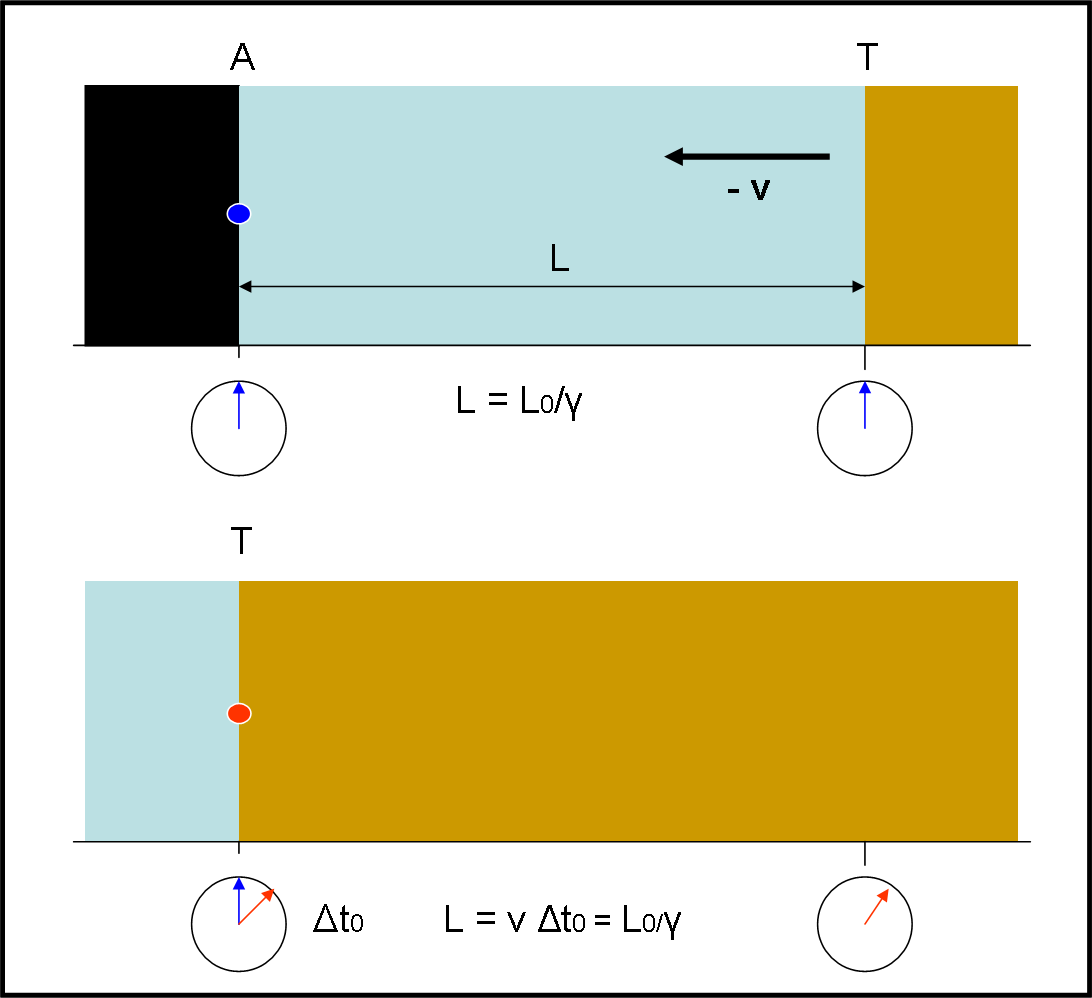
Il sistema del muone la misura (teoricamente) con due orologi diversi che indicano lo stesso tempo. Questa lunghezza vale, perciò:

L = L₀/γ

Ne segue che nel tempo proprio che misura la vita del muone la distanza da percorrere si è ristretta.

Per una migliore comprensione della situazione e per dimostrare che le due “osservazioni” sono perfettamente coerenti, poniamoci nei due sistemi e descriviamo ciò che succede.

(1) Sistema terrestre

Il muone si muove con velocità di modulo v e percorre i 10 km della distanza A-T. La distanza è una distanza propria dato che è misurata nel sistema terrestre. Non è un tempo proprio, invece, quello misurato tra la partenza e l’arrivo del muone (è osservato da due orologi del sistema terrestre). Abbiamo quindi, come già dimostrato, la relazione:

L0 = v γ Δt0     …. (1)

(2) Sistema del muone

Il muone vede il punto T della Terra venirgli incontro con velocità di modulo v. La distanza tra A (quando è nato) e B (quando muore) viene contratta nella direzione del moto (in qualche modo è misurata sfruttando due orologi del sistema del muone. Il tempo di vita è invece un tempo proprio, misurato da un solo orologio). Vale perciò la relazione:

L = L₀/γ = v Δt₀

Da cui si ricava:

L₀ = v γ Δt₀     …. (2)

La (1) e la (2) sono perfettamente uguali!

Come ampiamente previsto (Einstein non era un fessacchiotto…) i due sistemi di riferimento riescono a descrivere in modo identico la nascita del muone in A e la sua morte in T.

E’ più favola la favola o la realtà? Teniamo conto che noi osserviamo da Terra e quindi osserviamo realmente i muoni che arrivano fino al suolo. Ma, se osserviamo un fenomeno fisico, esso deve rimanere immutato anche nel sistema dei muoni. La relatività sembra "apparenza", ma è , invece, la realtà dei fatti fisici.

Concludiamo qui questa prima parte fondamentale. In seguito passeremo alle conseguenze della relatività sulle altre grandezze fisiche (e vedremo che anche la massa ne è influenzata) e alla sua rappresentazione nel diagramma di Minkowski.

 

QUI la favola del muone raccontata per i più piccoli dall'amico Muo e da Mago Albertino.

Finalmente anche Gatto Gualtiero si è deciso a miagolarci del concetto di Relatività da Giordano Bruno (ebbene sì, proprio lui è stato il primo) fino ad Albert Einstein, passando per Galileo e Newton! Ascoltiamolo in miagoloso silenzio...