Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento

 

Ho detto che i due gemelli possono fare a meno di conoscere la relatività ristretta e le sue formule per arrivare a un risultato assolutamente non simmetrico (e questo non inficia assolutamente la RR). A loro basta mantenersi in contatto visivo o radio e contare il numero di invii e di ricezioni dei segnali. In poche parole, sfruttano solo la costanza della velocità della luce. Noi, invece, per costruire il disegno esplicativo dobbiamo conoscere bene ciò che capita nel diagramma di Minkowski e sfruttare la trasformazione di Lorentz. Tuttavia, per far ciò, basta utilizzare solo e soltanto delle rette e le loro intersezioni: un gioco da ragazzi!

Una parola in più sulla simmetria che non si mantiene. Sappiamo benissimo che ogni formula della RR può essere tranquillamente invertita. Quello che vede il sistema S’ deve essere visto anche dal sistema S. La trasformazione di Lorentz ce lo impone. Se per chi viaggia è il gemello a terra che resta giovane, deve valere anche l’opposto: per chi sta fermo è l’astronauta a invecchiare di meno. Il fatto che, alla fine, troviamo un risultato UNICO e non simmetrico non vuole assolutamente dire che la RR è da buttare. Vuole solo dire che la sua applicazione ha evidenziato una situazione che non può far parte della RR. Ciò che noi stiamo per fare è dimostrare che il risultato unico, intollerabile dalla RR, può essere trovato lavorando solo con lei…

Ci tengo a dirvi che considero questo metodo come la soluzione forse più intuitiva del celebre paradosso, dato che mostra graficamente come sia realmente il viaggiatore a invecchiare di meno e come anche quest’ultimo non può che essere pienamente d’accordo su questo risultato. Ovviamente, lo ripeto ancora, basterebbe dire che per tornare indietro è necessario decelerare e accelerare, ma sarebbe sbrigativo e scaricherebbe sulla relatività generale il compito della dimostrazione. Basta, invece, considerare trascurabile il periodo di tempo in cui si cambia velocità (cosa fisicamente plausibile) e tutto scorre secondo una logica estremamente efficace e immediata.

Andrò avanti con molta “cautela” non tralasciando nessun passaggio, anche il più semplice. Per seguire l’intera faccenda è solo necessario conoscere la trasformazione di Lorentz e la strana geometria del piano di Minkowski in cui oltre a una rotazione degli assi, esiste un invariante che non segue la geometria euclidea (in altre parole, è facile tracciare la curva di calibrazione, la ormai ben nota iperbole equilatera, luogo delle unità di misura degli assi trasformati da Lorentz). Tutto il resto è pura geometria aiutata da banalissime formule.

Pronti… via!

Per ottenere il risultato voluto dobbiamo dimostrare che, qualunque sia il riferimento scelto, sia il gemello terrestre che quello spaziale arrivano alla stessa identica soluzione: è l’astronauta che invecchia di meno. Se entrambi raggiungono la stessa conclusione cade automaticamente il paradosso.

Gli assi t e x sono stati scelti come al solito, in modo da far sì che la traiettoria della luce sia sempre una retta inclinata di 45°. Per semplicità di lettura, consideriamo come unità di tempo l’anno e come unità di distanza l’anno luce. Ne segue che possiamo considerare c = 1 e scrivere il rapporto v/c semplicemente come v. Disegniamolo nella Fig. 1, anche se sarebbe del tutto inutile, ma è bene partire dal banale per cercare di non fare mai salti concettuali troppo bruschi. Nella stessa figura inseriamo la traiettoria dell’astronave. E’ immediato vedere a quale velocità sta andando: 3/5 di quella della luce. D’altra parte si nota subito che percorre 3 anni luce in 5 anni.

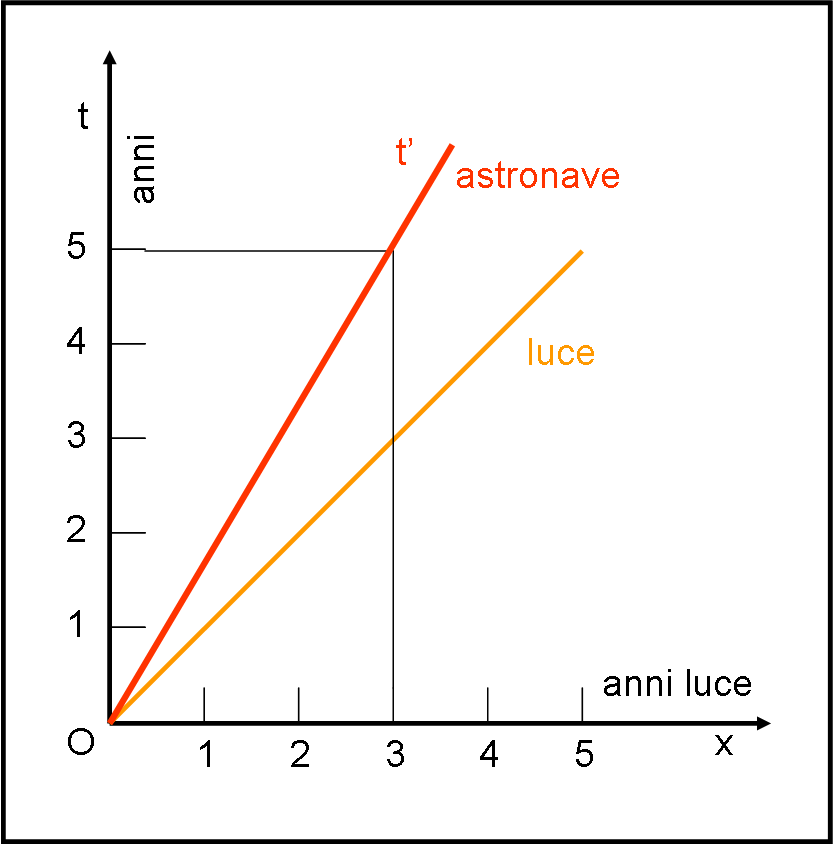
Abbiamo scelto questo valore dato che porta a numeri interi e più facilmente comprensibili. Tuttavia, troveremo le formule generali che servono al nostro scopo e questa scelta apparirà subito molto utile.

Ricordiamo subito come si determina la retta tracciata in rosso. Nel sistema di riferimento della figura essa ha equazione:

t = x/β = x/v

Basta rileggere quanto scritto QUI. Essa è una retta passante per l’origine di entrambi i sistemi e con coefficiente angolare uguale all’inverso della velocità dell’astronave (c = 1, ricordiamo).

Fin qui, direi che tutto è estremamente banale e immediato (e già descritto precedentemente).

Lasciamo che l’astronave parta per il suo viaggio con v/c = 3/5 e occupiamoci di cosa si deve fare a terra e sull’astronave per mantenere un contatto diretto e continuo.

L’impegno preso è  inviare un segnale luminoso ogni anno. Ovviamente, il gemello terrestre lo invia ogni anno terrestre e il gemello astronauta ogni anno trascorso secondo il suo orologio. Ripeto ancora, il tutto è visto nel sistema terrestre. Il tempo dell’astronauta è, come già detto,  anche il suo tempo biologico e quindi è più che ovvio che lui si riferisca al suo orologio per mandare i segnali.

Attenzione: non esiste nessuna connessione tra l’arrivo del segnale sull’astronave e l’invio di quello di ritorno. Sia il gemello terrestre che quello spaziale mandano i segnali a distanza di un anno esatto, ognuno misurato con il proprio orologio. Non aspettano l’arrivo dei segnali del gemello per agire, ma lo fanno seguendo un  ritmo predisposto fin dall’inizio. Tra poco, vedremo che i segnali sembreranno talvolta simultanei. Non confondiamoci! Questo fatto deriva solo dalla scelta della velocità, ideale per potere eseguire facilmente i calcoli necessari e per la grafica. Ribadiamo ancora, i due gemelli mandano i segnali solo e soltanto allo scadere di un loro anno.

Nel piano di Minkowski, il gemello terrestre descrive, ovviamente, la retta verticale del tempo t, in quanto è considerato fermo. Allo scadere esatto del primo anno manda il segnale al gemello. Quello che vogliamo trovare è il momento di arrivo di questo segnale sull’astronave. Mettiamoci nei panni dell’astronauta: che bello non sentirsi completamente solo anche se la luce ha una lentezza quasi insopportabile.

Disegnare graficamente quanto detto a parole è veramente immediato, dato che gli anni terrestri sappiamo bene come scorrono con la scala decisa fin dall’inizio (anno e anno luce). Più difficile è trovare il momento di arrivo sull’astronave nonché sapere quando l’astronauta deve inviare il suo segnale annuale. In poche parole, bisogna conoscere la scala del tempo lungo l’asse t’ che rappresenta la traiettoria dell’astronave vista nel sistema terrestre.

La faccenda non ci crea grossi problemi, dato che già sappiamo benissimo come fare a trovare l’unità di misura su ogni traiettoria al variare della velocità del sistema in moto. Lo abbiamo fatto sia graficamente che attraverso un po’ di matematica, definendo la ormai famosa curva di calibrazione, l’iperbole che ci permette di descrivere il luogo dei punti che mantiene la stessa unità di misura. Essa ci regala un invariante non euclideo che ci è stato e ci sarà molto utile.

Siamo, quindi, in grado di utilizzare la curva di calibrazione per determinare la “lunghezza” dell’anno dell’astronauta e poi, in qualche modo, valutare graficamente il momento di arrivo della luce del gemello terrestre. Tuttavia, dato che vogliamo prendere sempre maggiore dimestichezza con la geometria di Minkowski, ci dedichiamo a un problemino di geometria elementare, da svolgere nel piano x,t. Ci serve anche come ripasso di molte cose che abbiamo imparato sulla retta.

Per trovare l’evento “arrivo sull’astronave della luce mandata dopo un anno da terra” basta trovare l’intersezione tra la retta descritta dall’astronave e quella descritta dalla luce partita all’istante relativo al primo anno terrestre.

Le due rette (scritte nelle coordinate terrestri) sono:

t = x/v

t = x + 1           …. (1)

La prima è la traiettoria dell’astronave, la seconda la traiettoria della luce che parte al verificarsi dell’evento (0,1). Ricordiamo, infatti, che il coefficiente angolare deve essere uguale a 1 (retta a 45°) e che il termine noto deve essere uguale all’ordinata (t) relativa all’ascissa (x) uguale a 0 (partenza del segnale).  La stessa retta acquista subito un carattere più generale e può essere usata anche per gli anni successivi, inserendo al posto di “1” i valori 2, 3, 4, … ecc. In parole povere la retta

t = x + N

dove N è un numero intero che vale 1, 2, 3, ecc. e permette di  descrive tutte le traiettorie parallele della luce inviate da terra anno dopo anno.

(1) è un sistemino veramente ridicolo, la cui soluzione ci fornisce le coordinate x_A’ e t_A’ del punto intersezione A’. In realtà, a noi serve solo il valore di t_A’, ma tanto vale risolverlo completamente.

Dalla prima equazione abbiamo che:

x = vt

sostituendo nella seconda:

t = vt + 1

t - vt = 1

t(1 - v) = 1

t_A’ = 1/(1 - v)

sostituendo nella prima si ha:

x/v = 1/(1 - v)

x_A’ =  v/(1- v)

Quello che abbiamo trovato è la “componente” nel sistema terrestre x,t, mentre a noi interessa il valore t’_A’ misurato lungo l’asse t’.

Ci viene in aiuto immediato la trasformazione di Lorentz che ci dice:

t’_A’ = t_A’/γ = t_A’(1 – v²)^1/2

Da cui:

t’_A’ = (1 – v²)^1/2/(1 - v)     …. (2)

Questa formula ci dà il tempo di arrivo (misurato sull’orologio dell’astronave) del segnale inviato da Terra un anno dopo la partenza da O.

Conoscere questo valore vuole anche dire determinare l’unità di misura sull’asse t’. Come vedete, siamo tornati alla curva di calibrazione e cose del genere. La RR e la sua rappresentazione grafica è come una “frittata”: la si può girare come si vuole, ma i risultati sono sempre gli stessi. Non è nemmeno difficile capire che la “componente” t_A’ non fa altro che esprimere e determinare il concetto di dilatazione del tempo. ma ci torneremo a suo… tempo. Torniamo al nostro segnale giunto, finalmente, sull’astronave. Dopo quanto tempo dalla partenza da O il gemello vagabondo lo vede arrivare secondo il suo orologio?  Avendo scelto per il nostro viaggio v = 3/5 si ottiene, attraverso la (2):

t’_A’ = 2

A questo punto è immediato sapere anche quando arriva il segnale del secondo anno terrestre e quello del terzo e via dicendo. Basta inserire N = 2 , 3, … nella retta descritta dalla luce.

Non stiamo a riscrivere il sistemino (1), ma è immediato capire che il segnale terrestre arriva sull’astronave a un tempo locale che è sempre doppio di quello di partenza da terra (sempre misurato localmente). Così il segnale del secondo anno terrestre arriva al gemello astronauta dopo quattro dei suoi anni e quello dei tre anni terrestri dopo sei anni, tempo locale dell’astronave.

Ricapitoliamo… Cosa significano questi numeri? Dopo un anno dalla partenza, il gemello terrestre manda un segnale luminoso che  arriva sull’astronave del  gemello spaziale dopo due dei suoi anni dalla partenza. Se il terrestre lo invia dopo due anni, questo arriva sull’astronave dopo quattro ; se lo invia dopo tre arriva sull’astronave dopo sei, ecc.

Il risultato è sicuramente interessante e deriva dalla scelta fatta per v. Ad esempio, se avessimo scelto v =1/2 avremmo trovato un valore di t’_A’ uguale a 1.73, molto meno semplice da disegnare. La situazione non sarebbe comunque cambiata per il nostro scopo, ma ci sarebbe stato una discordanza temporale tra l’arrivo dei segnali sull’astronave e sulla loro partenza. Ricordiamoci, infatti, che anche l’astronauta deve mandare i suoi segnali cadenzati anno per anno.

La cosa importante è che abbiamo comunque trovato non solo il momento dell’arrivo dei segnali, ma anche la scala dell’asse t’. Infatti, dato che OA’ deve essere uguale a 2 anni, la sua metà ci regala proprio l’unità su t’. Un altro metodo (ma in fondo è sempre la stessa frittata girata come si vuole) per determinare l’unità di misura del sistema in movimento a seguito della trasformazione di Lorentz.

Comunque sia, possiamo adesso procedere solo in modo grafico, senza più alcuna formula! Non dite che non siete contenti… Segniamo in Fig. 2 quello che abbiamo appena trovato.

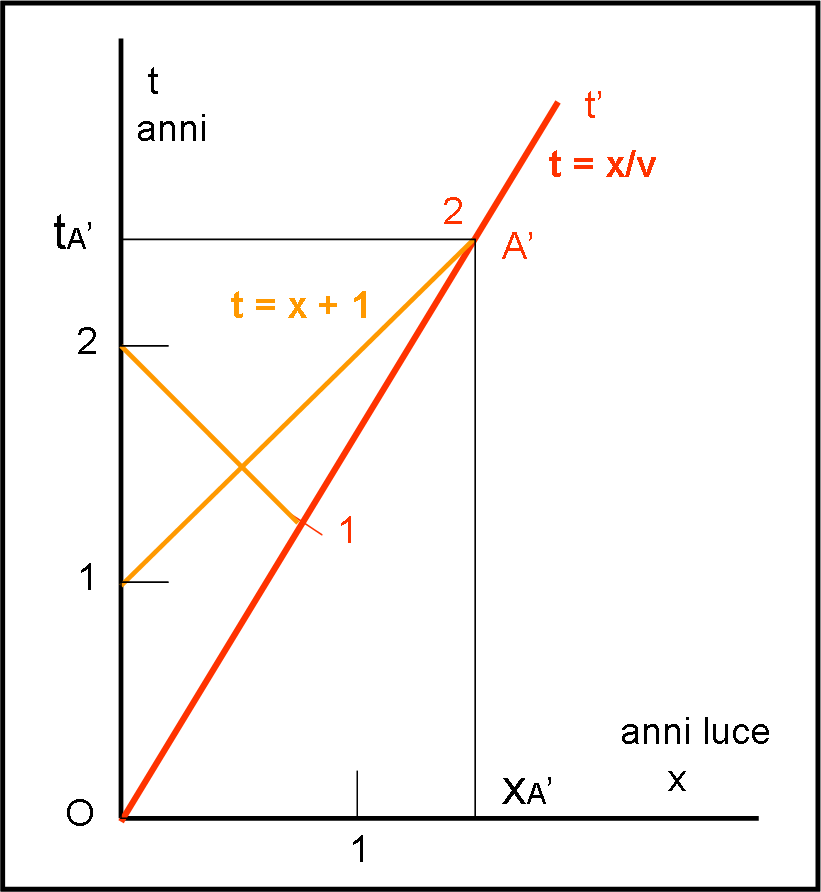
Attenzione: ho usato un metodo puramente geometrico per determinare i momenti di arrivo della luce. L’ho considerato più immediato e molto utile per rinfrescare un po’ del “corso” di matematica. Tuttavia, date la trasformazione di Lorentz  e la curva di calibrazione si poteva ottenere la soluzione in vari modi.  Tuttavia, il succo era ottenere il grafico risolvente e poco importa come l’abbiamo ottenuto…

Qualcuno potrebbe dirmi: “Sì, va bene, l’astronauta manda il suo segnale ogni anno dei suoi, ma quando arriveranno questi segnali sulla Terra?”. Come dicevo, possiamo risolvere la faccenda lavorando solo graficamente e il risultato apparirà immediato. Tuttavia, se vogliamo fare i raffinati, la risposta si può dare anche senza tracciare linee sulla figura.

Le formule, che abbiamo usato precedentemente per trovare l’intersezione tra la traiettoria descritta dall’astronave e il segnale annuale terrestre, possono essere usate tali e quali invertendo astronave e Terra (Fig. 3).

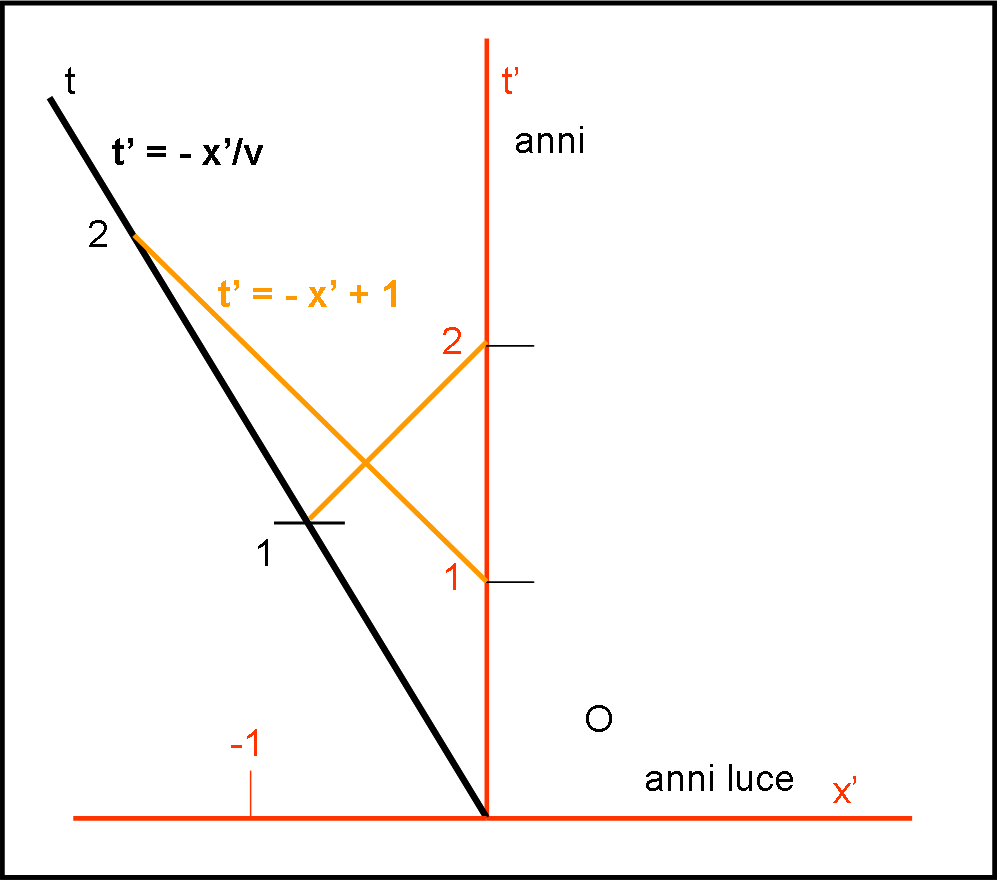
Sappiamo molto bene, infatti, che per l’astronauta è la Terra che viaggia a velocità –v. Se mettiamo t’ al posto di t, la traiettoria della Terra sarà ribaltata rispetto a quella dell’astronave, ma anche la traiettoria della luce lo sarà. Il sistema di prima diventa perciò, rispetto al sistema fisso astronave:

t’ = - x’/v

t’ = - x’ + 1

da cui si ottiene nuovamente:

t’ = vt’ + 1

Per trovare il valore nelle coordinate in movimento t (questa volta è il sistema terrestre che si muove) si applica pari pari la trasformazione di Lorentz come prima e si ha nuovamente t = (1 - v²)^1/2/(1 – v). Per v = - 3/5  si ottiene perciò ancora t = 2. Provare per credere…

Ne segue che, a causa del valore della velocità scelta, il primo segnale terrestre arriva sull’astronave dopo due anni dal lancio ed è concomitante con  il lancio dall’astronave del suo secondo segnale che arriva a Terra dopo 4 anni dal lancio. A questo punto, come dicevamo, la faccenda diventa una questione puramente grafica.

Disegniamo in Fig. 4 i primi anni di viaggio… e i segnali inviati e ricevuti dai due gemelli. Per una migliore visibilità, usiamo colori diversi per la luce che parte da terra e luce che parte dall’astronave. La prima la coloriamo di blu, la seconda di verde.

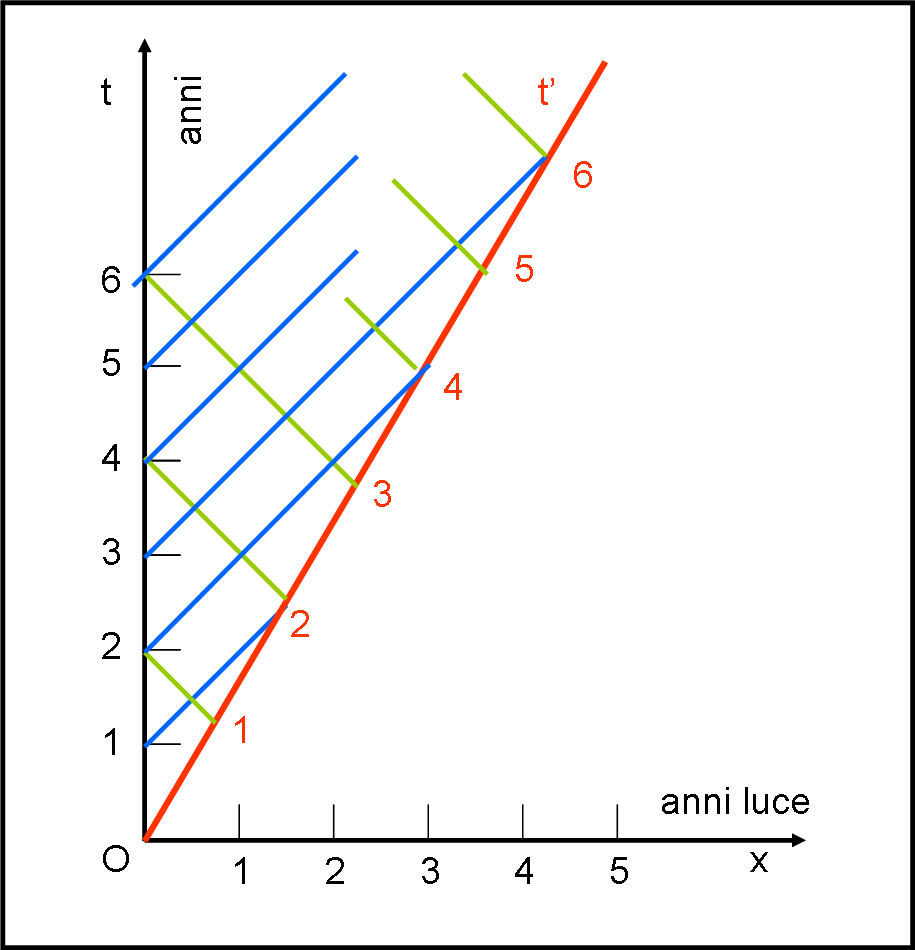
Cosa possiamo concludere, per adesso? Che sia l’astronave che la Terra ricevono il segnale altrui ogni due anni. Tutto è perfettamente simmetrico, come ci dobbiamo aspettare dalla RR. Dopo sei anni di viaggio, la Terra ha inviato sei segnali e ne ha ricevuto tre; stessa identica cosa per l’astronave. I segnali inviati dopo i primi tre anni li abbiamo solo accennati per questioni di spazio…

Potremmo andare avanti all’infinito e la situazione non cambierebbe assolutamente, in perfetto accordo con la RR. Potremmo anche vedere molto bene la dilatazione dei tempi osservata per il sistema in moto. Basterebbe tracciare le parallele a x (linee di simultaneità per il sistema Terra) o, simmetricamente, le parallele a x’ (non disegnato in figura) per determinare la dilatazione perfettamente simmetrica dei tempi osservati sul sistema considerato in moto. Ma, tralasciamo questo aspetto (fondamentale) e proseguiamo con il nostro viaggio. Lo analizzeremo successivamente andando a cercare dilatazione dei tempi e contrazione delle lunghezze…

Il gemello astronauta decide di tornare a Terra dopo aver raggiunto una distanza da Terra (nel sistema terrestre) di 3 anni luce. Ciò vuol dire che nel sistema Terra sono passati esattamente 5 anni. D’altra parte la velocità dell’astronave è proprio 3/5 di quella della luce. Continuiamo, però, a disegnare il tutto nel sistema terrestre. L’inversione di marcia dell’astronave vuole allora dire che essa inizia a muoversi con velocità -3/5.

Possiamo fare questo giochino sul diagramma di Minkowski? Sicuramente sì, dato che il tempo necessario a invertire la direzione (e quindi la decelerazione e la successiva accelerazione) è del tutto trascurabile. Graficamente possiamo permettercelo tranquillamente.

L’intero viaggio, con l’invio e il ricevimento dei segnali, è chiaramente mostrato in Fig. 5. Consideriamo anche come segnale mandato quello relativo al punto di arrivo dell’astronave sulla Terra. In questa situazione entrambi i segnali partono e arrivano simultaneamente dato che l’evento è unico.

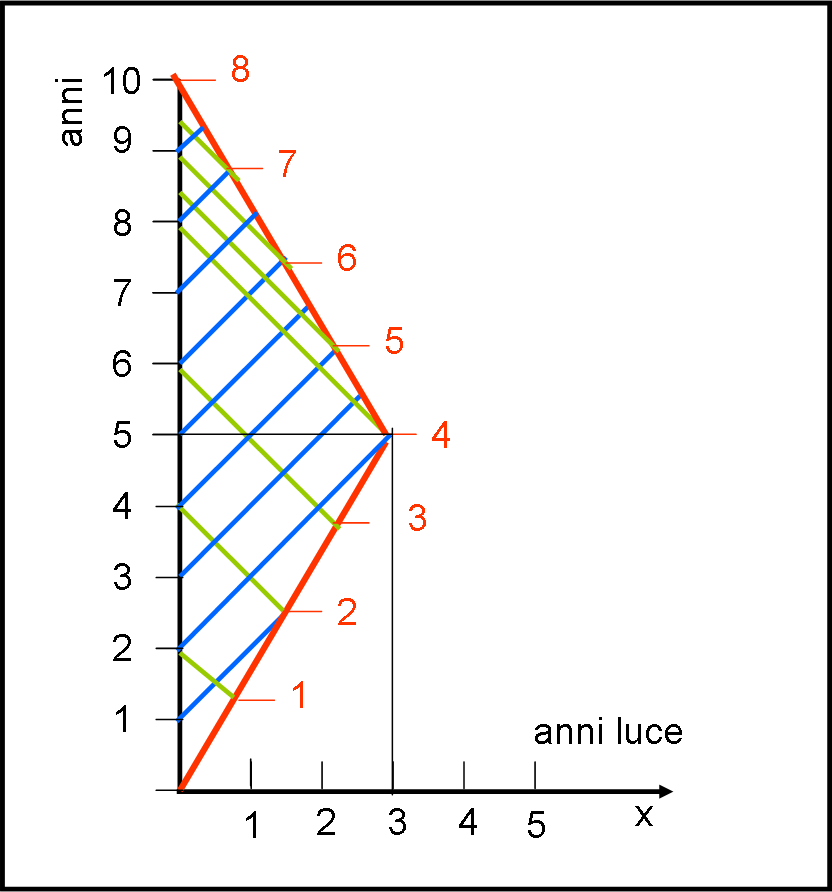
Lascio a voi riflettere sulla figura. Ma risulta chiaro che le cose nel viaggio di ritorno cambiano drasticamente. Dopo l’inversione di rotta i segnali arrivano con frequenza maggiore sia per l’astronauta che per il terrestre: ben due ogni anno locale (graficamente si vede molto bene, ma si potrebbero anche calcolare gli istanti di arrivo, utilizzando sempre il solito sistemino iniziale). Tuttavia, una differenza c’è… Il viaggiatore riceve per metà del viaggio (andata) i segnali del gemello ogni due anni, mentre li riceve ogni mezzo anno per l’altra metà del viaggio (ritorno). Il terrestre, invece, riceve quelli dell’astronauta ogni due anni per ben otto dei suoi anni. Solo dopo, comincia a riceverli ogni mezzo anno. La simmetria non si conserva di certo.

In conclusione, dal punto di vista dell’osservatore terrestre la situazione è abbastanza chiara.  Lui ha mandato ben dieci segnali, mentre ne ha ricevuto solo otto. Il gemello astronauta deve concludere, anche se con un po’ di sorpresa, che è proprio vero! Ha ricevuto dieci segnali, mentre ne ha mandati solo otto. Per lui sono passati otto anni, mentre per il terrestre ne sono passati dieci. Il gemello astronauta deve essere veramente più giovane! Il diagramma di Minkowski, con l’aggiunta di qualche segnale luminoso, ha risolto il paradosso.

Per chi ha voglia di riflettere, questo cambiamento di frequenza nell’arrivo dei segnali luminosi rispecchia perfettamente l’effetto doppler relativistico, che, nel caso di una sola coordinata, coincide perfettamente con quello ben noto a tutti noi. A suo tempo potremo anche parlarne un po’ più estesamente.

Cosa ci resta ancora da fare? Dimostrare che il fenomeno dell’invecchiamento UNIVOCO può essere confermato anche cambiando sistema di riferimento. In altre parole, il fenomeno deve rimanere lo stesso anche se si ci mette dal punto di vista dell’astronauta e si descrive il viaggio sotto questa nuova luce. Un esercizio molto utile per “pasticciare” nel nostro “amico” diagramma.

Imponiamo, perciò, come sistema di riferimento “fisso” quello dell’astronave alla sua partenza e vediamo a che soluzione si arriva. Il tutto è riportato in Fig. 6.

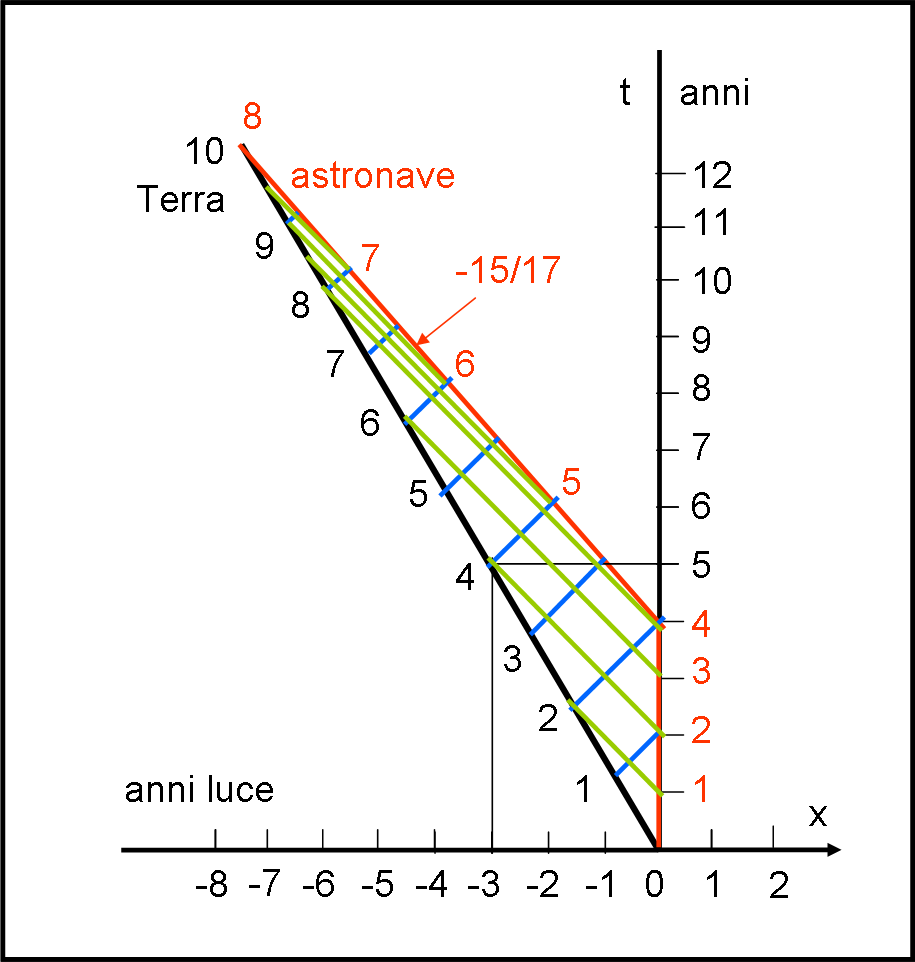
Per i primi quattro anni dell’astronave si segue la retta verticale. D’altra parte sappiamo benissimo che essa impiega quattro dei suoi anni per arrivare al punto di cambiamento di rotta. Rispetto a questa linea verticale la traiettoria della Terra sarà determinata costantemente dalla retta che corrisponde a una velocità -3/5. Anche su questo non ci piove, dato che abbiamo applicato soltanto  la RR. La Terra ovviamente percorre tre anni luce in cinque anni, così come faceva l’astronauta nel caso precedente.

Possiamo tracciare tranquillamente i segnali mandati dall’astronauta (luce verde) che colpiscono la Terra ogni due anni, in perfetto accordo con quanto successo nel grafico precedente. Questo fatto capita per ben otto anni terrestri, analogamente a prima.

Ed ecco che giungiamo al punto chiave del nuovo grafico: l’astronave cambia rotta e lascia il sistema di riferimento iniziale. Quale sarà la traiettoria descritta dall’astronauta rispetto alla linea di partenza? Beh… deve muoversi verso sinistra con velocità  -3/5, ma non basta. In questo modo si muoverebbe parallelamente alla Terra e noi vogliamo, invece, che torni a casa! Per ottenerlo dobbiamo sommare un’altra velocità -3/5. Eccoci finalmente alla composizione relativistica delle velocità! Per ottenere la velocità con cui si muove l’astronave rispetto alla traiettoria iniziale (durata 4 dei suoi anni) è necessario applicare la formula che abbiamo trovato nel capitolo relativo proprio a questo argomento.

u = (u’ + v)/(1 + u’v)

che nel nostro caso, diventa:

u = (-3/5 -3/5)/(1 + 3/5 x 3/5) = - 6/5/(1 + 9/25) = - 6 x 25/5 x 34 = -6 x 5/34 = -30/34 = -15/17

La retta che descrive la traiettoria dell’astronave fino al suo ritorno a terra avrà quindi come coefficiente angolare -17/15.  In realtà, non  vi era nemmeno bisogno di calcolarla… Quanto deve essere lungo il viaggio della Terra lo sapevamo già: 10 dei suoi anni. Dopo quattro anni di astronave “ferma” basta congiungere l’evento (0,4) dell’astronave con l’evento corrispondente a dieci anni terrestri…

Comunque sia, abbiamo ottenuto un bel triangolo spostato verso sinistra, in cui possiamo continuare a far partire e arrivare i segnali luminosi tra astronave e Terra e viceversa.

Chi non ci crede, può anche provare a calcolare nuovamente i punti di partenza e di arrivo con le solite rette usate precedentemente, ma troverà, ovviamente, ciò che si vede nella figura.

Dopo quattro dei suoi anni, il tempo sull’astronave scorre molto più lentamente rispetto a prima e raggiunge la Terra ogni mezzo anno dei suoi. Quelli blu mandati da terra, dopo due volte che hanno raggiunto l’astronave ogni due anni (in modo speculare a quanto successo con la Terra considerata ferma), iniziano anche loro a raggiungere l’astronave ogni mezzo anno. Non ci resta che fare i conti e si trova, senza troppa sorpresa, che nuovamente l’astronave riceve dieci segnali da Terra (ossia sa che sulla Terra sono passati dieci anni), mentre il gemello astronauta ne ha inviati solo otto (ossia è invecchiato solo di otto anni).

Abbiamo ritrovato lo stesso risultato di prima, pur avendo cambiato sistema di riferimento. Il diagramma di Minkowski ha permesso di risolvere il paradosso (sempre che si tratti veramente di paradosso) in modo puramente grafico e estremamente “pratico”, basandosi solo sull’invio e la ricezione di segnali luminosi mandati con cadenza annuale.

L’unica cosa che cambia macroscopicamente è la durata dell’intero viaggio misurata nel tempo di riferimento del tragitto iniziale dell’astronave: ben 12.5 anni. Risultato assolutamente non imprevisto, dato che l’orologio della Terra deve andare più piano per tutto il viaggio.

Quando il gemello torna a Terra sa benissimo di essere il più giovane, senza bisogno di effettuare calcoli vari. E’ bastato che contasse quanti segnali mandava e quanti ne riceveva.

Oltre che a risolvere il paradosso utilizzando solo e soltanto la RR, dimostrando che non è lei che “sbaglia” ma è il tipo di viaggio che non rispetta le sue regole, questo esercizio permette di divertirsi un “sacco” con il diagramma, cambiando per esempio le velocità… Chi vuole provare può anche farlo, ma la resa grafica si complica non poco e temo possa confondere i meno preparati. Per cui vi prego di non inserire figure più complicate tra i commenti. Oltretutto, io non ci sarò e il “circolo” chiude i battenti per l’intera settimana.

Se questo esercizio sarà compreso molto bene, diventerà veramente uno scherzo ricavare rapidamente dilatazione dei tempi e contrazione delle lunghezze, lavorando solo graficamente sul diagramma.

A presto e incrociamo le dita sia per l'operazione che per il "circolo". Siamo comunque in buone mani per entrambe le cose (neurochirurgo e SMA)!

 

QUI tutti (o quasi) gli articoli riguardanti il paradosso dei gemelli