Categorie: Relatività
Tags: paradosso dei gemelli relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:26
Tutto ciò che avreste voluto sapere su quei paradossali gemelli!
Questo articolo è inserito nella sezione d'archivio dedicata alla Relatività Ristretta
In questo approfondimento vengono passati in rassegna alcuni articoli particolarmente significativi riguardanti il famoso “paradosso dei gemelli”. Abbiamo cercato di metterli nell'ordine che ci è apparso più logico, ma tenete presente che sono stati scritti a distanza di tempo l'uno dall'altro, nell'arco di quattro anni, quindi non meravigliatevi se non vi sembreranno perfettamente concatenati. Riteniamo, tuttavia, che nell'insieme essi riescano a trattare l'argomento in modo sufficientemente esaustivo, nell'ambito della Relatività Ristretta.
Un GRAZIE a tutti i collaboratori che, a vario titolo, mi hanno aiutato, nel tempo, a portare a compimento questo progetto: sostenendolo e migliorandolo con consigli e osservazioni, partecipando alla scrittura di articoli, correggendo i miei errorini formali, infine assemblando questo articolone riassuntivo. Sto parlando di Paolo, Arturo, Umberto, Maurizio e... ahimè mi tocca ringraziare pure lui... PapalScherzone (ha fatto meno di tutti, ma purtroppo c'è anche il suo zampino papalliano in tutto questo).
Prima di metterci in marcia vi proponiamo la lettura di un quesito a cui due autori del blog, con approcci diversi ma egualmente validi, forniscono la propria risposta.
Se vi sentirete perfettamente a vostro agio in questa lettura preliminare, significa che già possedete una ottima conoscenza del problema e degli strumenti per la sua soluzione. I testi successivi, su cui forse avrete già meditato, risulteranno scorrevoli e ben comprensibili.
In caso contrario sarà necessario impegnarvi un po' di più per trarne insegnamento, converrà consultare i link che vi troverete e “studiare”. Al termine del percorso provate a tornare a questo quesito ed all'esame delle relative risposte. Certamente, a quel punto, vi sarà tutto perfettamente chiaro.
I prerequisiti per affrontare l'argomento li trovate in questi due approfondimenti:
LE BASI DELLA RELATIVITA' RISTRETTA
LO SPAZIOTEMPO DI MINKOWSKI: L'UNIVERSO IN UN FOGLIO
IL "COMANDANTE" VI DA' IL BENVENUTO A BORDO
E VI AUGURA BUON VIAGGIO TRA I GEMELLI
PRONTI?? VIA!
*********************************************************************************************************
QUESITO PRELIMINARE:
LA MINIMA DISTANZA RELATIVISTICA
La domanda è estremamente semplice e si riferisce alla Fig. 1. Siamo nel diagramma di Minkowski e AB è un intervallo spaziotemporale. Ricordo che questo intervallo è un invariante relativistico e rimane costante per ogni sistema di riferimento. Lo conosciamo molto bene e l’abbiamo già usato per descrivere le curve di calibrazione. La formula che lo esprime è:
s2 = T’2 = T2 – x2
Vi chiedo: “Qual è la distanza relativistica MINORE tra l’evento A e l’evento B? L’intervallo rettilineo rosso o quello curvilineo verde?”.
Ovviamente non mi basta la risposta (50% di probabilità), ma dovete dimostrare geometricamente il risultato che avete “scelto”e, poi, utilizzarlo per dimostrare immediatamente il paradosso dei gemelli.
Mi attendo che facciate anche il viceversa: partendo dal risultato relativo al paradosso dei gemelli, trovare immediatamente la soluzione del quiz.
Buon divertimento!
P.S.: la soluzione esatta e generale si ottiene attraverso l’operazione di integrale. Ma io non VOGLIO questi slanci… eruditi. Si può ottenere lo stesso risultato (altrettanto valido) senza alcun integrale e mettendosi in un caso particolare, ma più che significativo.
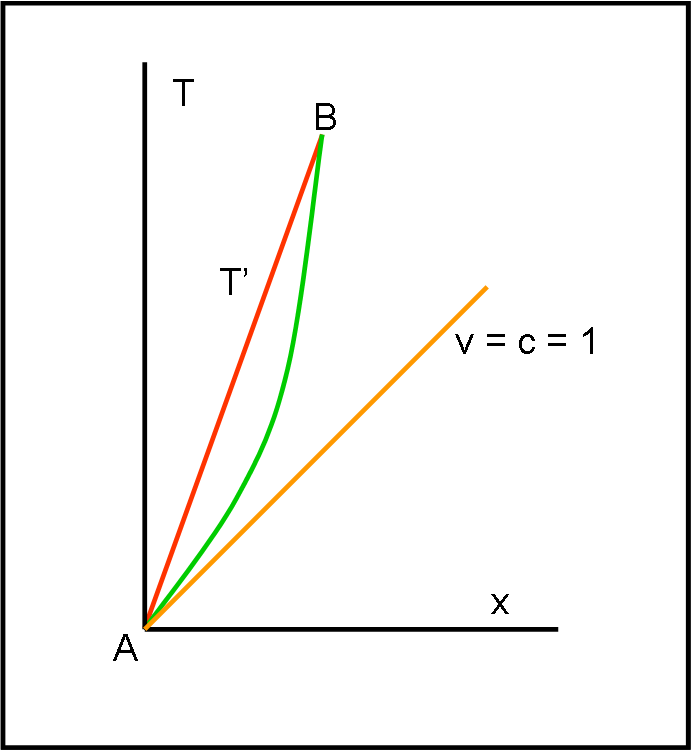
Figura 1
Risposte
Paolo
Alcune brevi premesse...
Il diagramma rappresenta tre diversi sistemi:
1) quello “fermo” rappresentato dagli assi ( linee nere) T e x; a 90° tra di loro
2) quello in movimento a velocità 0,35C (linea rossa) che dal suo punto di vista si sposta solo nel tempo, ossia lungo il suo asse T' (x'=0). Infatti solo per altri sistemi esterni questo sistema si muove anche nello spazio;
3) quello in movimento lungo la linea verde.
Quest'ultimo sistema è diverso dagli altri due, poiché la sua velocità non è costante (ossia varia nel tempo e nello specifico ad un certo punto, in prossimità di C, decelera).
Dato che la curva ha due lunghi tratti che sono riducibili ad una retta (velocità costante), ho approssimato tale percorso spazio-temporale, come se si trattasse di due velocità, una che contraddistingue la prima parte del percorso (A-C) stimabile in 0,71C e l'altra ( C-B) che contraddistingue la seconda parte del percorso stimabile in 0,15C, dopo la decelerazione.
Quindi l'asse del tempo T'' , visto da sistemi esterni, in prossimità dell'evento C cambia, per cui varia l'inclinazione della retta che lo rappresenta ( linea spezzata blu) e variano anche le rispettive linee di simultaneità (una per il tratto A-C e l'altra per il tratto C-B).
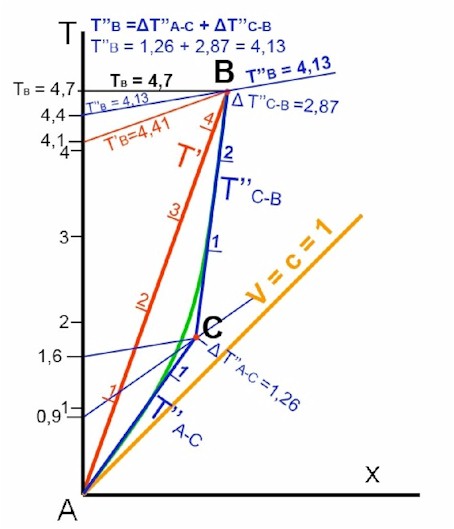
Nella figura ogni sistema (assi del tempo: T, T' e T'') ha le sue unità di misura che rappresentano il tempo segnato dal proprio orologio fisso, mentre le linee di simultaneità rappresentano il tempo segnato da tutti gli orologi del sistema di riferimento posizionati su tale linea (linee nere, rosse o blu come i relativi assi del tempo).
Per un ipotetico osservatore che viaggia lungo l'asse T'' (X''=0), l'orologio fisso rimane sempre lo stesso, ossia non cambia certo in prossimità di C , è quando viene visto da sistemi di riferimento esterni che la sua rappresentazione cambia profondamente.
Nello specifico: nel tratto A-C, l'asse T'' adotta l'unità di misura relativa a v =0,71C, mentre nel tratto C-B adotta l'unità di misura relativa a v=0,15C e di conseguenza cambiano anche le due rispettive linee di simultaneità.
Quindi per coprire l'intero percorso impiega un certo tempo, dato dalla somma dell'intervallo di tempo A-C (misurato con la sua specifica unita di misura) e dell'intervallo di tempo C-B (misurato con la sua specifica unita di misura).
Conseguentemente, l'orologio del sistema T'' ,quando arriva in B, segnerà un tempo:
T’’B =ΔT’’A-C + ΔT’’C-B = 1,26 + 2,87 = 4,13
I valori 1,26 e 2,87 sono stati ricavati usando le unità di misura adottate dall'asse T'' rispettivamente nei due tratti A-C e C-B.
A questo punto basta confrontare il tempo segnato dall'orologio fisso di T'' (T''B=4,13) con quello segnato dall'orologio fisso di T' (T'B = 4,41), per rendersi conto che il viaggiatore che segue la linea verde (approssimata a due rette blu) “percorre” la distanza spazio temporale A-B in un tempo più breve: il suo tempo è più dilatato di quello dell'altro viaggiatore.
Non resta che confrontare cosa vede ogni sistema di riferimento.
Per il sistema fermo (nero) quando l'unico orologio fisso del sistema in movimento (rosso) T' segna 4,41, i suoi orologi (linea simultaneità nera) segnano T=4,7, per cui segnano un tempo maggiore di T', ossia il tempo (rosso visto da nero) sembra dilatarsi.
Per il sistema in movimento (rosso) quando l'unico orologio fisso del sistema fermo T segna 4,1 i suoi orologi (linea simultaneità rossa) segnano T=4,41, per cui segnano un tempo maggiore di T, ossia anche per il sistema in movimento il tempo dell'altro sistema (nero visto da rosso) sembra dilatarsi.
Una perfetta simmetria per cui ad entrambi i sistemi sembra che sia il tempo altrui a dilatarsi.
Una simmetria destinata a rompersi osservando il sistema T''.
Per il sistema fermo (nero) quando l'unico orologio fisso del sistema in movimento (blu) T'' segna 4,13 (arrivo in B), i suoi orologi (linea simultaneità nera) segnano T=4,7, per cui segnano un tempo maggiore di T'', ossia il tempo (blu visto da nero) sembra dilatarsi.
Per il sistema in movimento (blu) quando l'unico orologio fisso del sistema fermo T segna 4,4 i suoi orologi (linea simultaneità blu) segnano T''=4,13, per cui segnano un tempo (nero visto da blu) minore di T.
Sia per il sistema fermo sia per il sistema in movimento il tempo T'' 4,13 ( del sistema in movimento) è sempre inferiore a T e la simmetria valida prima per sistemi che si muovono a velocità costante, si è rotta.
La situazione è ancora più chiara confronto il sistema in movimento rosso T' con quello blu T''.
Entrambi partono da A inseme ed insieme arrivano in B, solo che chi viaggia nel sistema blu invecchia meno, dato che quando arriva in B il suo orologio fisso (tempo proprio T''=4,13) segna un tempo minore dell'orologio fisso di T' (tempo proprio T'=4,41).
La rottura della simmetria dovuta alla velocità non costante di T'', sembra rispondere al paradosso dei gemelli (in questo caso uno dei due invecchia davvero meno dell'altro).
In ultimo, una piccola considerazione sull'approssimazione della curva verde.
Guardando la figura in prossimità di C ho tracciato due diverse linee di simultaneità blu, una si riferisce alla prima parte del percorso e l'altra alla seconda parte.
Una parte della curva verde non coincide con le due rette ed in questo tratto la velocità cambia da V=0,71C a V=0,15C (decelerazione), per cui l'inclinazione della retta di simultaneità cambia, passando repentinamente da quella che congiunge C all'asse T=0,9 a quella che congiunge C all'asse T=1,6.
In pratica ho approssimato questo tratto, ottenendo un ipotetico “evento” C di intersezione tra le due rette.
In questo modo tale evento C subisce istantaneamente un salto temporale (misurato dal sistema fermo sull'asse T, da 0,9 a 1,6, ma lo stesso discorso si potrebbe fare misurandolo sull'asse T' del sistema rosso), che in realtà avviene più lentamente in un certo intervallo di tempo, dato che la curva verde (a differenza delle rette blu) indica un passaggio graduale da V=0,71 C a V=0,15C.
Umberto
La distanza relativistica MINORE tra l’evento A e l’evento B è quella curvilinea di colore verde.
vista l'indipendenza della distanza relativistica, possiamo supporre di metterci nel sistema di riferimento nel quale la velocità con cui viene percorso il segmento AB è zero. Ciò equivale a compiere una rotazione nel diagramma di Minkowski per cui il segmento AB viene a coincidere con un segmento sull'asse dei tempi di coordinate A(0,0) , B (0,T')
la curva verde subirà anch'essa una rotazione in modo che i suoi estremi coincidano con A,B.
Nei diagrammi di Minkowski il segmento di retta rappresenta la distanza massima rispetto alle spezzate che uniscono due estremi;(vale la disuguaglianza triangolare al contrario) ciò si può capire nel nostro esempio dal fatto che essendo nulla la componente spaziale la lunghezza del segmento AB è semplicemente T', mentre se dobbiamo calcolare la lunghezza della spezzata (una sommatoria degli intervalli) avremmo a che fare con termini sia temporali che spaziali; nella formula della distanza relativistica, a causa del segno meno che sottrae dalla parte temporale
al quadrato la parte a spaziale al quadrato avremmo perciò una somma totale minore di T' (le parti temporali si ottengono proiettando i vertici della spezzata sull'asse dei tempi)
potremmo estendere a spezzate sempre con più lati fino al limite per ottenere la curva.
Se questo è vero si risolve subito il paradosso dei gemelli, in quanto la spezzata del gemello in moto che inverte la rotta diventa un caso particolare di questo problema.
cari amici,
anche se siete solo due devo dire che avete azzeccato il problemino. Umberto è stato molto sintetico ed esauriente, mentre Paolo, come sempre, ha descritto completamente la situazione senza approfittare di generalizzazioni che renderebbero il tutto più semplice e immediato.
COME DISTRUGGERE "OSSERVATIVAMENTE" IL PARADOSSO DEI GEMELLI
Innanzitutto, vediamo come sia semplicissimo calcolare graficamente quanto passi più lentamente il tempo per chi viaggi a grande velocità su un’astronave, se misurato da un osservatore fermo. Sfruttiamo il fattore di Lorentz, proprio quello che ci permette di valutare la dilatazione del tempo in funzione della velocità di una astronave.
Eliminiamo, innanzitutto, un errore che si commette spesso. Si legge e si sente dire che il tempo per chi viaggia su un sistema in rapido movimento passa più lentamente. Questa affermazione è sbagliata concettualmente. E’ giusto dire che il tempo dell'astronauta passa più lentamente per chi osserva il viaggiatore da un sistema esterno in quiete, ossia che rimane fermo. Ci torneremo sicuramente sopra varie volte, ma è bene eliminare subito questo concetto veramente deleterio. Un’astronave che si avvicina sempre più a un buco nero, ossia acquista una velocità sempre più prossima a quella della luce, appare fermarsi sull’orizzonte degli eventi a un osservatore esterno. Per il viaggiatore, il tempo passa normalmente ed egli attraversa l’orizzonte senza alcun problema. Questo fatto ci porta al tempo proprio che sarà fondamentale nella relatività speciale.
L’orologio di chi viaggia e quello di chi sta fermo girano nello stesso modo, ma è quello dell’astronave che rallenta se visto dall’osservatore esterno. E', nuovamente, solo e soltanto un problema di sistema di riferimento
Poniamo per semplicità X = v/c, ossia X sia il rapporto tra la velocità dell’astronave e quella della luce. In altre parole, esso ci dice a quale frazione della velocità della luce sta viaggiando la nave spaziale. X = 0.1 vuol dire che va a un decimo di c, 0.9 che va a 9/10, e via dicendo. Ovviamente, se v = 0, X = 0 (astronave ferma) non vi è dilatazione del tempo. Se, invece, v = c, X = 1 la dilatazione è massima e l’orologio dell’astronave appare fermarsi. La formula che lega il tempo T’ di chi sta fermo con quello T di chi si muove è data da:
T = T’ (1 - X2)½ … (1)
Per adesso, prendiamola per buona, ma la ricaveremo in modo molto semplice...
Poniamo, inoltre, Y = T/T’. Y indica, così, il rapporto tra il tempo di chi viaggia e quello di chi sta fermo. In altre parole, di quanto rallenta l’orologio di bordo rispetto a quello di chi sta a terra. Ovviamente, come già detto, Y = 0 se X =1. Il che vuol dire che andando alla velocità della luce l’orologio di bordo non gira più. Ciò vorrebbe dire che per un fotone (se potesse avere un orologio) il tempo non passerebbe, se visto da terra… Tuttavia lui viaggia e come e quindi ci raggiunge sicuramente.
La formula (1) diventa:
Y = (1 – X2)½ e ancora (con passaggi elementari):
X2 + Y2 = 1 … (2).
Accidenti! La (2) non è altro che l’equazione di una circonferenza che ha il centro nell’origine degli assi X e Y. Con questo cerchio possiamo fare molte cose. Notate che ormai il tempo è diventato coordinata a tutti gli effetti...
La Fig. 1 (a sinistra) ci illustra questa semplice, ma utilissima rappresentazione.
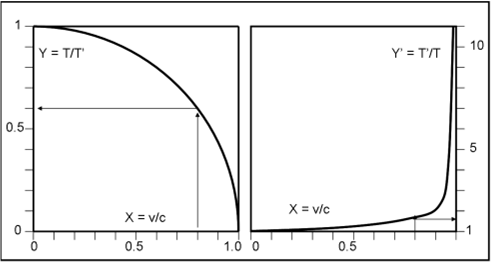
Scegliendo la velocità di crociera si può subito sapere di quanto si dilaterà il tempo dell’astronauta, ossia di quanto il suo orologio girerà più piano di quello terrestre. Ad esempio, se decidiamo che viaggi all’80% della velocità della luce, l’orologio dell’astronave rallenterà del 60%. In altre parole segnerà l’anno 6 quando il nostro segnerà l’anno 10 (sempre che si sia partiti entrambi da zero).
La Fig. 1 (a destra) illustra il viceversa. Ossia rappresenta Y’ = 1/Y in funzione sempre del rapporto X. Y’ è ovviamente il rapporto tra il tempo nostro e quello dell’astronave. Rispetto a quest’ultimo, il nostro orologio viaggia sempre più velocemente a mano a mano che si avvicina alla velocità della luce. Quando la raggiunge, il nostro tempo (T’) è infinito, l’orologio gira in modo pazzesco! Un fotone vede scorrere tutto l’Universo in un attimo. Se invece la velocità dell’astronave diventa zero il nostro tempo e quello dell’astronave diventano nuovamente uguali (Y’ = 1).
La perfetta simmetria
Quanto detto dimostra ancora una volta che le conclusioni sono relative al sistema di riferimento scelto. Se consideriamo il nostro tempo come riferimento, quello dell’astronauta viaggia più lentamente andando verso lo zero. Se consideriamo come riferimento il suo, è il nostro che viaggia in modo sempre più rapido tendendo a infinito.
In entrambi i casi, però, stiamo considerando noi fermi e l’astronauta in viaggio. Lui, però, cosa vede? Esattamente la stessa cosa, ribaltata. Per lui, che può giustamente considerarsi fermo, siamo noi che andiamo a velocità più o meno alta e che subiamo una dilatazione del tempo. La sua astronave è ferma ed è la Terra che si muove a velocità altissima. Ne consegue che nel suo sistema di riferimento è il nostro orologio che appare girare più lentamente, ecc., ecc.
In parole semplici: i due sistemi di riferimento sono inerziali e quindi è possibile invertire completamente i risultati. Un’astronave che viaggia rispetto a una Terra ferma porta alle stesse conclusioni di un’astronave ferma che vede la Terra viaggiare a grande velocità. Ne consegue che per chi sta a terra sarà l’astronauta a invecchiare di meno (è lui che si muove). Per l’astronauta è invece chi sta sulla terra a restare giovane (è la Terra che si muove).
Siamo arrivati nuovamente al paradosso dei gemelli. La relatività ristretta, che si occupa solo di sistemi inerziali, ossia che si muovono uno rispetto all’altro con velocità rettilinea uniforme, comporta questa assurdità: entrambi i personaggi devono invecchiare di meno, dato che entrambi applicano correttamente le formule della dilatazione del tempo.
Il paradosso dei gemelli è ancora oggi spunto per dibattiti più o meno sensati e più o meno complicati. Tuttavia, come tutti i paradossi, non è difficile risolverlo. Basta scegliere le giuste condizioni per affrontarlo. Quello dei gemelli si scioglie come neve al Sole se passiamo alla relatività generale, ossia se si considerano sistemi NON inerziali, sistemi di riferimento che si muovano uno rispetto all’altro con velocità non uniforme, ossia sistemi accelerati.
Ecco che diventa fondamentale conoscere le basi della meccanica classica. Anche lei dice che se si passa da un sistema inerziale a uno accelerato le regole cambiano e uno stesso fenomeno deve essere descritto in modo diverso. Nascono addirittura delle forze fittizie, come quella centrifuga o quella di Coriolis. Ed ecco anche perché, per parlare di Universo, di tempo relativo, di spazio-tempo, ecc., ecc., è necessario conoscere la fisica elementare. Senza di lei il salto verso la relatività diventa un’impresa senza speranza.
Innanzitutto, ribadiamo ancora una volta che il paradosso dei gemelli perde di significato quando il moto dell’astronave e quello della Terra vengono considerati nell’ambito della relatività generale. La Terra può essere considerata un sistema inerziale, ma non certo l’astronave, la quale, per raggiungere una certa velocità deve accelerare e, per tornare a casa, decelerare. Il che implica un moto accelerato e quindi un sistema non inerziale. La simmetria si è rotta. Ne consegue che solo l’astronauta subisce una variazione del proprio tempo e ne conserva il segno al suo ritorno sulla Terra. E’ veramente invecchiato di meno, perché solo lui ha subito accelerazioni e decelerazioni.
Nel libro “L’Infinito Teatro del cosmo” avevo presentato un metodo relativamente semplice per risolvere il paradosso anche ragionando solo nell’ambito della relatività ristretta. Si analizzava il sistema di riferimento dell’astronave che, pur mantenendosi inerziale, cambiava direzione dopo aver raggiunto la stella. Ne conseguiva un “salto” temporale che permetteva di confrontare gli anni effettivi dei gemelli e dare ragione a chi stava sulla terra e pensava di invecchiare di più.
L’osservazione diretta non tradisce mai
Giocherellando, però, con le figure che vi ho mostrato prima, mi è venuto spontaneo considerare anche un altro modo per risolvere il paradosso: un modo puramente “empirico”, ossia osservativo.
Si può dimostrare che chi viaggia è veramente invecchiato di meno, pur mantenendo immutata la simmetria apparente tra chi viaggia e chi sta fermo, come impone la relatività ristretta.
Attenzione, però: non si risolve veramente il paradosso, ma, seguendo cosa succede, si arriva a una conclusione univoca. In altre parole, ci si disinteressa del problema “teorico” o concettuale sulla perfetta inversione dei sistemi di riferimento dettata dalla relatività ristretta, ma si valuto solo ciò che capita osservativamente.
Ciò che mi piace in questo approccio è il fatto che si deve partire dal caro e amato cono di luce.
Solo un accenno, ma quanto basta per capire tutte le connessioni che esistono tra le grandezze in gioco. Attraverso di lui si può fare di tutto e di più… e Minkowski ce lo insegnerà.
Disegniamo, allora, in Fig. 2, il cono di luce della Terra come “sfondo”. Lo mettiamo orizzontale. Lo spazio, ossia la distanza tra la Terra e tutto il “resto” sia l’asse delle ordinate. Le distanze su di esso si misurano in anni luce. L’asse delle ascisse è invece il tempo terrestre, espresso in anni. Sia T’ questo tempo. La linea di Universo della Terra è, ovviamente, proprio l’asse del tempo.
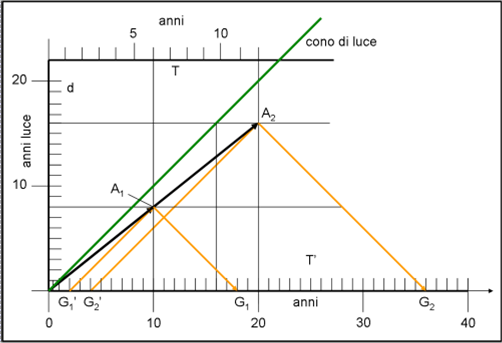
Il bordo superiore del cono di luce futuro, al tempo T’ = 0, è la linea verde, inclinata di 45°. L’inclinazione ottenuta dipende dal fatto che l’unità delle ascisse è l’anno e quello delle ordinate l’anno luce: in un anno di tempo, la luce percorre proprio una distanza di un anno luce. Ricordiamo che, per definizione stessa di velocità della luce, niente, originatosi sulla Terra, può superare la linea verde. Teniamo bene a mente che stiamo vedendo tutto nel sistema di riferimento della Terra intesa come immobile.
Facciamo partire l’astronave A (linea nera), al tempo T = T’ = 0, a un velocità che sia pari all’80% di quella della luce. La Fig. 2 illustra l’astronave inviata nello spazio per sempre (non è previsto il ritorno). Dopo 10 anni terrestri l’astronave giunge sulla stella A1 che dista 8 anni luce da noi. Questo è un dato di fatto, dato che la sua velocità è stata proprio scelta così: v = 0.8c (circa 240 000 km/sec). L’astronauta guarda il suo orologio. Sembra tutto normale, ma sa che rispetto a quello terrestre esso è andato più piano e gli è facile calcolare di quanto attraverso la Fig. 1 che si è portato dietro: essa ci dice che vale T = 0.6 T’, ossia T = 0.6 · 10 = 6 anni. Il suo orologio nel sistema di riferimento terrestre segna 6. Ma, a noi, per adesso, interessa poco quello che vede il viaggiatore…
Possediamo ormai telescopi fantastici e vogliamo vedere direttamente il suo orologio. Quando, però potremo vederlo? Beh… si deve, comunque, aspettare che la sua luce arrivi fino a noi. Per ottenere questo bisogna aspettare 8 anni (la stella dista 8 anni luce da noi). L’orologio dell’astronave, che segna l’anno 6, viene visto sulla Terra in G1, nell’anno 10 + 8 = 18. Dalla pura osservazione possiamo dire che quando l’orologio dell’astronauta segna 6 noi siamo già a 18. Il suo orologio è andato tre volte più lento del nostro.
Anche l’astronave è munita di un fantastico telescopio. Cosa osserva l’astronauta quando giunge in A1? Vede la luce che giunge dalla Terra partita nell’anno 2 da G1’. In altre parole, l’orologio terrestre segna 2 mentre il suo (secondo la Fig. 1) segna 6. Per l’astronauta l’orologio sulla Terra è andato tre volte più piano del suo. Fino a qui nessun problema: cambiando sistema di riferimento si è invertita la visione degli eventi. La simmetria è perfetta e la relatività ristretta è soddisfatta. Ricordatevi che stiamo eseguendo osservazioni perfettamente realistiche. Nessuno può dire che quanto descritto non sia giusto.
L’astronauta riparte (anzi, non si è mai fermato se no avrebbe variato velocità) e giunge dopo altri 10 anni terrestri sulla stella A2 che dista da noi 16 anni luce. Per raggiungerla ha, ovviamente impiegato, totalmente, 20 anni terrestri. Tuttavia, cosa segna il suo orologio ? Beh… facile a dirsi, visto che la velocità è sempre la stessa e che la distanza percorsa da A1 a A2 è nuovamente 8 anni luce. La dilatazione del tempo non cambia e quindi l’orologio segna 6 anni in più di prima, ossia 12.
Notate che sulla parte alta della figura ho inserito la scala del tempo dell’astronauta (il suo orologio visto nel sistema di riferimento terrestre), ottenuta proprio moltiplicando il tempo terrestre per il fattore 0.6. Posso inserire questa scala nel sistema di coordinate terrestri. Se cambiassi sistema di riferimento questa scala non sarebbe più valida, ovviamente. Inoltre, questa scala di tempo vale solo per la velocità scelta. Se cambio velocità, cambia il fattore di Lorentz e quindi anche la scala. Nell’esempio che stiamo descrivendo, però, questa scala è del tutto valida per guardare l’ora del viaggiatore spaziale nel nostro sistema di riferimento.
In A2, quindi, l’orologio dell’astronauta segna 12. Quando viene visto sulla Terra questo orologio con questa ora? Ovviamente, in G2, nell’anno 36 (18 + 18). Cosa si dice sulla Terra? Che il tempo dell’astronauta ha continuato ad andare tre volte più lento del nostro. Tutto secondo le regole. E l’astronauta giunto in A2? Il suo orologio segna 12 (esso segna il tempo che si vedrebbe dalla Terra), mentre quello che vede sulla terra soltanto 4 (luce partita da G2’). Anche per l’astronauta le cose non cambiano. Sulla terra il tempo continua a viaggiare tre volte più lentamente del suo. La simmetria si mantiene perfetta, in accordo con la relatività ristretta.
Potremmo andare avanti all’infinito, ma le cose non cambierebbero. La nostra simulazione è perfettamente logica, esatta e si basa sulle pure osservazioni. Non solo, ma vi è completa simmetria tra chi viaggia e pensa di stare fermo e chi sta fermo ma viene visto viaggiare. Per sapere chi è veramente invecchiato di più bisognerebbe confrontare gli orologi a uno stesso istante in uno qualsiasi dei due sistemi di riferimento. Questo non potremmo mai farlo, dato che noi e l’astronauta ci allontaniamo sempre di più.
Tuttavia, possiamo provarci, cambiando la simulazione. Questa volta, infatti, quando l’astronauta arriva in A1 non prosegue verso A2, ma torna verso la Terra. Finalmente, sarà veramente possibile confrontare gli orologi nello stesso luogo. Manteniamo, ovviamente, sempre uguale la velocità dell’astronave (se no addio alla relatività ristretta) e teniamo conto del cambiamento di direzione valutando SOLO le osservazioni.
Consideriamo la Fig.3. Fino ad A1 tutto funziona come prima, con entrambi i protagonisti (noi e l’astronauta) che osservano l’orologio dell’altro andare tre volte più piano. Noi sulla Terra, siamo già nell’anno 18, in quanto abbiamo osservato l’orologio dell’astronauta quando era in A1 e segnava 6. Sappiamo, però, anche molto bene che il viaggio di andata e ritorno deve durare 20 anni. Questo è un dato di fatto, dato che la velocità dell’astronave è sempre la stessa e percorre 8 + 8 = 16 anni luce in 20 anni: 10 per arrivare in A1 e 10 per tornare sulla Terra. Nell’anno 20 la nave spaziale DEVE tornare.
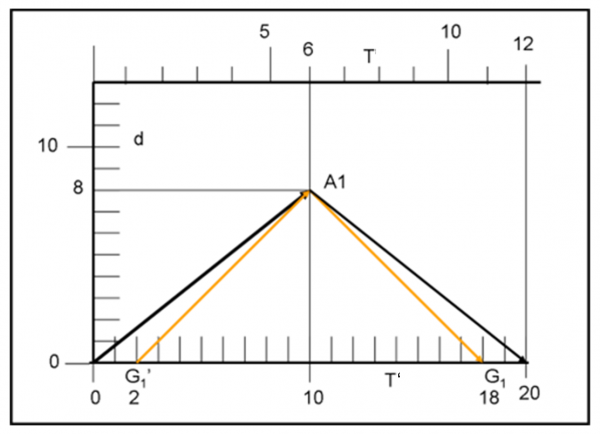
E infatti è così. Nel 20 la nave atterra. Cosa concludiamo noi sulla Terra? Che il viaggio di ritorno è stato rapidissimo: solo 2 anni. Nel 18 l’orologio era ancora in A1 e adesso eccolo davanti a noi! Nel 18 segnava 6 e adesso segna 12. DEVE sicuramente segnare 12 dato che nel viaggio di ritorno l’orologio dell’astronauta ha continuato a rallentare secondo il fattore di Lorentz.
Noi quindi vediamo il nostro che segna 20 e il suo che segna 12. Cosa vede l’astronauta appena giunto sulla Terra? Ovviamente la stessa cosa: il suo orologio segna 12 e quello della Terra segna 20. Accidenti! Ma, allora, il tempo è veramente passato più lentamente per l’astronauta. E’ lui che è invecchiato meno. Dov’è finito il paradosso? Non esiste più…
Un attimo, un attimo. Per cantare vittoria, dobbiamo ancora vedere se si è mantenuta la perfetta simmetria tra chi sta sull’astronave e chi sta sulla Terra. Dunque, per noi sulla Terra sono passati 2 anni (20 – 18), mentre l’orologio dell’astronauta ne segna ben 6 in più (12 – 6). Per l’esattezza, l’orologio spaziale ha viaggiato tre volte più veloce di quello terrestre.
Cosa dice, invece, l’astronauta? Il suo segna 6 anni in più di quando era in A1 (e quindi 12). Quello della Terra, invece, segna ben 18 anni di più (è infatti l’anno 20) di quando l’aveva osservato da A1 (20 – 2). Per lui l’orologio della Terra è andato tre volte più veloce del suo.
La simmetria è rispettata perfettamente anche nel viaggio di ritorno.
Da un punto di vista puramente osservativo, che è poi proprio la realtà, il viaggiatore è veramente il più giovane. Per lui sono passati 12 anni (il suo orologio segna 12), mentre per chi sta sulla Terra ne sono passati 20 (il nostro orologio segna 20).
Dov’è finito il paradosso? Praticamente non esiste più. E’ uno e uno soltanto colui che è invecchiato di meno. Proprio quello che ci direbbe la relatività generale.
E’ chiaro che abbiamo dimostrato la verità nascondendo il vero paradosso sotto il tappeto. Tuttavia, la dimostrazione è a prova di bomba. Come si spiega? Facile, in fondo. Nell’andata abbiamo considerato la nave allontanarsi da noi, al ritorno invece avvicinarsi. In un modo o nell’altro abbiamo rotto la costanza del moto rettilineo uniforme dell’astronave, senza toccare il nostro. E’ quindi ovvio che il paradosso sparisca automaticamente. Il paradosso (da un punta di vista concettuale) continua a esistere nella relatività ristretta, ma le “osservazioni” ci dimostrano che in un viaggio di andata e ritorno è l’astronauta a invecchiare di meno.
Divertitevi a ragionarci sopra, ma posso garantirvi che non fa una grinza… Ricordate sempre, però, che stiamo rappresentando il tutto nel sistema di riferimento della Terra, che è poi quello in cui si svolgono le osservazioni. L’orologio dell’astronauta rallenta perché viene riferito a questo sistema. Nulla toglie però che lui possa sentirsi fermo e osservi la Terra muoversi…
Non dannatevi troppo, però… è solo un piccolo antipasto, per i più esperti, sul quale torneremo appena ci saremo tolti “dai piedi” la relatività galileiana e legheremo in modo indissolubile la coordinata tempo con quella spazio, secondo la regola di Lorentz.
Ricordate , ancora, che il tempo appare passare più lentamente sull’astronave per chi guarda da terra, ma è un po’ come la forza centrifuga che esiste realmente anche se apparente. Il suo orologio va realmente più piano, per noi, e questo è un dato di fatto. Anche se torna a casa non può recuperare il tempo… perso, dato che ha continuato a viaggiare ad alta velocità.
DIVERTIAMOCI A PREPARARE IL PARADOSSO DEI GEMELLI
Vi sono moltissimi modi per presentare, descrivere e risolvere il paradosso dei gemelli. Impostiamolo per quello che è, utilizzando un approccio oltremodo intuitivo. Vi prego di non cercare di trarre affrettate conclusioni (sicuramente giuste) ma che sarebbe meglio “toccare” al momento giusto e con la comprensione completa del diagramma di Minkowski.
Stabiliamo, per gradi, in cosa consiste veramente il paradosso. Abbiamo visto che il tempo per chi viaggia a grande velocità appare scorrere più lentamente per un osservatore che sta fermo (o, meglio, che si considera fermo). Come al solito, immaginiamo che il viaggiatore sia un astronauta e chi sta sulla Terra il suo gemello sedentario. Al momento di partire per le stelle essi devono perciò avere la stessa età. Durante il volo, eseguito a velocità costante (sistema inerziale), il tempo del viaggiatore sembra, perciò, scorrere al rallentatore rispetto a quello che viene misurato nel sistema terrestre.
Questo fatto non può certo meravigliarci dato che deriva direttamente dalla trasformazione di Lorentz e, di conseguenza, dalla relatività della simultaneità. Già a questo punto nasce un problema che non si evidenzia mai abbastanza bene, nelle varie trattazioni che si trovano un po’ ovunque. Quali sono veramente i due sistemi di riferimento? Si parla sempre di “chi sta sulla Terra” e di “chi viaggia sull’astronave”, ma è bene definirli un po’ meglio. Ci aiuta la Fig. 1.
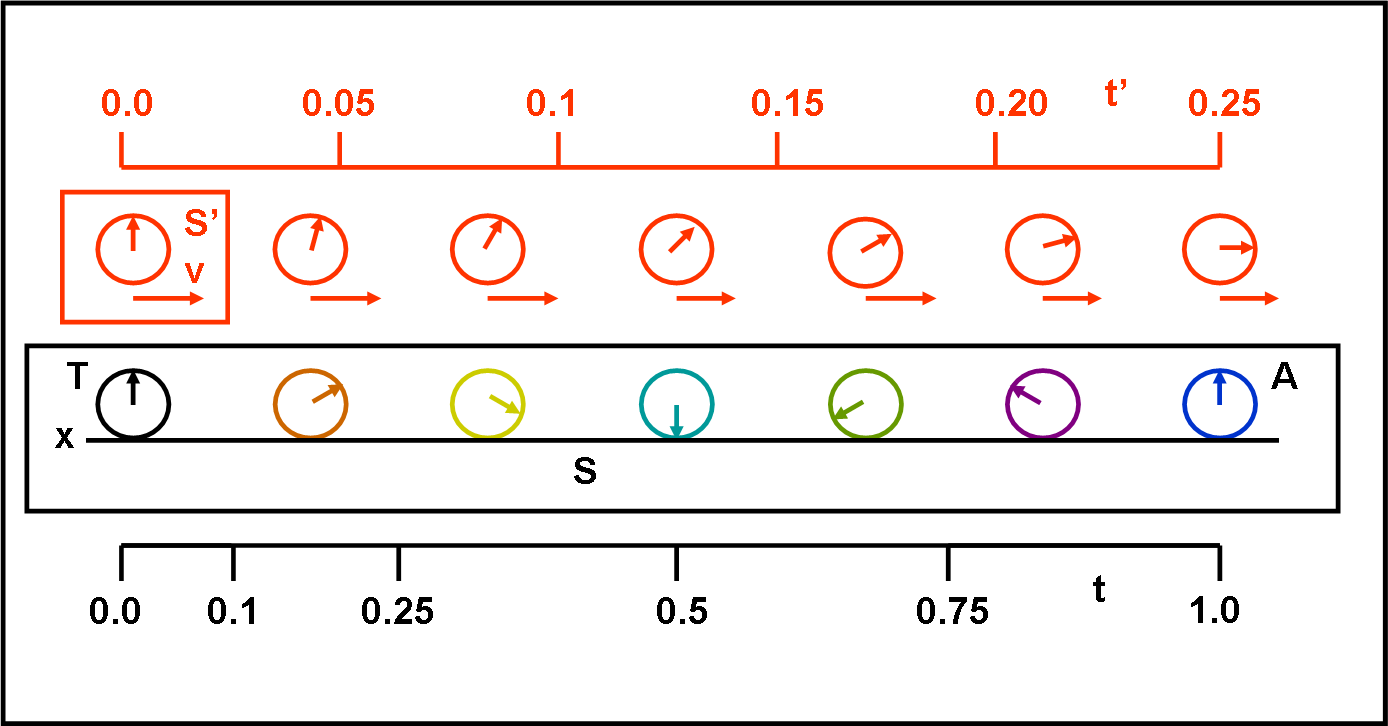
Mentre il viaggiatore (in rosso) rappresenta da solo il sistema di riferimento in moto S’ (non abbiamo bisogno di alti personaggi solidali con lui), l’osservatore a Terra nel sistema S (in nero) ha bisogno di mettere al lavoro molti altri amici che riescano a osservare ciò che capita al viaggiatore. Non facciamo, perciò, lo sbaglio di dire che è sempre lo stesso osservatore che vede il viaggiatore. Ciò è impossibile, dato che la luce impiegherebbe un certo tempo per giungere fino a lui, complicando tutta la faccenda (ne faremo uso, in seguito, ma al momento evitiamo una possibile ulteriore confusione).
Interviene alla grande la definizione di sistema di riferimento. Esso è composto da infiniti osservatori, che si trovano in posizioni diverse, ciascuno con il proprio orologio e distanziati attraverso un regolo unitario. Una struttura che si muove o che sta ferma (anche se “star fermo” non ha un senso fisico) in modo solidale. Un sistema di riferimento va costruito molto bene, come avevamo fatto all’inizio della descrizione della RR. Sono questi infiniti osservatori che possono verificare ciò che capita al viaggiatore che si muove con velocità v e non certo solo il gemello sedentario. Questo fatto non va mai dimenticato.
Detto in parole che ormai conoscete molto bene, la vera differenza sta nel fatto che il viaggiatore (il sistema di riferimento in moto) utilizza un solo orologio, il suo, mentre nel sistema fermo si è costretti a utilizzare molti orologi, ognuno coincidente con la posizione raggiunta dal viaggiatore.
La Fig. 1 cerca di illustrare molto bene questa situazione. Il sistema S’ si muove rispetto al sistema S e durante il suo movimento basta un unico orologio per scandire il tempo. In S, invece, devono essere utilizzati orologi diversi per effettuare il confronto. Si capisce molto bene, quindi, che ricadiamo nuovamente nel problema della simultaneità che è relativa al sistema che si considera. E da questo fatto si arriva facilmente, attraverso la trasformazione di Lorentz, a un tempo che appare scorrere più lentamente per l’orologio in movimento rispetto a quello segnato dagli orologi degli osservatori fermi.
Nella Fig. 1 abbiamo inserito anche i due assi del tempo relativi ai due sistemi. Rispetto al tempo corrispondente agli orologi dell’asse nero, che compiono un giro completo (loro sono comunque sincronizzati), l’orologio rosso compie solo un quarto di giro. Questo è quello che conferma l’orologio posto in A quando vede passare il viaggiatore spaziale S’ con il suo orologio. Dato che l’orologio della Terra T è sincronizzato con quello di A si dice, solitamente, che il gemello fermo in T vede scorrere più lentamente il tempo del gemello sull’astronave. Il discorso è sicuramente valido, ma si rischia di perdere per strada il concetto di simultaneità che deriva dall’uso di uno o di più orologi.
Anche se tutti gli orologi del sistema fisso sono stati sincronizzati, sappiamo ormai molto bene che essi appaiono NON sincronizzati quando si assiste a un fenomeno che avviene su un sistema in movimento. Da ciò segue la relatività della simultaneità e la dilatazione del tempo. Ripeto, nessuno sbaglia e gli orologi sono veramente sincronizzati nel sistema terrestre, ma essi appaiono sfasati rispetto a quello del viaggiatore.
Scusate le continue ripetizioni, ma proprio in questo concetto sta il nocciolo vero di tutta la RR.
Finché tutto prosegue in questo modo, il rallentamento apparente continua e la dilatazione del tempo non smette assolutamente. Tuttavia, basterebbe cambiare il sistema di riferimento dell’osservatore per ottenere lo stesso identico risultato. Non per niente la trasformazione di Lorentz è perfettamente simmetrica. Se, infatti, fosse il viaggiatore a considerarsi fermo, egli sarebbe costretto ad ammettere che è l’orologio terrestre a girare più lentamente. Questa volta, infatti, l’orologio della Terra (quello del gemello sedentario) è più che sufficiente a descrivere il tempo del suo sistema che si muove solidalmente mentre scorre davanti all’astronave. Il gemello dello spazio, invece, è costretto a utilizzare orologi solidali con il suo sistema, posti teoricamente lungo lo spazio percorso dall’unico orologio del gemello terrestre. E’ adesso lui che si muove rispetto all’astronauta ed è il suo orologio che sembra rallentare.
Il paradosso non è certo questo! La relatività speciale ci ha insegnato che la simultaneità e tutte le sue conseguenze sono relative al sistema di riferimento usato per descriverle. Nessuno commette un errore, ma vede solo in modo diverso. I muoni ci hanno insegnato che questa situazione, a prima vista assurda, non lo è per niente, dato che per entrambi i sistemi si ottiene lo stesso processo fisico, in accordo con la relatività. Per uno si dilata il tempo, per l’altro si contrae la lunghezza e tutto, alla fine, torna perfettamente: il fenomeno fisico rimane inalterato.
Tuttavia, ricordiamolo ancora, se si vive in un sistema di riferimento le conseguenze della RR sono reali a tutti gli effetti. Se niente cambia il movimento relativo, il “mondo” del viaggiatore spaziale e “quello” dell’osservatore stabile sulla Terra rimangono inalterati. Ognuno vive la sua realtà e può anche misurarla facilmente.
Per avvicinarci ancora di più al paradosso dei gemelli, riprendiamo la Fig. 1 e trasformiamola nella Fig. 2. Sono solocambiati gli orologi! Invece di usare quelli “meccanici” o “atomici” vogliamo usare un orologio biologico: la crescita della barba. Essa si allunga di una certa quantità in funzione del tempo. Se il tempo rallenta deve rallentare anche la sua crescita. Abbiamo preso la barba, ma potevamo prendere il battito del cuore o qualsiasi altra funzione fondamentale del nostro corpo. Se ammettiamo che il cuore ha a disposizione un certo numero N di battiti prima di farci addormentare per sempre, è ovvio che se rallenta il numero di battiti aumenta il tempo necessario a raggiungere N. Insomma, si invecchia “veramente” di meno. La Fig. 2 è del tutto identica alla Fig. 1, anche se adesso tutti gli amici del gemello sedentario si confrontano con la barba che cresce molto meno della loro e diventano sempre più … tristi. Ancora una volta, il gemello sedentario non può confrontarsi direttamente con il gemello in volo. Lo può fare solo attraverso la barba dei suoi amici che deve crescere esattamente come la sua (le barbe sono state… sincronizzate).
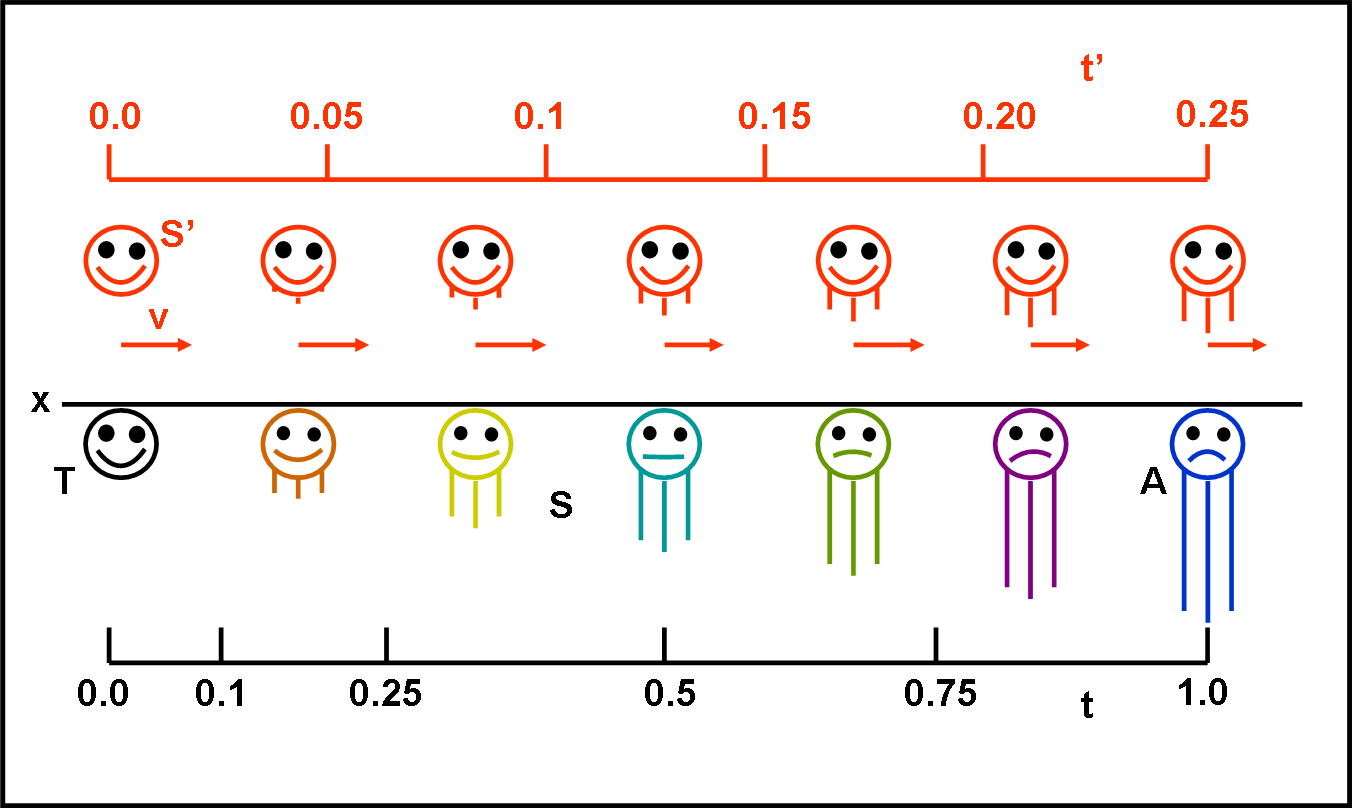
Figura 2
E’ inutile dire che se invertissimo i sistemi di riferimento sarebbe il gemello astronauta a vedere la sua barba crescere sempre di più.
Riflettendo su questi concetti e sulla loro origine non ci si deve sbalordire più di tanto dell’invecchiamento relativo, che è del tutto simile alla dilatazione dei tempi relativa.
Insomma, alla fine si conclude che non c’è niente di male e niente di sconvolgente se sia il viaggiatore che l’osservatore terrestre “vedano” la stessa cosa, ossia un loro invecchiamento precoce rispetto a chi si muove.
Queste considerazioni, che derivano direttamente dalla relatività della simultaneità (e non da un effettivo errore di sincronizzazione degli orologi) ci fanno capire che non esiste nessun paradosso. Tutto è perfettamente spiegabile con la RR. In modo del tutto simile alla favola del muone.
Il vero paradosso nasce quando il viaggiatore vuole confrontare il proprio orologio proprio con quello del fratello gemello sulla Terra e non con uno dei tanti amici di quest’ultimo. Uno potrebbe dire che avendo continuato a viaggiare alla stessa velocità, anche se ha invertito la direzione, dovrebbe rimanere sempre più giovane di chi è rimasto sulla Terra. Ma alla stessa conclusione si giunge invertendo gli attori. Per il viaggiatore dovrebbe invecchiare di meno il gemello terrestre.
Fin qui non ci sarebbe nessun paradosso, anche se non vi sarebbe una vera soluzione. Quando s’incontrano cosa succede veramente? Tornano alla stessa età? O cos’altro? Dato che nella RR tutto è perfettamente simmetrico, uno si potrebbe aspettare che quando il viaggiatore torna al punto di partenza le differenze di tempo apparente si annullino in qualche modo.
E’ proprio a questo punto che nasce il paradosso, dato che quando i due gemelli s’incontrano è proprio il viaggiatore a essere invecchiato di meno. Si è rotta la simmetria della RR? No, nemmeno per sogno, il vero motivo è che si è rottal’inerzialità dei sistemi di riferimento. Quello della Terra non ha mutato la sua velocità (o il suo star fermo, che è la stessa cosa), mentre l’astronauta ha dovuto cambiar direzione. Sappiamo molto bene che anche solo cambiare direzione vuol dire introdurre un’accelerazione e tutta la RR cade! La spiegazione sembra ovvia, anche se è un po’ come passare la castagna bollente al vicino… La RR non può risolverlo e può pensarci la relatività generale che tratta proprio con le accelerazioni e che accetta la mancanza di simmetria.
Non pensiamo che sia un discorso veramente concluso. Ancora oggi si sta discutendo sulla necessità di passare realmente alla relatività generale per superarlo. Sicuramente è più facile. Noi, però, dobbiamo ancora completare l’analisi della RR e non vogliamo addentrarci nelle curvature dello spaziotempo (ogni cosa a suo … tempo). L’esercizio che cercheremo di fare è allora risolvere il paradosso con la sola RR, tenendo, però, in conto che il sistema in movimento, pur rimanendo inerziale, ha cambiato direzione. Assumeremo, però, che è mutata la direzione, ma non il modulo della velocità. Un’esperienza praticamente impossibile senza una qualche forza che agisca sull’astronave, ma che si può ottenere, considerando trascurabili i pochi istanti necessari alla decelerazione e all’accelerazione.
In altre parole, possiamo ricostruire perfettamente il viaggio di andata e ritorno solo attraverso la RR. La vera novità di questo approccio, che utilizza il diagramma di Minkowski a piene mani, è quello di dimostrare che anche con la sola RR il risultato non è simmetrico: il viaggiatore invecchia di meno e questo viene confermato sia dal sistema che viaggia sia dal sistema che è fermo!
Qualcuno potrebbe dirmi: “Non è assolutamente una novità. Tu stesso hai dimostrato in altri articoli che il cambiamento di direzione comporta un’esauriente spiegazione della mancanza di simmetria finale”. Sì, avrebbe ragione… ma la vera novità è che questa volta troveremo la medesima conclusione sia mettendoci nel sistema terrestre sia in quello del viaggiatore. L’importante è che i due gemelli mantengano sempre un contatto “visivo” e facciano un po’ di conti.
E’ inutile continuare, dato che, per andare avanti, Minkowski non deve avere più segreti e deve anche essere introdotta la composizione relativistica delle velocità.
Per adesso c’è abbastanza materia su cui riflettere. Impostare bene un esercizio è già una buona parte della soluzione.
Ciò che abbiamo descritto con tante parole e figure apparentemente banali rinsalda le basi della relatività della simultaneità, della dilatazione dei tempi e della diversa scala temporale che ogni sistema deve adottare. Non consideriamolo come una semplice ripetizione…
I DUE GEMELLI MANTENGONO IL CONTATTO E IL PARADOSSO SPARISCE
I due gemelli possono fare a meno di conoscere la relatività ristretta e le sue formule per arrivare a un risultato assolutamente non simmetrico (e questo non inficia assolutamente la RR). A loro basta mantenersi in contatto visivo o radio e contare il numero di invii e di ricezioni dei segnali. In poche parole, sfruttano solo la costanzadella velocità della luce. Noi, invece, per costruire il disegno esplicativo dobbiamo conoscere bene ciò che capita nel diagramma di Minkowski e sfruttare la trasformazione di Lorentz. Tuttavia, per far ciò, basta utilizzare solo e soltanto delle rette e le loro intersezioni: un gioco da ragazzi!
Una parola in più sulla simmetria che non si mantiene. Sappiamo benissimo che ogni formula della RR può essere tranquillamente invertita. Quello che vede il sistema S’ deve essere visto anche dal sistema S. La trasformazione di Lorentz ce lo impone. Se per chi viaggia è il gemello a terra che resta giovane, deve valere anche l’opposto: per chi sta fermo è l’astronauta a invecchiare di meno. Il fatto che, alla fine, troviamo un risultato UNICO e non simmetrico non vuole assolutamente dire che la RR è da buttare. Vuole solo dire che la sua applicazione ha evidenziato una situazione che non può far parte della RR. Ciò che noi stiamo per fare è dimostrare che il risultato unico, intollerabile dalla RR, può essere trovato lavorando solo con lei…
Ci tengo a dirvi che considero questo metodo come la soluzione forse più intuitiva del celebre paradosso, dato che mostra graficamente come sia realmente il viaggiatore a invecchiare di meno e come anche quest’ultimo non può che essere pienamente d’accordo su questo risultato. Ovviamente, lo ripeto ancora, basterebbe dire che per tornare indietro è necessario decelerare e accelerare, ma sarebbe sbrigativo e scaricherebbe sulla relatività generale il compito della dimostrazione. Basta, invece, considerare trascurabile il periodo di tempo in cui si cambia velocità (cosa fisicamente plausibile) e tutto scorre secondo una logica estremamente efficace e immediata.
Andrò avanti con molta “cautela” non tralasciando nessun passaggio, anche il più semplice. Per seguire l’intera faccenda è solo necessario conoscere la trasformazione di Lorentz e la strana geometria del piano di Minkowski (vedi approfondimento QUI ) in cui oltre a una rotazione degli assi, esiste un invariante che non segue la geometria euclidea (in altre parole, è facile tracciare la curva di calibrazione, la ormai ben nota iperbole equilatera, luogo delle unità di misura degli assi trasformati da Lorentz). Tutto il resto è pura geometria aiutata da banalissime formule.
Pronti… via!
Per ottenere il risultato voluto dobbiamo dimostrare che, qualunque sia il riferimento scelto, sia il gemello terrestre che quello spaziale arrivano alla stessa identica soluzione: è l’astronauta che invecchia di meno. Se entrambi raggiungono la stessa conclusione cade automaticamente il paradosso.
Gli assi t e x sono stati scelti come al solito, in modo da far sì che la traiettoria della luce sia sempre una retta inclinata di 45°. Per semplicità di lettura, consideriamo come unità di tempo l’anno e come unità di distanza l’anno luce. Ne segue che possiamo considerare c = 1 e scrivere il rapporto v/c semplicemente come v. Disegniamolo nella Fig. 1, anche se sarebbe del tutto inutile, ma è bene partire dal banale per cercare di non fare mai salti concettuali troppo bruschi. Nella stessa figura inseriamo la traiettoria dell’astronave. E’ immediato vedere a quale velocità sta andando: 3/5 di quella della luce. D’altra parte si nota subito che percorre 3 anni luce in 5 anni.
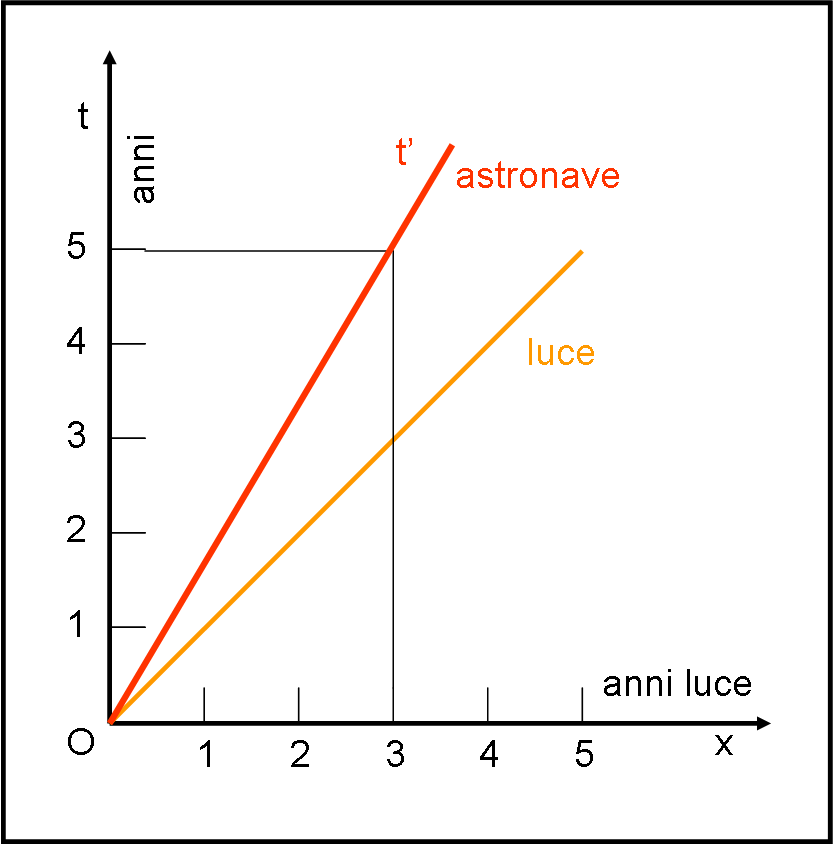
Figura 1
Abbiamo scelto questo valore dato che porta a numeri interi e più facilmente comprensibili. Tuttavia, troveremo le formule generali che servono al nostro scopo e questa scelta apparirà subito molto utile.
Ricordiamo subito come si determina la retta tracciata in rosso. Nel sistema di riferimento della figura essa ha equazione:
t = x/β = x/v
Essa è una retta passante per l’origine di entrambi i sistemi e con coefficiente angolare uguale all’inverso della velocità dell’astronave (c = 1, ricordiamo).
Fin qui, direi che tutto è estremamente banale e immediato (e già descritto precedentemente).
Lasciamo che l’astronave parta per il suo viaggio con v/c = 3/5 e occupiamoci di cosa si deve fare a terra e sull’astronave per mantenere un contatto diretto e continuo.
L’impegno preso è inviare un segnale luminoso ogni anno. Ovviamente, il gemello terrestre lo invia ogni anno terrestre e il gemello astronauta ogni anno trascorso secondo il suo orologio. Ripeto ancora, il tutto è visto nel sistema terrestre. Il tempo dell’astronauta è, come già detto, anche il suo tempo biologico e quindi è più che ovvio che lui si riferisca al suo orologio per mandare i segnali.
Attenzione: non esiste nessuna connessione tra l’arrivo del segnale sull’astronave e l’invio di quello di ritorno. Sia il gemello terrestre che quello spaziale mandano i segnali a distanza di un anno esatto, ognuno misurato con il proprio orologio. Non aspettano l’arrivo dei segnali del gemello per agire, ma lo fanno seguendo un ritmo predisposto fin dall’inizio. Tra poco, vedremo che i segnali sembreranno talvolta simultanei. Non confondiamoci! Questo fatto deriva solo dalla scelta della velocità, ideale per potere eseguire facilmente i calcoli necessari e per la grafica. Ribadiamo ancora, i due gemelli mandano i segnali solo e soltanto allo scadere di un loro anno.
Nel piano di Minkowski, il gemello terrestre descrive, ovviamente, la retta verticale del tempo t, in quanto è considerato fermo. Allo scadere esatto del primo anno manda il segnale al gemello. Quello che vogliamo trovare è il momento di arrivo di questo segnale sull’astronave. Mettiamoci nei panni dell’astronauta: che bello non sentirsi completamente solo anche se la luce ha una lentezza quasi insopportabile.
Disegnare graficamente quanto detto a parole è veramente immediato, dato che gli anni terrestri sappiamo bene come scorrono con la scala decisa fin dall’inizio (anno e anno luce). Più difficile è trovare il momento di arrivo sull’astronave nonché sapere quando l’astronauta deve inviare il suo segnale annuale. In poche parole, bisogna conoscere la scala del tempo lungo l’asse t’ che rappresenta la traiettoria dell’astronave vista nel sistema terrestre.
La faccenda non ci crea grossi problemi, dato che già sappiamo benissimo come fare a trovare l’unità di misura su ogni traiettoria al variare della velocità del sistema in moto. Lo abbiamo fatto sia graficamente che attraverso un po’ di matematica, definendo la ormai famosa curva di calibrazione, l’iperbole che ci permette di descrivere il luogo dei punti che mantiene la stessa unità di misura. Essa ci regala un invariante non euclideo che ci è stato e ci sarà molto utile.
Siamo, quindi, in grado di utilizzare la curva di calibrazione per determinare la “lunghezza” dell’anno dell’astronauta e poi, in qualche modo, valutare graficamente il momento di arrivo della luce del gemello terrestre. Tuttavia, dato che vogliamo prendere sempre maggiore dimestichezza con la geometria di Minkowski, ci dedichiamo a un problemino di geometria elementare, da svolgere nel piano x,t. Ci serve anche come ripasso di molte cose che abbiamo imparato sulla retta.
Per trovare l’evento “arrivo sull’astronave della luce mandata dopo un anno da terra” basta trovare l’intersezione tra la retta descritta dall’astronave e quella descritta dalla luce partita all’istante relativo al primo anno terrestre.
Le due rette (scritte nelle coordinate terrestri) sono:
t = x/v
t = x + 1 …. (1)
La prima è la traiettoria dell’astronave, la seconda la traiettoria della luce che parte al verificarsi dell’evento (0,1). Ricordiamo, infatti, che il coefficiente angolare deve essere uguale a 1 (retta a 45°) e che il termine noto deve essere uguale all’ordinata (t) relativa all’ascissa (x) uguale a 0 (partenza del segnale). La stessa retta acquista subito un carattere più generale e può essere usata anche per gli anni successivi, inserendo al posto di “1” i valori 2, 3, 4, … ecc. In parole povere la retta
t = x + N
dove N è un numero intero che vale 1, 2, 3, ecc. e permette di descrive tutte le traiettorie parallele della luce inviate da terra anno dopo anno.
(1) è un sistemino veramente ridicolo, la cui soluzione ci fornisce le coordinate xA’ e tA’ del punto intersezione A’. In realtà, a noi serve solo il valore di tA’, ma tanto vale risolverlo completamente.
Dalla prima equazione abbiamo che:
x = vt
sostituendo nella seconda:
t = vt + 1
t - vt = 1
t(1 - v) = 1
tA’ = 1/(1 - v)
sostituendo nella prima si ha:
x/v = 1/(1 - v)
xA’ = v/(1- v)
Quello che abbiamo trovato è la “componente” nel sistema terrestre x,t, mentre a noi interessa il valore t’A’ misurato lungo l’asse t’.
Ci viene in aiuto immediato la trasformazione di Lorentz che ci dice:
t’A’ = tA’/γ = tA’(1 – v2)1/2
Da cui:
t’A’ = (1 – v2)1/2/(1 - v) …. (2)
Questa formula ci dà il tempo di arrivo (misurato sull’orologio dell’astronave) del segnale inviato da Terra un anno dopo la partenza da O.
Conoscere questo valore vuole anche dire determinare l’unità di misura sull’asse t’. Come vedete, siamo tornati alla curva di calibrazione e cose del genere. La RR e la sua rappresentazione grafica è come una “frittata”: la si può girare come si vuole, ma i risultati sono sempre gli stessi. Non è nemmeno difficile capire che la “componente” tA’ non fa altro che esprimere e determinare il concetto di dilatazione del tempo. ma ci torneremo a suo… tempo. Torniamo al nostro segnale giunto, finalmente, sull’astronave. Dopo quanto tempo dalla partenza da O il gemello vagabondo lo vede arrivare secondo il suo orologio? Avendo scelto per il nostro viaggio v = 3/5 si ottiene, attraverso la (2):
t’A’ = 2
A questo punto è immediato sapere anche quando arriva il segnale del secondo anno terrestre e quello del terzo e via dicendo. Basta inserire N = 2 , 3, … nella retta descritta dalla luce.
Non stiamo a riscrivere il sistemino (1), ma è immediato capire che il segnale terrestre arriva sull’astronave a un tempo locale che è sempre doppio di quello di partenza da terra (sempre misurato localmente). Così il segnale del secondo anno terrestre arriva al gemello astronauta dopo quattro dei suoi anni e quello dei tre anni terrestri dopo sei anni, tempo locale dell’astronave.
Ricapitoliamo… Cosa significano questi numeri? Dopo un anno dalla partenza, il gemello terrestre manda un segnale luminoso che arriva sull’astronave del gemello spaziale dopo due dei suoi anni dalla partenza. Se il terrestre lo invia dopo due anni, questo arriva sull’astronave dopo quattro ; se lo invia dopo tre arriva sull’astronave dopo sei, ecc.
Il risultato è sicuramente interessante e deriva dalla scelta fatta per v. Ad esempio, se avessimo scelto v =1/2 avremmo trovato un valore di t’A’ uguale a 1.73, molto meno semplice da disegnare. La situazione non sarebbe comunque cambiata per il nostro scopo, ma ci sarebbe stato una discordanza temporale tra l’arrivo dei segnali sull’astronave e sulla loro partenza. Ricordiamoci, infatti, che anche l’astronauta deve mandare i suoi segnali cadenzati anno per anno.
La cosa importante è che abbiamo comunque trovato non solo il momento dell’arrivo dei segnali, ma anche la scala dell’asse t’. Infatti, dato che OA’ deve essere uguale a 2 anni, la sua metà ci regala proprio l’unità su t’. Un altro metodo (ma in fondo è sempre la stessa frittata girata come si vuole) per determinare l’unità di misura del sistema in movimento a seguito della trasformazione di Lorentz.
Comunque sia, possiamo adesso procedere solo in modo grafico, senza più alcuna formula! Non dite che non siete contenti… Segniamo in Fig. 2 quello che abbiamo appena trovato.
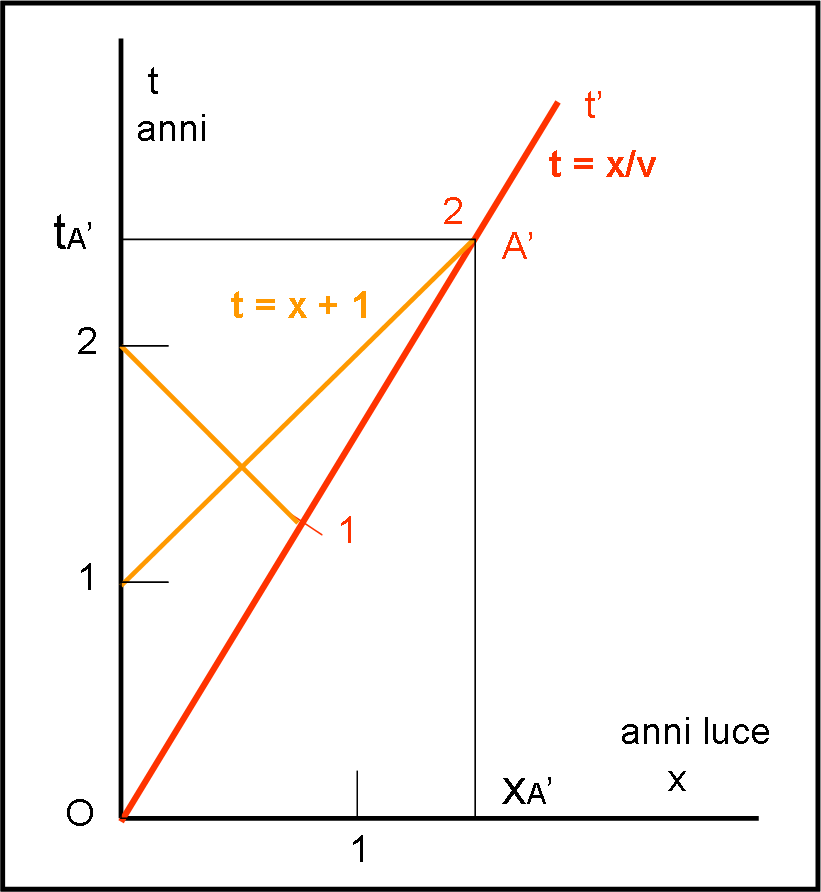
Figura 2
Attenzione: ho usato un metodo puramente geometrico per determinare i momenti di arrivo della luce. L’ho considerato più immediato e molto utile per rinfrescare un po’ del “corso” di matematica. Tuttavia, date la trasformazione di Lorentz e la curva di calibrazione si poteva ottenere la soluzione in vari modi. Tuttavia, il succo era ottenere il grafico risolvente e poco importa come l’abbiamo ottenuto…
Qualcuno potrebbe dirmi: “Sì, va bene, l’astronauta manda il suo segnale ogni anno dei suoi, ma quando arriveranno questi segnali sulla Terra?”. Come dicevo, possiamo risolvere la faccenda lavorando solo graficamente e il risultato apparirà immediato. Tuttavia, se vogliamo fare i raffinati, la risposta si può dare anche senza tracciare linee sulla figura.
Le formule, che abbiamo usato precedentemente per trovare l’intersezione tra la traiettoria descritta dall’astronave e il segnale annuale terrestre, possono essere usate tali e quali invertendo astronave e Terra (Fig. 3).
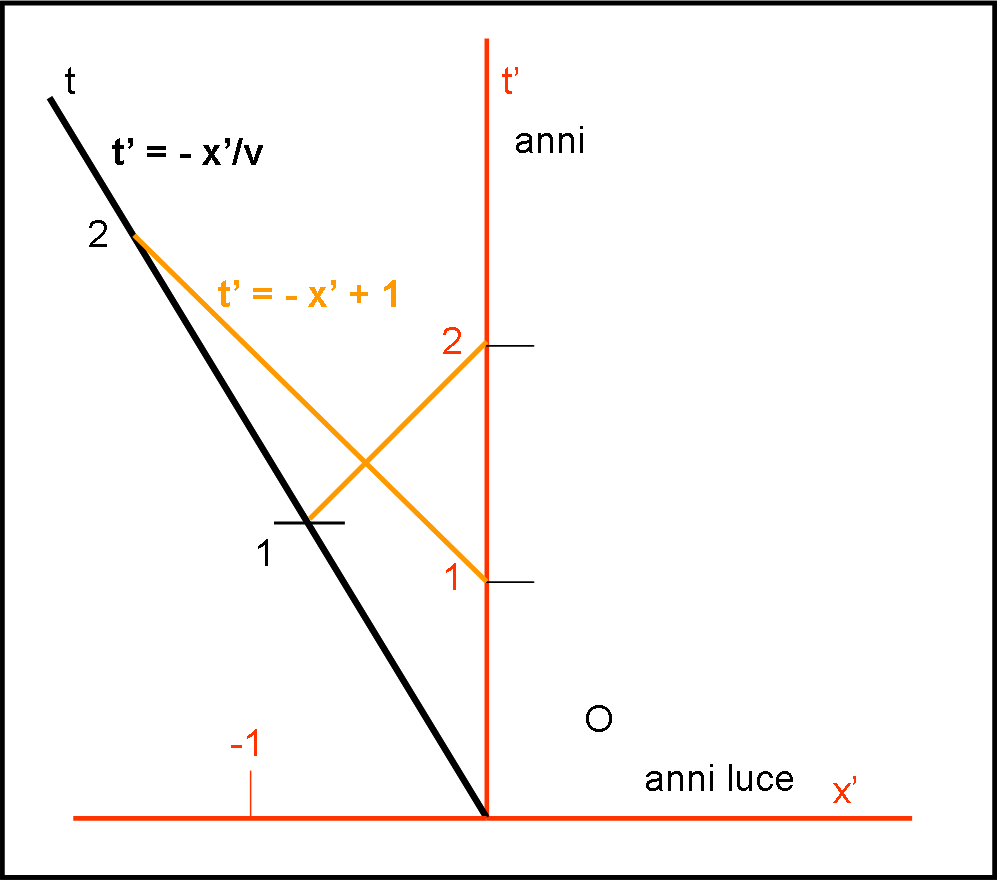
Figura 3
Sappiamo molto bene, infatti, che per l’astronauta è la Terra che viaggia a velocità –v. Se mettiamo t’ al posto di t, la traiettoria della Terra sarà ribaltata rispetto a quella dell’astronave, ma anche la traiettoria della luce lo sarà. Il sistema di prima diventa perciò, rispetto al sistema fisso astronave:
t’ = - x’/v
t’ = - x’ + 1
da cui si ottiene nuovamente:
t’ = vt’ + 1
Per trovare il valore nelle coordinate in movimento t (questa volta è il sistema terrestre che si muove) si applica pari pari la trasformazione di Lorentz come prima e si ha nuovamente t = (1 - v2)1/2/(1 – v). Per v = - 3/5 si ottiene perciò ancora t = 2. Provare per credere…
Ne segue che, a causa del valore della velocità scelta, il primo segnale terrestre arriva sull’astronave dopo due anni dal lancio ed è concomitante con il lancio dall’astronave del suo secondo segnale che arriva a Terra dopo 4 anni dal lancio. A questo punto, come dicevamo, la faccenda diventa una questione puramente grafica.
Disegniamo in Fig. 4 i primi anni di viaggio… e i segnali inviati e ricevuti dai due gemelli. Per una migliore visibilità, usiamo colori diversi per la luce che parte da terra e luce che parte dall’astronave. La prima la coloriamo di blu, la seconda di verde.
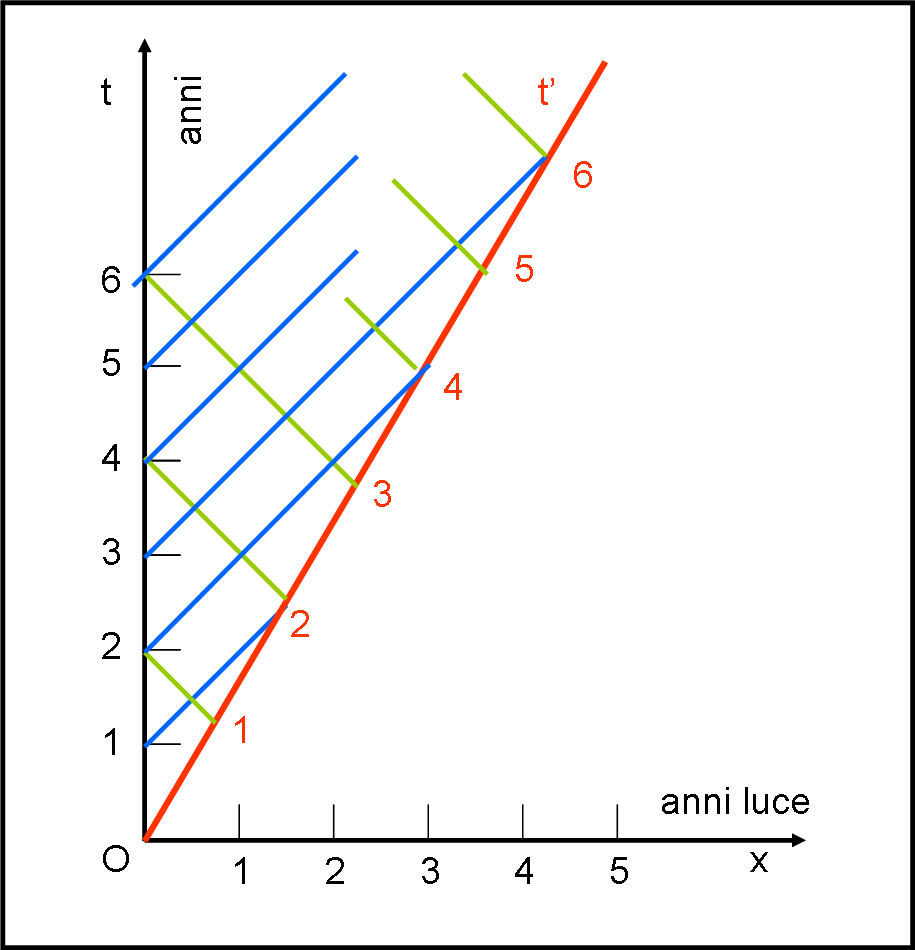
Figura 4
Cosa possiamo concludere, per adesso? Che sia l’astronave che la Terra ricevono il segnale altrui ogni due anni. Tutto è perfettamente simmetrico, come ci dobbiamo aspettare dalla RR. Dopo sei anni di viaggio, la Terra ha inviato sei segnali e ne ha ricevuto tre; stessa identica cosa per l’astronave. I segnali inviati dopo i primi tre anni li abbiamo solo accennati per questioni di spazio…
Potremmo andare avanti all’infinito e la situazione non cambierebbe assolutamente, in perfetto accordo con la RR. Potremmo anche vedere molto bene la dilatazione dei tempi osservata per il sistema in moto. Basterebbe tracciare le parallele a x (linee di simultaneità per il sistema Terra) o, simmetricamente, le parallele a x’ (non disegnato in figura) per determinare la dilatazione perfettamente simmetrica dei tempi osservati sul sistema considerato in moto. Ma, tralasciamo questo aspetto (fondamentale) e proseguiamo con il nostro viaggio. Lo analizzeremo successivamente andando a cercare dilatazione dei tempi e contrazione delle lunghezze…
Il gemello astronauta decide di tornare a Terra dopo aver raggiunto una distanza da Terra (nel sistema terrestre) di 3 anni luce. Ciò vuol dire che nel sistema Terra sono passati esattamente 5 anni. D’altra parte la velocità dell’astronave è proprio 3/5 di quella della luce. Continuiamo, però, a disegnare il tutto nel sistema terrestre. L’inversione di marcia dell’astronave vuole allora dire che essa inizia a muoversi con velocità -3/5.
Possiamo fare questo giochino sul diagramma di Minkowski? Sicuramente sì, dato che il tempo necessario a invertire la direzione (e quindi la decelerazione e la successiva accelerazione) è del tutto trascurabile. Graficamente possiamo permettercelo tranquillamente.
L’intero viaggio, con l’invio e il ricevimento dei segnali, è chiaramente mostrato in Fig. 5. Consideriamo anche come segnale mandato quello relativo al punto di arrivo dell’astronave sulla Terra. In questa situazione entrambi i segnali partono e arrivano simultaneamente dato che l’evento è unico.
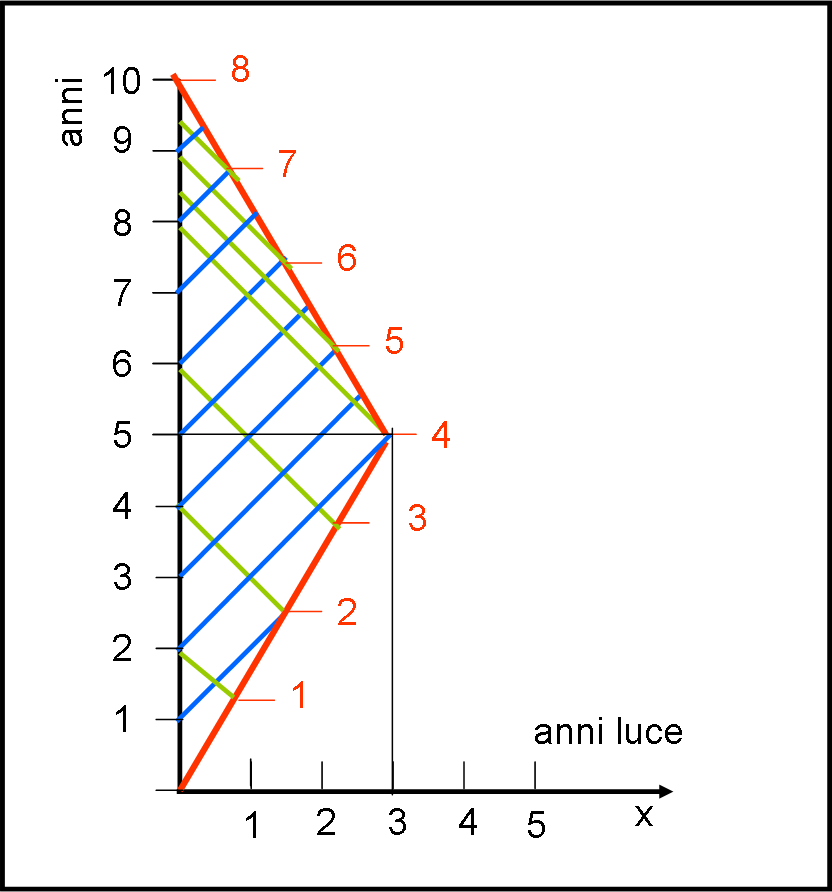
Figura 5
Lascio a voi riflettere sulla figura. Ma risulta chiaro che le cose nel viaggio di ritorno cambiano drasticamente. Dopo l’inversione di rotta i segnali arrivano con frequenza maggiore sia per l’astronauta che per il terrestre: ben due ogni anno locale (graficamente si vede molto bene, ma si potrebbero anche calcolare gli istanti di arrivo, utilizzando sempre il solito sistemino iniziale). Tuttavia, una differenza c’è… Il viaggiatore riceve per metà del viaggio (andata) i segnali del gemello ogni due anni, mentre li riceve ogni mezzo anno per l’altra metà del viaggio (ritorno). Il terrestre, invece, riceve quelli dell’astronauta ogni due anni per ben otto dei suoi anni. Solo dopo, comincia a riceverli ogni mezzo anno. La simmetria non si conserva di certo.
In conclusione, dal punto di vista dell’osservatore terrestre la situazione è abbastanza chiara. Lui ha mandato ben dieci segnali, mentre ne ha ricevuto solo otto. Il gemello astronauta deve concludere, anche se con un po’ di sorpresa, che è proprio vero! Ha ricevuto dieci segnali, mentre ne ha mandati solo otto. Per lui sono passati otto anni, mentre per il terrestre ne sono passati dieci. Il gemello astronauta deve essere veramente più giovane! Il diagramma di Minkowski, con l’aggiunta di qualche segnale luminoso, ha risolto il paradosso.
Per chi ha voglia di riflettere, questo cambiamento di frequenza nell’arrivo dei segnali luminosi rispecchia perfettamente l’effetto doppler relativistico, che, nel caso di una sola coordinata, coincide perfettamente con quello ben noto a tutti noi. A suo tempo potremo anche parlarne un po’ più estesamente.
Cosa ci resta ancora da fare? Dimostrare che il fenomeno dell’invecchiamento UNIVOCO può essere confermato anche cambiando sistema di riferimento. In altre parole, il fenomeno deve rimanere lo stesso anche se si ci mette dal punto di vista dell’astronauta e si descrive il viaggio sotto questa nuova luce. Un esercizio molto utile per “pasticciare” nel nostro “amico” diagramma.
Imponiamo, perciò, come sistema di riferimento “fisso” quello dell’astronave alla sua partenza e vediamo a che soluzione si arriva. Il tutto è riportato in Fig. 6.
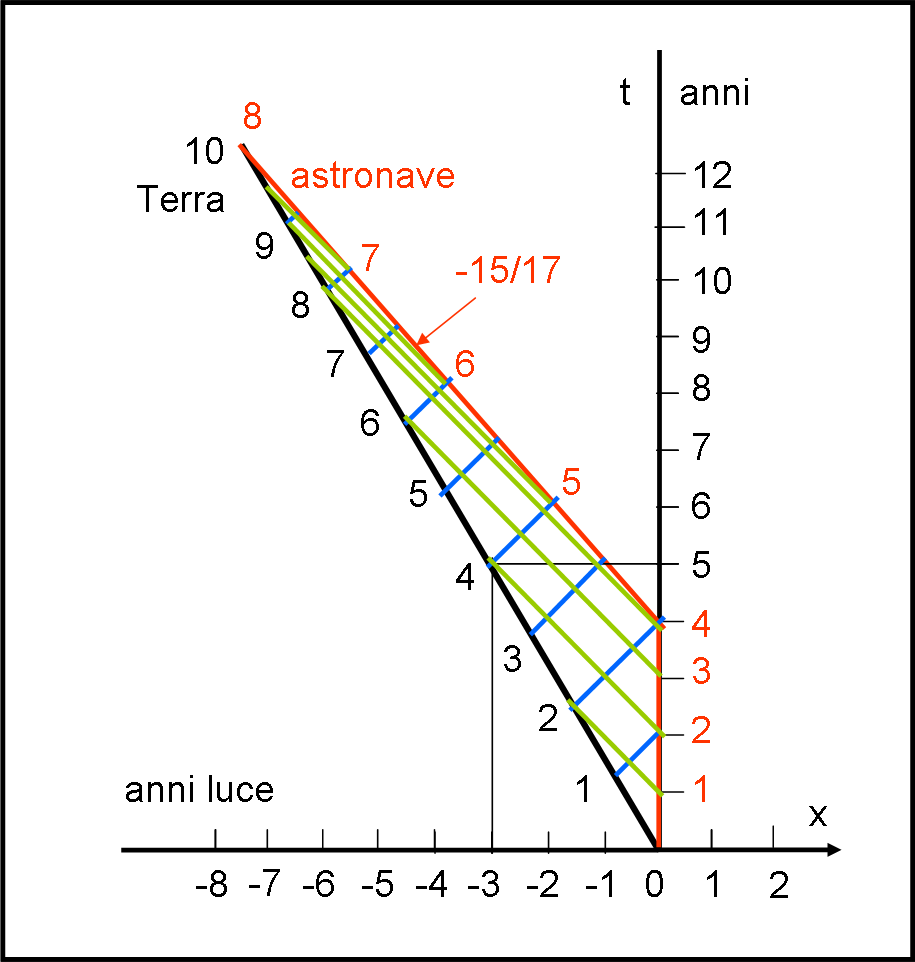
Per i primi quattro anni dell’astronave si segue la retta verticale. D’altra parte sappiamo benissimo che essa impiega quattro dei suoi anni per arrivare al punto di cambiamento di rotta. Rispetto a questa linea verticale la traiettoria della Terra sarà determinata costantemente dalla retta che corrisponde a una velocità -3/5. Anche su questo non ci piove, dato che abbiamo applicato soltanto la RR. La Terra ovviamente percorre tre anni luce in cinque anni, così come faceva l’astronauta nel caso precedente.
Possiamo tracciare tranquillamente i segnali mandati dall’astronauta (luce verde) che colpiscono la Terra ogni due anni, in perfetto accordo con quanto successo nel grafico precedente. Questo fatto capita per ben otto anni terrestri, analogamente a prima.
Ed ecco che giungiamo al punto chiave del nuovo grafico: l’astronave cambia rotta e lascia il sistema di riferimento iniziale. Quale sarà la traiettoria descritta dall’astronauta rispetto alla linea di partenza? Beh… deve muoversi verso sinistra con velocità -3/5, ma non basta. In questo modo si muoverebbe parallelamente alla Terra e noi vogliamo, invece, che torni a casa! Per ottenerlo dobbiamo sommare un’altra velocità -3/5. Eccoci finalmente alla composizione relativistica delle velocità! Per ottenere la velocità con cui si muove l’astronave rispetto alla traiettoria iniziale (durata 4 dei suoi anni) è necessario applicare la formula che abbiamo trovato nel capitolo relativo proprio a questo argomento.
u = (u’ + v)/(1 + u’v)
che nel nostro caso, diventa:
u = (-3/5 -3/5)/(1 + 3/5 x 3/5) = - 6/5/(1 + 9/25) = - 6 x 25/5 x 34 = -6 x 5/34 = -30/34 = -15/17
La retta che descrive la traiettoria dell’astronave fino al suo ritorno a terra avrà quindi come coefficiente angolare -17/15. In realtà, non vi era nemmeno bisogno di calcolarla… Quanto deve essere lungo il viaggio della Terra lo sapevamo già: 10 dei suoi anni. Dopo quattro anni di astronave “ferma” basta congiungere l’evento (0,4) dell’astronave con l’evento corrispondente a dieci anni terrestri…
Comunque sia, abbiamo ottenuto un bel triangolo spostato verso sinistra, in cui possiamo continuare a far partire e arrivare i segnali luminosi tra astronave e Terra e viceversa.
Chi non ci crede, può anche provare a calcolare nuovamente i punti di partenza e di arrivo con le solite rette usate precedentemente, ma troverà, ovviamente, ciò che si vede nella figura.
Dopo quattro dei suoi anni, il tempo sull’astronave scorre molto più lentamente rispetto a prima e raggiunge la Terra ogni mezzo anno dei suoi. Quelli blu mandati da terra, dopo due volte che hanno raggiunto l’astronave ogni due anni (in modo speculare a quanto successo con la Terra considerata ferma), iniziano anche loro a raggiungere l’astronave ogni mezzo anno. Non ci resta che fare i conti e si trova, senza troppa sorpresa, che nuovamente l’astronave riceve dieci segnali da Terra (ossia sa che sulla Terra sono passati dieci anni), mentre il gemello astronauta ne ha inviati solo otto (ossia è invecchiato solo di otto anni).
Abbiamo ritrovato lo stesso risultato di prima, pur avendo cambiato sistema di riferimento. Il diagramma di Minkowski ha permesso di risolvere il paradosso (sempre che si tratti veramente di paradosso) in modo puramente grafico e estremamente “pratico”, basandosi solo sull’invio e la ricezione di segnali luminosi mandati con cadenza annuale.
L’unica cosa che cambia macroscopicamente è la durata dell’intero viaggio misurata nel tempo di riferimento del tragitto iniziale dell’astronave: ben 12.5 anni. Risultato assolutamente non imprevisto, dato che l’orologio della Terra deve andare più piano per tutto il viaggio.
Quando il gemello torna a Terra sa benissimo di essere il più giovane, senza bisogno di effettuare calcoli vari. E’ bastato che contasse quanti segnali mandava e quanti ne riceveva.
Oltre che a risolvere il paradosso utilizzando solo e soltanto la RR, dimostrando che non è lei che “sbaglia” ma è il tipo di viaggio che non rispetta le sue regole, questo esercizio permette di divertirsi un “sacco” con il diagramma, cambiando per esempio le velocità…
Se questo esercizio sarà compreso molto bene, diventerà veramente uno scherzo ricavare rapidamente dilatazione dei tempi e contrazione delle lunghezze, lavorando solo graficamente sul diagramma.
IL PARADOSSO DEI GEMELLI NON ESISTE REALMENTE
(PER CHI HA CAPITO LA RELATIVITA')
Questo articolo affronta il paradosso dei gemelli nella forma da molti usata come la più ovvia, ma che lo è solo apparentemente. Si sente dire: “Basta tener conto della RG è tutto diventa banale”. Sì, ma come e perché? Più che una spiegazione, l’articolo vuole essere una possibile fonte di discussione, dato che l’interpretazione che viene data è abbastanza personale e non da tutti accettata.
Abbiamo affrontato il paradosso dei gemelli in vari modi e tutti corretti, utilizzando solo la RR (relatività ristretta). In particolare, il diagramma di Minkowski ce l’ha mostrato chiaramente: il massimo tempo proprio indica chiaramente la traiettoria seguita nello spaziotempo a velocità costante (o da fermo). Se la velocità non è costante, dato che cambia direzione, il tempo proprio diminuisce. Sembrerebbe quasi di poter concludere che il tempo passa più lentamente per colui che si muove REALMENTE (un’assurdità nella RR dato che sembra pretendere un sistema assoluto di riferimento).
Frase, questa, che fa rizzare capelli in testa, lavorando in RR. Essa ci dice che è impossibile stabilire chi si muove e chi sta fermo. Entrambi i gemelli, nel proprio sistema di riferimento, vedono rallentare l’orologio di chi si muove. Per risolvere la questione bisogna assolutamente modificare il sistema di riferimento. Insomma sembra quasi necessario restare nella RR per risolvere il paradosso, malgrado si dica sovente che tutto si risolverebbe più facilmente nella RG (relatività generale) in quanto l’astronave accelera, decelera, accelera di nuovo e poi decelera per tornare a casa.
Permettetemi di dire che sono “frasi fatte”, che, in realtà non dimostrano un bel niente. A meno di non interpretarle correttamente (sempre che ci si riesca).
La faccenda è più complicata del previsto e in questo ci viene incontro la parte finale della nostra trattazione della RG, quando cercavamo di far MUOVERE una pallina, immersa in un campo di gravità, e ottenere il massimo tempo proprio. Avevamo visto che si riusciva a ottenere il risultato voluto lanciando in alto la pallina. Essa subiva un’accelerazione, una decelerazione, una nuova accelerazione e infine l’urto finale sulla terra. Insomma, era necessario un gioco combinato di RR e RG. Vi era, in fondo, anche una decelerazione finale, istantanea, che trasformava una certa velocità in velocità nulla in un tempo uguale a zero.
In tutto ciò torna ad avere valore chi si muove e chi non si muove. Ciò che era assurdo nella RR non lo é più nella RG. Nella RG, noi che siamo fermi sappiamo benissimo chi è che si muove, ma lo sa anche chi si muove (cosa che nella RR non era vero).
Come fa a saperlo? Facilissimo: chi subisce gli effetti di un’accelerazione o decelerazione sa benissimo di non essere in un sistema inerziale e quindi sa benissimo di muoversi! Abbiamo detto una banalità? Neanche per sogno… ancora adesso vi sono diatribe e discussioni a proposito. Il paradosso dei gemelli, utilizzando la RG, solleva problemi ben più grandi di quando viene trattato solo con la RR. Fatemelo dire con altre parole…
Chi è convinto di stare fermo non ha nessuna prova di muoversi e può continuare a sentirsi nella RR. Lui vede partire l’astronave ed è convinto che sia lei che si sta muovendo. Se rimaniamo nella RR, l’astronave può permettersi di dire lo stesso e per lei è chi sta fermo che si muove con velocità uguale e contraria. Vi è una perfetta simmetria. Solo una rottura di questa simmetria (cambiamento il sistema) può fare ringiovanire il viaggiatore.
Se io viaggiassi a velocità costante, cosa farebbe la pallina che tengo in mano e lascio libera? starebbe ferma nella stessa identica posizione di prima. Se, invece, la vedessi cadere, capirei subito che sono in un campo accelerato, ad esempio un campo gravitazionale (principio di equivalenza).
Chi è accelerato sa anche che il suo orologio rallenta sempre di più a mano a mano che si avvicina alla massa. In qualche modo, è consapevole di viaggiare e di subire un rallentamento del suo orologio. In poche parole, e lo abbiamo anche detto nella trattazione della RG, bisogna tener presente sia la RR sia la RG: la loro combinazione ci regala la traiettoria percorsa da chi si muove realmente, ossia la geodetica.
La faccenda è quindi molto diversa. Riassumiamola ancora: chi sta fermo continua a sentirsi fermo e quindi non può che concludere che sia il viaggiatore a invecchiare di meno. Il paradosso di chi torna a terra, però, scompare, perché anche il viaggiatore sa di essersi mosso e quindi di essere rimasto più giovane. Lui ha sentito l’accelerazione e i suoi effetti (pallina che cade sul pavimento) e quindi non può che prevedere la sua effettiva giovinezza, dato che ha dovuto muoversi.
In altre parole ancora: il paradosso dei gemelli nella RG si risolve molto semplicemente ammettendo che entrambi i fratelli sanno chi si sta muovendo. Il primo perché lui non sente accelerazione, il secondo perché la sente. Il paradosso si scioglie. Ricordiamoci ancora che chi si muove impiega meno tempo a percorrere una certa traiettoria e quindi DEVE restare più giovane.
Nel web ne potete leggere di tutti i colori e leggere spiegazioni che sembrano illuminanti e che poi si mostrano completamente errate. Ve ne cito una che, a prima vista, sembrerebbe essere accurata e decisiva e… invece… (la potenza dei video…).
L’idea di base sembrerebbe giusta, soprattutto quando l’astronauta inverte la rotta. Si dice chiaramente che per tornare indietro il pilota deve accelerare. Facendo questo è come (principio di equivalenza) che si creasse un campo gravitazionale. Il viaggiatore è decisamente più vicino all’origine del campo fittizio di non quanto non lo sia la Terra e quindi la RG dice che il suo orologio DEVE girare molto più lentamente o -se preferite- quello della Terra deve girare molto più in fretta.
Durante il viaggio erano nella RR, ma nell’inversione sono ENTRAMBI nella RG. Anche il viaggiatore capisce che sta ringiovanendo rispetto al terrestre. Si dice anche giustamente che l’accelerazione alla partenza gioca di meno (in quel caso lui sarebbe più “in alto” rispetto a chi sta a Terra) e il suo orologio girerebbe più velocemente, ma in modo meno drastico di quanto succede nel pianeta alieno in cui la Terra è decisamente molto “più in alto”.
Sembrerebbe una buona spiegazione, anche perché alla fine si dice una sacra verità: entrambi sanno chi è che ha viaggiato.
In realtà (ma è una mia spiegazione che può anche essere confutata viste le polemiche ancora in corso), se ci poniamo in queste condizioni, vuol dire che anche chi sta sulla Terra si muove, ossia risente del fittizio campo di gravità che sente il viaggiatore. Se non si muovesse non dovrebbe assolutamente sentire niente e il suo orologio non dovrebbe accelerare. Accettare questa situazione vorrebbe, in pratica, dire che chi entra in un campo di gravità obbliga anche chi ne è del tutto estraneo a sentirne gli effetti. Ma questo non è vero! La gravità e i suoi effetti spaziotemporali sono sentiti solo da chi li sta subendo e non da chi ne sta fuori. E’ solo il cono di luce del viaggiatore che si piega. Quello esterno resta com’è… non c’è nessuna simmetria!
L’errore commesso in questa visione troppo semplicistica si può anche comprendere in altro modo.
Nel video si tratta solo l’accelerazione… Ma che dire della decelerazione? Essa produrrebbe qualcosa di uguale e contrario e il viaggiatore, mentre decelera arrivando nei pressi del pianeta alieno, risentirebbe della gravità che ha origine sulla Terra e che impone al suo orologio (molto più “in alto”) di girare molto più velocemente di quello terrestre. Insomma, secondo me, nascondendo una parte sotto la sabbia, si è reso comprensibile e convincente un qualcosa che non lo è affatto.
In particolare c’è una frase alla fine del video che mi lascia molto dubbioso: “Sia chi sta sulla Terra che chi viaggia é convinto di essere sempre stato fermo durante tutto il tempo”.
No, su questo io non sono d’accordo… Questa è, ovviamente, una mia visione della spiegazione, ma se qualcuno vede una interpretazione diversa me lo faccia sapere. Non sono affatto sicuro di essere nel giusto… come tanti altri ben più bravi di me…
Riflettiamo ancora un po’ sul paradosso. Se io fossi sicuro di stare fermo potrei concludere che chi si muove ha l’orologio più lento? Assolutamente SI. Prendiamo il muone, anzi due muoni: uno fermo e uno che arriva ad alta velocità sulla Terra. Normalmente si considera il muone che arriva a velocità costante e il discorso torna perfettamente, perché non ci si cura di cosa vede e sente il muone. Tuttavia, si può dire benissimo che il più giovane è quello che ha viaggiato! Noi siamo capaci di dirlo con certezza. E, in fondo, lo potrebbe dire anche il muone in viaggio, perché sa che sta subendo gli effetti della gravità! Si sente sicuramente diverso da suo fratello che non si è mosso. Il tempo in cui nascono i due muoni (quello terrestre e quello atmosferico) è un tempo terrestre (per esempio), ma appena l’alieno si muove, cambia il suo tempo e la simultaneità. E’ come se lui fosse ben più avanti del fratello a riposo. L’osservatore a terra, l’unico che valuta la situazione finale, direbbe che ha vissuto più a lungo, sia in RR che in RG.
L’esempio si può fare ancora meglio entrando in laboratorio. Costruisco due muoni. Uno lo lascio fermo, mentre l’altro lo faccio muovere velocemente lungo una circonferenza attorno al gemello, magari attraverso un campo magnetico costruito “ad hoc”. State pur certi che il muone fermo morirebbe prima del fratello in moto, ma non ci sarebbe nessun paradosso, dato che entrambi i muoni sanno benissimo chi dei due è in movimento! Quello fermo perché vede girare il fratello; quello in moto perché sente l’accelerazione e quindi non può nascondersi la verità.
Non prendete per oro colato tutto ciò che ho detto… A questi livelli “quasi filosofici” la discussione è ancora aperta e vede anche insulti reciproci. Un consiglio? Continuiamo a risolvere il paradosso con la sola RR… è molto meglio! Ma stiamo molto attenti a video che sembrano spiegare tutto attraverso immagini accattivanti…
TANTI EVENTI E TRE SISTEMI: IL PARADOSSO È SERVITO!
In questo articolo cerchiamo di descrivere, in modo estremamente accurato, le condizioni che accompagnano il paradosso dei gemelli, basandoci essenzialmente sulla relatività della simultaneità e parlando soltanto di eventi. Assumiamo, ovviamente, come già dedotte le trasformazioni di Lorentz per passare da un sistema di riferimento a un altro e la rappresentazione nel diagramma di Minkowski. Abbiamo così in mano tutti i dati per poter risolvere, nel modo preferito, un paradosso che tale, in realtà, non è, ma deriva solo da una violazione della relatività ristretta. In particolare, si dimostra che una soluzione banale e ovvia si ottiene solo con almeno tre sistemi di riferimento (a meno di non passare alla relatività generale, dove il paradosso cessa di esistere).Vediamo, inoltre, come anche altri approcci trattati precedentemente abbiano pari valore e non si discostino molto uno dall’altro.
Consideriamo, in Fig. 1, come sistema “fermo” quello che contiene sia la Terra che Alpha Centauri.
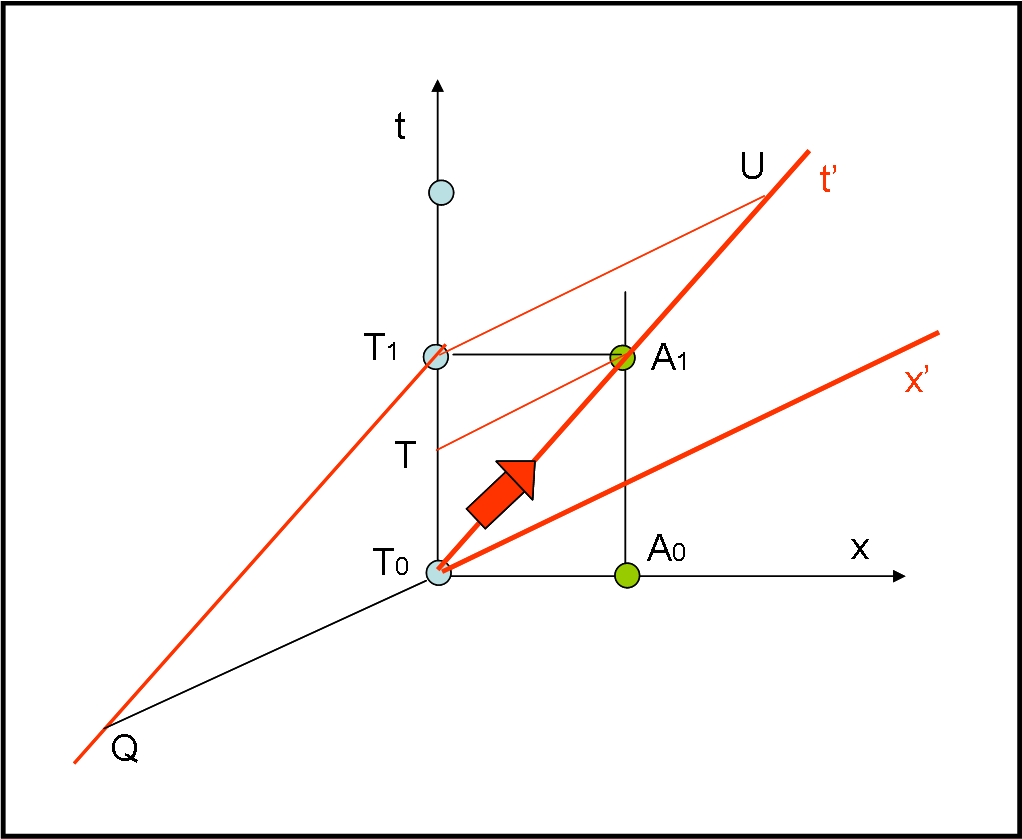
Le coordinate degli eventi in questo sistema S siano x e t. La Terra (azzurra) e Alpha (verde) sono, perciò separate solo da una distanza pari a 4 anni luce che si mantiene costante. I pallini azzurri sono eventi che hanno tutti la stessa distanza tra di loro (in particolare, 0) e quindi il tempo che si misura lungo l’asse t è un tempo proprio per questo sistema. Analogamente, i due pallini verdi sono eventi che mantengono la stessa distanza (in particolare, 4 anni luce) e, quindi, anche la linea parallela a t che li unisce misura un tempo proprio. La differenza di tempo tra gli eventi T1 e T0 è un tempo proprio, così come la differenza di tempo tra gli eventi A1 e A0. Se l’evento T1 ha la stessa t di A1 gli eventi T1 e A1 sono simultanei, ad esempio t = 5 anni. Notiamo che abbiamo scelto come unità di misura, di x e t, l’anno luce e l’anno, in modo avere c = 1.
Se volessimo andare da T0 ad A1 dovremmo impartire una certa velocità ad una ipotetica astronave, tale da percorrere (per esempio) i 4 anni luce in 5 anni, ossia tale da essere v = 0.8 c. Introduciamo, allora, un nuovo sistema di riferimento S’ solidale con l’astronave, di assi x’ e t’ (rossi). In questo sistema di riferimento il tempo si misura lungo t’ e le distanze lungo x’, per cui l’intervallo di tempo t’ che intercorre tra T0 e A1 diventa un tempo proprio. Notiamo, infatti, che la differenza di distanza tra gli eventi T0 e A1 rimane costante (in particolare, 0).
Nel sistema S, la differenza tra i tempi t relativi agli eventi T0 e A1 è invece un tempo improprio, dato che i due eventi non hanno la stessa coordinata x (una è 0 e la seconda è 4). Analogamente gli eventi T0 e T1 non hanno la stessa distanza nel sistema S’ (la distanza si misura lungo l’asse x’): il primo ha x’ = 0, il secondo ha x’ = T0Q = T1U . Ne segue che la differenza di tempo t’ tra gli eventi T1 e T0 non è un tempo proprio. Lo sarebbe invece la differenza dei tempi tra T1 e Q oppure tra U e T0
In maniera analoga si possono stabilire gli eventi simultanei nei vari sistemi. Nel sistema S l’evento T1 è simultaneo all’evento A1, mentre nel sistema S’ l’evento A1 è simultaneo all’evento T, così come l’evento T1 è simultaneo all’evento U e T0 all’evento Q
In conclusione, impariamo una facile regola per riconoscere due eventi qualsiasi rappresentati in sistemi diversi: se in dato sistema la coordinata x (spazio) è la stessa, la differenza tra i due tempi corrispondenti misura un tempo proprio per tale sistema. Se, invece, i due eventi hanno la stessa coordinata temporale, i due eventi sono simultanei in tale sistema. In caso contrario, abbiamo tempi non propri o impropri ed eventi non simultanei.
Notiamo che stiamo parlando di sistemi riferimento, i quali sono caratterizzati da una miriade di orologi perfettamente sincronizzati dislocati per tutto lo spaziotempo, per cui non c’è bisogno, per un certo osservatore, di vedere direttamente un orologio di un altro sistema, distante spazialmente da lui (ossia attendere che la luce lo raggiunga), dato che c’è sempre un orologio del primo sistema vicino a lui.
Questa parte introduttiva è stata inserita per capire bene cosa s’intende per tempo proprio e tempo improprio: tutto dipende dalla differenza di coordinate misurate nei sistemi di riferimento. Detto in altre parole, tutto dipende dalla relatività della simultaneità degli eventi, la vera base di tutta la RR.
Fatte queste premesse fondamentali, possiamo cercare di affrontare il paradosso dei gemelli G (sedentario) e G’ (astronauta), basandoci solo e soltanto sulle coordinate dei vari eventi che caratterizzano il problema. Scoprendo presto che due sistemi non possono bastare, andiamo a calcolare tutte le coordinate degli eventi fondamentali in tresistemi di riferimento, in modo da avere un quadro completo di tempi propri, impropri e di eventi simultanei. I sistemi sono S, quello terrestre e di Alpha; S’, quello relativo al viaggio di andata dell’astronave; S”, quello relativo al viaggio di ritorno dell’astronave sulla Terra.
Il sistema terrestre
Immaginiamo, allora. che un’astronave parta realmente per Alpha Centauri all’istante t = t’ = 0, così come rappresentato in Fig. 2 con una velocità di 0.8 c.
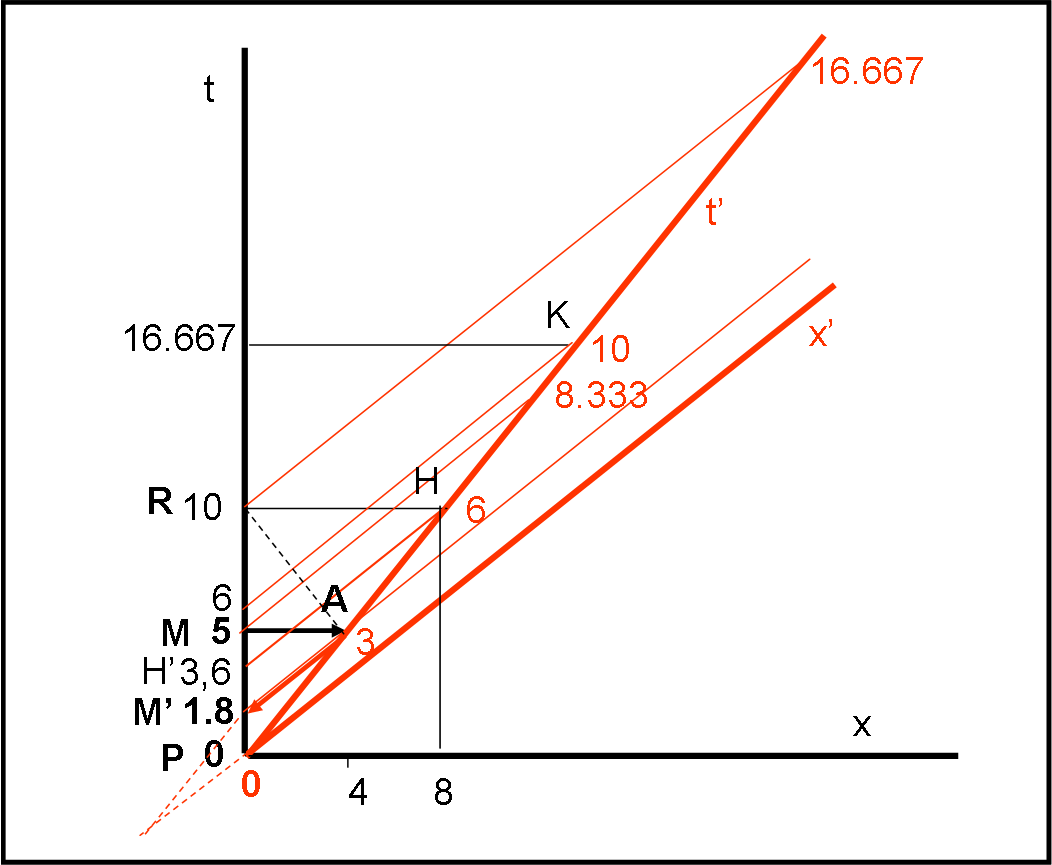
Calcoliamo subito il valore del fattore di Lorentz γ, che ci servirà presto e che ben conosciamo:
1/γ = √(1 – v2) = √1 – 0.82 = 0.6 (c = 1)
Facciamo pure viaggiare l’astronave senza fermarla mai e cerchiamo di fare chiarezza sui vari eventi che ci possono interessare. I primi tre, i più ovvi, sono
L’evento P: partenza dell’astronave dalla Terra
L’evento A : arrivo dell’astronave su Alpha Centauri
L’evento R : ritorno dell’astronave sulla Terra
A questi ne aggiungeremo altri, un po’ alla volta
Richiamiamo le trasformazioni di Lorentz che permettono di passare dal sistema di riferimento S’ (viaggio di andata) al sistema terrestre S (e viceversa).
x’ = γ(x – vt) …. (1)
t’ = γ(t – vx/c2) = γ(t – vx) …. (2)
Consideriamo gli eventi P, A, R nel sistema di riferimento terrestre S. Essi sono definiti dalle coordinate (x, t) e risulta, immediatamente:
PS (0,0)
AS (4,5)
RS (0,10)
Esse si derivano facilmente, calcolando il tempo necessario all’astronave per raggiungere Alpha e per tornare indietro nel sistema S. La velocità è 0.8, per cui il tempo per arrivare su A che dista 4 anni luce, deve essere 5 anni. La stessa cosa succede per tornare indietro. Notiamo subito che il tempo che trascorre andando da RS a PS è un tempo proprio. Ci torneremo sopra molte altre volte, dato che vogliamo fare le cose in modo ultra accurato, calcolando anche coordinate non veramente necessarie, in modo da permettere approcci anche diversi.
Aggiungiamo subito l’evento mediano M (evento in cui da Terra si considera che l’astronave sia arrivata in A)
MS (0,5)
Possiamo subito dire che, nel sistema, S l’evento M è simultaneo ad A (stesso tempo) e che tra lui e gli eventi di partenza e di arrivo, gli intervalli temporali sono ancora tempi propri. In poche parole, potremmo già concludere che l’orologio unico della Terra segna 10 anni tra partenza e arrivo dell’astronave (o astronavi… ?) e che nel suo sistema l’astronave arriva su Alpha dopo 5 anni. Tuttavia, il tempo t trascorso per andare dall’evento P all’evento A non è un tempo proprio nel sistema S, dato che le rispettive x non sono uguali.
Spostiamoci, adesso, nel sistema S’ di coordinate x’ e t’
Il sistema del gemello astronauta
Calcoliamo gli stessi eventi di prima nel sistema di riferimento dell’astronave S’ utilizzando la (1) e la (2), dato che ormai conosciamo le loro coordinate x e t nel sistema S.
x’P = γ(xP – vtP)
x’P = (0 – 0.8·0)/0.6 = 0
t’P = γ(tP – vxP)
t’P= (0 – 0.8·0)/0.6 = 0
PS’ (0,0)
Beh… questo era ovvio, dato che l’origine è comune ed è proprio P.
Passiamo all’evento A, le cui coordinate sono adesso calcolate nel Sistema S’
x’A = (4 – 0.8·5)/0.6 = 0
t’A= (5 – 0.8·4)/0.6 = 3
AS’ (0, 3)
La differenza dei tempi tra gli eventi A e P nel sistema S’ è un tempo proprio, dato che la coordinata x’ è rimasta costante, in particolare 0. Ciò vuol dire, in altre parole, che basta un solo orologio dell’astronave per misurare l’intervallo di tempo trascorso.
Calcoliamo anche le coordinate dell’evento M (l’evento del sistema terrestre che corrisponde all’arrivo dell’astronave in A) in S’, ricordando che A e M sono simultanei nel sistema terrestre S.
x’M = (0 – 0.8 ·5)/0.6 = - 6.6667
t’M = (5 – 0.8·0)/0.6 = 8.3333
MS’ (- 6.6667, 8.3333)
Se confrontiamo AS’ (0. 3) con MS’(-6.6667, 8.3333) ci accorgiamo subito che nel sistema S’ il punto A non è simultaneo a M. Ecco che compare il punto chiave di tutta la RR: non si mantiene la simultaneità tra due eventi le cui coordinate sono calcolate in sistemi inerziali diversi. Nel sistema S’, l’evento simultaneo di A sull’asse del tempo t di S, deve avere la stessa t’ di A. Questo evento è sicuramente interessante e lo chiamiamo M’. Calcoliamo, innanzitutto, il suo t nel sistema terrestre (la x è zero per definizione)
Possiamo utilizzare la (2), ricavando la t corrispondente al valore t’ = 3
t’M’ = γ(tM’ – vxM’)
3·0.6 = tM’ - 0
tM’ = 1.8
M’S (0, 1.8)
Immediatamente, otteniamo le sue coordinate nel sistema S’, sapendo già che t’ = 3 (deve essere simultaneo ad AS’)
x’M’ = γ(xM’ – vtM’)
x’M’ = (0 – 0.8·1.8)/0.6 = - 2.4
M’S’ (- 2.4, 3)
Controlliamo, per sicurezza, gli eventi A e M’ nel sistema S’: AS’ (0, 3) e M’S’ (- 2.4, 3). Come previsto (e costruito) i due eventi hanno la stessa coordinata temporale e quindi sono simultanei.
Siamo giunti a un punto”imbarazzante”: L’astronave è arrivata su Alpha e tutto fila liscio con la RR che conosciamo, dato che stiamo lavorando con due sistemi inerziali. Non ci stupiamo di certo che il tempo proprio dell’astronauta sia risultato di 3 anni, mentre l’evento simultaneo al suo arrivo su Alpha, misurato nel riferimento S della Terra, sia di solo 1.8 anni. I due eventi P e M’ misurati in S’ non danno un tempo proprio (M’S’(- 2.4, 3) e PS’(0,0)), mentre è un tempo proprio per il sistema S, per il quale abbiamo M’S (0,1.8) e PS(0,0) (stessa coordinata x). La x’ dell’evento M’S’ è individuata dalle linee sottili rosse tratteggiate.
L’astronave non può invertire la rotta
Non possiamo certo fare invertire la rotta della nostra astronave, dato che in questo caso passeremmo in un altro sistema inerziale dove le coordinate degli eventi cambierebbero nuovamente (per adesso almeno). Possiamo, però, tranquillamente continuare a far volare la nostra astronave lungo la sua traiettoria e vedere come misura, nel suo sistema S’, l’ultimo evento, calcolato precedentemente nel sistema S, ossia il punto R di ritorno dell’astronave previstodalla Terra. La RR non può tradirci.
x’R = (0 – 0.8·10)/0.6 = -13.3333
t’R = (10 – 0.8·0)/0.6 = 16.6667
RS’ (-13.3333, 16.6667)
Non stupiamoci queste strane coordinate. L’astronave se ne sta andando nello spazio e non può certo confrontare direttamente il suo orologio con quello del gemello rimasto sulla Terra, mentre noi volevamo che i due gemelli si incontrassero veramente. Risulta ovvio che il paradosso non ha senso se i sistemi di riferimento inerziali sono solo due: i due gemelli non si potranno mai incontrare. Tuttavia, potrebbero comunque confrontare i loro orologi! Ricordiamoci dei famosi orologi che dislocati ovunque in ogni sistema di riferimento.
Quello che potremmo fare è utilizzare un orologio solidale con la Terra che si trovi proprio lungo la traiettoria dell’astronave. Questo orologio misura lo stesso tempo di quelli terrestri. In altre parole, potremmo vedere che coordinate ha un evento H nel sistema S’ che sia simultaneo con l’evento R nel sistema terrestre: una specie di gemello terrestre “virtuale”
tH = 10
xH = 8
t’H = γ(tH – vxH) = (10 – 0.8·8)/0.6 = 6 anni
Stupendo! Questo basterebbe a dirci che se l’astronauta percorresse due volte la distanza tra la Terra e Alpha (8 anni luce) (in fondo è del tutto equivalente ad andare e tornare) impiegherebbe solo 6 anni contro i 10 dell’orologio misurati dal sistema terrestre. Purtroppo, questo ragionamento può essere immediatamente ribaltato…
Per capire che non abbiamo risolto un bel niente, basterebbe calcolare l’evento terrestre simultaneo all’evento H nel sistema di S’.
Per l’astronauta il punto H ha coordinate
HS’(0, 6)
Qual è l’evento H’ simultaneo a H sull’asse t terrestre? Imponiamo che xH’ = 0 (asse del tempo t)
t’H’ = γ(tH’ – vxH’)
6 · 0.6 = tH’
tH’ = 3,6 anni
Accidenti! Se il sistema dell’astronauta avesse un orologio dei suoi, vicino a questo punto H’ si accorgerebbe che mentre per lui sono passati 6 anni, per l’orologio terrestre sarebbero passati solo 3.6 anni.
Ribadiamo che la RR funziona benissimo e che ogni gemello considera l’altro più giovane solo e soltanto per colpa di un diversa simultaneità. La faccenda è del tutto simmetrica: il tempo non proprio (ossia improprio) è legato a quello proprio corrispondente attraverso quel rompiscatole del fattore γ, che nasce proprio dalla simultaneità relativa degli eventi nei due sistemi
Lo possiamo vedere bene considerando l’evento K. Il tempo proprio dell’astronave vale 10, mentre l’orologio terrestre virtuale vicino a lui (sincronizzato con quello della Terra) segna 16.6667. Analogamente, però, quando l’orologio virtuale (sincronizzato con quello dell’astronave) è vicino a R (dove l’orologio terrestre indica 10) segna 16.6667. Nessuno dei due è più giovane dell’altro o, se preferite, lo sono tutti e due.
Un gemello in più
Non c’è niente da fare: per confrontare veramente l’età, gli orologi dei due gemelli devono venire a contatto: quelli virtuali seguono implacabilmente la RR e l’inerzia dei sistemi. Bisogna inventarsi qualcosa che non sia il solito cambio di direzione repentina che fa gridare allo scandalo molti lettori…
Dobbiamo far tornare l’astronauta sulla Terra per poter realmente vedere chi è il più vecchio, faccia a faccia. In qualche modo quei 3 anni che l’astronauta misura quando arriva su Alpha, devono conservarsi anche tornando indietro. Solo in questo modo potremmo concludere qualcosa di risolutivo.
In altre parole, l’astronauta dovrebbe misurare un tempo proprio di 6 anni tra andata e ritorno e verificare che, anche per lui, il gemello terrestre giungerebbe allo stesso evento dopo 10 anni di tempo proprio.
Il modo migliore è inserire un altro gemello G” che invece di partire dalla Terra, partisse da un luogo posto nel sistema Terra-Alpha, ma a 8 anni luce dalla Terra, con la stessa velocità del gemello viaggiatore G’. G” partirebbe nello stesso momento dell’altro (t” = t’ = 0) e arriverebbe su Alpha nello stesso momento di G’, con la stessa età. Misurerebbe, però, tutti gli eventi posti sulla linea temporale della Terra in un sistema S”, anch’esso perfettamente inerziale.
La differenza fondamentale sarebbe che G” arriverebbe sulla Terra proprio al verificarsi dell’evento R. Potrebbe veramente confrontare il suo orologio con quello di G.
Cosa dovremmo fare in pratica? Considerare come gemello di partenza quello del sistema S’ (G’) e come gemello di arrivo quello del sistema S” (G”). Saremmo sicuri che, sostituendo G’ con G”, al loro arrivo simultaneo su Alpha, l’orologio del gemello G” misurerebbe veramente 6 anni nel momento dell’evento R. L’importante è verificare che per entrambi i gemelli viaggiatori il tempo passato sulla Terra sia veramente 10 anni. A quel punto il paradosso sarebbe risolto (con un piccolo trucco) e potremmo “fregare” la RR in modo truffaldino.
Non ce ne sarebbe nemmeno bisogno, ma per dare a tutti la possibilità di giocare con i vari eventi e riunirli in un unico schema, conviene ricalcolare tutti gli eventi del sistema Terra nel nuovo sistema S”. Nella Figura 3 il nuovo sistema è quello azzurro.
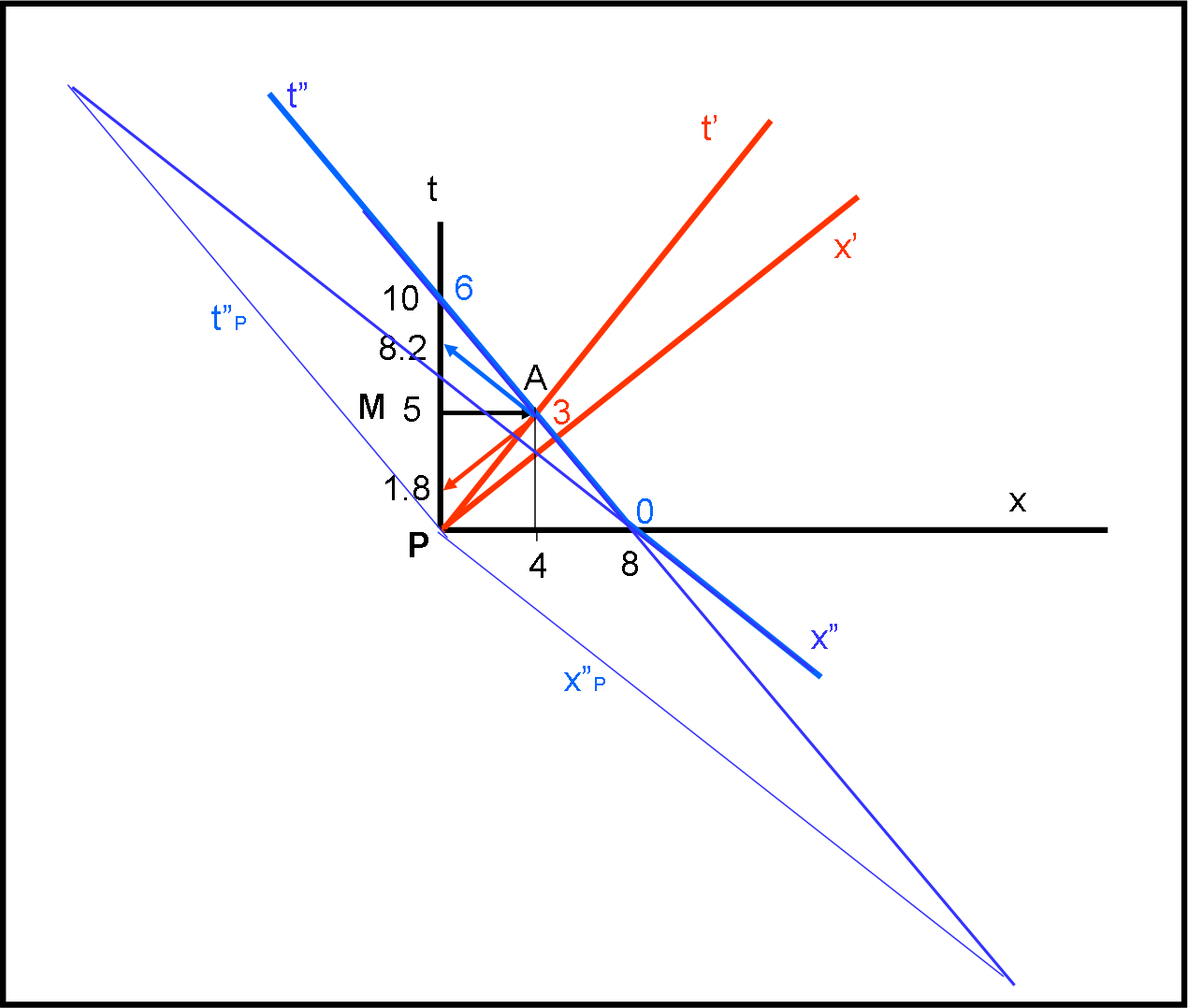
Le trasformazioni di Lorentz per passare da S a S” diventano:
x” = γ(x – 8 + vt) …. (3)
t” = γ(t + v(x - 8)) …. (4)
Notiamo che x” = 0 per x = 8 e t = 0, così come t”, e la velocità ha, ovviamente segno invertito.
A questo punto possiamo ricalcolare tutte le coordinate degli eventi terrestri precedenti. Lascio a voi il compito (un lavoro di pura routine) e fatemi riportare solo i risultati finali:
PS” (-13.3333, -10.6667)
M’S”(-10.9333, -7.6667)
M S”(-6.6667, -2.3333)
R S” (0, 6)
A S” (0, 3)
Abbiamo anche calcolato l’evento A e, come previsto, ci dice che il gemello G” arriva su Alpha con la stessa età e allo stesso istante di G’.
A questi aggiungiamo il punto M”, che altri non è che il punto dell’asse del tempo terrestre simultaneo ad A nel sistema di riferimento S” (analogo a M’ che è simultaneo ad A in S’). Lo calcoleremo anche in S e S’, per completezza.
M’’S (0, 8.2)
M”S’(- 10.9333, 13.6667)
M”S”(- 2.4, 3)
Nella Fig. 3 sono indicate le coordinate di PS”, per meglio comprendere come lavorare graficamente su sistemi non ortogonali… non è cosa molto banale e bisogna farci un po’ la mano (molto meglio fidarsi delle formule).
Il trucco
E’ giunta l’ora di fare una bella Tabella 1 con tutti gli eventi e le loro coordinate nei tre sistemi (ma non dite niente al gemello sedentario…), seguita dalla Fig. 4, che riporti i tempi calcolati nei vari sistemi di riferimento utilizzati.

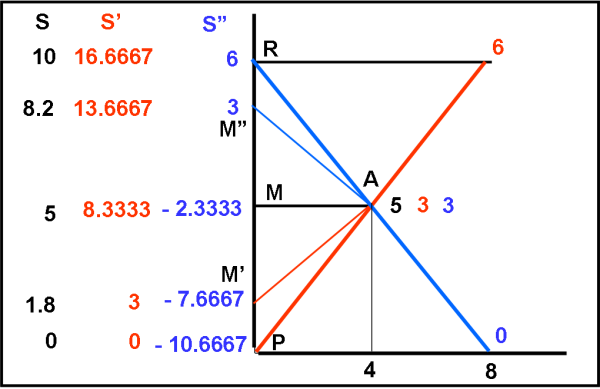
Innanzitutto, vediamo che quando G’ e G” si incontrano in A il loro orologio segna 3 ore. Questo vuol dire che, con un po’ di tecnologia avanzata, potrebbero scambiarsi gli orologi o, addirittura, cambiare astronave! G’, dopo aver fatto il viaggio fino ad Alpha, potrebbe spostarsi nell’astronave di G” e ritornare a Terra. Sarebbe proprio lui a confrontarsi con G e il trucco sarebbe solo quello di aver cambiato astronave (identiche, ovviamente). Purtroppo, G” se ne andrebbe nello spazio profondo. A voi (e a loro) la scelta.
Qualsiasi sia la decisione presa, il gemello (G' o G") che torna a Terra (evento R) è più che sicuro di avere impiegato 6 anni e il suo orologio lo dimostra (ha sempre calcolato un tempo proprio).
L’importante, adesso, è calcolare il tempo passato dal gemello G e verificare che sia proprio di 10 anni. Ma, deve essere 10 anni per tutti e tre i gemelli! Una garanzia fondamentale per concludere che essere rimasto più giovane è una realtà e non una strana magia.
Il gemello G fa in fretta a calcolare il suo tempo: i tempi dei vari eventi trascorsi sono stati tutti misurati con il suo orologio. Possiamo calcolare intervallo per intervallo o fare la differenza tra l’ultimo e il primo, ma il risultato non può che essere 10 anni.
Il gemello G’ (rosso) misura un intervallo di tempo tra R e P che risulta 16.6667. Però sa benissimo che è un tempo improprio rispetto a quello trascorso in S da G. Per trovare il tempo trascorso da G deve tener conto del fattore 1/γ. Ricordiamo che il tempo proprio si ottiene da quello improprio moltiplicandolo per 1/γ = 0.6. G’, quindi, per sapere il tempo proprio del gemello G non fa altro che scrivere:
tRP = t’RP 0.6 = 16.6667·0.6 = 10 anni
Perfetto, anche lui conferma che G è invecchiato di più.
Il gemello G” (azzurro) può fare lo stesso discorso e misurare la differenza di tempo tra R e P e poi moltiplicarla per 0.6. Il suo tempo improprio risulta
t”RP = 6 - (- 10.6667) = 16.6667.
Com'era ovvio... è lo stesso misurato dal gemello G’. Facendo lo stesso calcolo di prima conferma anche lui che per il gemello G sono passati 10 anni.
Volendo essere ancora più raffinati, potremmo calcolare il tempo improprio di G’ da P ad A e trasformarlo in tempo proprio di G per arrivare a M. Non stupiamoci se esso risulta 8.3333 che diventa un tempo proprio di 5 anni. A questo punto lascia il campo al gemello G” (oppure lo calcola lui stesso se cambia astronave) e misura il tempo improprio per arrivare in R. Presto fatto: 6 - (-2.3333) = 8.3333. il che comporta un tempo proprio di G uguale nuovamente a 5 anni per andare da M a P. Ne segue, nuovamente, che anche per G” (o per G’ che ne ha preso il posto) il tempo trascorso da G è proprio 5 + 5 = 10 anni. Tutti sono d’accordo che il gemello viaggiatore che riabbraccia G rimane più giovane di ben 4 anni.
Conclusioni
Questo articolo è sicuramente un po’ strano… Vuole, in pratica, calcolare solo, in modo estremamente semplice, le coordinate di tutti gli eventi che possono essere utili per confrontare tre sistemi di riferimento inerziali. Non consideriamolo, quindi, difficile… dato che ci sono sempre due sole formulette da utilizzare. A questo punto abbiamo in mano tutti i dati per potere immaginare inversioni di rotta, salti temporali o quello che vogliamo. Io ho utilizzato un sistema un po’ truffaldino, ma non poi tanto se cambiamo astronave in A, per dimostrare che il paradosso si risolve solo e soltanto utilizzando tre sistemi di riferimento: siamo comunque riusciti a far incontrare i due gemelli iniziali e dimostrare che uno è realmente più vecchio. L’astronave che continua a viaggiare nello spazio dimostra, però, che con due soli sistemi di riferimento inerziali il paradosso non ha alcun senso, dato che la RR non perde affatto la sua simmetria.
Penso che possiate divertirvi a giocare con i numeri che si sono ricavati nell’articolo e che i concetti di tempo proprio e di simultaneità siano stati (perfettamente) chiariti. Inoltre, visualizzare graficamente le coordinate che si ottengono facilmente con le trasformazioni di Lorentz è un esercizio che può dare molta soddisfazione (bravo Minkowski).
Possiamo considerare questa trattazione come quella iniziale o finale relativa al paradosso dei gemelli e forse quella che riesce a spiegare meglio tutte le stranezze che appaiono, cercando di non cambiare astronave.
Altri approcci
Tuttavia, il paradosso può essere affrontato in vari modi, come abbiamo già visto. Quello che io giudico più rapido e concettualmente più “professionale” è quello che si basa sull’invariante relativistico. Qualsiasi percorso si discosti da quello rettilineo che unisce due eventi, utilizzando un solo orologio (il tempo proprio), si effettua in un tempo minore. Nel caso dei gemelli, è quindi ovvio che il tempo proprio misurato dal gemello G sia più lungo di quello trascorso da una o due astronavi che vadano fino ad Alpha e poi tornino indietro. Addirittura, potremmo anche usare veramente una sola astronave tenendo conto di accelerazioni e decelerazioni e inversioni di marcia, integrando sul tutto il percorso e considerando sistemi di riferimento inerziali variabili continuamente (Fig. 5).
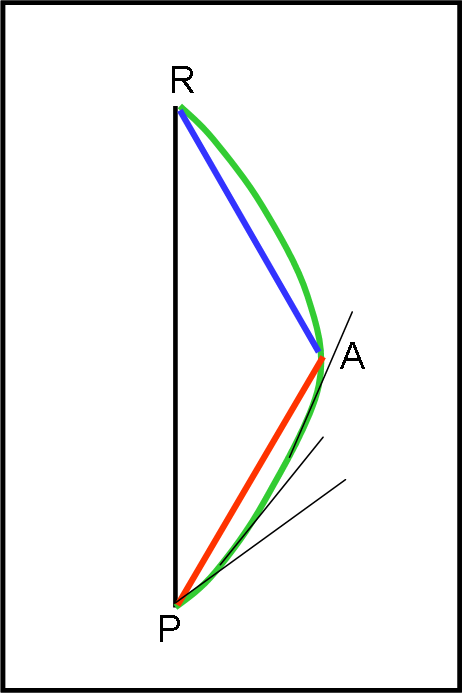
Nell’ambito dell’invariante relativistico non mi dispiace nemmeno la soluzione in cui si confrontano direttamente tempi propri utilizzando l’iperbole di calibrazione. Compare un salto temporale che sembra strano, ma che è il salto temporale effettivo lavorando solo con tempi propri (Fig. 6). In realtà, non è un salto temporale, ma il tempo proprio che manca al sistema "fermo" per pareggiare i due tempi propri del viaggiatore, In pratica è un semplice confronto di "distanze" spaziotemporali.
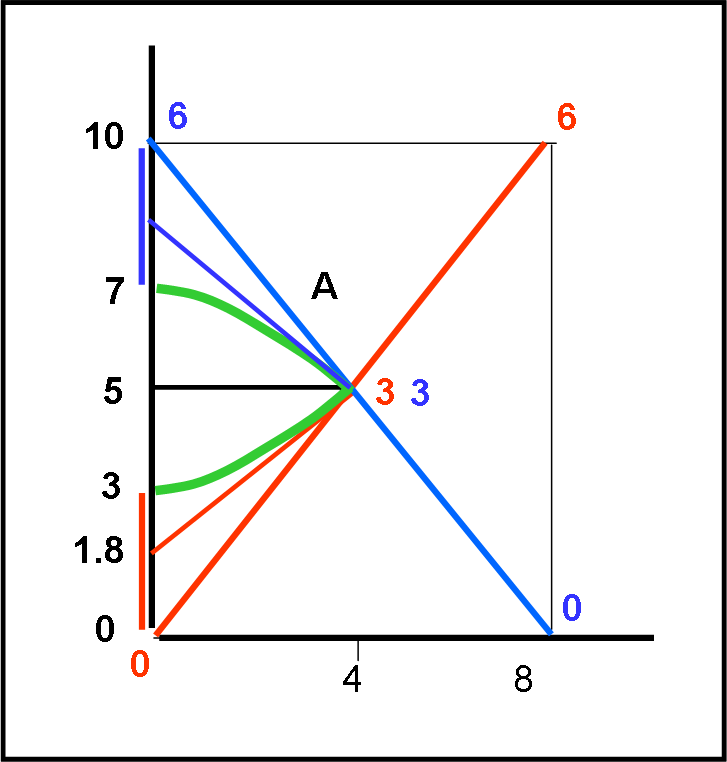
Come già detto, mi piace meno la soluzione che fa uso di … telescopi per vedere l’orologio del l’altro gemello. E’ sicuramente efficace, ma utilizza più che altro la velocità finita della luce e l’effetto doppler relativistico. In qualche modo mischia due effetti e non può assolutamente evitare che la RR entri in ballo in qualche modo. In ogni modo lo abbiamo usato anche noi, per non farci mancare niente.
I più teorici potrebbero dire: tutte approssimazioni o trucchi, il vero metodo è tenere in conto la relatività generale. Tutto si spiega durante l’inversione di marcia dell’astronave. Durante quella fase l’astronave decelera e accelera e quindi subisce una deformazione spazio temporale non simmetrica. L’orologio del terrestre che fino a un certo momento andava più lentamente, si mette a girare come un forsennato dato che quello dell’astronave sembra quasi fermarsi. Ma, come detto varie volte, è del tutto inutile infilarsi nelle equazioni della RG per un problema che si delinea molto bene anche senza di lei.
Infine, non trascuriamo nemmeno la favola di Muo1 e Muo2. In fondo, potremmo lavorare solo sulla contrazione delle distanze e ottenere la soluzione, non preoccupandoci più di tanto se la particella inverte la rotta. In fondo, si “raddoppia” la vecchia favola di Muo.
I DUE GEMELLI DIVERSI I Papallicoli
Nonostante le gigantesche limitazioni, gli ominidi del terzo pianeta del sistema solare, in qualche modo erano riusciti a costruire astronavi in grado di viaggiare a velocità prossime a quelle della luce salvaguardando i fragili organismi viventi al loro interno.
La vicina stella Alpha Centauri distava solo 4 anni luce ed i terricoli avevano costruito quattro stazioni spaziali distanziate fra loro di 1 anno luce, l’ultima delle quali in orbita intorno ad Alpherra, il terzo pianeta della stella Alpha Centauri.
La stazione Alpha 1 distava un anno luce dalla Terra, Alpha 2 due anni luce, Alpha 3 tre anni luce e Alpha 4 quattro anni luce.
I terricoli sapevano molto bene che la distanza tra la Terra e le 4 stazioni spaziali era sempre la stessa, pertanto queste appartenevano tutte allo stesso sistema di riferimento.
Inoltre, qualunque segnale proveniente da Alpha 1, viaggiando alla velocità della luce, avrebbe impiegato esattamente 1 anno per raggiungere la Terra, così come qualunque segnale proveniente da Alpha 2 avrebbe impiegato 2 anni per raggiungere la Terra e così via.
Sulla Terra ancora tutti ricordavano quando era arrivata la notizia che su Alpha 1 era scoppiato un incendio. Nessuno sulla Terra poteva far nulla per aiutarli, poiché quell’incendio era accaduto un anno prima, visto che la notizia aveva impiegato esattamente 1 anno per arrivare fino a Terra.
I grandi orologi presenti nelle 4 stazioni spaziali erano stati tutti sincronizzati con quello terrestre, proprio tenendo conto del tempo necessario alla luce (onde radio comprese) per percorrere la distanza che separava le stazioni spaziali dalla Terra.
Pertanto quando su Alpha 1 era scoppiato l’incendio, l’orologio della stazione indicava che erano le 14:00 del 13 gennaio 2098, mentre la notizia dell’incendio era arrivata sulla Terra esattamente alle 14:00 del 13 gennaio 2099.
Sulla Terra alle 14:00 del 13 gennaio 2098, mentre su Alpha 1 scoppiava l’incendio, era in corso il torneo di lanci lunari, su Alpha 2 l’equipaggio giocava ad Astropoker (ma sulla Terra lo avrebbero saputo 2 anni dopo), su Alpha 3 festeggiavano il compleanno di Angelo del deserto (ma sulla Terra lo avrebbero saputo 3 anni dopo), su Alpha 4 si divertivano a contare le orbite compiute intorno ad Alpherra (ma sulla Terra lo avrebbero saputo 4 anni dopo).
Nella Figura sottostante, viene rappresentato il ritardo con cui l’informazione proveniente dalle stazioni spaziali, che viaggia alla velocità della luce, giunge sulla Terra.
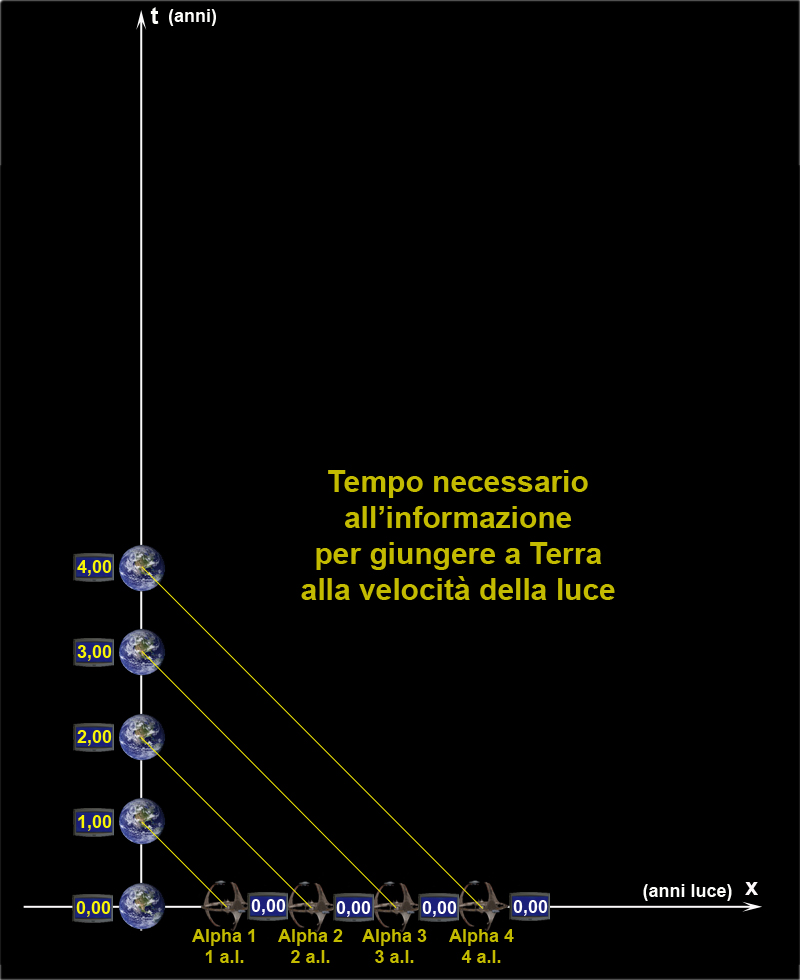
Il 1 gennaio del 2100 era previsto il lancio di un’astronave per un viaggio di andata e ritorno verso Alpha Centauri.
Sull’astronave sarebbe salito il Sig. Flash, gemello del Sig. Stop, che al contrario del fratello non aveva alcuna intenzione di avventurarsi nello spazio.
L’astronave era in grado di raggiungere in un tempo brevissimo una velocità costante di crociera pari all’80% della velocità della luce (V = 0,8 c).
Per il gemello rimasto a Terra, abituato a ragionare solo secondo il suo sistema di riferimento, tutto sembrava scontato.
All’andata Flash avrebbe raggiunto la stazione Alpha 1 dopo 1,25 anni (T = S/V = 1/0,8 = 1,25), Alpha 2 dopo 2,5 anni (T = 2/0,8 = 2,5), Alpha 3 dopo 3,75 anni (T = 3/0,8 = 3,75), Alpha 4 dopo 5 anni (T = 4/0,8= 5).
Come previsto, la stazione Alpha 1 aveva segnalato l’arrivo dell’astronave dopo 1,25 anni dalla partenza ed ovviamente tale segnalazione era arrivata sulla Terra 1 anno dopo, ossia dopo 2,25 anni dalla partenza (Tempo arrivo informazione T + 1 anno = 1,25 + 1), Alpha 2 aveva segnalato il passaggio dopo 2,5 anni dalla partenza e la segnalazione era giunta a Terra dopo altri 2 anni (2,5 + 2 = 4,5 anni dalla partenza), Alpha 3 aveva segnalato il passaggio dopo 3,75 anni dalla partenza e la segnalazione era giunta a Terra dopo altri 3 anni (3,75 + 3 = 6,75 anni dalla partenza), Alpha 4 aveva segnalato il passaggio dopo 5 anni dalla partenza e la segnalazione era giunta a Terra dopo altri 4 anni (5 + 4 = 9 anni dalla partenza).
Il gemello rimasto a Terra era perfettamente soddisfatto. Tutto sembrava svolgersi proprio come si aspettava.
Durante il viaggio di ritorno Flash aveva raggiunto la stazione Alpha 3 dopo 1,25 anni da Alpha Centauri, o meglio dopo 6,25anni dalla partenza (5 + 1,25) e tale segnalazione per giungere fino alla Terra aveva impiegato altri 3 anni (6,25 + 3 = 9,25anni), dopo 7,5 anni dalla partenza (5 + 2,5) aveva raggiunto Alpha 2 e la segnalazione aveva impiegato altri 2 anni per arrivare a Terra (7,5 +2 = 9,5 anni), dopo 8,75 anni aveva raggiunto Alpha 1 (5 +3,75) e la segnalazione aveva impiegato un altro anno per giungere a Terra (8,75 +1 = 9,75 anni) ed infine dopo 10 anni dalla partenza (5 +5 = 10) Flash era tornato sulla Terra.
Il gemello rimasto a Terra ha disegnato anche una figura per mostrare il viaggio di andata e ritorno dell’astronave, così come lui lo ha immaginato.
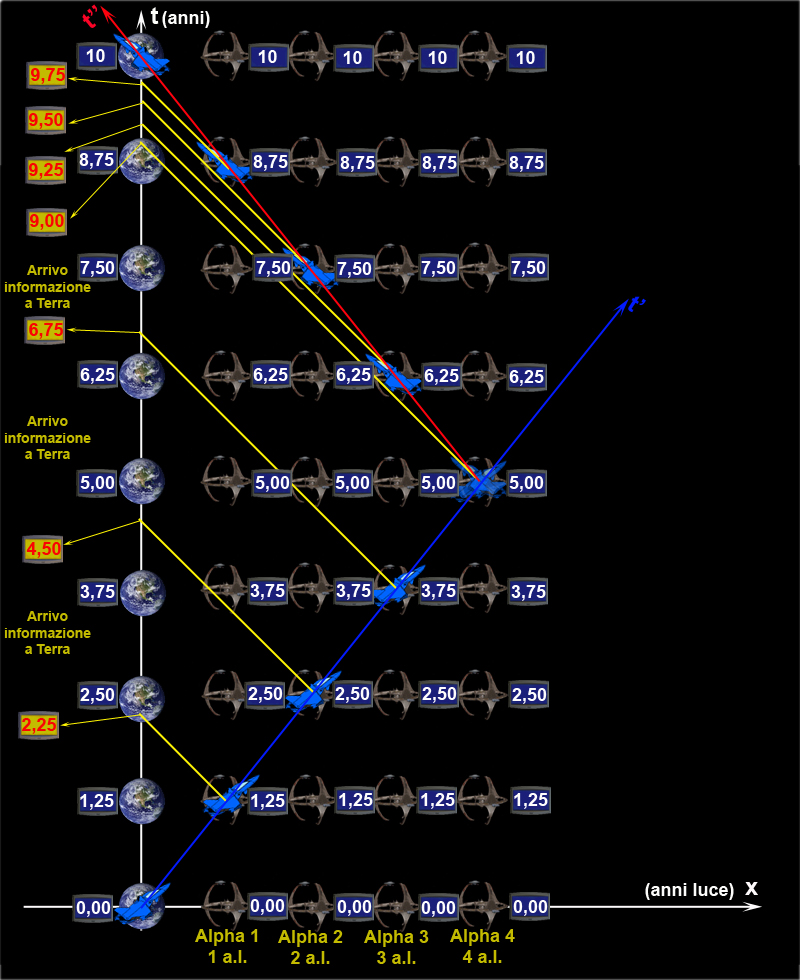
Il Sig. Stop continua ad essere convinto che tutto sia andato esattamente come previsto, finché Flash non scende dall’astronave.
Accidenti esclama Stop, caro fratello il viaggio spaziale sembra aver frenato il tuo invecchiamento e sembri decisamente più giovane di me.
Cosa hai mangiato per tenerti così in forma?
Flash, invece, non può far altro che esclamare: ma cosa ti è successo? Sono passati solo 6 anni, ma sembri invecchiato di 10!
Come sono passati solo 6 anni? Ne sono passati 10 e non 6, come indica chiaramente il mio orologio terrestre!
No, ne sono passati solo 6, replica Flash, come indica chiaramente l’orologio della mia astronave.
Ma scusa dice Stop, come può essere che tu abbia percorso 10 anni luce (5 all’andata e 5 al ritorno) in soli 6 anni?
Hai forse viaggiato più veloce della luce?
Flash ci pensa un po’ prima di rispondere a Stop.
Guarda il diario di bordo dell’astronave ed esclama: ah dimenticavo, secondo gli strumenti di Bordo il percorso era di 2,4 anni luce all’andata e 2,4 anni luce al ritorno.
Stop che fino ad allora riteneva il suo sistema di riferimento perfetto e infallibile, non sa più cosa pensare.
Caro fratello esclama Stop è del tutto evidente che la strumentazione dell’astronave è difettosa.
Ti sbagli di grosso, risponde Flash, gli strumenti funzionano benissimo… e poi come spieghi che io sono più giovane di te?
A questo punto i due gemelli decidono di chiedere aiuto ad Albert, che segue i viaggi delle astronavi dalla torre di controllo.
Albert, rassicura i due gemelli che gli strumenti funzionano perfettamente e che quando si trovano nello stesso sistema di riferimento le misure delle distanze spaziali e del tempo funzionano benissimo, altrimenti…
Altrimenti cosa, rispondono perplessi i due gemelli?
Per rispondere, Albert invita Flash e Stop ad analizzare con calma il viaggio di andata e ritorno, osservando i dati in possesso della torre di controllo.
Quando l’astronave è passata dalla stazione spaziale Alpha 1, l’orologio della stazione, sincronizzato con quello della Terra, segnava che erano passati 1,25 anni dalla partenza (tempo improprio), ma dalla stazione spaziale si vedeva chiaramente che l’unico orologio dell’astronave (tempo proprio) indicava che erano passati solo 0,75 anni.
Albert mostra ai due gemelli una tabella con indicato cosa segnavano gli orologi delle stazioni spaziali sincronizzati con quello terrestre e cosa indicava l’unico orologio dell’astronave visto dalle stazioni spaziali:
|
Stazione Spaziale |
Orologi sincronizzati con la Terra |
Orologio dell’astronave |
|
Alpha 1 (Andata) |
1,25 anni dalla partenza |
0,75 anni dalla partenza |
|
Alpha 2 (Andata) |
2,5 anni dalla partenza |
1,5 anni dalla partenza |
|
Alpha 3 (Andata) |
3,75 anni dalla partenza |
2,25 anni dalla partenza |
|
Alpha 4 (Andata) |
5 anni dalla partenza |
3 anni dalla partenza |
|
Alpha 3 (Ritorno) |
6,25 anni dalla partenza |
3,75 anni dalla partenza |
|
Alpha 2 (Ritorno) |
7,5 anni dalla partenza |
4,5 anni dalla partenza |
|
Alpha 1 (Ritorno) |
8,75 anni dalla partenza |
5,25 anni dalla partenza |
|
Terra 4 (Ritorno) |
10 anni dalla partenza |
6 anni dalla partenza |
Ma come è possibile esclama STOP, il tempo è il tempo per chiunque e l’astronave non può viaggiare più veloce della luce!
Ti sbagli di grosso risponde Albert, il tempo, così come la misura delle distanze non è uguale per tutti, non è assoluto, ma relativo e dipende dal sistema di riferimento.
L’astronave di Flash per la Terra si muove e la sua distanza dal pianeta e dalle stazioni spaziali varia continuamente, per cui non appartiene al sistema di riferimento terrestre.
E come la mettiamo con le distanze percorse, chiede STOP?
Albert, non si scompone minimamente e presenta un'altra tabella che mostra anche la diversa misura delle distanze:
|
Stazione Spaziale |
Distanza dalla Terra misurata dal suo sistema di riferimento |
Distanza misurata dall’astronave appena ha raggiunto alla partenza la velocità di crociera |
|
Alpha 1 (Andata) |
1 anno luce |
0,6 anni luce |
|
Alpha 2 (Andata) |
2 anni luce |
1,2 anni luce |
|
Alpha 3 (Andata) |
3 anni luce |
1,8 anni luce |
|
Alpha 4 (Andata) |
4 anni luce |
2,4 anni luce |
|
Stazione Spaziale |
Distanza da Alpha Centauri misurata dal sistema di riferimento terrestre |
Distanza misurata dall’astronave appena ha raggiunto al ritorno la velocità di crociera |
|
Alpha 1 (Andata) |
1 anno luce |
0,6 anni luce |
|
Alpha 2 (Andata) |
2 anni luce |
1,2 anni luce |
|
Alpha 3 (Andata) |
3 anni luce |
1,8 anni luce |
|
Alpha 4 (Andata) |
4 anni luce |
2,4 anni luce |
Stop è sempre più perplesso...
Voi delle torri di controllo usate sempre i dati come meglio credete, ma non c’è alcuna spiegazione per giustificare queste misure così diverse.
Flash al contrario del fratello, invece è molto curioso e non ama gli atteggiamenti dogmatici.
Lui si sente un po’ come Giordano Bruno, ama volare non solo fisicamente e i dogmi gli ricordano un po’ quel terribile rogo costato la vita a chi aveva osato mettere in discussione le indiscutibili certezze sposate dalla dottrina ecclesiastica dell’epoca.
Pertanto chiede ad Albert di spiegargli come tutto ciò sia possibile.
Il controllore non può fare a meno di ricordare che nel passato un suo omonimo aveva già spiegato quanto tempo e spazio fossero indissolubili e relativi.
Basta una semplice trasformazione per trovare la relazione tra il tempo proprio misurato con un unico orologio in un sistema di riferimento e quello improprio misurato da diversi orologi sincronizzati fra loro di un altro sistema di riferimento:
ΔT proprio = ΔT improprio/γ (dilatazione del tempo)
Dato che l’astronave viaggia a 0,8 c ci vuole un attimo per calcolare il valore di 1/γ
1/γ = √(1 – (v/c)2) = √(1 – 0,82) = √(1 – 0,64) = √0,36 = 0,6
ΔT proprio = ΔT improprio x 0,6
Applicando questa trasformazione è facile ricavare proprio i dati della prima tabella, ossia l'intervallo di tempo intercorso dalla partenza.
Infatti l’unico orologio dell’astronave segna un tempo proprio, mentre gli orologi delle stazioni spaziali sincronizzati con la Terra segnano un tempo improprio.
|
Stazione Spaziale |
Tempo improprio del sistema terrestre |
Tempo proprio dell’astronave ΔT proprio = ΔT improprio x 0,6 |
|
Alpha 1 (Andata) |
1,25 anni dalla partenza |
1,25 x 0,6 = 0,75 anni |
|
Alpha 2 (Andata) |
2,5 anni dalla partenza |
2,50 x 0,6 = 1,5 anni |
|
Alpha 3 (Andata) |
3,75 anni dalla partenza |
3,75 x 0,6 = 2,25 anni |
|
Alpha 4 (Andata) |
5 anni dalla partenza |
5 x 0,6 = 3 anni |
|
Alpha 3 (Ritorno) |
6,25 anni dalla partenza |
6,25 x 0,6 = 3,75 anni |
|
Alpha 2 (Ritorno) |
7,5 anni dalla partenza |
7,5 x 0,6 = 4,5 anni |
|
Alpha 1 (Ritorno) |
8,75 anni dalla partenza |
8,75 x 0,6 = 5,25 anni |
|
Terra 4 (Ritorno) |
10 anni dalla partenza |
10 x 0,6 = 6 anni |
Albert, oltre alla tabella, mostra anche un’animazione che riproduce il viaggio di andata e ritorno dell’astronave visto dal sistema terricolo e confronta il tempo proprio (dell’astronave) con il tempo improprio (della Terra e delle stazioni spaziali).
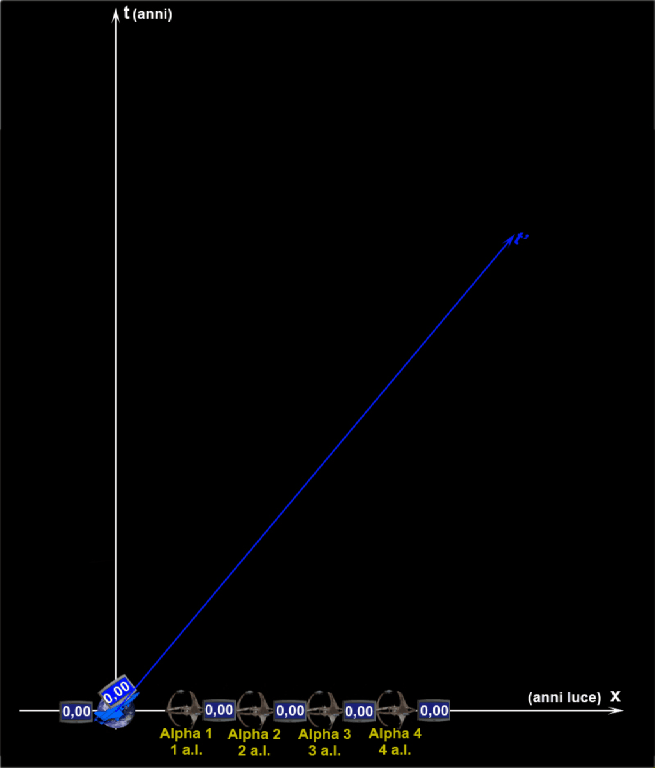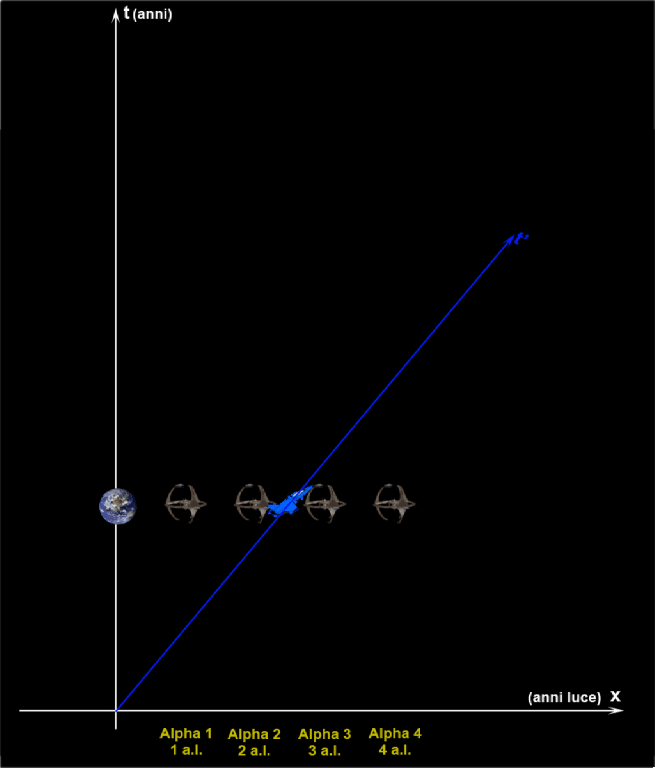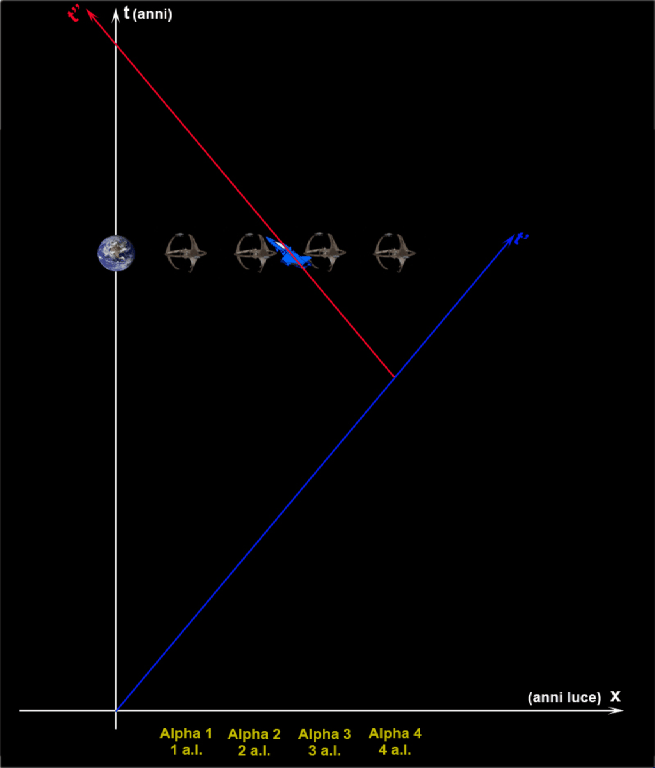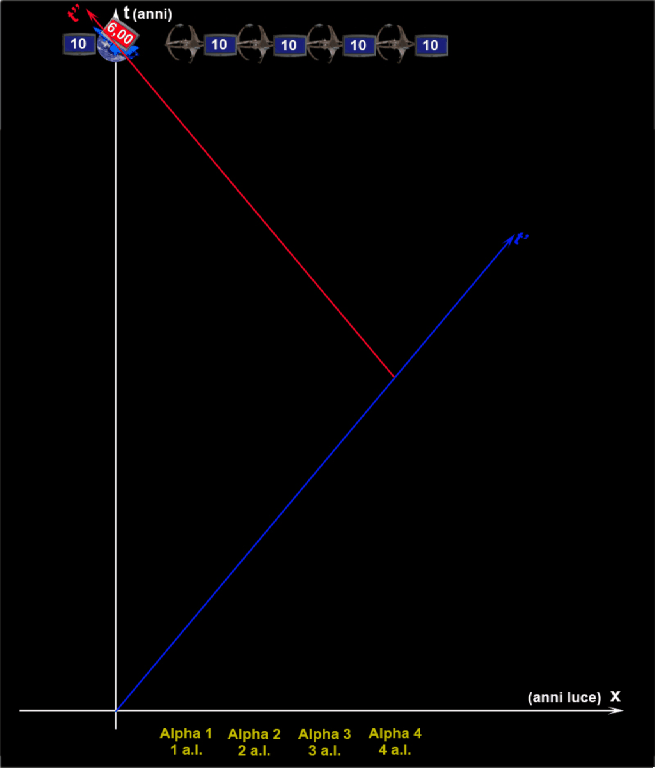
Dopo la spiegazione di Albert, i dati rilevati dalle varie stazioni spaziali durante il passaggio dell'astronave non appaiono più così misteriosi!
Albert però non ha finito.
Se cambia la misura del Tempo deve cambiare anche la misura dello spazio... d'altronde la velocità della luce è sempre la stessa per tutti i sistemi di riferimento.
Anche i dati della seconda tabella, dice Albert, non hanno nulla di misterioso.
Anche in questo caso è possibile applicare una semplice trasformazione per confrontare la misura della lunghezza (distanza) propria di un sistema di riferimento con la misura della lunghezza impropria di un altro sistema di riferimento.
La distanza tra la Terra e le stazioni spaziali è una Lunghezza propria dato che per la Terra ed il suo sistema di riferimento tale distanza non varia mai, mentre per l'astronave su cui viaggia Flash le stazioni spaziali si avvicinano a velocità pari all'80% di quella della luce, per cui la distanza si accorcia (lunghezza impropria) secondo la relazione:
L (lunghezza impropria) = Lo (Lunghezza propria) /γ = Lo x 0,6 (contrazione delle lunghezze)
Anche in questo caso, Albert ha una tabella da mostrare:
|
Stazione Spaziale |
Distanza dalla Terra misurata dal suo sistema di riferimento Lo (Lunghezza propria) |
Distanza misurata dall’astronave appena ha raggiunto alla partenza la velocità di crociera L (lunghezza impropria) = Lo x 0,6 |
|
Alpha 1 (Andata) |
1 anno luce |
1 x 0.6 = 0,6 anni luce |
|
Alpha 2 (Andata) |
2 anni luce |
2 x 0.6 =1,2 anni luce |
|
Alpha 3 (Andata) |
3 anni luce |
3 x 0.6 =1,8 anni luce |
|
Alpha 4 (Andata) |
4 anni luce |
4 x 0.6 =2,4 anni luce |
|
Stazione Spaziale |
Distanza da Alpha Centauri misurata dal sistema di riferimento terrestre Lo (Lunghezza propria) |
Distanza misurata dall’astronave appena ha raggiunto al ritorno la velocità di crociera L (lunghezza impropria) = Lo x 0,6 |
|
Alpha 3 (Ritorno) |
1 anno luce |
1 x 0.6 = 0,6 anni luce |
|
Alpha 2 (Ritorno) |
2 anni luce |
2 x 0.6 =1,2 anni luce |
|
Alpha 1 (Ritorno) |
3 anni luce |
3 x 0.6 =1,8 anni luce |
|
Terra (Ritorno) |
4 anni luce |
4 x 0.6 =2,4 anni luce |
Albert, ha anche rappresentato le diverse distanze rilevate dall’astronave, in una semplice figura.

Albert, non può fare a meno di rivolgersi a Stop: come vedi, oltre ad essere in perfetto accordo con i dati rilevati, nessuno ha viaggiato più veloce della luce... per l'astronave il tempo proprio di viaggio è più breve rispetto a quello improprio misurato del sistema terrestre, ma le distanze si sono accorciate.
L'aiuto controllore, un certo Sig. Lorentz, però non è molto soddisfatto dalla spiegazione fornita da Albert.
Mi sembra che manchi qualcosa, dice Lorentz.
Se non ricordo male, ogni sistema di riferimento dovrebbe misurare il tempo dell'altro come rallentato, ma allora come mai solo Flash al ritorno è più giovane?
Albert, non si scompone minimamente, poiché sa bene che Lorentz ha ragione.
Fortunatamente oltre all'astronave di Flash, ci sono molte altre astronavi in viaggio, che si muovono a velocità 0,8 c.
Tra queste Albert sceglie di contattare solo quelle che si muovono nella stessa direzione e verso dell'astronave su cui viaggia Flash.
In tal modo la distanza tra queste astronavi non cambia mai, per cui se gli orologi sono sincronizzati, queste rappresentano il sistema di riferimento di Flash, ovviamente diverso da quello della Terra (per il sistema Terra la distanza delle astronavi cambia continuamente).
Ora è il sistema di Flash che vede muovere spazialmente la Terra, le stazioni spaziali ed Alpha Centauri e che per misurare il loro moto deve usare orologi posti su astronavi diverse. Perciò, misura un tempo improprio con i suoi molteplici orologi posizionati sulle varie astronavi, mentre l'unico orologio della Terra misura un tempo proprio.
Quando l'astronave di Flash raggiunge Alpha Centauri, un'altra astronave del suo sistema di riferimento (stessa velocità in modulo direzione e verso) si trova in prossimità della Terra.
I loro orologi sono sincronizzati e la distanza tra queste astronavi non cambia mai, per cui entrambi gli orologi indicano che sono passati 3 anni dalla partenza.
Il pilota dell'astronave che si trova in prossimità della Terra vede chiaramente che mentre il suo orologio segna che sono passati 3 anni quello della torre di controllo terrestre indica che sono passati solo 1,8 anni dalla partenza.
Pertanto, per il sistema di riferimento delle astronavi solidali con Flash è il tempo proprio della Terra che si è dilatato(scorre più lentamente).
ΔT proprio = ΔT improprio/γ = ΔT proprio = ΔT improprio x 0,6 = 3 x 0,6 = 1,8 anni
Non a caso alla Torre di controllo terricola, durante il viaggio di andata, considerando i passaggi di Flash dalle stazioni spaziali, risultano i seguenti dati:
|
Stazione Spaziale |
Intervallo di Tempo improprio del sistema solidale con l’astronave di Flash (andata) |
Intervallo di Tempo proprio dell’unico orologio della Torre di controllo terricola ΔT proprio = ΔT improprio x 0,6 |
|
Alpha 1 (Andata) |
0,75 anni dalla partenza |
0,75 x 0,6 = 0,45 anni |
|
Alpha 2 (Andata) |
1,5 anni dalla partenza |
1,5 x 0,6 = 0,9 anni |
|
Alpha 3 (Andata) |
2,25 anni dalla partenza |
2,25 x 0,6 = 1,35 anni |
|
Alpha 4 (Andata) |
3 anni dalla partenza |
3 x 0,6 = 1,8 anni |
Albert, ha anche rappresentato in una semplice figura il viaggio di andata ed il confronto tra tempo proprio e tempo improprio, visto dal sistema delle astronavi solidali con Flash.
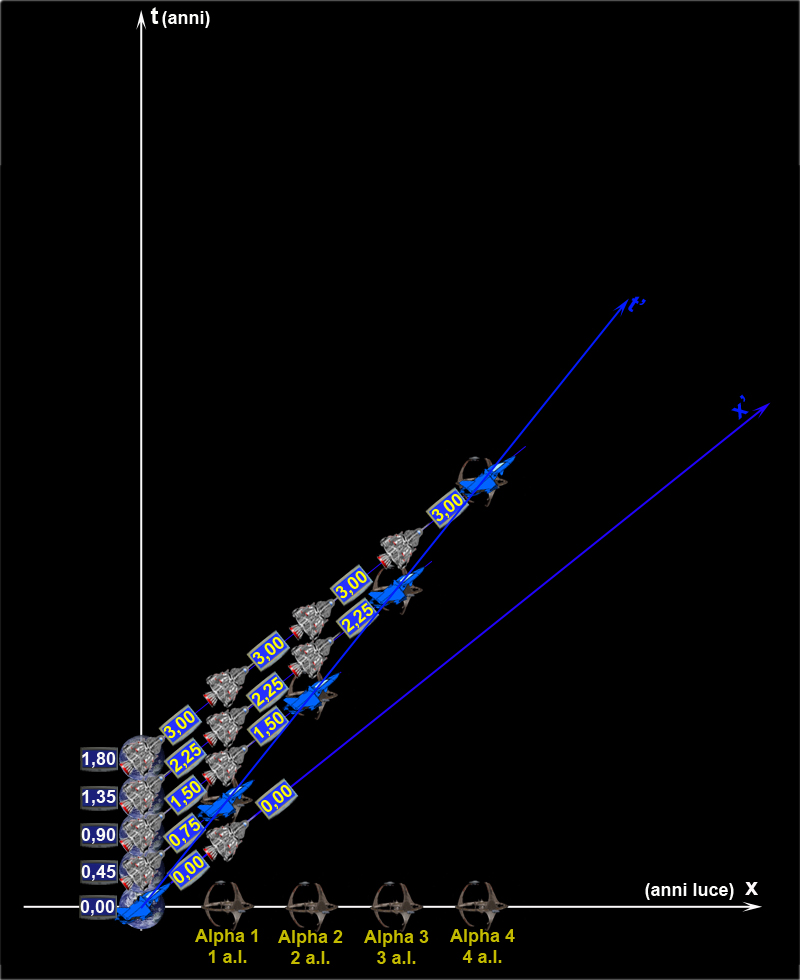
Una perfetta simmetria, afferma Albert: per il sistema di riferimento della Terra è il tempo dell'astronave che scorre più lentamente, mentre per il sistema di riferimento delle astronavi è il tempo della Terra che rallenta.
Una simmetria destinata a rompersi con l'inversione di rotta dell'astronave, esclama Albert!
Quando l'astronave di Flash inizia il viaggio di ritorno, cambia il suo sistema di riferimento.
E' un po' come un'autostrada in cui le macchine viaggiano tutte alla stessa velocità costante, ma mentre quelle che viaggiano su una corsia mantengono sempre la stessa distanza fra loro (stesso sistema di riferimento) quelle che viaggiano nell'altra corsia, in senso inverso, mutano continuamente la loro distanza rispetto a chi viaggia nella corsia opposta (altro sistema di riferimento).
Pertanto dopo l’inversione di rotta, sono le astronavi che viaggiano verso la Terra a velocità 0,8c che viaggiano in solido con Flash e che rappresentano il suo nuovo sistema di riferimento.
Quando l'astronave di Flash riparte da Alpha Centauri verso la Terra a velocità di crociera di 0,8c, tra le varie astronavi che appartengono al nuovo sistema di riferimento di Flash (ritorno) ve ne è una che si trova in prossimità della Terra.
Gli orologi di queste astronavi sono tutti sincronizzati e la loro distanza dall’astronave di Flash non cambia mai, per cui tutti gli orologi indicano che sono passati poco più di 3 anni dalla partenza.
Cambiando sistema di riferimento gli eventi che per Flash risultavano simultanei all’andata, non lo sono più al ritorno.
Infatti quando l’astronave di Flash raggiunge Alpha Centauri al termine del viaggio di andata, tra le astronavi appartenenti al primo sistema di riferimento (andata) i cui orologi sincronizzati segnano tutti 3 anni, quella in prossimità della Terra nota che l’orologio della Torre di controllo terrestre indica che sono passati 1,8 anni dalla partenza, mentre quando Flash inizia il viaggio di ritorno, tra le astronavi appartenenti al secondo sistema di riferimento (ritorno) i cui orologi sincronizzati segnano tutti 3 anni, quella in prossimità della Terra nota che l’orologio della Torre di controllo terrestre indica che sono passati 8,2 anni dalla partenza.
E’ un po’ come se durante la manovra di inversione di rotta, con il cambio di sistema di riferimento, per Flash il suo gemello rimasto a Terra sia invecchiato da 1,8 a 8,2 anni.
Un sorta di salto temporale!
Durante il ritorno, l'intervallo di tempo ΔT da considerare per il confronto tra tempo proprio (dell’orologio terricolo) e tempo improprio (degli orologi sincronizzati delle astronavi solidali con il percorso di ritorno di Flash) è quello che manca per raggiungere la Terra.
Quando Flash raggiunge la Terra, per la torre di controllo terricola sono passati 10 anni dalla partenza e questo è un evento certo.
Per l'astronave il percorso di ritorno non può che durare come quello di andata (visto che il modulo della velocità è lo stesso, ossia 0,8c), quindi per Flash mancano 3 anni per raggiungere la Terra.
Pertanto, usando il sistema di riferimento delle astronavi solidali con il percorso di ritorno di Flash, l’intervallo di tempo mancante per raggiungere la Terra è pari a 3 anni ed applicando la solita trasformazione, dove il tempo degli orologi del sistema delle astronavi è quello improprio e quello della torre di controllo sulla Terra è quello proprio, quest’ultimo risulta pari a:
ΔT proprio = ΔT improprio x 0,6 = 3 x 0,6 = 1,8 anni all’arrivo a Terra
Per ricavare il tempo che segna l’orologio della Torre di controllo terricola dalla partenza dell’astronave, e non quello che manca affinché l’astronave raggiunga la Terra, basta tener conto che quando Flash arriva a Terra, l’orologio terricolo deve segnare 10 anni.
Pertanto:
T proprio (dalla partenza) = 10 anni - ΔT proprio
T proprio (dalla partenza) = 10 anni – (3 x 0,6) = 8,2 anni dalla partenza.
Albert, mostra come tale indicazione sia in accordo con i dati rilevati:
|
Stazione Spaziale |
Intervallo di Tempo improprio del sistema solidale con l’astronave di Flash (ritorno) |
Intervallo di Tempo proprio dell’unico orologio della Torre di controllo terricola ΔT proprio = ΔT improprio x 0,6 T proprio (dalla partenza) =10 - ΔT proprio |
|
Alpha 4 (Ritorno) |
3 anni all’arrivo a Terra, 3 anni dalla partenza |
3 x 0,6 = 1,8 anni all’arrivo a Terra 10 - 1,8 = 8,2 anni dalla partenza |
|
Alpha 3 (Ritorno) |
2,25 anni all’arrivo a Terra, 3,75 anni dalla partenza |
2,25 x 0,6 = 1,35 anni all’arrivo a Terra, 10 - 1,35 = 8,65 anni dalla partenza |
|
Alpha 2 (Ritorno) |
1,5 anni all’arrivo a Terra, 4,5 anni dalla partenza |
1,5 x 0,6 = 0,9 anni all’arrivo a Terra, 10 - 0,8 = 9,1 anni dalla partenza |
|
Alpha 1 (Ritorno) |
0,75 anni all’arrivo a Terra, 5,25 anni dalla partenza |
0,75 x 0,6 = 0,45 anni all’arrivo a Terra, 10 - 0,45 = 9,55 anni dalla partenza |
|
Terra (Ritorno) |
0 anni all’arrivo a Terra; 6 anni dalla partenza |
0 x 0,6 = 0 anni all’arrivo a Terra 10 - 0 = 10 anni dalla partenza |
Albert, ha anche rappresentato in una semplice figura il viaggio di ritorno visto dal nuovo sistema delle astronavi solidali con Flash.
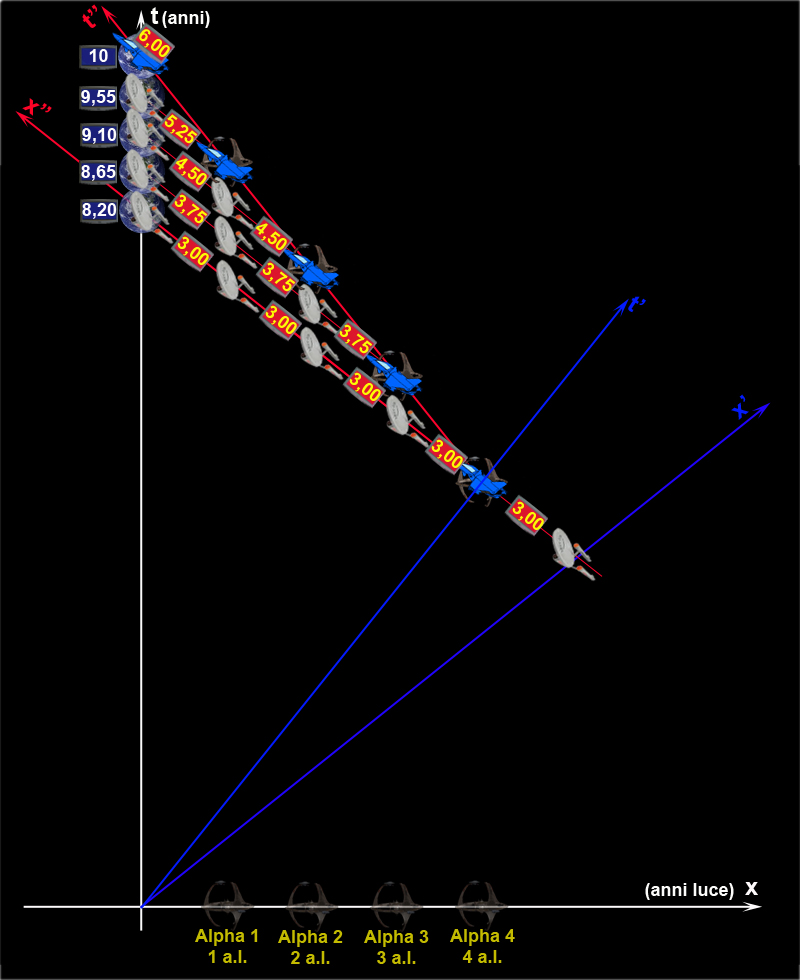
Infine, Albert mostra anche un’animazione che riproduce il viaggio, secondo il sistema delle astronavi solidali con Flash, sia all’andata, sia al ritorno con relativo cambio di sistema di riferimento.

Non è la velocità in sé che consente a Flash di tornare più giovane (anche perché se per la Terra è Flash che si muove, per Flash è la Terra che prima si allontana e poi si avvicina... non esistono sistemi di riferimento privilegiati), ma l'inversione di rotta ed il conseguente cambio del sistema di riferimento.
Ora anche Stop, nonostante i suoi pregiudizi, è costretto ad ammettere che se per lui sono passati 10 anni dalla partenza di Flash, per quest'ultimo ne sono passati solo 6!
L’andata e ritorno di Flash ha compiuto il miracolo di ottenere due gemelli, nati nello stesso giorno, ma che ora hanno ben 4 anni di differenza!
QUIZ: UN VIAGGIO SU ALPHA CENTAURI
(e tante discussioni conseguenti)
Il quiz che vi propongo è banalissimo, ma si riferisce al paradosso dei gemelli, gioia e dolore di molti appassionati. La soluzione è quasi immediata, ma noi ne approfitteremo per tornarci sopra e discuterne con calma, per cercare di eliminare qualsiasi concetto sia rimasto ancora un po’ confuso. Soprattutto, vedremo l’importanza della simultaneità, del significato di sistema di riferimento e del ruolo che gioca la velocità della luce.
L’osservatore G’ parte da una piattaforma spaziale e viaggia alla velocità v = 0.8 c verso Alpha Centauri, che dista dalla piattaforma 4 anni luce. Quando raggiunge la stella, inverte subito la rotta e ritorna alla piattaforma, sempre alla stessa velocità. Quando G’ ritorna alla piattaforma, confronta la sua età con quella del fratello gemello G, che è sempre rimasto sulla piattaforma. Quali sono le età di G e G’, se al momento della partenza avevano 30 anni ?
Notiamo bene che vogliamo che i due gemelli si incontrino realmente (distanza tra loro = 0).
SOLUZIONE (PRIMA PARTE)
Avrete capito subito che il quiz, di cui questo articolo è soluzione, è stato predisposto per fare (una volta per tutte) chiarezza sul paradosso dei gemelli. Ragione per cui risolviamo il problema in vari modi, accorgendoci che, alla fine, si usa sempre lo stesso concetto, quello del cambiamento di sistema di riferimento inerziale.
Non aspettatevi un riassunto o una rielaborazione di quanto già si può trovare negli approfondimenti di questo Circolo. Per dimostrare certi concetti rimanderò costantemente a loro. Solo così, si può realmente inserire il problema particolare in un contesto più generale e completo. Inoltre, una bella rinfrescata non fa mai male.
Se leggete in giro per la rete, troverete decine e decine di spiegazioni, spesso in contrapposizione. Alcune sono decisamente errate, altre affrontano il paradosso sotto condizioni diverse. In qualche caso si preferisce non chiamarlo nemmeno paradosso, anche se è nato proprio per mettere in difficoltà la teoria della relatività. Non potrò, perciò, essere esaustivo, ma mi limiterò a presentarvi TRE METODI (che sono poi quattro o anche cinque) che sembrano molto diversi, ma che in fondo esprimono sempre lo stesso concetto: la Relatività Ristretta si applica solo e soltanto a due sistemi inerziali in movimento reciproco o, quantomeno, solo in questa situazione si ha una perfetta simmetria. Le cose non funzionano più se i sistemi diventano tre… mi spiegherò meglio.
Innanzitutto, chiariamo subito un fatto: il paradosso si risolve immediatamente (anche se non è poi così ovvio per tutti), giudicando il problema come un qualcosa legato alla Relatività Generale. In realtà, non esiste astronave che possa partire, arrivare in un certo luogo, invertire marcia e ritornare al punto di partenza senza accelerare e decelerare. Questa semplice constatazione esclude una trattazione mediante la sola RR e quindi giudica il paradosso non realistico, in quanto patrimonio della RG, dove il risultato (il gemello viaggiatore risulta più giovane del gemello che sta fermo) è del tutto ammissibile dato che solo uno dei due risente di un campo accelerato, con le conseguenze del caso.
In realtà, attraverso integrazioni si potrebbe anche utilizzare la RR come un approccio valido istante per istante e arrivare comunque alla soluzione simile a quella della RG. Ricordiamo, infatti, che la RG si costruisce proprio approssimandola punto a punto con la RR, ma non complichiamoci la faccenda che è giù abbastanza controversa di per sé.
Consideriamo, allora il nostro quiz e vediamo di rispondere, ragionando nei modi più semplici e intuitivi. Ovviamente, per ogni metodo che useremo è fondamentale conoscere le basi della RR e, ancora meglio, saper disegnare nel diagramma di Minkowski.
Il metodo più rapido si ricollega al quiz della volta precedente, ossia a quello che doveva portare alla comprensione del concetto di tempo proprio. Ricordiamo ancora che per tempo proprio (uguale in ogni sistema di riferimento) si intende il tempo segnato da un solo orologio che misuri il tempo in un sistema che non si muova spazialmente. Vi ricorderete che abbiamo risolto il quiz della volta scorsa proprio imponendo l’uguaglianza a zero della posizione iniziale e finale. Questa asserzione ci riporta alla relatività classica di Galileo (di cui abbiamo parlato QUI alle vedi figure 4 e 5 e QUI in modo ultrasemplificato adatto anche ai più piccoli): non è possibile dimostrare che si sia in moto o fermi in un sistema inerziale. In altre parole, non esiste un sistema di riferimento assoluto e ogni sistema può considerarsi immobile. Quante volte abbiamo usato questo concetto parlando di Coriolis? Tante, forse troppe…
Chi sta sulla Terra vive chiaramente un suo tempo proprio e può usare un solo orologio per misurare il tempo. La stella Alpha Centauri (AC) appartiene allo stesso sistema di riferimento (la distanza rimane invariata) e quindi il suo orologio è perfettamente sincronizzato con quello della Terra. Durante tutto il viaggio dell’astronave del gemello astronauta, il sistema Terra-AC si sente immobile e il tempo passato tra l’evento “partenza dell’astronauta” e l’evento “ritorno dell’astronauta”, è un tempo proprio del suo sistema. Lo si può misurare tranquillamente con un solo orologio e non ci vuole molto a calcolare quanto sarà lungo: la stella dista 4 anni luce. Viaggiando a 0.8c, ci si impiega 5 anni. Il ritorno è perfettamente analogo, per cui non ci sono problemi a prevedere un tempo proprio di 10 anni.
Prima di proseguire, immaginiamo che i gemelli conoscano i rudimenti della RR e quindi sappiano che il Sig. Einstein ha dimostrato che l’orologio di chi viene considerato in moto appaia a chi sta fermo rallentare sempre di più al crescere della velocità. Se l’astronave andasse alla velocità della luce, l’orologio verrebbe addirittura visto fermo. Lo hanno imparato utilizzando l’orologio di luce e lo hanno anche descritto graficamente, utilizzando il diagramma di Minkowski.
Tuttavia, sanno benissimo che la faccenda è perfettamente simmetrica. Il gemello sull’astronave si sente immobile e per lui è la Terra (o la stazione spaziale) che si muove con una velocità uguale e contraria. Sarà lui, adesso, che giudica l’orologio del sistema Terra andare più piano del suo. Il succo di tutto, come abbiamo spiegato a lungo nell’approfondimento sulle basi della RR, è la relatività della simultaneità: ciò che è simultaneo per un sistema non lo è per l’altro. Il diagramma di Minkowski ne dà una dimostrazione immediata che potete trovare nell’approfondimentorelativo e, in particolare, descrivendo le figure 33 e 34. Cosa vuol dire tutto ciò?
Se l’astronave continuasse a viaggiare nello spazio senza tornare indietro, non esisterebbe nessun paradosso: ognuno dei due sistemi vedrebbe l’orologio dell’altro rallentare e penserebbe che è il gemello in movimento che si mantiene decisamente più giovane (il suo orologio non solo meccanico, ma anche biologico, sembra viaggiare più lentamente). Se volessimo veramente confrontare i tempi dei due sistemi dovremmo usare i relativi tempi propri. Questi sono uguali per tutti i sistemi, per cui, in realtà, l’età sarebbe la stessa. Attenzione, però, che i sistemi sono considerati alla Einstein, ossia muniti di infiniti orologi e righelli e non c'è bisogno di inviare segnali.
Torniamo, allora al nostro quiz. Il gemello fermo sulla piattaforma (solidale con la Terra) risponde a una domanda molto ambigua: “Quanto tempo impiegherà il mio gemello ad andare su Alpha Centauri?”. Per poterlo veramente confrontare con il suo tempo proprio non può eseguire il calcoletto basato su “data una velocità e una distanza spaziale posso trovare il tempo impiegato dal mio gemello per arrivare su Alpha Centauri”. Vi è un grave errore di fondo (e questo ci riporta al quiz precedente): quello che sta calcolando non è un tempo proprio, dato che il punto di partenza e il punto di arrivo per lui hanno una certa distanza (4 anni luce). Ne segue che il tempo trovato NON può essere il tempo proprio dell’astronauta, per il quale la posizione spaziale non cambia: lui deve solo aspettare che Alpha Centauri arrivi da lui. Il tempo necessario sarà il vero tempo proprio dell’astronauta.
Ripeto ancora il concetto: una cosa è il tempo proprio del gemello terrestre che intercorre tra un evento (partenza) e un altro (arrivo), entrambi appartenenti al suo sistema di riferimento; un’altra cosa è il calcolo che lui potrebbe fare del tempo di viaggio dell’astronave che appartiene a un altro sistema, in movimento. Facendo questo calcolo misura un tempo improprio, dato che il tempo proprio può essere misurato solo da chi si sente fermo e usa un solo orologio.
Sappiamo benissimo come calcolare questo tempo proprio (ricordiamo l’orologio di luce). Basta dividere il tempo improprio calcolato sulla Terra (immaginata ferma) per il fattore di Lorentz γ.
Immaginiamo di fare il calcolo per la prima metà del viaggio, durante il quale i due sistemi sono veramente inerziali. Essendo la velocità di 0.8c, si deriva che
1/γ = √(1 – (v/c)2) = √(1 – 0.82) = √(1 – 0.64) = √0.36 = 0.6
Il tempo improprio tIT misurato da Terra è di 5 anni, da cui segue che il tempo proprio dell’astronauta tPA risulta:
tPA = 0.6 tIT = 0.6·5 = 3 anni
Fino a qui non esiste nessun risultato paradossale. L’astronauta misurerebbe una cosa simile calcolando il tempo proprio del sistema Terra, dato che sappiamo che spostandosi nello spazio del sistema Terra (dalla Terra ad AC) il tempo che vede passare nel sistema Terra è un tempo improprio.
Tuttavia, il problema sembrerebbe banalissimo (e lo è) per entrambi i sistemi. Il ritorno non dovrebbe cambiare le cose e quando l’astronauta ritornerà a casa tutto si sistemerà in qualche modo.
E invece, il risultato è ben diverso. Basta pensare che il ritorno dell’astronave alla Terra comporta un ulteriore tempo di 5 anni per il sistema Terra, per ovvi motivi di simmetria. Tempo improprio era e tempo improprio rimane. L’orologio non può sbagliare e segna 10 anni. Il risultato è corretto, in quanto tra l’evento partenza e l’evento ritorno è stato usato un solo orologio. Ma non può sbagliare nemmeno il tempo proprio dell’astronauta: se era 3 anni all’andata DEVE essere per simmetria 3 anni anche al ritorno. Se fosse così la RR sembrerebbe andare a farsi friggere… Purtroppo sembra proprio così, in quanto il gemello sulla Terra nell’evento ritorno ha 30 + 10 = 40 anni e l’astronauta 30 + 6 = 36.
Tutta da buttare la RR? Nemmeno per sogno, dato che sono stai usati TRE sistemi inerziali. Quello della terra-AC, quello dell’astronauta che raggiunge AC e quello dell'astronauta che da AC torna sulla Terra, invertendo il verso del moto. In pratica cosa succede? Cercherò di esprimerlo con parole semplici e senza calcoli. Dobbiamo tornare alle figure 33 e 34 che abbiamo già studiato.
Quando l’astronauta arriva su Alpha Centauri l’asse spazio x’ del suo sistema dimostra che è valida la RR, dato che lui incontra l’asse delle t (verticale) del sistema Terra ben prima dei 5 anni (vedi figura successiva, dove al posto di AC abbiamo inserito S). Vedrebbe quindi più giovane il gemello terrestre. Quando però riparte, dopo avere invertito la rotta, il suo nuovo asse x” incontra l’asse t molto più in alto di prima. In poche parole, in un tempo praticamente zero per l’astronauta, sulla Terra è passato un tempo estremamente lungo. Invertendo la rotta, è come se fosse subentrato un secondo astronauta che parte da AC a un tempo decisamente più grande rispetto a quello corrispondente all’arrivo del primo astronauta. In parole molto semplici il tempo passato sulla Terra tra A e B (non certo trascurabile) si annulla con l’inversione della rotta per l’astronauta.
Tuttavia, non voglio battere troppo su questo procedimento (il più classico). Basta dire che devo paragonare il tempo trascorso tra due eventi sulla Terra e sull’astronave. Non vi è dubbio che devo confrontare i 10 anni con i 6 calcolati usando la RR sia all’andata che al ritorno . Ricordiamo ancora che il tempo proprio si misura con un solo orologio, mentre il tempo improprio ha bisogno di almeno due orologi e tutto si riduce a un problema di simultaneità relativa.
Il quiz sarebbe risolto, dimostrando nel contempo la motivazione del cosiddetto paradosso. Esso non esiste, dato che la soluzione si trova, introducendo un terzo sistema di riferimento o -se preferite- un cambiamento repentino di sistema e quindi un salto repentino dell’asse di simultaneità da x’ a x”, come illustra in modo qualitativo la figura precedente.
N.B.: PapalScherzone si è irritato un pochino e mi ha ordinato di essere un po' più chiaro... Come dirgli di no? E, allora, in appendice,
trovate una spiegazione più dettagliata... E che sia contento e non mi chieda di più!
Si può, però, sintetizzare e dimostrare l’intera faccenda (oltre che risolvere il paradosso), considerando i due triangoli uguali T1S2M e T2S2M. Essi descrivono l’invariante relativistico, da cui si dimostra che il lato T1S2 è sempre più corto di T1M e analogamente per quello di sopra. In poche parole il percorso T1S2T2 si svolge in un tempo sempre minore di T1T2. Per comprendere meglio il risultato basta riflettere sulle Fig. 45 e 46 dell’approfondimento su Minkowski. Tra parentesi, nello stesso modo si può trattare anche un moto accelerato, integrando su una linea curva, che evidenzi accelerazioni continue e regolari.
Con l’invariante e la sua definizione si risolve il nostro problemino, così come fatto da Oreste QUI, per determinare il tempo proprio, che è proprio l’invariante.
Ricordiamo, adesso, un altro metodo che, come già ho fatto presente in altre discussioni, non amo in modo particolare. O, almeno, non lo amo quando viene utilizzato al posto della RR. Ossia, utilizzare realmente un astronauta e un osservatore terrestre (e non i loro sistemi in generale), tali da potere osservare ciascuno l’orologio dell’altro (o accorgimenti del genere). In pratica, si deve tener conto del tempo necessario ai segnali luminosi per partire e per arrivare. Il metodo tiene conto, perciò, anche del tempo che la luce impiega a raggiungere effettivamente i due gemelli. In qualche modo si mischia la vera RR con un suo effetto, ossia l’effetto doppler relativistico, che abbiamo pubblicato QUI. Come ben descritto da Umberto, esso permette la soluzione, ma invito ad andare direttamente nell’approfondimento di Minkowski, dove il tutto è descritto anche cambiando sistema di riferimento (capitolo: Manteniamo il contatto visivo e il paradosso si dissolve, da Fig. 24 a 29).
Non possiamo dimenticare che per tracciare le linee del diagramma di Minkowski si deve usare la dilatazione dei tempi e quindi la RR entra di prepotenza nella trattazione, così come succede per il calcolo dell’effetto doppler relativistico. Tuttavia, non voglio continuare a discutere la validità “profonda” di questo metodo che potete trovare in vari siti del web. Addirittura, si può anche ricavare la RR partendo da questo effetto e cento altre variazioni sul tema.
Io penso, comunque, che quanto scritto nei vari approfondimenti sia più che sufficiente per avvicinarsi adeguatamente alla RR. Non chiedetemi, perciò, di entrare nei dettagli di altri metodi che non mi sembrano né più corretti e nemmeno più semplici. Direi che per capire l’essenza della RR e risolvere il paradosso dei gemelli ne abbiamo a sufficienza.
A questo punto, direi di aver non solo risolto il quiz, ma anche aver girato e rigirato il paradosso dei gemelli in modo sufficientemente completo e intuitivo.
Permettetemi, però, di proporvi (nel prossimo articolo) una specie di favola, che ricorda tanto quella del nostro amico Muo (QUI), anzi la potremmo chiamare la “doppia” favola di Muo1 e di suo fratello gemello Muo2. In fondo, potrebbe essere il modo migliore e più intuitivo per capire e risolvere il paradosso, così come è stato banale comprendere la favola di Muo. Nello stesso articolo vedremo anche una versione tipica del nostro amico Maurizio, alias (quando vuole) Oreste Pautasso.
Appendice:
Facciamo riferimento alla figura precedente...
Gli orologi dei due gemelli sono sincronizzati alla partenza. Cosa ci diranno alla fine del viaggio?
Per G (gemello terrestre) l’evento M è simultaneo a S2.
Per G’ l’evento A e simultaneo a S2.
Per G’ l’evento B è simultaneo a S2.
Ossia A è simultaneo a B… per G’ il tempo AB non esiste.
Potrebbe bastare così, ma si può andare nei dettagli
Ci mettiamo nei panni di G
tT1T2 = tT1M + tMT2
Come valuta G il tempo misurato da G’?
t’T1S2T2 = t’T1S2 + t’S2T2.
Per G, che è istruito, t’ T1S2 e t’ S2T2 sono tempi propri (misurati da chi non si muove) per cui può scrivere (sapendo che M e S2sono simultanei nel suo sistema):
t’ T1S2T2 = tT1M /γ + tMT2/γ
Secondo G il tempo che misura G’ è minore del suo:
t’ T1S2T2 = (tT1M + t MT2)/γ
t’ T1S2T2 < (tT1M + t MT2) = tT1T2
t’ T1S2T2 < tT1T2
Quanto riportato è il ragionamento di G, che sa calcolare il tempo passato da G’.
Cosa pensa G’ del tempo passato da G:
tT1T2 = tT1A + tBT2
dato che il tempo AB non esiste
Adesso può calcolare il tempo del suo orologio
t’T1S2T2 = t’T1S2 + t’S2T2
Ma sa anche che S2 è simultaneo ad A e, contemporaneamente, a B e quindi può calcolare, sapendo che t’T1S2 e t’S2T2 sono tempi propri, che:
t’T1S2T2= (tT1A + tBT2)/γ
t’ T1S2T2 < (tT1A + t BT2) = tT1T2
t’ T1S2T2 < tT1T2
Per entrambi i sistemi il tempo passato dal gemello viaggiatore è minore di quello del terrestre
SOLUZIONE (SECONDA PARTE): GEMELLI IPERBOLICI
Vi propongo un ulteriore modo per arrivare subito a risolvere il paradosso dei gemelli che spero sia ancora più intuitivo. La RR non cambia di certo, ma viene sfruttata solamente l’iperbole di calibrazione (QUI fig. 31 e seguenti).
La situazione è sempre la stessa, illustrata nella figura che segue
La linea verticale del tempo è quella relativa al tempo che trascorre per un orologio che è solidale con la Terra. A noi interessano due eventi che hanno la stessa posizione spaziale (Terra), ma tempi diversi. Esso sono la partenza e l’arrivo dell’astronave che raggiunge Alpha Centauri. Lo calcoleremo a posteriori.
Disegniamo le iperboli di calibrazione per ogni unità di tempo annuo terrestre 1, 2, 3,…. Esse ci permettono di stabilire immediatamente il corrispondente tempo annuo unitario relativo all’astronave che va verso Alpha Centauri con v = 0.8c.
Vediamo che all’arrivo su Alpha sono passati 3 anni sulla rotta dell’astronave (sistema in moto).
Ciò vuol dire che invertendo la rotta deve capitare la stessa cosa rispetto all’evento arrivo dell’astronave sulla Terra. Partendo dalla posizione dell’astronave all’anno 3 (in Alpha), basta invertire il sistema di iperboli e si otterrà l’evento “arrivo” sulla linea temporale della Terra.
Per costruzione il numero di anni passati sull’astronave sono 3 + 3 = 6 anni. Quanti sono quelli passati sulla Terra? Molti di più… basta segnare gli anni terrestri fino a incontrare l’evento arrivo astronave sulla Terra. Il calcolo è presto fatto: sono passati 10 anni.
Viaggiando sull’astronave e invertendo la rotta si sono saltati 4 anni terrestri.
NEWS del 1/8/2020: Ma se esiste il paradosso dei gemelli, esiste anche il paradosso del muone? Parliamone...
NEWS del 17/2/2022: Il paradosso è degli orologi e non dei gemelli
**************************************************************************************************
E ora... RICREAZIONE PER TUTTI !!! (anche per il "comandante")
SCHERZYAMO SUL PARADOSSO DEI GEMELLI:
LO SPIRITO DELLA VELOCITA'
In questo circolo si è parlato spesso del celebre paradosso dei gemelli, dimostrando, così, che non esiste un unico modo per risoverlo, ma lo si può fare con approcci diversi. Ciò che non si era ancora fatto finora era scherzarci (ops... scherzYarci) sopra. Potevamo forse perdere un'occasione del genere? Certo che no! Ecco a voi, quindi, tre racconti che in comune hanno la ricerca di un'applicazione concreta al paradosso e, al contempo, confermano che è sempre possibile affrontare un problema con approcci diversi. Leggete fino in fondo, il divertimento è assicurato, parola di PapalScherzone!
A proposito di approcci diversi ad uno stesso problema, prima di passare alla lettura dei racconti, fatemi raccontare una barzelletta...
In un campo di golf di un circolo lussuosissimo, frequentato solo da VIP e da celebri professionisti, vi sono tre amici che stanno giocando: uno è un cardinale potentissimo, un altro è un medico chirurgo e ricercatore di assoluto rilievo e il terzo un celebre ingegnere. Purtroppo nella buca successiva c’è una grande confusione e i giocatori perdono un sacco di tempo. I nostri tre personaggi chiamano subito il direttore del club e manifestano la loro impazienza. Il direttore spiega il motivo: “Abbiate pazienza, carissimi soci… ma davanti a voi c’è un gruppo di vigili del fuoco a cui abbiamo dato il permesso di giocare a seguito del loro atto eroico di alcuni anni fa. La sede del circolo si incendiò e solo con enorme sprezzo del pericolo i vigili riuscirono a salvare persone e cose. Era il minimo che potevano concedergli, anche perché, nell’attraversare le fiamme, sono diventati tutti ciechi per il calore intensissimo”.
“Oh, mio Dio” esclama il cardinale “d’ora in poi, ogni sera, pregherò per quei poveri fratelli così eroici”. “Un momento, un momento…” dice il chirurgo “ho da poco messo a punto una tecnica sperimentale innovativa che riesce a ridare la vista anche a casi che sembravano irrisolvibili. Mandatemi quei cari vigili e farò di tutto per loro”. Infine, dopo aver ciondolato la testa, l’ingegnere sussurra: “E farli giocare di… notte?”.
In sintonia con lo spirito della barzelletta, la prima storia è stata scritta da un ricercatore un po’ sognatore, la seconda da un ingegnere con molto senso pratico e la terza da un tipo che, come ormai sappiamo bene, è capace di grande versatilità e non ha avuto problemi questa volta a calarsi nella parte del cardinale (o quasi!).
UN REGALO TEMPORALE (Prof. sogn. Enzone Zappalà)
Muo1 vuole molto bene al suo gemello Muo2 e vorrebbe fargli un regalo davvero speciale. Muo1 vive nel sistema terrestre e non ha grandi problemi a usare i righelli regalategli dal mago Albertino per misurare la distanza di Alpha Centauri, che sta nel suo stesso sistema. Esattamente 4 Anni Luce.
Si rivolge al suo gemello Muo2 e gli chiede: “Hai voglia di andare fino a quella stella e poi tornare indietro?” Muo2 risponde: “Accidenti… ma è un viaggio lunghissimo, dovrei avere un’astronave velocissima… e poi perché me lo chiedi?”. Muo1 risponde: “E’ un viaggio fantastico e posso trovare l’astronave necessaria. Verrei anch’io con te, ma il medico mi ha detto che non potrei resistere a certe velocità. Tuttavia, tu puoi farlo e vedrai che al tuo ritorno sarai molto contento…”.
Muo2, che è sempre stato un amante dell’avventura, non può che ringraziare il fratello e decide di partire con l’astronave (costruita, ovviamente, dal mago) che viaggia a una velocità che è l’ottanta per cento di quella della luce. Muo1 fa un calcoletto molto banale che vale nel suo sistema solidale con la Terra e con Alpha Centauri e dice a Muo2: “La stella dista 4 anni luce, la velocità v è 0.8 (ponendo quella della luce = 1), da cui segue che per raggiungere la stella, secondo me impiegherai un tempo t dato da
t = spazio/velocità = 4/0.8 = 5 anni
Tornando subito indietro passeranno altri 5 anni. Adesso abbiamo solo 30 anni. Quando tornerai ne avrò, ovviamente, 40 (io vivo nel sistema della Terra e di Alpha Centauri)… e avremo ancora tanto tempo da passare assieme. Ricordati comunque di portare con te i righelli del mago Albertino… non si mai”
Tutto è pronto e Muo2 parte verso Alpha Centauri alla velocità preventivata.

Accidenti, qualcosa deve essere andata di traverso… a lui sembra di rimanere fermo. Vede invece chiaramente che la stella gli si avvicina a grande velocità. Utilizza i suoi righelli e, quando Alpha Centauri lo raggiunge, non può che meravigliarsi: “Accidenti, Muo1 ha sbagliato i calcoli… la distanza che ho percorso non è assolutamente di 4 Anni Luce ma solo di 2.4! Peccato non essermi portato un orologio. Poco male, basta che ripeta il calcoletto fatto da Muo1:
t = 2.4/0.8 = 3 anni.
“Ma…allora ho impiegato meno tempo del previsto. Eppure avevo visto con i miei occhi e i righelli di Muo1 che la stella si trovava a 4 anni luce. Che abbia preso dei righelli più corti? Boh… vedremo…” e riparte immediatamente verso la Terra. Anche lei, come previsto, gli viene incontro a velocità pazzesca. Ha, comunque, tempo per pensare e si ricorda di una favola sentita da bambino, in cui il mago Albertino era riuscito a fare arrivare fino a terra un piccolo Muo, accorciando la distanza tra lui e la Terra…
“Chissà…” dice fra sé e sé “magari non era una favola, ma proprio la verità. Che Muo1 si sia messo d’accordo con il mago per farmi una sorpresa?” Il viaggio procede e, come ormai previsto, la distanza tra Alpha Centauri e la Terra non è cambiata: sempre 2.4 Anni Luce. Di conseguenza anche il tempo del ritorno deve essere stato di soli 3 anni. 3 + 3 uguale 6, per cui Muo2 dovrebbe avere solo 36 anni invece dei 40 previsti.
Scende dall’astronave e gli basta poco per capire che quella è proprio la realtà. Non c’è dubbio alcuno: lui ha veramente 36 anni, ma Muo ne ha 40.
In un lampo capisce tutto e non può che abbracciare il fratello “Grazie Muo1 sei proprio fantastico e ti voglio un bene dell’anima… Che magnifico regalo mi hai fatto… mi hai regalato quattro anni!”.
Intanto, però guarda verso il cielo e si accorge che il mago Albertino sta sorridendo da dietro una nuvola. Sorride anche lui e capisce che è stato un altro dei suoi trucchetti e che le favole sono spesso decisamente vere.
Ovviamente, la favola si spiega benissimo con la contrazione delle lunghezze: sia all’andata che al ritorno (e poco importa se l’astronave ha cambiato direzione) la distanza tra Terra e Alpha Centauri si è ridotta in accordo con il fattore di Lorentz, nello stesso modo in cui si era ridotta per il piccolo Muo della favola.
GIOVANILISMO SPAZIALE (Ing. prat. Maurizio Bernardi)
In fila, per cortesia! State in fila! In ogni caso verrete chiamati in ordine alfabetico, quindi non è il caso di spingere per farsi avanti.
L'ufficiale addetto agli imbarchi sbuffò nel microfono e il rumore scaturì, ingigantito dai potenti amplificatori, negli altoparlanti disseminati sul piazzale antistante la grande astronave, dove una imponente folla di ultra-settantacinquenni attendeva la chiamata.
Da quando il motore a curvatura era uscito dai telefilm di Star Trek per entrare nella quotidianità, centinaia di veicoli spaziali si avvicendavano senza sosta negli spazioporti, trasportando merci e passeggeri fino ai più sperduti confini della galassia.
All'INPS non era parso vero di vedersi aprire quella via di uscita. Il deficit di gestione, ormai fuori controllo (nessuno sapeva più dire nemmeno a quanto ammontasse) poteva venire rallentato, forse addirittura fermato, semplicemente con un modesto investimento, nettamente inferiore a quello che era stato stanziato nel secolo precedente per surgelare gli aspiranti al pensionamento.
Bastava affittare qualche nave spaziale, imbarcare tutti quelli a cui mancava qualche anno per raggiungere i requisiti minimi per la pensione e spedirli verso una destinazione relativamente vicina: Alfa Centauri, Sirio, Procione, tutta roba che stava nel giro di una dozzina di anni luce.

Per esempio: ti mancavano 10 anni per arrivare ai 90 prescritti come minima età pensionabile? Ottimo, una gita verso Alfa Centauri era quel che ci voleva: 5 anni anni alla velocità di 0,8c all'andata e altri 5 al ritorno e saresti arrivato giusto in tempo, pronto per la pensione. Così dicevano gli spot dell'INPS, e così era scritto sui milioni di depliant distribuiti ai contribuenti.
Ma la verità era leggermente diversa.
Nei 5 anni del viaggio di andata l'effetto della contrazione della lunghezza avrebbe dimezzato il percorso e l'equipaggio ed i passeggeri sarebbero invecchiati solo di 3 anni. Altrettanto nel viaggio di ritorno. In conclusione i 10 anni sarebbero passati solo sul pianeta Terra e, al loro sbarco, gli aspiranti pensionati si sarebbero sentiti dire: “Eh, ma siete troppo giovani per andare in pensione, per voi il tempo si è dilatato, avete solo 6 anni in più di quando siete partiti...” E allora, ecco pronta la soluzione: un secondo viaggetto di parcheggio per far passare il tempo residuo e arrivare alla soglia agognata. Intanto le casse dell'Istituto potevano riprendere fiato e non si poteva escludere che in tutto quel tempo qualche nuova riforma, qualche nuovo disegno di legge, qualche rimodulazione dei parametri di aspettativa di vita, non spostassero un po' più in avanti i termini di decorrenza del diritto al trattamento pensionistico. In tal caso si sarebbe reso necessario un terzo e forse un quarto viaggio spaziale. Ma per dei giovanotti sotto i cento anni sarebbe stato puro divertimento.
IN VINO VERITAS (Sua quasi Emin. Oreste Pautasso)
La sede dell'Enoteca Vaticana, intitolata a Urbano VIII, all'anagrafe Maffeo Barberini, si elevava alle pendici delle zone pedemontane dei Castelli Romani. Era l'ultimo avamposto della tradizione vitivinicola dello Stato Pontificio, dopo che l'antica tradizione aveva subito l'attacco della espansione edilizia ed erano progressivamente scomparse tutte le vigne che, in epoca pontificia, esistevano anche entro la stessa città, ove erano famosi, per la pregevolezza del prodotto che ne derivava, i cosiddetti terreni casalini, con vigneti impiantati sui ruderi delle case.
Con il tempo l’agricoltura dei Castelli Romani, famosa anche per le produzioni ortofrutticole, quali i broccoli di Albano, le pesche di Castel Gandolfo, i cavoli e i carciofi di Velletri, si andò specializzando nella coltivazione delle viti; in un primo periodo coesisterono sia quelle da vino che quella da tavola, della cui importanza rimane traccia nel grandioso pergolato sull’Appia Nuova in località ancora denominata Uva di Roma. Successivamente, la viticoltura preferì rivolgersi quasi esclusivamente alla produzione di uva da vino in vigneti specializzati.
Nella fascia altimetrica ancora superiore, i colli che rasentano l’altitudine propria della montagna, sono investiti a castagneti. Si tratta di boschi impiantati dai papi per sopperire alle esigenze alimentari delle popolazioni che, in montagna, non potevano usufruire dei frutti della coltivazione dei campi. Nel tempo i castagni da frutto sono stati in gran parte sostituiti in castagni da legname e la raccolta dei marroni è (ahimé!) proibita.
L’attuale assortimento delle varietà di vitigni utilizzate, è il frutto del lunghissimo e tenace lavoro di una speciale commissione di cardinali che, tra la fine del XIX e l'inizio del XX secolo, a seguito della distruzione dei vigneti per l’infestazione della fillossera, riordinò tutti i vitigni locali, definendone le caratteristiche.
La missione del Reverendo Istituto, oltre alla protezione delle tradizioni, è centrata sulla valorizzazione commerciale dei prodotti mediante strategie che avvicinino i fedeli alla consumazione consapevole e illuminata.
E proprio la luce entra prepotentemente in questa storia come portatrice di una nuova testimonianza del sovrannaturale!
Il Cardinale Reggente, biologo molecolare che aveva gettato il camice alle ortiche, un Barberini, lontano discendente di quel Maffeo che ben conosciamo per avere avuto qualche "screzio" con Galileo Galilei, aveva avuto una geniale ispirazione per rivitalizzare non solo il business dell'Enoteca Vaticana, ma anche quel sentimento religioso che, nel XXVII secolo, aveva ormai raggiunto i minimi storici in tutta la popolazione mondiale.
Invece di operare sul prodotto si sarebbe dovuto agire sul consumatore. Stupire con effetti veramente speciali, insinuare nella mente del popolo (dei fedeli, ma soprattutto degli infedeli) la certezza che un ritiro spirituale può realmente produrre risultati “reali”. Occorreva un miracolo, o almeno qualcosa che gli somigliasse, come fare invecchiare il vino più velocemente del bevitore, un paradosso temporale che, però, nei suoi ricordi di addetto ai lavori, la scienza era in grado di offrire...
Sì, ora i mezzi c'erano, bastava organizzarsi.
La fondazione Templeton venne incaricata di allestire a tempo di record un'astronave in grado di raggiungere una velocità di poco inferiore alla velocità della luce (c), per la precisione l'80%, circa 240.000 km/sec.

A bordo sarebbero saliti enologi volontari non credenti, scettici, atei dichiarati che avrebbero garantito e testimoniato l'attendibilità della dimostrazione. Una partita di vini da invecchiamento sarebbe stata stivata nell'astronave per il confronto finale con un identico assortimento rimasto a terra, sotto la responsabilità dell'Enoteca Vaticana che avrebbe apposto sigilli ai locali della cantina fino al ritorno dei viaggiatori spaziali.
La posta in gioco era molto alta: il vino rimasto sul pianeta, accudito dai religiosi, avrebbe mostrato una qualità superiore a quello che era rimasto a contatto con la microsocietà degli spaziali non credenti? Oppure sarebbe avvenuto il contrario? Cosa si poteva dedurre dal risultato?
L'opinione condivisa dalle due parti era che, salvo il caso di parità, la correlazione vino-fede-non fede, poteva avere un significato probatorio. Poteva essere un segno, se non proprio una prova, di esistenza della divinità, o viceversa. Insomma lo slogan avrebbe potuto essere “in vino veritas”.
L'astronave partì e il tempo trascorse. Una notte, proprio alla data programmata, fece ritorno e, all'alba di un giorno memorabile, le bottiglie vennero stappate e i vini degustati.
Non ci fu nessuna discussione, nessuna contestazione, il vino dei religiosi era decisamente superiore, come se fosse invecchiato molto di più di quello degli astronauti non credenti.
Le reti televisieve si scatenarono, i prezzi delle bottiglie dell'Enoteca Vaticana schizzarono alle stelle (cioè... no, fino alle stelle no...), raggiunsero i massimi storici e li superarono ripetutamente. Pellegrini da ogni parte del mondo giunsero ai Castelli Romani per visitare i luoghi del miracolo e acquistare damigiane di vino pontificio. E va da sé che le chiese tornarono a riempirsi di fedeli, desiderosi di riconciliarsi con quel Dio che, visto il miracolo compiuto sul vino, non poteva non esistere!
Nessuno ebbe la curiosità di leggere il diario di bordo della nave ammiraglia su cui, giorno per giorno, anno dopo anno, il comandante Brachetto aveva annotato minuziosamente i tempi della traversata. Riportiamo solo uno stralcio della registrazione audio al momento del ritorno.
“Giornale di bordo del comandante Brachetto, anno domini 2666, notte della vigilia. Il viaggio della "Giordano Bruno" si è concluso con pieno successo questa notte. Un primo bilancio scientifico della spedizione non può prescindere dalla constatazione che tutte le nostre conoscenze sugli effetti del moto relativistico sono state confermate. Le distanze non solo appaiono ridotte ma sono effettivamente contratte in proporzione inversa al fattore di Lorentz. Mentre la Giordano Bruno manteneva la sua lunghezza di 160 metri, il tragitto dalla Terra Ad Alfa Centauri si contraeva da 4 a 2.4 anni luce. Questo fenomeno è indiscutibilmente da attribuire alla nostra velocità 0.8c, a cui corrisponde un valore di Gamma = 0.6, come tutti gli studenti delle elementari sanno (perfino quelli delle scuole cattoliche). Le conseguenze sul tempo di percorrenza sono evidenti a tutti: una rotta più breve implica un tempo (proprio) proporzionalmente più breve".
Se qualcuno si fosse dato la pena di leggere queste testimonianze il "miracolo" si sarebbe probabilmente sgonfiato e il Cardinal Barberini avrebbe finito i suoi giorni coperto di vergogna... invece gli furono riservati funerali in pompa magna quando, rivelatosi inopinatamente "esperto" pilota di elicotteri, a causa del sovraccarico di damigiane, perse il controllo del velivolo mentre si stava recando in San Pietro per portare in dono al pontefice una ricca selezione di quei vini che avevano decretato il successo degli uomini di fede contro i miscredenti... Sic transit gloria mundi.
Purtroppo nessuno si diede questa pena e la verità giacque per secoli, gelosamente custodita in una antica chiavetta usb in cui Brachetto aveva archiviato il diario di bordo, sepolta nelle segrete sotterranee di Castel Sant'Angelo, in una cassa di legno, tra bottiglie di vin santo ormai svaporato.
Quando, nell'anno domini 3421, Bruno Giordanini, l'archeologo sovraintendente agli scavi, riuscì (non per miracolo, ma grazie a sofisticatissimi strumenti e tecniche) a restaurare la chiavetta e ad ascoltare il file audio, non seppe trattenere lacrime di emozione e di rabbia, al pensiero che neppure il vino avesse potuto far trionfare una verità così semplice ed evidente.
******************************************************************************************
A questo punto, cari amici lettori, se avete apprezzato lo sforzo titanico sostenuto per sviscerare in lungo e in largo il paradosso di questi gemelli e se vi siete divertiti con i tre racconti finali (in particolare l'ultimo), contravvenendo alle nostre regole etiche non scritte, vi chiediamo di esprimere concretamente la vostra riconoscenza inviandoci un contributo per acquistare le tute ignifughe necessarie a fronteggiare eventuali "screzi" con discendenti di Urbano VIII... chi è interessato a mantenere in vita questo blog e, soprattutto, alcuni suoi autori nonché il suo fondatore, può offrire il proprio sostegno economico tramite il modulo dei contatti in home page e riceverà le istruzioni del caso.
(Ovviamente si fa per scherzyare ![]() ... forse...
... forse... ![]() )
)



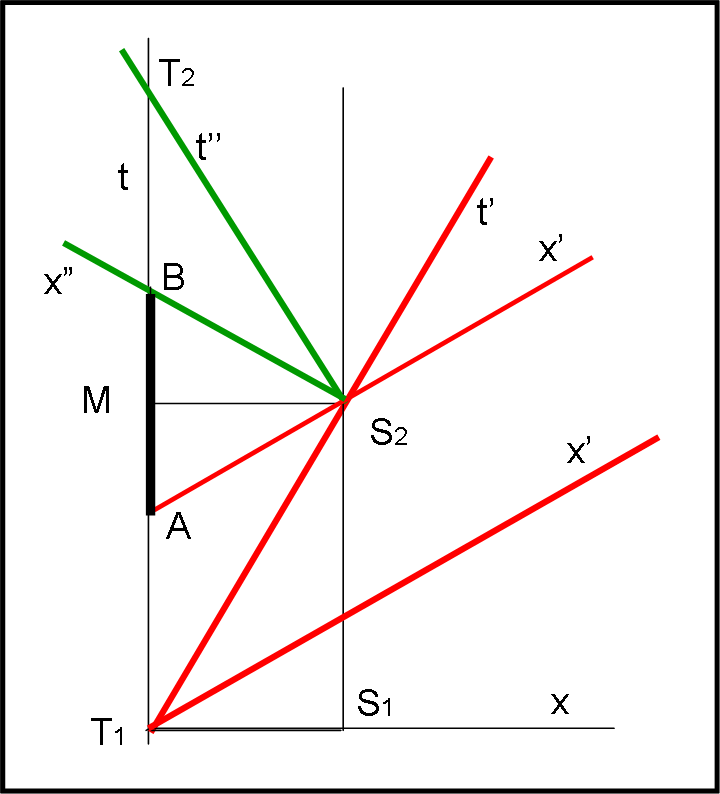
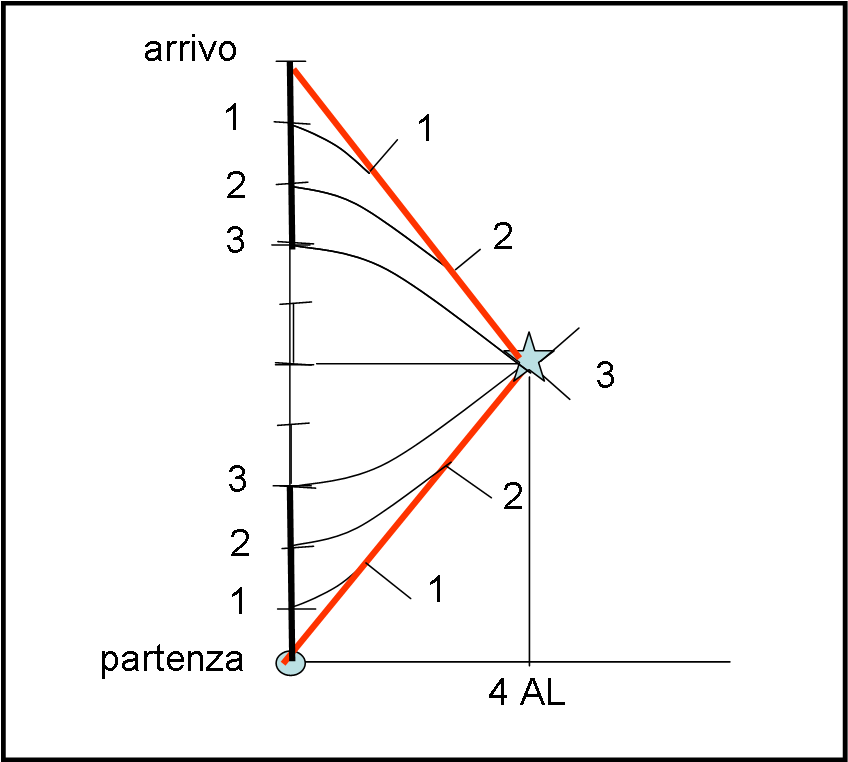




26 commenti
Riporto il messaggio inviato al prof: Zappalà in privato poiché non avevo visto che avrei potuto lasciare un commento pubblico.
Propongo un diverso approccio alla risoluzione del problema: come ho riferito ad altri esponenti della comunità scientifica (in attesa di risposta) io penso che sia fondamentale considerare che uno dei due gemelli debba arrivare (con un' astronave e naturalmente a velocità sostenuta per poter meglio verificare la dilatazione temporale) in una determinata posizione (ad esempio nelle vicinanze di una stella) che sia ad una certa distanza fissa dalla Terra stessa. Se consideriamo fermo il gemello astronauta la trattazione non è simmetrica; in questo caso infatti non sarà solo la Terra a muoversi ma sarà tutta la distanza Terra - stella a spostarsi (e quindi a contrarsi). Quando consideriamo il gemello viaggiatore a muoversi è una situazione diversa perché è solo l'astronave a contrarsi (rispetto al gemello che è rimasto sulla Terra), mentre la distanza Terra - stella è fissa e non cambia. Se invece consideriamo l'astronave ferma tutto l' Universo è in movimento e, poiché le distanze in movimento si contraggono (per le trasformazioni di Lorentz), viene sì percorsa la distanza Terra - stella ma quella contratta e non quella effettiva secondo un terrestre. Considero per questo che non c'è simmetria ed è chiaro che, nel caso in cui la Terra si spostasse per qualche strano motivo della distanza Terra - stella relativa al sistema di riferimento terrestre e se ovviamente l'astronauta rimanesse fermo ad aspettarci, allora sarebbe sicuramente il gemello rimasto sulla Terra a misurare lo stesso tempo di viaggio.
Volendo, si può inoltre immaginare che alla coda dell’ astronave del gemello viaggiatore sia agganciata un'asta rigida di lunghezza pari alla distanza Terra – stella (e con direzione parallela alla distanza Terra – stella stessa). Quando l'astronave è in moto, il gemello rimasto sulla Terra vede l'asta in movimento (quindi contratta) ed è proprio quando vedrà terminare il passaggio dell'asta davanti ai suoi occhi che saprà il tempo segnato dal cronometro del fratello quando arriverà a destinazione (anche per lui infatti la distanza Terra - stella che "gli viene incontro" è contratta ed è questa la trattazione simmetrica in cui non si avverte il fenomeno della dilatazione temporale).
L’astronave non è comunque arrivata; se per la Terra quando termina il passaggio dell’asta è trascorso un tempo t, sul cronometro del fratello viaggiatore è indicato un tempo minore.
Come ben sappiamo il gemello astronauta arriva prima a destinazione rispetto al sistema di riferimento solidale con l'astronave, la distanza Terra-stella è infatti fissa nel sistema di riferimento solidale con chi è rimasto sulla Terra (perché non si è contratta) e all'astronave occorrerà quindi più tempo per percorrerla interamente. Considerando poi il viaggio di ritorno (e naturalmente le fasi di accelerazione e di decelerazione di cui possiamo anche determinarne i tempi propri con integrali, come ad esempio riportato in un libro di Penrose) si evince che il gemello che ha viaggiato sarà più giovane del fratello al suo ritorno.
Spero di essere stato chiaro nello spiegare perché il paradosso non sussiste e mi farà molto piacere se rispondendomi commenterete questa mia opinione. Non so se quest'approccio sia stato già proposto da altri, ma sono soddisfatto ad averci pensato autonomamente per la sua semplicità.
Buona estate (e buon lavoro perché sono sicuro che avete ancora tanto da raccontarci), Massimiliano.
Ovviamente il messaggio è stato inviato al prof. Zappalà (con un punto solo e non al prof: con due punti ) e a tutti gli autori del blog ma, a parte gli scherzi, fa piacere che altri lettori affascinati da tale paradosso possano leggerlo.
In tanti lavoriamo e diamo soluzioni affinché il paradosso dei gemelli (che paradosso non è) rimanga confinato all'interno della teoria della relatività ristretta, senza dover ricorrere alla teoria della relatività generale. (avvalendoci unicamente delle trasformazioni di Lorentz e dei diagrammi spazio-tempo di Minkowski)
Sì, è ovvio che se il gemello viaggiatore visiterà luoghi in cui i campi gravitazionali sono particolarmente intensi potrà avvantaggiarsene per essere ancora più giovane del fratello al suo ritorno, ma questa è un'altra storia!
Idealmente ritengo che si possano sempre considerare due punti in moto relativo tra loro (indipendentemente dalle forze apparenti che agiscono su corpi dotati di massa) e le trasformazioni di Lorentz, fino ad adesso mai contraddette in quanto il postulato relativo alla costanza della velocità della luce è stato sempre verificato, devono valere in qualsiasi contesto (anche in uno spazio-tempo euclideo).
caro Massimiliano,
si può girare come si vuole, ma tutto si risolve sempre, solo e soltanto, con l'assunzione del sistema di riferimento che si considera come fermo. La vera importanza sta nel fatto che il gemello torna sulla Terra e non la passa senza fermarsi. Ricordiamo che la dilatazione dei tempi ha la velocità al quadrato e quindi il segno non conta.
La storia del muone in moto e di quello fermo fa vedere benissimo la differenza tra i due orologi, ma il muone, se la sua età viene misurata nel sistema Terra, appare più giovane.
Grazie per la sua tempestiva risposta, ribadisco comunque che è sempre possibile considerare il viaggio (della Terra) rispetto al sistema di riferimento dell'astronave o del muone e, se li consideriamo fermi dal punto di vista di osservatori solidali con essi, sarà la Terra a partire e a doversi fermare (senza passare)!
E' per questo che la contrazione delle lunghezze gioca secondo me un ruolo importante, ancora grazie e buone vacanze!
caro Massimilano,
volevo aggiungere che quanto tu dici non è altro che il caso del muone che è trattabile con la sola RR. C'è tanto alone di mistero attorno al paradosso dei gemelli solo perché si pensa alle persone fisiche, ma il paradosso sparisce se pensiamo, come è giusto fare, ai sistemi di riferimento.
Preferisco risponderti meglio con un breve articolo che non fa altro che applicare la storia del muone al caso dei gemelli (gemelli un po' strani per la verità...).
Caro Vincenzo, per approfondire i miei messaggi precedenti, continuo a sottolineare che qualsiasi sistema di riferimento può considerarsi fermo rispetto ad un altro e, tornando all’ esempio del gemello in viaggio con la sua astronave, anche il gemello viaggiatore può benissimo ritenere che la Terra abbia iniziato ad accelerare e si sia allontanata per poi riavvicinarsi fino a fermarsi (sebbene queste accelerazioni e decelerazioni non siano reali).
I due moti descritti sembrano simmetrici ma non lo sono.
Se consideriamo il moto dal punto di vista del sistema di riferimento solidale con la Terra, l’astronave tra andata e ritorno avrà percorso una distanza 2*d .
Se consideriamo invece il moto secondo il sistema di riferimento solidale con l’astronave, la Terra tra andata e ritorno avrà percorso una distanza contratta 2*a*d (dove il parametro a , seppur difficile da calcolare, è tale che 0 < a < 1).
A prescindere che tali distanze possano essere misurate o meno, esse sono diverse, ed è per questo che quando i due gemelli torneranno nella stessa posizione solo uno dei due sarà più giovane dell’altro.
Per quanto riguarda i muoni, so che molti di loro nascono negli strati superiori dell'atmosfera, in seguito agli urti tra le molecole d'aria ed i raggi cosmici provenienti dall'esterno. Non è purtroppo possibile dotarli di telecamere che possano registrare come la Terra (e tutto l'Universo) si muova contratto relativamente ad esso, però siamo fortunati in quanto conosciamo il loro tempo di vita medio a riposo (in laboratorio e quando sono fermi rispetto a noi).
Poiché alcuni di essi provenienti dall'atmosfera riescono a raggiungere la superficie terrestre percorrendo lunghi tragitti (anche dell'ordine di 100 km e ben più lunghi di quelli che percorrerebbe l'Universo contratto alla stessa velocità e nel breve tempo di vita media che conosciamo) è proprio da questo che capiamo che per loro il tempo trascorre più lento.
Finisco col dirti che è un vero piacere discutere con te di tali affascinanti argomenti, grazie ancora!
Scusami l'errore non voluto nel mio messaggio precedente: la frase corretta è
"Non è purtroppo possibile dotarli di telecamere che possano registrare come la Terra (e tutto l'Universo) si muova contratto relativamente ad essi, ... "
So che avresti capito, ma è meglio non creare ambiguità (soprattutto per i lettori del blog adesso non esperti con la teoria della relatività ristretta, ma che potrebbero apportare in futuro i propri contributi approfondendo l'argomento)
... è meglio non creare ambiguità (soprattutto per i lettori del blog adesso non esperti di teoria della relatività ristretta (e non con la teoria ..., purtroppo in Italiano non sono stato mai bravissimo!)
Con questo non voglio affatto dire che tutti i lettori del blog non siano esperti di relatività. (Figuriamoci!)
Mi riferivo soltanto a chi ha iniziato a studiare tale affascinante teoria da poco e che approfondendo potrà contribuire molto in futuro e penso in particolare agli studenti delle Scuole Superiori.
"Non è purtroppo possibile dotarli di telecamere che possano registrare come la Terra e tutto l'Universo si muovano contratti relativamente ad essi, (essi si riferisce ai muoni) ... "
Scusatemi ancora, anche da questo capisco che mi occorre una visita oculistica al più presto!!!!!
caro Massimiliano,
appunto... non creiamo ambiguità. Contrazione delle distanze e dilatazione dei tempi sono due facce della stessa medaglia. L'importante è aver capito la storia del muone. Un muone che nasce sulla Terra nello stesso momento di uno che viaggia verso la Terra, vive di meno! Su questo non c'è alcun dubbio e rientra nella RR. Il succo di questa differenza sta nel fatto che il muone che viaggia è costretto, all'improvviso, a trasferirsi nel sistema Terra e quindi il suo orologio (cuore) continua a "ricordare" i battiti che aveva durante il viaggio. Risulta più giovane a tutti gli effetti. Dov'è la differenza con il paradosso dei gemelli? Mi sa che tu stai dicendo la stessa cosa. Se nessuno lo fermasse all'improvviso, ci sarebbe una situazione simmetrica, ma obbligandolo a fermarsi la diversità di età risulta manifesta solo in un senso (almeno per gli osservatori terrestri!). Quello che conta non è il gemello in sé, ma il cambiamento di sistema di riferimento.
Ti prego evitiamo complicazioni ulteriori... tutto ciò è detto e ridetto nell'articolo.
Visto che si parla di muone, ci sta anche questo in aggiunta all'articolo:
http://www.infinitoteatrodelcosmo.it/2018/09/28/superman-la-relativita-diventa-banale-1-la-dilatazione-dei-tempi/
Io ritengo che se il muone viaggiatore non si fermasse all'improvviso per tornare a Terra sarebbe lo stesso più giovane dell'altro (anche se quest'ultimo rimasto sulla Terra salisse in astronave). Per me non dipende dal sistema di riferimento; comunque hai ragione, evitiamo ulteriori complicazioni! L'importante è averti riferito ciò che penso del paradosso dei gemelli (che paradosso non è)
Ti saluto.
E perché mai Massimiliano? I due sistemi sono inerziali entrambi... la RR deve essere simmetrica. L'asimmetria viene data dal fatto che uno cambia sistema improvvisamente. Mettiti pure nella parte del muone che viaggia e che si sente fermo...
Proverò a chiarirmi:
se consideriamo ferma la Terra, l' astronave percorre (rispetto alla Terra) una certa distanza (il doppio della distanza Terra - stella) e mentre trascorre il tempo terrestre,
se consideriamo ferma l'astronave, l'universo contratto percorre (rispetto all'astronave) una distanza contratta (quindi minore) e naturalmente mentre trascorre il tempo dell'astronave.
Per questo non c'è simmetria (le distanze non sono le stesse) e, poiché analizzando il moto secondo il punto di vista terrestre la distanza è maggiore, sarà il gemello solidale con tale sistema di riferimento ad essere più vecchio rispetto all'altro (anche se al momento del ritorno del fratello entrasse in astronave con lui)
Secondo me bisogna riflettere proprio su questo:
se l'astronave è in viaggio allora è solo l'astronave a contrarsi (secondo il gemello rimasto sulla Terra) e, se invece consideriamo l'astronave ferma, è tutto l' Universo a contrarsi e a muoversi rispetto ad essa alla stessa velocità.
Poi come dicevi tu, le trasformazioni di Lorentz sono simmetriche.
Quando due moti sono simmetrici tra loro i tempi devono essere gli stessi, ma occorre fare attenzione a considerare due moti che apparentemente sono simmetrici e che analizzandoli più approfonditamente non lo sono.
Caro Massimiliano,
ti invito ad aspettare fino a domani (devo fare le figure) e poi a commentare la soluzione che propongo... ossia Muone=gemello
Se riesci a distruggermela ne sarò, comunque, contento...
Ma no, non voglio distruggere nulla, però è bello confrontarsi perché è grazie a questi dibattiti che la scienza progredisce. Per quanto riguarda il lavoro che stai per fare sicuramente sarà utilissimo e te ne sono già grato in anticipo. Tieni presente però che occuparsi di Fisica in un certo senso è come occuparsi di Filosofia, ad esempio ho saputo che qualche Fisico, considerando lo spazio - tempo quantizzato, ritiene che il secondo postulato relativo alla costanza della velocità della luce possa essere contraddetto. Ancora non è successo, ma se dovesse accadere in futuro le trasformazioni di Lorentz dovrebbero essere rivisitate e a quel punto anche il contenuto dei nostri messaggi forse in futuro non avrà più senso. Ma, a pensarci bene, avremmo speso il nostro tempo per occuparci dei fenomeni naturali e, anche se avessimo detto delle stupidaggini agli occhi dei posteri, sicuramente ci saremo divertiti a ragionare e a esporre le proprie opinioni.
perfettamente d'accordo. Accettiamo ciò che sappiamo oggi, poi vedremo...
In attesa del tuo lavoro, ti propongo una semplice situazione: immaginiamo che un gemello (inizialmente sulla Terra) arrivi ad una distanza di 17,32 anni-luce per poi tornare indietro.
Poniamo che la sua velocità all'andata ed al ritorno sia costante e del valore v = 0,866 c (una bella velocità, quasi il 90% della velocità della luce); ho scelto tale valore in modo che il fattore di Lorentz equivalga a 2.
Tra andata e ritorno, rispetto ad un terrestre, trascorrono 40 anni (20 per l'andata e 20 per il ritorno)
Quindi, per chi è rimasto sulla Terra, sono trascorsi 40 anni ed è stata percorsa una distanza doppia di 17,32 anni-luce (34,64 anni-luce)
Secondo l'astronauta l'Universo è in movimento rispetto ad esso e si è perciò contratto; essendo il fattore di Lorentz uguale a 2, ogni distanza è per lui la metà rispetto a come misurato sulla Terra.
Sempre rispetto al gemello in astronave, la Terra (che si è inizialmente allontanata per poi tornare indietro) non ha percorso tra andata e ritorno 34,64 anni-luce ma la metà di tale valore che ovviamente equivale a 17,32 anni-luce (essendo stato scelto il fattore di Lorentz uguale a 2 è chiaro che tale valore coincide con la distanza di andata rispetto ad un terrestre, ma si può scegliere un altro valore della velocità e operare con un fattore di Lorentz diverso)
Riassumendo, rispetto al gemello astronauta, la Terra tra andata e ritorno ha percorso (sempre alla velocità v = 0,866 c ) una distanza di 17,32 anni-luce e perciò sono trascorsi solo 20 anni.
Dov'è perciò la simmetria? Sono due moti che di uguale hanno solo la velocità.
Per il gemello terrestre l'astronave ha percorso 34,64 anni-luce in 40 anni ,
per il gemello in astronave la Terra ha percorso 17,32 anni-luce in 20 anni .
Quando i due ritorneranno nella stessa posizione, il gemello rimasto sulla Terra sarà più vecchio rispetto all'altro e questo vale a prescindere dal sistema di riferimento.
Se l'astronave non si fermasse e se il gemello riuscisse in qualche modo a salire in astronave (cambiando sistema di riferimento) continuerebbe ad essere più vecchio dell'altro.
Sono consapevole del fatto che il problema possa essere risolto in altri modi, non ne ho dubbi.
Preferisco però che la soluzione sia ricavata nel modo più semplice possibile.
no Massimiliano,
quanto tu dici direbbe che il muone non rispetta la simmetria della RR e, invece, sappiamo tutti che è la dimostrazione più classica della RR. L'articolo è apparso...
Vincenzo, ti invito nuovamente a riflettere sulle mie considerazioni relative ai sistemi di riferimento (ed è un invito rivolto a tutti i lettori di cui sarò grato di conoscere le proprie considerazioni al riguardo).
Se il gemello rimasto ad aspettare sulla Terra riuscisse a salire in astronave sarà sempre più vecchio rispetto al fratello che in astronave c'è sempre stato da quando è partito.
Per ognuno dei due fratelli il tempo trascorso nel passato non cambia e rimane cucito addosso (e questo vale per tutti, non solo per i due gemelli).
La simmetria non è violata se uno dei due gemelli lascia il suo sistema di riferimento per essere poi solidale con un altro sistema di riferimento, rileggendo attentamente il mio semplice esercizio proposto si evince che durante il viaggio la simmetria tra i due sistemi di riferimento non c'è.
caro Massimiano,
la RR afferma che se i sistemi inerziali sono due il tempo passa più lentamente nel sistema che viene visto dall'altro muoversi ad alta velocità. Qui deve esserci la completa simmetria. Ognuno dei due oggetti, appartenenti a due sistemi diversi, deve vedere l'altro oggetto invecchiare di meno. E questo capita sia per il muone terrestre che per il muone spaziale. Quando il muone che viaggia passa vicino alla Terra (ma non ci sarebbe bisogno di passare vicino, basterebbe un qualsiasi orologio di quel sistema di riferimento solidale con la Terra o con il muone viaggiatore) DEVE vedere il muone terrestre più GIOVANE (la RR dice questo!). Il che vuol dire che se il terrestre saltasse sull'astronave risulterebbe più giovane. Esattamente la stessa cosa capita a ranghi invertiti, dato che non esiste un sistema assoluto di riferimento. Basta cambiare il sistema fisso nel diagramma di Minkowski e invertire il moto. Dato che v cambia in -v il fattore di dilatazione NON può cambiare.
Quello che dico io è tutta un'altra cosa...
Questa è la RR, c'è poco da fare!
Se il gemello salirà sull'astronave, ritengo che solo gli intervalli di tempo futuri saranno quelli misurati da qualsiasi osservatore solidale con l'astronave stessa.
Ma il tempo trascorso nel passato non cambia e lui ormai è più vecchio anche se, da ora in poi, misurerà insieme al fratello un tempo minore rispetto a chi è rimasto sulla Terra.
Questa è la mia opinione a prescindere da quelle di altri studiosi, ho sempre rispettato l'interpretazione di tale paradosso studiata da altri , ad esempio con i diagrammi spazio-tempo di Minkowski (in cui si considerano le curve di calibrazione e le "rotazioni" dello spazio-tempo) e con l'effetto doppler relativistico anche se, a dire la verità, secondo me con i diagrammi spazio-tempo di Minkowski occorre essere attenti a quello che si rappresenta.
E' rispettando rigorosamente i due postulati di Einstein sulla relatività ristretta ed applicando poi sempre rigorosamente le trasformazioni di Lorentz che sono arrivato a tali conclusioni, sei libero comunque di non darmi ragione (questo è il bello).
Sì, ho capito quello che dici. Se fosse la Terra a muoversi rispetto all'astronave (e percorrendo una distanza rispetto all'astronave stessa che non è quella contratta (attenzione!), il tempo proprio di viaggio secondo i terrestri sarebbe minore del tempo misurato dall'astronauta, ma questa è un'altra storia e non ha niente a che fare con l'esercizio che ti ho proposto. (è proprio vero che parli di tutt'altra cosa!)
(1) il tempo proprio è SEMPRE lo stesso in tutti i sistemi inerziali (invariante relativistico)... non facciamo confusione.
(2) Con le frasi seguenti:
"Se il gemello salirà sull'astronave, ritengo che solo gli intervalli di tempo futuri saranno quelli misurati da qualsiasi osservatore solidale con l'astronave stessa.
Ma il tempo trascorso nel passato non cambia e lui ormai è più vecchio anche se, da ora in poi, misurerà insieme al fratello un tempo minore rispetto a chi è rimasto sulla Terra."
Continui a pensare al sistema Terra, ma devi sforzarti di portare tutto sul sistema astronave e per quel sistema è chi sta sulla Terra che è più giovane (è lei che ha viaggiato a grande velocità). Il tempo proprio rimane sempre lo stesso, ma ricorda che il tempo proprio è quello misurato da un solo orologio... La contrazione delle distanze è legata alla dilatazione del tempo. In un caso ha importanza per potere riportare il tutto allo stesso tempo proprio.
Temo che tu stia facendo un po' di confusione... (sempre ammettendo che io capisca bene ciò che vorresti dire...)
Ti consiglierei il mio libro La Favola di Muo dove tutto questo "intreccio" di tempi propri e impropri e di contrazione è spiegato a livello estremamente divulgativo (sul sito si trova anche una piccola errata corrige).
Caro Vincenzo,
mi dispiace per l'ambiguità, ho detto tempo proprio per intendere il tempo di viaggio relativo al sistema di riferimento solidale con chi viaggia (che è minore rispetto al sistema di riferimento solidale di chi si ritiene fermo)
Per me è il quadrato dell'intervallo tra due eventi ad essere invariante, intendo Δs2 = c2 · Δt2 - Δx2 che può essere di tipo spazio se Δs2 < 0 , di tipo luce se Δs2 = 0 oppure di tipo tempo se Δs2 > 0 .
(nessun problema, adesso siamo d'accordo su quello di cui si sta parlando)
Ti ho detto come si analizza il moto secondo il sistema di riferimento astronave (e quindi mi sono sforzato, eccome!), secondo me è giusto quello che dico io e non come la pensi tu.
Sei libero di avere altre opinioni e ritenere che le mie siano inesatte (ma anch'io ho la stessa libertà)
Nessuno di noi due riuscirà a convincere l'altro, ormai ho capito che è così.
Ti ringrazio comunque perché ho condiviso attimi di cultura, lasciamo ai posteri valutare quale sarà l'esatta interpretazione del paradosso.